Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data
Abstract
:1. Introduction
1.1. Polar Motion Variations due to Mass Redistribution
1.2. Hydrological/Cryospheric Excitation of PM from Hydrological and Climate Models
1.3. Hydrological/Cryospheric Excitation of PM from GRACE and GRACE-FO
2. Materials and Methods
2.1. HAM/CAM from Different GRACE and GRACE-FO Data Types
- Jet Propulsion Laboratory (JPL), Pasadena, CA, USA—JPL RL06 solution;
- Center for Space Research (CSR), Austin, TX, USA—CSR RL06 solution;
- GeoForschungsZentrum (GFZ) Potsdam, Germany—GFZ RL06 solution.
2.2. Observed Hydrological Signal in PM Excitation
3. Results
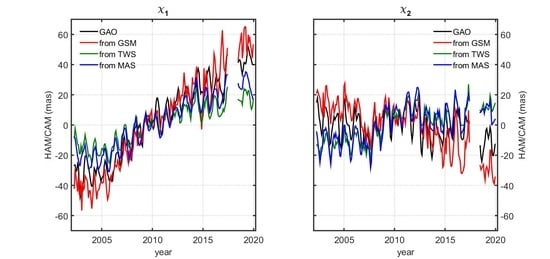
3.1. Internal Consistency of GRACE- and GRACE-FO-Based HAM/CAM Estimates
3.2. External Validation of GRACE- and GRACE-FO-Based HAM/CAM Estimates
- June 2003 to December 2004 (initial period of the GRACE mission),
- June 2007 to December 2008 (best GRACE performance),
- June 2015 to December 2016 (terminal phase of the GRACE mission).
3.3. External Validation of GSM–Based, TWS–Based and MAS-Based HAM/CAM from JPL
4. Discussion
4.1. Sources of Differences between HAM/CAM Obtained from Various GRACE and GRACE-FO Data Types
4.2. Sources of Differences between HAM/CAM Obtained from GRACE and GRACE-FO Data Provided by Different Data Centers (CSR, JPL, GFZ)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barnes, R.T.H.; Hide, R.; White, A.A.; Wilson, C.A. Atmospheric angular momentum fluctuations, length-of-day changes and polar motion. Proc. R. Soc. A Math. Phys. Eng. Sci. 1983, 387, 31–73. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Greiner-Mai, H. Decade variations of the Earth’s rotation and geomagnetic core-mantle coupling. J. Geomagn. Geoelectr. 1993, 45, 1333–1345. [Google Scholar] [CrossRef]
- Adhikari, S.; Caron, L.; Steinberger, B.; Reager, J.T.; Kjeldsen, K.K.; Marzeion, B.; Larour, E.; Ivins, E.R. What drives 20th century polar motion? Earth Planet. Sci. Lett. 2018, 502, 126–132. [Google Scholar] [CrossRef] [Green Version]
- Youm, K.; Seo, K.W.; Jeon, T.; Na, S.H.; Chen, J.; Wilson, C.R. Ice and groundwater effects on long term polar motion (1979–2010). J. Geodyn. 2017, 106, 66–73. [Google Scholar] [CrossRef]
- Brzeziński, A.; Nastula, J.; Kołaczek, B. Seasonal excitation of polar motion estimated from recent geophysical models and observations. J. Geodyn. 2009, 48, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Chao, B.F.; O’Connor, W.P. Global surface-water-induced seasonal variations in the Earth’s rotation and gravitational field. Geophys. J. Int. 1988, 94, 263–270. [Google Scholar] [CrossRef] [Green Version]
- Göttl, F.; Schmidt, M.; Seitz, F. Mass-related excitation of polar motion: An assessment of the new RL06 GRACE gravity field models. Earth Planets Space 2018, 70. [Google Scholar] [CrossRef]
- Nastula, J.; Wińska, M.; Śliwińska, J.; Salstein, D. Hydrological signals in polar motion excitation—Evidence after fifteen years of the GRACE mission. J. Geodyn. 2019, 124, 119–132. [Google Scholar] [CrossRef]
- Nastula, J.; Śliwińska, J. Prograde and retrograde terms of gravimetric polar motion excitation estimates from the GRACE monthly gravity field models. Remote Sens. 2020, 12, 138. [Google Scholar] [CrossRef] [Green Version]
- Śliwińska, J.; Wińska, M.; Nastula, J. Terrestrial water storage variations and their effect on polar motion. Acta Geophys. 2019, 67, 17–39. [Google Scholar] [CrossRef] [Green Version]
- Śliwińska, J.; Nastula, J.; Dobslaw, H.; Dill, R. Evaluating gravimetric polar motion excitation estimates from the RL06 GRACE monthly-mean gravity field models. Remote Sens. 2020, 12, 930. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Zhou, Y.H. Seasonal excitation of polar motion. J. Geodyn. 2012, 62, 8–15. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R.; Grötzsch, A.; Brzeziński, A.; Thomas, M. Seasonal polar motion excitation from numerical models of atmosphere, ocean, and continental hydrosphere. J. Geophys. Res. 2010, 115, B10406. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L. Satellite gravimetry and mass transport in the earth system. Geod. Geodyn. 2018, 10, 402–415. [Google Scholar] [CrossRef]
- Brzezinski, A. Polar motion excitation by variations of the effective angular momentum function: Considerations concerning deconvolution problem. Manuscr. Geod. 1992, 17, 3–20. [Google Scholar]
- Eubanks, T.M. Variations in the orientation of the Earth. In Contributions of Space Geodesy to Geodynamics: Earth Dynamics: Geodynamic Series; Smith, D.E., Turcotte, D.L., Eds.; American Geophysical Union: Washington, DC, USA, 1993; Volume 24, pp. 1–54. [Google Scholar]
- Brzeziński, A.; Nastula, J.; Kołaczek, B.; Ponte, R.M. Oceanic excitation of polar motion from interannual to decadal periods. In International Association of Geodesy Symposia, Proceedings of the IAG General Assembly, Sapporo, Japan, 30 June–11 July 2003; Sansò, F., Ed.; Springer: New York, NY, USA, 2003; Volume 128, pp. 591–596. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D. Atmospheric and oceanic excitation of the Earth’s wobbles during 1980–2000. J. Geophys. Res. Solid Earth 2003, 108, 2370. [Google Scholar] [CrossRef] [Green Version]
- Nastula, J. The regional atmospheric contributions to the polar motion and EAAM excitation functions. In Gravity, Geoid and Marine Geodesy, Proceedings of the International Symposium No. 117, Tokyo, Japan, 30 September–5 October 1996; Segawa, J., Fujimoto, H., Okubo, S., Eds.; Springer: Berlin/Heidelberg, Germany; pp. 281–288. [CrossRef]
- Nastula, J.; Ponte, R.M. Further evidence for oceanic excitation of polar motion. Geophys. J. Int. 1999, 139, 123–130. [Google Scholar] [CrossRef] [Green Version]
- Nastula, J.; Ponte, R.M.; Salstein, D.A. Regional signals in atmospheric and oceanic excitation of polar motion. In Polar Motion: Historical and Scientific Problems; Dick, S., McCarthy, D., Luzum, B., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2000; pp. 463–472. [Google Scholar] [CrossRef] [Green Version]
- Nastula, J.; Ponte, R.M.; Salstein, D.A. Comparison of polar motion excitation series derived from GRACE and from analyses of geophysical fluids. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Nastula, J.; Salstein, D.A.; Kołaczek, B. Patterns of atmospheric excitation functions of polar motion from high–resolution regional sectors. J. Geophys. Res. 2009, 114, B04407. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R. Hydrological excitations of polar motion, 1993–2002. Geophys. J. Int. 2005, 160, 833–839. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Chao, B.F.; Shum, C.K.; Tapley, B.D. Hydrological and oceanic excitations to polar motion and length-of-day variation. Geophys. J. Int. 2000, 141, 149–156. [Google Scholar] [CrossRef]
- Hinnov, L.A.; Wilson, C.R. An estimate of the water storage contribution to the excitation of polar motion. Geophys. J. R. Astron. Soc. 1987, 88, 437–459. [Google Scholar] [CrossRef] [Green Version]
- Nastula, J.; Pasnicka, M.; Kolaczek, B. Comparison of the geophysical excitations of polar motion from the period 1980.0–2007.0. Acta Geophys. 2011, 59, 561–577. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Kołaczek, B. Assessment of the global and regional land hydrosphere and its impact on the balance of the geophysical excitation function of polar motion. Acta Geophys. 2016, 64, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Wińska, M.; Nastula, J.; Salstein, D.A. Hydrological excitation of polar motion by different variables from the GLDAS model. J. Geod. 2017, 17, 7110. [Google Scholar] [CrossRef] [Green Version]
- Wińska, M.; Śliwińska, J. Assessing hydrological signal in polar motion from observations and geophysical models. Stud. Geophys. Geod. 2018, 63, 95–117. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Arsenault, K.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Güntner, A. Improvement of global hydrological models using GRACE data. Surv. Geophys. 2008, 29, 375–397. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Famiglietti, J.; Landerer, F.; Chambers, D.; Reager, J.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Wouters, B.; Bonin, J.A.; Chambers, D.P.; Riva, R.E.M.; Sasgen, I.; Wahr, J. GRACE, time-varying gravity, Earths system dynamics and climate change. Rep. Prog. Phys. 2014, 77, 116801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Göttl, F.; Murböck, M.; Schmidt, M.; Seitz, F. Reducing filter effects in GRACE-derived polar motion excitations. Earth Planets Space 2019, 71, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Meyrath, T.; van Dam, T. A comparison of interannual hydrological polar motion excitation from GRACE and geodetic observations. J. Geodyn. 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Seoane, L.; Nastula, J.; Bizouard, C.; Gambis, D. Hydrological excitation of polar motion derived from GRACE gravity field solutions. Int. J. Geophys. 2011. [Google Scholar] [CrossRef]
- Seoane, L.; Biancale, R.; Gambis, D. Agreement between Earth’s rotation and mass displacement as detected by GRACE. J. Geodyn. 2012, 62, 49–55. [Google Scholar] [CrossRef]
- Śliwińska, J.; Nastula, J. Determining and evaluating the hydrological signal in polar motion excitation from gravity field models obtained from kinematic orbits of LEO satellites. Remote Sens. 2019, 11, 1784. [Google Scholar] [CrossRef] [Green Version]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M. GRACE-FO: The gravity recovery and climate experiment follow-on mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Gross, R. Theory of earth rotation variations. In VIII Hotine-Marussi Symposium on Mathematical Geodesy; Sneeuw, N., Novák, P., Crespi, M., Sansò, F., Eds.; Springer: Cham, Switzerland, 2015; Volume 142, pp. 41–46. [Google Scholar]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice-age terminal deglaciation: The global ICE-6G C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef] [Green Version]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Rowlands, D.D.; Luthcke, S.B.; McCarthy, J.J.; Klosko, S.M.; Chinn, D.S.; Lemoine, F.G.; Boy, J.-P.; Sabaka, T.J. Global mass flux solutions from GRACE: A comparison of parameter estimation strategies—Mass concentrations versus Stokes coefficients. J. Geophys. Res. 2010, 115, B01403. [Google Scholar] [CrossRef]
- Luthcke, S.; Sabaka, T.; Loomis, B.; Arendt, A.; McCarthy, J.; Camp, J. Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J. Glaciol. 2013, 59, 613–631. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Śliwińska, J.; Salstein, D. Mass and motion terms of atmospheric and oceanic angular momentum contributions to polar motion excitation. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 8–13 April 2018. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2018, 93, 621–633. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; von Storch, J.S. Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Dobslaw, H.; Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high–resolution model of non–tidal atmosphere and ocean mass variability for de–aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Gross, R.S.; Lavallée, D.A.; Blewitt, G.; Clarke, P.J. Consistency of Earth rotation, gravity, and shape measurements. In Observing Our Changing Earth, Proceedings of the International Association of Geodesy Symposia, Perugia, Italy, 2–13 July 2007; Sideris, M.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 133. [Google Scholar] [CrossRef] [Green Version]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Nastula, J.; Salstein, D.A.; Popiński, W. Hydrological excitations of polar motion from GRACE gravity field solutions. Int. Assoc. Geod. Symp. 2016, 2011, 513–519. [Google Scholar] [CrossRef]
- Encarnação, J.T.; Save, H.; Tapley, B.; Rim, H.-J. Accelerometer parameterization and the quality of gravity recovery and climate experiment solutions. J. Spacecr. Rocket. 2020, 57, 740–752. [Google Scholar] [CrossRef]
- Dahle, C.; Murböck, M.; Flechtner, F.; Dobslaw, H.; Michalak, G.; Neumayer, K.H.; Abrykosov, O.; Reinhold, A.; König, R.; Sulzbach, R.; et al. The GFZ GRACE RL06 monthly gravity field time series: Processing details and quality assessment. Remote Sens. 2019, 11, 2116. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar] [CrossRef] [Green Version]
- Flechtner, F.; Landerer, F.; Save, H.; Dahle, C.; Bettadbur, S.; Watkins, M.; Webb, F. NASA and GFZ GRACE follow-on mission: Status, science, advances. In Proceedings of the EGU General Assembly 2020 (online meeting), 4–8 May 2020; pp. 4–8. [Google Scholar] [CrossRef]
















| (a) | ||||||||
| RMSE (mas) | Correlation Coefficients | |||||||
| GRACE | GRACE-FO | GRACE | GRACE-FO | |||||
| χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | |
| CSR GSM/JPL GSM | 4.86 | 5.42 | 3.34 | 2.21 | 0.83 | 0.83 | 0.88 | 0.93 |
| CSR GSM/GFZ GSM | 15.32 | 10.70 | 3.10 | 4.04 | 0.29 | 0.50 | 0.86 | 0.75 |
| GFZ GSM/JPL GSM | 14.63 | 12.43 | 4.61 | 3.70 | 0.40 | 0.33 | 0.75 | 0.79 |
| CSR TWS/JPL TWS | 1.71 | 2.89 | 1.00 | 1.43 | 0.96 | 0.92 | 0.97 | 0.87 |
| CSR TWS/GFZ TWS | 5.00 | 6.55 | 2.01 | 3.26 | 0.68 | 0.69 | 0.88 | 0.62 |
| GFZ TWS/JPL TWS | 4.99 | 7.18 | 1.74 | 3.01 | 0.69 | 0.62 | 0.91 | 0.69 |
| (b) | ||||||||
| RMSE (mas) | Correlation Coefficients | |||||||
| GRACE | GRACE-FO | GRACE | GRACE-FO | |||||
| χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | |
| CSR GSM/mean GSM | 5.80 | 3.85 | 1.50 | 1.79 | 0.75 | 0.90 | 0.97 | 0.95 |
| JPL GSM/mean GSM | 5.17 | 5.31 | 2.48 | 1.52 | 0.82 | 0.83 | 0.94 | 0.96 |
| GFZ GSM/mean GSM | 9.85 | 7.52 | 2.37 | 2.48 | 0.83 | 0.78 | 0.92 | 0.90 |
| CSR TWS/mean TWS | 1.86 | 2.38 | 0.89 | 1.35 | 0.95 | 0.95 | 0.98 | 0.89 |
| JPL TWS/mean TWS | 1.84 | 2.92 | 0.67 | 1.14 | 0.95 | 0.92 | 0.99 | 0.92 |
| GFZ TWS/mean TWS | 3.28 | 4.48 | 1.21 | 2.04 | 0.87 | 0.86 | 0.96 | 0.89 |
| Time Series | STD of Series (mas) | Trend (mas/year) | ||||||
|---|---|---|---|---|---|---|---|---|
| GRACE | GRACE-FO | GRACE | GRACE-FO | |||||
| χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | |
| GAO | 7.77 | 9.23 | 4.32 | 7.08 | 5.12 (0.51) | −0.16 (0.61) | 3.39 (2.85) | 2.80 (4.66) |
| CSR GSM | 7.33 | 8.98 | 5.62 | 5.89 | 6.38 (0.48) | −2.33 (0.59) | −3.16 (3.70) | −6.33 (3.87) |
| JPL GSM | 8.76 | 9.39 | 7.07 | 5.86 | 6.05 (0.58) | −2.07 (0.62) | 0.15 (4.65) | −3.11 (3.86) |
| GFZ GSM | 15.82 | 11.86 | 6.20 | 5.79 | 4.67 (1.04) | −3.79 (0.78) | −2.75 (4.08) | −8.25 (3.81) |
| CSR TWS | 5.83 | 7.51 | 4.18 | 3.01 | 2.40 (0.38) | 1.87 (0.50) | −3.48 (2.75) | −0.54 (1.98) |
| JPL TWS | 5.92 | 7.45 | 4.17 | 2.74 | 2.36 (0.39) | 1.91 (0.49) | −1.07 (2.74) | 1.90 (1.81) |
| GFZ TWS | 6.60 | 8.86 | 4.38 | 4.25 | 2.05 (0.44) | 0.86 (0.58) | −1.99 (2.68) | −1.91 (2.80) |
| Time Series | STD of Series (mas) | Trend (mas/year) | ||||||
|---|---|---|---|---|---|---|---|---|
| GRACE | GRACE-FO | GRACE | GRACE-FO | |||||
| χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | |
| GAO | 7.77 | 9.23 | 4.32 | 7.08 | 5.12 (0.51) | −0.16 (0.61) | 3.39 (2.85) | 2.80 (4.66) |
| JPL GSM | 8.76 | 9.39 | 7.07 | 5.86 | 6.05 (0.58) | −2.07 (0.62) | 0.15 (4.65) | −3.11 (3.86) |
| JPL TWS | 5.92 | 7.45 | 4.17 | 2.74 | 2.36 (0.39) | 1.91 (0.49) | −1.07 (2.74) | 1.90 (1.81) |
| JPL MAS | 6.82 | 9.22 | 5.21 | 4.23 | 3.48 (0.45) | 1.78 (0.61) | −3.17 (3.43) | −4.91 (2.79) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śliwińska, J.; Wińska, M.; Nastula, J. Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data. Remote Sens. 2020, 12, 3490. https://doi.org/10.3390/rs12213490
Śliwińska J, Wińska M, Nastula J. Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data. Remote Sensing. 2020; 12(21):3490. https://doi.org/10.3390/rs12213490
Chicago/Turabian StyleŚliwińska, Justyna, Małgorzata Wińska, and Jolanta Nastula. 2020. "Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data" Remote Sensing 12, no. 21: 3490. https://doi.org/10.3390/rs12213490
APA StyleŚliwińska, J., Wińska, M., & Nastula, J. (2020). Preliminary Estimation and Validation of Polar Motion Excitation from Different Types of the GRACE and GRACE Follow-On Missions Data. Remote Sensing, 12(21), 3490. https://doi.org/10.3390/rs12213490