Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Field (Ground-Truth) Data
2.3. UAS Data
2.4. Digital Terrain Model (DTM) Data
3. Methods
3.1. UAS Image Orientation
- The InSO method based on image tie-points and 5 irregularly distributed GCPs;
- The GNSS-SO1 method based on tie-points, 5 GCPs and non-PPK single-frequency carrier-phase GNSS data (absolute positioning);
- The GNSS-SO2 method based on tie-points, 5 GCPs and using PPK dual-frequency carrier-phase GNSS data (relative positioning).
3.2. UAS Point Cloud Generation
3.3. Extraction and Calculation of Point Cloud (PC) Metrics
3.4. Generation and Validation of Lorey’s Mean Height (HL) Models
- The validation over the independent validation dataset of 33 plots (HV), which was not used to derive the models. The HL estimates from the developed models were compared with corresponding field data and evaluated by means of adjusted coefficients of determination (R2adj), mean error (ME) (Equation (2)), relative mean error (ME%) (Equation (3)), root mean square error (RMSE) (Equation (4)), and relative root mean square error (RMSE%) (Equation (5)):where is the predicted (UAS estimated) Lorey’s mean height of plot i, is the observed (from field data) Lorey’s mean height of plot i, n is the number of plots, and is the mean of the observed values.
- The LOOCV statistical method [46,47], based on 66 sample plots, was used for the model’s development. LOOCV is the iterative procedure of n iterations, where n is the number of all measurements (field plots). In n iterations (n = 66), one measurement was removed from the dataset and the selected model wasfitted using the remaining n-1 measurements. The model was then validated using the removed measurement. After the process of n-1 iterations was done, the model accuracy was estimated by averaging validation results (residuals) from all iterations.
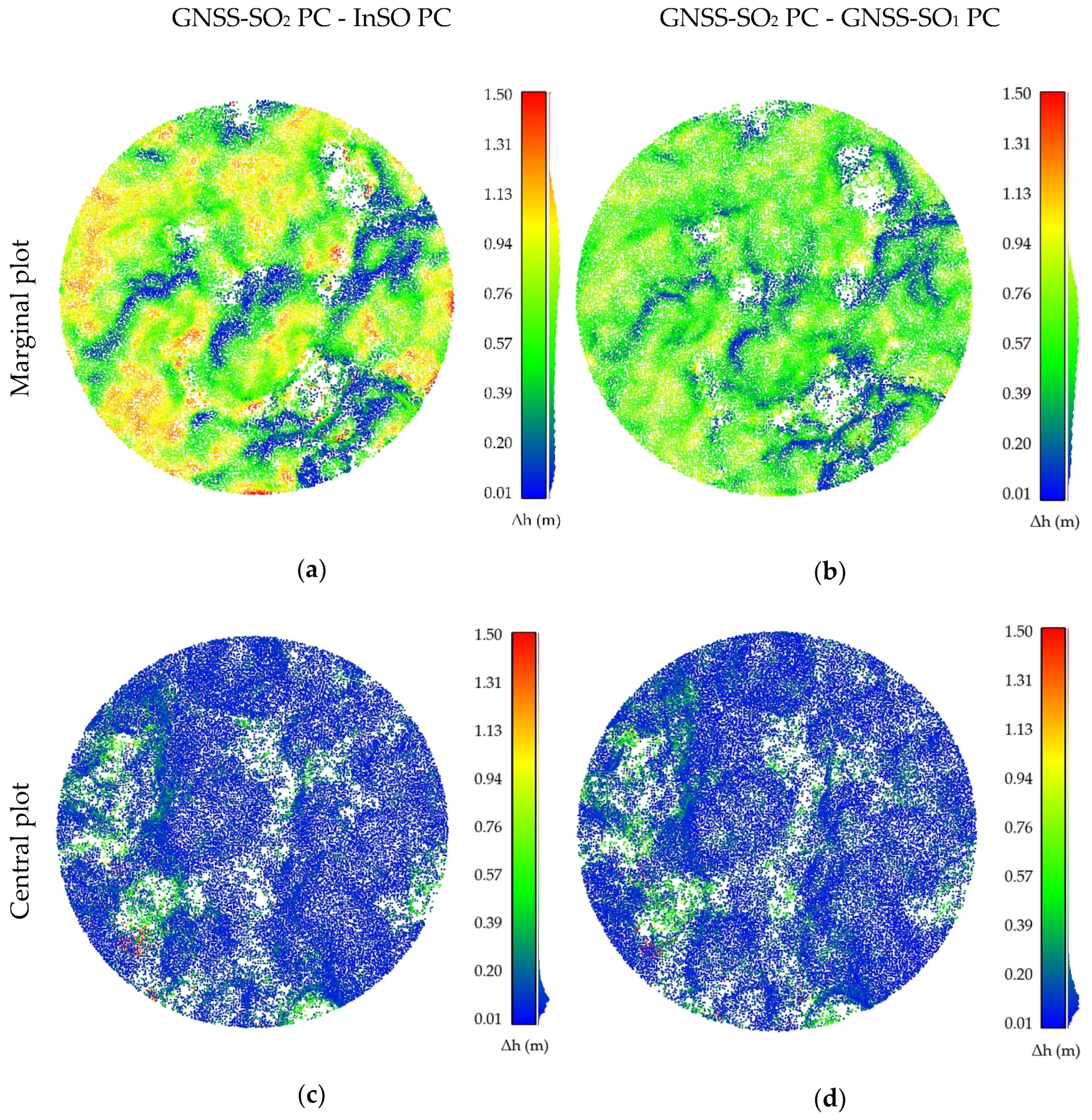
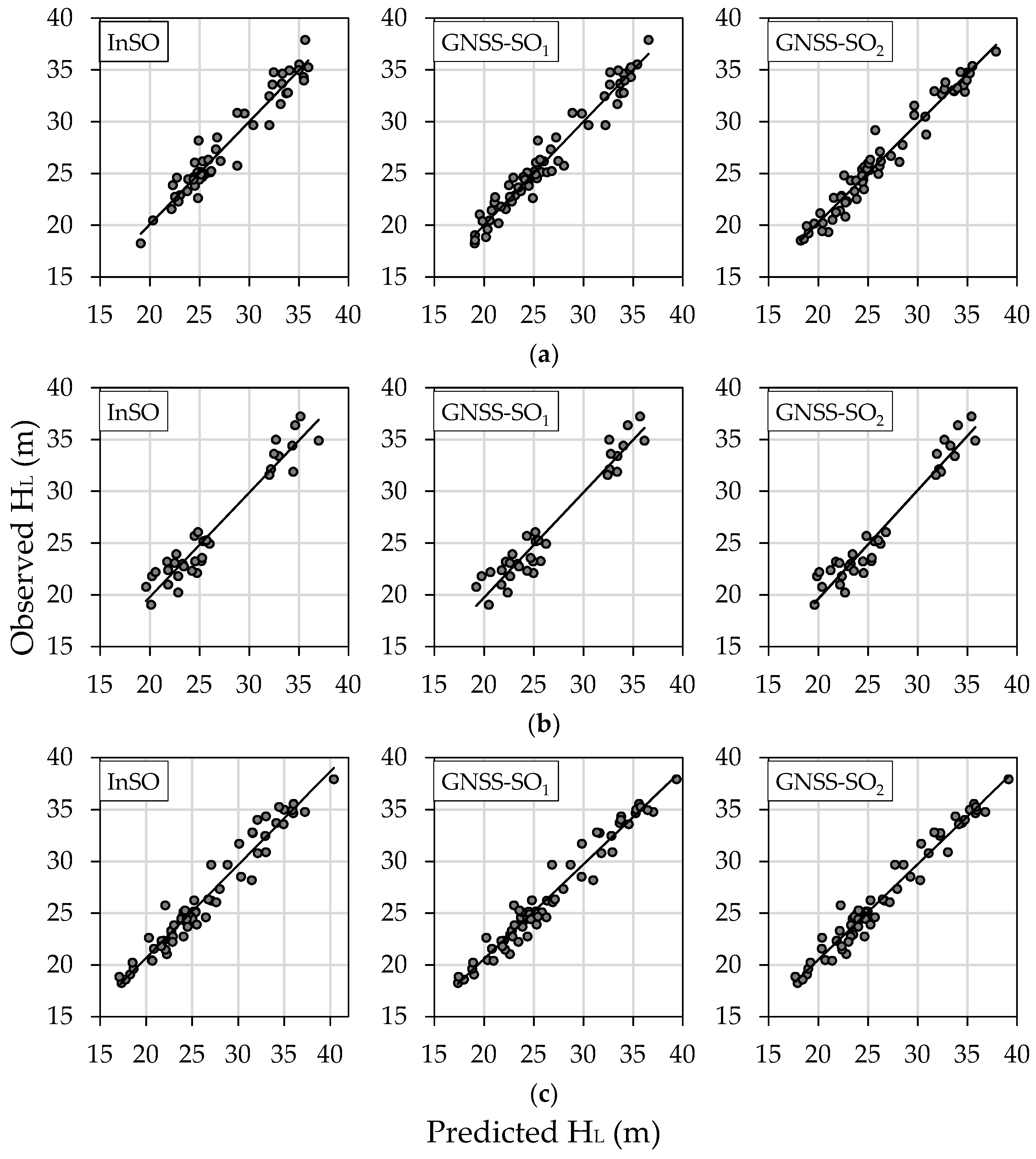
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Coops, N.C.; Hilker, T.; Wulder, M.; St-Onge, B.; Newnham, G.; Siggins, A.; Trofymow, J.A. Estimating canopy structure of Douglas-fir forest stands from discrete-return LiDAR. Trees 2007, 21, 295–310. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Comparison of four types of 3D data for timber volume estimation. Remote Sens. Evniron. 2014, 155, 325–333. [Google Scholar] [CrossRef]
- Smreček, R.C.; Michnová, Z.V.; Sačkov, I.; Danihelová, Z.; Levická, M.; Tuček, J. Determining basic forest stand characteristics using airborne laser scanning in mixed forest stands of Central Europe. iForest 2018, 11, 181–188. [Google Scholar] [CrossRef]
- Ørka, H.O.; Bollandsås, O.M.; Hansen, E.H.; Næsset, E.; Gobakken, T. Effects of terrain slope and aspect on the error of ALS-based predictions of forest attributes. Forestry 2018, 91, 225–237. [Google Scholar] [CrossRef]
- Balenović, I.; Simic Milas, A.; Marjanović, H. A Comparison of Stand-Level Volume Estimates from Image-Based Canopy Height Models of Different Spatial Resolutions. Remote Sens. 2017, 9, 205. [Google Scholar] [CrossRef]
- Rahlf, J.; Breidenbach, J.; Solberg, S.; Næsset, E.; Astrup, R. Digital aerial photogrammetry can efficiently support large-area forest inventories in Norway. Forestry 2017, 90, 710–718. [Google Scholar] [CrossRef]
- Kangas, A.; Gobakken, T.; Puliti, S.; Hauglin, M.; Næsset, E. Value of airborne laser scanning and digital aerial photogrammetry data in forest decision making. Silva Fenn. 2018, 52, 19. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Coops, N.C.; White, J.C. Digital Aerial Photogrammetry for Updating Area-Based Forest Inventories: A Review of Opportunities, Challenges, and Future Directions. Curr. Forestry Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
- Noordermeer, L.; Bollandsås, O.M.; Ørka, H.O.; Næsset, E.; Gobakken, T. Comparing the accuracies of forest attributes predicted from airborne laser scanning and digital aerial photogrammetry in operational forest inventories. Remote Sens. Environ. 2019, 226, 26–37. [Google Scholar] [CrossRef]
- Strunk, J.; Packalen, P.; Gould, P.; Gatziolis, D.; Maki, C.; Andersen, H.E.; McGaughey, R.J. Large Area Forest Yield Estimation with Pushbroom Digital Aerial Photogrammetry. Forests 2019, 10, 397. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.O.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
- Giannetti, F.; Chirici, G.; Gobakken, T.; Næsset, E.; Travaglini, D.; Puliti, S. A new approach with DTM-independent metrics for forest growing stock prediction using UAV photogrammetric data. Remote Sens. Environ. 2018, 213, 195–205. [Google Scholar] [CrossRef]
- Krause, S.; Sanders, T.G.; Mund, J.-P.; Greve, K. UAV-Based Photogrammetric Tree Height Measurement for Intensive Forest Monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Whitehead, K.; Hugenholtz, C.H.; Myshak, S.; Brown, O.; LeClair, A.; Tamminga, A.; Barchyn, T.E.; Moorman, B.; Eaton, B. Remote sensing of the environment with small unmanned aircraft systems (UASs), part 2: Scientific and commercial applications. J. Unmanned Veh. Syst. 2014, 2, 86–102. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Snavely, N.; Seitz, S.M.; Szeliski, R. Modeling the World from Internet Photo Collections. Int. J. Comput. Vis. 2008, 80, 189–210. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic Structure from Motion: A New Development in Photogrammetric Measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Mlambo, R.; Woodhouse, I.H.; Gerard, F.; Anderson, K. Structure from Motion (SfM) Photogrammetry with Drone Data: A Low Cost Method for Monitoring Greenhouse Gas Emissions from Forests in Developing Countries. Forests 2017, 8, 68. [Google Scholar] [CrossRef]
- Goodbody, T.R.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; Crawford, P. Assessing the status of forest regeneration using digital aerial photogrammetry and unmanned aerial systems. Int. J. Remote Sens. 2018, 39, 5246–5264. [Google Scholar] [CrossRef]
- Iglhaut, J.; Cabo, C.; Puliti, S.; Piermattei, L.; O’Connor, J.; Rosette, J. Structure from Motion Photogrammetry in Forestry: A Review. Curr. Forestry Rep. 2019, 5, 155–168. [Google Scholar] [CrossRef]
- Dall’Asta, E.; Thoeni, K.; Santise, M.; Forlani, G.; Giacomini, A.; Roncella, R. Network Design and Quality Checks in Automatic Orientation of Close-Range Photogrammetric Blocks. Sensors 2015, 15, 7985–8008. [Google Scholar] [CrossRef]
- Micheletti, N.; Chandler, J.H.; Lane, S.N. Structure from motion (SFM) photogrammetry. In Geomorphological Techniques; Clarke, L.E., Nield, J.M., Eds.; British Society for Geomorphology: London, UK, 2015; pp. 1–12, Online edition, Chapter 2, Section 2.2. [Google Scholar]
- Carrivick, J.L.; Smith, M.W.; Quincey, D.J. Structure from Motion in the Geosciences; John Wiley & Sons: Hoboken, NJ, USA, 2016; p. 197. [Google Scholar] [CrossRef]
- Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS precise point positioning for UAV photogrammetry. Photogramm. Rec. 2018, 33, 427–447. [Google Scholar] [CrossRef]
- Zhang, H.; Aldana-Jague, E.; Clapuyt, F.; Wilken, F.; Vanacker, V.; Van Oost, K. Evaluating the potential of post-processing kinematic (PPK) georeferencing for UAV-based structure-from-motion (SfM) photogrammetry and surface change detection. Earth Surf. Dynam. 2019, 7, 807–827. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial accuracy of UAV-derived orthoimagery and topography: Comparing photogrammetric models processed with direct geo-referencing and ground control points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- Padró, J.C.; Muñoz, F.J.; Planas, J.; Pons, X. Comparison of four UAV georeferencing methods for environmental monitoring purposes focusing on the combined use with airborne and satellite remote sensing platforms. Int. J. Appl. Earth Obs. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Gašparović, M.; Seletković, A.; Berta, A.; Balenović, I. The Evaluation of Photogrammetry-Based DSM from Low-Cost UAV by LiDAR-Based DSM. South-East Eur. For. 2017, 8, 117–125. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Saloň, Š.; Chudý, F.; Tunák, D. Accuracy of Photogrammetric UAV-Based Point Clouds under Conditions of Partially-Open Forest Canopy. Forests 2017, 8, 151. [Google Scholar] [CrossRef]
- Tuominen, S.; Balazs, A.; Saari, H.; Pölönen, I.; Sarkeala, J.; Viitala, R. Unmanned aerial system imagery and photogrammetric canopy height data in area-based estimation of forest variables. Silva Fenn. 2015, 49, 1348. [Google Scholar] [CrossRef]
- Ota, T.; Ogawa, M.; Mizoue, N.; Fukumoto, K.; Yoshida, S. Forest Structure Estimation from a UAV-Based Photogrammetric Point Cloud in Managed Temperate Coniferous Forests. Forests 2017, 8, 343. [Google Scholar] [CrossRef]
- Tuominen, S.; Balazs, A.; Honkavaara, E.; Pölönen, I.; Saari, H.; Hakala, T.; Viljanen, N. Hyperspectral UAV-imagery and photogrammetric canopy height model in estimating forest stand variables. Silva Fenn. 2017, 51, 7721. [Google Scholar] [CrossRef]
- Balenović, I.; Jurjević, L.; Simic Milas, A.; Gašparović, M.; Ivanković, D.; Seletković, A. Testing the Applicability of the Official Croatian DTM for Normalization of UAV-based DSMs and Plot-level Tree Height Estimations in Lowland Forests. Croat. J. For. Eng. 2019, 40, 163–174. [Google Scholar]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and Digital Aerial Photogrammetry Point Clouds for Estimating Forest Structural Attributes in Subtropical Planted Forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L.; Yang, B.; Xu, Z.; Wang, G. Estimation of Forest Structural Attributes Using Spectral Indices and Point Clouds from UAS-Based Multispectral and RGB Imageries. Remote Sens. 2019, 11, 800. [Google Scholar] [CrossRef]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Varma, S.; Simon, R. Bias in error estimation when using cross-validation for model selection. BMC Bioinform. 2006, 7, 91. [Google Scholar] [CrossRef]
- Dragčević, D.; Pavasović, M.; Bašić, T. Accuracy validation of official Croatian geoid solutions over the area of City of Zagreb. Geofizika 2016, 33, 183–206. [Google Scholar] [CrossRef]
- Stereńczak, K.; Mielcarek, M.; Wertz, B.; Bronisz, K.; Zajączkowski, G.; Jagodziński, A.M.; Ochał, W.; Skorupski, M. Factors influencing the accuracy of ground-based tree-height measurements for major European tree species. J. Environ. Manage. 2019, 231, 1284–1292. [Google Scholar] [CrossRef]
- Michailoff, I. Zahlenmässiges Verfahren für die Ausführung der Bestandeshöhenkurven [Numerical estimation of stand height curves]. Cbl. und Thar. Forstl. Jahrbuch 1943, 6, 273–279. [Google Scholar]
- Pepe, M.; Fregonese, L.; Scaioni, M. Planning airborne photogrammetry and remote-sensing missions with modern platforms and sensors. Eur. J. Remote Sens. 2018, 51, 412–436. [Google Scholar] [CrossRef]
- Terrasolid Ltd. 2012: Terrascan. Available online: http://www.terrasolid.fi/en/products/terrascan (accessed on 19 December 2019).
- Gašparović, M.; Simic Milas, A.; Seletković, A.; Balenović, I. A novel automated method for the improvement of photogrammetric DTM accuracy in forests. Šumar. List 2018, 142, 567–576. [Google Scholar] [CrossRef]
- Balenović, I.; Gašparović, M.; Simic Milas, A.; Berta, A.; Seletković, A. Accuracy Assessment of Digital Terrain Models of Lowland Pedunculate Oak Forests Derived from Airborne Laser Scanning and Photogrammetry. Croat. J. For. Eng. 2018, 39, 117–128. [Google Scholar]
- Rehak, M.; Skaloud, J. Time synchronization of consumer cameras on Micro Aerial Vehicles. ISPRS J. Photogramm. 2017, 123, 114–123. [Google Scholar] [CrossRef]
- Vautherin, J.; Rutishauser, S.; Schneider-Zapp, K.; Choi, H.F.; Chovancova, V.; Glass, A.; Strecha, C. Photogrammetric accuracy and modeling of rolling shutter cameras. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 139–146. [Google Scholar]
- AgiSoft LLC. 2018: AgiSoft PhotoScan Professional (Version 1.4.3). Available online: http://www.agisoft.com/downloads/installer/ (accessed on 19 December 2019).
- Jurjević, L.; Balenović, I.; Gašparović, M.; Simić Milas, A.; Marjanović, H. Testing the UAV-based Point Clouds of Different Densities for Tree- and Plot-level Forest Measurements. In Proceedings of the 6th Conference for Unmanned Aerial Systems for Environmental Research, FESB, Split, Croatia, 27–29 June 2018; p. 56. [Google Scholar] [CrossRef]
- McGaughey, R.J. FUSION/LDV: Software for LiDAR Data Analysis and Visualization; Version 3.80; USDA Forest Service Pacific Northwest Research Station: Seattle, WA, USA, 2018; p. 209. [Google Scholar]
- Hill, T.; Lewicki, P. STATISTICS: Methods and Applications; StatSoft, Inc.: Tulsa, OK, USA, 2007; p. 800. [Google Scholar]
- Cassotti, M.; Grisoni, F.; Todeschini, R. Reshaped Sequential Replacement algorithm: An efficient approach to variable selection. Chemometr. Intell. Lab. 2014, 133, 136–148. [Google Scholar] [CrossRef]
- Seifert, E.; Seifert, S.; Vogt, H.; Drew, D.; van Aardt, J.; Kunneke, A.; Seifert, T. Influence of Drone Altitude, Image Overlap, and Optical Sensor Resolution on Multi-View Reconstruction of Forest Images. Remote Sens. 2019, 11, 1252. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Wang, M.; Beelen, R.; Eeftens, M.; Meliefste, K.; Hoek, G.; Brunekreef, B. Systematic evaluation of land use regression models for NO2. Environ. Sci. Technol. 2012, 46, 4481–4489. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]



| Forest Attribute | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|
| Age (years) | 43 | 148 | 86 | 41 |
| Mean dbh (cm) | 17.0 | 69.4 | 32.8 | 14.0 |
| Lorey’s mean height (m) | 18.2 | 37.9 | 26.3 | 5.2 |
| Stem density (trees∙ha−1) | 56 | 1840 | 534 | 375 |
| Basal area (m2∙ha−1) | 13.7 | 56.4 | 29.9 | 7.6 |
| Volume (m3∙ha−1) | 158.0 | 963.5 | 398.8 | 149.3 |
| UAS | Trimble UX5 HP |
|---|---|
| Type | Fixed wing |
| Weight | 2.4 kg |
| Wingspan | 1 m |
| Battery | 14.8 V, 6600 mAh |
| Endurance | 40 min |
| Camera | Sony ILCE-7R |
| Sensor size | Full Frame (35.9 × 24 mm) |
| Field of view | W 55°, H 37° |
| Image size | 7360 × 4912 |
| Focal length | 35 mm |
| GNSS receiver | Dual-frequency L1/L2 (GPS, Glonass, Beidou, Galileo ready) |
| Flight | Mean Error | Mean Absolute Error | Median Absolute Deviation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E (m) | N (m) | h (m) | E (m) | N (m) | h (m) | E (m) | N (m) | h (m) | |
| First | −0.45 | −1.35 | 0.80 | 3.28 | 1.35 | 0.87 | 2.93 | 0.13 | 0.40 |
| Second | −1.06 | 0.23 | 3.04 | 2.94 | 0.26 | 3.04 | 2.58 | 0.12 | 0.47 |
| Variable Group | Variable (Abbreviation and Description) |
|---|---|
| Height metrics | hmin—minimum height; hmax—maximum height; hmean—mean height; hmode—mode height |
| Height variability metrics | SD—standard deviation; VAR—variance; CV—coefficient of variation; IQ—interquartile distance; Skew—skewness; Kurt—kurtosis; AAD—average absolute deviation; MADmed—Median of the absolute deviations from the overall median; MADmode—Median of the absolute deviations from the overall mode; CRR—Canopy relief ratio ((mean − min)/(max − min)); SQRTmeanSQ—Generalized mean for the 2nd power (Elevation quadratic mean); CURTmeanCUBE—Generalized mean for the 3nd power (Elevation cubic mean); L1, L2, L3, L4—L moments; LCV—moment coefficient of variation; Lskew—moment skewness; Lkurt—moment kurtosis |
| Height percentiles | Ph (h = 1st, 5th, 10th, 20th, 25th, 30th, 40th, 50th, 60th, 70th, 75th, 80th, 90th, 95th, 99th percentiles) |
| Canopy cover metrics | CCh—percentage of points above h (h = 2 m, 5 m, 10 m, 15 m, 20 m, 25 m, 30 m, mean, mode) |
| Orientation Method | Model |
|---|---|
| InSO | HL = 3.085 + 0.485·hmax + 0.641·AAD + 0.291·SQRTmeanSQ |
| GNSS-SO1 | HL = 2.365 + 0.529·hmax + 0.511·CURTmeanCUBE + (−6.202)·Lkurt + (−0.180)·P5 |
| GNSS-SO2 | HL = 0.864 + 0.298·SD + 0.880·P95 |
| Dataset | Orientation Method | R2adj | RMSE (m) | RMSE% (%) | ME (m) | ME% (%) |
|---|---|---|---|---|---|---|
| Modeling dataset | InSO | 0.943 | 1.182 | 4.488 | < 0.001 | < 0.001 |
| GNSS-SO1 | 0.953 | 1.067 | 4.050 | < 0.001 | < 0.001 | |
| GNSS-SO2 | 0.958 | 1.024 | 3.888 | < 0.001 | < 0.001 | |
| Validation (HV) | InSO | 0.921 | 1.458 | 5.551 | 0.169 | 0.643 |
| GNSS-SO1 | 0.925 | 1.403 | 5.344 | 0.167 | 0.637 | |
| GNSS-SO2 | 0.935 | 1.361 | 5.183 | 0.068 | 0.259 | |
| Validation (LOOCV) | InSO | 0.937 | 1.276 | 4.843 | −0.015 | −0.056 |
| GNSS-SO1 | 0.948 | 1.150 | 4.365 | −0.007 | −0.026 | |
| GNSS-SO2 | 0.955 | 1.069 | 4.057 | 0.001 | 0.004 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurjević, L.; Gašparović, M.; Milas, A.S.; Balenović, I. Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes. Remote Sens. 2020, 12, 404. https://doi.org/10.3390/rs12030404
Jurjević L, Gašparović M, Milas AS, Balenović I. Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes. Remote Sensing. 2020; 12(3):404. https://doi.org/10.3390/rs12030404
Chicago/Turabian StyleJurjević, Luka, Mateo Gašparović, Anita Simic Milas, and Ivan Balenović. 2020. "Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes" Remote Sensing 12, no. 3: 404. https://doi.org/10.3390/rs12030404
APA StyleJurjević, L., Gašparović, M., Milas, A. S., & Balenović, I. (2020). Impact of UAS Image Orientation on Accuracy of Forest Inventory Attributes. Remote Sensing, 12(3), 404. https://doi.org/10.3390/rs12030404








