Parsing Synthetic Aperture Radar Measurements of Snow in Complex Terrain: Scaling Behaviour and Sensitivity to Snow Wetness and Landcover

Abstract

This study investigates the spatial signatures of seasonal snow in Synthetic Aperture Radar (SAR) observations at different spatial scales and for different physiographic regions. Sentinel-1 C-band (SAR) backscattering coefficients (BSC) were analyzed in the Swiss Alps (SA), in high elevation forest and grasslands in Grand Mesa (GM), Colorado, and in North Dakota (ND) croplands. GM BSC exhibit 10 dB sensitivity to wetness at small scales (~100 m) over homogeneous grassland. Sensitivity decreases to 5 dB in the presence of trees, and it is demonstrated that VH BSC sensitivity enables wet snow mapping below the tree-line. Area-variance scaling relationships show minima at ~100 m and 150–250 m, respectively, in barren and grasslands in SA and GM, increasing up to 1 km and longer in GM forests and ND agricultural fields. The spatial organization of BSC (as described by 1D-directional BSC wavelength spectra) exhibits multi-scaling behavior in the 100–1000 m range with a break at (180–360 m) that is also present in UAVSAR L-band measurements in GM. Spectral slopes in GM forested areas steepen during accumulation and flatten in the melting season with mirror behavior for grasslands reflecting changes in scattering mechanisms with snow depth and wetness, and vegetation mass and structure. Overall, this study reveals persistent patterns of SAR scattering variability spatially organized by land-cover, topography and regional winds with large inter-annual variability tied to precipitation. This dynamic scaling behavior emerges as an integral physical expression of snowpack variability that can be used to model sub-km scales and for downscaling applications.

1. Introduction

Seasonal snow-covered area (SCA) plays an important role in the Earth’s water cycle. SCA inter-annual variability is tied to the Earth’s climate because its high surface albedo governs the energy exchange between the land surface and the atmosphere in the cold regions of the world [1,2,3,4], where seasonal snowpacks represent the most important freshwater resource (quantified as snow water equivalent SWE). Natural hazards in regions of complex terrain such as avalanches and spring flash-floods often occur during the transition from snow-on to snow-free conditions [5,6,7]. This transition is characterized by changes in snowpack thermodynamics resulting in changes in snow stratigraphy, and snow microstructure (e.g., snow grain size distribution) and composition (e.g., ice versus liquid water content, LWC) leading to snowmelt. The advantage of remote sensing is that it can be used effectively to monitor large areas at high spatial and temporal resolution, thus reducing the need for ground measurements in remote regions. The challenge is that indirect measurements based on the spectral reflectance, emission or backscattering of electromagnetic radiation require inverse models to convert measurements to meaningful geophysical variables.

The visible and near-infrared ranges of the electromagnetic spectrum are used in optical remote sensing to distinguish snow-covered surfaces from other land cover types. The high reflective properties of snow in the visible range of the spectrum depend on snow wetness, snow grain size, impurity content, snow surface roughness and snowpack stratigraphy. The grain size of fresh dry snow is very small and increases with LWC (LWC >1% by volume is associated with significant changes in radiometric properties [8,9,10]. A complicating factor in mountainous regions is the emergence of heterogeneous stratigraphy due to intra-seasonal variability in atmospheric forcing as cycles of diurnal snow surface melting and refreezing that translate into significant grain coarsening of the snowpack top layer [11] are followed by snowfall forming a new surface layer of small grainsize. A major limitation in optical remote sensing is cloud contamination that exhibits a pronounced diurnal cycle in mountainous regions. By contrast, sensors operating at microwave frequencies can make measurements under all weather conditions, and microwave radiometer data have been extensively used in the past despite their coarse spatial resolution [12,13,14,15,16,17]. Indeed, deeper measurement depths in the microwave range have long been leveraged to probe snowpack bulk physical properties [18,19,20]. Nevertheless, detection of wet snow is especially problematic for passive microwave remote sensing because its high emissivity is similar to snow-free surfaces [17,21]. Active microwave systems such as Synthetic Aperture Radar (SAR) have the advantage of high spatial resolution along with multi-polarization and multi-incidence angle capabilities that enable wet snow detection [22,23,24,25,26].

SAR backscattering is determined by the sensor and sensing geometry parameters including the transmitted signal wavelength, incidence angle and polarization on the one hand, and by the radiative and geometrical properties of the snowpack on the other [27]. The total snowpack backscatter (BSC) can be decomposed into three main components attributed to the interaction of the radar electromagnetic (EM) signal at the air–snow interface, snow–soil interface, and between snowpack layers (volume scattering) depending on the wavelength of the incident wave [27]. The principal properties that determine the three scattering components are surface roughness of the snow and soil, snow wetness and grain size [28]. The absorption loss is high for wet snow, so the scattering at the snow–soil interface can be neglected in those circumstances (Figure 1; [28,29]). The absorption coefficient increases with LWC, and thus volume scattering varies inversely with snow wetness [30]. Given fixed snow wetness and density, volume scattering and snow albedo increase with grain size as per Rayleigh scattering theory for longer wavelengths (e.g., X-, C- and L-band) [31]. At higher frequencies, dense media theory is required to capture scattering behavior [32,33]. Attenuation of the microwave signal in dry snowpacks is very small, and thus the backscatter is dominated by interactions between the ground surface and the snowpack [27,34,35]. In the longer microwave wavelengths (e.g., C- and L-band), the dielectric contrast at the air–snow boundary is small for dry snow, and thus most of the power incident upon the snow surface is transmitted across the boundary and the backscatter at the air–snow interface can be ignored. For dry snow (Figure 1), the total BSC is, therefore, a combination of volume scattering and surface scattering at the snow–ground interface. Volume scattering is practically undetectable at C- and L-bands for shallow snowpacks, in which case, the backscatter at the snow–ground interface is dominant [36].

The sensitivity of backscattering coefficients to snow cover condition in the Alps was examined by many in the past, including Matzler (1996) and Strozzi et al. (1997) [30,37]. In particular, Strozzi and Matzler (1998) [38] demonstrated that C-band radar measurements with an incidence angle of 30° could be used to distinguish wet from dry snow and snow-free areas. The capability to discriminate between dry-refrozen and wet snow at microwave frequencies is similarly well established [19,39]. Nagler and Rott (2000) [25] used ERS-2 (European Remote Sensing satellite 2) and RADARSAT-1 imagery to identify wet snow in the Austrian Alps. This work was followed by an improved approach using dual polarimetric bi-temporal Sentinel-1 SAR data to monitor snowmelt [26]. To integrate across scales from the SAR nominal measurement scale (10 s of m) to landscape scale, including the scales representative of unambiguous physical processes in state-of-the-art models (100 m–kms), remains, however, a critical challenge [40].

The goal of this study is to investigate the temporal evolution of the spatial signatures of seasonal snow in SAR observations at different spatial scales and for different physiographic regions using multi-temporal Sentinel-1 dual-polarization C-band observations. L-band UAVSAR (Uninhabited Aerial Vehicle Synthetic Aperture Radar) observations are also available for one of the study regions. The focus is on quantifying and interpreting the impact of spatial variability on SAR BSC imagery with an eye toward inferring constraints for physically based snow models using spectral scaling analysis. In particular, the temporal evolution of the spectral slope (scaling factor) and local changes in spectral slope (scaling breaks) with scale are interpreted considering the snowpack condition, land-cover, and landform. This information can be used to capture (parameterize) scale-aware subgrid-scale variability in coupled snow hydrology–microwave models, and to downscale snow products (e.g., passive microwave) as illustrated by [41] for soil moisture. In addition, the scaling characteristics can be used to upscale or downscale the results of coupled-snow hydrology–microwave models observing system simulators (OSS) to the desired scale in forward mode and in data-assimilation experiments. The study regions and the data are described in Section 2. Section 3 describes the processing steps followed to derive the BSC from Sentinel-1 measurements, including the Cloud–Pottier (CP) decomposition the dual-polarization SAR data to derive the Alpha and entropy parameters. Section 4 presents the results of the multi-temporal analysis of backscattering, Entropy and Alpha parameters for different regions, and the spatial scaling analysis toward elucidating how the SAR BSC intensity changes with topography and land cover, followed by conclusion and discussion concerning the suitability of SAR measurements in Section 5. Supplementary data presented in tables and figures are referred to using the notation S# throughout the manuscript.

2. Data and Study Area

2.1. Study Regions

Three different study sites characterized by deep seasonal snowpacks (depth > 1 m) were selected to investigate the snowpack properties from Sentinel-1 SAR imagery (Figure 2). The first study region is Grand Mesa, Colorado (CO), USA (38°54′–39°06′N, 107°42′–108°20′W). This is one of NASA’s Snow Experiment (SnowEx) primary field sites, where an intense field campaign was conducted in February 2017, hereafter referred to as SnowEx’17. SnowEx’s primary goal is to enable development and/or systematic evaluation of alternative snow remote-sensing technologies methods and retrieval algorithms using extensive in-situ measurements [42,43].

The second study region is in the Swiss Alps around Davos (46°39′–47°1′N, 9°36′E–10°10′E). The Swiss Federal Office of Meteorology and Climatology (MeteoSwiss) maintains climatological stations to monitor weather and snowpack properties at different terrain elevations in this region, with most located above the tree-line. The Swiss Alps site is characterized by steep complex topography in the 800–3000 m elevation range and heterogeneous land cover including barren land, grassland, deciduous forests, urban areas, and lakes. In contrast, Grand Mesa is characterized by elevated flat terrain with complex land cover (Figure 3) including grassland, shrubs, and meadows of closed canopy evergreen forest with deciduous forest in adjacent slopes [42,43]. SNOTEL stations (automated system of SNow and climate sensors with TELemetry) are located within and close to the Grand Mesa region. Because of the high elevation of the Alps and Grand Mesa, a third study region of modest topography was selected in the agricultural region of Golden Valley country, North Dakota (ND), USA (46°59′–46°43′N and 103°48′–104°14′W). The main crops in the area include wheat, oats, rye, barley, flax and corn.

2.2. Data

Sentinel-1 C-Band SAR Data—Sentinel-1 was launched in 2014 as part of the European Copernicus program. It consists of a constellation of two satellites, each carrying a dual- polarization imaging C-band (5.405 GHz) Synthetic Aperture Radar (SAR). The Sentinel-1 Level-1 single-look complex (SLC) data in the Interferometric Wide (IW) swath mode processed to 15 × 15 m² in the same orbital configuration (12-day revisit cycle) are used in this study. The SLC data consist of co- (VV) and cross- (VH) polarization BSC intensity and relative phases between the two polarization channels. The Sentinel-1 data over Grand Mesa and North Dakota are acquired in descending mode with a relative orbit number of 129 and 56, respectively, whereas the Swiss Alps data are acquired in the ascending mode with a relative orbit number of 15.

Table 1. Sentinel-1 SLC data used in the Grand Mesa, Colorado study region.

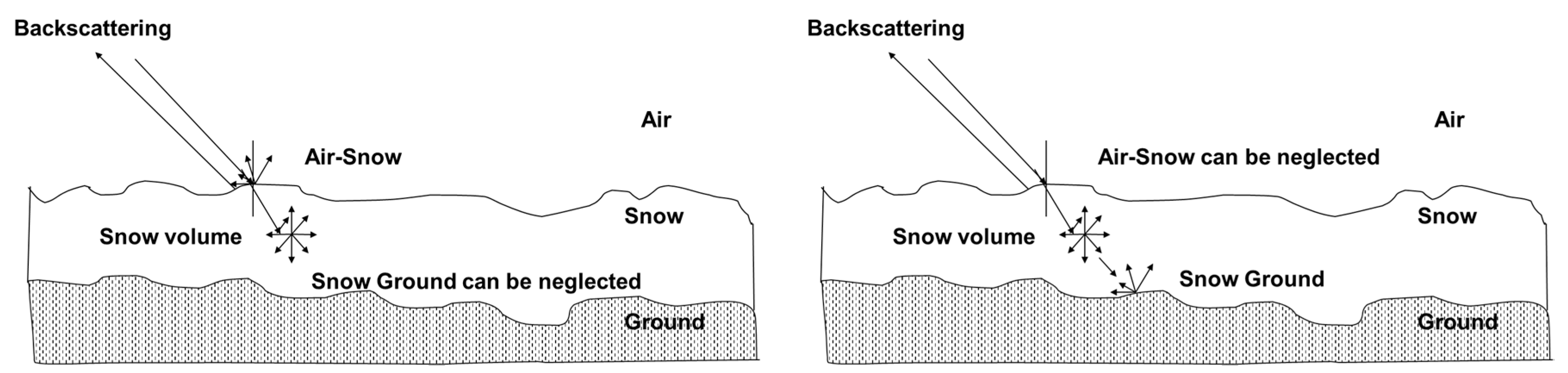
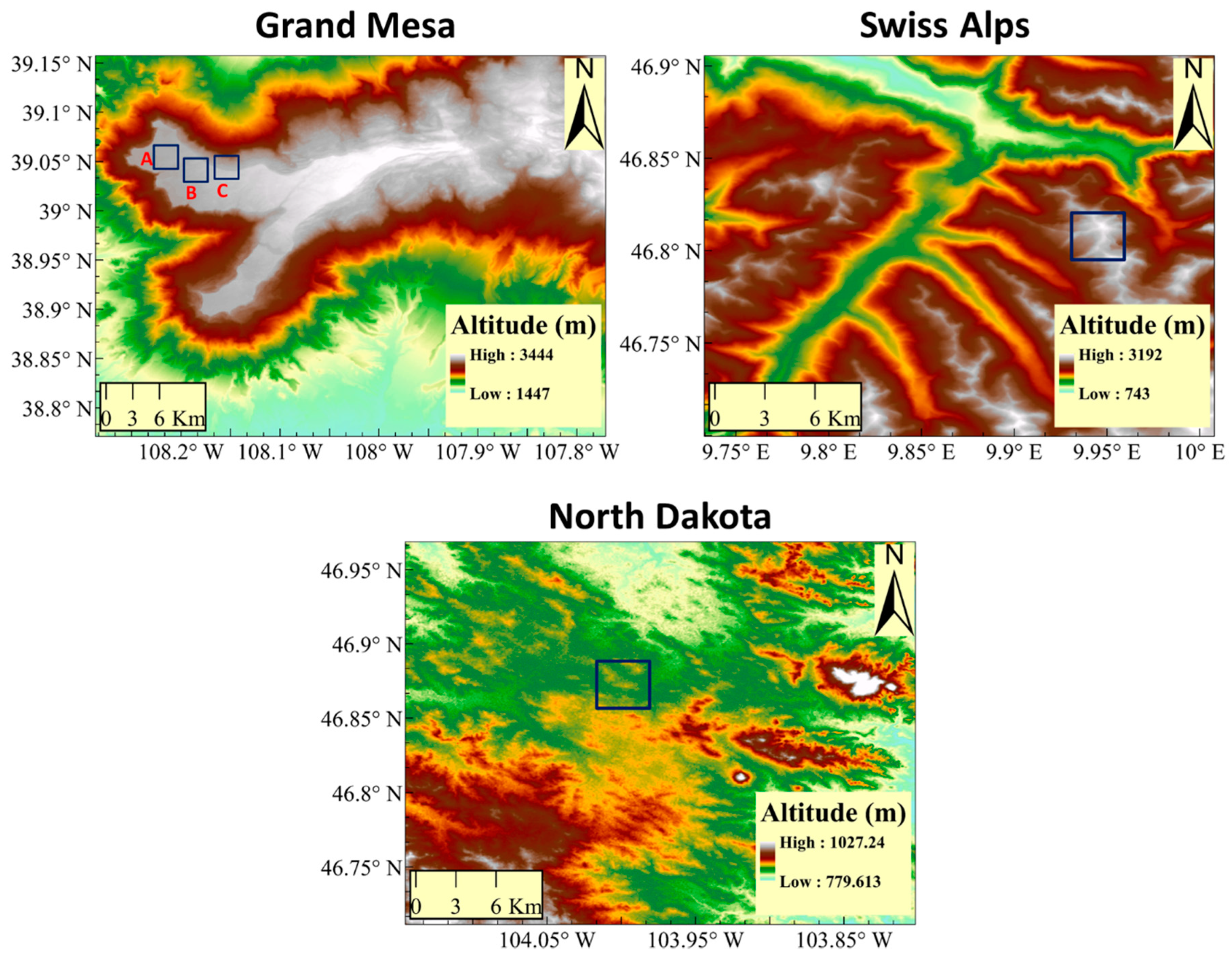
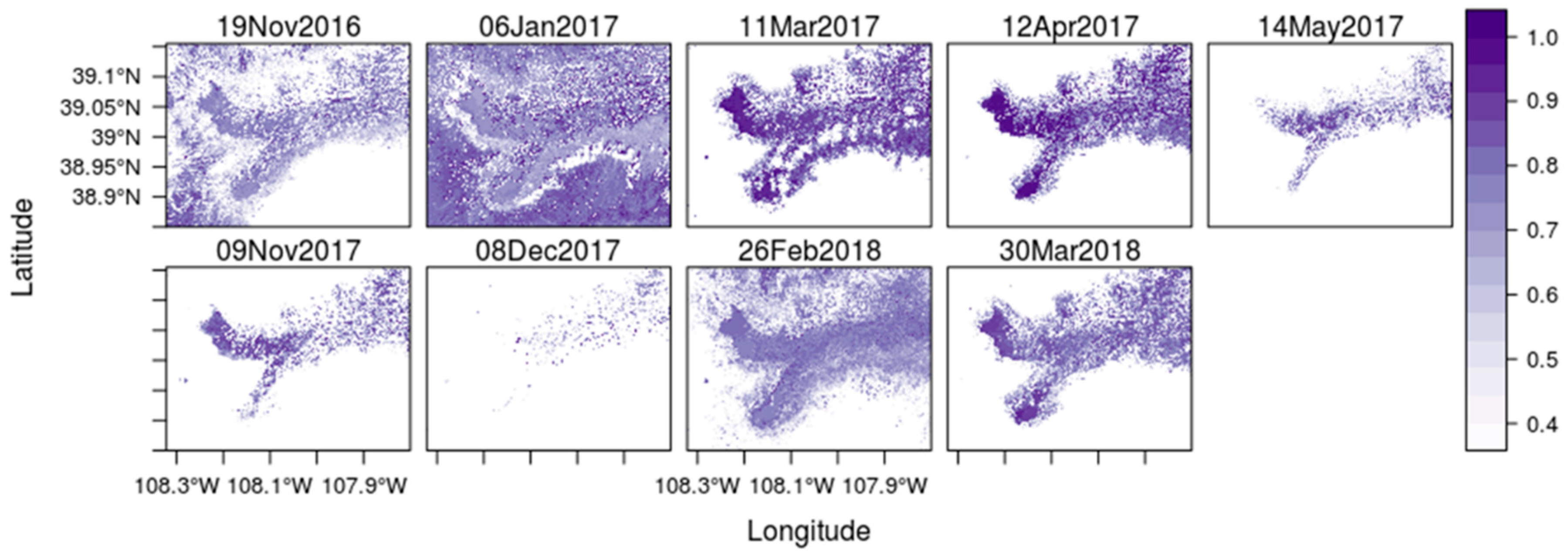
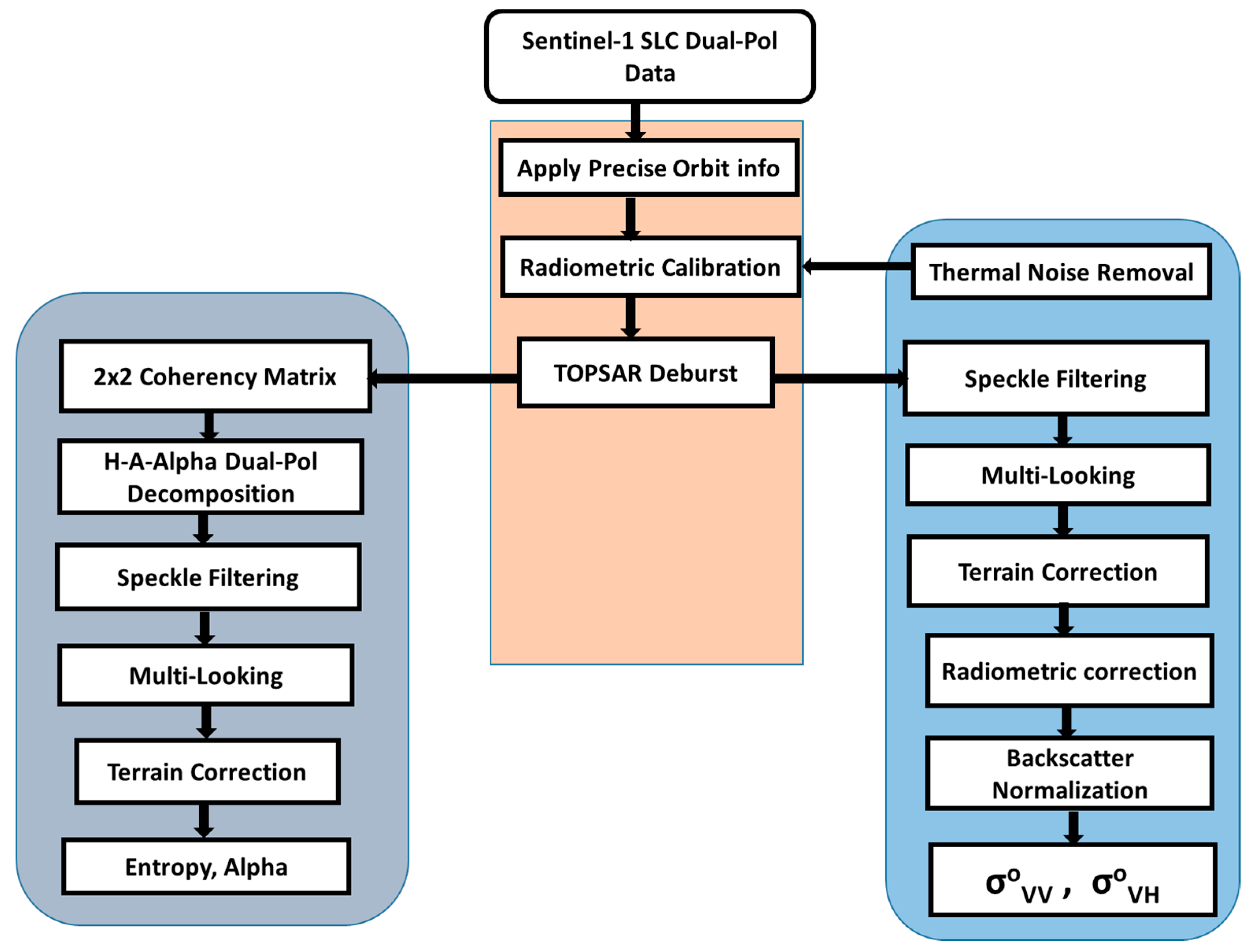
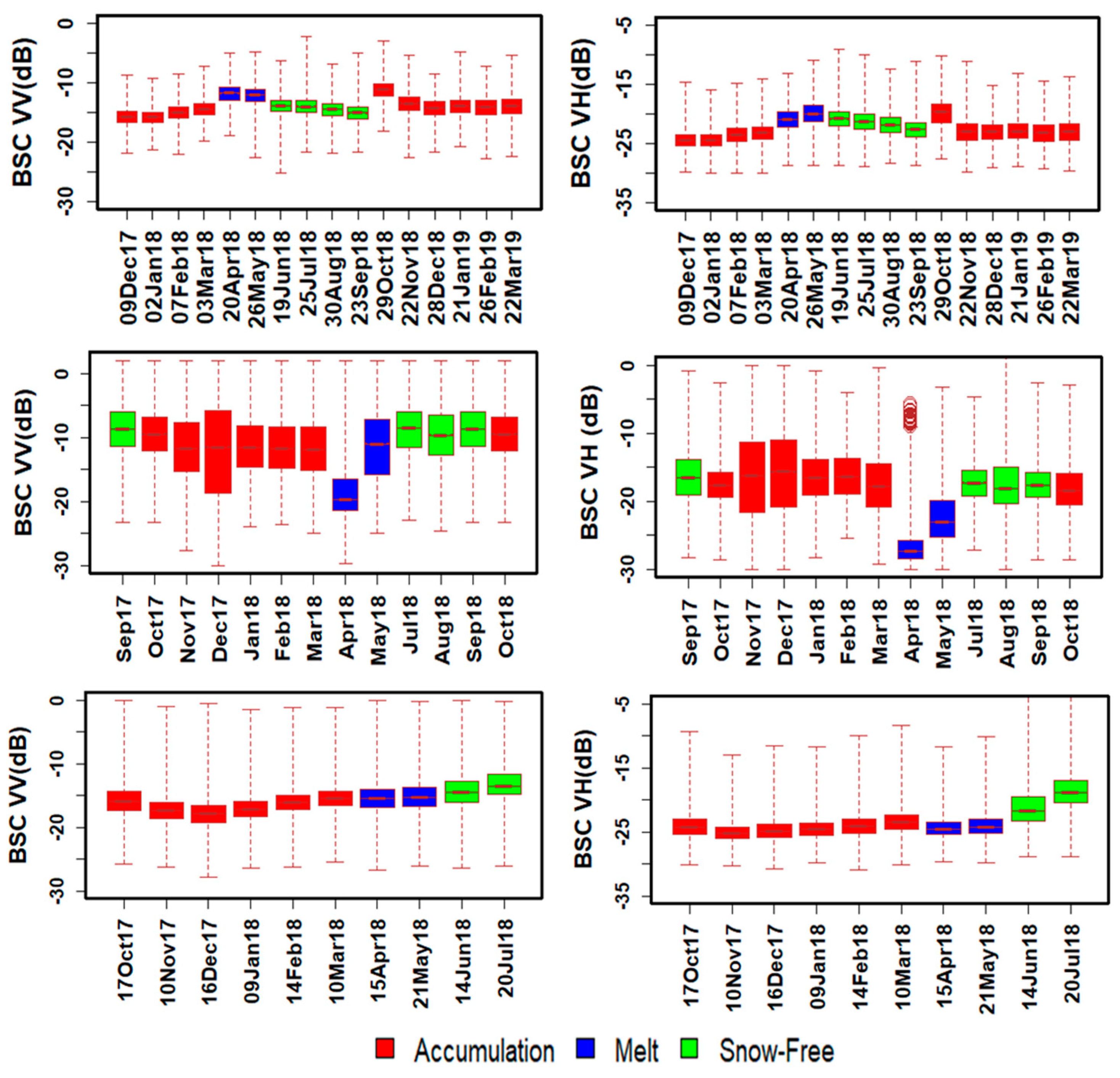
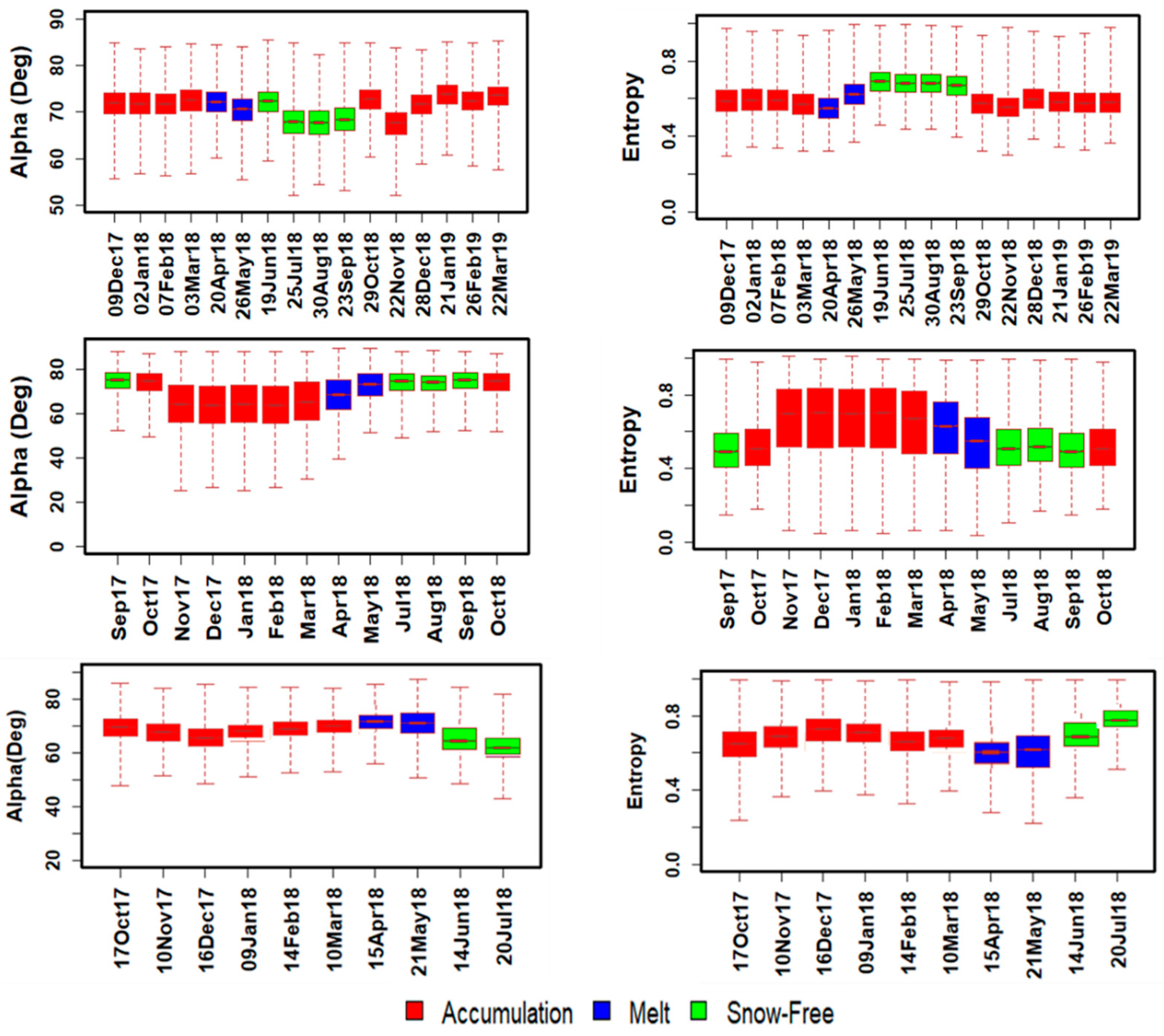
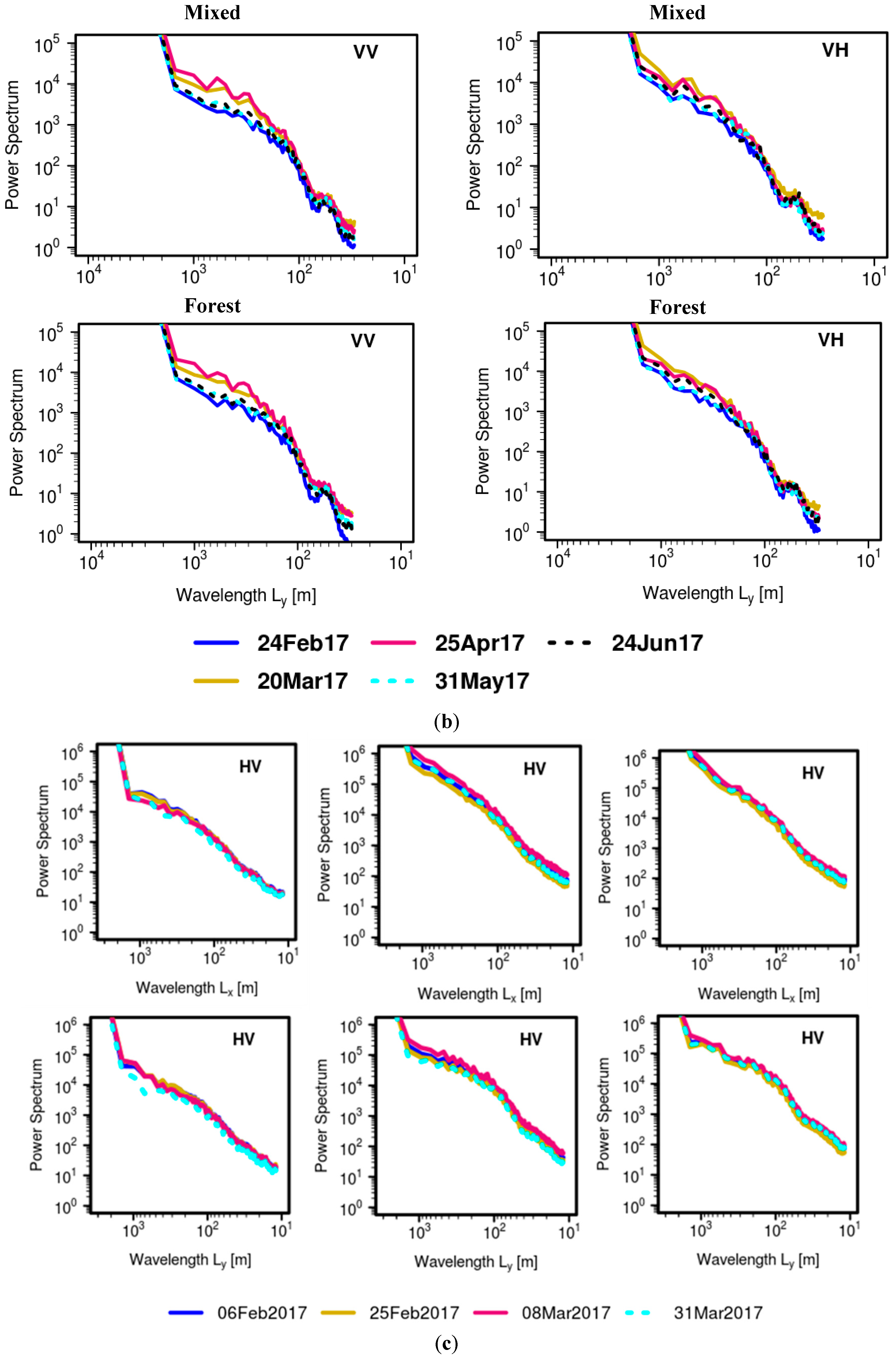
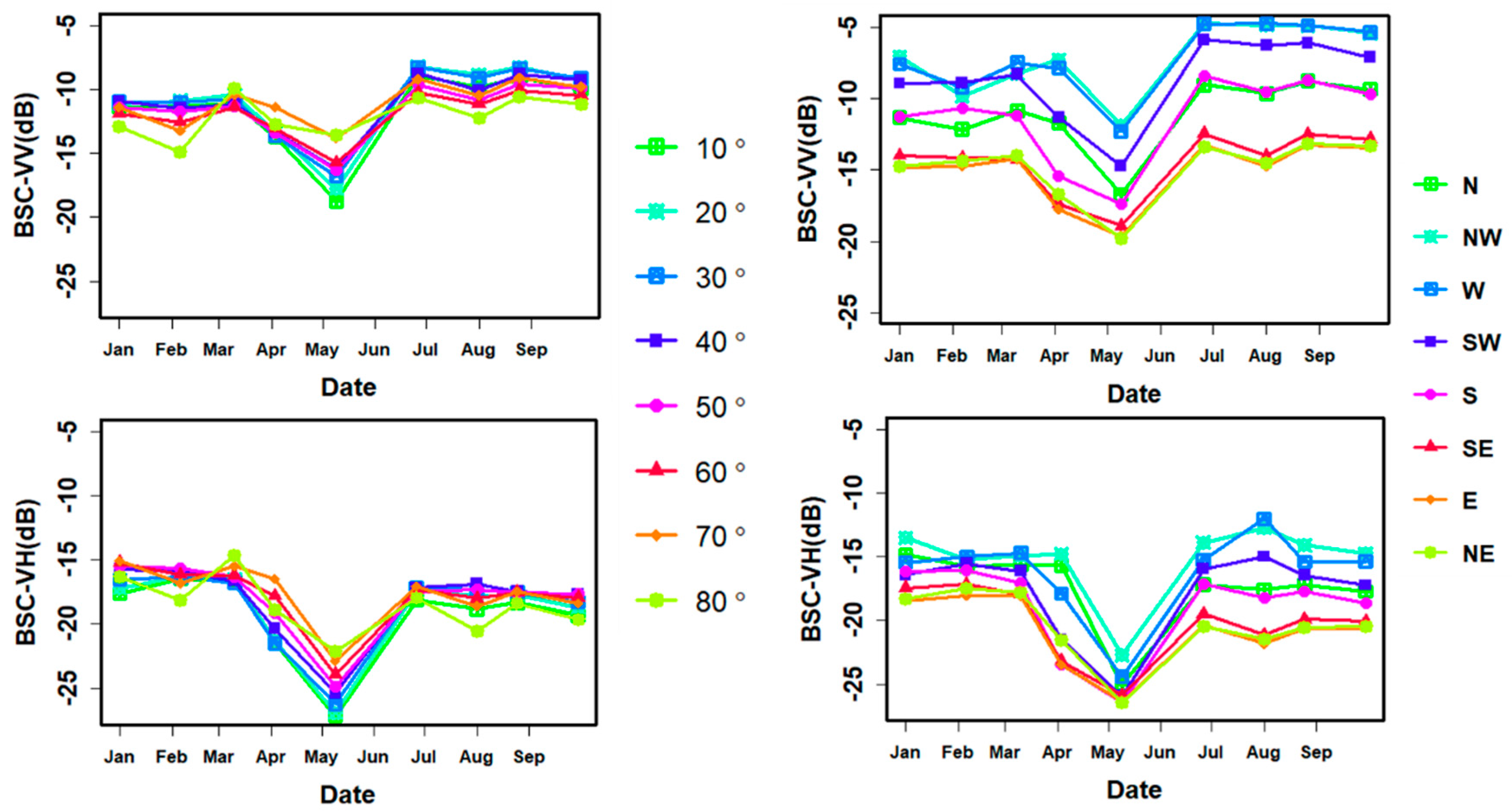
Year	Mode	Polarization	Incidence Angle Range	Acquisition Dates
2017	Interferometric Swath	VV, VH	38.7–46.3	07 Jan, 24 Feb, 08 Mar, 20 Mar, 01 Apr, 25 Apr, 07 May, 31 May, 24 Jun
2018	Interferometric Swath	VV, VH	38.7–46.3	02 Jan, 07 Feb, 03 Mar, 20 Apr, 26 May, 19 Jun, 25 Jul, 30 Aug, 23 Sep, 29 Oct, 22 Nov, 28 Dec
2019	Interferometric Swath	VV, VH	38.7–46.3	21 Jan, 26 Feb, 22 Mar

,

Table 2. Sentinel-1 SLC data used in Davos, Swiss Alps study region.

Year	Mode	Polarization	Incidence Angle Range	Acquisition Dates
2018	Interferometric Swath	VV, VH	30.4–46.0	18 Jan, 30 Jan, 11 Feb, 23 Feb, 19 Mar, 31 Mar, 12 Apr, 06 May, 18 May, 30 May, 10 Aug

and

Table 3. Sentinel-1 SLC data used in Dickinson, North Dakota study region.

Year	Mode	Polarization	Incidence Angle Range	Acquisition Dates
2017	Interferometric Swath	VV, VH	30.4–46.0	17 Oct, 10 Nov, 16 Dec
2018	Interferometric Swath	VV, VH	30.4–46.0	19 Jan, 14 Feb, 10 Mar, 15 Apr, 21 May, 14 Jun, 20 Jul

provide summaries of Sentinel-1 data used in this study for each year and geographic region.

UAVSAR Data—The Uninhabited Aerial Vehicle Synthetic Aperture Radar (UAVSAR) is NASA’s L-band airborne full-polarimetric SAR system with high spatial resolution (1.7 m × 1 m) and swath coverage of more than 16 km (https://airbornescience.jpl.nasa.gov/instruments/uavsar). UAVSAR L-band data acquired over the Grand Mesa during the SnowEx’17 field campaign are used here to contrast against Sentinel-1 C-band data. Specifically, four UAVSAR images acquired in the same orbit from Feb–Mar 2017 are used to contrast the spatial variability of L-band BSC in Grand Mesa conditional on land-cover against Sentinel-1 C-band BSC.

Terrain Data—The NASA/NGA Shuttle Radar Topography Mission (SRTM) C-band 30 m (1 arcsec) Digital Elevation Model (DEM) is used in this study to process the Sentinel-1 SAR data and for scaling analyses. The same data were used to process the UAVSAR data over the Grand Mesa at 5 m resolution. U.S. Geological Survey (USGS) National Elevation Data (NED) at 1 m, 10 m and 30 m resolution are also available for Grand Mesa and were used in this study as baseline to assess the influence of the DEM on SAR processing.

Landsat-8 Data—In order to confirm the presence of snow in the Sentinel-1 data, 30 m resolution snow cover maps were generated from Landsat-8 data for the Grand Mesa, Swiss Alps and North Dakota regions on cloud-free days during 2017 and 2018. A summary of Landsat-8 data used in this study for all study regions is presented in

Table 4. Landsat-8 data acquisitions.

Region	Year	Acquisition Date
Grand Mesa	2016	15 Aug, 16 Sep, 03 Nov, 19 Nov
	2017	06 Jan, 11 Mar, 12 Apr, 14 May, 15 Jun, 01 Jul, 03 Sep, 05 Oct, 09 Nov, 08 Dec
	2018	26 Feb, 30 Mar, 17 May, 02 Jun, 04 Jul, 22 Sep, 25 Nov
Swiss Alps	2016	25 Aug, 29 Nov, 08 Dec
	2017	25 Jan, 30 Mar, 17 May, 29 Jun, 15 Jul, 22 Sep, 15 Oct, 16 Nov, 02 Dec
	2018	13 Feb, 24 Mar, 02 Apr, 25 Apr, 12 Sep, 28 Nov, 14 Dec
	2019	22 Jan, 16 Feb, 23 Feb
North Dakota	2017–2018	17 Dec, 02 Jan, 10 Feb, 14 Mar, 15 Apr, 26 May, 11 Jun, 20 Jul

. A threshold-based normalized difference snow index (NDSI) binary algorithm with a threshold value of 0.4 was applied to generate SCA maps. The NDSI is derived from the spectral reflectance of Landsat-8 Band 3 (0.53–0.59 µm, B_VIS) and Band 6 (1.57–1.65 µm, B_SWIR):

$$NDSI=\frac{B_{VIS}-B_{SWIR}}{B_{VIS}+B_{SWIR}}$$

(1)

Snow cover is maximum over Grand Mesa from November through to March and minimum from June to September for the 2016–2019 period (Figure 4). June and July images serve as snow-free baseline. Snow cover over the Swiss Alps shows similar seasonality (Figure 5), although snow accumulation begins in September and decreases in October due to the warmer temperatures and high precipitation in the form of rainfall rather than snow [44]. In North Dakota, considerable snow accumulation occurs during February and March, when the entire study region is covered with snow until it melts in April (Figure 6).

Land-cover Classification—The spectral variability vegetation index (SVVI) is used to classify vegetation due its refined sensitivity as compared to NDVI (Normalized Difference Vegetation Index) and application to both natural and agricultural land-uses [45]. SVVI is calculated as the difference between the standard deviation (SD) of all Landsat bands (excluding thermal) and the SD of all three infrared bands, as follows

$$SVVI=SD\left({\rho }_{allbands}\right)-SD\left({\rho }_{NIRandSWIR}\right)$$

(2)

SVVI derived from Landsat-8 data over Grand Mesa was used here to distinguish grassland, forest and snow-cover features, as shown in Figure 7. Nevertheless, despite superior performance as compared to NDVI (not shown), the SVVI-based classification cannot distinguish between grasslands and forested areas during the melting season (Mar, Apr, and May 2017), and ambiguity and misclassification remain at the edges of complex terrain (e.g., Jan 2017).

3. Methods

3.1. Backscattering Coefficient Estimation

The standard framework for processing the Sentinel-1 Single Look Complex (SLC) data is presented in Figure 8. Radiometric and geometric corrections are applied to the Sentinel-1 SAR data to derive the normalized backscattering coefficients. Thermal noise due to the background energy of the SAR receiver is removed from the VV and VH intensity images (this background energy is independent of the received signal of the SAR sensor). Next, radiometric calibration was performed which converts the digital number of the image pixel to the corresponding backscatter intensity for both polarization channels, and phase information is preserved to extract the coherency matrix (https://sentinel.esa.int/web/sentinel/technical-guides/sentinel-1-sar).

The Terrain Observation with Progressive Scans SAR (TOPSAR) technique is applied in the IW mode of Sentinel-1 acquisitions to achieve large swath widths with enhanced radiometric performance [46]. The IW mode acquisition consists of three swaths. Each swath has a single image for each polarization channel, thus a single SLC image consists of six images for dual-polarization channels. Due to the coherent addition of scattered signals within a pixel, constructive and destructive interference occurs depending on the relative phase of each scattered signal. Speckle is an inherent problem of the SAR system, and the Lee speckle filter [47] with a width of five pixels (75 m) was applied to remove the speckles of the backscattered elements. SAR data have different topographical distortions (i.e., layover, foreshortening, shadowing) that depend on acquisition geometry. A geometric terrain correction is necessary to convert the data from slant range geometry into a gridded map. Specifically, the Range–Doppler terrain correction is applied, which is a robust approach that takes into account topography, and orbit and velocity information from the satellite.

While computing the Sentinel-1 backscattering coefficient (BSC), local terrain variation and their impact on the BSC are not considered. Therefore, the local incidence angle is used to represent the local terrain variation as proposed by Kellendorfer et al. (1998) [48]. This is called the radiometric corrected backscattering coefficient. The BSC of an illuminated target area is highly dependent on the incident angle of the signal. At small incidence angles, the backscattered intensity is high compared to that at higher incidence angles over the same illuminated area. Thus, the cosine correction [49] is applied to the georeferenced data to minimize the backscatter variation due to the incidence angle. Finally, radiometric and geometric corrected normalized BSC coefficients for VV and VH polarization channels are derived.

3.2. Coherency Metrics (Entropy–Alpha Estimation)

The CP (Cloude–Pottier) polarimetric decomposition [50,51] is an incoherent decomposition technique based on the eigenvalues and eigenvectors from the coherency matrix that was originally developed for fully polarimetric SAR data (intensity and phase at HH, VV, and HV polarizations). The Entropy and Alpha parameters obtained from the CP decomposition reveal scattering characteristics of the SAR signal that can be tied to scattering mechanisms of the snowpack [52,53,54]. Here, a modified CP decomposition approach is applied to the Sentinel-1 data coherency matrix generated from the debursted SLC image (Section 3.1), which includes only VV and VH channels. The scattering matrix captures the complete scattering characteristics of each pixel in an image as follows,

$$S=\left[\begin{array}{cc}0& S_{VH}\\ S_{VH}& S_{VV}\end{array}\right]$$

(3)

where S_VV, S_VH and S_HV represent the co- and cross-pol BSC at VV, VH and HV polarization, respectively. Due to the constraints of the reciprocity theorem, the cross-polarization elements in the scattering matrix are similar in the monostatic backscattering case, i.e., S_HV = S_VH. These elements can be represented by the corresponding Pauli vector, k_p:

$$k_p={\left[\begin{array}{cc}{S}_{VV}& 2S_{VH}\end{array}\right]}^T$$

(4)

where the operator T represents the conjugate transpose. The coherency matrix [T₂] is obtained from the product of the Pauli vector and its conjugate:

$$\langle \left[T_2\right]\rangle =\langle k_p·k_p{}^{T*}\rangle$$

(5)

Using the eigenvalue- and eigenvector-based incoherent target decomposition technique, [T₂] can be decomposed into its corresponding rank-1 coherency matrix T₂ as follows:

$$T_2={\displaystyle \sum }_{i=1}^2{\lambda }_i{\left[T_2\right]}_i$$

(6)

where λ_i are the eigenvalues of the rank-1 coherency matrix. The normalized eigenvalues (P_i) can be interpreted as pseudo probability measures derived from the eigenvalues:

$$P_i=\frac{{\lambda }_i}{{{\displaystyle \sum }}_{i=1}^2{\lambda }_i}$$

(7)

Shannon’s Entropy (H) is subsequently estimated from the normalized eigenvalues (P_i):

$$H={\displaystyle \sum }_{i=1}^2-P_i{\log }_2{P}_i$$

(8)

Following [47], the eigenvectors u of the averaged coherency matrix can be expressed as

$$u={\left[\begin{array}{cc}\cos \alpha e^{j\varphi }& \sin \alpha \cos \beta e^{j\left(\delta +\varphi \right)}\end{array}\right]}^T$$

(9)

This could be further written as a revised eigenvector parameterization of a 2 × 2 unitary matrix as

$$\left[\begin{array}{cc}{u}_1& u_2\end{array}\right]=\left[\begin{array}{cc}\cos {\alpha }_1{e}^{j{\varphi }_1}& \cos {\alpha }_2{e}^{j{\varphi }_2}\\ \sin {\alpha }_1\cos {\beta }_1{e}^{j\left({\delta }_1+{\varphi }_1\right)}& \sin {\alpha }_1\cos {\beta }_2{e}^{j\left({\delta }_2+{\varphi }_2\right)}\end{array}\right]$$

(10)

where ${\alpha }_1$, ${\alpha }_2$ represent the target’s scattering mechanisms, and β, δ and ϕ are used for the estimation of target orientation angles. The roll invariant mean dominant scattering parameter $\widehat{\alpha }$ is calculated in terms of the pseudo probabilities as follows:

$$\widehat{\alpha }={\displaystyle \sum }_{i=1}^2{P}_i{\alpha }_i$$

(11)

In the remainder of the manuscript, $\widehat{\alpha }$ is referred to as Alpha. Generally, it is expected that Entropy is low for fresh snow cover and increases with wetness. Conversely, Alpha is high for fresh snow and decreases with wetness. Entropy and Alpha, respectively, increase and decrease with surface roughness. Entropy is high (>0.7) for vegetated areas, whereas Alpha takes values in the intermediate range (30°–50°) [52,53].

3.3. Scaling Analyses

The spatial characteristics of snowpack properties as captured by SAR measurements were examined by quantifying the changes in the variance as a function of area, and by tracking changes in the spatial statistics between overpasses based on the slope of the power spectra of individual images as per Kim and Barros (2002) [55]. To isolate homogeneous areas for scaling analysis, backscattering images for Grand Mesa, Swiss Alps, and the North Dakota areas were subset into areas of homogeneous land cover with areas ~4–16 km². The BSC intensity images were aggregated from 225 m² to ~16 km² using the aggregation scheme summarized in

Table 5. Scaling scheme for spatial analyses.

Number of Pixels (Range Direction)	Number of Pixels (Azimuth Direction)	Total Number of Pixels	Pixel Area Range × Azimuth (m2)
1	1	1	15 × 15
2	2	4	30 × 30
4	4	16	60 × 60
8	8	64	120 × 120
16	16	256	240 × 240
32	32	1024	480 × 480
64	64	4096	960 × 960
128	128	16,384	1920 × 1920

. Note that the speckle removal described in Section 3.1 to improve the signal-to-noise ratio (SNR) is expected to introduce a scaling break above and below the LRS filter scale.

Given the small size (<20 km²) of the homogenous areas of interest, instead of using 2D FT to calculate the power spectra, 1D FTs are conducted for rows and columns separately, and the average in the zonal (x) and meridional (y) directions is calculated for scaling analysis as following [56,57]. If $k_x \left({\lambda }_x\right)$ and $k_y \left({\lambda }_y\right)$ are wavenumbers (wavelengths) corresponding to the $x$ and $y$ directions, in the range of scales where the power spectrum $|{\mathrm{F}}^{\prime }\left(k_{\gamma }\right){|}^2$ exhibits power-law behavior

$$|{\mathrm{F}}^{\prime }\left(k_{\gamma }\right){|}^2=C{k}_{\gamma }^{{\beta }_{\gamma }}$$

(12)

where $\gamma$ can be $x$ or $y$ and $C$ is a constant, the spectral slope ${\beta }_{\gamma }$ along direction $\gamma$ is estimated by applying the log transform to Equation (12) as follows:

$$log\left\{\frac{|{\mathrm{F}}^{\prime }\left(k_{\gamma }\right){|}^2}{C}\right\}= {\beta }_{\gamma }log\left(k_{\gamma }\right)$$

(13)

The spectral slope is the metric (scaling factor) that explains the transfer of backscatter energy across scales. A change in slope between adjacent scales (scaling break) is indicative of a change in scaling behavior. Here, the underlying premise is that scaling breaks and changes in scaling factor can be attributed to physical changes in the snowpack that impact backscattering mechanisms.

3.4. Snow Wetness Mapping

The BSC difference between wet and dry snow or snow-free surfaces has long been explored to detect and map wet snow [23]. The threshold polarization ratio algorithm proposed by [26] to map wet snow was applied to the Sentinel-1 SAR data for the three study regions. Both VV and VH polarization BSC ratios with respect to a reference image (e.g., summer conditions) as a function of the local incidence angle were utilized to determine the appropriate threshold values to detect wet snow based on LandSat-8 visible imagery and SCA-NDSI maps. Different threshold values were estimated for each of the three study regions due to different topography and SAR viewing geometry. Following [26], the reference image is the average of multiple SAR images from summer and early winter for snow-free conditions to reduce noise. Results from the analysis of BSC variance with scale (see Section 4) suggest a minimum is reached at ~250 m, and, therefore, the wet snow detection algorithm is applied to the SAR data at 240 m resolution to strike a balance between spatial resolution and accuracy. BSC image pairs are co-registered based on the SRTM 30m DEM and a multichannel intensity filter was applied [58]. Finally, weighted averages of R_VV = VV_winter/VV_summer and R_VH = VH_winter/VH_summer at different times were determined based on the local incidence angle following Nagler et al. (2016) [26].

The most commonly used wet snow mapping algorithm [25] was successfully applied previously to map wet snow at high elevations above the treeline, and it worked well in this study for North Dakota and the Swiss Alps areas, but it failed in Grand Mesa due to the presence of evergreen forest. To address this limitation, the approach from [26] was modified to take advantage of VH BSC sensitivity (~5 dB for on–off snow in the forest). The backscattering coefficients (VV and VH) derived for summer (reference) and all winter Sentinel 1 overpasses with the same acquisition geometry (descending mode in Grand Mesa) are used to calculate the ratios R_VV = VV_winter/VV_summer and R_VH = VH_winter/VH_summer. A weighted average polarization R_Avg image is then estimated as follows:

$$R_{Avg}=W{R}_{VH}+\left(1-W\right)R_{VV}$$

(14)

where R_VV and R_VH are backscattering coefficient ratios of winter and summer reference SAR imageries for both VV and VH polarizations, respectively. R_VH ratios over the forest region during the melting season are always below −0.5, in contrast with R_VV and R_VH ratios over grassland that fall within the range [−0.5, 2]. Sensitivity analyses of both polarization ratios over different land cover types reveal that the VH and VV ratios over the forest region have high (low) variability with snow on and off, as discussed in Section 4.3. Consequently, the weight W is calibrated based on two VH BSC thresholds, $R_{{VH}_1}$ and $R_{{VH}_2}$, inferred from R_VH BSC histograms:

$$IF \left(R_{VH}<R_{{VH}_1}\right) then \left\{=0.1\right\}$$

(15)

$$IF \left(R_{{VH}_1}\le R_{VH}\le R_{{VH}_2}\right) then \left\{=k\left[1+\frac{\left(R_{{VH}_2}-R_{VH}\right)}{R_{{VH}_2}-R_{{VH}_1}}\right]\right\}$$

(16)

$$R_{Avg}=W{R}_{VH}+\left(1-W\right)R_{VV}$$

(17)

where k = 0.5, $R_{{VH}_1}$ = −0.5 and $R_{{VH}_2}$ = 2. Discrimination of wet from dry snow and snow-free areas over forest and other land covers is done based on the threshold of −1.2 dB of the average polarization ratio image (R_Avg). This value is selected based on the histogram of polarization ratio images over the different land cover classes based on the analyses of snow cover during the accumulation (October–March), melting (April–May) and snow-free (July–August) seasons.

4. Results and Discussion

4.1. Temporal Variability of SAR Measurements over Complex Terrain

The temporal variability of backscatter measurements over snow-covered areas has been documented for many different geographic regions with a focus on sensitivity to snow condition and snow mass [9,10,27,30,35,36,37,59]. Generally, BSC slightly increases over the course of the (dry) snow accumulation season [60]. The change of snow BSC from snow-free BSC is strongly dependent on (1) local weather, including winds and precipitation regimes, (2) local soils and vegetation, and (3) the timing of the snow and snow-free observations.

Here, the temporal evolution of Sentinel-1 BSC sensitivity for Grand Mesa, Swiss Alps, and North Dakota is shown in Figure 9, taking advantage of multiple overpasses of Sentinel-1 C-Band dual-polarization (VV and VH). Seasonal BSC intensity is significantly different over grassland for both polarizations in Grand Mesa. VH BSC is 3 dB lower for dry snow vis-à-vis snow-free conditions, but VV BSC shows no difference, although VV BSC differs by 5 dB between fresh snow (Dec–Jan) and melting season conditions (Apr–May). This is in contrast with [30], the authors of which reported that the backscattering coefficient for dry snow was 5 dB lower than snow-free conditions at C- band irrespective of the polarization in the Swiss Alps at mid-elevations (~2500 m), which highlights the importance of regional controls in seasonal backscattering. Sentinel-1 data over the Grand Mesa were acquired in descending mode at 07:00 LT (Local Time), and thus, the surface of the snowpack is always frozen in late winter at the time of overpass. Diurnal melt–refreeze processes (Figure S1a–f) result in increased snow surface roughness as well as rough ice–water and, or ice–soil snowpack interfaces due to the refreezing of the daytime meltwater that can percolate deep into the snowpack [61]. Melt–refreeze cycles along with increases in diffuse scattering caused by the larger snow grain sizes in old snow and due to wind sintering explain the BSC increase from early spring (smooth wet snow) to late-spring and early-summer conditions (refrozen crusted wet snow) [62,63,64]. In early winter, from December to March, dielectric discontinuities in the snowpack tied to heterogeneous stratigraphy strongly impact the backscattering signal. In particular, if the event-scale snow accumulation is small, heterogeneous layering in the snowpack leads to strong backscattering [65]. In the Swiss Alps, the Sentinel-1 data were acquired in ascending pass at 19:15 LT. Both VV and VH BSC are ~5 dB higher in the accumulation season than in Grand Mesa and in North Dakota due to strong scattering at the dry snowpack–ground interface because of the rock surfaces and steep terrain. In April–May, VV and VH BSC decrease both relative to dry-snow and snow-free conditions due to surface melting. Indeed, the Sentinel-1 imagery shows strong spatial organization of BSC behavior with slope and aspect, and thus direct solar radiation, which is indicative of afternoon surficial melting preceding the late afternoon overpass in the Swiss Alps (see Section 4.3 below). Over North Dakota, the Sentinel-1 BSC measurements were collected in descending mode at 07:00 LT as in Grand Mesa, and they show similar seasonality. The co-polarization backscattering decreases from October to December, subsequently increasing as snow mass accumulates.

Overall, the analysis for the three regions shows evolution of backscattering behavior that is consistent with snowpack wetness and melt–refreeze processes depending on the overpass time (ascending in the Swiss Alps versus descending in the Grand Mesa and North Dakota), reflecting the diurnal cycle of snow surface condition and time-of-the-year (season). Higher temporal variability in the Alps than in the smooth topography of North Dakota or Grand Mesa, despite the high elevation of the latter, is indicative of distinct surface melt patterns depending on slope and aspect. The high values of Entropy and Alpha parameters for the three study regions (Figure 10, Alpha > 50 and Entropy in the 0.5–0.9 range) are similar to those of rough landscapes such as forests and urban areas [50], making it difficult to separate the different dominant scattering mechanisms, and thus it is not possible to discriminate among snow-cover types. In addition, the Sentinel-1 polarimetric data consist only of VV and VH channels and lack HH information (see Section 3.2). Nevertheless, the changes observed in Entropy and Alpha can be used to differentiate snow-on/snow-free conditions at high spatial resolution. The Entropy values are higher for snow-free as compared to snow-on conditions in Grand Mesa and North Dakota, whereas the opposite is true in the Swiss Alps. Conversely, snow-free season Alpha values are low for Grand Mesa and North Dakota, and high for the Swiss Alps compared to other seasons. This is attributed to the presence of vegetation in Grand Mesa and North Dakota, while measurements in the Alps are above the tree-line.

Note that, in addition to surface radiative effects, wind-driven coarsening and roughing of the snowpack surface should also be influenced by the diurnal cycle of ridge-valley wind patterns, thus introducing persistent spatial variability that varies locally with time-of-day and with landform. Therefore, BSC sensitivity in complex terrain is necessarily regional and even local. The advantage of satellite revisits is that it is possible to learn a local climatology (time-varying patterns) of BSC sensitivity from tracking its variability in space and time, which can be interpreted subsequently in the light of snow physical conditions using a snow physics model or ground-based observations. More extensive discussion follows in Section 4.2 in the context of scaling analysis.

4.2. Space-Time Scaling Behavior

Variance Scaling—To examine the evolution of spatial variability with time, we first focus on the relationship between variance (2nd order moment of the spatial distribution of BSC) with area for three (4 × 4 km²) areas of homogeneous land-cover identified in Figure 3 as (A) grassland, (B) mixed (grassland mixed with evergreen forest), and (C) evergreen forest in Grand Mesa. The changes in variance as a function of area are examined in Figure 11. The variability of the multi-temporal BSC for both VV and VH polarization in (A) is maximum at a 15 × 15 m² spatial scale (the nominal resolution of the processed data) and decreases gradually with increasing area to a minimum in the [250–500 m²] range for region A (Figure 11) and increases again for larger spatial scales up to 16 km². The shape of the variance-area curve of VH polarization on 29 October 2018, is different from other dates between 0.01 and 2 km² due to rain-on-snow (RoS) and melting followed by melt–refreeze cycles (Figure S2) in the previous week, resulting in higher surface roughness and higher spatial variability across scales up to 2 km². Since the SAR data over Grand Mesa is acquired at 07:00 AM LT, this change is explained by overnight freezing of the snowpack, including deeper layers due to rainfall impact and ponding on the snowpack surface, and infiltration. For area B with mixed forest and grassland, the variability decreases gradually from 15 × 15 m² to 4 × 4 km² (Figure 11), and the observed variability is more than 200% higher than the variability of homogeneous grassland both in time and space, with a minimum between 0.4 and 0.8 km². This behavior is attributed to the characteristic length scales of land-cover within B, that is the variance is minimum at the spatial scales corresponding to uniform land-cover (e.g., grass meadows versus forest-patch length-scales). Finally, the variability observed at A, B and C was maximum in summer (snow-free) and decreases to a minimum in early winter (fresh snow cover). Warm weather episodes during the accumulation season result in surface melt followed by overnight refreeze (e.g., 20 April 2018). Over forested areas (areas B and C), the minimum variance is reached at larger spatial scales in the range 1–2 km², although it increases at larger scales due to changes in topography at the edges of area C (see Figure 2 and Figure 3).

The variability of both VV and VH polarization BSC intensities in the Swiss Alps at the nominal Sentinel-1 resolution is much higher than for Grand Mesa due to the steep terrain (Figure 12), but it drops very quickly to reach a minimum at ~0.01 km² for both polarizations. High BSC variability observed in April and May at very small scales during the melt season is tentatively attributed to a combination of increased snow surface roughness due to the overnight freeze of previous day melt at the surface of the wet snowpack as well as wet snow absorption at lower elevations at the time of overpass consistent with [27,66].

Over the smooth topography of North Dakota, BSC variability also decreases gradually with spatial scale (Figure 13) reaching a minimum at field scale (1 km²). Maximum variability in the snow free season (June and July) is tied to spatial organization of growing row crops in this mostly agricultural land.

Spectral Scaling—The spectral slope (scaling factor) of the 1D directional Power Spectra of BSC for the different regions as a function of time are used here to characterize the spatial organization of BSC with scale for different land- and snow-cover conditions. Through the snow season of 2017, the power spectra exhibit persistent multi-scaling behavior for Grand Mesa in the x-(Figure 14a) and y- (Figure 14b) directions for both polarizations within the range of wavelengths (90–900 m) over which the spectral slope is estimated (in between black dashed vertical lines in the top left power spectrum graph) with a strong scaling break at ~180 m (green vertical line) corresponding to a flattening of the spectra at larger scales (longer wavelengths). Tables S1a–c present a summary of the spectral slopes for each direction, polarization, and at both small- and large-scales (90–180 m, 180–900 m for grassland; and 90–250 m, 250–1500 m for mixed and forest land-cover) in 2017. Results for 2018 are presented in Table S2a–c. Comparison of the scaling behavior of BSC fields (Figure 14a,b), DEM data (not shown) and vegetation indices (e.g., SVVI, Figure S4) suggest that land-cover (vegetation) and snow condition govern the scaling behavior of BSC, with mixed and forested areas exhibiting very similar behavior pointing to the dominant role of trees in the evolution of BSC space–time structure. The scaling behavior at small scales (<100 m) over Grand Mesa shows negligible temporal sensitivity and the spectral slope is consistent with the SRTM DEM at the same scales. Further, multi-scaling SVVI spectra over the forest area suggest that multi-scaling artefacts associated with small-scale topography (landform) are cancelled by the presence of vegetation.

The power spectra for UAVSAR BSC L-band HV polarization over Grand Mesa in 2017 are shown in Figure 14c. Table S1d presents the spectral slope summary of HV UAVSAR for the slope ranges of 30–180 m, 180–900 m. The UAVSAR BSC images cover an area smaller than Sentinel-1 and were collected over a two-month period during the accumulation season (Feb–March). In the common range of scales, the behavior of UAVSAR L-band is consistent with Sentinel-1 C-band: the first scaling break is in the 100–200 m scale range and scaling factors are persistent in the snow accumulation season when the dominant backscattering mechanism is at the snow–ground interface. This independence of frequency suggests that the physical basis of BSC scaling behavior is robust for dry snow conditions and there is, therefore, potential to explore multi-frequency SAR data for retrieving snow properties without extensive calibration using ground observations [34].

The intra-seasonal persistence of spectral slopes during the accumulation season is present in 2018 as well, but the spectral slopes change dramatically (see selected spectra in Figure 14d, and Figure S5a,b). The changes between the two years reflect changes in the spatial organization of BSC linked to snowfall and local meteorology. Specifically, large differences in precipitation regimes during the accumulation season (January–February–March) in 2017 (>160 cm snowfall; >330 mm rainfall) compared to 2018 (~80 cm snowfall; >210 mm rainfall) result in much deeper snowpacks (>2 factor), more complex stratigraphy, and spatial heterogeneity. These effects are apparent by inspecting the differences in VV-x spectra between Sentinel-1 overpasses in 2017 for scales 100–1000 m (Figure 14a) that are largely absent in 2018 (Figure 14d, Figure S5a,b). The distinct behavior is more significant for grassland (area A in Figure 2 and Figure 3) and mixed (area B in Figure 2 and Figure 3) land-cover where wind redistribution effects are stronger in Grand Mesa.

Figure 15a,b show there are significant differences in spectral slopes between grassland and mixed and forest areas with high (low) spectral slope ratios in the y-direction (x-direction) for snow-free conditions in late May (5/31) and before the full greening of the Mesa by end of June (6/24, see Figure S6 for NDVI maps). Note the increasingly steeper slopes for VV BSC in the x-direction in the forest as snow wetness increases and peaks by the end of April (4/25) for snow-on conditions in contrast with the behavior for grassland in the y-direction (Figure 15b). The decreases after the onset of the melting season show that attenuation due to snow wetness on the ground counterbalances volume scattering by the canopy above leading to a significant increase in spectral slope ratios. No significant differences between mixed and forest land-cover classes suggest a saturation of sensitivity in the melting season when trees are present. Interestingly, greening of the grassland smooths the BSC fields by introducing homogeneous volume and surface scattering effects due to the growing grass layer, whereas exposure of the full tree architecture (trunk, branches, and canopy, and greening of deciduous trees where present) results in higher variability associated with increased heterogeneous volume and surface scattering. The ambiguity that emerges for the magnitude of BSC in the forest areas at C-band (UAVSAR data are not available after March 31) due to wet snow conditions illustrates the challenges of snow mass retrieval, whereas changes in spectral slope documented here can be used to map the under-canopy snow wetness condition. The persistence of the scaling behavior during the snow season (e.g., VV grassland in the x-direction, VV-forest in the y-direction) indicates that the local spatial patterns of BSC variability (i.e., spatial statistics) are robust in time, and thus can be learned from repeat measurements. Differences such as those quantified for VH in the x-direction for grassland and forested areas in end of March (3/26) capture distinct behavior after fresh snowfall. The reliability of these patterns in the accumulation season, hereafter referred to as snowform, and the ability to detect wet snow in the melting season is in keeping with previous work [41,66] and supports the notion that subgrid scale variability can be parameterized using scaling principles as done elsewhere for other geophysical variables [55,67,68,69,70]. The large inter-annual variability illustrated for the case of Grand Mesa suggests that, whereas reliable snowform tied to topography and vegetation explains the scaling breaks, BSC intensity and space–time structure in the same region reflect snow surface and snowpack properties (snow depth, surface roughness, microphysics, LWC) that are significantly different depending on weather and snowfall regime. Therefore, the spectral slopes can be viewed as an emergent metric of snowpack heterogeneity across scales.

The Sentinel-1 BSC spectra over the Swiss Alps shows multi-scaling behavior with scaling breaks at ~180 m and ~360 m for snow-on conditions (Figure 16, Table S3) with single-scaling for snow-free conditions. Note that the selected area (Figure 2) for scaling analysis is above the tree-line, and thus vegetation should not be playing a role here. At pixels where meteorological stations exist in the Swiss Alps (Figure S3a), the relationship between BSC and snow depth is ambiguous (Figure S7a,b). This suggests that snow mass is wrapped on the terrain filling (accumulating) the terrain roughness (depressions) at scales below 360 m. The variation of VV and VH BSC with slope (Figure 17a) is only apparent in the spring (Apr–May) during the melt season. There is, however, high all-year sensitivity to aspect (sun exposure, ascending and descending pass acquisitions and local incidence angle) with a difference of 7 dB between the North-East and North-West slopes for VV polarization in contrast with the North and South slopes that show the same BSC for all seasons (Figure 17b). As in Grand Mesa, the sensitivity to aspect captures differences in insolation patterns that are indicative of spatial variability on daytime surface melt followed by nocturnal refreeze cycles that strongly impact the microphysics of the snow surface during the accumulation season. Wet snow attenuation effects consistent with the minimum BSC magnitude independent of slope and aspect (Figure 17a,b) explain the distinct spectral slopes at small scales on May 18, 2018 in the y-direction (Figure 16, bottom row). Nonlinear behavior of heterogeneous snowpacks in the melt season reflects the changing patterns of SCA for scales <360 m (see also [8,71]).

In North Dakota (Figure 18, Table S4), temporally varying multi-scaling BSC behavior with breaks at ~90 m and ~360 m shows strong differentiation between snow-on and snow-free conditions especially in the VH polarization. The changes in scattering geometry and scattering mechanism are attributed to crop planting and growth in the summer.

The impact of wind-driven snow redistribution is out of the scope of this work. In particular, it is expected that “snowform” should reflect wind climatology in the planetary boundary layer that is closely modulated by regional topography and landform. This likely explains the contrasting variance-area relationships in Grand Mesa and the Swiss Alps with minima consistent with the second scaling break at scales 180–360 m and in the smooth topography of North Dakota where the variance-area scaling is monotonic in the range ~100–1000 m even as the BSC spectra exhibit an intermediate scaling break. Note that the methodology followed is general, albeit analysis metrics of the scaling behavior are specific to the areas analyzed here, which were selected purposefully to highlight differences and similarities at sub-km scales. For example, large-scale orography (latitudinal in the Swiss Alps, longitudinal in the Rockies), ridge-valley effects, and altitudinal changes in land-cover are not specifically addressed.

4.3. Wet Snow Mapping

Figure 19a–c show wet snow maps of the Grand Mesa, Swiss Alps, and North Dakota area. In Grand Mesa, wet snow is detected not only in grass and barren land but also in the forested areas, which can be confirmed through the spectral slope changes as well. High variability in the wet snow cover area (WSCA) is observed irrespective of the type of land cover reflecting weather variability: for example, about 26% of the area was covered with wet snow on 1 April 2017 and it was reduced to 8% on 13 April 2017 due to cold temperatures and snowfall between the two SAR acquisitions. Whereas the minimum WSCA occurs by the end of May, the time rate of WSCA change in the forested areas is slower compared to other land covers, suggesting that light extinction through the canopy plays a significant role in reducing incoming shortwave radiation, and thus preserving the snowpack. As expected, the algorithm effectively detects wet snow above the tree line in the Swiss Alps (Figure 19b), capturing weather-related variability such as new snowfall and melting events in April and May. Figure 19c shows the wet snow changes over North Dakota. Even though the region is mostly agricultural land, the BSC ratio-based wet snow map approach works well, showing a decreasing trend from a maximum of 58% WSCA in April of to 18% in May. The results are consistent with Landsat imagery of the region that is mostly snow-free by the end of May. However, the BSC changes during the snow melt [71] can potentially lead to the temporary underestimation of wet snow areas. Using the summer BSC image as a reference for wet snow mapping can lead to overestimation in areas of densely vegetated deciduous forest and underestimation for dry snow in barren areas with high BSC, both relatively small in Grand Mesa. Also, the selection of threshold for the wet snow mapping is highly dependent on local soil surface, vegetation covers and observation period, and thus it should be calibrated locally.

5. Conclusions

ESA’s spaceborne Sentinel-1 dual-polarization SAR data offers high spatial and temporal polarimetric BSC imagery to monitor seasonal snowpacks globally. This study reports a comprehensive effort to examine the spatial information content of these data in the light of snow physics. First, the data show large ambiguity in the relationship between BSC magnitude and snow mass, with the underlying ground surface dominating the signal during snow accumulation and a difference in BSC magnitude greater than 5 dB attributed to rocky terrain. In GM, BSC exhibit 10 dB sensitivity to wetness at small scales (~100 m) over homogeneous grassland. Sensitivity decreases to 5 dB in the presence of trees, and it is demonstrated that VH BSC sensitivity enables wet snow mapping below the tree-line. VV and VH BSC trends (positive, negative) in the early snow melting season strongly depend on the time of data acquisition (morning, evening), which demonstrates the importance of melt–refreeze cycles on surface roughness and microphysics. Parameters Entropy and Alpha derived from the coherency matrix showed little sensitivity to snowpack changes during the accumulation season in all cases, which is attributed in part to the lack of full polarimetric information in Sentinel-1 data.

Previously, [26] demonstrated a wet snow mapping algorithm that was adopted here to map wet snow using Sentinel-1 data. The algorithm that worked well in the Swiss Alps failed in Grand Mesa due to the presence of vegetation. Here, a modified version of the algorithm was implemented, successfully taking advantage of the sensitivity of BSC VH (and spectral slopes) to snow wetness conditions, especially in forested areas. This opens the possibility of global mapping of wet snow below the tree-line, albeit further testing and development toward generalization is required.

Area-variance scaling relationships show minimum variance at ~100 m in the Alps, 150–250 m in Grand Mesa, increasing up to 1 km and longer for forested areas in Grand Mesa and agricultural fields in North Dakota. These scales can be viewed as measurement optima, that is the scales at which the average of the measured BSC Lm is representative of the local mean value of the field measured at scale l (Lm > l). Spectral analysis reveals two scaling regimes at sub-km scale with scaling breaks around ~180–360 m. These scaling regimes as measured by the spectral slopes are reliable within the same accumulation season and exhibit strong sensitivity to snow mass and snow wetness when trees are present. This is in keeping with work in the peer-reviewed literature, highlighting the reliability of snowpack melting patterns at regional scale consistent with topography and landform, as discussed in Section 4.2. Nevertheless, large inter-annual variability as illustrated for the case of Grand Mesa suggests that snowmelt patterns organized by topography and vegetation can explain the scaling breaks at small scales, the regional spatial variability of snowpack conditions (surface roughness, microphysics, LWC) varies strongly with local weather including snowfall that determines snow accumulation, and wind-driven snow redistribution. Indeed, variance-area and spectral scaling differences between regions of complex topography (Grand Mesa and the Swiss Alps) and smooth topography in North Dakota suggest the hypothesis that BSC multi-scaling behavior may be attributed to scattering mechanisms controlled by heterogeneous stratigraphy and surface roughness at small mesoscales (100s of m) vis-à-vis snow mass modulated by regional winds (snow-form) at larger mesoscales (kms).

This work demonstrates time-varying spectral slopes are an emergent metric of the overall scattering behavior of heterogeneous snowpacks. More extensive multi-year multi-site analysis is required to investigate whether the scaling break positions identified here are fixed conditional on climate, topography and land-cover, that is cold region physiography, or they also exhibit inter-annual variability as the spectral slopes, for example, in response to changes in wind climatology. Further research will focus on elucidating the scattering budget (volume scattering, surface and interface scattering) of heterogeneous snowpacks and developing model constraints and a data assimilation framework to capture snow physics heterogeneity at sub-km scale.