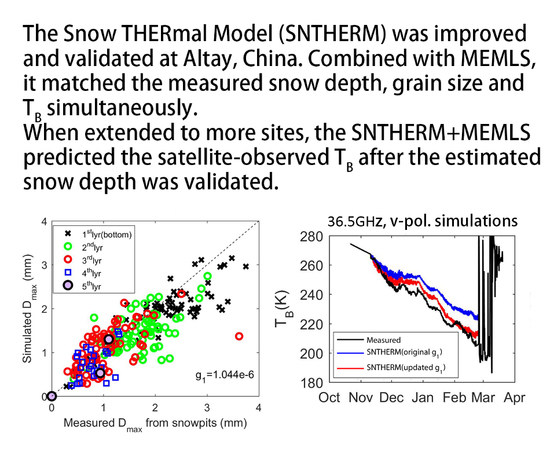
Validation of the SNTHERM Model Applied for Snow Depth, Grain Size, and Brightness Temperature Simulation at Meteorological Stations in China
Abstract
:1. Introduction
2. The Altay Experiment, Study Area, and the Datasets Utilized
2.1. The Altay Experiment
2.2. The Study Area and the Datasets Utilized
3. Models
3.1. Snow Thermal Model (SNTHERM) Introduction
3.2. Snow Thermal Model (SNTHERM) Improvement
3.3. Brightness Temperature Model
4. Results
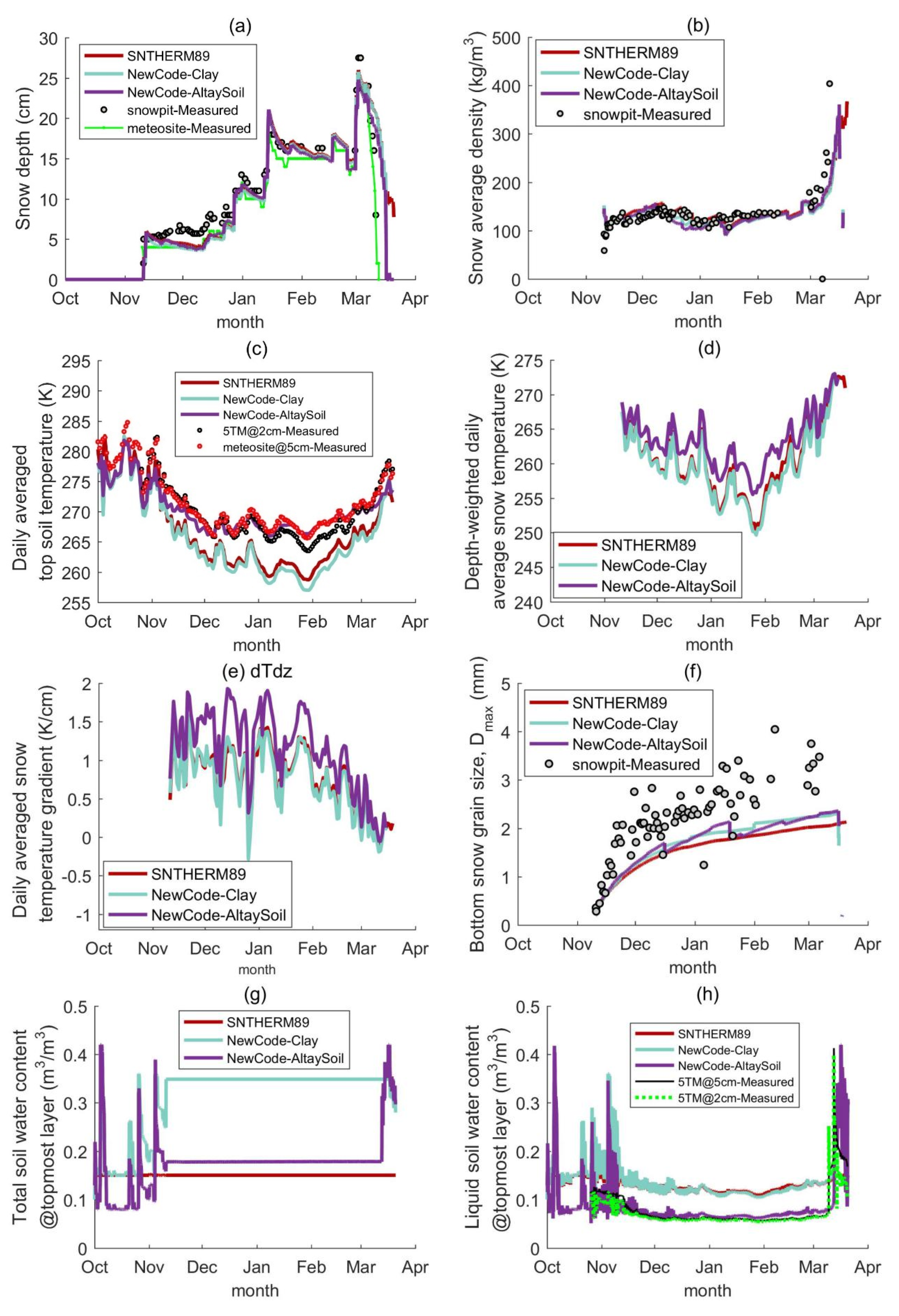
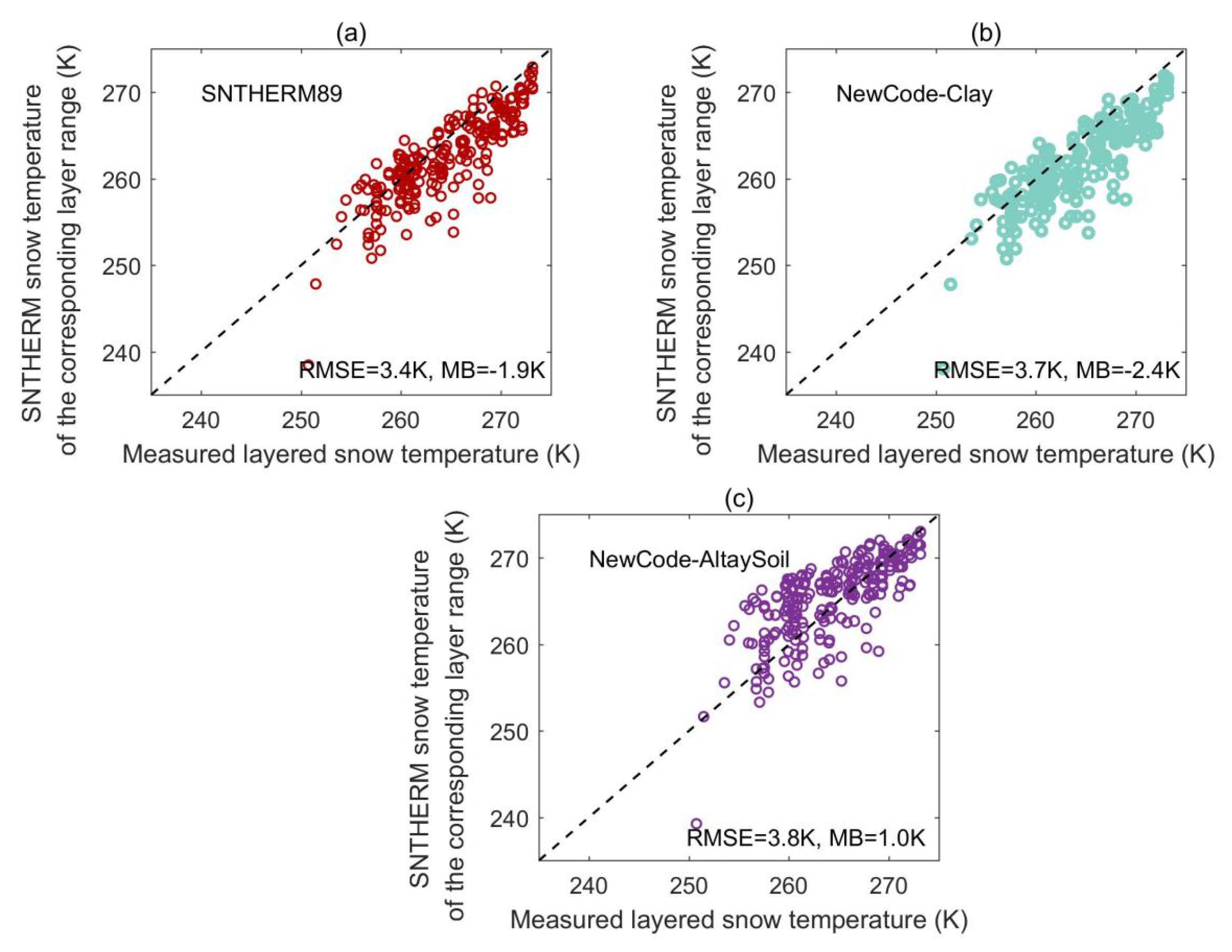
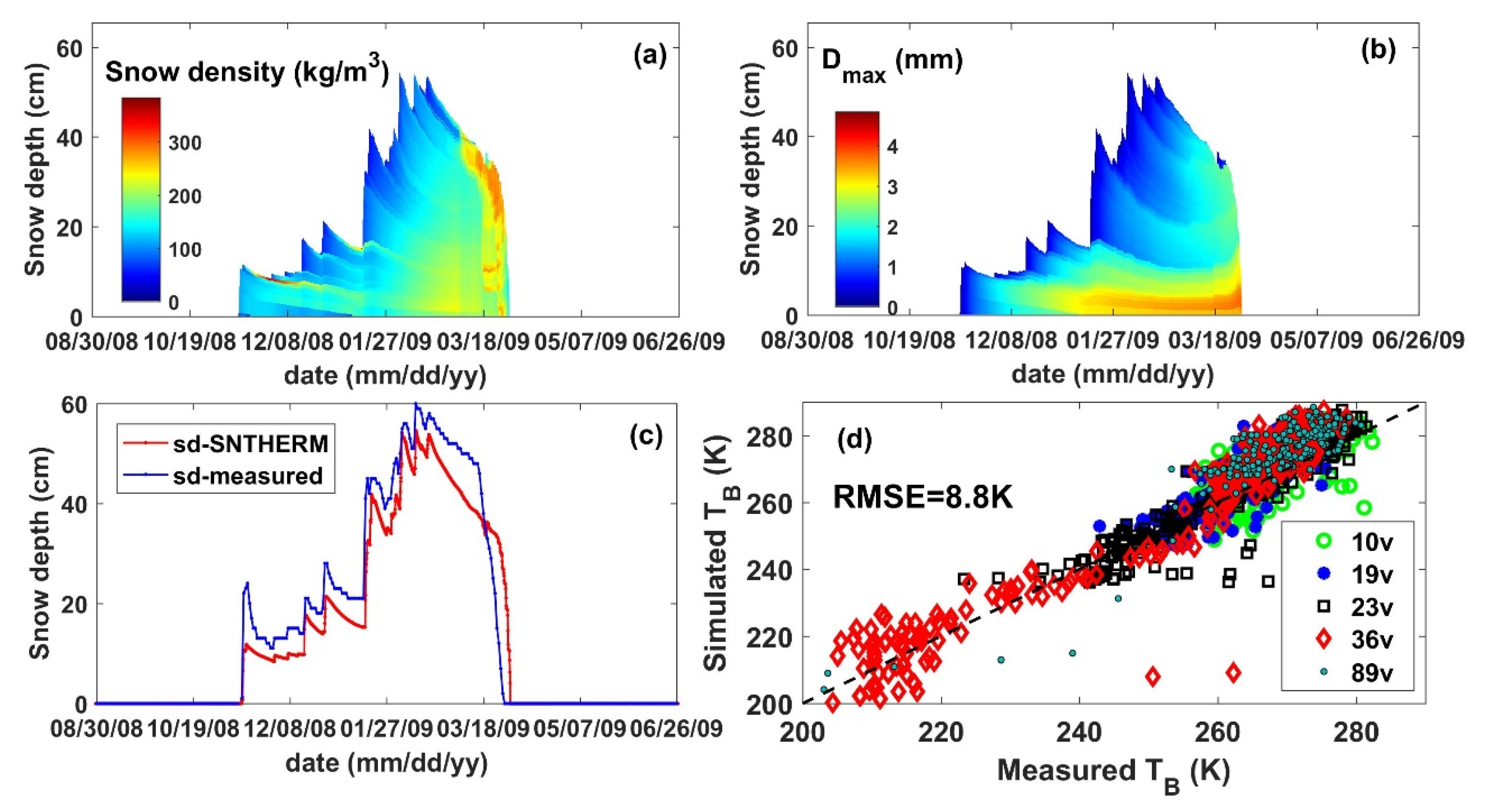
4.1. The Revised Soil Modeling in SNTHERM and the Validation Based on the Altay Experiment
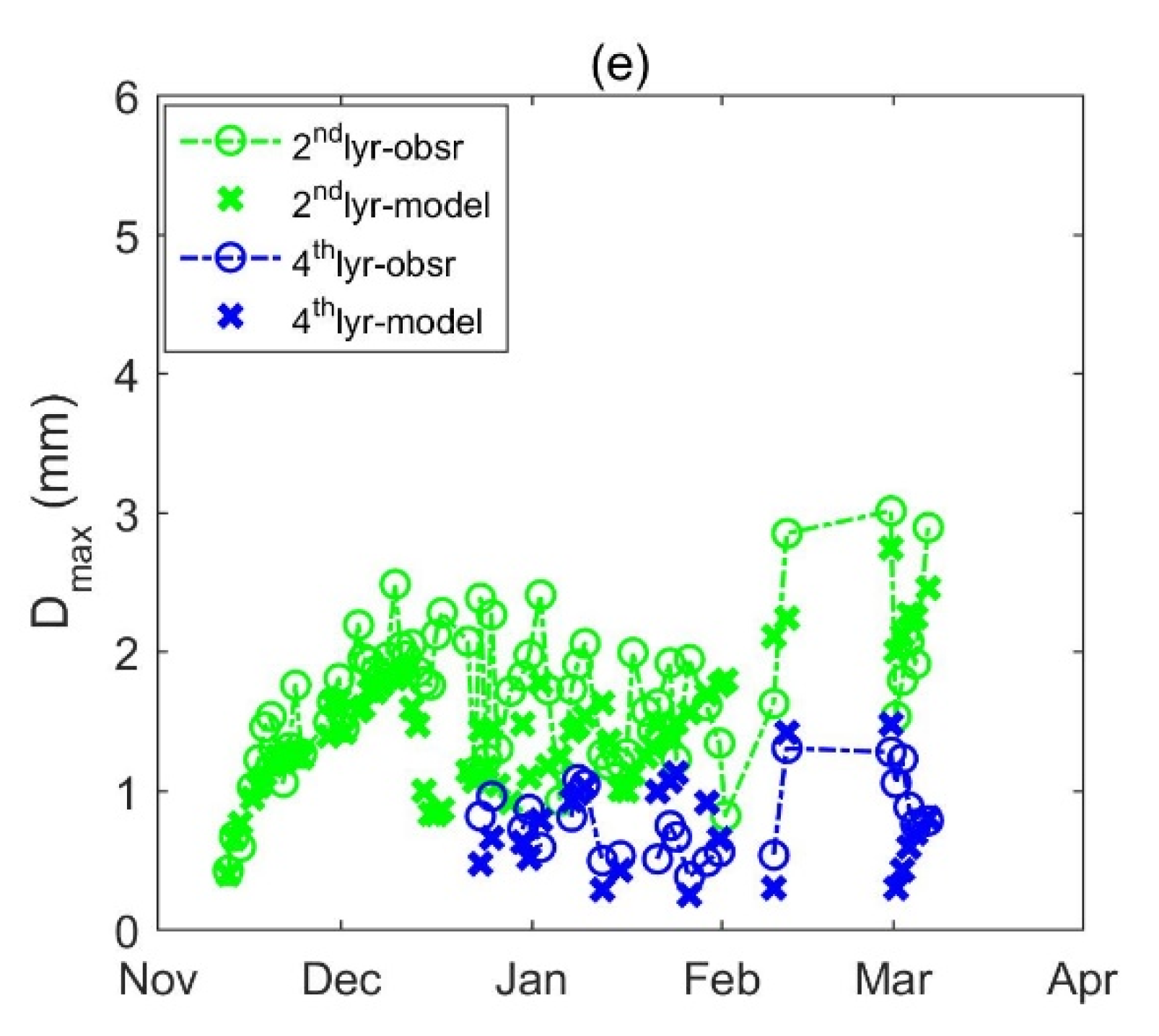
4.2. The Grain for the Altay Experiment
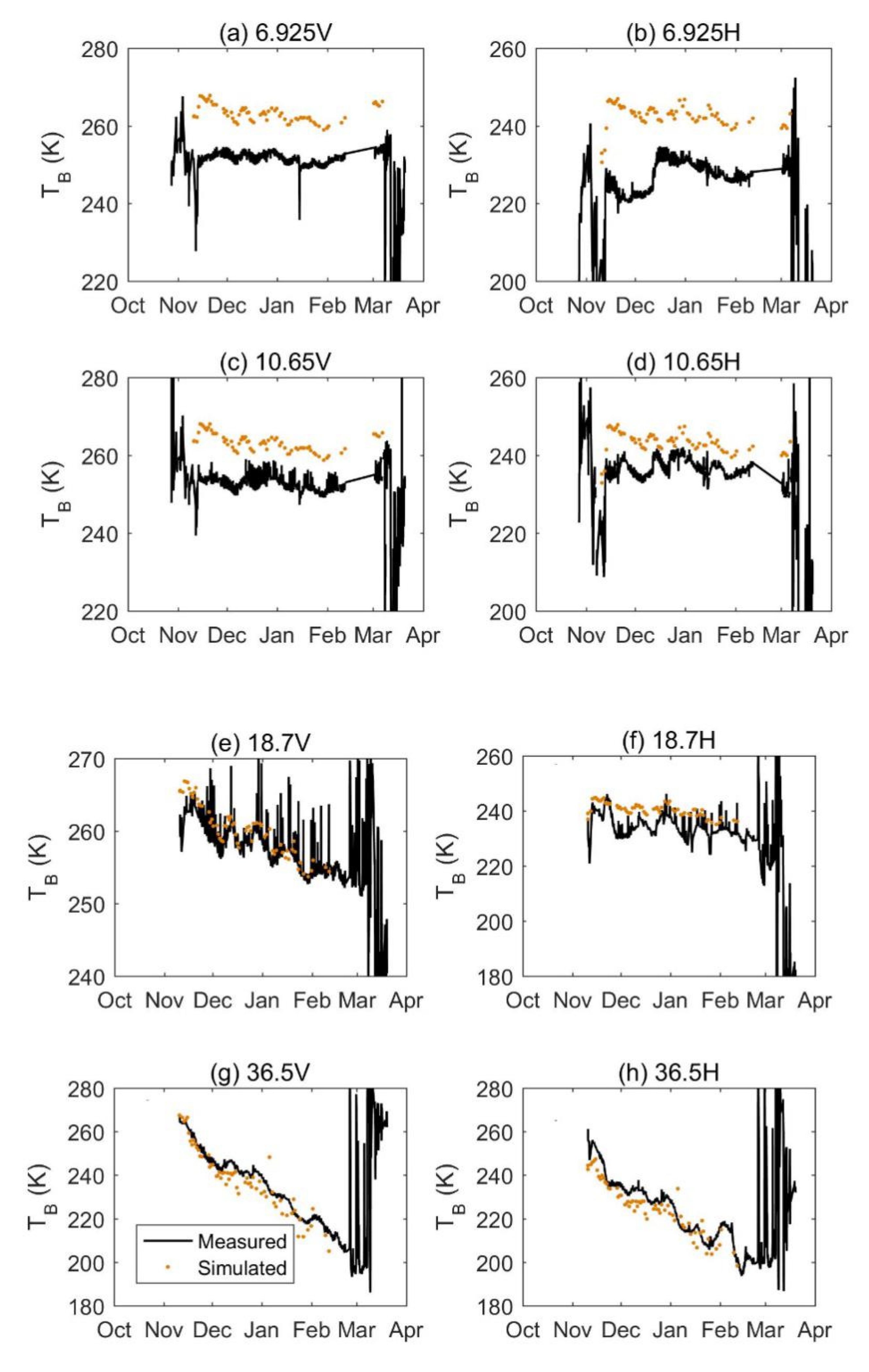
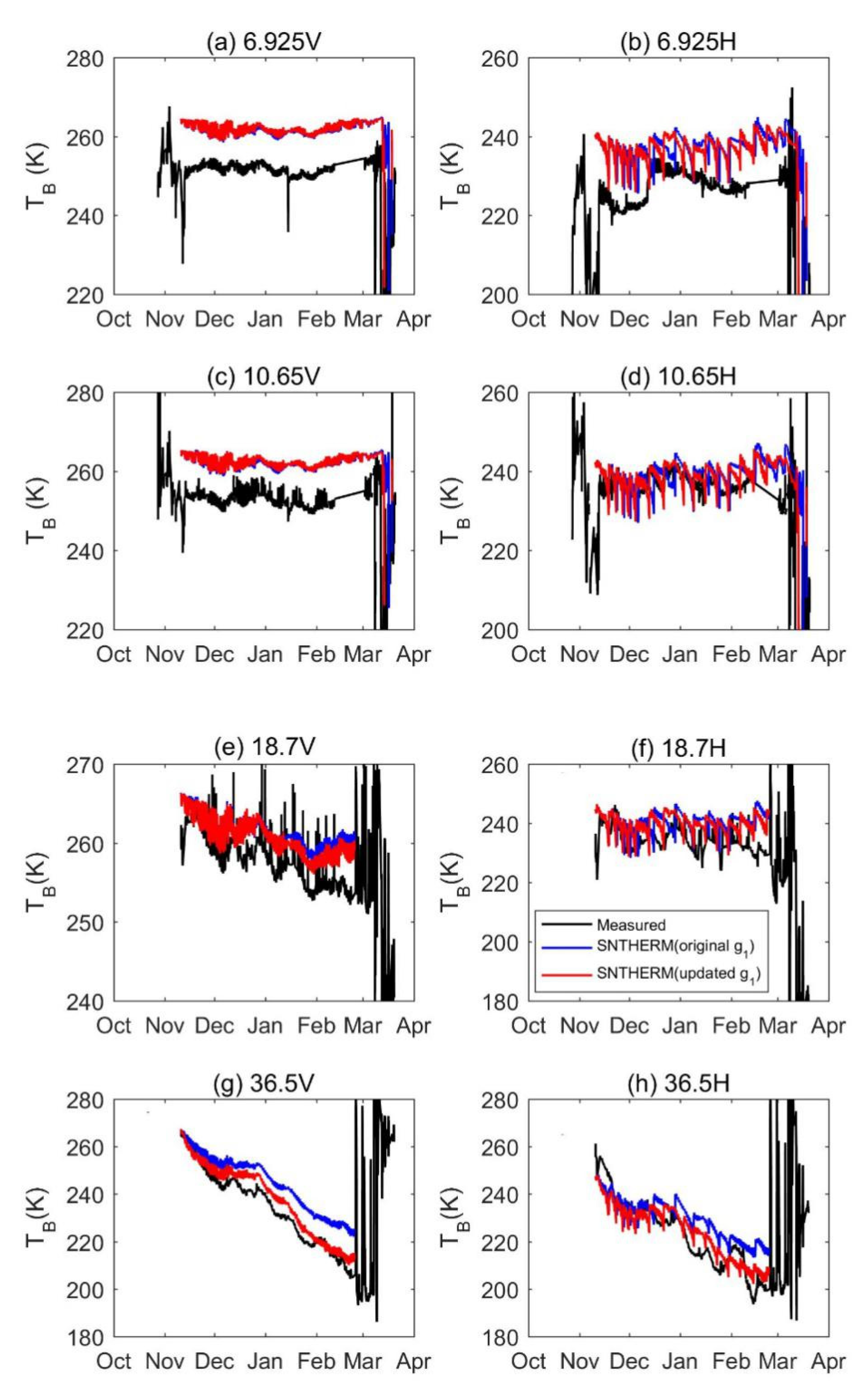
4.3. Brightness Temperature Simulation for the Altay Experiment
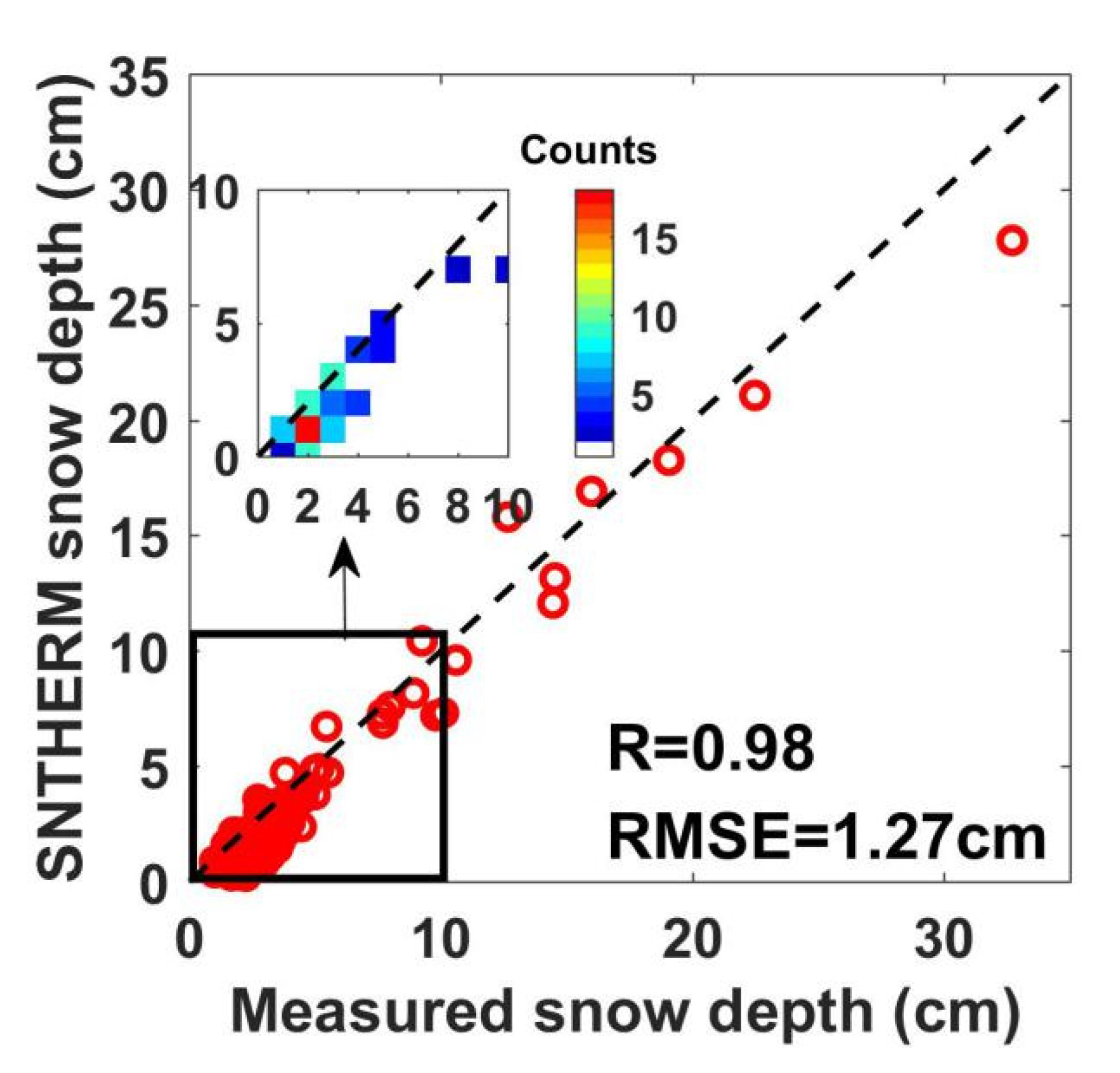
4.4. Validation of Snow Depth at the 102 Sites
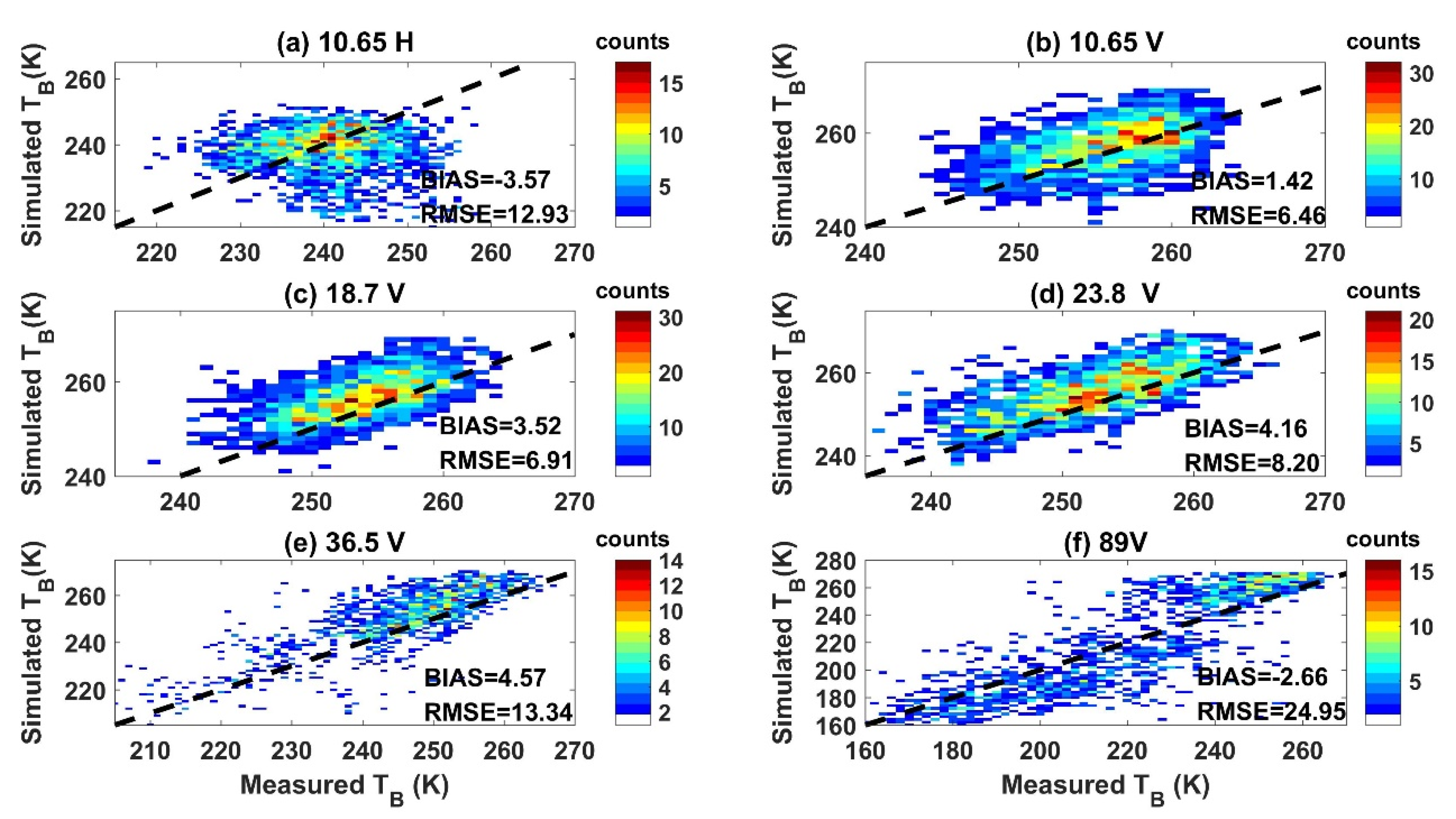
4.5. Validation of the Brightness Temperature at the 102 Sites
5. Discussions
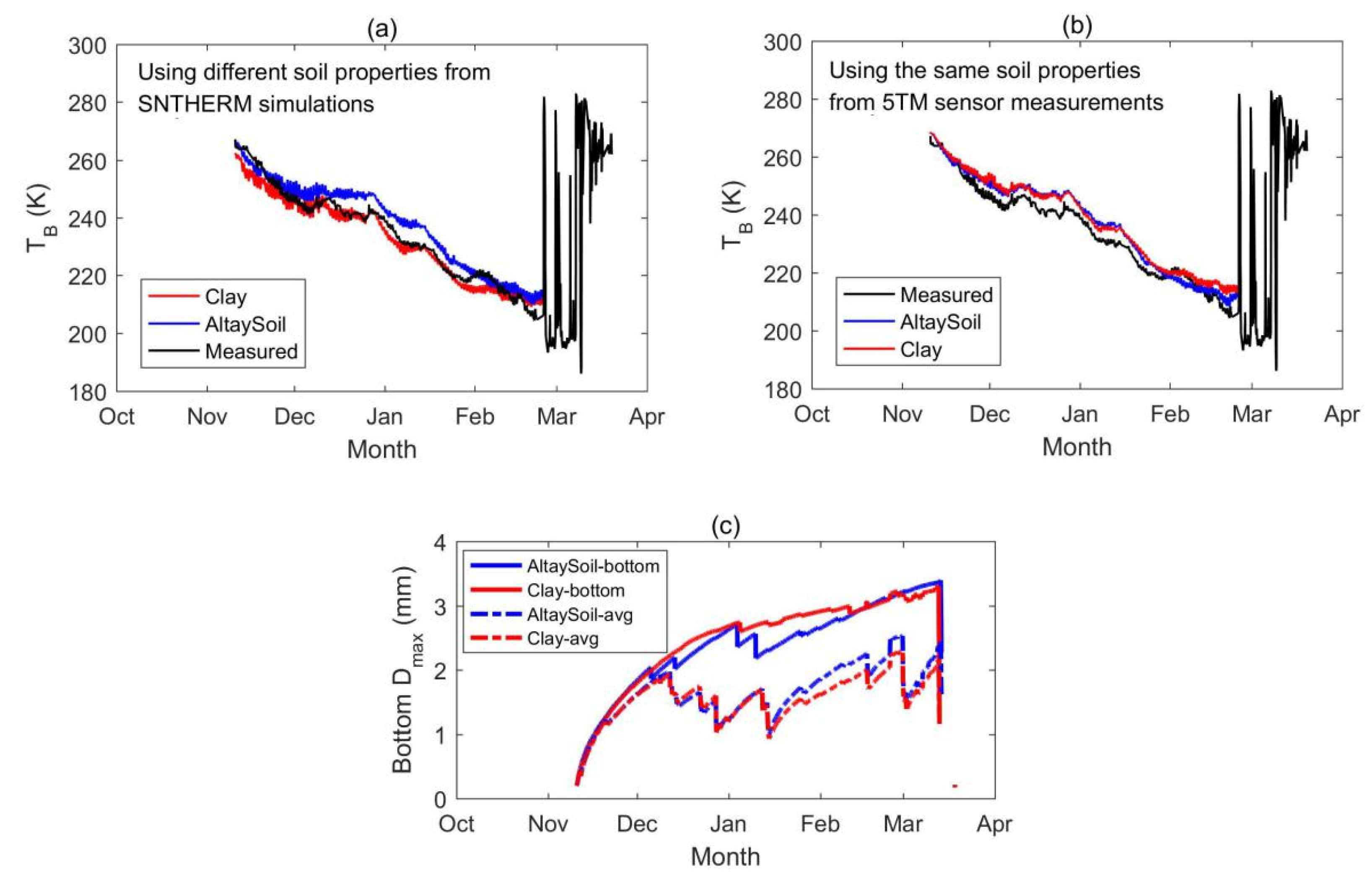
5.1. Analysis of the Influence of Soil Parameter Setting on the Brightness Temperature Simulation
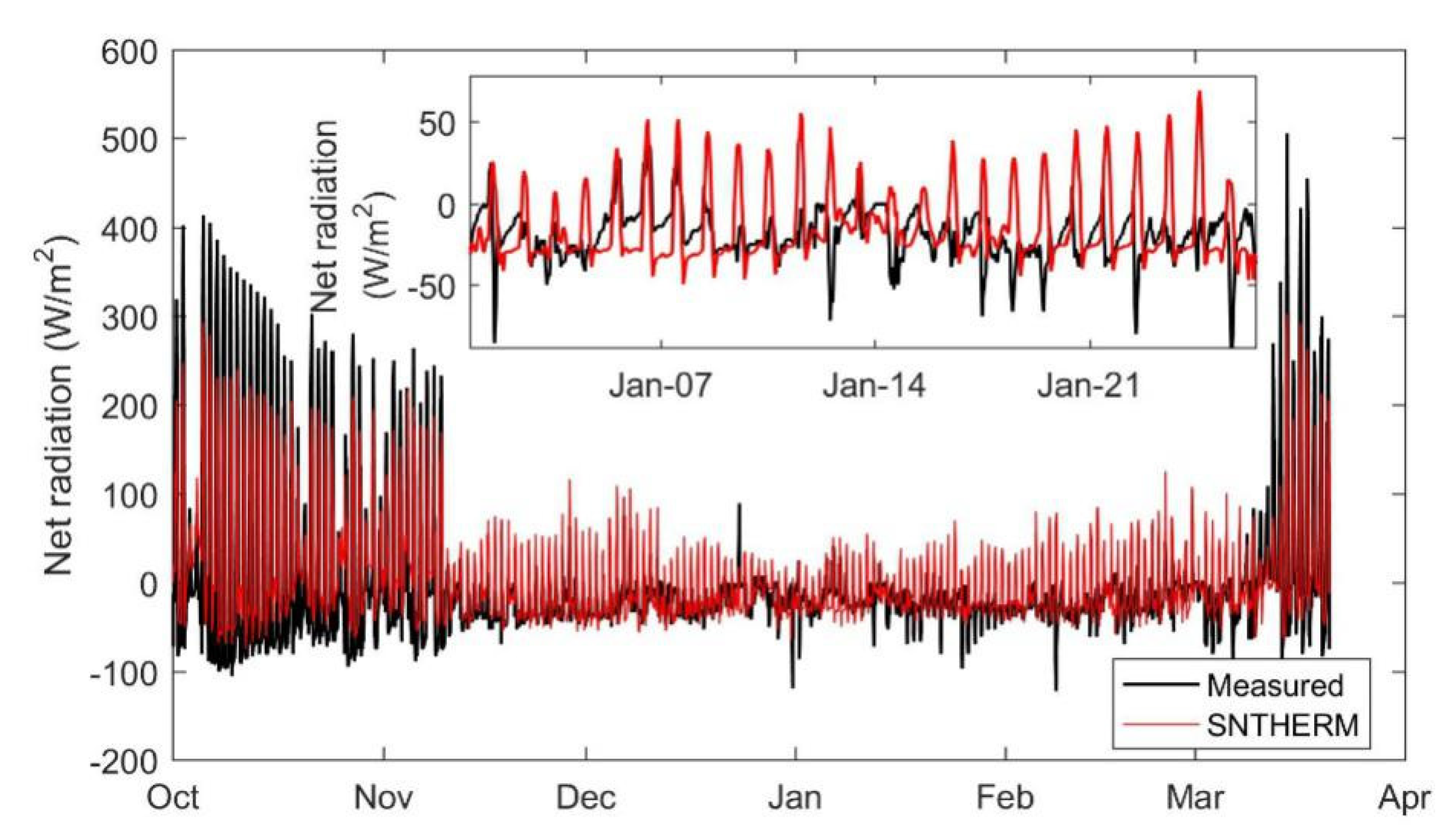
5.2. Evaluation the Use of GLDAS Downwelling Longwave Radiation
5.3. Error Analysis for the Brightness Temperature Simulation at 102 Stations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Minimum Bug Fixing Required for a Normal Operation of the SNTHERM89 Code
References
- Brucker, L.; Royer, A.; Picard, G.; Langlois, A.; Fily, M. Hourly simulations of the microwave brightness temperature of seasonal snow in Quebec, Canada, using a coupled snow evolution-emission model. Remote Sens. Environ. 2011, 115, 1966–1977. [Google Scholar] [CrossRef]
- Kim, R.S.; Durand, M.; Li, D.; Baldo, E.; Margulis, S.A.; Dumont, M.; Morin, S. Estimating alpine snow depth by combining multifrequency passive radiance observations with ensemble snowpack modeling. Remote Sens. Environ. 2019, 226, 1–15. [Google Scholar] [CrossRef]
- Sun, Z.W.; Yu, P.S.; Xia, L. Progress in study of snow parameter inversion by passive microwave remote sensing. Remote Sens. Land. Resour. 2015, 27, 9–15. [Google Scholar]
- Qu, X.; Hall, A. On the persistent spread in snow-albedo feedback. Clim. Dyn. 2014, 42, 69–81. [Google Scholar] [CrossRef]
- Essery, R.; Li, L.; Pomeroy, J. A distributed model of blowing snow over complex terrain. Hydrol. Process. 1999, 13, 2423–2438. [Google Scholar] [CrossRef]
- Brown, R.D.; Brasnett, B.; Robinson, D. Gridded North American monthly snow depth and snow water equivalent for GCM evaluation. Atmos. Ocean 2003, 41, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Hardiman, S.C.; Kushner, P.J.; Cohen, J. Investigating the ability of general circulation models to capture the effects of Eurasian snow cover on winter climate. J. Geophys. Res. Atmos. 2008, 113, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Gong, G. Land surface insulation response to snow depth variability. J. Geophys. Res. Atmos. 2010, 115, D08107. [Google Scholar] [CrossRef]
- Langlois, A.; Royer, A.; Derksen, C.; Montpetit, B.; Dupont, F.; Gota, K. Coupling the snow thermodynamic model SNOWPACK with the microwave emission model of layered snowpacks for subarctic and arctic snow water equivalent retrievals. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Essery, R. A factorial snowpack model (FSM 1.0). Geosci. Model Dev. 2015, 8, 3867–3876. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.L.; Dickinson, R.E.; Robock, A.; Vinnikov, K.Y. Validation of the snow submodel of the biosphere-atmosphere transfer scheme with Russian snow cover and meteorological observational data. J. Clim. 1997, 10, 353–373. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Bonan, G.B.; Flanner, M.G.; Kluzek, E.; Lawrence, P.J.; Levis, S.; Swenson, S.C.; Thornton, P.E. Technical Description of Version 4.0 of the Community Land Model (CLM); NCAR/TN-478 + STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2010; pp. 61–72. [Google Scholar]
- Dutra, E.; Balsamo, G.; Viterbo, P.; Miranda, P.M.A.; Beljaars, A.; Schar, C.; Elder, K. An improved snow scheme for the ECMWF land surface model: Description and offline validation. J. Hydrometeorol. 2010, 11, 899–916. [Google Scholar] [CrossRef]
- Douville, H.; Royer, J.F.; Mahfouf, J.F. A new snow parameterization for the Météo-France climate model: Part I: Validation in stand-alone experiments. Clim. Dyn. 1995, 12, 21–35. [Google Scholar] [CrossRef]
- Boone, A.A.; Etchevers, P. An intercomparison of three snow schemes of varying complexity coupled to the same land surface model: Local-scale evaluation at an alpine site. J. Hydrometeorol. 2001, 2, 374–394. [Google Scholar] [CrossRef] [Green Version]
- Best, M.J.; Pryor, M.; Clark, D.B.; Rooney, G.G.; Essery, R.L.H.; Ménard, C.B.; Edwards, J.M.; Hendry, M.A.; Porson, A.; Gedney, N.; et al. The Joint UK Land Environment Simulator (JULES), model description—Part 1: Energy and water fluxes. Geosci. Model Dev. 2011, 4, 677–699. [Google Scholar] [CrossRef] [Green Version]
- Cox, P.M.; Betts, R.A.; Bunton, C.B.; Essery, R.L.H.; Rowntree, P.R.; Smith, J. The impact of new land surface physics on the GCM simulation of climate and climate sensitivity. Clim. Dyn. 1999, 15, 183–203. [Google Scholar] [CrossRef]
- Wang, T.; Ottlé, C.; Boone, A.; Ciais, P.; Brun, E.; Morin, S.; Krinner, G.; Piao, S.; Peng, S. Evaluation of an improved intermediate complexity snow scheme in the ORCHIDEE land surface model. J. Geophys. Res. Atmos. 2013, 118, 6064–6079. [Google Scholar] [CrossRef]
- Verseghy, D.L. Canadian Land Surface Scheme for. Int. J. Climatol. 1991, 11, 111–133. [Google Scholar] [CrossRef]
- Vionnet, V.; Brun, E.; Morin, S.; Boone, A.; Faroux, S.; Le Moigne, P.; Martin, E.; Willemet, J.-M. The detailed snowpack scheme Crocus and its implementation in SURFEX v7.2. Geosci. Model Dev. 2012, 5, 773–791. [Google Scholar] [CrossRef] [Green Version]
- Lehning, M.; Bartelt, P.; Brown, B.; Fierz, C.; Satyawali, P. A physical SNOWPACK model for the Swiss avalanche warning Part II. Snow microstructure. Cold Reg. Sci. Technol. 2002, 35, 147–167. [Google Scholar] [CrossRef]
- Jordan, R.E. A One-Dimensional Temperature Model for a Snow Cover: Technical Documentation for SNTHERM.89; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1991. [Google Scholar]
- Lemmetyinen, J.; Pulliainen, J.; Rees, A.; Kontu, A.; Qiu, Y.; Derksen, C. Multiple-layer adaptation of HUT snow emission model: Comparison with experimental data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2781–2794. [Google Scholar] [CrossRef]
- Durand, M.; Kim, E.J.; Margulis, S.A.; Molotch, N.P. A first-order characterization of errors from neglecting stratigraphy in forward and inverse passive microwave modeling of snow. IEEE Geosci. Remote Sens. Lett. 2011, 8, 730–734. [Google Scholar] [CrossRef]
- Montpetit, B.; Royer, A.; Roy, A.; Langlois, A.; Derksen, C. Snow microwave emission modeling of ice lenses within a snowpack using the microwave emission model for layered snowpacks. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4705–4717. [Google Scholar] [CrossRef]
- Pan, J.; Jiang, L.; Zhang, L. Comparison of the multi-layer HUT snow emission model with observations of wet snowpacks. Hydrol. Process. 2014, 28, 1071–1083. [Google Scholar] [CrossRef]
- Li, D.; Durand, M.; Margulis, S.A. Large-scale high-resolution modeling of microwave radiance of a deep maritime alpine snowpack. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2308–2322. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Long, D.G. Volume-scattering models and land observations. In Microwave Radar and Radiometric Remote Sensing, 2nd ed.; The University of Michigan Press: Ann Arbor, MI, USA, 2014; pp. 461–548. [Google Scholar]
- Change, A.T.C.; Foster, J.L.; Hall, D. Nimbus-7 SMMR Derived Monthly Global Snow Cover and Snow Depth. Ann. Glaciol. 1987, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Royer, A.; Roy, A.; Montpetit, B.; Saint-Jean-Rondeau, O.; Picard, G.; Brucker, L.; Langlois, A. Comparison of commonly-used microwave radiative transfer models for snow remote sensing. Remote Sens. Environ. 2017, 190, 247–259. [Google Scholar] [CrossRef] [Green Version]
- Durand, M.; Kim, E.J.; Margulis, S.A. Quantifying uncertainty in modeling snow microwave radiance for a mountain snowpack at the point-scale, including stratigraphic effects. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1753–1767. [Google Scholar] [CrossRef]
- Kwon, Y.; Forman, B.A.; Ahmad, J.A.; Kumar, S.V.; Yoon, Y. Exploring the utility of machine learning-based passive microwave brightness temperature data assimilation over terrestrial snow in high Mountain Asia. Remote Sens. 2019, 11, 2265. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Margulis, S.A.; Durand, M.T.; Musselman, K.N. Assessment of snow grain-size model and stratigraphy representation impacts on snow radiance assimilation: Forward modeling evaluation. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4551–4564. [Google Scholar] [CrossRef]
- Sandells, M.; Essery, R.; Rutter, N.; Wake, L.; Leppänen, L.; Lemmetyinen, J. Microstructure representation of snow in coupled snowpack and microwave emission models. Cryosphere 2017, 11, 229–246. [Google Scholar] [CrossRef] [Green Version]
- Kang, D.H.; Tan, S.; Kim, E.J. Evaluation of Brightness Temperature Sensitivity to Snowpack Physical Properties Using Coupled Snow Physics and Microwave Radiative Transfer Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10241–10251. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Kontu, A.; Pulliainen, J.; Vehviläinen, J.; Rautiainen, K.; Wiesmann, A.; Mätzler, C.; Werner, C.; Rott, H.; Nagler, T.; et al. Nordic Snow Radar Experiment. Geosci. Instrum. Methods Data Syst. 2016, 5, 403–415. [Google Scholar] [CrossRef] [Green Version]
- Sturm, M.; Holmgren, J.; Liston, G.E. A seasonal snow cover classification system for local to global applications. J. Clim. 1995. [Google Scholar] [CrossRef] [Green Version]
- Mätzler, C. Relation between grain-size and correlation length of snow. J. Glaciol. 2002, 48, 461–466. [Google Scholar] [CrossRef] [Green Version]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Wiesmann, A.; Mätzler, C. Extension of the Microwave Emission Model of Layered Snowpacks to Coarse-Grained Snow. Remote Sens. Environ. 1999, 70, 317–325. [Google Scholar] [CrossRef]
- Corona, J.A.I.; Muñoz, J.; Lakhankar, T.; Romanov, P.; Khanbilvardi, R. Evaluation of the snow thermal model (SNTHERM) through continuous in situ observations of snow’s physical properties at the CREST-SAFE field experiment. Geosciences 2015, 5, 310–333. [Google Scholar] [CrossRef] [Green Version]
- Davis, R.E.; Hardy, J.P.; Ni, W.; Woodcock, C.; McKenzie, J.C.; Jordan, R.; Li, X. Variation of snow cover ablation in the boreal forest: A sensitivity study on the effects of conifer canopy. J. Geophys. Res. Atmos. 1997, 102, 29389–29395. [Google Scholar] [CrossRef]
- Pan, J.; Durand, M.; Sandells, M.; Lemmetyinen, J.; Kim, E.J.; Pulliainen, J.; Kontu, A.; Derksen, C. Differences between the HUT snow emission model and MEMLS and their effects on brightness temperature simulation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2001–2019. [Google Scholar] [CrossRef]
- Beaudoing, H.K.; Rodell, M. GLDAS Noah Land Surface Model L4 3 hourly 0.25 × 0.25 degree V2.1; NASA Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2016. Available online: https://disc.gsfc.nasa.gov/datacollection/GLDAS_NOAH025_3H_2.1.html (accessed on 30 April 2018).
- Brodzik, M.J.; Long, D.G.; Hardman, M.A.; Paget, A.; Armstrong, R. MEaSUREs Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR; Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar] [CrossRef]
- Tian, X.; Xie, Z.; Dai, A. A land surface soil moisture data assimilation system based on the dual-UKF method and the Community Land Model. J. Geophys. Res. 2008, 113, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Rawlins, M.A.; Nicolsky, D.J.; McDonald, K.C.; Romanovsky, V.E. Simulating soil freeze/thaw dynamics with an improved pan-Arctic water balance model. J. Adv. Model. Earth Syst. 2013, 5, 659–675. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Decharme, B.; Boone, A.; Delire, C.; Noilhan, J. Local evaluation of the Interaction between Soil Biosphere Atmosphere soil multilayer diffusion scheme using four pedotransfer functions. J. Geophys. Res. Atmos. 2011, 116, 1–29. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.M.; Lee, H. Improved simulation of the terrestrial hydrological cycle in permafrost regions by the Community Land Model. J. Adv. Model. Earth Syst. 2012, 4, 1–15. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Slater, A.G. Incorporating organic soil into a global climate model. Clim. Dyn. 2008, 30, 145–160. [Google Scholar] [CrossRef]
- Wei, S.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China data set of soil properties for land surface modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar] [CrossRef]
- Bi, H.; Ma, J.; Zheng, W.; Zeng, J. Comparison of soil moisture in GLDAS model simulations and in situ observations over the Tibetan Plateau. J. Geophys. Res. Atmos. 2016, 121, 2658–2678. [Google Scholar] [CrossRef] [Green Version]
- Montpetit, B.; Royer, A.; Wigneron, J.P.; Chanzy, A.; Mialon, A. Evaluation of multi-frequency bare soil microwave reflectivity models. Remote Sens. Environ. 2015, 162, 186–195. [Google Scholar] [CrossRef]
- Shi, J. An automatic algorithm on estimating sub-pixel snow cover from MODIS. Quat. Sci. 2012, 32, 6–15. [Google Scholar]
- Hao, S.; Jiang, L.; Shi, J.; Wang, G.; Liu, X. Assessment of MODIS-Based Fractional Snow Cover Products Over the Tibetan Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 533–548. [Google Scholar] [CrossRef]









| Parameters | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| SNTHERM soil modelling structure | Original SNTHERM89 code | New SNTHERM with soil water movement | New SNTHERM with soil water movement |
| Soil type | clay soil type | extended clay soil type with hydraulic parameters added | Altay site-specific soil type |
| Soil texture | Not determined | 22% sand, 20% silt, 58% clay | 35% sand, 46% silt, 19% clay |
| Specific density [kg/m3] | 2700 | ||
| Bulk density [kg/m3] | 1000 | 1323 | |
| Heat capacity [J·kg−1·K−1]1 | 800 | 832.4 | |
| Dry soil thermal conductivity [W·m−1·K−1] | 0.113 | 0.156 | |
| Thermal conductivity of dry solids [W·m−1·K−1] | 3.43 | 6.06 | |
| Plasticity index2 | 0.23 | 0.1 | |
| Soil albedo | 0.4 | ||
| Soil emissivity | 0.9 | ||
| Irreducible volumetric water content [m3/m3] | Not used | 0 | 0.004 |
| Saturated volumetric water content [m3/m3] | Not used | 0.36 | 0.42 |
| Saturated hydraulic conductivity [cm/min]4 | Not used | 0.00294 | 0.0164 |
| α [1/cm] 4 | Not used | 0.00855 | 0.348 |
| n | Not used | 1.08 | 1.50 |
| m | Not used | 0.07 | 0.33 |
| Initial soil temperature status | Temperature measurements at −5, −10, −15, −20, −40, −80, −160, and −320 cm depth | ||
| Soil temperature boundary condition | Time-varying temperature at −320 cm depth | ||
| Initial soil water content status | 10% volumetric water content for all layers | 10% volumetric water content for layers above −22 cm depth, and 20% for the layers below | |
| Soil water content status boundary condition | Constant bottom layer soil moisture | ||
| Error (K) | 6.925 V | 10.65 V | 18.7 V | 36.5 V | 6.925 H | 10.65 H | 18.7 H | 36.5 H |
|---|---|---|---|---|---|---|---|---|
| Simulated using snow pit measurements | 11.32 | 9.71 | 2.56 | 5.54 | 16.96 | 7.30 | 8.07 | 6.11 |
| (11.12) | (9.45) | (1.86) 1 | (−3.16) | (16.25) | (6.70) | (7.51) | (−3.51) | |
| Simulated using SNTHERM predictions with updated g1 | 10.58 | 9.75 | 3.24 | 4.43 | 11.85 | 5.30 | 7.40 | 6.37 |
| (10.30) | (9.59) | (2.75) | (3.37) | (10.46) | (2.55) | (5.91) | (0.95) | |
| Simulated using SNTHERM predictions with original g1 | 10.30 | 9.52 | 3.88 | 10.95 | 11.97 | 5.76 | 8.26 | 10.29 |
| (9.99) | (9.34) | (3.35) | (10.04) | (10.58) | (2.78) | (6.56) | (6.52) |
| Difference (Clay−AltaySoil) | Average Difference | Maximum Difference |
|---|---|---|
| Difference in 36.5 V TB caused by soil parameter inputs | −5.18 K | −9.98 K |
| Difference in 36.5 V TB caused by the influence of soil parameter inputs on Dmax | 0.78 K (with difference in average Dmax: −0.09 mm; bottom Dmax: 0.1 mm) | 4.66 K (with difference in average Dmax: −0.27 mm; bottom Dmax: 0.51 mm) |
| Difference in 36.5 V TB caused by different g1 * | 6.93 K | 14.06 K |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Pan, J.; Chang, S.; Xiong, C.; Shi, J.; Liu, M.; Che, T.; Wang, L.; Liu, H. Validation of the SNTHERM Model Applied for Snow Depth, Grain Size, and Brightness Temperature Simulation at Meteorological Stations in China. Remote Sens. 2020, 12, 507. https://doi.org/10.3390/rs12030507
Chen T, Pan J, Chang S, Xiong C, Shi J, Liu M, Che T, Wang L, Liu H. Validation of the SNTHERM Model Applied for Snow Depth, Grain Size, and Brightness Temperature Simulation at Meteorological Stations in China. Remote Sensing. 2020; 12(3):507. https://doi.org/10.3390/rs12030507
Chicago/Turabian StyleChen, Tao, Jinmei Pan, Shunli Chang, Chuan Xiong, Jiancheng Shi, Mingyu Liu, Tao Che, Lifu Wang, and Hongrui Liu. 2020. "Validation of the SNTHERM Model Applied for Snow Depth, Grain Size, and Brightness Temperature Simulation at Meteorological Stations in China" Remote Sensing 12, no. 3: 507. https://doi.org/10.3390/rs12030507
APA StyleChen, T., Pan, J., Chang, S., Xiong, C., Shi, J., Liu, M., Che, T., Wang, L., & Liu, H. (2020). Validation of the SNTHERM Model Applied for Snow Depth, Grain Size, and Brightness Temperature Simulation at Meteorological Stations in China. Remote Sensing, 12(3), 507. https://doi.org/10.3390/rs12030507