Next Article in Journal
Recognition of Water Colour Anomaly by Using Hue Angle and Sentinel 2 Image
Previous Article in Journal
Operational Monitoring and Damage Assessment of Riverine Flood-2014 in the Lower Chenab Plain, Punjab, Pakistan, Using Remote Sensing and GIS Techniques
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 4
10.3390/rs12040715
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Joint Inversion of GPS, Leveling, and InSAR Data for The 2013 Lushan (China) Earthquake and Its Seismic Hazard Implications

by
Zhicai Li
1,*,
Yangmao Wen
2,
Peng Zhang
1,
Yang Liu
2 and
Yong Zhang
2,3
1
Department of Geodesy, National Geomatics Center of China, Beijing 100830, China
2
School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
3
Department of Earthquake Monitoring and Predication, China Earthquake Administration, Beijing 100036, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(4), 715; https://doi.org/10.3390/rs12040715
Submission received: 7 January 2020 / Revised: 19 February 2020 / Accepted: 19 February 2020 / Published: 21 February 2020
Browse Figures
Versions Notes

Abstract

:
On 20 April 2013, a moment magnitude (Mw) 6.6 earthquake occurred in the Lushan region of southwestern China and caused more than 190 fatalities. In this study, we use geodetic data from nearly 30 continuously operating global positioning system (GPS) stations, two periods of leveling data, and interferometric synthetic aperture radar (InSAR) observations to image the coseismic deformation of the Lushan earthquake. By using the Helmert variance component estimation method, a joint inversion is performed to estimate source parameters by using these GPS, leveling, and InSAR data sets. The results indicate that the 2013 Lushan earthquake occurred on a blind thrust fault. The event was dominated by thrust faulting with a minor left-lateral strike–slip component. The dip angle of the seismogenic fault was approximately 45.0°, and the fault strike was 208°, which is similar to the strike of the southern Longmenshan fault. Our finite fault model reveals that the peak slip of 0.71 m occurred at a depth of ~12 km, with substantial slip at depths of 6–20 km. The estimated magnitude was approximately Mw 6.6, consistent with seismological results. Furthermore, the calculated static Coulomb stress changes indicate that the 2013 Lushan earthquake may have been statically triggered by the 2008 Wenchuan earthquake.

Graphical Abstract

1. Introduction

On 20 April 2013, an earthquake with a moment magnitude (Mw) of 6.6 struck Lushan County, Ya’an city, Sichuan Province, southwestern China, generating considerable economic losses in the local region [1,2]. The event was the result of a thrust earthquake that occurred in this area following the 2008 Mw 7.9 Wenchuan earthquake. The focal mechanism solution released by the United States Geological Survey (USGS) revealed a focal depth of approximately 12.3 km and a fault with a dip of 33° [3]. After this event, both near-field and far-field broadband digital seismic data were used to constrain the seismic source rupture process and focal mechanism in combination with other relevant information [4,5,6,7,8,9]. For example, Zhao et al. [5] used waveform data from the Global Seismographic Network (GSN)/Integrated Research Institutions for Seismology (IRIS), China Earthquake Networks Center (CENC) and Sichuan regional seismic network to perform a focal mechanism inversion; their findings indicated that the mainshock was a thrust earthquake that occurred on a fault with a dip of 45°. Liu et al. [6] reported that the main rupture asperity was located around the hypocenter with a range of ~28 km, and the peak slip was approximately 1.5 m. Considering the rupture source process, Wang et al. [9] reported that the dip was 38.5°, and the maximum slip occurred at depths of 10–12 km. However, no obvious surface rupture was observed in a field geological survey, and thus the Lushan earthquake was classified as a typical blind reverse-fault earthquake [10].
With an increasing amount of data, a variety of researchers have carried out a large number of inversions of the coseismic deformation associated with the 2013 event using global positioning system (GPS), leveling, interferometric synthetic aperture radar (InSAR), and strong motion and gravity data either separately or jointly [11,12,13,14,15,16,17,18,19,20]. For example, Jiang et al. [11] used observations from 33 continuously operating GPS (CGPS) stations to invert the coseismic slip distribution; their results suggested that the rupture was dominated by thrust faulting with a slight but still statistically significant left-lateral strike–slip component. Liu et al. [13] used InSAR data to image the coseismic deformation and calculated a further distributed slip model. Hao et al. [12] employed two campaigns of precise leveling observations across the southern section of the Longmenshan fault (LMSF) zone to quantify the coseismic vertical deformation and suggested that the seismogenic fault was dominated by a thrust component. Tan et al. [16] combined near-field coseismic offsets acquired both by continuously operating and by campaign GPS stations as well as seismic strong motion stations to reveal the rupture model and analyze its tectonic implications. Zhang et al. [18] jointly inverted local strong motion data and geodetic (including GPS and InSAR) measurements to obtain a robust model of the rupture process. Most recently, Huang et al. [20] performed a joint inversion with leveling, GPS, InSAR, and strong motion data to constrain the fault geometry and slip distribution.
Nevertheless, due to differences among the data sets, the findings of the previous studies all contrasted considerably with regard to the details of the fault geometry and coseismic slip distribution. The main difference among these results is the dip angle of the rupture plane, which varies by about 8°. This discrepancy may be attributed to the low spatial resolution of far-field seismic waveforms and an insufficient amount of near-field geodetic data. As a result, previous studies generally assumed that the rupture plane was rectangular with a single dip angle; thus, the geometry of the rupture surface at depth could not be finely constrained.
Strain accumulation and stress change due to the mainshock have also been rigorously discussed in previous researches [21,22,23,24]. For instance, Shan et al. [21] calculated the co- and post-seismic stress changes caused by the 2008 Mw 7.9 Wenchuan and 2013 Ms 7.0 Lushan earthquakes to investigate their relationship and the stress changes on the major faults in this region. Zhang et al. [18] found a Coulomb stress change of approximately 0.5 MPa that occurred on the secondary fault segments simultaneously with the initiation of coseismic slip on the main fault of the 2013 event, indicating that the slip was likely triggered by coseismic slip on the main blind thrust fault. In addition, Lin et al. [24] investigated the Coulomb stress changes during the 2017 Mw 6.5 Jiuzhaigou and 2013 Mw 6.6 Lushan earthquakes and discussed their relationships to the 2008 Wenchuan earthquake.
In this paper, in addition to the CGPS data as used in Jiang et al. [11], we collected measurement data from six CGPS stations (two of them situated atop the footwall of the seismogenic fault responsible for the 2013 Lushan earthquake); these GPS data will provide better constraints for the slip distribution inversion along the rupture plane. We first acquired CGPS observed coseismic deformation around the seismogenic fault area of the Lushan earthquake, as well as InSAR data and leveling data. Then, we adopted a two-step method to retrieve the source parameters associated with this event to determine the geometry of the seismogenic fault and to estimate the slip distribution along the fault plane using these GPS, leveling, and InSAR data. Finally, we calculated the Coulomb stress change based on our preferred slip model and discussed the relationship to the Wenchuan earthquake.

2. Tectonic Background

The Lushan earthquake occurred in a region characterized by complex tectonism to the immediate north of an area that can be referred to as a triple junction, with the Songpan–Ganzi block to the northwest, the Chuandian block to the southwest and the Sichuan Basin to the east [18] (Figure 1). The epicenter of the Lushan earthquake is located in the southern segment of the LMSF zone, which also hosted the 2008 Wenchuan Mw 7.9 earthquake to the northeast. The LMSF constitutes the boundary between the Songpan–Ganzi block and the Sichuan Basin; this boundary is characterized by crustal shortening caused by the southeastward movement of the Songpan–Ganzi block and collision with the South China Block [10]. The Songpan–Ganzi block is bounded by the Xianshuihe fault (XSHF) to the west, while to the south, the Anninghe fault (ANHF) separates the Chuandian block from the Sichuan Basin (Figure 1). Both the XSHF and the ANHF are large and active strike–slip faults with dextral strike–slip rates of >10 mm/yr and 3–8 mm/yr, respectively [25]. In contrast, the LMSF experiences movement of less than 3 mm/yr with both thrust and dextral strike–slip components, as determined from the surface geology and GPS measurements [26,27].
Through a field geological survey, the Lushan earthquake was classified as a typical blind reverse-fault earthquake [10]. Li et al. [28] found that the Lushan event was initiated along a detachment fault underneath the front range of the LMSF between the Shuangshi–Dachuan fault (SDF) and the Xinkaidian fault (XF) based on observations of surface cracks. Xu et al. [10] found several northeast-striking imbricate reverse faults in the southern segment of the LMSF, but no apparent earthquake surface rupture zones were located along these active faults or their adjacent areas. Based on an analysis of precisely relocated aftershocks, most aftershocks were confined to depths from 5 to 20 km, while few earthquakes occurred in the shallow crust [29].

3. Data and Methods

3.1. GPS Data

We collected nearly two years (2013–2014) raw GPS data from near-field GPS stations surrounding the epicenter of the Lushan earthquake managed by different agencies, including 10 permanent GPS sites from the Crustal Movement Observation Network of China, 10 regional CGPS stations deployed by Dr. Jiang from the China Earthquake Administration, two CGPS stations (YAAN and SCQL) from the Sichuan Provincial Seismological Bureau, and six CGPS stations constructed by the Sichuan Bureau of Surveying, Mapping and Geoinformation (SBSMG) (Figure 1, blue squares). Two sites (QLA1 and MINS) from the SBSMG were atop the footwall of the seismogenic fault, which we believe will provide better constraints on the fault distribution than those offered in previous researches [11,18,20].
We used BERNESE 5.2 software [32] to process the raw data, including the implementation of daily solutions and adjustments. The data processing of a daily solution mainly includes data preprocessing, baseline combination, eliminating integer ambiguities, and calculating free network solutions. Pseudorange and phase processing modes were adopted for the integer ambiguity elimination strategy with a quasi-ionosphere-free (QIF) wide-lane (WL) ambiguity resolution strategy based on the pseudorange and an L5 strategy based on the phase. To maintain the regional framework throughout China and establish a connection with the global framework during the daily solutions, six International Global Navigation Satellite System (GNSS) Service (IGS) stations throughout China and its adjacent areas, namely, BJFS, DAEJ, IISC, POL2, TCMS, and ULAB, were used to acquire joint daily solutions. During the daily network adjustment process, Solution Independent Exchange (SINEX) files of global daily solutions from the CODE Data Processing and Analysis Center were downloaded and converted into normal equation files, which were then superimposed onto the aforementioned normal equation files of daily solutions. By fixing the aforementioned six IGS stations and global framework stations, the regional daily solutions and global framework daily solutions were integrated. With the baseline constraint, all stations under the IGB08 framework were used as baseline framework points. Additionally, a priori unit weight mean error of all the reference points were set as 0.001 m for the baseline constraint [33,34,35]. For the least-square constraint, the global seven-parameter transformation method was adopted instead of the block adjustment three-parameter transformation method [36,37,38]. Finally, single-day net solution time series with high stability and high reliability were obtained. Figure 2 illustrates examples of the high-precision time series of LS05 and SCTQ, from which coseismic deformation can be clearly observed.
After acquiring high-precision single-day measurements, we calculated the coseismic deformation produced by the Lushan earthquake with a five-day daily position time series before and after the earthquake. By averaging the preseismic and postseismic positions and subtracting the latter from the former, we obtained the coseismic deformation in the region. Here, we subtracted the coseismic deformation and preseismic deformation from the postseismic deformation to define a new time series, and we propose using the standard deviation of this new time series to evaluate the coseismic deformation error. The weighted root mean squared (wrms) is as follows:
w r m s = n n − 1 ∑ i = 1 n ( y i − y ¯ ) 2 σ i 2 ∑ i = 1 n σ i − 2
where y i stands for the site position before or after the earthquake from the new time series, y ¯ describes its average, and n is the number of GPS observations in the new time series. The corresponding coseismic deformation error, rms, is calculated on the error propagation law as, r m s = w r m s p r e 2 + w r m s p o s t 2 . The coseismic deformation from these CGPS stations are documented in Table 1 and Figure 3a. The largest coseismic displacement was approximately 68.0 mm horizontally and 82.6 mm vertically at site LS05, which are in good agreement with the results from Jiang et al. [11].

3.2. Leveling Data

The leveling data is from the work of Hao et al. [12]. Here we just give a simple illustration of the leveling observation. A historical leveling line is located in the southwestern part of the study area across the LMSF starting at Jiajiang, after which it passes through Ya’an and Lushan and ends at Xiaojin in the southeast (Figure 1). With a length of approximately 294 km, this leveling line traverses the Xinkaidian fault (XF) and the Shuangshi–Dachuan (SDF) ruptures. The China State Bureau of Surveying and Mapping took first-order measurements from Jiajiang to Ya’an in October 1985 and from Ya’an to Xiaojin in July 1986. After the 2008 Wenchuan earthquake, the SBSMG carried out second-order leveling remeasurements along this route from April to November 2010 and embedded the benchmarks that ruptured during the earthquake. Based on these two periods of leveling measurement data, the vertical crustal deformation across the southern segment of the LMSF between 1985/1986 and 2008 was obtained. In 2013, the Second Crustal Deformation Monitoring Center, China Earthquake Administration, acquired first-order precise leveling measurements along the Ya’an–Baoxing route within three months after the Lushan earthquake struck Sichuan Province. Similarly, the vertical deformation was calculated along this route based on the two leveling data sets from 2010 and 2013. The calculated deformation also included the interseismic crustal deformation from 2010 to 2013 (prior to the occurrence of the Lushan earthquake) and the effects of afterslip and viscoelastic relaxation following the 2008 Wenchuan earthquake [12].
The following methods were employed by Hao et al. [12] to remove the impacts of crustal deformation before the Lushan earthquake first, they computed the interseismic vertical deformation rate by subdividing the vertical deformation during 1985–2010 by the time interval; next, they determined the corresponding vertical deformation from 2010 to 2013 and subtracted it from the two leveling data sets described above. Additionally, they adopted a cubic spline function to interpolate the interseismic vertical deformation rate of the newly added benchmarks during 2010 and 2013. By these means, they finally obtained the coseismic deformation of the Lushan earthquake according to leveling observations (Table 2 and Figure 4a). Based on theoretical estimates and analyses of the vertical deformation results in the cases of some earthquakes, including the 2008 Wenchuan earthquake, the postseismic vertical deformation caused by afterslip and viscoelastic relaxation in the lower crust was determined to range from approximately several millimeters to centimeters. Thus, these effects were disregarded when the coseismic deformation of the Lushan earthquake was calculated. For more details about instruments and data process strategy for the leveling observations, please refer to the work of Hao et al. [12].

3.3. InSAR Data

We employed Canada RADARSAT-2 single look complex (SLC) data to obtain the coseismic deformation of the Lushan earthquake along the satellite line of sight (LOS). Considering the coverage area and temporal–spatial baseline, we selected a pair of ascending SAR images, acquired on 10 January 2013 and 10 May 2013 with a perpendicular baseline of 186.3 m, to acquire the interferogram. The SAR data were processed by Switzerland GAMMA software [39] in two-pass differential interferometry mode [40]. The interferogram was corrected for the effects of topography using a 90-m-resolution Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) and MDA-provided orbit data. The interferograms were filtered using a power spectrum filter to reduce the effects of phase noise, unwrapped with the branch-cut method [41,42], and finally geocoded into the World Geodetic System 1984 (WGS84) coordinate system.
The interferograms resolve coseismic displacements only to the east of the Lushan epicenter, primarily in the Sichuan Basin and on the footwall of the thrust fault (Figure 5a). Large LOS signals were observed far from the fault in the Sichuan Basin, where an earthquake of this magnitude would not produce such significant coseismic ground displacements. These signals were likely caused by factors such as atmospheric turbulence. Excluding these errors, the InSAR-derived displacements qualitatively agree well with those observed by the GPS measurements. The standard deviation and decay distance estimated from a 1D covariance function [43] for the interferogram were 1.2 cm and 25.6 km, respectively.

4. Joint Inversion

Based on the coseismic deformation determined from the GPS, leveling, and InSAR measurements, we used an elastic half-space dislocation model [44] to retrieve the fault geometry and slip distribution of the Lushan earthquake. Here, a two-step method was adopted to estimate the source parameters associated with this event. The first step was to determine the geometry of the seismogenic fault by a nonlinear inversion method while assuming a uniform slip model composed of a rectangular fault plane. The second step was to estimate the slip distribution along the fault plane based on a linear inversion method.
The horizontal and vertical GPS coseismic displacements from 28 sites were adopted in the inversion. Their mean square errors in the east, north and vertical directions were 1.5 mm, 1.6 mm and 5 mm, respectively, as detailed in Table 1. Taking into account the computational efficiency and the feasibility of the inversion, a resolution-based downsampling method [45] was used to deduce the observations of the InSAR surface deformation field. Finally, 762 points with corresponding incidence and azimuth angles were derived from millions of observations.
The relative weighting ratio P i among the observed values in the joint inversion process was determined by the Helmert variance component estimation method [46] according to the corresponding mean square error σ i . The relative weighting ratio of the GPS horizontal deformation: GPS vertical deformation: leveling: InSAR observation was finally determined to be 1.000: 0.052: 0.021: 0.010.

4.1. Uniform Slip Inversion

During the nonlinear inversion, we employed a hybrid optimization algorithm based on multi-peak particle swarm optimization (M-PSO) [47] to retrieve the seismogenic fault parameters, including the fault position, strike, dip angle, length, depth, width, and slip. A Monte Carlo bootstrap method [48] was used to estimate the uncertainty of each fault parameter. Based on the statistical characteristics of the one-dimensional covariance function, the uncertainty of each fault parameter was estimated by using 100 combined observation data points with errors. Table 3 lists all the estimated fault parameters and their errors. The inversion results demonstrate that the errors were relatively small and that the seismogenic fault could be characterized by a blind fault with a dip of approximately 45° that generated an Mw 6.56 earthquake.

4.2. Distributed Slip Inversion

With the fault geometry determined, the slip distribution along the fault plane can be inverted based on classic elastic dislocation theory. The optimal fault was extended to 36 km along the strike and 40 km along the dip, and the fault plane was divided into 1440 patches, each with a size of 1 km × 1 km. The constrained least-square method was used to solve the objective function:
F ( s ) = ‖ G s − d ‖ 2 + κ 2 ‖ L s ‖ 2
where G is Green’s matrix, d represents the observation data, s is the slip of each patch, and L is the second-order finite difference approximation of the Laplace operator used to avoid a slip distribution characterized by nonphysical oscillations. κ 2 is a smoothing factor. In this study, we first analyzed the changing trends of the model roughness (ψ) and residuals (ξ) with the variation of smoothing weight [47]. To obtain the trade-off between the roughness (ψ) and residual (ξ), we built a Log-function f( κ ) = log(ψ + ξ), which indicated a single minimum at κ 2   = 2.5 (grey solid line in Figure 6).
Figure 7 shows the slip distributions and uncertainty based on the joint inversion of GPS, leveling, and InSAR observations. The results show that the seismogenic fault is mainly a thrust fault with a left-lateral strike–slip component. The total energy released was approximately 6.1 × 1018 Nm (Mw 6.58), which is comparable to that estimated in the GCMT catalog but greater than that predicted by the USGS. The maximum fault slip was 0.71 m at a depth of approximately 13 km (21–25 km wide), and the average slip error was approximately 2–3 cm.
Figure 3, Figure 4 and Figure 5 show the observed and simulated deformation and residuals for the GPS, leveling, and InSAR measurements, respectively, from the best-fitting slip model. Clearly, the coseismic deformation observed by the GPS, leveling, and InSAR observations can be effectively explained by the slip distribution model without any significant residual in the near field. The significant residuals of the interferogram are in the Sichuan Basin (Figure 5c), far from the epicenter, which is mainly attributed to the atmospheric effect. The standard deviations between the observed and simulated GPS, leveling, and InSAR values were 5.1 mm, 2.4 mm and 4.2 mm, respectively, from our joint inversion model.

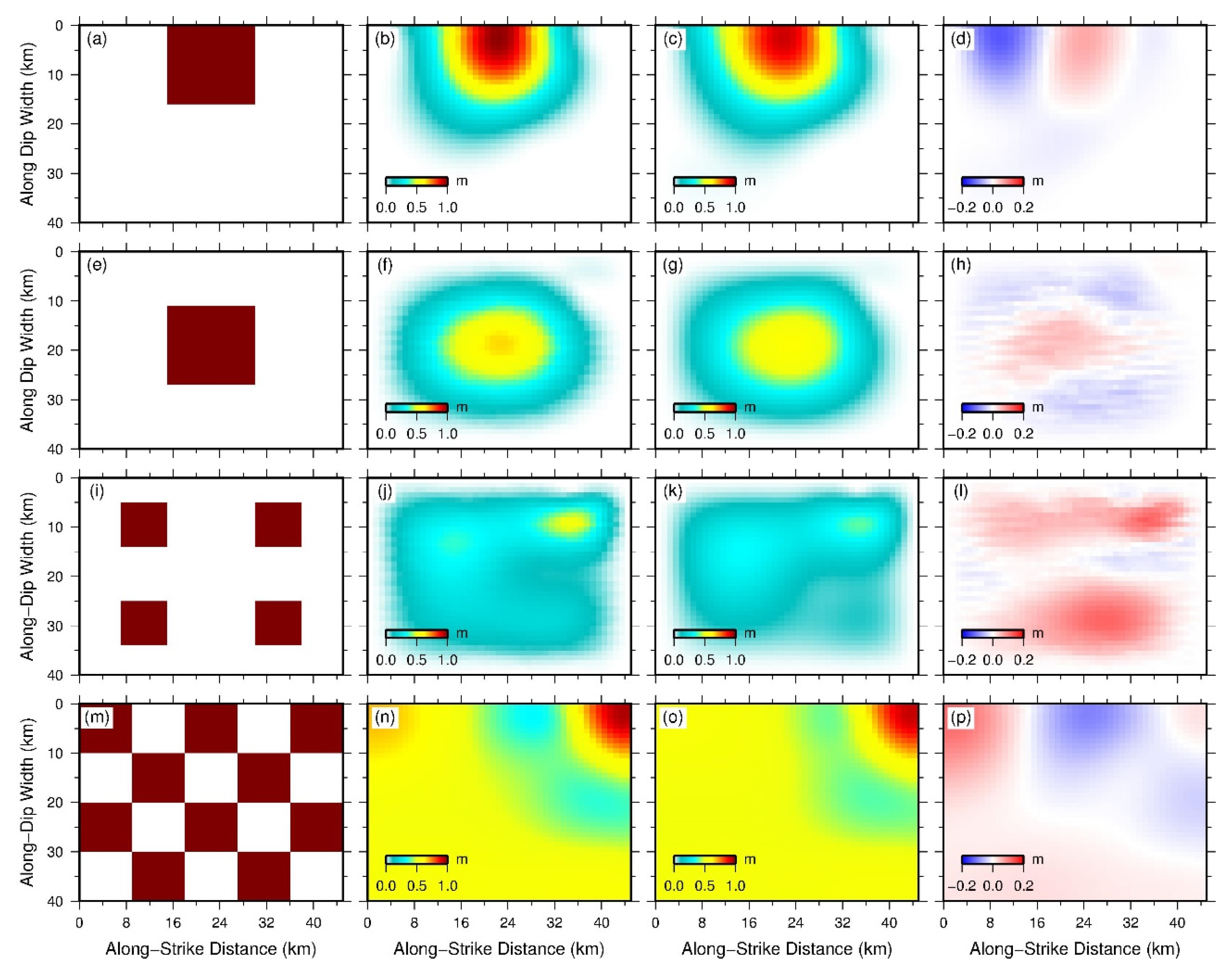
4.3. Checkerboard Tests

Additionally, to assess the reliability of the obtained slip model, we performed checkerboard tests, for which we first construct four kinds of input models: a model with single-patch at the shallowest subfaults, a model with single-patch at the middle subfaults, a model comprising four patches, and a 10-patch classic model (Figure 8a,e,i,m). For these models, the slip of each patch was set to 1 m with a rake angle of 90°. The checkerboard tests at the shallowest and middle subfaults were conducted to confirm high resolution at the surface to middle depth (Figure 8a,b,e,f). The tests also showed that the most of the slip patches were smeared in the retrieved slip distribution mode for the complex configurations (Figure 8i-p) while large asperity patch could be recovered easily in the resulting slip models (Figure 8a–h), which is similar to the result of Huang et al. [20]. Furthermore, the two new CGPS stations of QLA1 and MINS at the nearfield of the seismogenic fault were also tested to find whether they will affect the result of the slip distribution. We found that the QLA1 and MINS stations increased ~10% maximum slip (Figure 8d,h,l,p), which proved that two CGPS stations could provide more constraint to the slip distribution. These results suggest that the slip asperity of four or less patches can be well determined from the joint inversion of GPS, leveling, and InSAR observations.

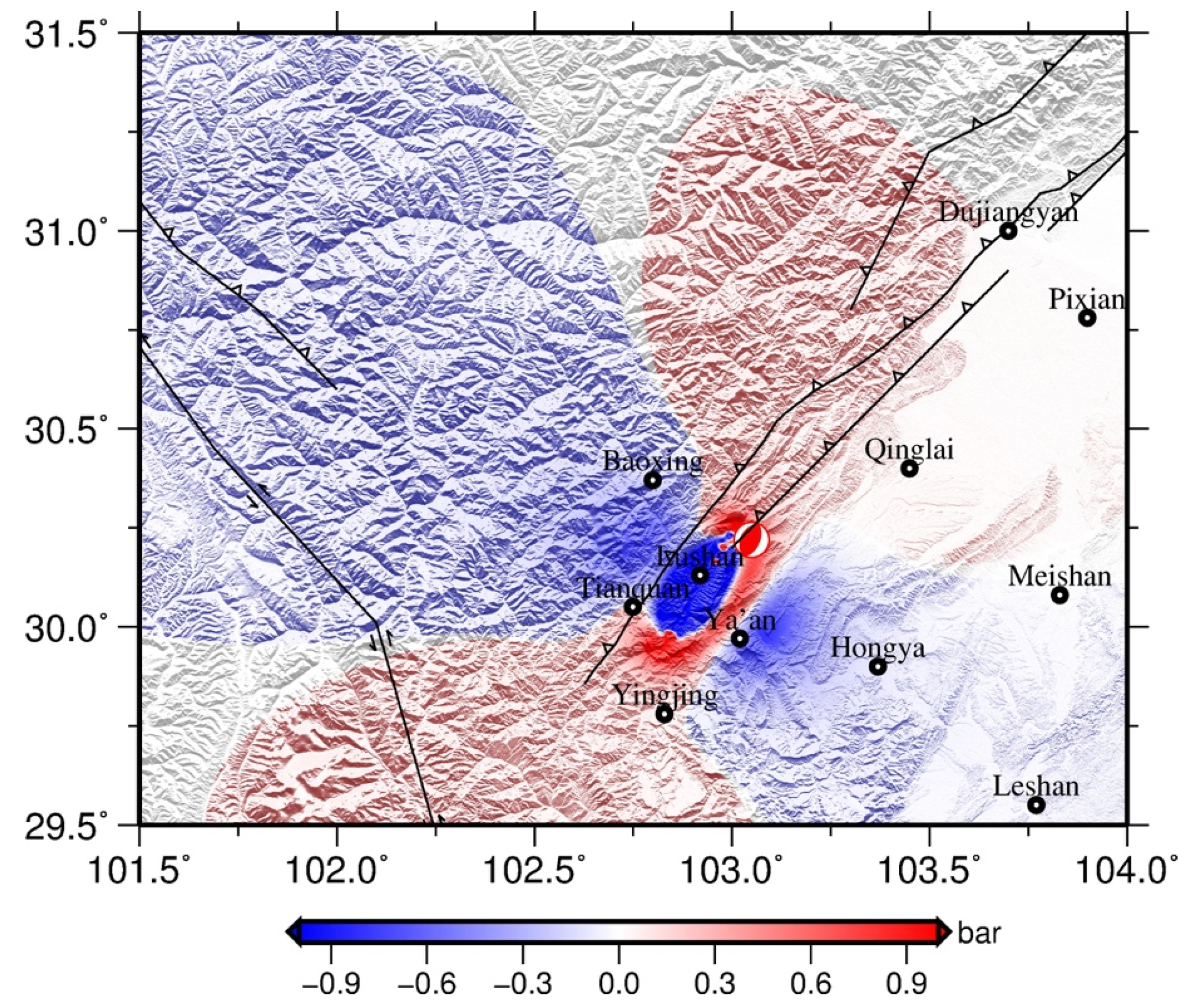
5. Coseismic Stress Changes

Variations in regional stresses due to coseismic displacements are likely affected by the surrounding faults and seismic activity. To estimate the stress field, we used the static Coulomb stress change method by King et al. [49]. According to Coulomb’s failure law, the static Coulomb failure stress Δ C F S on a given fault surface should obey the following formula:
Δ C F S = Δ τ + μ ′ Δ σ
where Δ τ is the variation in the shear stress parallel to the fault surface, Δ σ is the variation in the stress vertically perpendicular to the fault plane (release is represented as a positive value), and μ ′ is the friction coefficient. When the Coulomb stress increases, it will accelerate the rupture process on the fault plane; in contrast, when the Coulomb stress decreases, stress relief will occur, thereby suppressing fault rupture. It is worth noting that the Coulomb stresses that could trigger an earthquake are often smaller than tectonic stresses, and a Coulomb stress as low as 0.1 bar is sufficient to trigger an earthquake [49,50].
In this study, we used Coulomb v3.4 software [51], which was developed based on MATLAB, to calculate the variations in the static Coulomb stresses generated by the Lushan earthquake. The effective friction coefficient and shear elasticity modulus were set to be 0.4 and 3.32 × 1010 N/m2, respectively [52]. The specific fault parameters in our region of investigation, that is, the strike, dip, and rake, were 208°, 43°, and 83° (the same as the rupture fault), respectively, as determined from our inversion model (Table 3). The calculated Coulomb stress distribution at a depth of 13 km (which is nearly the depth of maximum slip) is shown in Figure 9, revealing that the Coulomb stress increased in the epicentral area by more than 0.45 bar.
Next, we calculated the stress changes on nearby active faults (Figure 1) caused by the Wenchuan and Lushan earthquakes. The parameters of these active faults were adopted from Table 2 of Shan et al. [53]. The Coulomb stress changes along the surrounding faults caused by the Wenchuan and Lushan earthquakes (both separately and jointly) are shown in Figure 10. As a result of the Wenchuan earthquake, the Coulomb stress changes increased on the following faults: the middle part of the XSHF, the Wenchuan–Qingchuan fault (WQF), the Longriba fault (LRBF), the Beichuan–Yingxiu fault (BYF), and the southern segment of the Pengxian–Guanxian fault (PGF) (Figure 10a). As a result of the Lushan earthquake, the Coulomb stress changes increased on the following faults: the PGF and the southern segment of the BYF (Figure 10b). From these increases in the Coulomb stress changes, we can conclude that the Coulomb stress changes accumulated mainly along the PGF due to the Wenchuan earthquake, although we further deduce that the Lushan earthquake ultimately ruptured the PGF (Figure 10c).

6. Discussion

Using GPS, leveling, and InSAR data, the fault geometry and slip characteristics of the 2013 Lushan earthquake (Table 3) were retrieved based on an elastic half-space dislocation model. This investigation presents the full application of high-quality geodetic observations in the study area. From the joint inversion of geodetic data, our model indicates that a one-segment fault is good for fitting the observed near-field deformation (Figure 3, Figure 4 and Figure 5). The observed and modeled displacements from the GPS, InSAR, and leveling data were well fit, especially in the footwall of the seismogenic fault, due to the addition of observations from six CGPS stations. The findings agree well with those of Jiang et al. [11] and Huang et al. [20] but differ from those of Zhang et al. [18]. Jiang et al. [11] found that a one-segment fault geometry based on a layered half-space model [54] can be fit well with CGPS observations, while Zhang et al. [18] reported that a four-segment fault geometry based on a homogeneous elastic half-space model can be fit well when constrained by both CGPS and InSAR data. Huang et al. [20] used GPS, InSAR, leveling, and strong motion data to study different fault geometries based on a homogeneous elastic half-space model and a layered half-space model separately, based on the data residuals, and found that a one-segment fault model constrained by GPS and leveling data can provide a better fit in the near field than other fault models.
Because of the availability of more near-field CGPS observations from the footwall of the seismogenic fault, our slip distribution model precludes the presence of obvious deformation in the upper crust (Figure 7) and demonstrates that the seismogenic fault is a blind thrust fault, which is in agreement both with the geological survey by Xu et al. [10] and with the study of Huang et al. [20] but different from the results from Jiang et al. [11] and Zhang et al. [18]. Huang et al. [20] verified that their slip distribution model yields no slip on the subfault patches near the surface, while the models developed by Jiang et al. [11] and Zhang et al. [18] presented coseismic slip on the near-surface subfaults. Our checkerboard tests also confirmed that there was no significant slip near the surface (Figure 8). Wen et al. [55] studied the asperities on the deep part of the seismogenic fault responsible for the 2015 Pishan earthquake in Xinjiang; they reported the presence of partial ruptures on the ramp fault at depths of 14–18 km that truncate the strata from the Paleozoic to the bottom of the Paleocene and transfer slip from the Proterozoic decollement beneath the area to the shallow Eocene layer beneath the Tarim Basin. Our research proves that the 2013 Lushan Mw 6.6 earthquake occurred along a blind thrust fault in a boundary zone between the Longmenshan fault and Sichuan Basin. These two moderate earthquakes, namely, the Pishan and Lushan events, illustrate that crustal material migrates outward from the deformed front within the Tibetan Plateau, causing lateral compression.
The centroid depth based on the uniform slip model was 7.4 km, and the maximum slip occurred at a depth of ~12 km. These depths are shallower than those reported by the GCMT and USGS but are basically consistent with the GPS-derived results by Jiang et al. [11], with the main slip occurring at a depth of 13 km. One reason for this discrepancy is the variability of the local crust throughout a seismic array. In this paper, a homogeneous and elastic half-space model was adopted, but this model represents only a first-order approximation of the real crust. Moreover, in some cases, the focal depth of a layered crustal model is shallower than that of a half-space model [56]. A second possible reason is that the depth of the focal mechanism is the initial rupture depth, while the modeled depth is the centroid depth or peak slip depth of the fault. Based on over 80 finite-hypocenter rupture models of more than 50 large earthquakes, Mai et al. [57] concluded that shallow crustal ruptures tend to propagate upward from deeper layers along the fault plane. Another explanation for the shallow centroid depth of the model in this paper is the distribution of ground measurements. Near-field and far-field deformation are induced by seismic waves; in our model, near-field (0-100 km) observations, including InSAR, GPS, and leveling data, were used to provide strong constraints on the shallow slip distribution along the fault.
The optimal slip model shows that the rupture of the 2013 Lushan earthquake was dominated by thrust faulting (with an 11% left-lateral strike–slip component), which is in agreement with two previous geodetic inversions [11,20] but disagrees with the findings of Zhang et al. [18]. The main reason for this may be that our model employs a one-segment fault geometry to perform the inversion, similar to the models of Jiang et al. [11] and Huang et al. [20], while Zhang et al. [18] utilized four subfaults. The peak slip in our study was characterized by a 0.66 m thrust component and a 0.08 m left-lateral strike–slip component with a dip angle of approximately 45°; these values are larger than the thrust component (0.57 m) and smaller than the left-lateral strike–slip component (0.20 m) of Jiang et al. The difference between these two models is affected mainly by the different geodetic data sets used. We employed GPS, leveling, and InSAR data to perform our joint inversion, while the model of Jiang et al. used only GPS data. Our maximum fault slip was approximately 0.71 m at a depth of approximately 13 km, which agrees well with the maximum slip of Jiang et al. (0.61 m) but is less than the maximum slip of both Huang et al. (1.2 m) and Zhang et al. (1.61 m) [11,18,20]. The total energy released was approximately 6.1 × 1018 Nm, which is close to that of Huang et al. (7.63 × 1018 N m) but 30% smaller than that of Jiang et al. (9.5 × 1018 N m), and 67% smaller than that of Zhang et al. (1.8 × 1019 N m). Again, the differences among these studies may be affected by the different data sets. We utilized 2 CGPS stations on the footwall of the seismogenic fault, and these stations are very close to the epicenter; this may provide better constraints on the inversion than other studies, leading to a lower moment.
The changes in the ΔCFS calculated from the uniform slip model and the slip distribution model show that the Coulomb stress increased in the epicentral area by more than 0.45 bar (shown in Figure 9), which is larger (by more than 0.3 bar) than the increase in the epicentral area reported by Lin et al. [24] using teleseismic broadband waveforms. We depict the stress changes on nearby active faults caused by the Wenchuan and Lushan earthquakes in Figure 10. Following the Lushan earthquake, the CFS increased on the PGF and BYF by nearly 0.1 bar and 0.2 bar, respectively, which agree well with the results of Lin et al. [24]; it is possible that this stress change will result in future earthquakes. Following the Wenchuan earthquake, the CFS increased on the following faults (as shown in Figure 10a): the middle part of the XSHF, the WQF, the LRBF, the BYF and the southern segment of the PGF. Our results demonstrate that the Wenchuan earthquake increased the CFS by up to 0.2 bar at the hypocenter of the Lushan earthquake, which exceeded the threshold value (0.1 bar) of earthquake triggering [58]. Lin et al. [24] found that the Wenchuan earthquake had a significant impact on the surrounding area and verified that the Lushan earthquake was probably promoted (possibly triggered) by the 2008 Wenchuan earthquake. There were few aftershocks or smaller events about Mw 6 that occurred in this area between the 2008 Wenchuan and 2013 Lushan events. The coseismic static Coulomb stress changes induced by these small events would not significantly affect the stress distribution pattern in the studied area, such as the 2017 Mw 6.5 Jiuzhaigou earthquake [24].

7. Conclusions

In this study, the fault geometry and slip distribution of the 2013 Lushan earthquake were inverted by jointly using GPS, leveling, and InSAR data. We investigated the rupture parameters of the seismogenic fault by employing the Helmert variance component estimation method to determine the relative weighting ratio among the GPS, leveling, and InSAR observations.
The inversion demonstrated that the 2013 Mw 6.6 Lushan earthquake occurred along a blind thrust fault, which was dominated by thrust faulting with a minor left-lateral strike–slip component. The dip angle of the seismogenic fault was approximately 45.0°, and the fault strike was 208°, which is generally consistent with the strike of the southern LMSF. The slip was concentrated mainly at depths of 6–20 km and the peak slip was 0.71 m, which occurred at a depth of approximately 12 km. The estimated moment magnitude was approximately Mw 6.6, which is consistent with the results from seismological studies but smaller than other geodetic inversions.
Finally, we calculated the static Coulomb stress changes triggered by the Lushan and Wenchuan earthquakes. The results show that the Lushan event increased the static Coulomb stress changes in the epicentral area by more than 0.45 bar. In addition, the Coulomb stress changed by the Wenchuan earthquake due to surrounding faults increased the stress by up to 0.2 bar at the hypocenter of the Lushan earthquake, confirming that the Lushan earthquake was probably promoted by the 2008 Wenchuan earthquake.

Author Contributions

Z.L. and Y.W. conceived and designed the experiments; Z.L. and P.Z. performed and analyzed the experiments; Z.L., Y.W., P.Z., and Y.L. wrote the paper; Y.Z. performed the data processing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was co-supported by the National Key Research and Development Program of China (No. 2016YFB0501405) and the National Natural Science Foundation of China (Nos. 41274030, 41774011, 41874011, 41974004).

Acknowledgments

We wish to acknowledge two anonymous reviewers for their comments and suggestions on improving the manuscript. We appreciate the GPS observations from the Crustal Movement Observation Network of China, Zaiseng Jiang of the China Earthquake Administration, the Sichuan Provincial Seismological Bureau, and the Sichuan Bureau of Surveying, Mapping and Geoinformation. We thank Ming Hao at the Second Monitoring Center, China Earthquake Administration, for providing the leveling data. All figures were constructed using Generic Mapping Tools (GMT) version 4.5.1 [59].

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Chen, X.; Cui, P.; You, Y.; Yang, Z.; Kong, Y. Secondary mountain disasters induced by the 4·20 Lushan earthquake and disaster mitigation. Earth Sci. Front. 2013, 20, 29–30. (In Chinese) [Google Scholar]
  2. Liu, J.; Yi, G.; Zhang, Z.W.; Guan, Z.J.; Ruan, X.; Long, F.; Du, F. Introduction to the Lushan, Sichuan M7.0 earthquake on 20 April 2013. Chin. J. Geophys. 2013, 56, 1404–1407. (In Chinese) [Google Scholar] [CrossRef]
  3. USGS. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/usb000gcdd/executive (accessed on 10 November 2019).
  4. Zhang, Y.; Xu, L.S.; Chen, Y.T. Rupture process of the Lushan 4.20 earthquake and preliminary analysis on the disaster-causing mechanism. Chin. J. Geophys. 2013, 56, 1408–1411. (In Chinese) [Google Scholar] [CrossRef]
  5. Zhao, B.; Gao, Y.; Huang, Z.B.; Zhao, X.; Li, D.H. Double difference relocation, focal mechanism and stress inversion of Lushan Ms 7.0 earthquake sequence. Chin. J. Geophys. 2013, 56, 3385–3395. (In Chinese) [Google Scholar] [CrossRef]
  6. Liu, R.F.; Chen, Y.T.; Zou, L.Y.; Chen, S.F.; Liang, J.H.; Zhang, L.W.; Han, X.J.; Ren, X.; Sun, L. Determination of parameters for the 20 April 2013 Lushan Mw6.7 (Ms7.0) earthquake in Sichuan Province. Acta Seismol. Sin. 2013, 35, 652–660. (In Chinese) [Google Scholar]
  7. Liu, C.; Zheng, Y.; Ge, C.; Xiong, X.; Hsu, H. Rupture process of the Ms7.0 Lushan earthquake, 2013. Sci. China Earth Sci. 2013, 56, 1187–1192. [Google Scholar] [CrossRef]
  8. Xu, X.; Chen, G.; Yu, G.H.; Cheng, J.; Xi-Bin, T.; Zhu, A.; Wen, X.-Z. Seismogenic structure of Lushan earthquake and its relationship with Wenchuan earthquake. Earth Sci. Front. 2013, 20, 11–20. (In Chinese) [Google Scholar]
  9. Wang, W.; Hao, J.L.; Yao, Z.X. Preliminary result for rupture process of Apr. 20, 2013, Lushan Earthquake, Sichuan, China. Chin. J. Geophys. 2013, 56, 1412–1417. (In Chinese) [Google Scholar] [CrossRef]
  10. Xu, X.; Wen, X.; Han, Z.; Chen, G.; Li, C.; Zheng, W.; Zhang, S.; Ren, Z.; Xu, C.; Tan, X.; et al. Lushan MS7.0 earthquake: A blind reserve-fault event. Chin Sci Bull. 2013, 58, 3437–3443. [Google Scholar] [CrossRef] [Green Version]
  11. Jiang, Z.; Wang, M.; Wang, Y.; Wu, Y.; Che, S.; Shen, Z.; Bürgmann, R.; Sun, J.; Yang, Y.; Liao, H.; et al. GPS constrained coseismic source and slip distribution of the 2013 Mw6.6 Lushan, China, earthquake and its tectonic implications. Geophys. Res. Lett. 2014, 41, 407–413. [Google Scholar] [CrossRef]
  12. Hao, M.; Wang, Q.; Liu, L.; Shi, Q. Interseismic and coseismic displacements of the Lushan Ms7.0 earthquake inferred from leveling measure-ments. Chin. Sci. Bull. 2014, 59, 5129–5135. [Google Scholar] [CrossRef]
  13. Liu, Y.; Wang, C.; Shan, X.; Zhang, G.; Qu, C. Result of SAR differential interferometry for the co-seismic deformation and source parameter of the Ms7.0 Lushan earthquake. Chin. J. Geophys. 2014, 57, 2495–2506. [Google Scholar] [CrossRef]
  14. Deng, M.; Sun, H.; Xu, J.; Zhu, Y. Theoretical simulation of co-seismic and post-seismic deformations and gravity changes of Lushan earthquake. Earth Sci. J. China Univ. Geosci. 2014, 39, 1373–1382. (In Chinese) [Google Scholar] [CrossRef]
  15. Yang, G.H.; Zhu, S.; Liang, H.; Yang, B. Pre-seismic and co-seismic deformation of Ms 7.0 earthquake in Lushan. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 121–127. (In Chinese) [Google Scholar]
  16. Tan, K.; Wang, Q.; Ding, K.; Li, H.; Zou, R.; Nie, Z.S.; Wang, D.; Yang, S.; Qiao, X. Rupture models of the 2013 Lushan earthquake constrained by near field displacements and its tectonic implications. Chin. J. Geophys. Chin. Ed. 2015, 58, 3169–3182. (In Chinese) [Google Scholar] [CrossRef]
  17. Liu, Q.; Wen, X.Z.; Shao, Z.G. Joint inversion for coseismic slip of the 2013 MS7.0 Lushan earthquake from GPS, leveling and strong motion observations. Chin. J. Geophys. 2016, 59, 2113–2125. (In Chinese) [Google Scholar] [CrossRef]
  18. Zhang, G.; Hetland, E.; Shan, X.; Martin, V.; Liu, Y.; Zhang, Y.; Qu, C. Triggered slip on a back reverse fault in the Mw6.8 2013 Lushan, China earthquake revealed by joint inversion of local strong motion accelerograms and geodetic measurements. Tectonophysics 2016, 672–673, 24–33. [Google Scholar] [CrossRef] [Green Version]
  19. Xu, C.J.; Zhou, L.X.; Yin, Z. Construction and geodesy slip inversion analysis of 2013 Ms 7.0 Lushan in China earthquake’s curved fault model. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 1665–1672. (In Chinese) [Google Scholar]
  20. Huang, Y.; Qiao, X.; Freymueller, J.T.; Wang, Q.; Yang, S.; Tan, K.; Zhao, B. Fault geometry and slip distribution of the 2013 Mw 6.6 Lushan earthquake in China constrained by GPS, InSAR, leveling, and strong motion data. J. Geophys. Res. Solid Earth 2019, 124, 7341–7353. [Google Scholar] [CrossRef]
  21. Shan, B.; Xiong, X.; Zheng, Y.; Diao, F. Stress changes on major faults caused by 2013 Lushan earthquake, and its relationship with 2008 Wenchuan earthquake. Sci. China Earth Sci. 2013. (In Chinese) [Google Scholar] [CrossRef]
  22. Wang, M.; Jia, D.; Shaw, H.J.; Hubbard, J.; Plesch, A.; Li, Y.; Liu, B. The 2013 Lushan earthquake: Implications for seismic hazards posed by the range front blind thrust in the Sichuan basin, China. Geology 2014, 42, 915–918. [Google Scholar] [CrossRef] [Green Version]
  23. Wang, Z.; Su, J.; Liu, C.; Cai, X. New insights into the generation of the 2013 Lushan Earthquake (Ms 7.0), China. J. Geophys. Res. Solid Earth 2015, 120, 3507–3526. [Google Scholar] [CrossRef]
  24. Lin, X.; Chu, R.; Zeng, X. Rupture processes and Coulomb stress changes of the 2017 Mw 6.5 Jiuzhaigou and 2013 Mw 6.6 Lushan earthquakes. Earth Planets Space 2019, 71, 81. [Google Scholar] [CrossRef]
  25. Wang, Y.; Wang, E.; Shen, Z.; Wang, M.; Gan, W.; Qiao, X.; Meng, G.; Li, T.; Tao, W.; Yang, Y.; et al. GPS-constrained inversion of present-day slip rates along major faults of the Sichuan–Yunnan region. China Sci. China Earth Sci. 2008, 51, 1267–1283. [Google Scholar] [CrossRef]
  26. Densmore, A.L.; Ellis, M.A.; Li, Y.; Zhou, R.; Hancock, G.S.; Richardson, N. Active tectonics of the Beichuan and Pengguan faults at the eastern margin of the Tibetan Plateau. Tectonics 2007, 26, TC4005. [Google Scholar] [CrossRef] [Green Version]
  27. Shen, Z.; Lu, J.; Wang, M.; Burgmann, R. Contemporary crustal deformation around southeast borderland of Tibetan plateau. J. Geophys. Res. 2005, 110, B11409. [Google Scholar] [CrossRef] [Green Version]
  28. Li, Y.; Jia, D.; Wang, M.; Shaw, J.; He, J.; Lin, A.; Xiong, L.; Rao, G. Structural geometry of the source region for the 2013 Mw 6.6 Lushan earthquake: Implication for earth- quake hazard assessment along the Longmen Shan. Earth Planet. Sci. Lett. 2014, 390, 275–286. [Google Scholar] [CrossRef]
  29. Fang, L.; Wu, J.; Wang, W.; Du, W.; Su, J.; Wang, C.; Cai, Y. Aftershock observation and analysis of the 2013 Ms 7.0 Lushan earthquake. Seismol. Res. Lett. 2015, 86, 1135–1142. [Google Scholar] [CrossRef] [Green Version]
  30. Ziewonski, A.M.; Chou, T.A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
  31. Ekström, G.; Nettles, M.; Dziewonski, A.M. The global CMT project 2004-2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200–201, 1–9. [Google Scholar] [CrossRef]
  32. Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2. In User Manual, Astronomical Institute, University of Bern; Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar] [CrossRef]
  33. Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
  34. Yao, Y.B. Research on the Alorithm and Realization of Post-Processing for GPS Precise Positioning and Orbit Determination; Wuhan University: Wuhan, China, 2004. [Google Scholar]
  35. Gao, C.; Zhao, Y.; Wan, D. The weight determination of the double difference observation in GPS carrier phase positioning. Sci. Surv. Mapp. 2005, 30, 28–32. [Google Scholar]
  36. Borkowski, K.M. Accurate algorithms to transform geocentric to geodetic coordinates. Bull. Géod. 1989, 63, 50–56. [Google Scholar] [CrossRef]
  37. Wang, J.X. Correlations among parameters in seven-parameter transformation model. J. Geod. Geodyn. 2007, 27, 43–46. [Google Scholar]
  38. Li, J.L.; Liu, L.; Qiao, S.B.; Guo, L. Discussion on the determination of transformation parameters of 3D cartesian coordinates. Sci. Surv. Mapp. 2010, 35, 76–78. [Google Scholar]
  39. Werner, C.; Wegmller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and Interferometric Processing Software. In Proceedings of the ERS-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2001. [Google Scholar]
  40. Rosen, P.A.; Hensley, S.; Peltzer, G.; Simons, M. Updated repeat orbit interferometry package released. EOS Trans. Am. Geophys. Union 2004, 85, 47. [Google Scholar] [CrossRef]
  41. Goldstein, R.; Werner, C. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
  42. Goldstein, R.; Zebker, H.; Werner, C. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef] [Green Version]
  43. Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
  44. Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
  45. Lohman, R.B.; Simons, M. Some thoughts on the use of InSAR data to constrain models of surface deformation: Noise structure and data downsampling. Geochem. Geophys. Geosyst. 2005, 6, 359–361. [Google Scholar] [CrossRef]
  46. Xu, C.; Liu, Y.; Wen, Y.; Wang, R. Coseismic slip distribution of the 2008 Mw 7.9 Wenchuan earthquake from joint inversion of GPS and InSAR data. Bull. Seismol. Soc. Am. 2010, 100, 2736–2749. [Google Scholar] [CrossRef]
  47. Feng, W.; Li, Z.; Elliott, J.R.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z. The 2011 MW 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef] [Green Version]
  48. Parsons, B.; Wright, T.; Rowe, P.; Andrews, J.; Jackson, J.; Walker, R.; Khatib, M.; Talebian, M.; Bergman, E.; Engdahl, E. The 1994 Sefidabeh (eastern Iran) earthquakes revisited: New evidence from satellite radar interferometry and carbonate dating about the growth of an active fold above a blind thrust fault. Geophys. J. Int. 2006, 164, 202–217. [Google Scholar] [CrossRef] [Green Version]
  49. King, G.C.P.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 78, 935–953. [Google Scholar]
  50. Ziv, A.; Rubin, A.M. Static stress transfer and earthquake triggering: No lower threshold in sight? J. Geophys. Res. Solid Earth 2000, 105, 13631–13642. [Google Scholar] [CrossRef]
  51. Toda, S.; Stein, R.S.; Richards-Dinger, K.; Bozkurt, S.B. Forecasting the evolution of seismicity in southern California: Animations built on earthquake stress transfer. J. Geophys. Res. Solid Earth 2005, 110, 361–368. [Google Scholar] [CrossRef]
  52. Steck, L.K.; Phillips, W.S.; Mackey, K.; Begnaud, M.L.; Stead, R.J.; Rowe, C.A. Seismic tomography of crustal P and S across Eurasia. Geophys. J. Int. 2009, 177, 81–92. [Google Scholar] [CrossRef] [Green Version]
  53. Shan, B.; Xiong, X.; Zheng, Y.; Diao, F. Stress changes on major faults caused by Mw7.9 Wenchuan earthquake, May 12, 2008. Sci. China Earth Sci. 2013, 52, 593–601. [Google Scholar] [CrossRef]
  54. Wang, R.; Lorenzo-Martín, F.; Roth, F. PSGRN/PSCMP—A new code for calculating co-and post-seismic deformation, geoid and gravity changes based on the viscoelastic-gravitational dislocation theory. Comput. Geosci. 2006, 32, 527–541. [Google Scholar] [CrossRef] [Green Version]
  55. Wen, Y.; Xu, C.; Liu, Y.; Jiang, G. Deformation and source parameters of the 2015 Mw 6.5 earthquake in Pishan, Western China, from Sentinel-1A and ALOS-2 data. Remote Sens. 2016, 8, 134. [Google Scholar] [CrossRef] [Green Version]
  56. Jiang, G.; Wen, Y.; Liu, Y.; Xu, X.; Fang, L.; Chen, G.; Gong, M.; Xu, C. Joint analysis of the 2014 Kangding, southwest China, earthquake sequence with seismicity relocation and InSAR inversion. Geophys. Res. Lett. 2015, 42, 3273–3281. [Google Scholar] [CrossRef]
  57. Mai, P.M.; Spudich, P.; Boatwright, J. Hypocenter locations in finite-source rupture models. Bull. Seismol. Soc. Am. 2005, 95, 965–980. [Google Scholar] [CrossRef]
  58. Ma, K.; Chan, C.; Stein, R. Response of seismicity to Coulomb stress triggers and shadows of the 1999 Mw = 7.6 Chi-Chi, Taiwan, earthquake. J. Geophys Res. 2005. [Google Scholar] [CrossRef] [Green Version]
  59. Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 12 00715 g001 550
Figure 1. Tectonic setting of the 2013 Lushan earthquake with the locations of mapped faults (solid black lines), continuously operating global positioning system (CGPS) stations from Jiang et al. [11] (black squares), new CGPS stations in this study (blue squares), leveling points (black triangles with red infill), epicenters of earthquakes with Ms > 5.0 between 1976 and November 2019 from the Global Centroid Moment Tensor (GCMT) catalog (red bench ball; the circle size scales with the magnitude [30,31]), and the epicenter of the 2013 Lushan earthquake and 2008 Wenchuan earthquake (red star). Nearly 30 CGPS stations and 20 leveling points were used to constrain the surface deformation. The white circles represent the aftershocks after the mainshock of the Lushan earthquake. The red lines are the surface projections of the fault model. Acronyms: LMSF: Longmenshan fault; XSHF: Xianshuihe fault; ANHF: Anninghe fault; LJF: Lijiang fault; LRBF: Longriba fault; EKLF: East Kunlun fault; HYF: Huya fault; MJF: Minjiang fault; XF: Xinkaidian fault; SDF: Shuangshi–Dachuan fault.
Figure 1. Tectonic setting of the 2013 Lushan earthquake with the locations of mapped faults (solid black lines), continuously operating global positioning system (CGPS) stations from Jiang et al. [11] (black squares), new CGPS stations in this study (blue squares), leveling points (black triangles with red infill), epicenters of earthquakes with Ms > 5.0 between 1976 and November 2019 from the Global Centroid Moment Tensor (GCMT) catalog (red bench ball; the circle size scales with the magnitude [30,31]), and the epicenter of the 2013 Lushan earthquake and 2008 Wenchuan earthquake (red star). Nearly 30 CGPS stations and 20 leveling points were used to constrain the surface deformation. The white circles represent the aftershocks after the mainshock of the Lushan earthquake. The red lines are the surface projections of the fault model. Acronyms: LMSF: Longmenshan fault; XSHF: Xianshuihe fault; ANHF: Anninghe fault; LJF: Lijiang fault; LRBF: Longriba fault; EKLF: East Kunlun fault; HYF: Huya fault; MJF: Minjiang fault; XF: Xinkaidian fault; SDF: Shuangshi–Dachuan fault.
Remotesensing 12 00715 g001
Remotesensing 12 00715 g002 550
Figure 2. Time series of CGPS stations in the Lushan region.
Figure 2. Time series of CGPS stations in the Lushan region.
Remotesensing 12 00715 g002
Remotesensing 12 00715 g003a 550Remotesensing 12 00715 g003b 550
Figure 3. GPS-observed (red arrow) and jointly inverted (blue arrow) horizontal coseismic deformation (a), horizontal residuals between the observed and inverted deformation (b), GPS-observed (red arrow) and inverted (blue arrow) vertical coseismic deformation (c), and vertical residuals between the observed and inverted deformation (d).
Figure 3. GPS-observed (red arrow) and jointly inverted (blue arrow) horizontal coseismic deformation (a), horizontal residuals between the observed and inverted deformation (b), GPS-observed (red arrow) and inverted (blue arrow) vertical coseismic deformation (c), and vertical residuals between the observed and inverted deformation (d).
Remotesensing 12 00715 g003aRemotesensing 12 00715 g003b
Remotesensing 12 00715 g004 550
Figure 4. Leveling-observed (red arrow) and leveling-inverted (blue arrow) vertical coseismic deformation (a) and vertical residuals between the observed and jointly inverted deformation (b).
Figure 4. Leveling-observed (red arrow) and leveling-inverted (blue arrow) vertical coseismic deformation (a) and vertical residuals between the observed and jointly inverted deformation (b).
Remotesensing 12 00715 g004
Remotesensing 12 00715 g005 550
Figure 5. Interferometric synthetic aperture radar (InSAR)-observed coseismic deformation (a), jointly inverted InSAR coseismic deformation (b), and InSAR residuals between the observed and inverted deformation (c).
Figure 5. Interferometric synthetic aperture radar (InSAR)-observed coseismic deformation (a), jointly inverted InSAR coseismic deformation (b), and InSAR residuals between the observed and inverted deformation (c).
Remotesensing 12 00715 g005
Remotesensing 12 00715 g006 550
Figure 6. A trade-off curve line associated with the model. The dashed and dash-dotted black lines show the trends of model roughness (ψ) and the residuals (ξ) of modeled simulations after normalizing, respectively, while the solid grey line represents log(ξ + ψ).
Figure 6. A trade-off curve line associated with the model. The dashed and dash-dotted black lines show the trends of model roughness (ψ) and the residuals (ξ) of modeled simulations after normalizing, respectively, while the solid grey line represents log(ξ + ψ).
Remotesensing 12 00715 g006
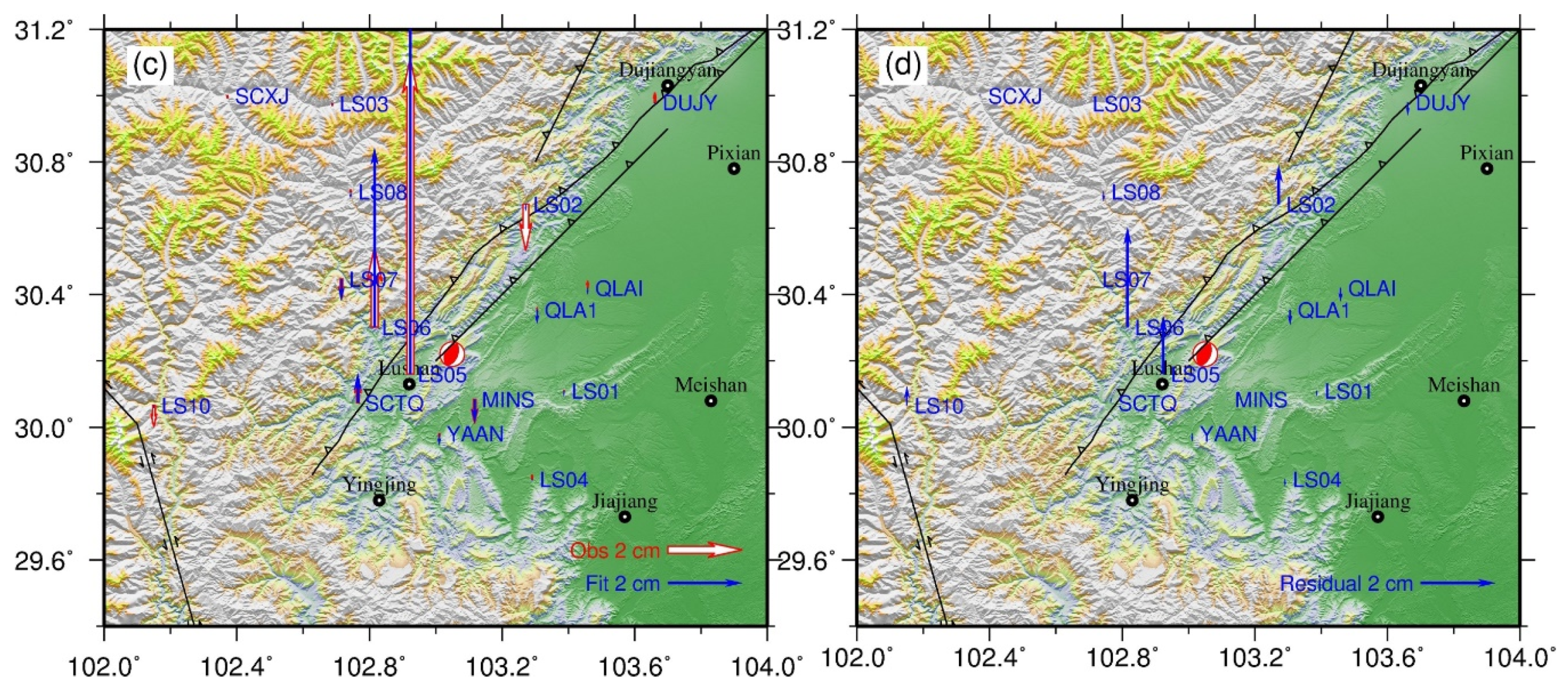
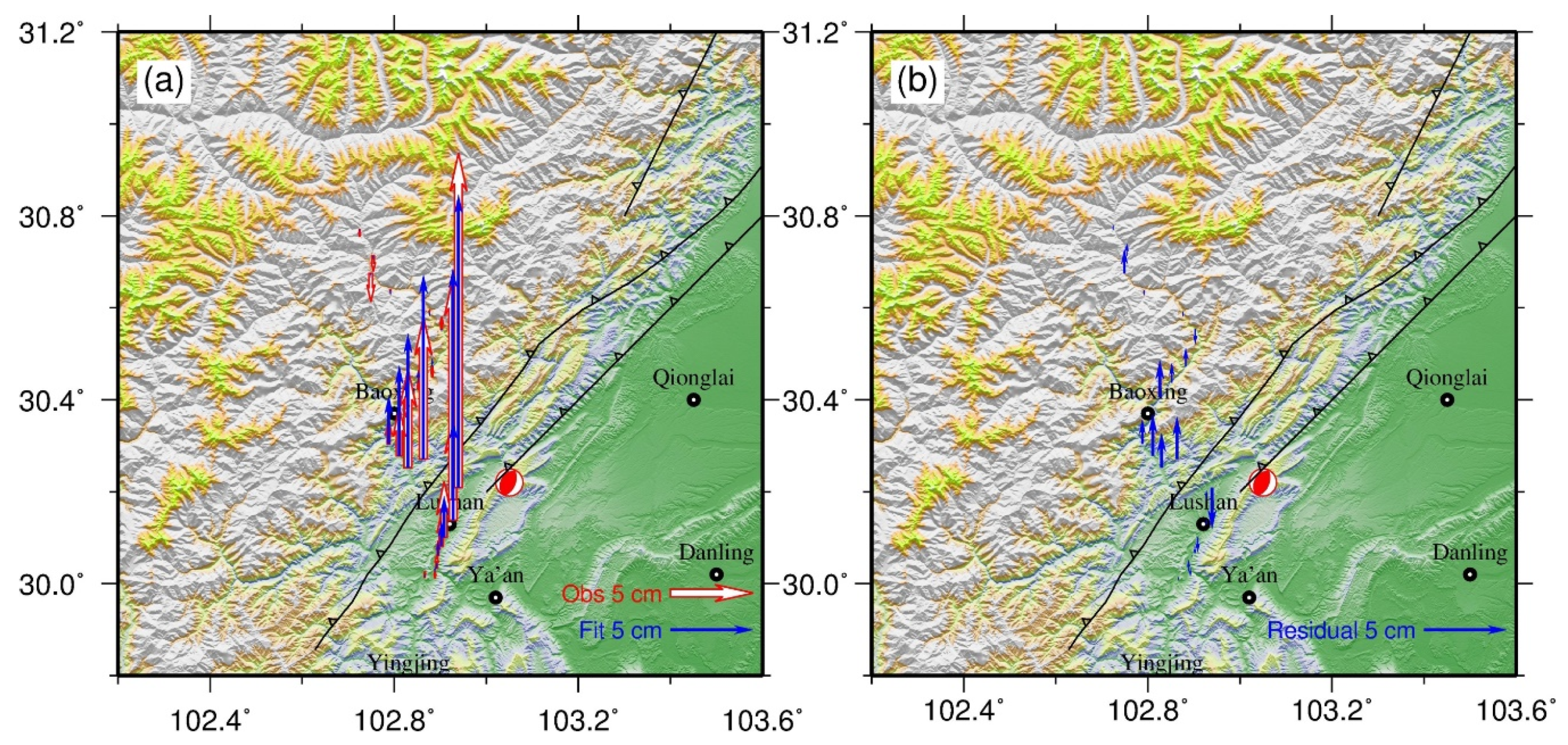
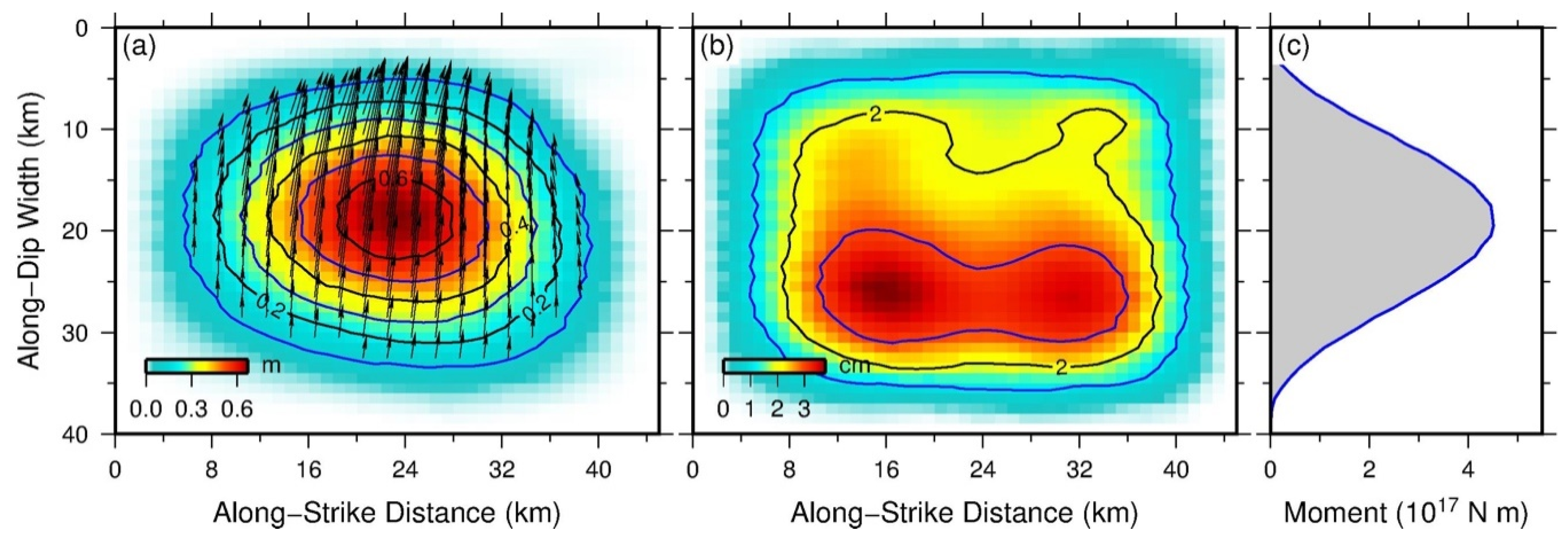
Remotesensing 12 00715 g007 550
Figure 7. The distributed slip model of the Lushan earthquake (a), standard deviation of the slip from a Monte Carlo bootstrap estimation with 100 perturbed data sets (b), and sum of the released moment with the distance along the strike (c). The lines (black and blue) show contours of the slip (a) and standard deviation of the slip (b) every 0.1 m and 1 cm, respectively.
Figure 7. The distributed slip model of the Lushan earthquake (a), standard deviation of the slip from a Monte Carlo bootstrap estimation with 100 perturbed data sets (b), and sum of the released moment with the distance along the strike (c). The lines (black and blue) show contours of the slip (a) and standard deviation of the slip (b) every 0.1 m and 1 cm, respectively.
Remotesensing 12 00715 g007
Remotesensing 12 00715 g008 550
Figure 8. Checkerboard tests for different asperities. (a) single-patch fault model at the shallowest subfault with 1 m slip and a rake angle of 90°, (b) the corresponding retrieved slip distribution from the single-patch fault with all observations (GPS, leveling, and InSAR), (c) the corresponding retrieved slip distribution from the single-patch fault without QLA1 and MINS CGPS stations, (d) the difference between (b) and (c), (e) single-patch fault model at the middle subfault with 1 m slip and a rake angle of 90°, (f) the corresponding retrieved slip distribution from the single-patch fault with all observations (GPS, leveling, and InSAR), (g) the corresponding retrieved slip distribution from the single-patch fault without QLA1 and MINS CGPS stations, (h) the difference between (f) and (g), (i) four-patch fault model with 1 m slip and a rake angle of 90°, (j) the corresponding retrieved slip distribution from the four-patch fault with all observations (GPS, leveling, and InSAR), (k) the corresponding retrieved slip distribution from the four-patch fault without QLA1 and MINS CGPS stations, (l) the difference between (j) and (k), (m) 10-patch classic model with 1 m slip and a rake angle of 90°, (n) the corresponding retrieved slip distribution from the 10-patch classic model with all observations (GPS, leveling, and InSAR), (o) the corresponding retrieved slip distribution from the 10-patch classic model without QLA1 and MINS CGPS stations, (p) the difference between (n) and (o).
Figure 8. Checkerboard tests for different asperities. (a) single-patch fault model at the shallowest subfault with 1 m slip and a rake angle of 90°, (b) the corresponding retrieved slip distribution from the single-patch fault with all observations (GPS, leveling, and InSAR), (c) the corresponding retrieved slip distribution from the single-patch fault without QLA1 and MINS CGPS stations, (d) the difference between (b) and (c), (e) single-patch fault model at the middle subfault with 1 m slip and a rake angle of 90°, (f) the corresponding retrieved slip distribution from the single-patch fault with all observations (GPS, leveling, and InSAR), (g) the corresponding retrieved slip distribution from the single-patch fault without QLA1 and MINS CGPS stations, (h) the difference between (f) and (g), (i) four-patch fault model with 1 m slip and a rake angle of 90°, (j) the corresponding retrieved slip distribution from the four-patch fault with all observations (GPS, leveling, and InSAR), (k) the corresponding retrieved slip distribution from the four-patch fault without QLA1 and MINS CGPS stations, (l) the difference between (j) and (k), (m) 10-patch classic model with 1 m slip and a rake angle of 90°, (n) the corresponding retrieved slip distribution from the 10-patch classic model with all observations (GPS, leveling, and InSAR), (o) the corresponding retrieved slip distribution from the 10-patch classic model without QLA1 and MINS CGPS stations, (p) the difference between (n) and (o).
Remotesensing 12 00715 g008
Remotesensing 12 00715 g009 550
Figure 9. Coulomb stress changes caused by the Lushan earthquake (received fault strike/dip/rake: 208.0°/43.0°/83.0°; depth: 13 km; frictional coefficient: 0.4).
Figure 9. Coulomb stress changes caused by the Lushan earthquake (received fault strike/dip/rake: 208.0°/43.0°/83.0°; depth: 13 km; frictional coefficient: 0.4).
Remotesensing 12 00715 g009
Remotesensing 12 00715 g010 550
Figure 10. Coulomb stress changes along the surrounding faults caused by the Wenchuan and Lushan earthquakes. Coulomb stress changes in the surrounding faults caused by the Wenchuan earthquake (a), Coulomb stress changes in the surrounding faults caused by the Lushan earthquake (b), and Coulomb stress changes in the surrounding faults caused by both the Wenchuan and the Lushan earthquakes (c).
Figure 10. Coulomb stress changes along the surrounding faults caused by the Wenchuan and Lushan earthquakes. Coulomb stress changes in the surrounding faults caused by the Wenchuan earthquake (a), Coulomb stress changes in the surrounding faults caused by the Lushan earthquake (b), and Coulomb stress changes in the surrounding faults caused by both the Wenchuan and the Lushan earthquakes (c).
Remotesensing 12 00715 g010
Table
Table 1. Coseismic displacements of the Lushan earthquake according to GPS observations.
Table 1. Coseismic displacements of the Lushan earthquake according to GPS observations.
SiteLong.
(°E)		Lat.
(°N)		E
(mm)		Se
(mm)		N
(mm)		Sn
(mm)		U
(mm)		Su
(mm)
BECH104.4531.620.51.3−1.31.5−3.15.8
DUJY103.6630.980.30.901.70.84.4
HANY102.6329.340.11.60.61.7−2.63.9
LS01103.3830.11−15.81.47.11.6−2.04.9
LS02103.2730.671.41.83.62.5−14.313.1
LS03102.6830.983.51.3−2.41.7−2.54.7
LS04103.2929.84−6.11.16.31.7−0.74.1
LS05102.9230.16−8.91.1−67.31.682.63.5
LS06102.8130.30−3.21.7−5.41.719.53.7
LS07102.7130.4424.71.1−18.21.5−7.32.8
LS08102.7430.716.80.9−10.21.6−1.33.8
LS09101.8630.954.52.0−2.71.42.55.5
LS10102.1530.063.71.8−1.61.3−7.64.3
MINS103.1130.08−21.01.918.72.2−8.36.1
MZHU104.1931.330.71.4−1.11.6−3.16.0
QLA1103.3030.35−10.61.40.21.5−1.54.6
QLAI103.4530.42−4.71.4−1.11.5−0.14.7
SCDF101.1230.981.81.3−1.31.51.04.5
SCJL101.5029.01−0.82.1−0.51.4−4.56.3
SCMB103.5328.840.21.801.5−0.23.9
SCMN102.1728.331.21.4−1.31.33.84.7
SCMX103.8531.671.01.2−0.61.6−2.04.1
SCSM102.3529.230.11.7−0.51.5−2.93.3
SCTQ102.7630.07−7.91.1−19.41.84.64.7
SCXD102.4328.30−0.71.9−2.32.0−1.88.2
SCXJ102.3731.003.11.2−2.61.0−2.64.7
SCYX102.5128.6502.7−1.81.62.97.0
YAAN103.0129.98−6.21.16.51.3−2.94.9
YAAN103.0129.98−6.21.16.51.3−2.94.9
Note: E, N, and U represent the coseismic deformation of east, north, and up direction, respectively. Se, Sn, and Su represent the coseismic deformation error of east, north, and up direction, respectively.
Table
Table 2. Coseismic displacements of the Lushan earthquake according to leveling observations.
Table 2. Coseismic displacements of the Lushan earthquake according to leveling observations.
Site
LONG.
(°E)		LAT.
(°N)		U
(mm)		 σ U
(mm)
Y165A102.8630.0100
CKFY001102.8830.03−8.20.9
FXG2167102.8930.034.30.6
DD42102.8930.065.10.9
DD41102.9030.0816.20.8
DD40102.9130.1030.00.7
DF37A(09)102.9330.1459.41.2
DD36102.9330.18130.31.0
DD35102.9430.21198.40.8
DD32102.8630.2782.11.7
DD30102.8330.2555.91.3
DF29(09)102.8130.2825.60.8
DD28102.7930.3010.61.0
DD23102.8330.41−16.21.6
DD22102.8530.44−8.30.9
DF23(09)102.8830.47−10.51.0
DF21(09)102.9030.553.61.5
DF20(09)102.8830.59−3.31.1
DD15102.7930.64−3.71.5
DF17(09)102.7530.67−21.01.1
DF16(09)102.7530.71−13.11.1
DD8102.7330.77−8.11.4
Note: U and σ U represent the vertical coseismic deformation and its error, respectively.
Table
Table 3. Focal mechanism solutions of the Lushan earthquake.
Table 3. Focal mechanism solutions of the Lushan earthquake.
SourceLongLatLengthDepthWidthStrikeDipRakeSlipMw
(°E)(°N)(km)(km)(km)(°)(°)(°)(m)
Uni. Model a102.98430.25824.37.415.0208.045.081.60.716.56
±0.7 km±0.8 km±2.3±1.3±3.4±4.7±1.3±7.9±0.17
Dist. Model b103.05230.22845040208.043.083.00.336.58
USGS BW c102.88830.308-19.0-2164793-6.5
GCMT d103.1230.22-21.9-21242100-6.6
Zhang et al. [18]--4504021063/40/10-1.66.8
Huang et al. [20]-- 208.542.1 1.26.53
Jiang et al. [11]102.94030.17922.57.717.0208.043.081.70.706.6
a Uni. Model is the uniform slip model. b Dist. Model is the distributed slip model. c USGC-BM is derived from body wave data by USGS. d GCMT is the Global CMT solution.

Share and Cite

MDPI and ACS Style

Li, Z.; Wen, Y.; Zhang, P.; Liu, Y.; Zhang, Y. Joint Inversion of GPS, Leveling, and InSAR Data for The 2013 Lushan (China) Earthquake and Its Seismic Hazard Implications. Remote Sens. 2020, 12, 715. https://doi.org/10.3390/rs12040715

AMA Style

Li Z, Wen Y, Zhang P, Liu Y, Zhang Y. Joint Inversion of GPS, Leveling, and InSAR Data for The 2013 Lushan (China) Earthquake and Its Seismic Hazard Implications. Remote Sensing. 2020; 12(4):715. https://doi.org/10.3390/rs12040715

Chicago/Turabian Style

Li, Zhicai, Yangmao Wen, Peng Zhang, Yang Liu, and Yong Zhang. 2020. "Joint Inversion of GPS, Leveling, and InSAR Data for The 2013 Lushan (China) Earthquake and Its Seismic Hazard Implications" Remote Sensing 12, no. 4: 715. https://doi.org/10.3390/rs12040715

APA Style

Li, Z., Wen, Y., Zhang, P., Liu, Y., & Zhang, Y. (2020). Joint Inversion of GPS, Leveling, and InSAR Data for The 2013 Lushan (China) Earthquake and Its Seismic Hazard Implications. Remote Sensing, 12(4), 715. https://doi.org/10.3390/rs12040715

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop