1. Introduction
The Strait of Gibraltar is the natural connection of the Mediterranean Sea with the world ocean, being a hot spot area in many senses. There, diverse and separated hydrodynamic phenomena occur over a wide range of spatial and temporal scales (from the small scales and submesoscale phenomena to inter-annual and climate variability). The complex hydrodynamic conditions influence the rich marine ecosystem in the adjacent coastal areas, e.g., [
1,
2,
3]. Furthermore, the region is of great socioeconomic relevance as a key passage for marine trade. Almost 1/6 of global sea traffic and 1/5 of global oil traffic transits through the Mediterranean basin, still being the shortest route between Europe and Asia [
4]. Then, it is not surprising that the Strait of Gibraltar and the adjacent Alboran Sea have been traditionally a focus area for many research and monitoring efforts since a long time ago, e.g., [
5,
6,
7]. Although the main characteristics of the prominent processes are reasonably known and modeling efforts capture most of them, an adequate operational forecast of the hydrodynamics conditions in this region remains a challenging task [
8]. Roughly, the water mass structure is close to a two-layer system characterized by an upper surface layer of Atlantic waters entering into the basin and denser Mediterranean waters outflowing below [
9]. The inflow of Atlantic water and the outflow of Mediterranean water are constrained by hydraulic control in the channel where the bottom relief, stratification, tidal, and wind regimes determine the variability of water exchanges through the strait, which are therefore linked to basin scale variability, e.g., [
10,
11].
The jet of Atlantic water forms and configures a quasi-permanent vortex or gyre in the western part (western Alboran vortex, WAG) of the Alboran Sea, which progresses further into the second half after Cape Tres Forcas (around 3
W) where it forms a second gyre (eastern Alboran gyre, EAG) and continues further to the east attached to the African coast as the Algerian current, e.g., [
12,
13] (see
Figure 1). This is the dominant general pattern of the surface circulation in the Alboran Sea, particularly in summer, emerging from the analysis of time series of sea level maps and model reanalysis [
14,
15] and often observed by in situ cruises, e.g., [
13]. Besides, the gyres may collapse or migrate until they are restored in the spring and early summer. These events appear to be induced by high frequency processes (tides and atmospheric fluctuations) requiring high resolution in space and time to be adequately analyzed and studied [
8].
Attempts to forecast the oceanographic conditions during a recent oceanographic experiment, the MEDESS-GIB experiment [
16], have shown that models reasonably reproduce the main pattern but fail to reproduce the variability of short scales and the details of the evolution of the Atlantic inflow around WAG, e.g., [
17]. Once models have the necessary spatial resolution and are able to reproduce the observed physical processes, as was the case of the MEDESS-GIB experiment, a way to improve the subsequent forecast is to have initial conditions and analyzed fields as close as possible to the truth. Furthermore, in the worst case, when and where operational systems are not working well and depending on the involved scales, an empirical approach using only real time field observations and assuming some kind of persistence may provide a reasonable first guess. Sea surface temperature (SST) is quite satisfactorily retrieved in real time and with enough resolution to reach fields at submesoscale. For the ocean velocity, altimetry offers the possibility to build maps of velocity fields interpolating along-track information. In this case, the resolution attained can reach the ocean mesoscale, although with limitations in terms of accuracy and reliability, e.g., [
18] and real time is not possible.
The operational estimation of ocean velocities from satellite observations remains a major problem in satellite oceanography. At present, multiple methods to estimate ocean currents from SST have been proposed with a wide range of performances, see [
19] for a review on this subject. In this study, we analyzed the possibility to retrieve real time high resolution fields making use of the surface quasi-geostrophic theory (SQG) [
20,
21]. SQG offers the theoretical body to derive high resolution surface velocity fields from a single infrared SST image [
21,
22,
23,
24,
25,
26]. This capability is of key importance for operational applications because it extends its usability in comparison with other techniques such as maximum cross correlation or optical flow that need a sequence of cloud-free images [
19]. Two conditions are necessary to apply the SQG framework to SST images: surface density fluctuations have to be strong enough to capture a significant amount of the near-surface dynamics [
22,
27] and SST has to be a proxy of density anomalies at the base of the mixed layer [
28]. In a pioneering work, LaCasce and Mahadevan [
29] demonstrated the applicability of the SQG framework in the Alboran Sea and showed that it was possible to retrieve the full 3D structure of ocean density and velocity fields from SST fields. Their reconstructed fields were quite similar to those observed in a CTD cruise; however, the work was flawed by the assumption that three-day cruises could be considered synoptic. Consequently, they had errors in both horizontal and vertical velocities.
In the present study, we went further by validating the reliability of using a time series of ocean velocity fields from SST covering the full area between the Strait of Gibraltar and the Alboran Sea. In particular, we analyzed the performance of the SQG approach when applied to infrared satellite measurements and compared to velocities derived from surface drifters. Moreover, we explored new approaches to overcome the limitations imposed by the lack of observations of ocean salinity.
This paper is organized as follows. We first briefly present the dataset used in
Section 2. We develop in detail the methodology to derive velocity fields applying a SQG-based methodology in
Section 3. In
Section 4, we present and validate the results comparing with field data from the MEDESS-GIB experiment. We finally discuss and conclude the major outcomes.
2. Data
On the frame of the MEDESS-4MS project (EU MED Program), an intensive Lagrangian experiment was organized in the Strait of Gibraltar to validate and test the operational systems running in this area [
16]. The experiment consisted od a quasi-synoptic deployment network of surface drifters distributed along the Strait of Gibraltar (
Figure 2). The experiment started on 9 September and lasted around three months from September to December 2014. The drifters used in the experiment were mostly of CODE type [
30] dragged at 1.5 m from the surface and a few units of oil-spills tracking drifters not used in this study, all set up with a sampling rate of 30 min. The dataset is available at PANGAEA (Data Publisher for Earth and Environmental Science) repository and all the quality control procedures and first view of the trajectories were described by Sotillo et al. [
17].
Geostrophic velocities used were derived from Near Real Time Absolute Dynamic Topography Maps (NRT-MADT) for the Mediterranean Sea generated by AVISO altimetry and distributed by the GlobCurrent project. Velocities were estimated from NRT-MADT using a nine-point stencil length, as described by Arbic et al. [
31]. During the period, most drifters remained in the Alboran Sea (from 9 September to 29 September,
Figure 2), but only 10 images with favorable cloud coverage were available. These images correspond to the AVHRR instrument from NOAA 19 platform for the period from 9 September at 03:08 GMT to 14 September at 02:12 GMT. Consequently, only the WAG could be simultaneously sampled by infrared instruments and drifters.
The used SSS corresponds to the Mediterranean and North Atlantic SMOS SSS maps V2.0 product from the Barcelona Expert Centre in Remote Sensing (BEC). These maps were derived from L1B Microwave Brightness Temperatures (MBT) products measured by SMOS and provided by ESA. Then, SMOS SSS daily L3 maps at
resolution were produced by means of a successive corrections analysis applied over time periods of nine days using influence radii adapted to the Mediterranean Sea, see [
32] and reference therein.
4. Comparison between Velocity Estimations
The eSQG model, together with the phase correction approach described in
Section 3.3, were used to derive velocities from all the available thermal images (
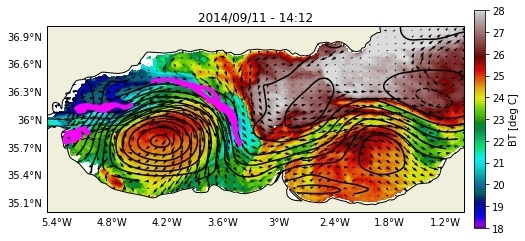
Figure 6 shows six of them). The resulting fields exhibit more temporal variability of the WAG than the velocity derived from SSH (
Figure 6 and
Figure 7). Indeed, thermal images shows that the WAG changes its shape significantly at temporal scales of the order of 12 h, but this variability is not observed in altimetric maps, which show an almost stationary vortex. A second major difference in the western part of the basin is the circulation east of the Strait of Gibraltar, the area between the strait and the vortex approximately limited by the meridian located at 4.8
W. There, altimetric maps show a northwards current while thermal images generate an eastwards current, indicating entrance of Atlantic waters into the Mediterranean Sea. The comparison between velocities derived from temperature and from sea level also show differences in the time evolution of the EAG. While the first shows an evolving vortex, altimetry shows an almost stationary bipolar structure. The differences between altimetric and thermal images are also evident comparing BT and buoyancy derived from SSH (
Figure 4). It is worth mentioning that, contrary to SST, buoyancy derived from SSH tends to be more representative of the patterns below the mixed layer rather than the ocean surface [
28] and, consequently, fields may not be fully comparable. Nevertheless, the temporal evolution of this vortex and its characteristics points to sampling limitations of the altimetric measurements rather than the difference between density anomalies in the Mixed Layer and below it. Finally, both fields seem to capture the separation of the west–east flow from the WAG located around longitude 3.55
W. The exception is for the AVHRR image of 10 September at 14:24, which shows currents that do not agree with other satellite images or altimetric maps. The reason for this disagreement relies on the failure of the phase correction approach for this particular image. Indeed, the separation between the EAG and the large extension of warm waters is not good enough to correct for their contribution to the flow on this side of the basin.
The velocity fields derived from altimetry and thermal images were compared to the in situ measurements provided by the drifters of the MEDESS-GIB experiment. A first comparison comes from the juxtaposition of trajectories with the instantaneous velocity fields (
Figure 6 and
Figure 7), which shows a strong tendency of drifter trajectories to move tangent to the velocity fields. There are, however, some exceptions, particularly in the area east of the Strait of Gibraltar where some drifters have swirling trajectories that do not agree with any of the velocity fields derived from satellite measurements. Although the temporal length of available thermal images is not long enough to analyze the penetration of drifters in the EAG, it is long enough to see the detachment of drifters from the WAG and their path towards the east, which is in agreement with the velocities seen from satellites. Notice that, in this area, swirling trajectories are also present and in disagreement with both velocity fields.
The velocities derived from surface drifters were compared to surface velocities derived from satellite observations by interpolating the latter onto the position and time of drifters (see
Figure 8). Since no correction for the presence of inertial oscillations was applied, only those drifter segments that did not show small loops were taken from the whole set of drifters depicted in
Figure 2. The global comparison between velocity components suggests a slightly better agreement between the velocities derived from SST than those derived from SSH (
Figure 9). This can be seen in the global correlations between reconstructed velocities and drifter velocities, which are
and
for the velocities derived from SST and
and
for the velocities derived from SSH. Since some ageostrophic corrections modify the speed but do not modify the direction of the geostrophic current, e.g., the cyclostrophic flow, it is interesting to compare velocity directions. Here, the correlation between the velocity directions diagnosed from satellite and those derived from drifter trajectories are quite similar:
for SST and
for SSH. Notice, however, that all correlations are well below 0.9. Another difference between the two types of velocities derived from satellite observations is their kinetic energy. Although velocities derived from SST are calibrated with altimetric data, the lack of small scale signals in altimetric maps implies that higher resolution velocities derived from SST have to be low-pass filtered for calibration (Equation (
8)) but the resulting field has higher kinetic energies closer to the kinetic energy of surface drifters (
Figure 9).
Figure 8 shows a relatively good agreement in the direction of currents, i.e., small angles between velocities and drifter trajectories, in the WAG for both the velocities derived from altimetry and velocities derived from thermal images. However, there is an important difference in the velocity angles observed in the velocities derived from SST with respect to drifter velocities for values around −1.5 rad (
Figure 9). This discrepancy is mainly due to the velocities in the eastern edge of the WAG. Moreover, between the Strait of Gibraltar and the WAG, altimetric velocities have angles that can be up to 90
with respect to the trajectories of drifters while, velocities derived from thermal images show significantly smaller angles. The above observations and the patterns seen in the velocity fields (
Figure 6 and
Figure 7) suggest that the agreement between satellite derived and in situ velocities may not be homogeneous and point to define three different areas: the area east of Gibraltar (the area between the Strait of Gibraltar and meridian located at 4.8
W), the WAG (between the meridians located at 4.8
W and 3.45
W), and the bifurcation area (east of the meridian located at 3.45
W), where part of the flow is trapped by the WAG and part of it flows eastwards towards the EAG (see
Figure 8). These areas were used to better quantify the agreement between in situ and satellite velocities. Taylor diagrams confirm that the ability to reconstruct velocities is better for WAG than for any other area (
Figure 10), although velocities derived from temperature have slightly higher correlations for the direction. In the area east of the bifurcation point, on the contrary, the performance is better for altimetry, although correlations are quite low for the orientation of the current. The opposite situation is found in the area east of Gibraltar, in which altimetry shows very poor performance. Interestingly, the meridional velocity is better reconstructed than the zonal velocity for both SSH- and SST-derived velocities.
Finally, the topology of the two velocity fields derived from satellite observations was unveiled by using the methodology presented by Jiménez Madrid and Mancho [
36], which has been already applied on altimeter datasets over the area of the Kuroshio Current [
37]. The idea was to produce a two-dimensional field covering the region, which computes at each point the arc length of the trajectory passing for the point. More precisely, by using synthetic trajectories obtained integrating forwards and backwards for a determined amount of time and getting the distance travelled, the arc lengths of the trajectory are computed for the central instant of the time series to have the maximum possible time period to integrate, i.e., 2.5 days (see
Appendix A for technical details).
Figure 11 depicts the arc length plots for both velocity fields. One can see both velocity fields are able to capture the two-vortex patterns typical of the Alboran Sea but with significant differences. First, altimetric field is more stable, i.e., vortex cores are clearly delimited and the flow of Atlantic water is very well defined by large arc length values. This indicates, as already stated, that the temporal evolution of the altimetric field is slow. On the contrary, thermal field shows the effect of rapidly evolving WAG producing a vaguer structure but it is still possible to see the vortex core and its contour. It is worth mentioning that the detection of EAG is challenging due to the similar temperature it has with respect to the Mediterranean waters. It is only seen thanks to the flow of fresh waters that clearly separates both structures. Notice the strong differences between them. Second, the thermal field is able to capture the entrance of Atlantic waters while the altimetric field is not. Indeed, the shadowed area in
Figure 11 is due to the particles that escape from the domain; consequently, it is not possible to track their evolution for the entire time period considered. It is worth remarking that, in the plot corresponding to the altimetric field, there are big regions of very low arc length values (purple color in the figure), showing the limitation of the altimetric fields when one approaches the coast in comparison to the velocities derived from SST.
5. Discussion
The circulation in the Alboran Sea is usually dominated by the presence of two large vortices that dominate the upper 100–300 m of the ocean [
34,
38]. These conditions are favorable to the exploitation of the eSQG approximation to retrieve surface current, as shown by LaCasce and Mahadevan [
29] and confirmed by the results shown in
Section 4. This opens the door to use SST to retrieve surface currents in this area, which allows resolving both the high frequency evolution of these vortices and the smaller scales structures that surround them [
12]. On the contrary, Altimeters have spatial and temporal sampling limitations. Alboran vortices, however, are large enough to be properly sampled by altimeters. Consequently, both velocities derived from infrared radiometers and velocities derived from radar altimeters show similar capabilities when compared with the trajectories of drifting buoys. Nevertheless, there are some relevant exceptions: the area east of Gibraltar. This area is not properly sampled by altimeters and, therefore, velocities diagnosed in this zone are significantly different from those observed by drifting buoys. On the contrary, velocities derived from thermal images give velocities with directions relatively close to the observed by drifters (
while
). The comparison between drifters and the geostrophic velocities derived from SST or SSH, however, has an important drawback: drifter trajectories have ageostrophic contributions not taken into account in the derivation of surface currents from SST nor SSH. In particular, drifters are affected by wind [
39] and inertial oscillations as well as ageostrophic contributions such as the cyclostrophic flow associated to the curvature of the Alboran vortex. Furthermore, drifter speed in the area east of Gibraltar showed some temporal behavior that suggest a relevant contribution from tides.
Although thermal images and altimeter maps have similar performances when the flow is dominated by structures large enough to be sampled by altimeters, both approaches have different latencies, with that of currents derived from SST being of the order of few hours (typically less than 4 h) (This is the time passed between satellite measurement and the delivery of surface currents derived from them. Notice that the time needed to estimate currents from SST is of the order of the time needed to compute the FFT). Of course, velocities have to be calibrated and independent measurements such as the ones provided by altimeters are necessary; however, when only the energy level has to be fixed, simultaneous data are not needed. On the contrary, it requires some time to get accurate altimetric measurements and near-real time maps can only use past data, which further limits the capability to resolve two-dimensional structures if not enough altimeters are available [
18]. Thermal images have, however, two main limitations. First, they can only be used under cloud-free situations, which restricts their applicability (particularly for those methods requiring consecutive cloud free images such optical flow and MCC). It is worth mentioning that the Mediterranean Sea is a quite favorable situation, with a relatively large fraction of cloud-free images (∼
). For moving clouds, gaps can be filled combining several images. One possible approach would be to compute vorticity from SST for several images, calibrate them, combine vorticities for a short enough period of time, and, finally, recompute the stream function inverting the vorticity.
A second limitation, as discussed above, is the need to correct for the impact of SSS. Presently, SSS measurements are not available in real time, although important advances have been done and it is already possible to detect the signature of the Atlantic waters in the Algerian basin [
26] and the key patterns in the Alboran Sea with low resolutions. This implies that other approaches are needed. Here, we explored a simple method that consists of detecting Mediterranean waters from thermal images and modifing y buoyancy to take into account the effect of salinity. Although this approach is very crude, it shows that it is able to correct the role of salinity and provide results similar to those provided by altimeters. This raises a question: To what extent can the approach here proposed be used in other areas of the ocean? As shown in
Section 3.3, there are two necessary conditions: the existence of water masses with salinities homogeneous enough to be considered constant and a way to identify such water masses from existing satellite observations. Multiple strategies are possible to identify water masses. In areas dominated by the presence of vortices of distinctive salinity, e.g., the Algerian basin [
26], vortex identification techniques can be used [
40,
41]. In areas where SST univocally identifies water masses, temperature can be used to identify the extension of water masses. In other cases, image processing techniques combined with oceanographic knowledge can be applied to satellite observations of temperature or chlorophyll to segment the image. Future improvements could include the use of new SSS products (if they are available in real time), climatological SSS, or the exploitation of the buoyancy derived from altimetry to give a better estimation of density anomalies. However, these approaches require the implementation of accurate numerical methods that are beyond the scope of this study.