Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment
Abstract
:1. Introduction
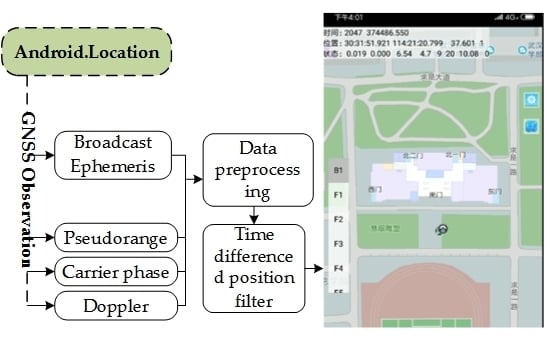
2. Data Collection
2.1. Static GNSS Data Collection
2.2. Dynamic GNSS Data Collection
3. Characteristics of Xiaomi Mi 8 Raw GNSS Observations
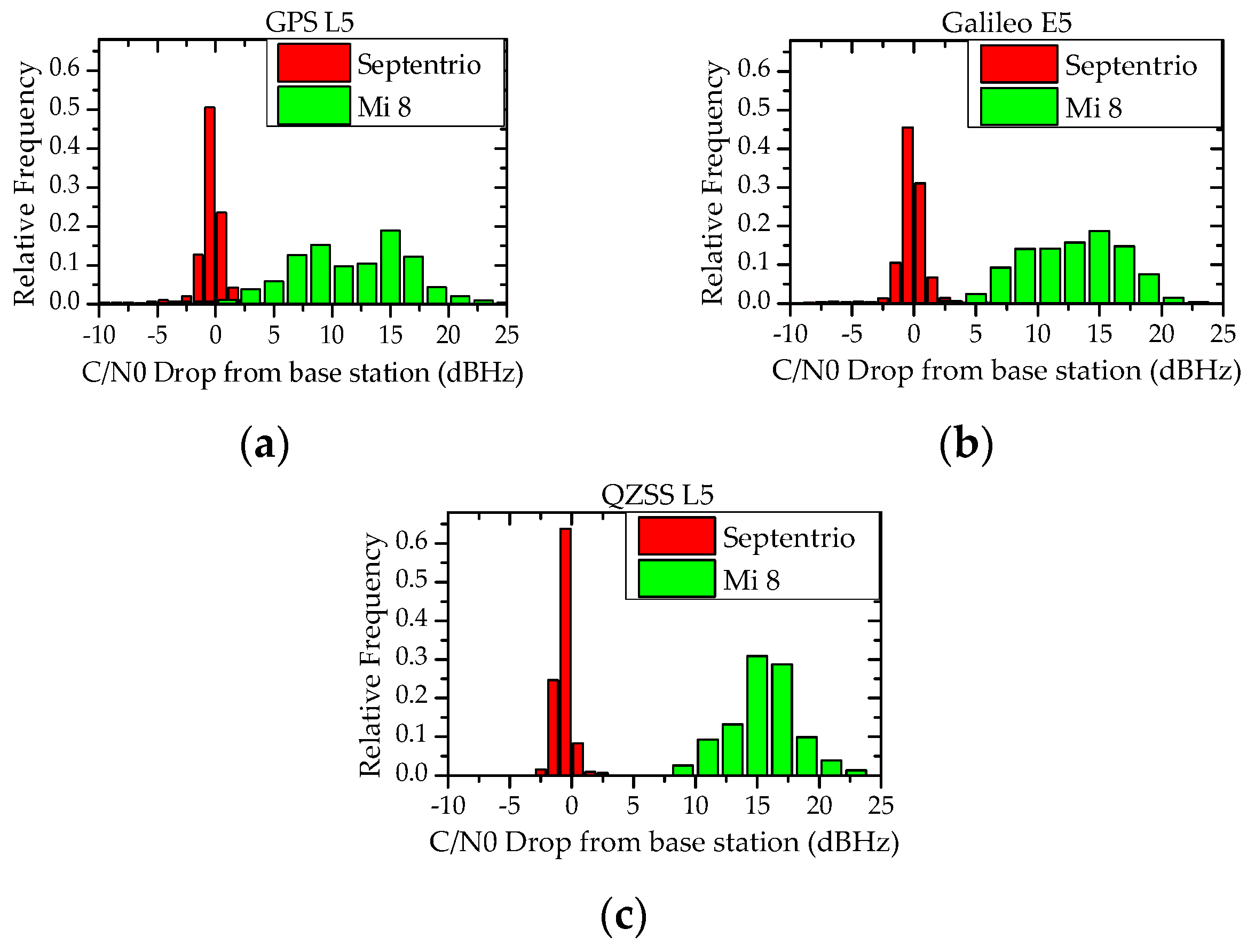
3.1. Carrier-to-Noise Density Ratio
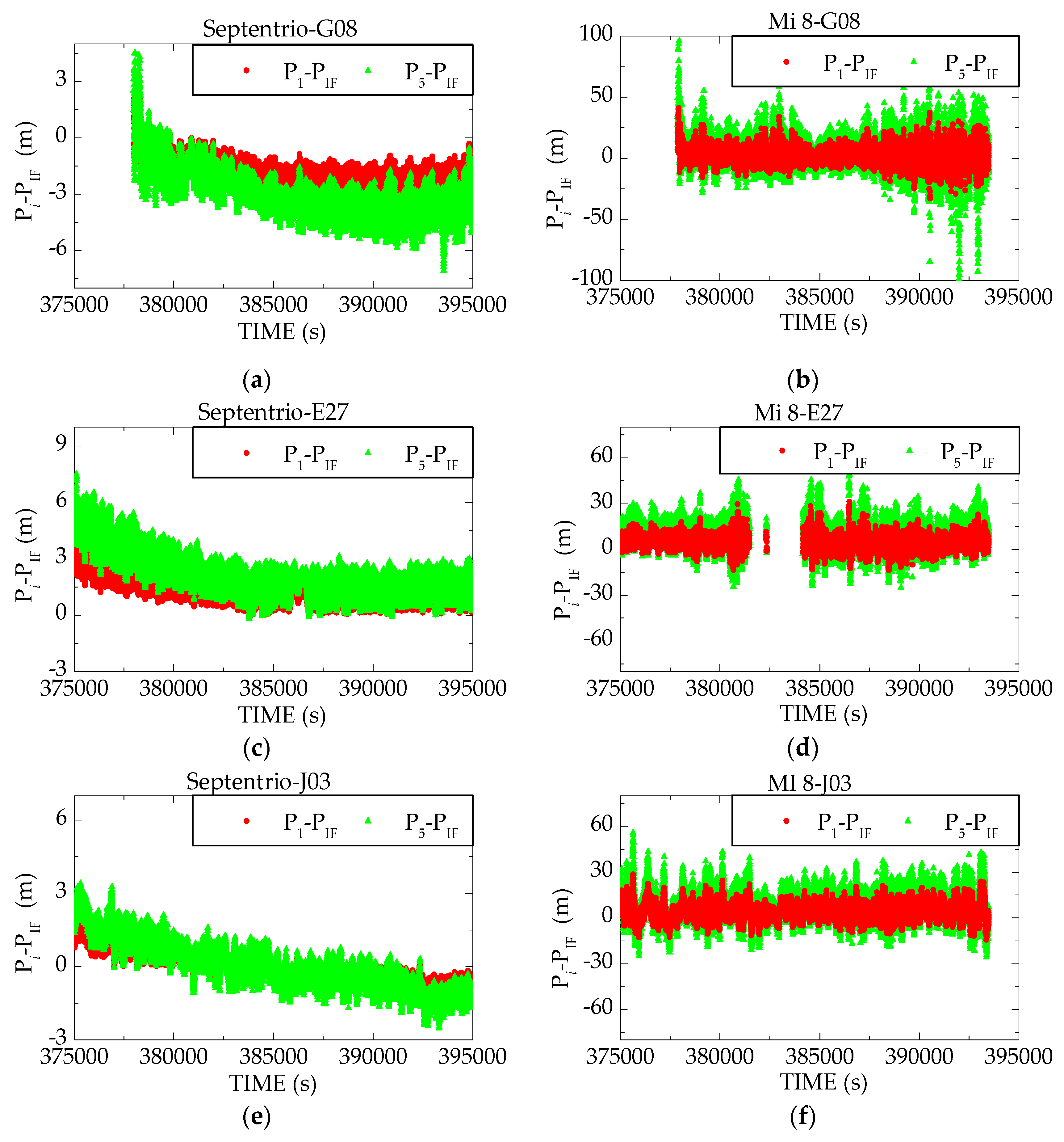
3.2. Pseudorange Observations
3.3. Carrier Phase Observations
4. Time Differenced Filter Algorithm
4.1. State Equation
4.2. Observation Equation
4.3. Filter Model
5. GNSS Positioning Performance of Xiaomi Mi 8
5.1. Positioning Strategies
5.2. Static Test Analysis
5.3. Dynamic Test Analysis
6. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
References
- The European GNSS Agency. GNSS Market Report 2017; The European GNSS Agency: Prague, Czech Republic, May 2017.
- Zhang, X.; Tao, X.; Feng, Z.; Xiang, S.; Wang, F. Quality assessment of GNSS observations from an Android N smartphone and positioning performance analysis using time-differenced filtering approach. GPS SOLUT 2018, 22, 70. [Google Scholar] [CrossRef]
- Küpper, A. Location-Based Services: Fundamentals and Operation; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Li, P.; Qin, T.; Hu, B.; Zhu, F.; Shen, S. Monocular Visual-Inertial State Estimation for Mobile Augmented Reality. In Proceedings of the 2017 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Nantes, France, 9–13 October 2017. [Google Scholar]
- Piras, M.; Lingua, A.; Dabove, P.; Aicardi, I. Indoor navigation using Smartphone technology: A future challenge or an actual possibility? In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Kim, J.; Lee, S.; Ahn, H.; Seo, D.; Park, S.; Choi, C. Feasibility of employing a smartphone as the payload in a photogrammetric UAV system. ISPRS J. Photogramm. Remote Sens. 2013, 79, 1–18. [Google Scholar] [CrossRef]
- Liu, W.; Shi, X.; Zhu, F.; Tao, X.; Wang, F. Quality analysis of multi-GNSS raw observations and a velocity-aided positioning approach based on smartphones. Adv. Space Res. 2019, 63, 2358–2377. [Google Scholar] [CrossRef]
- Pesyna, K.M.; Humphreys, T.E.; Heath, R.W.; Novlan, T.D.; Zhang, J.C. Exploiting antenna motion for faster initialization of centimeter accurate GNSS positioning with low-cost antennas. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1597–1613. [Google Scholar] [CrossRef]
- Li, G.; Geng, J. Characteristics of raw multi-GNSS measurement error from Google Android smart devices. GPS Solut. 2019, 23, 90. [Google Scholar] [CrossRef]
- Banville, S.; Diggelen, F. Precise GNSS for Everyone: Precise Positioning Using Raw GPS Measurements from Android Smartphones. GPS World 2016, 27, 43–48. [Google Scholar]
- Realini, E.; Caldera, S.; Pertusini, L.; Sampietro, D. Precise GNSS Positioning Using Smart Devices. Sensors 2017, 17, 2434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dabove, P.; Di Pietra, V. Towards high accuracy GNSS real-time positioning with smartphones. Adv. Space Res. 2019, 63, 94–102. [Google Scholar] [CrossRef]
- Gogoi, N.; Minetto, A.; Linty, N.; Dovis, F. A Controlled-Environment Quality Assessment of Android GNSS Raw Measurements. Electronics 2019, 8, 5. [Google Scholar] [CrossRef] [Green Version]
- Riley, S.; Lentz, W.; Clare, A. On the Path to Precision - Observations with Android GNSS Observables. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 25–29 September 2017. [Google Scholar]
- Staff, G.W. World’s First Dual-Frequency GNSS Smartphone Hits the Market. Available online: https://www.gpsworld.com/dual-frequency-gnss-smartphone-hits-the-market/ (accessed on 10 September 2019).
- Marco, F.; Joshua, C.; Malgorzata, S.; Maria, L.; Elisa, B.; William, R. Enabling High Accuracy Dynamic Applications in Urban Environments Using PPP and RTK on Android Multi-Frequency and Multi-GNSS Smartphones. In Proceedings of the 2019 European Navigation Conference (ENC), Warsaw, Poland, 9–12 April 2019. [Google Scholar]
- Crosta, P.; Zoccarato, P.; Lucas, R.; Pasquale, G. Dual Frequency Mass-market Chips: Test Results and Ways to Optimize PVT Performance. In Proceedings of the 31st International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Moore, S.K. Super-accurate GPS coming to smartphones in 2018. IEEE Spectr. 2017, 54, 10–11. [Google Scholar] [CrossRef]
- Shade, S.; Madhani, P. Android GNSS Measurements - Inside the BCM47755. In Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018. [Google Scholar]
- Robustelli, U.; Baiocchi, V.; Pugliano, G. Assessment of Dual Frequency GNSS Observations from a Xiaomi Mi 8 Android Smartphone and Positioning Performance Analysis. Electronics 2019, 8, 91. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Sun, M.; Zhou, C.; Zhang, P. Precise Point Positioning Using Dual-Frequency GNSS Observations on Smartphone. Sensors 2019, 19, 2189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elmezayen, A.; El-Rabbany, A. Precise Point Positioning Using World’s First Dual-Frequency GPS/GALILEO Smartphone. Sensors 2019, 19, 2593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, B.; Gao, C.; Liu, Y.; Sun, P. Real-time Precise Point Positioning with a Xiaomi MI 8 Android Smartphone. Sensors 2019, 19, 2835. [Google Scholar] [CrossRef] [Green Version]
- Takasu, T. RTKLIB Ver. 2.4. 2. Available online: https://github.com/tomojitakasu/RTKLIB_bin/tree/rtklib_2.4.3 (accessed on 15 November 2019).
- White Paper on Using GNSS Raw Measurements on Android Devices; European GNSS Agency: Prague, Czech Republic, 2017.
- Joseph, A. What is the difference between SNR and C/N0? InsideGNSS 2010, 5, 20–25. [Google Scholar]
- Hauschild, A.; Montenbruck, O.; Sleewaegen, J.M.; Huisman, L.; Teunissen, P.J.G. Characterization of Compass M-1 signals. GPS Solut. 2012, 16, 117–126. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Tiberius, C.C.J.M. Assessing receiver noise using GPS short baseline time series. GPS Solut. 2007, 11, 21–35. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Pirazzi, G.; Mazzoni, A.; Biagi, L.; Crespi, M. Preliminary performance analysis with a GPS+Galileo enabled chipset embedded in a smartphone. In Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017. [Google Scholar]
- Traugott, J. Precise Flight Trajectory Reconstruction Based on Time-Differential GNSS Carrier Phase Processing. Bachelor’s Thesis, Technical University of Munich, Munich, Germany, 28 October 2010. [Google Scholar]
- Wang, F.; Gong, X.; Sang, J.; Zhang, X. A Novel Method for Precise Onboard Real-Time Orbit Determination with a Standalone GPS Receiver. Sensors 2015, 15, 30403–30418. [Google Scholar] [CrossRef] [Green Version]
- Carcanague, S. Low-Cost GPS/GLONASS Precise Positioning Algorithm in Constrained Environment. Ph.D. Thesis, Institut National Polytechnique de Toulouse—INPT, Toulouse, France, 25 February 2014. [Google Scholar]
- Cabinet Office; Quasi-Zenith Satellite System Services Inc. Quasi-Zenith Satellite System Interface Specification Satellite Positioning, Navigation and Timing Service (IS-QZSS-PNT-003). 2018. Available online: https://qzss.go.jp/en/technical/ps-is-qzss/ps-is-qzss.html (accessed on 24 February 2020).
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Kazmierski, K.; Hadas, T.; Sośnica, K. Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning. Remote Sens. 2018, 10, 84. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Multi-GNSS signal-in-space range error assessment—Methodology and results. Adv. Space Res. 2018, 61, 3020–3038. [Google Scholar] [CrossRef]


















| Satellite | Frequency | Pseudorange Outlier Percentage (%) | |
|---|---|---|---|
| Static | Dynamic (Track 1) | ||
| GPS | L1 | 3.49 | 11.88 |
| L5 | 1.33 | 9.15 | |
| Galileo | E1 | 1.71 | 9.67 |
| E5 | 1.31 | 5.10 | |
| QZSS | L1 | 4.79 | 9.69 |
| L5 | 3.22 | 6.48 | |
| GLONASS | L1 | 42.08 | 43.86 |
| BeiDou | L1 | 19.61 | 23.65 |
| GNSS | Frequency | Static | Dynamic (Track 1) | Dynamic (Track 2) | ||||
|---|---|---|---|---|---|---|---|---|
| ADRS | Detected Cycle Slips | Cycle Slip Percentage (%) | ADRS | Cycle Slip Percentage (%) | ADRS | Cycle Slip Percentage (%) | ||
| G | L1 | 431 | 434 | 0.191 | 18,465 | 30.02 | 3311 | 45.32 |
| L5 | 546 | 586 | 0.627 | 5227 | 32.46 | 1187 | 42.89 | |
| E | E1 | 43 | 45 | 0.058 | 9734 | 25.27 | 1882 | 37.12 |
| E5 | 619 | 641 | 0.837 | 9280 | 24.09 | 2132 | 41.96 | |
| J | L1 | 516 | 517 | 0.810 | 4651 | 22.77 | 757 | 36.48 |
| L5 | 344 | 551 | 0.862 | 3752 | 18.37 | 630 | 30.31 | |
| R | L1 | 958 | 964 | 1.823 | 18,177 | 29.68 | 1401 | 62.25 |
| C | L1 | 3197 | 3199 | 0.715 | 9560 | 32.60 | 3821 | 52.62 |
| Setting Items | Details |
|---|---|
| Observations used | Uncombined L1/E1 and L5/E5 pseudorange and carrier phase measurements |
| GNSS orbit and clock | Broadcast ephemeris (F/NAV messages for Galileo) |
| Parameters to be estimated | Position, clock offsets |
| Weighting model |
|
| Ionospheric delay | Ionospheric delay correction model of each GNSS system |
| Tropospheric delay | Saastamoinen model |
| Satellite cutoff elevation | 10° |
| Parameter estimation method | Time differenced filter |
| TD Filter | SPP | SPP Availability (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C/N0 Dependent | SISRE Based | |||||||||
| E (m) | N (m) | U (m) | E (m) | N (m) | U (m) | E (m) | N (m) | U (m) | ||
| SF 1-G | 1.09 | 1.49 | 2.37 | 3.47 | 4.54 | 8.74 | 94.8 | |||
| SF-GE | 1.07 | 1.32 | 2.73 | 1.50 | 2.12 | 2.91 | 3.04 | 3.91 | 7.84 | 96.8 |
| SF-GEJ | 0.62 | 1.25 | 2.56 | 1.76 | 2.88 | 3.23 | 2.97 | 3.70 | 7.55 | 97.3 |
| SF-GEJC 2 | 0.95 | 1.98 | 3.29 | 1.37 | 2.49 | 3.12 | 3.02 | 3.82 | 7.38 | 98.0 |
| SF-GEJC without GEO | 0.45 | 1.24 | 2.60 | 1.11 | 2.26 | 3.14 | 3.06 | 3.80 | 7.70 | 97.7 |
| DF 3-G | 0.67 | 0.92 | 1.64 | 2.62 | 3.46 | 7.37 | 97.9 | |||
| DF-GE | 0.67 | 0.87 | 1.48 | 0.77 | 1.76 | 1.87 | 2.18 | 2.95 | 6.53 | 99.3 |
| DF-GE(L1+L5) | 0.66 | 1.07 | 1.70 | 0.82 | 1.54 | 1.96 | 4.62 | 4.45 | 9.87 | 89.1 |
| DF-GEJ | 0.62 | 0.83 | 1.45 | 0.80 | 1.84 | 1.97 | 2.10 | 2.66 | 6.17 | 99.6 |
| DF-GEJ(IONO-FREE) | 1.71 | 2.04 | 1.63 | 1.69 | 2.85 | 2.04 | 5.17 | 5.32 | 8.67 | 63.5 |
| DF-GEJC | 0.84 | 1.62 | 1.46 | 0.85 | 1.94 | 1.84 | 2.15 | 2.68 | 6.18 | 99.7 |
| DF-GEJC without GEO | 0.61 | 0.92 | 1.40 | 0.73 | 1.84 | 1.84 | 2.19 | 2.68 | 6.21 | 99.7 |
| Frequency-GNSS | E (m) | N (m) | U (m) | Availability (%) | Average Number of Observations |
|---|---|---|---|---|---|
| SF-G | 2.391 | 3.268 | 5.698 | 62.1 | 5.9 |
| SF-GE | 0.508 | 1.601 | 2.835 | 85.8 | 9.4 |
| SF-GEJ | 0.482 | 1.379 | 1.810 | 88.3 | 11.5 |
| SF-GEJC | 0.489 | 1.392 | 1.831 | 92.9 | 14.2 |
| DF-G | 1.332 | 1.539 | 2.031 | 77.1 | 7.1 |
| DF-GE | 0.592 | 1.238 | 2.047 | 92.7 | 14.7 |
| DF-GEJ | 0.506 | 1.252 | 1.875 | 94.9 | 19.0 |
| DF-GEJC | 0.460 | 1.131 | 1.941 | 97.8 | 22.1 |
| Frequency-GNSS | E (m) | N (m) | U (m) |
|---|---|---|---|
| SF-GEJC | 0.830 | 1.973 | 4.115 |
| DF-GEJC | 0.713 | 1.442 | 2.156 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Wang, F.; Sang, J.; Lin, X.; Gong, X.; Zhang, W. Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment. Remote Sens. 2020, 12, 744. https://doi.org/10.3390/rs12040744
Guo L, Wang F, Sang J, Lin X, Gong X, Zhang W. Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment. Remote Sensing. 2020; 12(4):744. https://doi.org/10.3390/rs12040744
Chicago/Turabian StyleGuo, Lei, Fuhong Wang, Jizhang Sang, Xiaohu Lin, Xuewen Gong, and Wanwei Zhang. 2020. "Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment" Remote Sensing 12, no. 4: 744. https://doi.org/10.3390/rs12040744
APA StyleGuo, L., Wang, F., Sang, J., Lin, X., Gong, X., & Zhang, W. (2020). Characteristics Analysis of Raw Multi-GNSS Measurement from Xiaomi Mi 8 and Positioning Performance Improvement with L5/E5 Frequency in an Urban Environment. Remote Sensing, 12(4), 744. https://doi.org/10.3390/rs12040744