1. Introduction
Hyperspectral Image (HSI) comprise hundreds of narrow and contiguous spectral bands, and each represents the measured intensity of a narrower range of light frequencies [
1]. The great spectral resolution of HSI improves the capability of precisely discriminating the surface materials of interest [
2,
3]. Such abundant spectral information makes it beneficial to a wide range of applications, especially in some cases that cannot be directly detected by humans. For most of these applications, HSI classification has been an active area of research in remote sensing research. Abundant spectral resolution is useful for classification problems but at the expense of much lower spatial resolution. Because of the low spatial resolution of HSI, the spectral signature of each pixel contains a mixture of different spectra, which is caused by the multiple components that form the ground surface materials. If a pixel is highly mixed in HSI data, it is very difficult to categorize it in the original feature space. Therefore, the presence of mixed pixels is one of the major obstacles affecting seriously the classifier accuracy [
4].
In recent years, in HSI data analysis, the spectral unmixing techniques [
5] have been employed to handle with the mixed pixel issue. The spectral unmixing includes two steps: (1) extracting the pure material spectra (endmembers) from the HSI and (2) calculating their relative proportions (abundances) of the HSI data [
6]. Spectral unmixing has been extensively studied as a possible solution in HSI analysis. Related research works and applications have been developed in many fields, such as HSI super-resolution, denoising, change detection, and so on [
7,
8,
9]. For instance, in Reference [
7], Lanaras et al. proposed a method which performs hyperspectral super-resolution by jointly coupled spectral unmixing. The proposed joint formulation significantly improves hyperspectral super-resolution. Yang et al. [
8] proposed a sparse representation framework that unifies denoising and spectral unmixing in a closed-loop manner. This method utilizes spectral information from spectral unmixing as feedback to correct spectral distortion, while denoising and spectral unmixing act as constraints to iteratively solve other constraints. In Reference [
9], a general framework for HSI change detection using sparse unmixing is proposed. This model has the potential to get more information than other change detection techniques.
Moreover, spectral unmixing also carries valuable information for the HSI classification problem. A brief review of existing HSI classification methods with spectral unmixing is given below. Generally, these algorithms can be divided into two groups. Firstly, spectral unmixing has been widely studied as a feature extraction strategy before classification [
10,
11,
12,
13]. For instance, in Reference [
10], unmixing results is used to improve classification performance in an alternative strategy and spectral unmixing can be used to extract suitable features for future classify images. Later, Dópido et al. [
11] quantitatively evaluated the unmixing-based feature extraction methods, and further proved that these features can effectively improve the accuracy of classification. This strategy was further explored in many works [
12,
13] and also proved that the unmixing before classification provided an effective solution for HSI classification. Secondly, several techniques are proposed to utilize the complementarity of the classification and spectral unmixing in a semi-supervised framework, where the abundance maps have been applied as a supplementary source for the multinomial logistic regression (MLR) classifier [
14,
15,
16,
17]. First, the framework utilizes the information provided by spectral unmixing to select new training samples for classification, and then it integrates the abundance maps and classification to obtain the final classification results. This strategy considers the output provided by both classification and unmixing simultaneously, which provides a joint approach for HSI interpretation and can effectively improve the classification results, particularly when the available training set is very limited.
More recently, the deep learning-based methods have shown state-of-the-art performance in HSI classification [
18,
19,
20,
21,
22], thanks to its great success in computer vision and the fast advancement of computing facilities [
23,
24,
25,
26,
27]. Instead of shallow manually-crafted features, deep learning network models can extract high-level, hierarchical and abstract features which are generally more robust to nonlinear processing. In Reference [
18], Pan et al., proposed a simplified deep learning model called R-VCANet [
18] (vertex component analysis network) based on the deep learning baseline PCANet [
27]. In recent studies, convolutional neural networks (CNNs) [
23] are most often used in deep learning-based methods for HSI classification [
19,
20,
21]. For example, a 3D CNN based on the 3D convolutional kernel is proposed in Reference [
19], and the discriminative spectral-spatial features and classification are performed in an end-to-end manner. Zhong et al. [
20] proposed a supervised spectral-spatial residual network (SSRN) based on the residual neural network (ResNet) [
24]. An SSRN consists of consecutive spectral and spatial residual blocks, which are used to extract spectral-spatial features of HSI.
Furthermore, dense convolutional networks (DenseNet) have demonstrated significant achievement in deep learning network models and have also been used for HSI classification [
28,
29,
30], particularly in limited training samples, because the dense connections have a regularizing effect, which reduces overfitting on tasks with smaller training set sizes [
31]. In Reference [
21], a 3D dense convolutional network with multiple scales dilated convolutions [
32] and a spectral-wise attention mechanism (MSDN-SA) is proposed for HSI classification with limited training samples. The 3D CNN has a very important characteristic, that is they can directly create hierarchical representations of spectral-spatial data. However, the number of parameters grows exponentially when convolution goes from 2D to 3D. Due to the additional kernel dimension, 3D network has more parameters than 2D CNN. A large number of parameters make it easily prone to over-fitting when there are only limited labeled samples. Besides, when the 3D network is applied to HSI classification, the power of 3D network comes at a considerable cost, namely the computational cost of applying them to new examples. It is necessary to design a network model for resource-efficient HSI classification with limited training samples [
33].
Considering the successful combination of HSI unmixing and classification, as well as the development of deep learning, we aimed at integrating spectral unmixing with deep learning-based classification algorithm to improve the classification accuracy. Little research has been undertaken on the combining of these two techniques. Recently, Alam et al. [
12] used spectral unmixing to generate abundance maps and then used abundance maps as the input for deep learning-based HSI classification. However, in some cases, it is important to take advantage of the unmixing and classification information in a complementary manner, but the algorithm [
12] uses the information provided by spectral separation before classification [
15].
Based on the above motivations, a novel 3D/2D dense network where multiple intermediate classifiers are integrated with the spectral unmixing method for HSI classification is proposed. For HSI data with mixed pixels, compared with state-of-the-art CNN, this model shows its superiority in terms of overall classification accuracy, especially in limited training samples. The three contributions of this paper can be summarized as follows.
Our model adopts a specially designed network with multiple intermediate classifiers that is trained end-to-end. A 3D/2D dense networks with multiple intermediate classifiers (3D/2DNets) are jointly optimized during training and early-exiting strategy is adopted for each sample during testing. This is a resource-efficient model concerning other deep learning-based HSI classifiers.
We proposed a spectral-spatial 3D/2D convolution (SSDC) for the proposed framework. It enables the network to incorporate fewer 3D convolutions, while taking advantage of 2D convolutions to obtain more spectral information feature maps and enhance feature learning capabilities, thereby reducing the training complexity of each round of spectral-spatial fusion, which reduces overfitting on tasks with limited training samples.
An adaptive spectral unmixing is proposed as a complementary source for classification. The endmember composition of each pixel is established by the probabilistic output of softmax adaptively.
The remainder of this paper is organized as follows. In
Section 2, we describe our approach for HSI classification. The experimental results are presented and discussed in
Section 3 and
Section 4. Finally, in
Section 5, the paper is summarized.
2. Proposed Methods
2.1. Overview
The proposed method aims to learn an early-exiting deep learning framework for HSI classification based on 3D/2D dense networks (denoted as 3D/2DNets) and adaptive spectral unmixing (ASU). The whole framework is abbreviated as ASU-3D/2DNets. We exploit the fact that HSI data is typically a combination of easy examples and hard examples. Based on the above facts, a 3D/2D dense network with early-exiting strategy is proposed, which can reduce the evaluation time without loss of accuracy. Furthermore, considering the pixels with a low probabilistic output are either mixed pixels or pixels that are difficult to classify due to spectral variability, we unmix the hard samples to get more accurate classification results.
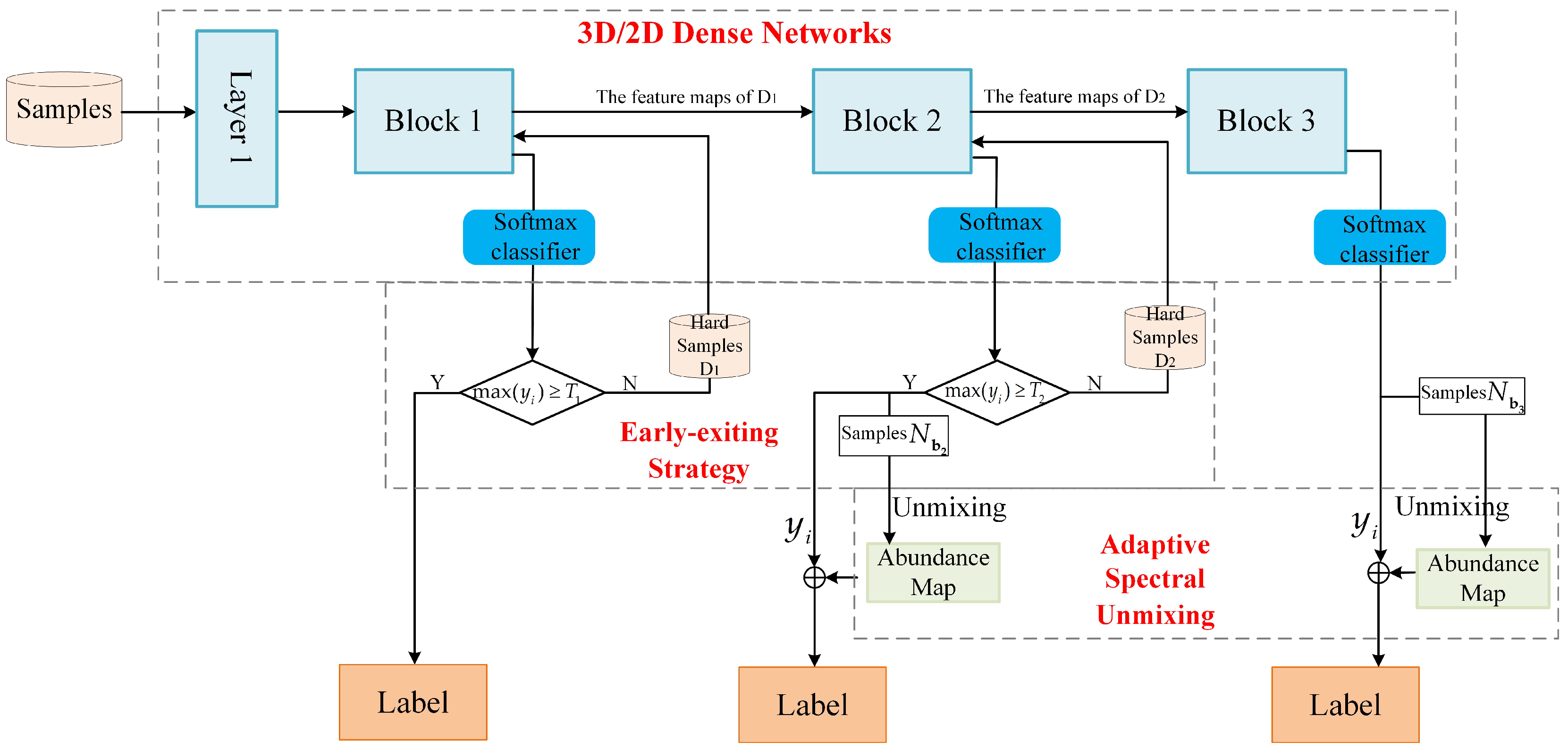
The framework of the proposed method is shown in
Figure 1. All available labeled samples are divided into three parts: training samples, validation samples, and testing samples. The method is mainly composed of three parts: 3D/2D dense networks; early-exiting strategy; and adaptive spectral unmixing.
3D/2D dense networks: To be specific, the 3D/2D dense networks composed of one convolution layer and three blocks, each block is connected to a classifier exit. In training processing, a 3D/2D dense network with multiple intermediate classifiers is jointly optimized.
Early-exiting strategy: Considering the existence of mixed pixels in HSI, the pixels in HSI classification can be divided into hard samples and easy samples. We intend to prioritize easy samples from early layer and difficult to classify samples (hard samples) from later layers. This process is called the early-exit strategy. All samples first pass the Block 1, each sample can be assigned to a class and the probability of each sample in the softmax layer is denote as , where , , i is the number of categories. If the softmax probability value of samples obtained in the classification process is greater than a chosen threshold , the system sends them down to exit; otherwise, it sends the samples (the hard samples ) to the Block 2. After the samples pass through the Block 2, if the softmax probability value of samples obtained in the classification process is greater than a chosen threshold , the system will send them to exit and future unmix them. Otherwise, the samples (the hard samples ) will be input into the Block 3 to continue to extract deeper features. The samples output from each block is represented as , , and , respectively.
Adaptive spectral unmixing: At the exit of the
Block 2, by considering the results of the coarse classification step and applying the fully constrained least squares (FCLS) [
34] method to each unlabeled pixel, spectral unmixing is performed to the unclassified pixels to obtain the abundance maps. As a result, abundance maps provide additional information about the composition of each pixel. Finally, the contribution degree of abundance maps and classification results are controlled by weight, and the final classification map is obtained.
Next, we will detail the 3D/2D dense networks with early-exiting strategy and adaptive spectral unmixing.
2.2. 3D/2D Dense Networks with Early-Exiting Strategy
Recently, two-dimensional multi-scale dense networks (MSDNets) is first proposed for resource-efficient image classification [
35]. MSDNets uses a cascade of intermediate early-exiting classifiers throughout the network. In these intermediate early-exiting classifiers setting, MSDNets can improve the average accuracy by reducing the amount of computation spent on easy samples to save up computation for hard samples [
35].
Based on the fact of that HSI data is typically a mix of easy examples and hard examples, we are trying to apply MSDNets to the HSI classification, thereby increasing the classification accuracy whilst reducing the computational requirements. As HSI data are 3D cubes, it is reasonable to extend the 2D model to the 3D model for HSI classification; however, greatly increasing on both computational complexity and memory usage has followed. To resolve this problem, an early-exiting dense network with mixed 3D and 2D convolutions (3D/2DNets) is proposed. In this section, we first give a detailed description of early-exiting dense networks. Then, a 3D/2D convolution based on spectral and spatial information is presented for early-exiting dense networks.
2.2.1. Dense Networks Architecture with Early-Exiting Strategy
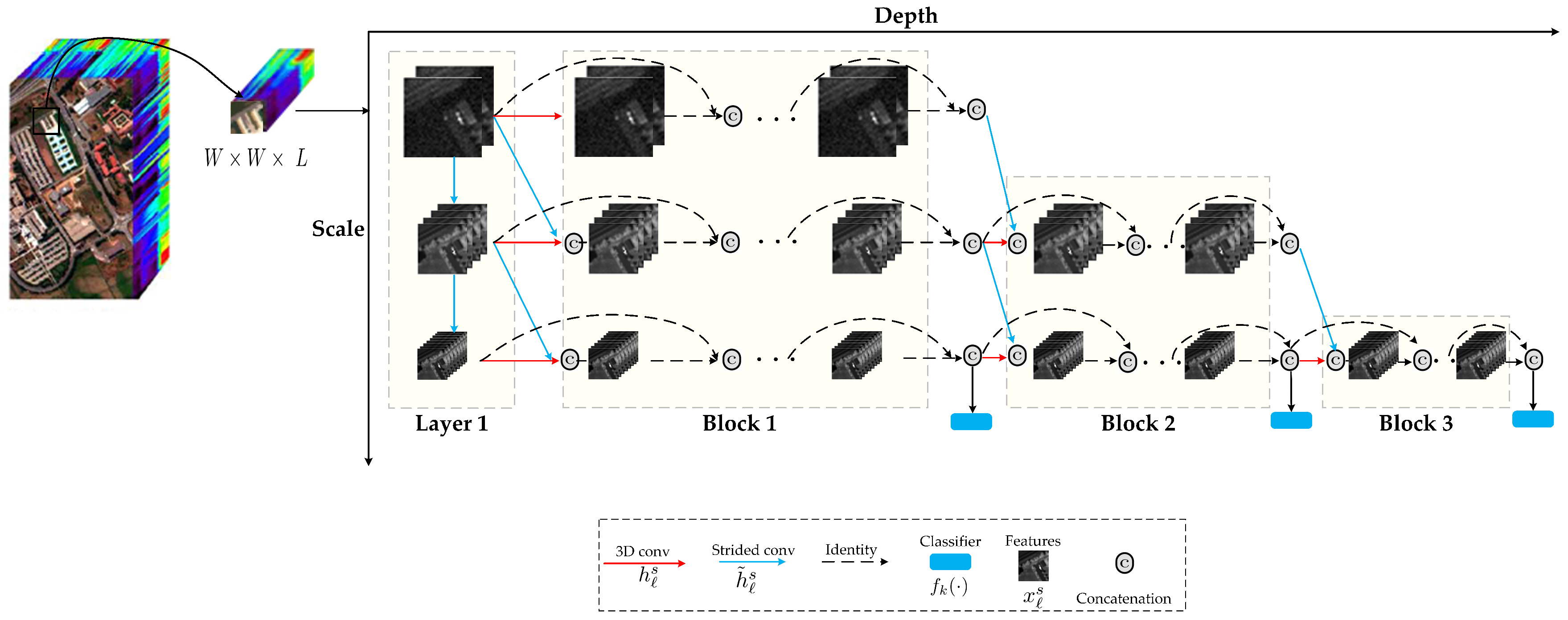
Figure 2 gives an illustration of the dense networks architecture with early-exiting strategy. As shown, the network is based on DenseNets [
31] and cascaded intermediate early-exiting classifiers throughout the network. Because coarse-scale features are important to classify the content of the sample patch into a single class, the network maintains a feature representation at multiple scales throughout the network, and all the classifiers only use the coarse-level features. We perform the early-exiting of the easy examples at early classifiers whilst propagating hard examples through the entire network, using the procedure described in
Section 2.1.
In sample extraction, we extract cube with the size , where W and L are the spatial size and the number of spectral bands, respectively. Each cube is extracted from a neighborhood window centered around a pixel, and the label of each sample is that of the pixel located in the center of this cube. Then, we feed 3D cube into the multi-scale dense networks model, which is itself composed of one convolution layer and three blocks, to obtain the classification result.
- (1)
The convolutional layer functions in the first layer ( ), ; denote a sequence of -sized 3D convolutions (Conv), the batch normalization layer with rectified linear unit (ReLU) function, and a 3D max pooling layer with -sized kernel, stride of 2. The output feature maps at ℓ layer and scale s are denoted as .
- (2)
For subsequent feature layers in each block, the transformations
and
are defined following the design in DenseNets [
32]: Conv(
)-BN-ReLU-Conv(
)-BN-ReLU. We set the number of output channels of the three scales to 6, 12, and 24, respectively. The output feature maps
produced at subsequent layers,
and scales
s, are a concatenation of transformed feature maps from all previous feature maps of scale
s and
(if
).
- (3)
Each classifier has two down-sampling convolutional layers with 128 dimensional filters, followed by a 3D average pooling layer and a linear layer. The classifier at layer ℓ uses all the features . Let denote the k th classifier, every sample traverses the network and exits after classifier if its prediction confidence (we use the maximum value of the softmax probability as a confidence measure) exceeds a pre-determined threshold T.
During training, we use cross entropy loss functions
for all classifiers and minimize a cumulative loss as follows:
where
D denotes the training set.
2.2.2. 3D/2D Convolutional Based on Spectral-Spatial Information
In HSI classification, a 3D convolution couples spectral-spatial information to effectively extract spectral-spatial features. Though promising, regarding 2D CNN, 3D CNN extends the spatial kernel to spectral-spatial space, which significantly increase the number of parameters, thus greatly increasing the computational complexity and memory usage, as well as increasing the network’s demand for huge training sets [
36]. It can be seen from the above analysis that the above facts limit the performance of existing 3D CNN on HSI classification, especially in dense convolution networks based on 3D convolution [
21]. There are currently some efforts to ameliorate the downside of the 3D convolution model in HSI classification. Zhong et al. [
20] first employed the style of residual connection to extract the spectral features by continuous 1D convolution, and then used 3D convolution to extract spatial information. Furthermore, in Reference [
37], the combination of a 2D spatial convolution and a 1D spectral convolution was used to replace spectral-spatial 3D convolution, which means that this network structure was no longer 3D CNN.
Recently, intertwined 3D/2D networks [
38,
39,
40] have shown up as a hybrid between 2D CNN and 3D CNN in human action recognition. In Reference [
38], a mixed convolutional tube (MiCT) was proposed to integrate 2D convolution with the 3D convolution to learn better spatio-temporal features. Compared to the 3D CNN, a benefit of using such 3D/2D networks is that the parameters involved in the networks are much reduced.
Inspired by this, to alleviate the drawback of 3D convolution in the HSI classification, inspired by Reference [
38], we proposed a spectral-spatial 3D/2D convolution (SSDC) for HSI, as illustrated in
Figure 3. The SSDC replaces each 3D convolution in the first layer of the proposed framework. Considering the HSI data has a lot of redundant spectral information among consecutive bands, this results in redundant information in feature maps along the spectral dimension. In the first layer, if all the bands are directly used in the network input, the 3D sample block will input too many parameters and increase the computational complexity. Therefore, the proposed SSDC is used to replace the 3D convolution used in the first layer network. It enables the network to incorporate fewer 3D convolutions, while taking advantage of 2D convolutions to obtain more spectral information feature maps and enhance feature learning capabilities, thereby reducing the training complexity of each round of spectral-spatial fusion, which reduces overfitting on tasks with limited training samples.
The shortcut in our SSDC is cross-domain [
38] is different from the residual connections in previous works [
21,
24]. The SSDC is obtained by 3D convolution mapping for the 3D inputs and a 2D convolution mapping for the 2D inputs. By introducing a 2D convolution to extract the 2D features information on each band, the 3D convolution in SSDC only needs to learn residual information along the spectral dimension. Thus, the cross-domain residual connection largely reduces the complexity of SSDC in 3D convolution kernels learning.
2.3. An Adaptive Endmember Selection of Unmixing
As described above, the method of combining classification and unmixing has achieved good results in pixel labeling, in which the abundance maps have been used as an auxiliary information source in the MLR classifier [
10,
11,
16]. However, all the above methods process all pixels in the same way, but the fact that hyperspectral data is that some samples may be not highly mixed (in this case, the coarse classification step may be sufficient to characterize them), and some samples may be highly mixed (in this case, spectral unmixing is particularly useful for enhancing the classification) [
15]. With the aforementioned issues in mind, adaptive spectral unmixing is introduced to the 3D/2D dense networks with early-exiting classifier. Through this network architecture, the easy examples were correctly classified and exited by the first classifier. The examples with low probabilistic outputs are either mixed pixels or pixels hard to classify due to spectral variability; we unmix the hard samples to achieve more accurate classification results. In general, adaptive spectral unmixing consists of two important parts, the collection of endmembers spectrum and adaptive endmember selection.
Firstly, in our framework, the spectral signatures used for unmixing purposes are not obtained by endmember extraction but are obtained by averaging the spectral signatures of each labeled category in the training set. Although the average endmembers will cause a decrease in spectral purity, it can reduce the effects of noise and/or average the subtle spectral variability of each spectral category, resulting in a more representative final endmember as a whole [
10,
13].
In the spectral unmixing of mixed pixels, the choice of endmembers is extremely important. We did a simple experiment, and
Figure 4 shows the classification results of each block output. In
Figure 4, we find the hard samples (maybe highly mixed), which are from the second and third classifiers, and the probabilistic output of top3—the top3 value refers to the top three in the maximum probability vector. As long as the correct probability is present, the prediction is correct; otherwise, the prediction error is close to 99% in second classifiers, and the probabilistic output of top5 is also 95% in third classifiers. So, we speculate that the endmember composition of a mixed pixel can represent its main component with a few endmembers instead of all endmembers, and according to the different spectral purity, different processing strategies should be adopted for different types of the pixel. This theory has also been verified in the literature [
15]. Therefore, we propose an endmember selection of unmixing in which the probabilistic output of softmax is exploited to determine the endmember set for each pixel.
To be specific, all samples first pass the first block, and every sample can be assigned to a class. If the probabilistic output obtained in the classification process is greater than a chosen threshold
T (
and
), the system sends it down to exit; otherwise, it sends the sample to the second block. It is worth mentioning that the easy examples were correctly classified and exited directly by the first classifier. For each sample output from the second classifier, we take the top3 result of the corresponding probabilistic output as the endmember, and for the sample output by the third classifier, we take the top5 of the probabilistic output classification result as the endmember.
where
is the selected endmember set of sample
i from the
k th classifier. If
, then
; if
, then
.
denotes endmember set.
Lastly, the adaptive endmembers are adopted for the fully constrained least squares (FCLS) [
34] unmixing model. As a result, abundance map provides additional information about the composition of each pixel. Finally, the contribution degree of abundance map and classification result is controlled by weight
, and the final classification map
is obtained as follows:
where function
is the probability obtained by the classification algorithm, i.e., the
kth classifier described in
Section 2.2.1; and function
is the abundance fraction obtained by the spectral unmixing with adaptive endmember
.