Spatiotemporal Distribution and Risk Assessment of Heat Waves Based on Apparent Temperature in the One Belt and One Road Region
Abstract
:1. Introduction
- A new heat wave calculation method, CHWT (Combined Heat Wave Threshold), is proposed, which considers the heterogeneity of heat wave thresholds temporally and spatially.
- The annual heat wave dataset for 1989–2018 in the OBOR region was calculated based on CHWT. The heat wave dataset includes Heat Waves Frequency (HWF), Heat Waves Total Duration (HWTD), Heat Waves Maximum Duration (HWMD), Heat Waves Maximum Apparent Temperature (HWMAT), Heat Waves Start Date (HWSD) and Heat Waves End Date (HWED).
- The spatiotemporal distribution of apparent temperature and heat waves in the OBOR region was identified.
- The heat wave risk of the OBOR region was assessed. We point out the high heat wave risk area, which is of great significance for residents life, enterprise investment and tourism planning.
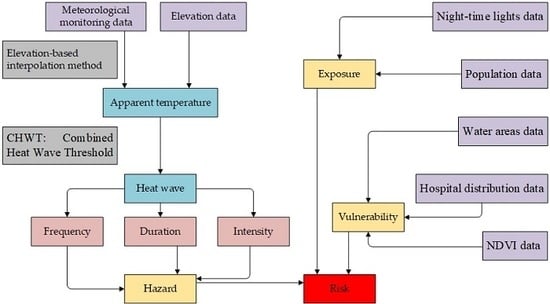
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. MissForest: Non-Parametric Missing Value Imputation
- We assume X = (X1, X2, …, Xp) to be a n × p-dimensional data matrix. For an arbitrary variable Xs with missing values, we can separate the dataset into four parts:y(s)obs: the observed values of variable Xs;y(s)mis: the missing values of variable Xs;x(s)obs: the variables other than Xs with observations;x(s)mis: the variables other than missing values of Xs with observations.
- First, an initial guess for the missing values is made in X using the mean/median imputation method. Second, the variables are sorted Xs, s=1, …, p according to the amount of missing values from small to large. For each variable Xs, the missing values are imputed by first fitting an RF with response y(s)obs and predictors x(s)obs; then, predicting the missing values y(s)mis by applying the trained RF to x(s)mis. The imputation procedure is repeated until the latest imputation result is not better than the previous one [48].
2.2.2. Elevation-Based Interpolation Method
- First, an initial correction of the temperature is made. The temperature at the given station is corrected to the zero plane. At this time, the temperature has no relationship with elevation but rather only the spatial correlation and spatial heterogeneity exist on the same plane, qualifying the use of a traditional interpolation method (such as Ordinary Kriging), defined as Equation (1):where Tc1 is first corrected temperature (°C), Ta is the monitoring station temperature (°C), and E is the monitoring station elevation (m).
- Then, the corrected temperature is interpolated to a synthetic mesh of 0.1° x 0.1°. Based on the first corrected temperature, the traditional interpolation method is used for interpolation. In this study, we use Kriging tool in arcpy software package provided by ArcGIS for interpolation, which uses the Ordinary Kriging method, spherical semi variance model and lag size is 0.371455. At this time, we obtained the temperature data covering the whole study area on the assumption of a zero plane, defined as Equation (2):where Ti is interpolated temperature (°C).
- Finally, the second temperature correction is performed. Using elevation data, the interpolated temperature data is corrected again to its actual elevation. At this time, the temperature data take topographic features into account, which can show the obvious vertical zonation, defined as Equation (3):where Tc2 is the second corrected temperature (°C).
2.2.3. Apparent Temperature
2.2.4. CHWT: Combined Heat Wave Threshold
3. Results
3.1. Dataset Validation
- 15% of the daily available monitoring stations are randomly selected as the verification set, which are discretely distributed in the whole study area at different altitudes. The apparent temperature of each station in the verification set is calculated as the real value.
- Using the elevation-based interpolation method, the daily apparent temperature grid data covering the whole study area are obtained from all available monitoring stations.
- The apparent temperature at the validation set stations are extracted from the daily apparent temperature grid data as the predictive value.
- By comparing the predictive value with the corresponding real value, the validation result is obtained.
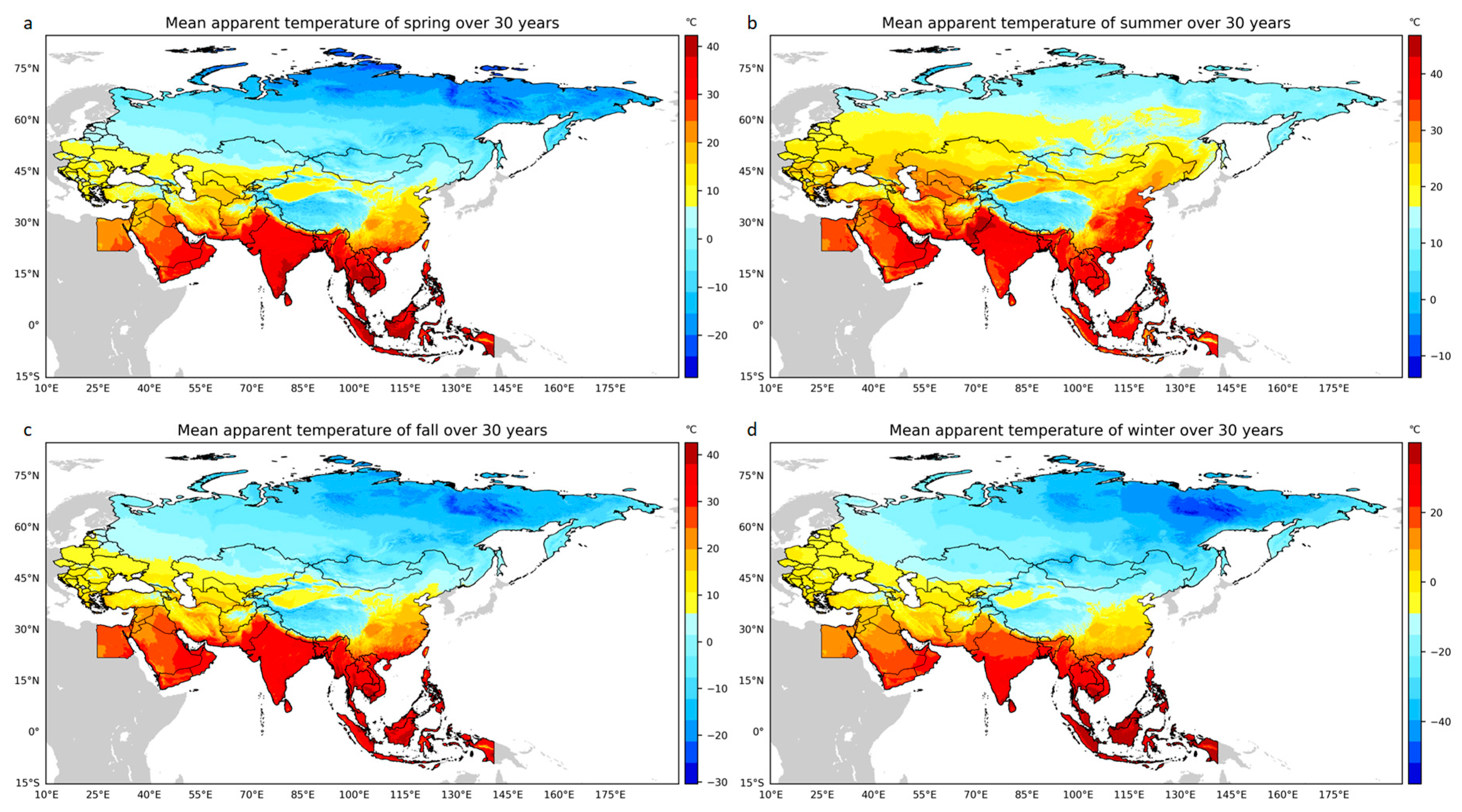
3.2. Seasonal Variation of Apparent Temperature for 1989–2018
3.3. Spatiotemporal Distribution of Heat Wave for 1989–2018
3.4. Heat Wave Risk Assessment
4. Discussion
4.1. Comparison with Other Results
4.2. Improvements and Limitations
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mazdiyasni, O.; Sadegh, M.; Chiang, F.; AghaKouchak, A. Heat wave Intensity Duration Frequency Curve: A Multivariate Approach for Hazard and Attribution Analysis. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J. The Current Situation of the One Belt and One Road Initiative and Its Development Trend. In Annual Report on the Development of the Indian Ocean Region (2017); Wang, R., Zhu, C., Eds.; Springer: Singapore, 2018; pp. 103–137. [Google Scholar] [CrossRef]
- Peng, C.; Regmi, A.D.; Qiang, Z.; Yu, L.; Chen, X.; Cheng, D. Natural Hazards and Disaster Risk in One Belt One Road Corridors. In Workshop on World Landslide Forum; Mikos, M., Tiwari, B., Yin, Y., Sassa, K., Eds.; Springer: Cham, Switzerland, 2017; pp. 1155–1164. [Google Scholar]
- Cui, P.; Su, F. Application of domestic high resolution satellite in “One Belt and One Road” natural disaster risk management. Satell. Appl. 2016, 8–11. [Google Scholar]
- Mazdiyasni, O.; AghaKouchak, A.; Davis, S.J.; Madadgar, S.; Mehran, A.; Ragno, E.; Sadegh, M.; Sengupta, A.; Ghosh, S.; Dhanya, C.T.; et al. Increasing probability of mortality during Indian heat waves. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [Green Version]
- Aboubakri, O.; Khanjani, N.; Jahani, Y.; Bakhtiari, B. The impact of heat waves on mortality and years of life lost in a dry region of Iran (Kerman) during 2005–2017. Int. J. Biometeorol. 2019, 63, 1139–1149. [Google Scholar] [CrossRef]
- Dadbakhsh, M.; Khanjani, N.; Bahrampour, A.; Haghighi, P.S. Death from respiratory diseases and temperature in Shiraz, Iran (2006–2011). Int. J. Biometeorol. 2017, 61, 239–246. [Google Scholar] [CrossRef]
- Khanjani, N.; Bahrampour, A. Temperature and cardiovascular and respiratory mortality in desert climate. A case study of Kerman, Iran. Iran. J. Environ. Health Sci. Eng. 2013, 10. [Google Scholar] [CrossRef] [Green Version]
- Ranandeh Kalankesh, L.; Mansouri, F.; Khanjani, N. Association of Temperature and Humidity with Trauma Deaths. Trauma Mon. 2015, 20, e23403. [Google Scholar] [CrossRef] [Green Version]
- Sharafkhani, R.; Khanjani, N.; Bakhtiari, B.; Jahani, Y.; Tabrizi, J.S. Physiological Equivalent Temperature Index and mortality in Tabriz (The northwest of Iran). J. Therm. Biol. 2018, 71, 195–201. [Google Scholar] [CrossRef]
- Wang, Y.; Nordio, F.; Nairn, J.; Zanobetti, A.; Schwartz, J.D. Accounting for adaptation and intensity in projecting heat wave-related mortality. Environ. Res. 2018, 161, 464–471. [Google Scholar] [CrossRef]
- Hatvani-Kovacs, G.; Belusko, M.; Pockett, J.; Boland, J. Assessment of Heatwave Impacts. In Fourth International Conference on Countermeasures to Urban Heat Island; Wong, N.H., Jusuf, S.K., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2016; Volume 169, pp. 316–323. [Google Scholar]
- Anderson, B.G.; Bell, M.L. Weather-related mortality: How heat, cold, and heat waves affect mortality in the United States. Epidemiology 2009, 20, 205–213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vliet, M.T.H.V.; Yearsley, J.R.; Ludwig, F.; Vögele, S.; Lettenmaier, D.P.; Kabat, P. Vulnerability of US and European electricity supply to climate change. Nat. Clim. Chang. 2012, 2, 676–681. [Google Scholar] [CrossRef]
- Vliet, M.T.H.V.; Sheffield, J.; Wiberg, D.; Wood, E.F. Impacts of recent drought and warm years on water resources and electricity supply worldwide. Environ. Res. Lett. 2016, 11, 124021. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Velicogna, I.; Kimball, J.S. Characterizing ecosystem response to water supply changes inferred from GRACE drought severity index and surface soil moisture anomalies from ESA CCI and SMAP. In Proceedings of the Agu Fall Meeting; American Geophysical Union: Washington, DC, USA, 2017. [Google Scholar]
- Varghese, B.M.; Hansen, A.; Nitschke, M.; Nairn, J.; Hanson-Easey, S.; Bi, P.; Pisaniello, D. Heatwave and work-related injuries and illnesses in Adelaide, Australia: A case-crossover analysis using the Excess Heat Factor (EHF) as a universal heatwave index. Int. Arch. Occup. Environ. Health 2019, 92, 263–272. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Kovats, R.S.; Lloyd, S.J.; Holt, T.; Tol, R.S.J. The Direct Impact of Climate Change on Regional Labor Productivity. Arch. Environ. Occup. Health 2009, 64, 217–227. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Holmer, I.; Lemke, B. Workplace heat stress, health and productivity–an increasing challenge for low and middle-income countries during climate change. Glob. Health Action 2009, 2, 2047. [Google Scholar] [CrossRef]
- Kjellstrom, T.; Freyberg, C.; Lemke, B.; Otto, M.; Briggs, D. Estimating population heat exposure and impacts on working people in conjunction with climate change. Int. J. Biometeorol. 2017, 62, 1–16. [Google Scholar] [CrossRef]
- Velde, M.V.D.; Wriedt, G.; Bouraoui, F. Estimating irrigation use and effects on maize yield during the 2003 heatwave in France. Agric. Ecosyst. Environ. 2010, 135, 90–97. [Google Scholar] [CrossRef]
- Ingvordsen, C.H.; Lyngkjær, M.F.; Peltonen-Sainio, P.; Mikkelsen, T.N.; Stockmarr, A.; Jørgensen, R.B. How a 10-day heatwave impacts barley grain yield when superimposed onto future levels of temperature and CO2 as single and combined factors. Agric. Ecosyst. Environ. 2018, 259, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Cai, W.; Yang, C.; Liu, S.; Dong, W.; Zhang, H.; Yu, G.; Chen, Z.; He, H.; Guo, W. Severe summer heatwave and drought strongly reduced carbon uptake in Southern China. Sci. Rep. 2016, 6, 18813. [Google Scholar] [CrossRef] [Green Version]
- Smoyer-Tomic, K.E.; Kuhn, R.; Hudson, A. Heat Wave Hazards: An Overview of Heat Wave Impacts in Canada. Nat. Hazards 2003, 28, 465–486. [Google Scholar] [CrossRef]
- Harrison, M.T.; Cullen, B.R.; Rawnsley, R.P. Modelling the sensitivity of agricultural systems to climate change and extreme climatic events. Agric. Syst. 2016, 148, 135–148. [Google Scholar] [CrossRef]
- Moura, D.J.D.; Vale, M.M.D.; Nääs, I.D.A.; Rodrigues, L.H.A. Estimating Poultry Production Mortality Exposed to Heat Wave Using Data Mining. In Proceedings of the Livestock Environment Viii, Iguassu Falls, Brazil, 31 August–4 September 2008. [Google Scholar]
- Baldwin, J.W.; Dessy, J.B.; Vecchi, G.A.; Oppenheimer, M. Temporally Compound Heat Wave Events and Global Warming: An Emerging Hazard. Earth Future 2019, 7, 411–427. [Google Scholar] [CrossRef] [Green Version]
- Raei, E.; Nikoo, M.R.; AghaKouchak, A.; Mazdiyasni, O.; Sadegh, M. Data Descriptor: GHWR, a multi-method global heatwave and warm-spell record and toolbox. Sci. Data 2018, 5, 15. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Li, M.; Liu, Z.; Dong, W.; Shi, P. Mapping Heat Wave Risk of the World; Springer: Berlin/Heidelberg, Germany, 2015; pp. 169–188. [Google Scholar] [CrossRef]
- Horton, R.M.; Mankin, J.S.; Lesk, C.; Coffel, E.; Raymond, C. A Review of Recent Advances in Research on Extreme Heat Events. Curr. Clim. Chang. Rep. 2016, 2, 242–259. [Google Scholar] [CrossRef]
- Lau, N.-C.; Nath, M.J. A model study of heat waves over North America: Meteorological aspects and projections for the twenty-first century. J. Clim. 2012, 25, 4761–4784. [Google Scholar] [CrossRef]
- Lee, Y.-Y.; Grotjahn, R. California Central Valley summer heat waves form two ways. J. Clim. 2016, 29, 1201–1217. [Google Scholar] [CrossRef]
- An, N.; Dou, J.; González, J.E.; Bornstein, R.D.; Miao, S.; Li, L. An observational case study of synergies between an intense heatwave and the urban heat island in Beijing. J. Appl. Meteorol. Climatol. 2020. [Google Scholar] [CrossRef]
- Ao, X.; Wang, L.; Zhi, X.; Gu, W.; Yang, H.; Li, D. Observed Synergies between Urban Heat Islands and Heat Waves and Their Controlling Factors in Shanghai, China. J. Appl. Meteorol. Climatol. 2019, 58, 1955–1972. [Google Scholar] [CrossRef] [Green Version]
- Founda, D.; Santamouris, M. Synergies between Urban Heat Island and Heat Waves in Athens (Greece), during an extremely hot summer (2012). Sci. Rep. 2017, 7, 10973. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Ye, X. Social media analytics for natural disaster management. Int. J. Geogr. Inf. Sci. 2017, 32, 49–72. [Google Scholar] [CrossRef]
- Zagorecki, A.T.; Johnson, D.E.A.; Ristvej, J. Data mining and machine learning in the context of disaster and crisis management. Int. J. Emerg. Manag. 2013, 9. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y. An Inter-comparison of Three Heat Wave Types in China during 1961-2010: Observed Basic Features and Linear Trends. Sci. Rep. 2017, 7, 45619. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.; Ebi, K.L.; Forsberg, B. Heatwave early warning systems and adaptation advice to reduce human health consequences of heatwaves. Int. J. Environ. Res. Public Health 2011, 8, 4623–4648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mistry, M.N. A High-Resolution Global Gridded Historical Dataset of Climate Extreme Indices. Data 2019, 4, 41. [Google Scholar] [CrossRef] [Green Version]
- Defrance, D. Dataset of global extreme climatic indices due to an acceleration of ice sheet melting during the 21st century. Data Brief 2019, 27, 104585. [Google Scholar] [CrossRef]
- Mandal, R.; Joseph, S.; Sahai, A.; Phani, M.K.; Dey, A.; Chattopadhyay, R.; Pattanaik, D. Real time extended range prediction of heat waves over India. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef]
- National Centers for Environmental Information, N. Global Historical Climate Network. National Centers for Environmental Information; NCEI: Asheville, NC, USA, 2019. [Google Scholar]
- Meng, J.; Li, C. Missing value interpolation of classified data based on random forest model. Stat. Inf. Forum 2014, 29, 86–90. [Google Scholar]
- Tang, F.; Ishwaran, H. Random forest missing data algorithms. Stat. Anal. Data Min. Asa Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Bühlmann, P. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-filled seamless SRTM data V4. International Centre for Tropical Agriculture (CIAT); Apartado Aéreo 6713: Cali, Colombia, 2008. [Google Scholar]
- Blaikie, P.; Cannon, T.; Davis, I.; Wisner, B. At risk: Natural Hazards, People’s Vulnerability and Disasters; Routledge: Abingdon, UK, 2005. [Google Scholar]
- Brooks, N.; Adger, W.N.; Kelly, P.M. The determinants of vulnerability and adaptive capacity at the national level and the implications for adaptation. Glob. Environ. Chang. 2005, 15, 151–163. [Google Scholar] [CrossRef]
- Cardona, O.D.; Van Aalst, M.K.; Birkmann, J.; Fordham, M.; Mc Gregor, G.; Rosa, P.; Pulwarty, R.S.; Schipper, E.L.F.; Sinh, B.T.; Décamps, H. Determinants of risk: Exposure and vulnerability. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; pp. 65–108. [Google Scholar]
- Kaźmierczak, A.; Cavan, G. Surface water flooding risk to urban communities: Analysis of vulnerability, hazard and exposure. Landsc. Urban Plan. 2011, 103, 185–197. [Google Scholar] [CrossRef]
- Earth Observation Group, E.O.G. Version 4 DMSP-OLS Nighttime Lights Time Series; National Centers for Environmental Information: Asheville, NC, USA, 2019. [Google Scholar]
- Center for International Earth Science Information Network, C.C.U. Gridded Population of the World, Version 4 (GPWv4): Basic Demographic Characteristics, Revision 11; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2018. [Google Scholar]
- Food and Agriculture Organization of the United Nations. FAO Geonetwork; FAO: Rome, Italy, 2015. [Google Scholar]
- OpenStreetMap contributors, O.S.M. OpenStreetMap; OpenStreetMap: London, UK, 2019. [Google Scholar]
- Eric, V. The Climate Data Guide: NDVI: Normalized-difference-vegetation-index: NOAA AVHRR; National Center for Atmospheric Research Staff (Eds): Asheville, NC, USA, 2018. [Google Scholar]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef] [Green Version]
- Städler, N.; Bühlmann, P. Pattern alternating maximization algorithm for high-dimensional missing data. arXiv Prepr. arXiv 2010, 1005, 1903–1928. [Google Scholar]
- Van Buuren, S.; Oudshoorn, K. Flexible Multivariate Imputation by MICE.; TNO: Leiden, The Netherlands, 1999. [Google Scholar]
- Meng, L.; Xiuli, W.; Yuanyuan, D. Comparison of several daily temperature interpolation methods. Anhui Agric. Sci. 2014, 8670–8674. [Google Scholar] [CrossRef]
- Chen, D.H.; Chen, Z.; Wang, S.Y.; Hu, L.I.; Zhang, X.S.; Geography, D.O.; Fuzhou University. Study on Spatial Interpolation of the Average Temperature in the Yili River Valley Based on DEM. Spectrosc. Spectr. Anal. 2011, 31, 1925–1929. [Google Scholar]
- Zhao, J.; Fei, L.; Fu, H.; Ying, T.; Hu, Z. A DEM-based partition adjustment for the interpolation of annual cumulative temperature in China. Proc. Spie 2007, 6753. [Google Scholar] [CrossRef]
- Pan, Y.; He, C.; Zhang, Q.; Chen, J. Smart distance searching and DEM-informed interpolation of surface air temperature of climatology in China. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; pp. 3782–3785. [Google Scholar]
- Ning, L.; Yongming, X.; Miao, H.; Xiaohan, W. Retrieval of Apparent Temperature in Beijing Based on Remote Sensing. J. Ecol. Environ. 2018, 27, 1113–1121. [Google Scholar] [CrossRef]
- Hodder, S.G.; Parsons, K. The effects of solar radiation on thermal comfort. Int. J. Biometeorol. 2007, 51, 233–250. [Google Scholar] [CrossRef]
- Steadman, R.G. A Universal Scale Of Apparent Temperature. J. Clim. Appl. Meteorol. 1984, 23, 1674–1687. [Google Scholar] [CrossRef]
- Masterson, J.; Richardson, F. Humidex, a method of quantifying human discomfort due to excessive heat and humidity, Environment Canada. Atmos. Environ. Serv. Downsviewont. 1979, 151, 1–79. [Google Scholar]
- Francesca Romana, D.A.A.; Boris Igor, P.; Giuseppe, R. Thermal environment assessment reliability using temperature--humidity indices. Ind. Health 2011, 49, 95–106. [Google Scholar]
- Xin-Yin, X.U.; Jun-Qi, Y.U.; Hong-Lian, L.I.; Yang, L. Comparative study on calculation methods of dew-point temperature. J. Meteorol. Environ. 2016, 32, 107–111. [Google Scholar] [CrossRef]
- Bobb, J.F.; Dominici, F.; Peng, R.D. A Bayesian Model Averaging Approach for Estimating the Relative Risk of Mortality Associated with Heat Waves in 105 U.S. Cities. Biometrics 2011, 67, 1605–1616. [Google Scholar] [CrossRef]
- Roetzel, A.; Tsangrassoulis, A.; Dietrich, U.; Busching, S. A review of occupant control on natural ventilation. Renew. Sustain. Energy Rev. 2010, 14, 1001–1013. [Google Scholar] [CrossRef]
- Zuo, J.; Pullen, S.; Palmer, J.; Bennetts, H.; Chileshe, N.; Ma, T. Impacts of heat waves and corresponding measures: A review. J. Clean. Prod. 2015, 92, 1–12. [Google Scholar] [CrossRef]
- Fischer, E.M.; Schär, C. Future changes in daily summer temperature variability: Driving processes and role for temperature extremes. Clim. Dyn. 2009, 33, 917. [Google Scholar] [CrossRef]
- Dole, R.; Hoerling, M.; Perlwitz, J.; Eischeid, J.; Pegion, P.; Zhang, T.; Quan, X.-W.; Xu, T.; Murray, D. Was there a basis for anticipating the 2010 Russian heat wave? Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Russo, S.; Dosio, A.; Graversen, R.; Sillmann, J.; Carrao, H.; Dunbar, M.; Singleton, A.; Montagna, P.; Barbosa, P.; Vogt, J. Magnitude of extreme heat waves in present climate and their projection in a warming world. J. Geophys. Res. Atmos. 2014, 19, 12500–12512. [Google Scholar] [CrossRef] [Green Version]
- Turner, J.; Overland, J. Contrasting climate change in the two polar regions. Polar Res. 2009, 28, 146–164. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, X.; Tao, J.; Wu, J.; Wang, J.; Shi, P.; Zhang, Y.; Yu, C. The impact of climate change and anthropogenic activities on alpine grassland over the Qinghai-Tibet Plateau. Agric. For. Meteorol. 2014, 189–190, 11–18. [Google Scholar] [CrossRef]
- Crichton, D. The risk triangle. Nat. Disaster Manag. 1999, 102, 103. [Google Scholar]
- Carrão, H.; Naumann, G.; Barbosa, P. Mapping global patterns of drought risk: An empirical framework based on sub-national estimates of hazard, exposure and vulnerability. Glob. Environ. Chang. 2016, 39, 108–124. [Google Scholar] [CrossRef]
- Prabnakorn, S.; Maskey, S.; Suryadi, F.X.; de Fraiture, C. Assessment of drought hazard, exposure, vulnerability, and risk for rice cultivation in the Mun River Basin in Thailand. Nat. Hazards 2019, 97, 891–911. [Google Scholar] [CrossRef]
- Qin, H.U.; Jiang, D.; Fan, G. Climate Change Projection on the Tibetan Plateau: Results of CMIP5 Models. Chin. J. Atmos. Sci. 2015, 39, 260–270. [Google Scholar]
- Perkins, E.S. A review on the scientific understanding of heatwaves—Their measurement, driving mechanisms, and changes at the global scale. Atmos. Res. 2015, 164–165, 242–267. [Google Scholar] [CrossRef]










| Abbreviation | Full Name | Definition |
|---|---|---|
| HWF | Heat waves frequency | Number of heat waves in a year |
| HWTD | Heat waves total duration | Total duration of heat waves in a year |
| HWMD | Heat waves maximum duration | Duration of the longest heat wave in a year |
| HWMAT | Heat waves maximum apparent temperature | The highest apparent temperature of each heat wave in a year |
| HWSD | Heat waves start date | Start date of the first heat wave in a year |
| HWED | Heat waves end date | End date of the last heat wave in a year |
| RTT | Relative temperature threshold | \ |
| ATT | Absolute temperature threshold | \ |
| CRTT | Climatological relative temperature threshold | Percentile threshold based on historical temperature series for a day |
| ARTT | Annual relative temperature threshold | Percentile threshold based on annual temperature series |
| DT | Duration threshold | \ |
| Factor | Data | Resolution | Time | Format |
|---|---|---|---|---|
| Hazard | Heat wave frequency | Annually, 0.1° | 1989–2018 | Grid |
| Heat wave duration | Annually, 0.1° | 1989–2018 | Grid | |
| Heat wave intensity | Annually, 0.1° | 1989–2018 | Grid | |
| Exposure | DMSP night-time lights data | Annually, 30″ | 2010 | Grid |
| CIESIN population data | 30″ | 2010 | Grid | |
| Vulnerability | FAO water areas data | / | 2012 | Vector |
| OSM hospital distribution data | Daily | October, 2019 | Vector | |
| AVHRR NDVI data | Daily, 0.05° | July 1, 2010 | Grid | |
| DRYAD GDP data | Five years, 10 km | 2015 | Grid |
| Date | Slope | R2 | P Value | MAE | NMAE | RMSE | NRMSE |
|---|---|---|---|---|---|---|---|
| January 1, 1989 | 0.9962 | 0.9959 | 2.994 × e−321 | 0.527 | 0.3166 | 1.2028 | 0.108 |
| March 1, 1996 | 0.9962 | 0.9943 | 0 | 0.5256 | 0.3087 | 1.3764 | 0.3027 |
| May 1, 2003 | 0.9967 | 0.9925 | 0 | 0.4709 | 0 | 1.1065 | 0 |
| July 1, 2004 | 0.9983 | 0.9833 | 0 | 0.4917 | 0.1174 | 1.2875 | 0.203 |
| September 1, 2011 | 0.9989 | 0.9696 | 1.0533 × e−312 | 0.6481 | 1 | 1.9982 | 1 |
| November 1, 2018 | 1.0023 | 0.9948 | 0 | 0.5922 | 0.6845 | 1.1411 | 0.0388 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, C.; Yang, F.; Wang, J.; Ye, Y. Spatiotemporal Distribution and Risk Assessment of Heat Waves Based on Apparent Temperature in the One Belt and One Road Region. Remote Sens. 2020, 12, 1174. https://doi.org/10.3390/rs12071174
Yin C, Yang F, Wang J, Ye Y. Spatiotemporal Distribution and Risk Assessment of Heat Waves Based on Apparent Temperature in the One Belt and One Road Region. Remote Sensing. 2020; 12(7):1174. https://doi.org/10.3390/rs12071174
Chicago/Turabian StyleYin, Cong, Fei Yang, Juanle Wang, and Yexing Ye. 2020. "Spatiotemporal Distribution and Risk Assessment of Heat Waves Based on Apparent Temperature in the One Belt and One Road Region" Remote Sensing 12, no. 7: 1174. https://doi.org/10.3390/rs12071174
APA StyleYin, C., Yang, F., Wang, J., & Ye, Y. (2020). Spatiotemporal Distribution and Risk Assessment of Heat Waves Based on Apparent Temperature in the One Belt and One Road Region. Remote Sensing, 12(7), 1174. https://doi.org/10.3390/rs12071174