Automated Feature-Based Down-Sampling Approaches for Fine Registration of Irregular Point Clouds

Abstract

The integration of three-dimensional (3D) data defined in different coordinate systems requires the use of well-known registration procedures, which aim to align multiple models relative to a common reference frame. Depending on the achieved accuracy of the estimated transformation parameters, the existing registration procedures are classified as either coarse or fine registration. Coarse registration is typically used to establish a rough alignment between the involved point clouds. Fine registration starts from coarsely aligned point clouds to achieve more precise alignment of the involved datasets. In practice, the acquired/derived point clouds from laser scanning and image-based dense matching techniques usually include an excessive number of points. Fine registration of huge datasets is time-consuming and sometimes difficult to accomplish in a reasonable timeframe. To address this challenge, this paper introduces two down-sampling approaches, which aim to improve the efficiency and accuracy of the iterative closest patch (ICPatch)-based fine registration. The first approach is based on a planar-based adaptive down-sampling strategy to remove redundant points in areas with high point density while keeping the points in lower density regions. The second approach starts with the derivation of the surface normals for the constituents of a given point cloud using their local neighborhoods, which are then represented on a Gaussian sphere. Down-sampling is ultimately achieved by removing the points from the detected peaks in the Gaussian sphere. Experiments were conducted using both simulated and real datasets to verify the feasibility of the proposed down-sampling approaches for providing reliable transformation parameters. Derived experimental results have demonstrated that for most of the registration cases, in which the points are obtained from various mapping platforms (e.g., mobile/static laser scanner or aerial photogrammetry), the first proposed down-sampling approach (i.e., adaptive down-sampling approach) was capable of exceeding the performance of the traditional approaches, which utilize either the original or randomly down-sampled points, in terms of providing smaller Root Mean Square Errors (RMSE) values and a faster convergence rate. However, for some challenging cases, in which the acquired point cloud only has limited geometric constraints, the Gaussian sphere-based approach was capable of providing superior performance as it preserves some critical points for the accurate estimation of the transformation parameters relating the involved point clouds.

1. Introduction

Accurate three-dimensional (3D) modeling of objects is an important task for various applications, such as industrial site modeling [1], 3D documentation of historical monuments [2], urban planning [3], infrastructure monitoring [4], and several civilian and military applications [5]. Three-dimensional reconstruction/representation of objects is currently achieved through either active or passive remote sensing systems [6]. Active sensors, such as laser scanners, directly provide a precise and dense point cloud, which is properly scaled, along with the scanned objects. Despite the high point density of laser scanning data, break-lines are not usually well defined by such data. The derived laser-based point cloud often lacks spectral information [7], especially when dealing with data collected by laser scanners onboard mobile platforms that have not been integrated with a photogrammetric system. Passive sensors, such as digital frame cameras, can provide semantic information to allow for the derivation of better and more reliable interpretation of the reconstructed objects. The main challenge in deriving 3D information from passive sensors is feature matching in overlapping imagery (i.e., automated identification of conjugate features in the involved images). Considering the complementary characteristics of the derived 3D data from active and passive sensors, the geospatial research community has advocated the integration of point clouds from these two data acquisition modalities [8]. In practice, the effective integration of such derived data depends on their alignment relative to a common reference frame, which is known as the registration problem [9].

The registration of 3D point clouds involves the estimation of the 3D transformation parameters (i.e., three rotation angles, three translations, and scale factor) that relate the reference frames of the different point clouds. However, when dealing with two point clouds that have been captured by well-calibrated laser scanners, only three translations and three rotation angles have to be estimated since the scale of the scanned objects is implicitly defined by the measured laser ranges [10]. According to Habib and Al-Ruzouq [11], a comprehensive registration process should address four issues: (1) the transformation parameters relating the involved datasets to a common reference frame, (2) the registration primitives used for the estimation of the transformation parameters, (3) the mathematical constraint describing the similarity metric between conjugate features after registration, and (4) the matching strategy controlling the framework for the automatic registration process. Depending on the final accuracy of the estimated transformation parameters, existing procedures can be categorized as either coarse or fine registration techniques [12]. Coarse registration is commonly used to establish rough alignment between the involved point clouds. The registration primitives utilized for coarse registration can be points [13,14,15,16,17,18,19], lines [10,11,20,21,22], or planar features.

The fine registration process starts from coarsely aligned point clouds to achieve more precise alignment of the involved datasets. The most commonly used approach for fine registration is the iterative closest point (ICP), where the transformation parameters are iteratively refined by generating pairs of corresponding points and minimizing the point-to-point distances [23,24]. Like the key point-based coarse registration process, point-to-point correspondence cannot always be assumed in the ICP approach. To circumvent this problem, different variants of the classical ICP algorithm have been introduced in the literature. For example, the iterative closest patch (ICPatch) approach utilizes the points in one point cloud and triangular patches in another point cloud as the registration primitives [25]. Instead of minimizing the point-to-point distance, the ICPatch approach is implemented by minimizing the sum of the squared normal distances between conjugate point-patch pairs. However, a Delaunay-based triangulated irregular network (TIN) is always required for one of the involved point clouds. In addition, the utilization of a Delaunay-based TIN always requires special treatment of the points originating from vertical structures (e.g., breaklines) as the Delaunay triangles are only meaningful for relatively horizontal surfaces. In order to compensate for the complex TIN generation process, the original ICPatch was further improved by Al-Durgham et al. [26]. In their procedure, rather than using the TIN patch, the geometric primitives chosen for the registration are matched pairs consisting of one query point in one-point cloud and its closest three points in another scan. Then, a tetrahedron search space (i.e., pyramid), which is established through extruding the centroid of the triangular patch along the normal direction with a given distance threshold, is used for the validation of candidate point-to-patch pairs. This improved approach only selects matched point-to-patch pairs, in which the transformed query point is inside the tetrahedron, for estimating the transformation parameters at each iteration of the fine registration procedure. An evaluation of various variants of the ICP was conducted by Rusinkiewicz and Levoy [27]. In their paper, the classical ICP algorithm was assumed to be composed of six different stages: (1) point selection, (2) matching strategy, (3) weighting assignment, (4) rejection criteria, (5) error metric, and (6) minimization method. Then, the ICP variants were classified into different categories according to their modifications to one or more of these stages. Interested readers can refer to their paper for more details regarding ICP and its variants in fine registration.

Although the current ICP and its variants (e.g., ICPatch) have demonstrated their feasibility in providing reliable point cloud registration, they do not consider the varying characteristics of 3D point clouds derived from the onboard active and passive sensors of various platforms. For example, the point density acquired from airborne laser scanners (ALS) is usually in the range of 1 to 40 points per square meter (pts/m²) [28], which is much lower than that for terrestrial laser scanner (TLS) or mobile terrestrial laser scanner (MTLS) data. This varying nature can lead to an unreliable estimation of the transformation parameters [29,30]. The potential challenges associated with the ICP and its variants for the fine registration of 3D point clouds derived from active and passive sensors can be summarized as follows:

• The derived laser-based/image-based point clouds usually include an excessive number of points [31]. Therefore, for these datasets, the conventional ICP-based registration, which utilizes the entirety of the available points, is time-consuming and even unnecessary. For example, there are usually thousands of points acquired along with a given planar feature within a high point density area. However, only a portion of them is required to represent a reliable planar surface, whereas the remaining points are redundant.
• Due to the nature of the utilized sensors, the acquired point clouds do not have a uniform point density. For example, the point clouds acquired by a TLS have a higher point density at locations closer to the scanner. Such variations in point density will negatively impact the accuracy of the registration procedure as they can lead to over-weighting of the points in high-density areas.
• The ICP method requires large overlapping areas among the datasets and a reasonable initial approximation of the transformation parameters in order to establish the primitive correspondence (i.e., a point to its nearest point in another scan or a point to its nearest patch) [31,32]. Nevertheless, even with considerable overlap and its initial high-quality parameters, the ICP algorithm and its variants can fail to reliably estimate the registration parameters due to the negative impact from linear/cylindrical objects and rough surfaces, which are usually partially represented by point clouds (i.e., neither a laser scanning nor an imaging system can capture/derive points that completely cover such neighborhood) [33].

1.1. Related Work for Existing Down-Sampling Approaches

At present, the point density of the derived point cloud is usually reduced either during the data collection or processing stages [33]. During the data collection stage, density reduction could be achieved by decreasing the scanning resolution (i.e., lowering pulse repetition frequency and/or scan rate). However, these approaches will reduce the point density throughout the entire area (i.e., areas farther from the scanning system will suffer from significant loss in detail). In addition, these approaches are only suitable for TLS and MTLS datasets. In other words, they cannot be applied to image-based point clouds, which are derived through dense image matching techniques. Alternatively, the point density of the collected point cloud can be thinned/adjusted through data processing, which is commonly known as down-sampling [34,35,36,37]. Current point cloud processing software, such as “CloudCompare” [38], have provided multiple down-sampling functions for reducing the involved point cloud to a preferred spatial density. In practice, three of the commonly used point cloud thinning down-sampling approaches are (1) random, (2) uniform, and (3) point-spacing [38]. Random down-sampling simply selects a specific number of points from the original dataset in a random manner. Uniform down-sampling removes the points according to the order in which the points are inserted in the input data file. Point-spacing down-sampling is based on a pre-specified minimum distance between neighboring points. Although uniform and point-spacing down-sampling approaches can achieve more homogeneous spatial distribution compared to the random down-sampling approach, none of the three approaches consider the local surface characteristics or the local point density variation within the involved point cloud. Therefore, a down-sampling strategy that could compromise further data processing activities such as registration and object reconstruction should be avoided. To achieve this objective, an “adaptive” down-sampling approach was recently proposed by Al-Durgham et al. [39] that is based on the fact that high point density is not crucial for identification and modeling within small local neighborhoods. Therefore, this new approach made it possible to randomly thin given point clouds in local neighborhoods that exhibit higher local point density when compared to a user-specified one. It is worth noting that due to the need of estimated point density, the performance of the adaptive down-sampling approach highly depends on an accurate local characterization process. In this work, the principal component analysis (PCA)-based classification approach was employed, which has been used to identify the local characteristics (i.e., planar, linear/cylindrical, and rough local neighborhoods) at each point and estimate the local point density within the established local neighborhoods. Lin et al. [33] demonstrated that using this adaptive down-sampling approach improved the point cloud segmentation process in terms of both the execution time and quality of the derived segments.

To date, several research efforts have been conducted to investigate the impact of incorporating different down-sampling approaches within fine registration strategies. Masuda et al. [40] adopted the random down-sampling approach for the ICP and demonstrated significant computational improvement using only a reduced number of points in the registration. However, in their work, the random down-sampling was conducted in each iteration of the ICP. In addition, the random selection failed to preserve features in areas with sparser point density, which led to an inaccurate estimate of the transformation parameters. Turk and Levoy [41] used the uniform down-sampling approach to accelerate the nearest point search process within the ICP registration; however, they found that it led to an imbalanced point distribution over various surfaces due to different local point densities. Weik [42] investigated the utilization of points with high-intensity gradients to improve the accuracy of the ICP-based registration. However, in his work, an algorithm is designed to use intensity values. Another down-sampling strategy for the ICP using three synthetically generated scenes to evaluate the ICP variant was proposed by Rusinkiewicz and Levoy [27]. In their work, a two-dimensional (2D) angular space is first generated according to the derived surface normal at each point. Then, points are uniformly selected in the angular space to assure that the distribution among the normal vectors is preserved during the down-sampling process. However, they found that some “unreliable” points, such as points from trees and other vegetation, may be included in the process for the estimation of transformation parameters, leading to an unstable alignment of the point clouds.

1.2. Aim of the Study

In response to the featured challenges, like the excessive number of points and the varying point density for point cloud fine registration, this paper focuses on fine registration, and it aims at introducing two alternative feature-based down-sampling approaches of irregular point clouds. These two approaches differ from the commonly used point cloud down-sampling techniques (random, uniform, and point-spacing) in that they consider the physical characteristics of the encompassing surfaces (i.e., planar, linear, and rough), the internal properties (e.g., local point density), and 3D spatial distribution of the point clouds (some existing down-sampling approaches merely consider point-to-point or point-to-scanner distances). In order to identify the nature of local neighborhoods, a principal component analysis (PCA)-based feature characterization process can be conducted while considering the noise level within the constituents of a point cloud [43]. Given the PCA-based feature classification (i.e., planar, linear, or rough) of local neighborhoods, the first approach selectively removes the redundant points in areas with high point densities while keeping points in lower density regions through the adaptive down-sampling strategy proposed by Al-Durgham et al. [39]. The second approach, on the other hand, starts by deriving the surface normal, which is presented on a Gaussian sphere, of a given point cloud using their local neighborhoods. Then, down-sampling is achieved by removing the points from peaks detected in the Gaussian sphere.

In this research, a fully automated registration procedure that incorporates the two down-sampling approaches is developed. During the registration process, the two involved point clouds are denoted as the “reference” and “source” point clouds, respectively. To be more specific, the reference point cloud is always kept fixed in the registration, while the source point cloud must be transformed into the reference coordinate system using the estimated parameters. It is worth noting that in the proposed procedure, only points identified from planar regions are considered in the down-sampling process, while linear and rough points are discarded. The motivation behind only using planar points is that linear/rough points may have negative impacts on the fine registration because neither point-to-point nor point-to-patch correspondences can be assumed. Given the down-sampled points, a modified ICPatch approach is adopted in the proposed procedure for the precise alignment of the involved point clouds. Compared to the original ICPatch, the advantages of the improved approach include higher computational efficiency, less sensitivity to the existence of erroneous points (i.e., outliers), and the capability of registering vertical surfaces, which cannot be effectively handled in the original ICPatch. In the remainder of this paper, the details of the two proposed approaches for point cloud down-sampling and fine registration are first introduced. Then, a comparative analysis, which comments on the computational efficiency and registration quality, is presented on both simulated and real datasets to evaluate the performance of the two proposed approaches. Finally, conclusions and recommendations for future work are introduced.

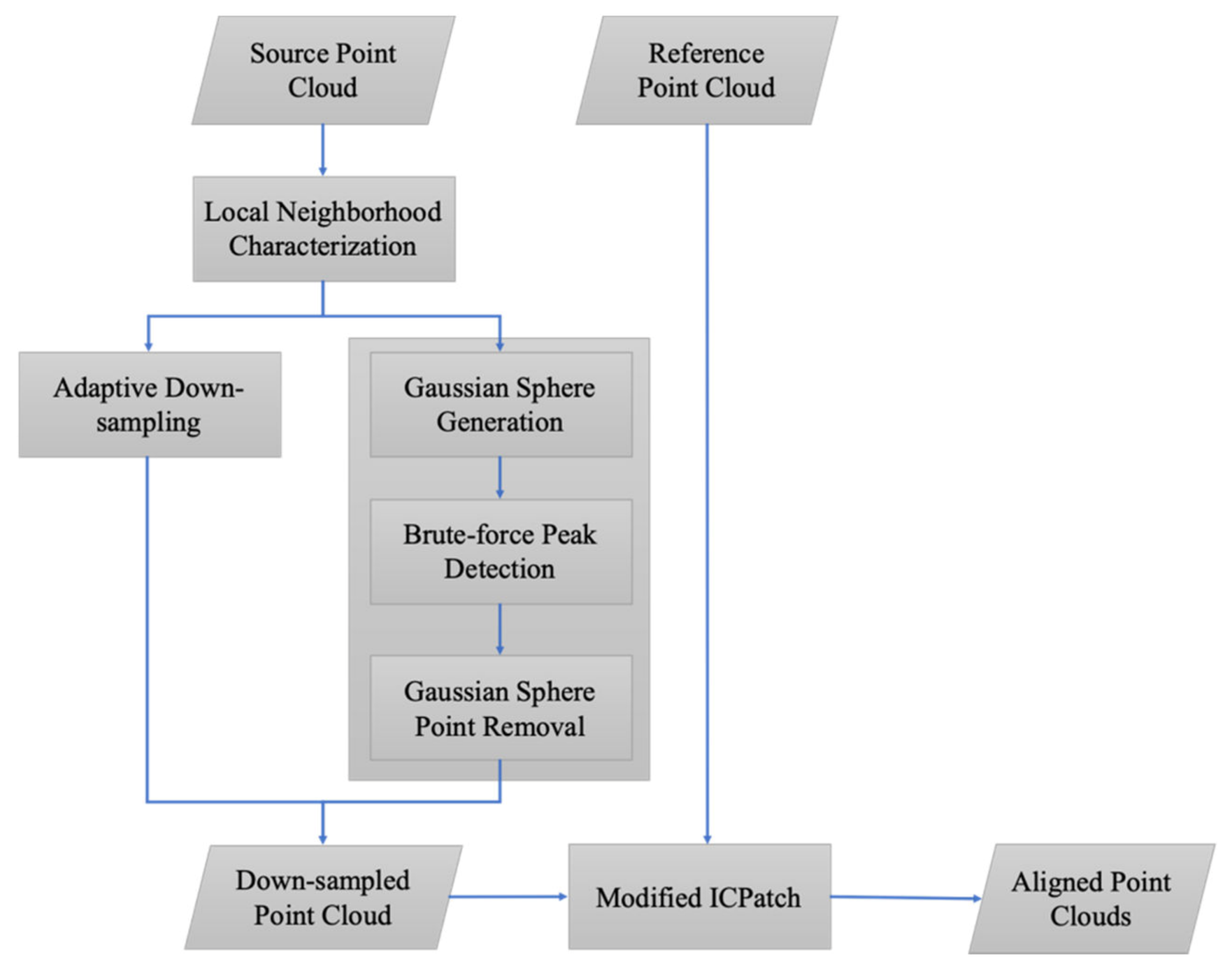
2. Methodology

As shown in Figure 1, the proposed registration procedures include three steps. In the first step, the source point cloud is initially classified as planar, linear/cylindrical, or rough, based on local neighborhoods. Then, the two proposed approaches are conducted on the points from the planar regions to reduce the data size. Finally, the down-sampled planar points are used within an improved ICPatch algorithm for fine registration. It is worth noting that in the proposed procedure, the down-sampling is only performed on the source point cloud, which has been classified as planar regions, since the total number of utilized geometric primitives (i.e., conjugate point-to-patch pairs) in the fine registration is determined by the number of query points in the source point cloud.

2.1. Local Neighborhood Characterization

During point cloud acquisition, incomplete point clouds that partially represent linear/cylindrical and rough surfaces are usually obtained. The proposed down-sampling and registration approaches are based on point-to-patch matches within planar regions of the involved point clouds for the fine registration, since either point-to-point or point-to-patch correspondences cannot be assumed for linear/cylindrical or rough surfaces. To identify planar points, a PCA-based characterization is used to classify the local neighborhood centered at each query point to a planar, linear/cylindrical, or rough region, through the inspection of the respective eigenvalues of the points-spread matrix relative to the centroid [44,45,46]. Specifically, the PCA-based local neighborhood characterization starts from selecting the n nearest neighbors $\left(P_n\right)$ of each query point in the source point cloud. In practice, a k-dimensional tree (k-d tree) data structure can be applied for organizing the point cloud and increasing the speed of the query search process [47]. Once the neighborhood search is completed, a covariance (point-spread) matrix can be derived as in Equations (1) and (2) using the 3D coordinates of the query point and its neighbors $\left(P_n\right),$ as well as the corresponding centroid ($\overline{P}$).

$$Co{v}_{3\times 3}=\frac{1}{n+1}{\displaystyle \sum }_{i=1}^{n+1}\left(P_i-\overline{P}\right){(P_i-\overline{P})}^T$$

(1)

$$\overline{P}=\frac{1}{n+1}{\displaystyle \sum }_{i=1}^{n+1}{P}_i$$

(2)

Then, an eigenvalue decomposition of the covariance matrix is used to evaluate the nature of the local neighborhood defined around the query point. In PCA, the eigenvectors represent the orientation of the neighborhood in the 3D space, while the eigenvalues define the extent of the neighborhood along with the directions of their corresponding eigenvectors. As shown in Equation (3), the eigenvalues (${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$) of the covariance matrix (Cov) are positive and can be ordered such that ${\lambda }_1\ge {\lambda }_2\ge {\lambda }_3>0$. Then, feature classification of the neighborhood can be decided according to the largest value of defined dimensionality measures $a_{1D}$, $a_{2D}$, and $a_{3D}$ [48], as in Equations (4)–(6). According to the derived dimensionality measures, linear/cylindrical, planar, or rough neighborhoods are reflected by situations in which $a_{1D}$, $a_{2D}$, or $a_{3D}$ is the largest one, respectively. As illustrated in Figure 2, a planar local neighborhood is identified when two of the eigenvalues are significantly larger than the third one, which leads to a much larger value of $a_{2D}$ when compared to $a_{1D}$ and $a_{3D}$. Once the planar local neighborhoods are classified, the local point density (LPD) of the identified planar point can be derived. The mathematical model for the local point density estimation of the planar neighborhood is presented as Equation (7), where $r_n$ is the distance between the query point in question and its n^th-farthest neighbor.

$$Co{v}_{3\times 3}=\left[\begin{array}{ccc}\overrightarrow{e_1}& \overrightarrow{e_2}& \overrightarrow{e_3}\end{array}\right]\left[\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right]\left[\begin{array}{c}{\overrightarrow{e_1}}^T\\ {\overrightarrow{e_2}}^T\\ {\overrightarrow{e_3}}^T\end{array}\right]$$

(3)

$$a_{1D}=\frac{\sqrt{{\lambda }_1}-\sqrt{{\lambda }_2}}{\sqrt{{\lambda }_1}}$$

(4)

$$a_{2D}=\frac{\sqrt{{\lambda }_2}-\sqrt{{\lambda }_3}}{\sqrt{{\lambda }_1}}$$

(5)

$$a_{3D}=\frac{\sqrt{{\lambda }_3}}{\sqrt{{\lambda }_1}}$$

(6)

$$LP{D}_{planar}=\frac{n+1}{\pi r_n^2}$$

(7)

2.2. Point Cloud Down-Sampling

Once the local neighborhood characterization is completed, the two proposed point cloud down-sampling approaches can be implemented to reduce the number of points along planar surfaces. The first proposed approach is based on an adaptive down-sampling procedure [33,39]. The second approach, on the other hand, is achieved by removing points from the detected peaks in a Gaussian sphere, which is generated from the surface normals derived from the local neighborhood characterization process.

2.2.1. Adaptive Down-Sampling

To achieve the desired point density along planar surfaces, a simple probability-based test, as shown in Equation (8), is conducted for the adaptive down-sampling approach. The conceptual basis of the equation is based on the fact that, given a uniformly distributed random number $r_i$ in the range of [0,1], for any planar neighborhood with local point density higher than the user-specified point density $LP{D}_d$ (i.e., ${\delta }_i\le 1$), the probability of maintaining a point is $P\left(r_i\le {\delta }_i\right)={\delta }_i$, while the probability of removing the point is $P\left(r_i>{\delta }_i\right)=1-{\delta }_i$. On the other hand, for the remaining planar surfaces, where the local point density $LP{D}_i$ is lower than the desired point density $LP{D}_d$, all points are maintained in the down-sampling process as the test value (${\delta }_i$) is always greater than 1. Interested readers can refer to Al-Durgham [39] for more details regarding the adaptive down-sampling approach. It is worth noting that although the adaptive down-sampling removes redundant points in areas with high point density while keeping the points in lower density regions, it does not ensure a balanced distribution of the surface normals within the source point cloud. In terms of fine registration, a balanced distribution of the surface normal is always necessary as it ensures sufficient geometric constraints for the accurate/reliable estimation of all the involved transformation parameters.

$${\delta }_i=\raisebox{1ex}{$LP{D}_d$}\!\left/ \!\raisebox{-1ex}{$LP{D}_i$}\right. ⟹ \{\begin{array}{c}{r}_i\le {\delta }_i maintain\\ r_i>{\delta }_i remove\end{array}$$

(8)

where, $LP{D}_d$ is the desired point density in pts/m², $LP{D}_i$ is the local point density of the $i^{th}$ planar local neighborhood in pts/m², and $r_i$ is a random number that is picked from a uniform distribution in the range [0,1].

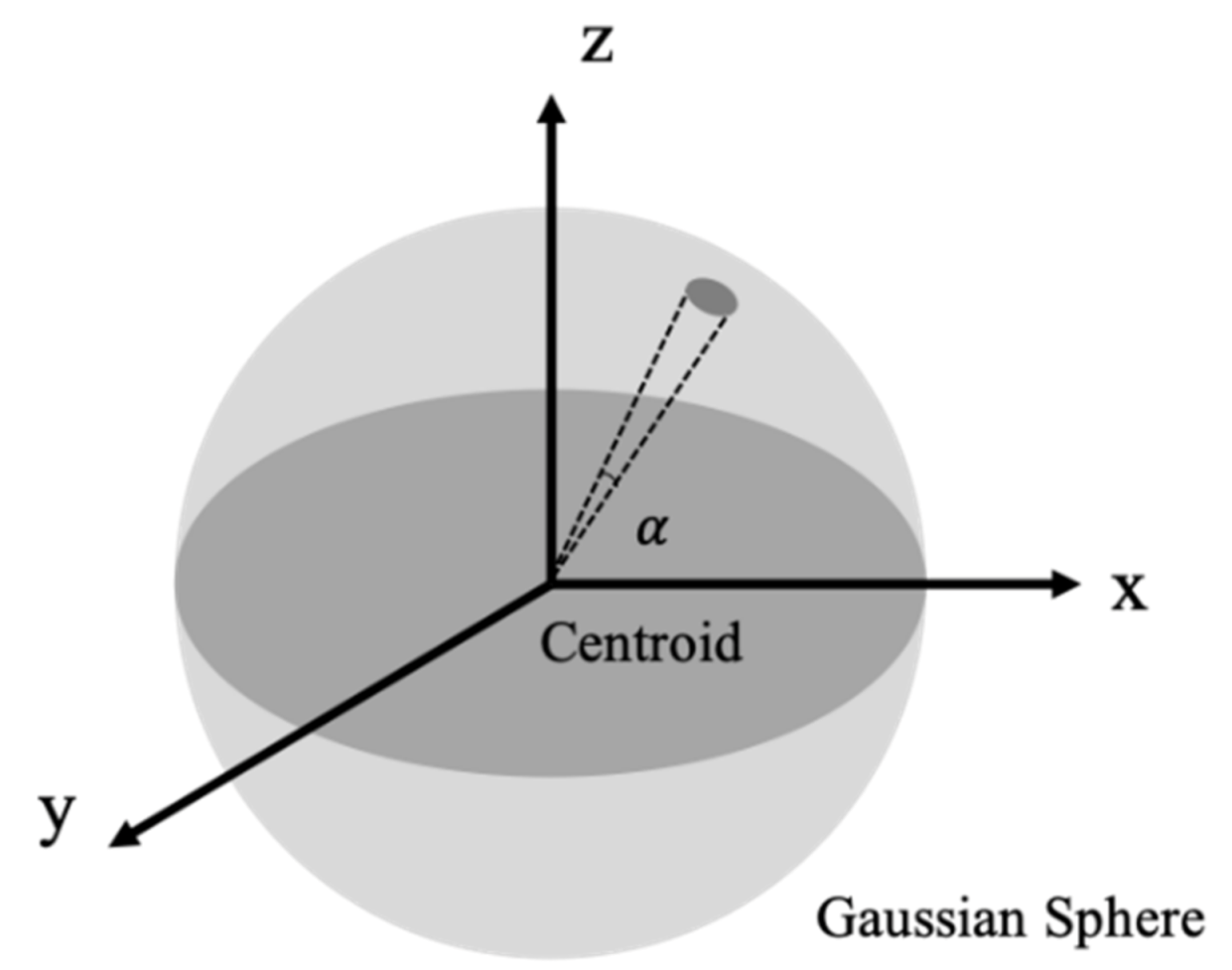
2.2.2. Gaussian Sphere-Based Down-Sampling

Motivated by the fact that points within the same planar region have a similar surface normal, the second approach begins by deriving the surface normal for the constituents of a given point cloud. The surface normal of the points along planar surfaces are derived through the local neighborhood characterization, which was introduced in Section 2.1 (i.e., the normal is the eigenvector that corresponds to the smallest eigenvalue of the covariance matrix). Then, these derived surface normals for all those points that are classified as part of planar neighborhoods are represented on a Gaussian sphere. The down-sampling is achieved thereafter by removing points from the detected peaks in the Gaussian sphere. In the remainder of this section, the Gaussian sphere-based approach is introduced through three steps: (1) Gaussian sphere generation, (2) brute force-based peak detection, and (3) Gaussian sphere-based point removal.

Gaussian Sphere Generation:

In order to down-sample the points that have a similar surface normal, a representation that groups the points into a different domain is required. The Gaussian sphere, also known as the extended Gaussian image (EGI), is a mapping of the surface normals of a specific object onto a sphere of unitary radius to represent the orientation attribute [49]. For any point cloud data, the EGI can be established by projecting the surface normal estimated for the constituents of a point cloud to a specific sphere. Figure 3 shows the Gaussian sphere created from a sample point cloud dataset. A practical approach to generate the Gaussian sphere starts by deriving the normals to the local neighborhoods for all the query points along the planar surfaces within the source point cloud (i.e., the eigen vector that corresponds to the smallest eigenvalue of the covariance matrix in the PCA analysis). Then, the derived eigenvector (i.e., surface normal) for each point is normalized into a unit vector, and these unit vectors are subsequently represented in the 3D space using a sphere with a unit radius. It is important to note that since the points with a similar surface normal are mapped onto the same location on the Gaussian sphere, planar regions that share a similar direction but are spatially disconnected contribute to a common peak. Therefore, the number of points within the planar regions can be reduced by down-sampling each corresponding peak on the derived Gaussian sphere.

Brute Force-Based Peak Detection:

In order to remove redundant points from each peak on the Gaussian sphere, it is necessary to identify existing concentration areas on the Gaussian sphere. A brute-force peak detection approach, which traverses the Gaussian sphere point cloud [43], was adopted in the proposed approach. More specifically, this approach begins by constructing a k-d tree structure for all the derived surface normals, which are represented on the Gaussian sphere. As shown in Figure 4, a pre-specified angular threshold $\mathsf{\alpha }$ can be used to determine the search radius for peak detection. Given the search radius, each of the involved points on the Gaussian Sphere is traversed to retrieve the one with the maximum number of neighboring points for peak detection. Once a peak is identified, the detected point, as well as all the points that fall into its neighborhood as determined by the angular threshold for the solid angle, are eliminated from the k-d tree structure. This peak detection and elimination process are repeated until the largest number of points within a given neighborhood are smaller than a predefined threshold. In practice, the angular threshold $\mathsf{\alpha }$ has to be determined according to the noise level within the constituents of the involved point cloud.

Gaussian Sphere-Based Point Removal:

A simple down-sampling strategy can be achieved by randomly removing the points from each of the detected peaks on the Gaussian sphere while using a constant reduction threshold. However, a single peak on the Gaussian sphere may correspond to multiple spatially-disconnected planar regions, which have close/similar normals in the object space. In addition, due to the nature of the data acquisition mechanism or the characteristics of the object surfaces, these spatially-disconnected planar regions are usually acquired with different point densities. Therefore, this down-sampling strategy, which relies on a constant reduction threshold on all the planar surfaces, can lead to an over-weighting problem for points in high-density areas. For example, Figure 5 shows a sample image for two parallel planes—$A$ and $A\prime$—with different point densities. According to the simple down-sampling strategy, both of the two planes will be thinned in a similar manner (i.e., the same percentage of points is removed from each plane). In order to overcome this issue for the fine registration procedure, the proposed point removal strategy begins by adopting a Euclidean clustering approach to group the points from the same peak on the Gaussian sphere into multiple disconnected planar surfaces. The adopted Euclidean clustering approach is conducted as follows:

• A distance threshold $d$ for the Euclidean clustering is first specified.
• Given the set of points $\left\{P\right\}$ belonging to the same peak, one point is randomly selected as the initial seed for the Euclidean clustering. Afterwards, this initial seed point is added to a list of temporary seed points $\left\{S\right\}$, and removed from $\left\{P\right\}$.
• If $\left\{S\right\}$ is not empty, the first point in the list is picked up as the current seed $s$ for the region-growing process. $s$ is then removed from $\left\{S\right\}$.
• Now that the current seed $s$ is determined, all points, which belong to $\left\{P\right\}$ and are within the distance threshold $d$ to $s$, have to be added to the list of current clusters $\left\{C\right\}$ and the list of seed points $\left\{S\right\}$. In the meantime, these selected points have to be removed from $\left\{P\right\}$.
• Steps 3 and 4 are repeated until $\left\{S\right\}$ is empty. Then, the group of points from the list $\left\{C\right\}$ are labeled to the same cluster.
• The process from Step 2 to 5 is repeated until no more clusters can be detected (i.e., $\left\{P\right\}$ is empty).

Given the groups of points derived from the Euclidean clustering, the reduction percentage is then separately estimated for each of the detected planar surfaces. More specifically, the derived reduction percentage aims to maintain a similar number of points on each of the detected planar surfaces with a given orientation after removing the redundant points. Different from the adaptive down-sampling approach, the Gaussian sphere-based point removal process does not rely on the estimated local point density (LPD).

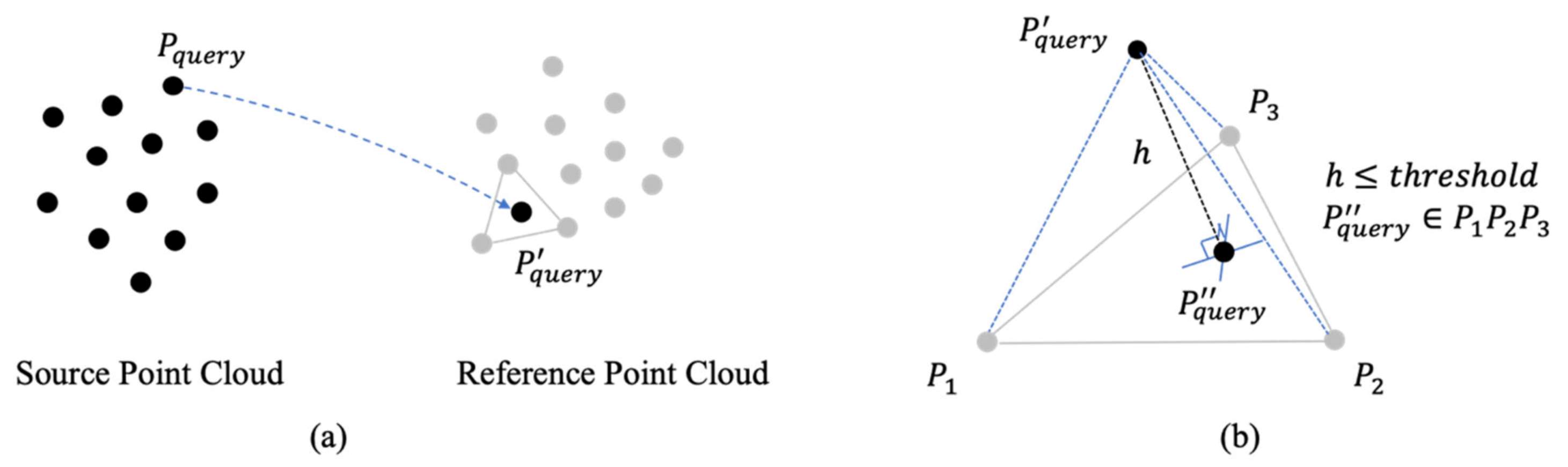
2.3. Improved ICPatch Registration

Once the down-sampling procedure is finalized, an improved ICPatch approach is implemented for the precise alignment of the involved point clouds. The ICPatch registration is performed between the source point cloud, which has been down-sampled through the introduced approaches, and the reference data. Instead of point-to-point correspondence, the geometric primitives chosen for the ICPatch registration are points and triangular patches [25]. Therefore, for any two overlapping point clouds, one (the source point cloud) is kept as is, and the other (the reference point cloud) is converted to a set of triangular patches. As it was mentioned earlier, a Delaunay TIN is conventionally utilized for the patch generation process. However, the generation of TIN can be very inefficient, and it cannot deal with vertical surfaces as the Delaunay triangles are only meaningful for relatively horizontal surfaces. Alternatively, the point-to-patch correspondences can be established by searching for the three closest points of each query point after applying the approximate transformation parameters (see Figure 6a). In practice, a 3D similarity transformation, which includes three rotation angles, three translation parameters, and one scale factor, is usually adopted for the point cloud registration, as in Equation (9). Although for any query point, the 3D similarity transformation leads to a pair of potential conjugate primitives (i.e., the query point and the corresponding triangular patch comprised of the three closest points) between the two involved point clouds, it is worth noting that the three closest points in the reference point cloud do not always represent a physical surface (e.g., sparse areas in the point cloud). In order to mitigate the impact of these invalid cases, only a subset of the derived point-to-patch correspondences is accepted and used for the estimation of transformation parameters. In the improved ICPatch approach, the point-to-patch correspondences are accepted only if the two following conditions are satisfied (See Figure 6b):

• The normal distance $h$ from the transformed query point $P_{query}^{\prime }$ to the corresponding triangular patch $P_1{P}_2{P}_3$, which is composed of the three closest points $P_1$, $P_2$, and $P_3$ in the reference point cloud, must be less than the pre-defined threshold.
• The projection of the transformed query point $P_{query}^{\prime }$ onto the triangular patch $P_1{P}_2{P}_3$,$P_{query}^{″}$, must be inside the patch.

  $$\left[\begin{array}{c}{X}_{P_{query}^{\prime }}\\ Y_{P_{query}^{\prime }}\\ Z_{P_{query}^{\prime }}\end{array}\right]=\left[\begin{array}{c}{T}_X\\ T_Y\\ T_Z\end{array}\right]+s·R_{3\times 3}\left(\omega ,\varphi ,\kappa \right)\left[\begin{array}{c}{X}_{P_{query}}\\ Y_{P_{query}}\\ Z_{P_{query}}\end{array}\right]$$

  (9)

  where, ${(X_{P_{query}},Y_{P_{query}},Z_{P_{query}})}^T$ is the coordinates for the query point $P_{query}$, ${(X_{P_{query}^{\prime }},Y_{P_{query}^{\prime }},Z_{P_{query}^{\prime }})}^T$ is the coordinates for the transformed query point $P_{query}^{\prime }$, $R$ is the rotation matrix relating the query and reference coordinate systems defined by the three rotation angles $\omega$, $\varphi$, and $\kappa$, ${(T_X,T_Y,T_Z)}^T$ is the translation vector relating the source and reference point clouds, and $s$ is the scale factor.

It is important to note that the improved ICPatch registration is different from the iterative closest projective point (ICPP) approach developed by Al-Durgham et al. [33], which is based on a tetrahedron (i.e., pyramid) search space for the validation of potential point-to-patch pairs. The tetrahedron is established through extruding the centroid of the triangular patch along the normal direction with a given distance threshold. The candidate point-to-patch match is accepted only if the transformed query point is inside the tetrahedron. The improved ICPatch utilized in this research only requires that the normal projection of the transformed query point is inside the triangular patch, and the normal distance from the point to the patch is less than the pre-specified distance threshold. Compared to the ICPP, which requires that the transformed query point must be inside the established tetrahedron, these conditions are less restrictive for the validation of all derived candidates.

Now that all valid point-to-patch correspondences between the source and reference point clouds are identified, two similarity measures, which are based on the co-planarity constraint, and the modified weight matrix strategy respectively, can be established for the calculation of the registration parameters. The mathematical models for the two different similarity measures are explained in the two following subsections.

Co-Planarity Constraint Approach:

In the co-planarity constraint, the transformed query point $P_{query}^{\prime }$ and the three closest points $P_1$, $P_2$, and $P_3$ are assumed to be coplanar. Therefore, the volume of the tetrahedron, whose vertices are $P_{query}^{\prime }$, $P_1$, $P_2$, and $P_3$, as shown in Figure 6b, should be zero. The mathematical expression for the tetrahedron volume can be expressed as Equation (10), where $\left(X_{P_{query}^{\prime }},Y_{P_{query}^{\prime }},Z_{P_{query}^{\prime }}\right)$ is the coordinates of the transformed query point $P_{query}^{\prime }$, as presented in Equation (9), and $\left(X_{P_1},Y_{P_1},Z_{P_1}\right)$, $\left(X_{P_2},Y_{P_2},Z_{P_2}\right)$, and $\left(X_{P_3},Y_{P_3},Z_{P_3}\right)$ are the 3D coordinates for the three points $P_1$, $P_2$, and $P_3$, respectively.

$$\det \left|\begin{array}{cccc}{X}_{P_{query}^{\prime }}& Y_{P_{query}^{\prime }}& Z_{P_{query}^{\prime }}& 1\\ X_{P_1}& Y_{P_1}& Z_{P_1}& 1\\ X_{P_2}& Y_{P_2}& Z_{P_2}& 1\\ X_{P_3}& Y_{P_3}& Z_{P_3}& 1\end{array}\right|=0$$

(10)

Modified Weight Matrix Approach:

For the modified weight matrix approach, the mathematical model relating the query point $P_{query}$ to one of its closest three points ($P_1$, $P_2$, or $P_3$) can be represented by Equation (11). The main difference between Equation (11) and the 3D similarity transformation as presented in Equation (9) is the misclosure vector ${\overline{e}}_{3\times 1}$, which is the sum of two components, ${(e_x,e_y,e_z)}^T$ and ${(d_x,d_y,d_z)}^T$. To be more specific, the first component ${(e_x,e_y,e_z)}^T$ is the random noise vector contaminating the observed point coordinates. On the other hand, the second component ${(d_x,d_y,d_z)}^T$ is the displacement vector, which describes the spatial offsets between the transformed query point $P_{query}^{\prime }$ and one of the triangular patch vertices (i.e., $P_1$, $P_2$, or $P_3$). Previous research [50] has shown that the displacement component ${(d_x,d_y,d_z)}^T$ can be eliminated from the least-squares adjustment by modifying the point weight matrix so that the normal distance from the transformed query point to the corresponding triangular patches is minimized.

$$\left[\begin{array}{c}{X}_{P_i}\\ Y_{P_i}\\ Z_{P_i}\end{array}\right]=\left[\begin{array}{c}{T}_X\\ T_Y\\ T_Z\end{array}\right]+s·R_{3\times 3}\left(\omega ,\varphi ,\kappa \right)\left[\begin{array}{c}{X}_{P_{query}}\\ Y_{P_{query}}\\ Z_{P_{query}}\end{array}\right]+{\overline{e}}_{3\times 1}$$

(11)

where,

$${\overline{e}}_{3\times 1}=\left[\begin{array}{c}{e}_x\\ e_y\\ e_z\end{array}\right]+\left[\begin{array}{c}{d}_x\\ d_y\\ d_z\end{array}\right]\mathrm{and}\left[\begin{array}{c}{e}_x\\ e_y\\ e_z\end{array}\right]~\left(0, {\sigma }_0^2{P}^{-1}\right)$$

In this research, the weight modification process is accomplished as follows: for each triangular patch, one can derive the rotation matrix $R_{XYZ}^{UVW}$, which transforms the point from the original reference coordinate system $\left(X, Y, Z\right)$ to the local coordinate system of the triangular patch $\left(U, V, W\right)$ (see Figure 7). In the patch local coordinate system $\left(U, V, W\right)$, $U$ and $V$ axes are within the patch plane, and the $W$ axis is normal to the patch plane. Then, the original weight matrix $P_{XYZ}$ is transformed to the patch local coordinate system $\left(P_{UVW}\right)$ according to the law of error propagation, as in Equation (12).

$$P_{UVW}=R_{XYZ}^{UVW}{P}_{XYZ}{(R_{XYZ}^{UVW})}^T$$

(12)

In the third step, the derived weight matrix of $P_{UVW}$ is then modified, as in Equation (13). This modification can be conceptually explained as only keeping weights along the $W$ axis, which is normal to the patch plane.

$$P_{UVW}^{\prime }=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& P_W\end{array}\right]$$

(13)

Finally, the modified weight matrix $P_{UVW}^{\prime }$ can be transformed back to the coordinate system of the reference point cloud according to Equation (14). Such a weight modification process will eliminate the impact of the displacement vector ${(d_x,d_y,d_z)}^T$ from the misclosure vector ${\overline{e}}_{3\times 1}$. Using the modified weight matrix $P_{XYZ}^{\prime }$, a point-based least-squares solution can be easily derived for the transformation parameters.

$$P_{XYZ}^{\prime }={(R_{XYZ}^{UVW})}^T{P}_{UVW}^{\prime }{R}_{XYZ}^{UVW}$$

(14)

It is worth noting that both of the two abovementioned similarity measures have to be implemented in an iterative procedure for the estimation of transformation parameters. Such an iterative procedure is repeated until convergence of the estimated transformation parameters or until there is no change for the identified point-to-patch correspondence. In this research, the modified weight matrix approach was adopted as it does not require a new implementation for the minimization of the introduced volumetric errors (i.e., co-planarity constraint). Given the modified weight matrix for each point-to-vertex correspondence, the transformation parameters can be easily estimated through the same least-squares adjustment process, which has been designed for point-to-point registration, without any change.

3. Experimental Results

Experiments utilizing simulated and real datasets were conducted to investigate the feasibility of the two proposed down-sampling approaches in providing reliable transformation parameters for the fine registration of 3D point clouds.

3.1. Simulated Dataset

There are two objectives for the experimental testing with the simulated dataset. The first objective was to evaluate the impact on the estimated transformation parameters when adding noise of different magnitudes to the simulated point cloud. The ability of the tested approaches to deal with introduced noise was evaluated by gradually increasing the noise level to a standard deviation of ±0.05 m. Only the two proposed approaches were tested for the first objective. The second objective was to evaluate the performance of the improved ICPatch using the implemented down-sampling approaches against two conventional strategies, which included using (1) all possible points and (2) a set of randomly down-sampled points. For the simulated dataset, a set of five planes with different orientation were simulated to emulate those in the vicinity of a building (i.e., facades, roofs, and ground surfaces) (see Figure 8). The ground coverage of the simulated dataset was 20 by 20 m, and the height range was 25 m. Both the source and reference point clouds were simulated on the five planes. For the two simulated point clouds, the maximum point density was 1600 pts/m², while the minimum point density was 25 pts/m². Then, the set of pre-defined 3D Euclidean transformation parameters shown in

Table 1. The three-dimensional (3D) Euclidean transformation parameters relating the coordinate systems of the simulated source and reference datasets.

${\mathit{T}}_{\mathit{X}} \left(\mathit{m}\right)$	${\mathit{T}}_{\mathit{Y}} \left(\mathit{m}\right)$	${\mathit{T}}_{\mathit{Z}} \left(\mathit{m}\right)$	$\mathit{\omega }°$	$\mathit{\varphi }°$	$\mathit{\kappa }°$
−0.15	−0.38	0.27	3.5	−2.8	1.6

was applied to the simulated reference points to transform it in a different coordinate system, while the simulated source points were kept as is. In the ICPatch registration, the approximate transformation parameters were set to 0 for both the rotation angles and translation parameters.

Table 2. Absolute rotation and translation differences for various noise values using the adaptive and Gaussian sphere-based down-sampling strategies.

Noise (m)	$\mathbf{∆}{\mathit{T}}_{\mathit{x}} \left(\mathit{m}\right)$	$\mathbf{∆}{\mathit{T}}_{\mathit{y}} \left(\mathit{m}\right)$	$\mathbf{∆}{\mathit{T}}_{\mathit{z}} \left(\mathit{m}\right)$	$\mathbf{∆}\mathit{\omega } (°)$	$\mathbf{∆}\mathit{\varphi } (°)$	$\mathbf{∆}\mathit{\kappa } (°)$
Adaptive down-sampling
0.01	0.002	0.001	0.002	0.002	0.003	0.001
0.02	0.001	0.002	0.002	0.004	0.005	0.002
0.03	0.001	0.010	0.012	0.011	0.002	0.010
0.04	0.011	0.001	0.014	0.010	0.008	0.019
0.05	0.003	0.022	0.006	0.005	0.019	0.011
Gaussian sphere-based down-sampling
0.01	0.004	0.003	0.001	0.002	0.001	0.001
0.02	0.007	0.010	0.002	0.003	0.006	0.004
0.03	0.009	0.011	0.011	0.007	0.003	0.007
0.04	0.009	0.004	0.006	0.012	0.016	0.028
0.05	0.004	0.025	0.007	0.011	0.027	0.031

illustrates the absolute rotation and translation differences between the estimated and true transformation parameters at each given noise level using the two proposed approaches. Figure 9 illustrates the comparison between the two proposed approaches with two traditional approaches (i.e., using a set of randomly selected points or all possible points) while using the modified ICPatch. Specifically, the comparison includes the convergence of each estimated transformation parameter as well as the derived Root Mean Square Error (RMSE) values (i.e., the RMSE of point-to-patch normal distances in ICPatch) for each test. This comparison was conducted only on the simulated dataset with a ±0.05 m noise level. Before conducting the two proposed down-sampling approaches, the PCA-based classification was applied on the simulated dataset to identify the nature of the defined local neighborhoods (i.e., determine whether they represent planar, linear, or rough regions). In this test, the number of neighboring points was set at 50 for the PCA-based classification. Now that all the defined local neighborhoods are classified, the adaptive down-sampling was applied to the identified planar points according to Equation (8) with a desired local point density of 20 pts/m². In the meantime, to ensure a compatible number of down-sampled points for the improved ICPatch registration, the Gaussian sphere-based approach only keeps about 790 points on each of the five detected peaks on the Gaussian sphere, and the random down-sampling is adjusted to a reduction percentage of roughly 3.9%.

Table 3. The number of points utilized in the four conducted tests: (1) adaptive down-sampling, (2) Gaussian sphere-based down-sampling, (3) random down-sampling, and (4) using all points—i.e., 100,709 points—in the source dataset.

	Number of Planar Point Features	Number of Down-Sampled Points for ICPatch
Adaptive	99,977	3944
Gaussian Sphere	99,977	3950
Random	---	3944
All Points	---	100,709

presents the number of points utilized in each of the conducted tests. To be specific, the total number of points in the source dataset was 100,709 points. Since both the adaptive and Gaussian sphere-based down-samplings were conducted on the points along the planar surfaces, the number of planar point features, which were derived from the local neighborhood characterization process, are presented in Column 2. The number of points utilized for the ICPatch is shown in Column 3.

Closer inspection of the derived results in Table 2 and Table 3 and Figure 9 reveals the following:

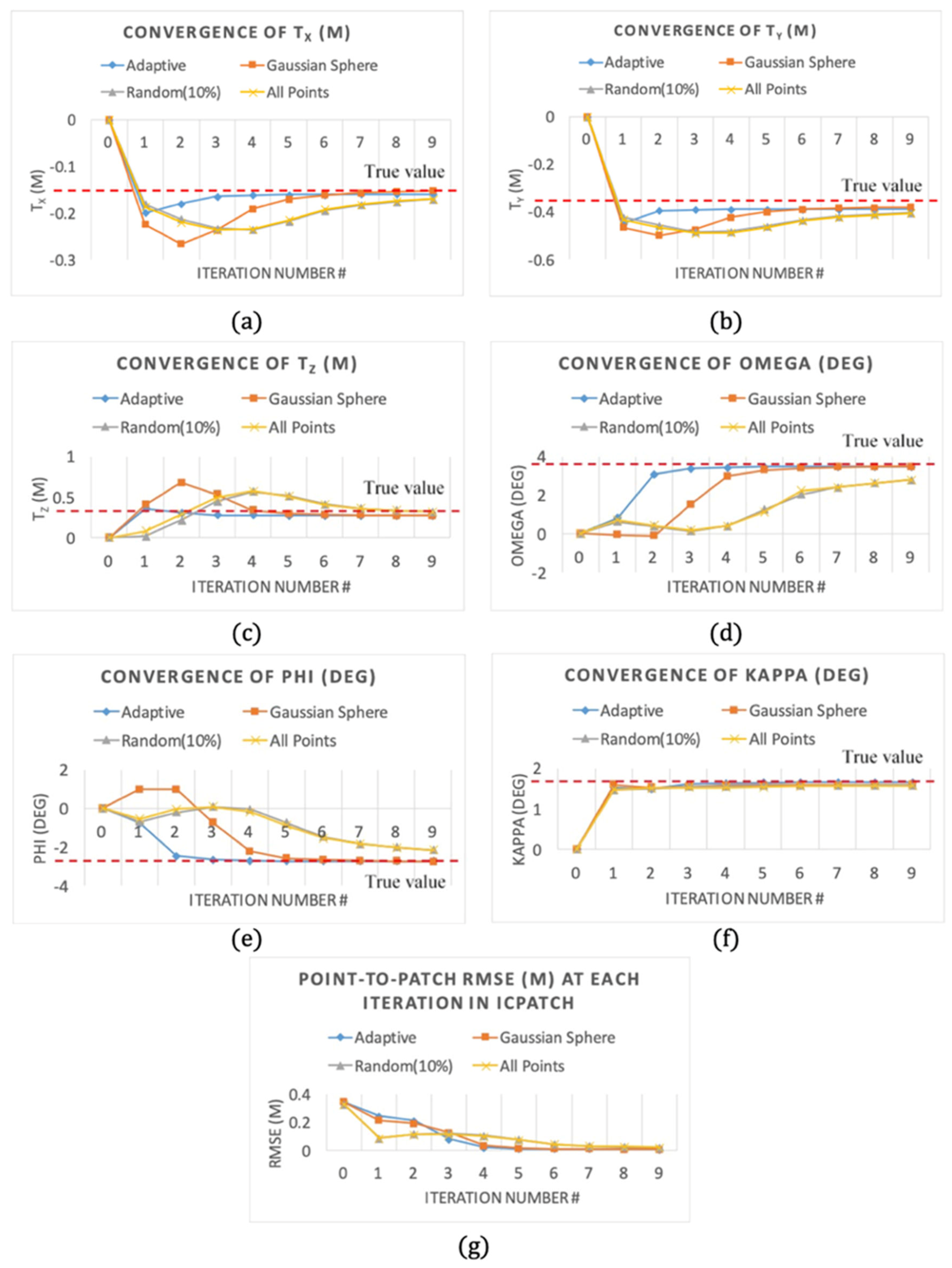
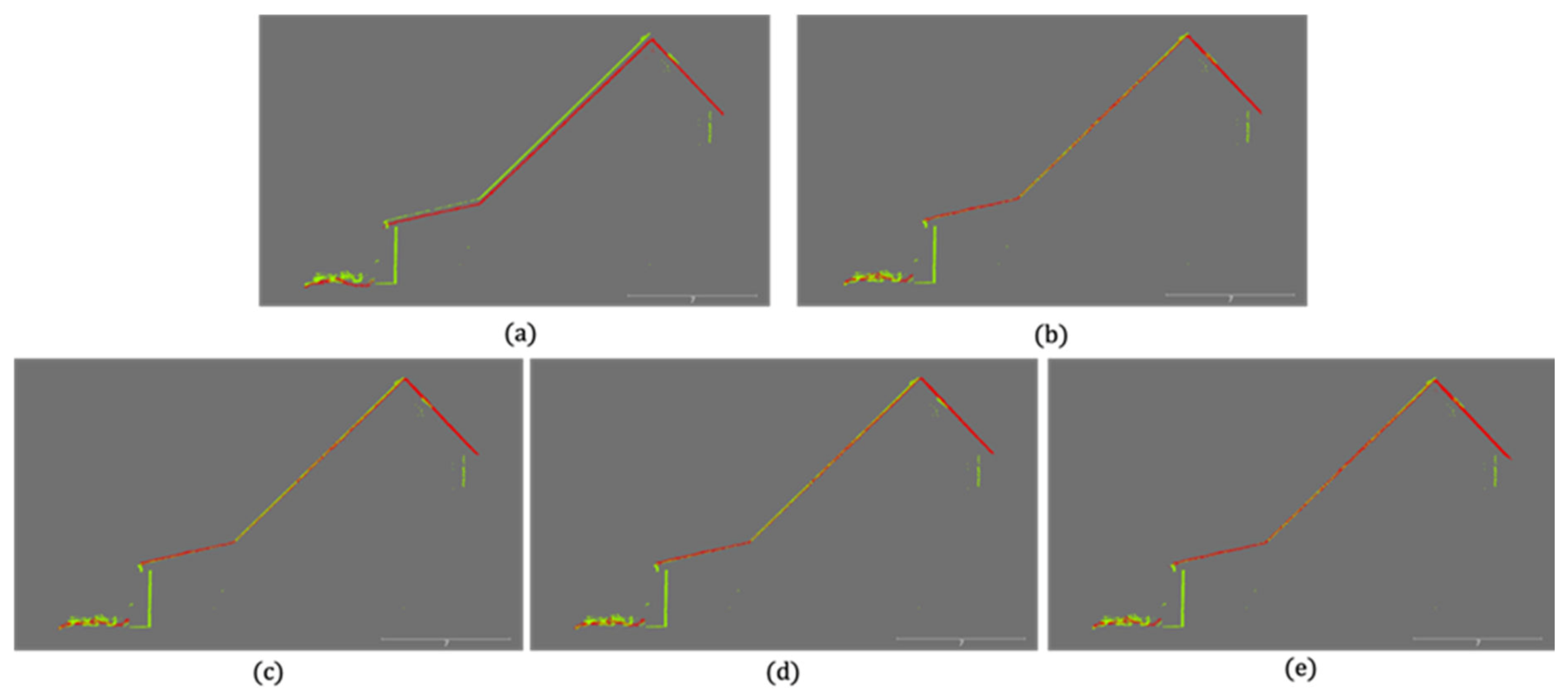
• For the simulated dataset with a gradually increasing noise level with a standard deviation up to $\pm 0.05$ m, the maximum absolute rotation and translation errors derived from the two proposed adaptive and Gaussian sphere down-sampling approaches were $0.019°$ and $0.031°$ and 0.0022 and 0.0025 m, respectively (highlighted in Table 2). This result indicates that both the adaptive and Gaussian sphere-based down-sampling approaches provided an accurate estimate for the transformation parameters.
• Compared to the two conventional strategies (random down-sampling or using all points), the two implemented proposed approaches exhibited a much faster convergence, which demonstrated that they were more efficient for the fine registration.
• The ICPatch registration using either a set of randomly selected points or all possible points demonstrated similar performance in terms of their convergence rate because the random down-sampling did not change the distribution of the utilized point clouds (i.e., after applying the random down-sampling, there were more points in the high point density area while there were fewer points in the low point density regions).
• As mentioned earlier, one may expect to see a faster convergence for the Gaussian sphere-based down-sampling approach as it is designed to maintain a similar number of points on each of the detected planar surfaces with a given orientation (i.e., better distribution of the points). However, as shown in Figure 9a–f, the proposed adaptive down-sampling approach exhibited a better convergence rate on both the estimated translation and rotation parameters. One possible explanation for the superior performance of the adaptive approach is it has less sensitivity to the noise level when compared to the Gaussian sphere-based approach.

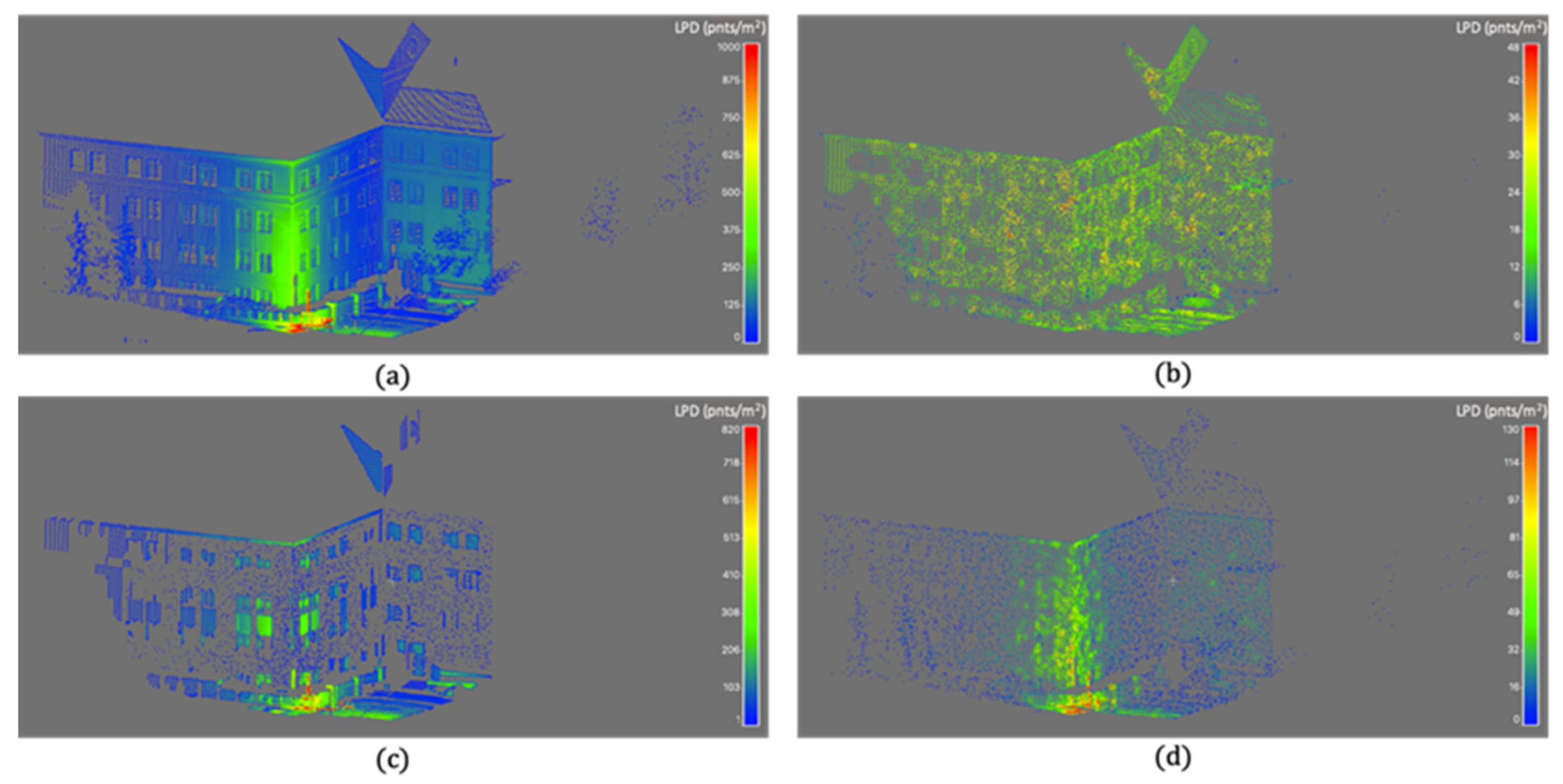
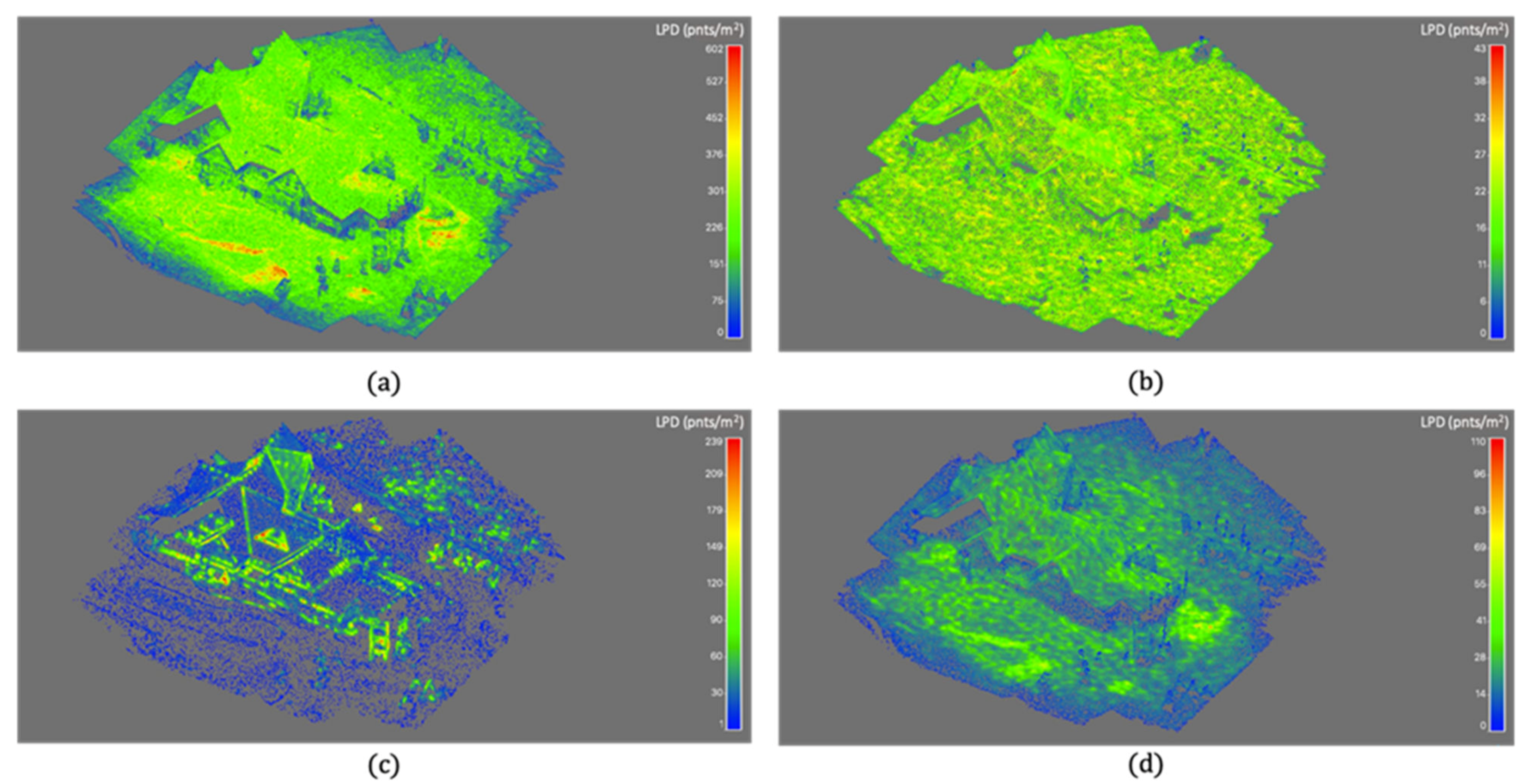
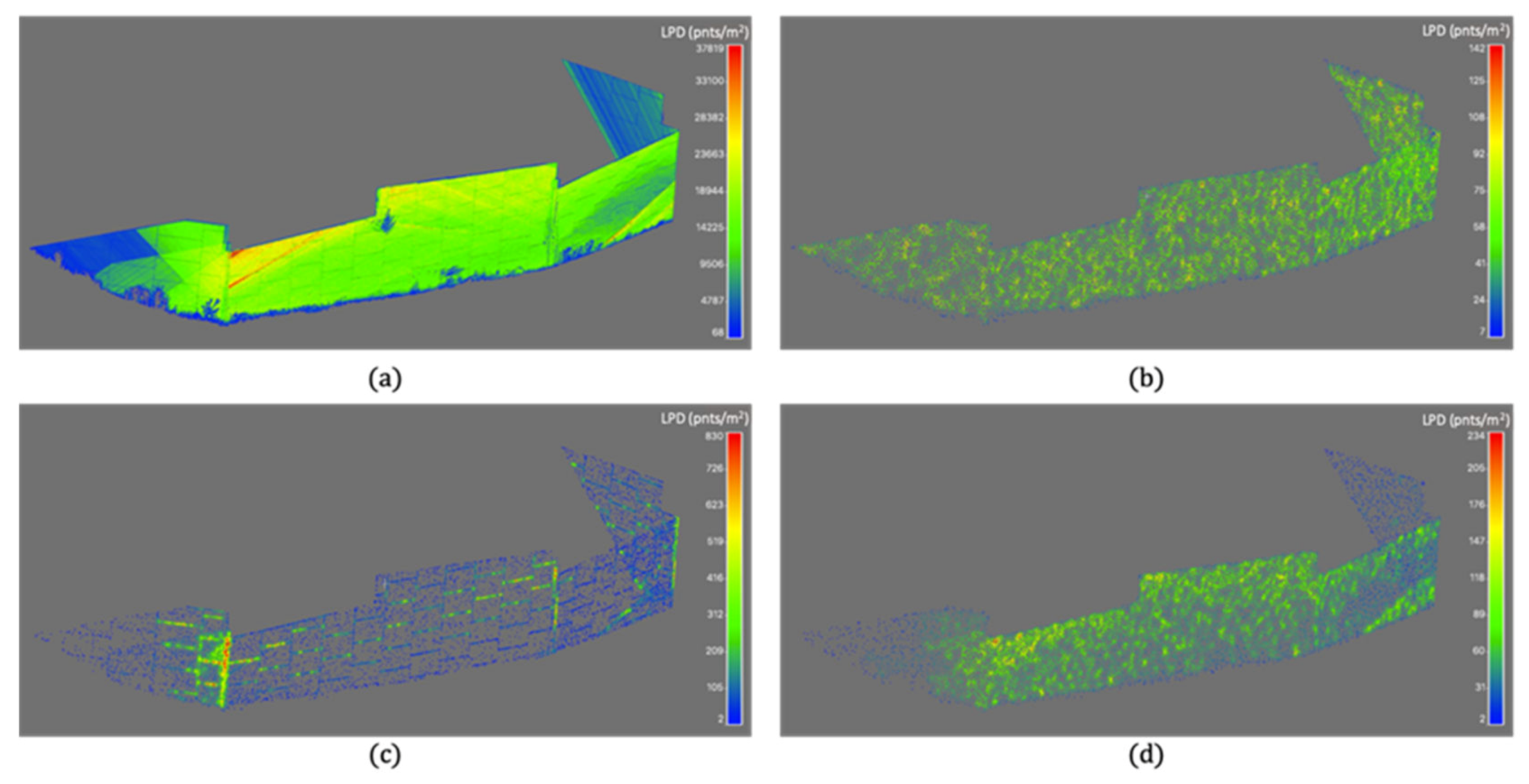
3.2. Real Dataset

In order to evaluate the performance of the proposed down-sampling approaches in providing reliable transformation parameters, this section presents experimental results from three real datasets, which include point clouds derived from (i) two TLS point clouds (Figure 10a, b), (ii) unmanned aerial vehicle (UAV) image-based and TLS point clouds (Figure 10c, d), and (iii) TLS and mobile mapping system (MMS) point clouds (Figure 10e, f). Similar to the experimental testing for the simulated dataset, the two proposed approaches and the two traditional approaches (i.e., random down-sampled and full point sets) were implemented on the real datasets for the comparative analysis. The details pertaining to these real datasets are described below.

Data Description

Real Dataset 1 has been generated from a static Leica HDS 3000 laser scanner viewing some of the building façades at a distance of 20 m. The two TLS point clouds (i.e., reference and source point clouds) have a total number of 66,541, and 143,779 points, respectively. Figure 10a and b illustrate the perspective views of the two point clouds.

Real Dataset 2 is composed of two point clouds, which are derived from a TLS and a UAV image-based point cloud in the vicinity of a building with a complex roof structure. The reference point cloud has a total number of 1,146,972 points, and it is acquired by a Faro Focus 3D terrestrial laser scanner at a distance of 15 m to the building. As can be seen in Figure 10c, the reference laser scan includes planar points from both building façades and roof surfaces. The source point cloud, which is shown in Figure 10d, is derived from a block of 201 images captured by a GoPro 3+ camera onboard a DJI Phantom 2 UAV over the building in question. The image-based point cloud, which is generated from automated aerial triangulation and dense image matching techniques [50,51], includes 1,983,108 points. Compared to the TLS point cloud, the UAV image-based one has a much lower point density on the building façades while most of the reconstructed points are on the ground and building roof surfaces.

Real Dataset 3 includes two-point clouds acquired at a smooth mechanically stabilized earth (MSE) wall that had piece-wise planar façades. The total length of the MSE wall is approximately 345 m with an average height of 7 m. The reference point cloud is scanned by Faro Focus X 330 at a distance of 25 m (Figure 10e), and it has 4,169,454 points. The source point cloud is captured from a fully calibrated vehicle-based MMS with two high-grade laser scanners (Riegl VUX-1HA and ZF Profiler 9012), as shown in Figure 10f, with a total number of 5,812,514 points. It is worth noting that due to the geometric characteristics of the involved planar surfaces (i.e., almost all points are on the planar surfaces parallel to the z-axis), the registration of the scanned scene in Real Dataset 3 can be very challenging. As can be seen in Figure 11, only a limited number of scanned points, which are on the narrow gaps among concrete panels, can provide additional constraints for estimating the translation parameter along the z-axis.

Using the results from real datasets, we compared the performance of the ICPatch registration on the three real datasets with different point down-sampling strategies: (a) adaptive down-sampling, (b) Gaussian sphere-based down-sampling, (c) random down-sampling, and (d) no down-sampling (i.e., using all points). Similar to the experiment for the simulated dataset, the PCA-based classification was first applied to each of the source point clouds to identify the nature of the defined local neighborhoods. For Real Datasets 1 and 3, 20 points have been used for defining the local neighborhoods. Real Dataset 2, on the other hand, uses 50 points to define the local neighborhood due to its relatively higher noise level. Then, the respective LPD for the classified planar local neighborhood was estimated according to Equation (7). The adaptive down-sampling was applied on all identified planar points according to Equation (8) after specifying the desired local point density. Given the total number of points maintained in the source point clouds after conducting the adaptive down-sampling, the reduction percentages were then adjusted for both the Gaussian sphere-based and random down-sampling approaches to ensure an identical number of points used in the ICPatch registration. The desired point density, total number of points in the original point cloud, and number of down-sampled points after conducting the adaptive down-sampling with the desired point density are presented in

Table 4. Parameters for the adaptive down-sampling approach.

	Desired Point Density (pts/m2)	Total Number of Points	Number of Down-Sampled Points
Real Dataset 1	20	143,779	23,059
Real Dataset 2	50	1,983,108	184,912
Real Dataset 3	20	5,812,514	20,420

.

Figure 12, Figure 13 and Figure 14 illustrate the point density maps for the original as well as adaptively, Gaussian sphere-based, and randomly down-sampled source point clouds in Real Datasets 1, 2, and 3, respectively. Through a closer inspection of these point density maps, one can observe that the adaptive down-sampling leads to relatively uniform LPD over the thinned point clouds (See Figure 12b, Figure 13b, and Figure 14b). This confirms the expectation that the adaptive down-sampling approach would reduce more points on the planar surface with higher point density while keeping all points in sparse areas. Different from the adaptive down-sampling, the Gaussian sphere-based approach aims at maintaining a similar number of points on each of the detected planar surfaces. Looking into the density maps in Figure 12c, Figure 13c, and Figure 14c, one can see that the Gaussian sphere-based down-sampling has significantly reduced points on big planar surfaces (e.g., building facades and roof-tops) while it has emphasized points on small/thin planar patches/areas (e.g., the roof edges, and joints between panels). It is worth noting that these emphasized points with various normal directions can be of great importance for the point cloud registration as they account for the accurate estimate of one or more transformation parameters. In terms of the random approach, a constant reduction rate was applied over the entire point cloud during the thinning procedure. As can be seen in Figure 12d, Figure 13d, and Figure 14d, after conducting the random down-sampling, dense areas preserve high point density while sparse regions remain sparse since this approach fails to consider the internal properties (i.e., local point density) of the involved point clouds.

In order to evaluate the derived registration outcomes, both qualitative and quantitative evaluation methodologies have been established for the comparative performance analysis. For qualitative evaluation, cross-sections over the aligned point clouds using the derived registration parameters from different down-sampling approaches have been generated over the three datasets and illustrated in Figure 15, Figure 16 and Figure 17, respectively (the reference point clouds are shown in green, and the source point clouds are visualized in red). A closer inspection of Figure 15 and Figure 16 reveals the fact that precise alignment can be achieved between the involved point clouds in Real Datasets 1 and 2 using either the original point cloud (i.e., all points) or the adopted point down-sampling approaches (i.e., adaptive, Gaussian Sphere-based, and random down-sampling). However, among all tests for Real Dataset 3, the Gaussian Sphere-based down-sampling led to the best alignment quality, which is visible at the joints gap between concrete panels, as shown in Figure 17d. As mentioned earlier, this superior performance of the Gaussian Sphere-based down-sampling is mainly caused by the high percentage of selected points within the joints (See Figure 14). Compared to other approaches, these points led to a correct estimate of the Z component for the translation parameters as well as the convergence to the correct alignment between the two involved point clouds. In this regard, one can claim that the proposed Gaussian Sphere-based approach can be more advantageous for dealing with challenging registration cases with very limited geometric constraints/variability.

For the quantitative evaluation,

Table 5. The statistics of ICPatch registration using the original (i.e., all points) as well as adaptively, Gaussian Sphere-based, and random down-sampled sourced point clouds for Real Datasets 1, 2, and 3.

	All Points	Adaptive	Gaussian Sphere	Random
Real Dataset 1
RMSE (m)	0.060	0.044	0.048	0.071
Execution time (s)	193.56	113.27	895.61	34.52
Real Dataset 2
RMSE (m)	0.050	0.029	0.033	0.050
Execution time (s)	3286.81	629.84	1617.63	334.76
Real Dataset 3
RMSE (m)	0.020	0.016	0.022	0.018
Execution time (s)	5425.13	300.44	1115.98	131.61

RMSE (Root Mean Square Error).

provides the derived RMSE values of the point-to-patch normal distance after performing the ICPatch registration as well as the total execution time of each conducted test for the three utilized experimental datasets. As can be seen in Table 5, for Real Datasets 1 and 2, the adaptive and Gaussian sphere-based provided similar point-to-patch RMSE values, which are 0.01 to 0.02 m less than the RMSE values derived from the two traditional approaches (i.e., random down-sampled and full points). For Real Dataset 3, the Gaussian sphere-based approach led to the highest point-to-patch RMSE value, which was 0.022 m. However, as shown in Figure 17, one has to note that among the four conducted ICPatch registrations for Real Dataset 3, only the Gaussian sphere-based approach achieved the correct alignment between the two involved point clouds. Considering the data characteristics in Real Dataset 3, the high RMSE value for the Gaussian sphere-based approach can be explained by the fact that compared to the scanned points on the planar concrete panels, points within the joints among these panels usually have a higher noise level. Since the Gaussian sphere-based approach selects a higher percentage of points within the joints (see Figure 14), a higher point-to-patch RMSE value is expected when compared to the other three approaches (i.e., adaptive, random down-sampled, and full points). In terms of the computational expenses, the experimental results confirm the expectation that the random down-sampling approach leads to the shortest execution time for all the three real datasets. On the other hand, due to the utilization of an inefficient brute-force approach for the peak detection, the Gaussian sphere-based down-sampling required the largest amount of time for Real Dataset 1 and the second-largest amount of time for Real Datasets 2 and 3 to complete the registration procedure.

Considering the observations drawn from both qualitative and quantitative analyses, we may argue that the adaptive down-sampling approach is capable of providing the best overall results for most of the common real datasets (e.g., Real Datasets 1 and 2) since it is able to provide a small RMSE value while completing the whole procedure within a relatively short execution time. However, for some challenging registration cases, like Real Dataset 3, the Gaussian sphere-based approach is recommended as it preserves a more balanced distribution of the surface normals in the down-sampled point cloud. Such balanced surface normal distribution is critical for the success of the accurate estimate of one or more transformation parameters relating to the involved point clouds.

4. Conclusions and Recommendations for Future Work

In this paper, two down-sampling approaches for the registration of 3D point clouds with non-uniform point density were introduced. The first approach utilizes an adaptive down-sampling strategy to remove redundant points in areas with high point density while keeping the points in lower density regions. The second approach begins by deriving the surface normal for each point and then the surface normals are projected onto a Gaussian sphere. Down-sampling is achieved by removing the points from the peaks detected in the Gaussian sphere. The experimental results confirmed that both the adaptive and Gaussian sphere-based down-sampling approaches can provide reliable estimates of transformation parameters in the presence of random noise in the utilized point clouds. Compared to the adaptive down-sampling, the Gaussian sphere-based approach implicitly detects all planar segments within the involved point cloud during the down-sampling process. Therefore, one can argue that these derived planar segments can be an additional advantage from the Gaussian sphere-based down-sampling.

In terms of the recommendation for future work, as previously noted, the Gaussian sphere-based down-sampling approach detects the peaks through a brute-force approach with a fixed search radius, which can be time-consuming and inefficient. Therefore, our future research will focus on the improvement of peak detection in the Gaussian sphere. Rather than adopting the brute-force strategy for peak detection, a more efficient search strategy will be determined. Furthermore, the utilization of an adaptive search radius, which can be derived while considering the local noise level, will be investigated.