CFAR Strategy Formulation and Evaluation Based on Fox’s H-function in Positive Alpha-Stable Sea Clutter

Abstract

The problem of target detection in impulsive non-Gaussian sea clutter has attracted a lot of attention in recent years. The positive alpha-stable (PαS) distribution has been validated as a suitable model for the impulsive non-Gaussian sea clutter. Since the probability density function (PDF) of the PαS variable cannot be expressed as a closed-form expression, the research into constant false alarm rate (CFAR) detectors in PαS distributed sea clutter is limited. This paper formulates and evaluates some CFAR detectors, such as Greatest Of-CFAR (GO-CFAR), Smallest Of-CFAR (SO-CFAR), Order Statistic-CFAR (OS-CFAR) and censored mean level (CML) detectors, in PαS distributed sea clutter. Firstly, the Fox’s H-function is adopted to express the PDF of the PαS variable, and the cumulative density function based on Fox’s H-function is derived in this paper. Then, by use of the properties of the H-function and PαS distribution, exact expressions of the probabilities of false alarm and detection for CFAR detectors in the PαS background are derived. Some CFAR properties of these detectors in the PαS background are also explored. Numerical results based on derived expressions are given and verified by Monte Carlo simulation. Some analyses of detection performance from a practical perspective are also given.

1. Introduction

The main goal of radar detection is to detect targets embedded in clutter. Detectors with a constant false alarm rate (CFAR) are needed when background clutter fluctuates with time. The cell averaging-CFAR (CA-CFAR) detector is a basic form of CFAR detector for single-pulse detection. The CA-CFAR is optimum under the assumption that the clutter samples are independent and identically distributed (IID) Gaussian variables [1]. Due to the considerable performance reduction of the CA-CFAR detector in nonhomogeneous situations, arising from the presence of clutter edges or interfering targets, some other detectors such as the Greatest Of-CFAR (GO-CFAR), Smallest Of-CFAR (SO-CFAR), Order Statistic-CFAR (OS-CFAR) and censored mean level (CML) detectors are proposed and studied [2,3,4]. GO-CFAR and SO-CFAR detectors are based on the mean level of reference samples. GO-CFAR has been proven to perform well against the clutter power transition in a nonhomogeneous Gaussian background and its performance loss in the homogeneous background is the smallest among the four detectors [5]. SO-CFAR has been proven to perform well when interfering targets or large clutter samples are present, but its performance loss in a homogeneous Gaussian background is the largest among the four detectors [5,6]. The OS-CFAR and CML detectors belong to the CFAR detectors, based on order statistics of reference samples. Compared with the GO-CFAR and SO-CFAR detectors, the OS-CFAR and CML detectors have more parameters that should be set a priori. In the OS-CFAR detector, the kth smallest reference sample is selected as the clutter power estimate. The detection performance loss of the OS-CFAR detector is tolerable, and it performs well in a situation with interfering targets when parameter $k$ is set accurately [1,5]. The CML detector has a small performance loss in a homogeneous Gaussian background and is quite robust in the presence of outliers when the number of censored samples is set accurately [1,5]. All of these detectors have been proven as CFAR in a Gaussian background. Besides, some other advanced adaptive CFAR strategies for multi-pulse detection in homogeneous or nonhomogeneous Gaussian backgrounds are also proposed and discussed [7,8,9]. The performances of CFAR detectors strongly depend on the clutter statistics. When the clutter distribution deviates from a Gaussian distribution, the CFAR properties and the detection performances of these detectors will change. In practice, the Gaussian distribution cannot approximately model the impulsive and heavy-tailed sea clutter [10,11,12,13]. Especially for some advanced systems with high resolution capability, or for detection with a low grazing angle, the probability of a false alarm (Pfa) inevitably increases due to the presence of spiky clutter samples. Therefore, finding an appropriate distribution to model the impulsive clutter is necessary for the analyses on the detectors.

To model the impulsive sea clutter, some distributions such as the K, Weibull and Pareto distributions are often used [3,14,15]. The K, Weibull and log-Normal distributions are commonly used to model the clutter amplitude, and the Pareto distribution is commonly used to model the clutter power distribution. The alpha-stable (αS) distribution is another distribution that is commonly used to model the impulsive clutter [6,16,17,18,19,20,21,22,23,24,25]. Differently from the distributions mentioned before, the αS model has two significant properties. Firstly, the αS distribution is derived from the generalized central limit theorem (GCLT). That means that the limiting distribution of the sum of the IID random variables (with finite or infinite variance) is the αS distribution. Secondly, the αS distribution is the only distribution that satisfies the stability property. Thus, the sum of two independent αS random variables with the same characteristic exponent is still the αS variable. Besides, in contrast to the exponentially decaying tails in the K and Weibull distributions, the αS distribution shows an algebraic decaying tail. Thus, the αS distribution can model highly impulsive clutter. The characteristic exponent α is a key parameter to decide the statistical properties of the αS distribution. The αS model becomes impulsive with a decrease in α.

The application of the αS distribution in modeling clutter focuses mainly on two aspects. One aspect is using the bivariate isotropic symmetric alpha-stable (SαS) distribution to model the complex clutter signal [16,17,18]. Another aspect is using the positive alpha-stable (PαS) distribution to model the clutter power [6,19,20,21,22,23,24,25]. The PαS distribution is a special case of the αS distribution family. For the PαS distribution, α is limited in the range of 0 to 1. That means that the PαS distribution can be used to model the highly impulsive signal. Some research [19,24,26] indicates that the clutter shows heavy-tailed characteristic properties in a high-resolution radar system and/or in the case of a low grazing angle, and suggests that some clutter power samples can be modeled as PαS variables. For example, [19] indicates that the power flow of some measured sea clutter in a low sea state 2 obtained by an X-band radar at a 0.9° grazing angle can be modeled by the PαS distribution. In this paper, the PαS distribution is chosen to model the clutter power samples.

Some previous research on the CFAR detectors in PαS backgrounds have been given in [6,20,21,22,23,24,25]. It is known that the probability density function (PDF) of the PαS variable cannot be expressed in a closed form except for in the case of a Pearson distribution (α = 1/2) [13]. Limited by this problem, much previous research just evaluates the CFAR detectors in the Pearson distribution [6,20,21,22,23]. In [20], some analyses on the CA, OS and CML detectors with homogeneous Pearson backgrounds are given. In [6], the performances of GO and SO detectors with homogeneous and nonhomogeneous Pearson backgrounds are studied. In [21], the performances of some decentralized CFAR detectors with homogeneous Pearson backgrounds with interfering targets are assessed. In [22], the decentralized CA, GO and SO detectors using fuzzy fusion rules in homogeneous Pearson backgrounds are assessed. In [23], the binary integrations of CA and OS detectors in homogeneous Pearson backgrounds are analyzed.

To deal with the problem that the PDF of the PαS variable usually cannot be expressed in a closed form, the Fox’s H-function is adopted to derive the PDF of the PαS variable in [24]. In this manner, the PDF of the PαS variable with an arbitrary value of $\alpha$ is expressed in a closed-form expression in terms of the H-function. Then, the CA-CFAR detector in a homogeneous PαS background is easily analyzed in [24]. Moreover, the CA-CFAR detector in a nonhomogeneous PαS background with an arbitrary value of α is formulated and analyzed in [25]. To date, other commonly-used CFAR detectors have not been formulated and studied in the PαS background with an arbitrary value of α, except for the CA-CFAR detector.

The main contribution of this study is the formulation and evaluation of the GO, SO, OS and CML detectors in a PαS background with an arbitrary value of α. Our study fills the gaps in the research regarding CFAR detectors in a PαS background. Specifically, the contributions can be summarized as:

• The Fox’s H-function is adopted to derive the expressions of Pfa and the probability of detection (Pd). Based on the PDF of the PαS distribution in [24], the closed-form cumulative density function (CDF) is derived based on the H-function. Then, by the use of certain properties of the H-function and PαS distribution, exact expressions of Pfa and Pd are derived.
• Certain CFAR properties of these detectors in the PαS background are explored based on the derived expressions. The detection performances in the PαS background are analyzed according to the numerical results based on the derived expressions and the Monte Carlo (MC) simulation [27] results.
• When calculating the Pfas and Pds, the H-function is transformed to Meijer’s G-function. Meijer’s G-function is available in some software and can be calculated directly.

The rest of this paper is organized as follows. In Section 2, GO, SO, OS and CML detectors are formulated in terms of the H-function in a PαS background. In Section 3, some numerical results based on the derived expressions and some MC simulation results are given. Finally, conclusions are given in Section 4.

2. Formulation of the CFAR Detectors in a PαS Background

In this section, some CFAR detectors are formulated in a PαS background. Firstly, the basic CFAR detection problem in a PαS background is introduced in Section 2.1. Then, based on Section 2.1, GO, SO, OS and CML detectors are formulated in a homogeneous PαS background. The GO, SO, and OS detectors are also formulated in a nonhomogeneous PαS background.

2.1. Basic CFAR Detection Problem in a PαS Background

Figure 1 shows the basic procedures of different CFAR detectors. The square law detector processes the received signal vector $r_0$ after matched filtering so that the square of the signal amplitude vector $r={\left|r_0\right|}^2$ is obtained. Note the signal vector $r$ is a vector in the time domain with each of its elements being the square of the signal amplitude in each range cell. Then, the outputs of the square law detector are input into a shift register (also called the detection window) of length $N+1$. The sample in the middle of the shift register is the test sample $D$. The leading $N/2$ and the lagging $N/2$ samples in the shift register are the reference samples. Firstly, the clutter estimate $Z$ is obtained using the reference samples. Different detectors have different estimation strategies. The CA-CFAR, GO-CFAR and SO-CFAR detectors belong to the CFAR detectors based on mean level of the reference samples. For these three detectors, the variables $U$ and $V$ are obtained by the leading $N/2$ and the lagging $N/2$ reference samples with $U=\frac{1}{N/2}{\displaystyle {\sum }_{i=1}^{N/2}{X}_i}$ and $V=\frac{1}{N/2}{\displaystyle {\sum }_{i=N/2+1}^N{X}_i}$. Then:

• For CA-CFAR: $Z=\left(U+V\right)/2$. In the CA-CFAR detector, the power estimate $Z$ is the mean of $N$ reference samples. The CA-CFAR detector is better than the other four detectors in a homogeneous Gaussian background.
• For GO-CFAR: $Z=\max \left(U,V\right)$. In the GO-CFAR detector, the power estimate $Z$ is the maximum of $U$ and $V$. The GO-CFAR detector has been proven to perform the best among the five detectors against the clutter power transition in a nonhomogeneous Gaussian background, and its performance loss in the homogeneous background is smaller than for SO-CFAR, OS-CFAR and CML detectors.
• For SO-CFAR: $Z=\min \left(U,V\right)$. In the SO-CFAR detector, the power estimate $Z$ is the minimum of $U$ and $V$. The SO-CFAR detector performs well when interfering targets or large clutter samples are present in the Gaussian background.

The OS-CFAR and CML detectors belong to the CFAR detectors based on order statistics of the reference samples. For these two detectors, the reference samples are firstly ordered with $X_{(1)}\le X_{(2)}\le \dots \le X_{(N)}$. Then:

• For OS-CFAR: $Z=X_{\left(k\right)}$. The $k$th smallest reference sample is selected as the power estimate. The detection performance loss of the OS-CFAR detector is tolerable, and it performs well in the situation with interfering targets when parameter $k$ is set accurately.
• For CML: The power estimate $Z={\displaystyle {\sum }_{k=1}^{N-p}{X}_{\left(k\right)}}$. In the CML detector, the largest $p$ reference samples are censored, and the mean of the remaining reference samples is adopted as the power estimate $Z$. The CML detector has a small performance loss in a homogeneous Gaussian background and is quite robust in the presence of outliers when $p$ is set accurately.

Secondly, the threshold can be obtained by multiplying the power estimate $Z$ and the scale parameter $T$.

Finally, a detection decision can be made by comparing the threshold $TZ$ and the test sample $D$. The decision that the target is present (${ℍ}_1$) or absent (${ℍ}_0$) can be made according to:

$$D\begin{array}{c}\stackrel{{ℍ}_1}{>}\\ \underset{{ℍ}_0}{<}\end{array}TZ$$

(1)

where $D$ is the test sample and $T$ represents the scale factor.

The Pfa for the CFAR detectors shown in Figure 1 can be expressed as:

$$\begin{array}{l}{P}_{fa}=E_Z\left[\mathrm{Pr}\left(D>TZ|{ℍ}_0\right)\right]={\displaystyle {\int }_0^{\infty }{f}_Z\left(z\right)\left[1-\mathrm{Pr}\left(D\le TZ|{ℍ}_0\right)\right]dz}=1-{\displaystyle {\int }_0^{\infty }{f}_Z\left(z\right)F_{D|{ℍ}_0}\left(Tz|{ℍ}_0\right)dz}\\ =1-{\displaystyle {\int }_0^{\infty }{F}_{D|{ℍ}_0}\left(Tz|{ℍ}_0\right)d{F}_Z\left(z\right)}=1-\left[F_{D|{ℍ}_1}\left(Tz|{ℍ}_0\right)F_Z\left(z\right)|\begin{array}{c}\infty \\ 0\end{array}-{\displaystyle {\int }_0^{\infty }{F}_Z\left(z\right)d{F}_{D|{ℍ}_0}\left(Tz|{ℍ}_0\right)}\right]\\ =T{\displaystyle {\int }_0^{\infty }{F}_Z\left(z\right)f_{D|{ℍ}_0}\left(Tz|{ℍ}_0\right)dz}\end{array}$$

(2)

where $E_Z[·]$ is the expectation, $\mathrm{Pr}(·)$ is the probability, $f_Z(·)$ and $F_Z(·)$ are the PDF and CDF of $Z$, and $f_{D|{ℍ}_0}\left(·|{ℍ}_0\right)$ and $F_{D|{\mathrm{H}}_0}\left(·|{ℍ}_0\right)$ are the PDF and CDF of $D$ under ${ℍ}_0$, respectively.

Then, the Pd for the CFAR detectors shown in Figure 1 can be expressed as:

$$\begin{array}{l}{P}_d=E_Z\left[\mathrm{Pr}\left(D>TZ|{ℍ}_1\right)\right]={\displaystyle {\int }_0^{\infty }{f}_Z\left(z\right)\left[1-\mathrm{Pr}\left(D\le TZ|{ℍ}_1\right)\right]dz}=1-{\displaystyle {\int }_0^{\infty }{f}_Z\left(z\right)F_{D|{ℍ}_1}\left(Tz|{ℍ}_1\right)dz}\\ =1-{\displaystyle {\int }_0^{\infty }{F}_{D|{ℍ}_0}\left(Tz|{ℍ}_1\right)d{F}_Z\left(z\right)}=1-\left[F_{D|{ℍ}_1}\left(Tz|{ℍ}_1\right)F_Z\left(z\right)|\begin{array}{c}\infty \\ 0\end{array}-{\displaystyle {\int }_0^{\infty }{F}_Z\left(z\right)d{F}_{D|{ℍ}_1}\left(Tz|{ℍ}_1\right)}\right]\\ =T{\displaystyle {\int }_0^{\infty }{F}_Z\left(z\right)f_{D|{ℍ}_1}\left(Tz|{ℍ}_1\right)dz}\end{array}$$

(3)

where $f_{D|{ℍ}_1}\left(·|{ℍ}_1\right)$ and $F_{D|{ℍ}_1}\left(·|{ℍ}_1\right)$ are the PDF and CDF of $D$ under ${ℍ}_1$, respectively.

Note that for different detectors in homogeneous or nonhomogeneous backgrounds, the power estimates $Z$ are different, and so are the PDFs $f_Z(·)$s. Therefore, Equations (2) and (3) are the basic forms of Pfa and Pd, which can formulate different detectors in both homogeneous and nonhomogeneous backgrounds.

In this study, the clutter power samples shown in Figure 1 are modeled by the PαS distribution. In Appendix A, certain measured sea clutter power data in the IPIX database [28] are proved to be in accordance with the PαS distribution. The PDF of the PαS distribution generally cannot be expressed in a closed form, and it is generally defined by its characteristic function (CF). A random variable $X_i$ is said to be a PαS random variable if, and only if, its CF (defined as the Laplace transform of the PDF) is in the form [29]:

$${\phi }_{X_i}\left(t\right)=\exp \left(-\gamma t^{\alpha }\right)$$

(4)

where $\alpha$ ($0<\alpha <1$) represents the characteristic exponent, which is a measure of the shape of the distribution; and $\gamma$ ($\gamma >0$) represents the dispersion or scale parameter, which behaves like the variance in the Gaussian distribution and measures the spread of the PαS distribution. The smaller the $\alpha$ is, the heavier the tail of the PαS distribution is.

In general, the PDF of the PαS variable cannot be expressed in a closed form except for in the case of $\alpha =1/2$. To deal with this problem, the PDF of the PαS variable is derived as a closed-form expression in terms of the Fox’s H-function in [24]. The Fox’s H-function is defined via a Mellin-Barnes type integral [30]:

$$H_{p,q}^{m,n}\left[z|{}_{\left(b_1,B_1\right),\cdots ,\left(b_q,B_q\right)}^{\left(a_{1,}{A}_1\right),\cdots ,\left(a_{p,}{A}_p\right)}\right]=\frac{1}{2\pi i}{\displaystyle {\int }_{ℒ}\frac{{\displaystyle \prod _{j=1}^m\mathsf{\Gamma }\left(b_j+B_{j}s\right)}{\displaystyle \prod _{i=1}^n\mathsf{\Gamma }\left(1-a_i-A_{i}s\right)}}{{\displaystyle \prod _{i=n+1}^p\mathsf{\Gamma }\left(a_i+A_{i}s\right)}{\displaystyle \prod _{j=m+1}^q\mathsf{\Gamma }\left(1-b_j-B_{j}s\right)}}{z}^{-s}ds}$$

(5)

where $z\ne 0$; $m$, $n$, $p$ and $q$ are integers with $0\le m\le q$ and $0\le n\le p$; $A_i$ and $B_j$ are positive real numbers; $a_i$ and $b_j$ are real or complex numbers; and $ℒ$ is the integral path, which should be chosen to separate the poles of $\mathsf{\Gamma }\left(b_j+B_{j}s\right)$ from the poles of $\mathsf{\Gamma }\left(1-a_i-A_{i}s\right)$. The Fox’s H-function has been studied comprehensively in [30].

In [24], the PDF of the PαS variable is derived through the Laplace transform of Equation (4). The closed-form PDF expression in terms of the Fox’s H-function can be written as:

$$f_X\left(z\right)=z^{-1}{H}_{1,1}^{0,1}\left[{\gamma }^{-1}{z}^{\alpha }{|}_{\left(1,\alpha \right)}^{\left(1,1\right)}\right]\equiv z^{-1}{H}_1\left({\gamma }^{-1}{z}^{\alpha }\right)$$

(6)

where $H_1\left({\gamma }^{-1}{z}^{\alpha }\right)$ is used to express $H_{1,1}^{1,0}\left[\gamma z^{-\alpha }{|}_{\left(0,1\right)}^{\left(0,\alpha \right)}\right]$ for brevity. Equation (6) gives a uniform PDF expression of the PαS variable with arbitrary $\alpha$ ($0<\alpha <1$).This PDF expression is convenient for the formulation and evaluation of the CFAR detectors. When $\alpha =1/2$, the H-function in the PαS distribution becomes the Pearson distribution [6,20,21,22,23], which has closed-form PDF expressions with respect to the elementary functions.

The CDF of the PαS variable is also necessary for the formulation and evaluation of the CFAR detectors, and it has not yet been given in previous research. In this paper, the CDF of the PαS variable is derived as a closed-form expression in terms of the H-function based on Equation (6). The CDF of a PαS variable $X$ can be expressed as:

$$F_X\left(z\right)=H_{1,1}^{0,1}\left[{\gamma }^{-1}{z}^{\alpha }{|}_{\left(0,\alpha \right)}^{\left(1,1\right)}\right]\equiv H_2\left({\gamma }^{-1}{z}^{\alpha }\right)$$

(7)

where $H_2\left({\gamma }^{-1}{z}^{\alpha }\right)$ is used to express $H_{1,1}^{0,1}\left[{\gamma }^{-1}{z}^{\alpha }{|}_{\left(0,\alpha \right)}^{\left(1,1\right)}\right]$ for brevity. The derivation process of Equation (7) is given in Appendix B. The PDF and CDF of the PαS variable have been expressed as closed-form expressions with regard to the H-function. Then, based on some properties of H-function and PαS distribution, the exact Pfa and Pd expressions of the CFAR detectors can be derived.

2.2. In a Homogeneous PαS Background

Here, the GO, SO, OS and CML detectors are formulated in a homogeneous PαS background. The clutter power samples are assumed to be IID and to follow a PαS distribution.

2.2.1. GO-CFAR

In order to derive the Pfa expression of the GO-CFAR detector, the PDF of the power estimate $Z$ and the CDF of the test sample $D$ under ${ℍ}_0$ are necessary. According to [3], the PDF of $Z$ in GO-CFAR detector can be written as:

$$f_Z^{GO}\left(z\right)=f_U\left(z\right)F_V\left(z\right)+f_V\left(z\right)F_U\left(z\right)$$

(8)

where $f_U\left(z\right)$ and $F_U\left(z\right)$ are the PDF and CDF of the variable $U$, shown in Figure 1. $f_V\left(z\right)$ and $F_V\left(z\right)$ are the PDF and CDF of the variable $V$, shown in Figure 1. According to the stability property of the PαS distribution, the variables $U$ and $V$ also follow a PαS distribution with the same characteristic exponent $\alpha$ and same scale parameter $2^{\alpha -1}{N}^{1-\alpha }\gamma$ [29]. According to the PDF and CDF expressions of the PαS variable in Equations (6) and (7), the PDFs and CDFs of $U$ and $V$ can be written as:

$$\begin{array}{l}{f}_U\left(z\right)=f_V\left(z\right)=z^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)\\ F_U\left(z\right)=F_V\left(z\right)=H_2\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)\end{array}$$

(9)

Then, the PDF of $Z$ can be obtained by substituting the PDFs and CDFs of $U$ and $V$ in Equation (9) into Equation (8):

$$f_Z^{GO}\left(z\right)=2z^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)H_2\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)$$

(10)

In Equation (10), the PDF of the clutter power estimate $Z$ in the GO-CFAR detector is also expressed in a brief closed form in terms of the H-function.

Under the assumption that the target is absent, the CDF of the test sample $D$ is the same as that in Equation (7):

$$F_{D|{ℍ}_0}\left(z|{ℍ}_0\right)=H_2\left({\gamma }^{-1}{z}^{\alpha }\right)$$

(11)

The Pfa is obtained by substituting Equations (10) and (11) into Equation (2):

$$P_{fa-hom}^{GO}=2{\displaystyle {\int }_0^{\infty }{z}^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)}{H}_2\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)\left[1-H_2\left(T{\gamma }^{-1}{z}^{\alpha }\right)\right]dz$$

(12)

By setting $\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$, the Pfa can be obtained and is expressed by Equation (T1.1) in

Table 1. The probabilities of a false alarm (Pfas) and probabilities of detection (Pds) of different detectors in a homogeneous positive alpha-stable (PαS) background.

	Probability of False Alarm	Probability of Detection
GO	$\begin{array}{l}{P}_{fa-hom}^{GO}=2{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)}\\ \times H_2\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)\left[1-H_2\left(T\mathsf{\Omega }\right)\right]d\mathsf{\Omega }\end{array}$(T1.1)	$\begin{array}{l}{P}_{d-hom}^{GO}=2{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)}\\ \times H_2\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)\exp \left[-T{\mathsf{\Omega }}^{1/\alpha }{\gamma }^{1/\alpha }/{\sigma }_s^2\right]d\mathsf{\Omega }\end{array}$(T1.2)
SO	$\begin{array}{l}{P}_{fa-hom}^{SO}=2{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)}\\ \times \left[1-H_2\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)\right]\left[1-H_2\left(T\mathsf{\Omega }\right)\right]d\mathsf{\Omega }\end{array}$(T1.3)	$\begin{array}{l}{P}_{d-hom}^{SO}=2{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)}\\ \times \left[1-H_2\left(2^{1-\alpha }{N}^{\alpha -1}\mathsf{\Omega }\right)\right]\exp \left(-T{\mathsf{\Omega }}^{1/\alpha }{\gamma }^{1/\alpha }/{\sigma }_s^2\right)d\mathsf{\Omega }\end{array}$(T1.4)
OS	$\begin{array}{l}{P}_{fa-hom}^{OS}=\frac{1}{\alpha }k\left(\begin{array}{c}N\\ k\end{array}\right){\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-k}}\\ \times {\left[H_2\left(\mathsf{\Omega }\right)\right]}^{k-1}{H}_1\left(\mathsf{\Omega }\right)\left[1-H_2\left(T^{\alpha }\mathsf{\Omega }\right)\right]d\mathsf{\Omega }\end{array}$(T1.5)	$\begin{array}{l}{P}_{d-hom}^{OS}=\frac{1}{\alpha }k\left(\begin{array}{c}N\\ k\end{array}\right){\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}\exp \left(-T{\mathsf{\Omega }}^{1/\alpha }{\gamma }^{1/\alpha }/{\sigma }_s^2\right)}\\ \times {\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-k}{\left[H_2\left(\mathsf{\Omega }\right)\right]}^{k-1}{H}_1\left(\mathsf{\Omega }\right)d\mathsf{\Omega }\end{array}$(T1.6)
CML	$\begin{array}{l}{P}_{fa-hom}^{CML}=\frac{1}{2\pi }{\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\left[g\left(\varphi \right)\right]}^{N-p}\exp \left(-j\varphi \psi \right)}}\\ \times \left[1-H_2\left(T^{\alpha }{\psi }^{\alpha }\right)\right]d\varphi d\psi \end{array}$(T1.7)	-

.

Then, the Pd will be discussed. Here, it is assumed that the target is Rayleigh fluctuating with parameter ${\sigma }_s^2$ and that the target signal power dominates the test sample. After the square-law detector, the test sample $D$ is exponentially distributed. Its CDF can be expressed as:

$$F_{D|{ℍ}_1}\left(z|{ℍ}_1\right)=\{\begin{array}{cc}1-\exp \left(-z/{\sigma }_s^2\right)\hfill & Tz\ge 0\hfill \\ 0\hfill & Tz<0\hfill \end{array}$$

(13)

By Substituting Equations (10) and (13) into Equation (3) and setting $\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$, Pd can be derived as Equation (T1.2) in Table 1.

2.2.2. SO-CFAR

According to [3], the PDF of $Z$ in the SO-CFAR detector is written as:

$$f_Z^{SO}\left(z\right)=f_U\left(z\right)\left[1-F_V\left(z\right)\right]+f_V\left(z\right)\left[1-F_U\left(z\right)\right]$$

(14)

Similar to the analysis in Section 2.2.1, Pfa can be obtained according to Equations (14), (9), (11) and (2). Pd can be obtained according to Equations (14), (9), (13) and (3). The Pfa and Pd in this case are expressed by Equations (T1.3) and (T1.4) in Table 1.

2.2.3. OS-CFAR

According to [31] (Equation (2.1.6)) and Equations (6) and (7), the PDF of the power estimate $Z$ can be expressed as:

$$f_Z^{OS}\left(z\right)=k\left(\begin{array}{c}N\\ k\end{array}\right){\left[1-H_2\left({\gamma }^{-1}{z}^{\alpha }\right)\right]}^{N-k}{\left[H_2\left({\gamma }^{-1}{z}^{\alpha }\right)\right]}^{k-1}{z}^{-1}{H}_1\left({\gamma }^{-1}{z}^{\alpha }\right)$$

(15)

Then, the Pfa and Pd can be obtained by substituting Equations (15) and (11) into Equation (2), substituting Equations (15) and (13) into Equation (3) and setting $\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$. The Pfa and Pd in this case are expressed by Equations (T1.5) and (T1.6) in Table 1.

2.2.4. CML

As shown in Figure 1, the estimated clutter power $Z$ is defined as the sum of the first $N-p$ smallest samples: $Z={\displaystyle {\sum }_{k=1}^{N-p}{X}_{\left(k\right)}}$.

Firstly, the PDF of $Z$ will be determined. Let $X_1,\dots ,X_N$ be the IID reference clutter samples. Let $Y_1,\dots ,Y_{N-p}$ represent the remaining samples by censoring the $p$ largest samples $X_i$ ($i=1,\dots ,N$). Then, $Z$ can be written as $Z={\displaystyle {\sum }_{i=1}^{N-p}{Y}_i}$. Note that a single $Y_i$ is able to have any rank from 1 to $N-p$, so $Y_i$s are IID variables [20]. The PDF of $Y_i$ can be expressed by the PDFs of the ranked samples: $f_{Y_i}\left(z\right)=1/\left(N-p\right)·{\displaystyle {\sum }_{k=1}^{N-p}{f}_{X_{\left(k\right)}}\left(z\right)}$. Similarly, it also holds to $X_i$ that:

$$f_{X_i}\left(z\right)=\frac{1}{N}{\displaystyle \sum _{k=1}^N{f}_{X_{\left(k\right)}}\left(z\right)}=\frac{N-p}{N}{f}_{Y_i}\left(z\right)+\frac{1}{N}{\displaystyle \sum _{k=N-p+1}^N{f}_{X_{\left(k\right)}}\left(z\right)}$$

(16)

Obviously, $f_{X_{\left(k\right)}}\left(z\right)$ is the same as the $f_Z^{OS}\left(z\right)$ in Equation (14). Then, by substituting Equations (6) and (15) into Equation (16) and solving for $f_{Y_i}\left(z\right)$, $f_{Y_i}\left(z\right)$ is obtained:

$$f_{Y_i}\left(z\right)=\frac{N}{N-p}{z}^{-1}{H}_1\left({\gamma }^{-1}{z}^{\alpha }\right)\left\{1-\frac{1}{N}{\displaystyle \sum _{k=N-p+1}^{N}k\left(\begin{array}{c}N\\ k\end{array}\right){\left[1-H_2\left({\gamma }^{-1}{z}^{\alpha }\right)\right]}^{N-k}{\left[H_2\left({\gamma }^{-1}{z}^{\alpha }\right)\right]}^{k-1}}\right\}$$

(17)

Then, the CF ${\phi }_{Y_i}\left(\tau \right)$ of $Y_i$ can be obtained according to the $f_{Y_i}\left(z\right)$ in Equation (17) (setting $\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$):

$$\begin{array}{ll}{\phi }_{Y_i}\left(\tau \right)& =\frac{N}{N-p}{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}{H}_1\left(\mathsf{\Omega }\right)}\exp \left(j{\gamma }^{1/\alpha }\tau {\mathsf{\Omega }}^{1/\alpha }\right)\left\{1-\frac{1}{N}{\displaystyle \sum _{k=N-p+1}^{N}k\left(\begin{array}{c}N\\ k\end{array}\right){\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-k}{\left[H_2\left(\mathsf{\Omega }\right)\right]}^{k-1}}\right\}d\mathsf{\Omega }\\ & \stackrel{def}{=}g\left({\gamma }^{1/\alpha }\tau \right)\end{array}$$

(18)

Then, the CF of $Z$ can be written as ${\left[g\left({\gamma }^{1/\alpha }\tau \right)\right]}^{N-p}$ and the PDF of $Z$ can be obtained:

$$f_Z^{CML}\left(z\right)=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }{\left[g\left({\gamma }^{1/\alpha }\tau \right)\right]}^{N-p}\exp \left(-jz\tau \right)d\tau }$$

(19)

Then, Pfa can be obtained by substituting Equations (19) and (11) into Equation (2) and setting $\varphi ={\gamma }^{1/\alpha }\tau$ and $\psi ={\gamma }^{-1/\alpha }z$. The Pfa here is expressed by Equation (T1.7) in Table 1.

For CML, the expression of Pd is so complex that its simple forms cannot be given at present. Therefore, only the Pfa of CML in a homogeneous background is given.

Table 1 gives the exact Pfa and Pd expressions of different CFAR detectors in a homogeneous background. The expressions are all derived from the basic Equations (2) and (3) in terms of the H-function. Through the derived expressions, some CFAR properties can be easily observed, and the Pfas and Pds can be calculated conveniently. In Table 1, Equations (T1.1), (T1.3), (T1.5) and (T1.7) show that the Pfas of these four detectors depend on the exponential characteristic exponent $\alpha$ and the scale parameter $T$. Moreover, (T1.5) and (T1.7) show that the Pfas of the OS and CML detectors also depend on their own parameter $k$ or $p$. In Equations (T1.1), (T1.3), (T1.5) and (T1.7) in Table 1, only the parameter $\mathsf{\Omega }$ ($\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$) is related to scale parameter $\gamma$, and the Pfas of these four detectors are the integrals with respect to $\mathsf{\Omega }$. Therefore, from Equations (T1.1), (T1.3), (T1.5) and (T1.7), a CFAR property of the GO, SO, OS and CML detectors in a homogeneous PαS background can be found, which is that the Pfas here are independent of the scale parameter $\gamma$. From Equations (T1.2), (T1.4) and (T1.6) in Table 1, it can be seen that the Pds of these four detectors are also the integrals with respect to $\mathsf{\Omega }$. Equations (T1.2), (T1.4) and (T1.6) also show that the Pds of the GO, SO and OS detectors are functions of ${\gamma }^{1/\alpha }/{\sigma }_s^2$, in which the ${\gamma }^{1/\alpha }$ is related to the statistical properties of the PαS distributed clutter power sample, and ${\sigma }_s^2$ is the power parameter of the exponentially distributed target power sample.

2.3. In a Nonhomogeneous Background

Since the CML detector in a nonhomogeneous PαS background is too complicated to formulate, only the GO, SO and OS detectors are formulated in a nonhomogeneous PαS background here.

2.3.1. GO-CFAR

In a nonhomogeneous background, it is assumed that a clutter boundary is present in the detection window. The leading $R$ samples in the detection window are relatively strong, with scale parameter $\mu \gamma$($\mu >1$), and the other $N-R$ samples in the detection window are relatively weak, with scale parameter $\gamma$. All of the strong and weak samples have the same characteristic exponent $\alpha$. Here, two situations in a nonhomogeneous background will be considered: 1. the test sample is immersed in weak clutter, and 2. the test sample is immersed in strong clutter:

1. Test sample immersed in weak clutter:

In this case, $U$ is the sum of $R$ strong samples and $N/2-R$ weak samples. $V$ is the sum of $N/2$ weak samples. Therefore, $U$ and $V$ can be rewritten as:

$$U=\frac{1}{N/2}\left({\displaystyle \sum _{i=1}^R{X}_i}+{\displaystyle \sum _{i=R+1}^{N/2}{X}_i}\right),V=\frac{1}{N/2}{\displaystyle \sum _{i=N/2+1}^N{X}_i}$$

(20)

According to the property of PαS in [29], $U$ and $V$ are still PαS random variables with the same characteristic exponent $\alpha$, and their scale parameters are $2^{\alpha }{N}^{-\alpha }\left(N/2-R+\mu R\right)\gamma$ and $2^{\alpha -1}{N}^{1-\alpha }\gamma$, respectively. By substituting the characteristic exponents and scale parameters of $U$ and $V$ into Equations (6) and (7), the PDFs and CDFs of $U$ and $V$ can be expressed as:

$$\begin{array}{ll}{f}_U\left(z\right)=z^{-1}{H}_1\left(2^{-\alpha }{N}^{\alpha }{\left(N/2-R+\mu R\right)}^{-1}{\gamma }^{-1}{z}^{\alpha }\right),& F_U\left(z\right)=H_2\left(2^{-\alpha }{N}^{\alpha }{\left(N/2-R+\mu R\right)}^{-1}{\gamma }^{-1}{z}^{\alpha }\right)\\ f_V\left(z\right)=z^{-1}{H}_1\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right),& F_V\left(z\right)=H_2\left(2^{1-\alpha }{N}^{\alpha -1}{\gamma }^{-1}{z}^{\alpha }\right)\end{array}$$

(21)

The PDF of $Z$ can be obtained by substituting Equation (21) into Equation (8):

$$f_Z^{GO}\left(z\right)=z^{-1}{H}_1\left[\frac{2^{-\alpha }{N}^{\alpha }{\gamma }^{-1}{z}^{\alpha }}{N/2-R+\mu R}\right]H_2\left(\frac{{\gamma }^{-1}{z}^{\alpha }}{2^{\alpha -1}{N}^{1-\alpha }}\right)+z^{-1}{H}_1\left(\frac{{\gamma }^{-1}{z}^{\alpha }}{2^{\alpha -1}{N}^{1-\alpha }}\right)H_2\left[\frac{2^{-\alpha }{N}^{\alpha }{\gamma }^{-1}{z}^{\alpha }}{N/2-R+\mu R}\right]$$

(22)

The Pfa and Pd are obtained by substituting Equations (22) and (11) into Equation (2), substituting Equations (22) and (13) into Equation (3) and setting $\mathsf{\Omega }={\gamma }^{-1}{z}^{\alpha }$. The Pfa and Pd in this case are expressed by Equations (T2.1) and (T2.2) in

Table 2. The Pfas and Pds of different detectors in a nonhomogeneous PαS background.

	Probability of False Alarm	Probability of Detection
GO Case 1	$\begin{array}{l}{P}_{fa-non1}^{GO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}[H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)}\\ +H_1\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)]H_2\left(T^{\alpha }\mathsf{\Omega }\right)d\mathsf{\Omega }\end{array}$ (T2.1)	$\begin{array}{l}{P}_{d-non1}^{GO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}[H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)}\\ +H_1\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)]\exp \left(-T{\mathsf{\Omega }}^{1/\alpha }\frac{{\gamma }^{1/\alpha }}{{\sigma }_s^2}\right)d\mathsf{\Omega }\end{array}$ (T2.2)
GO Case 2	$\begin{array}{l}{P}_{fa-non2}^{GO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}[H_1\left(\frac{{\mu }^{-1}\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)}\\ +H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)]H_2\left(\frac{T^{\alpha }\mathsf{\Omega }}{\mu }\right)d\mathsf{\Omega }\end{array}$ (T2.3)	$\begin{array}{l}{P}_{d-non2}^{GO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}[H_1\left(\frac{{\mu }^{-1}\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)}\\ +H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)]\exp \left(\frac{-T{\mathsf{\Omega }}^{\frac{1}{\alpha }}{\gamma }^{\frac{1}{\alpha }}}{{\sigma }_s^2}\right)d\mathsf{\Omega }\end{array}$ (T2.4)
SO Case 1	$\begin{array}{l}{P}_{fa-non1}^{SO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}\{H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)\left[1-H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)\right]}\\ +H_1\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)\left[1-H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)\right]\}{H}_2\left(T^{\alpha }\mathsf{\Omega }\right)d\mathsf{\Omega }\end{array}$ (T2.5)	$\begin{array}{l}{P}_{d-non1}^{SO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}\{H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)\left[1-H_2\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)\right]}\\ +H_1\left(\frac{\mathsf{\Omega }}{2^{\alpha -1}{N}^{1-\alpha }}\right)\left[1-H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{N/2-R+\mu R}\right)\right]\}\exp \left(\frac{-T{\mathsf{\Omega }}^{\frac{1}{\alpha }}{\gamma }^{\frac{1}{\alpha }}}{{\sigma }_s^2}\right)d\mathsf{\Omega }\end{array}$ (T2.6)
SO Case 2	$\begin{array}{l}{P}_{fa-non2}^{SO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}\{H_1\left(\frac{N^{\alpha -1}\mathsf{\Omega }}{2^{\alpha -1}\mu }\right)\left[1-H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)\right]}\\ +H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)\left[1-H_2\left(\frac{N^{\alpha -1}\mathsf{\Omega }}{2^{\alpha -1}}\right)\right]\}{H}_2\left(\frac{T^{\alpha }\mathsf{\Omega }}{\mu }\right)d\mathsf{\Omega }\end{array}$ (T2.7)	$\begin{array}{l}{P}_{d-non2}^{SO}=1-{\alpha }^{-1}{\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}\{H_1\left(\frac{N^{\alpha -1}\mathsf{\Omega }}{2^{\alpha -1}\mu }\right)\left[1-H_2\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)\right]}\\ +H_1\left(\frac{2^{-\alpha }{N}^{\alpha }\mathsf{\Omega }}{\mu R-uN/2+N-R}\right)\left[1-H_2\left(\frac{N^{\alpha -1}\mathsf{\Omega }}{2^{\alpha -1}}\right)\right]\}\exp \left(\frac{-T{\mathsf{\Omega }}^{\frac{1}{\alpha }}{\gamma }^{\frac{1}{\alpha }}}{{\sigma }_s^2}\right)d\mathsf{\Omega }\end{array}$ (T2.8)
OS Case 1	$\begin{array}{l}{P}_{fa-non1}^{OS}=\frac{1}{\alpha }{\displaystyle \sum _{i=k}^N{\displaystyle \sum _{j=\max \left(0,i-R\right)}^{\min \left(i,N-R\right)}\left(\begin{array}{c}N-R\\ j\end{array}\right)\left(\begin{array}{c}R\\ i-j\end{array}\right){\displaystyle {\int }_0^{\infty }{\mathsf{\Omega }}^{-1}}}}{H}_1\left(T^{\alpha }\mathsf{\Omega }\right){\left[H_2\left(\mathsf{\Omega }\right)\right]}^j\\ \times {\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-R-j}{\left[H_2\left(\frac{\mathsf{\Omega }}{\mu }\right)\right]}^{i-j}{\left[1-H_2\left(\frac{\mathsf{\Omega }}{\mu }\right)\right]}^{R-i+j}d\mathsf{\Omega }\end{array}$ (T2.9)	$\begin{array}{l}{P}_{d-non1}^{OS}=\frac{{\gamma }^{1/\alpha }}{2{\sigma }_s^2}{\displaystyle \sum _{i=k}^N{\displaystyle \sum _{j=\max \left(0,i-R\right)}^{\min \left(i,N-R\right)}\left(\begin{array}{c}N-R\\ j\end{array}\right)\left(\begin{array}{c}R\\ i-j\end{array}\right){\displaystyle {\int }_0^{\infty }{\left[H_2\left(\mathsf{\Omega }\right)\right]}^j{\left[H_2\left(\frac{\mathsf{\Omega }}{\mu }\right)\right]}^{i-j}}}}\\ \times {\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-R-j}{\left[1-H_2\left(\frac{\mathsf{\Omega }}{\mu }\right)\right]}^{R-i+j}\exp \left(\frac{-T{\mathsf{\Omega }}^{\frac{1}{\alpha }}{\gamma }^{\frac{1}{\alpha }}}{{\sigma }_s^2}\right){\mathsf{\Omega }}^{\frac{1}{\alpha }-1}\frac{T}{\alpha }d\mathsf{\Omega }\end{array}$ (T2.10)
OS Case 2	$\begin{array}{l}{P}_{fa-non2}^{OS}=\frac{1}{\alpha }{\displaystyle \sum _{i=k}^N{\displaystyle \sum _{j=\max \left(0,i-R\right)}^{\min \left(i,N-R\right)}\left(\begin{array}{c}N-R\\ j\end{array}\right)\left(\begin{array}{c}R\\ i-j\end{array}\right){\displaystyle {\int }_0^{\infty }{H}_1\left(\frac{T^{\alpha }\mathsf{\Omega }}{\mu }\right){\left[H_2\left(\mathsf{\Omega }\right)\right]}^j}}}\\ \times {\left[1-H_2\left(\mathsf{\Omega }\right)\right]}^{N-R-j}{\left[H_2\left({\mu }^{-1}\mathsf{\Omega }\right)\right]}^{i-j}{\left[1-H_2\left({\mu }^{-1}\mathsf{\Omega }\right)\right]}^{R-i+j}{\mathsf{\Omega }}^{-1}d\mathsf{\Omega }\end{array}$ (T2.11)	$P_{d-non2}^{OS}=P_{d-non1}^{OS}$ (T2.12)

.

2. Test sample immersed in strong clutter:

Similarly, in this situation, $U$ and $V$ are still the PαS random variables, with scale parameters $2^{\alpha -1}{N}^{1-\alpha }\mu \gamma$ and $2^{\alpha }{N}^{-\alpha }\left(\mu R-uN/2+N-R\right)\gamma$, respectively. Since the test sample is in a strong clutter region, the CDF of $D$ under ${ℍ}_0$ is expressed as:

$$F_{D|{ℍ}_0}^{high}\left(z|{ℍ}_0\right)=H_2\left({\mu }^{-1}{\gamma }^{-1}{z}^{\alpha }\right)$$

(23)

Similarly to the situation when the test sample is immersed in weak clutter, the Pfa and Pd here can be derived by Equations (T2.3) and (T2.4) in Table 2.

2.3.2. SO-CFAR

1. Test sample immersed in weak clutter:

Similarly to in the analyses in Section 2.3.1, the Pfa and Pd can be derived by Equations (T2.5) and (T2.6) in Table 2.

2. Test sample immersed in strong clutter:

Similarly to in the analyses in Section 2.3.1, the Pfa and Pd can be derived by Equations (T2.7) and (T2.8) in Table 2.

2.3.3. OS-CFAR

In a nonhomogeneous background for the OS-CFAR detector, it is still assumed that a clutter boundary is present in the detection window. Here, $R$ relatively strong samples are denoted as $X_i^{\prime }$s ($i=1,2,\dots ,R$), with a scale parameter $\mu \gamma$ ($\mu >1$), and $N-R$ relatively weak samples are denoted as $X_i^{″}$s ($i=1,2,\dots ,N-R$), with a scale parameter $\gamma$. The PDFs and CDFs of strong samples $X_i^{\prime }$ and weak samples $X_i^{″}$ are expressed as:

$$\begin{array}{l}{f}_{X_i^{\prime }}\left(z\right)=z^{-1}{H}_1\left({\mu }^{-1}{\gamma }^{-1}{z}^{\alpha }\right),F_{X_i^{\prime }}\left(z\right)=H_2\left({\mu }^{-1}{\gamma }^{-1}{z}^{\alpha }\right)\\ f_{X_i^{″}}\left(z\right)=z^{-1}{H}_1\left({\gamma }^{-1}{z}^{\alpha }\right),F_{X_i^{″}}\left(z\right)=H_2\left({\gamma }^{-1}{z}^{\alpha }\right)\end{array}$$

(24)

1. Test sample immersed in weak clutter:

According to [31], the CDF of $Z$ can be expressed as:

$$F_Z^{OS}\left(z\right)={\displaystyle \sum _{i=k}^N{\displaystyle \sum _{j=\max \left(0,i-R\right)}^{\min \left(i,N-R\right)}\left(\begin{array}{c}N-R\\ j\end{array}\right)\left(\begin{array}{c}R\\ i-j\end{array}\right){\left[F_{X_i^{″}}\left(z\right)\right]}^j}}{\left[1-F_{X_i^{″}}\left(z\right)\right]}^{N-R-j}{\left[F_{X_i^{\prime }}\left(z\right)\right]}^{i-j}{\left[1-F_{X_i^{\prime }}\left(z\right)\right]}^{R-i+j}$$

(25)

Similarly to in the analysis in Section 2.3.1, the Pfa and Pd can be derived by Equations (T2.9) and (T2.10) in Table 2.

2. Test sample immersed in strong clutter:

Similarly to in the analysis in Section 2.3.1, the Pfa in this case is expressed by Equation (T2.11) in Table 2. Here, the Pd is equal to that in Equation (T2.10), and it is expressed by Equation (T2.12) in Table 2.

Table 2 gives the exact Pfa and Pd expressions of the GO, SO and OS detectors in a nonhomogeneous background, and these expressions are also derived from the basic forms in Equations (2) and (3). From Table 2, it can be seen that the Pfa and Pd expressions in a nonhomogeneous background are more complicated than those in Table 1. However, these expressions also indicate certain CFAR properties of these detectors and can also be calculated precisely through particular numerical methods. From the equations in Table 2, it can be seen that the Pfas depend not only on the parameters $\alpha$, $T$, $N$ and $k$ (for OS), but also on the parameters $R$ and $\mu$, which represent the characteristics of the nonhomogeneous background. Similarly to in the analyses of the expressions in Table 1, a CFAR property can also be observed, which is that the Pfas in a nonhomogeneous background do not depend on the scale parameters of strong and weak clutter but depend on their ratio $\mu$. Equations (T2.2), (T2.4), (T2.6), (T2.8), (T2.10) and (T2.12) show that the Pds of the GO, SO and OS detectors are also a function of ${\gamma }^{1/\alpha }/{\sigma }_s^2$, in which the ${\gamma }^{1/\alpha }$ is related to the statistical properties of the PαS distributed clutter power sample, and ${\sigma }_s^2$ is the power parameter of the exponentially distributed target power sample.

3. Results and Discussion

In this section, numerical results based on the derived expressions in Table 1 and Table 2 are given and analyzed. Meanwhile the accuracy of the numerical results is verified by the results obtained through MC simulations [27]. Since Equation (T1.7) for the CML detector is too complex to calculate, the analyses of the CML detector are not given in this section. The Pfa and Pd of the CA-CFAR detector in a homogeneous PαS background have been derived in [24]. In a nonhomogeneous PαS background with a clutter boundary, the CA-CFAR detector has also been formulated and evaluated in [25]. Here, the analyses of CA-CFAR based on the derived Pfa and Pd expressions in [24,25] are adopted for comparison.

When calculating the derived expressions, the calculation of the H-function is necessary. The H-function cannot be found in the standard packages of certain software such as MATLAB and Maple. Some numerical methods to calculate the H-function directly have been put forward, such as that in [32]. In this study, the H-functions in the derived expressions are expressed by the G-function [30], which can be directly calculated in the most popular mathematical software. In Appendix C, the H-functions $H_1\left({\gamma }^{-1}{z}^{\alpha }\right)$ and $H_2\left({\gamma }^{-1}{z}^{\alpha }\right)$ are expressed by the G-function so that they can be calculated. The integrals in the derived expressions in Table 1 and Table 2 are calculated using the adaptive Gauss-Kronrod quadrature method, which can be found as the “quadgk” function in MATLAB. The relative error tolerance is set to 10⁻³ as the termination condition in the calculation of the integrals.

In the MC simulations in this paper, each MC simulation result is obtained through simulating 10⁸ random sets of test and reference samples according to the set parameters. The PαS distributed clutter power samples are generated according to [33,34]. In order to analyze the differences between the numerical results and MC results quantitatively, an index called the mean relative error (MRE) is introduced, which is defined as:

$$MRE=\frac{1}{M}{\displaystyle \sum _m^M\frac{\left|R{n}_m-R{m}_m\right|}{R{n}_m}}$$

(26)

where $M$ is the number of numerical or MC results, $R{n}_m$ is the $m$th numerical result and $R{m}_m$ is the $m$th MC result, respectively.

Since the traditional signal-to-clutter ratio (SCR) cannot be used in the PαS background [6,20], a generalized signal-to-clutter ratio (GSCR) is here defined as:

$$GSCR=10\log \frac{{\sigma }_s^{2\alpha }}{\gamma }$$

(27)

Obviously, ${\gamma }^{1/\alpha }/{\sigma }_s^2$ is a function of GSCR, and the Pds derived in Table 1 and Table 2 are all functions of ${\gamma }^{1/\alpha }/{\sigma }_s^2$. Therefore, the Pds can be seen as functions of GSCR.

3.1. In a Homogeneous PαS Background

Here, some results in a homogeneous PαS background based on the derived expressions are presented. Specifically, the following performance evaluation results are given:

• Figure 2: The real Pfa versus the designed Pfa in a homogeneous background.
• Figure 3: Pfa versus $\alpha$ (obtained using Equations (T1.1), (T1.3) and (T1.5) in Table 1).
• Figure 4: Pd versus GSCR (obtained using Equation (T1.2), (T1.4) and (T1.6) in Table 1).

To validate the accuracy of the derived expressions, some MC simulation results and MREs are also given in this part.

Figure 2 gives the real Pfas of the conventional CFAR detectors (for Gaussian) and the proposed CFAR detectors (for PαS) versus the designed Pfa, in a homogeneous PαS background, assuming $N=32$, $\alpha \in \left\{0.2,0.5,0.8\right\}$ and $k=28$ for the OS-CFAR detector. The conventional CFAR detectors are formulated in a Gaussian background, and their Pfa expressions can be found in [1]. Firstly, the scale parameters $T$ of the conventional detectors and the proposed detectors are calculated according to their Pfa expressions and the designed Pfa. Then, through the MC simulations with the calculated $T$s, the real Pfas of the conventional and proposed detectors in a homogeneous PαS background can be obtained. From Figure 4, it can be seen that the real Pfas of the conventional detectors designed for a Gaussian background are far larger than the designed Pfa, i.e., the conventional detectors are ineffective in a homogeneous PαS background. The real Pfas of the proposed detectors designed for a PαS background are almost the same as the designed Pfa.

Figure 3 gives the Pfas of four detectors versus $\alpha$, assuming $N=32$, $\gamma =1$, $T\in \left\{{10}^0,{10}^2,{10}^4\right\}$ and $k=28$ for OS-CFAR detector. Note that $k$ is a key parameter that decides the performance of OS detector. In some previous researches such as [28], the effect of $k$ on the performance of OS detector has been explored. According to the previous researches, we set $k=28$. The characteristic exponent $\alpha$ is a key parameter that decides the statistical properties of PαS distribution. From Figure 3, it can be observed that the change of Pfas with $\alpha$ depend on the parameter $T$. For example, the Pfas increase with $\alpha$ when $T$ is set to be a relatively small value such as 1. In practice, $T$ is always set to a relatively large value in order to obtain a relatively small Pfa. However, the larger the $T$ is, the more significant the Pfas decrease with the increase of $\alpha$. Therefore, the performance sensitiveness to $\alpha$ should be considered when setting the value of $T$ in practice.

Figure 4 gives the Pds versus the GSCRs, assuming $N=32$, $\alpha \in \left\{0.2,0.5,0.8\right\}$ and $k=28$ for the OS-CFAR detector and that the designed $\mathrm{Pfa}={10}^{-4}$. Note that a fixed Pfa corresponds to different values of $T$ in different detectors. From Figure 4, some conclusions can be made. On the one hand, the OS with $k=28$ performs better than other three detectors when GSCR is relatively large. Only within a small range of GSCR does the OS with $k=28$ perform worse than others. It is apparent that the OS with a proper $k$ is the best choice in a homogeneous PαS background. On the other hand, the SO is a better choice than the CA and GO for practice in a homogeneous background. It is worth noting that there are some differences between the CFAR detectors for a PαS background and the conventional CFAR detectors for a Gaussian background [1]. For the conventional CFAR detectors in a homogeneous Gaussian background, CA performs the best. However, for the CFAR detectors here in a homogeneous PαS background, both the OS and SO perform better than CA. Thus, the CA is no longer the best choice in a homogeneous PαS background.

Figure 3 and Figure 4 also give the MREs between the numerical results and the MC simulation results. From the MREs, it can be seen that most of the MREs are smaller than 1%, and the largest MRE is 6.5829%, which shows that the numerical results are consistent with the results obtained by the MC simulations. This also indicates that the derivation and calculation in the homogeneous background are correct.

3.2. In a Nonhomogeneous Background

Here, some results in nonhomogeneous PαS background based on the derived expressions are presented. Specifically, the following performance evaluation results are given:

• Figure 5: The real Pfa versus of the designed Pfa in a nonhomogeneous background.
• Figure 6: Pfa versus $\mu$ (obtained using Equations (T2.1), (T2.3), (T2.5), (T2.7), (T2.9) and (T2.11) in Table 2).
• Figure 7: Pfa versus $R$ (obtained using Equations (T2.2), (T2.4), (T2.6), (T2.8), (T2.10) and (T2.12) in Table 2).
• Figure 8: Pd versus Pfa (obtained using Equations (T2.2), (T2.4), (T2.6), (T2.8), (T2.10) and (T2.12) in Table 2).

To validate the accuracy of the derived expressions, some MC simulation results and MREs are also given.

Figure 5 gives the real Pfas of the conventional CFAR detectors for a Gaussian background and for the proposed CFAR detectors for a PαS background versus the designed Pfa in a nonhomogeneous PαS background, assuming $N=32$, $\alpha \in \left\{0.2,0.5,0.8\right\}$, $\mu =100$, $R=24$ and $k=28$ for the OS-CFAR detector. Similarly to in the operation in Figure 2, the scale parameters $T$ of the conventional and the proposed detectors are calculated through their Pfa expressions for the homogeneous case. Then, through the MC simulations with the calculated $T$s, the real Pfas of the conventional and proposed detectors in a nonhomogeneous PαS background can be obtained. From Figure 5, it can also be seen that the real Pfas of the conventional detectors designed for a Gaussian background are far larger than the designed Pfa, i.e., the conventional detectors are also ineffective in a nonhomogeneous PαS background. Although the real Pfas of the CFAR detectors for a PαS background are a little higher than the designed Pfa, the results are acceptable.

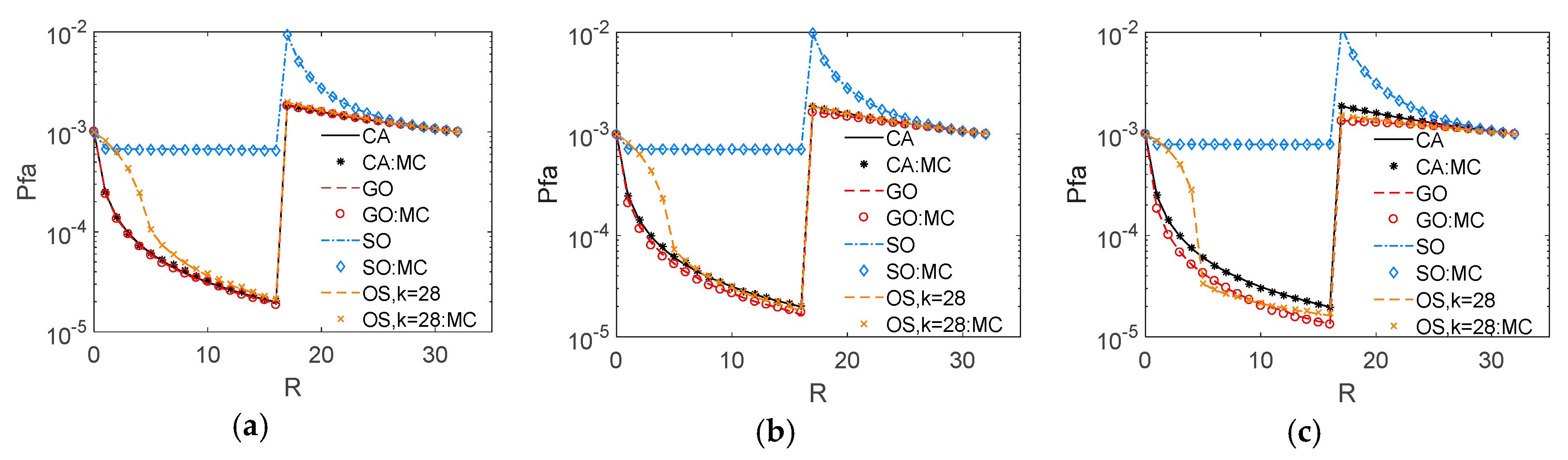
Figure 6 gives the Pfas versus the parameter $\mu$, assuming $N=32$, $\alpha \in \left\{0.2,0.5,0.8\right\}$, $\gamma =1$, $T={10}^3$ and $k=28$ for the OS-CFAR detector. Figure 6a–c gives the results when $R=8$, i.e., when the test sample is immersed in relatively weak clutter. Figure 6d–f gives the results when $R=24$, i.e., when the test sample is immersed in relatively strong clutter. From Figure 6a–c, it can be seen that the Pfa of the SO changes little with changes in $\mu$. That is because the clutter power estimate $Z$ and the test sample $D$ in the SO detector are almost unchanged with changes in $\mu$ in this case. In comparison, the Pfas of other three detectors apparently decrease with an increase in $\mu$. Figure 6d–f indicates that the Pfas of all detectors increase little with an increase in $\mu$ when the test sample is immersed in the strong clutter. Considering the two situations when the test sample is immersed in weak and strong clutter, a conclusion can be drawn that the SO is affected less by parameter $\mu$ than the other three detectors.

Figure 7 gives the Pfas versus $R$ when $N=32$, $\mu =100$, $\alpha \in \left\{0.2,0.5,0.8\right\}$, $\gamma =1$ and $k\in \left\{24,28\right\}$ for the OS-CFAR detector and when the designed $\mathrm{Pfa}={10}^{-3}$. Figure 7a–c also gives the results when $\alpha =0.2$,$\alpha =0.5$ and, respectively. When evaluating the detectors’ performances in a nonhomogeneous background, $R$ is a key parameter that should be taken into consideration [6,35]. From Figure 7, it can be seen that the Pfa decreases with an increase in $R$ when $R\le N/2$. For $R>N/2$, the Pfa increases with an increase in $R$. The results show that a sharp spike exists in the middle of each curve, which is caused by clutter power transition in the background. The lower the sharp spike is, the better the control of the Pfa is. Figure 7a–c shows that the SO detector performs the worst in the control of the sharp spike and that the GO detector performs the best. The CA and OS detectors perform a little worse than the GO in the control of the sharp spike. Thus, the GO is most robust among these four detectors against the clutter power transition in a nonhomogeneous PαS background. It is worth noting that this conclusion is the same as that about the conventional CFAR detectors in a nonhomogeneous Gaussian background [1].

Figure 8 gives the receiver operating characteristic (ROC) curves of the different detectors in a nonhomogeneous background when $N=32$, $\alpha \in \left\{0.2,0.5,0.8\right\}$, $\gamma =1$, $R\in \left\{8,24\right\}$, $\mu =100$ and $k=28$ for the OS-CFAR detector. In Figure 8a–f, the GSCR is set to 35, 13, 7, 55, 21 and 12dB, respectively, to make the ROC curves present well in the Pfa range of 10⁻⁴ to 10⁻¹. Figure 8a–c indicates that the OS ($k=28$) has the best detection performance and that other three detectors have almost the same detection performance when the test sample is immersed in relatively weak clutter. Figure 8d–f indicates that the OS ($k=28$) also has the best detection performance and that the SO is better than the CA and GO when the test sample is immersed in relatively strong clutter. Besides, it can also be seen from Figure 8 that the performance gaps among the different detectors reduces with an increase in $\alpha$. Therefore, considering the detection performance with a fixed Pfa, the OS ($k=28$) is the best choice among the four detectors irrespectively of whether the test sample is immersed in weak or strong clutter, and the SO is also a good choice when the test sample is immersed in strong clutter. Considering both the robustness against the clutter power transition shown in Figure 7 and the detection performance shown in Figure 8, the OS ($k=28$) has the best detection performance, with acceptable robustness against the clutter power transition.

Figure 6 and Figure 7 also give the MREs between the numerical results and the MC simulation results. From the MREs, it can be seen that most of the MREs are smaller than 1% and that the largest MRE is 2.6513%, which shows that the numerical results are consistent with the results obtained by the MC simulations. This also indicates that the derivation and calculation in a nonhomogeneous background are correct.

4. Conclusions

The PαS distribution performs well in modeling certain impulsive sea clutter power samples. This study develops several frequently-used CFAR detectors in PαS sea clutter. The exact expressions of Pfa and Pd are derived in terms of the H-function. Based on the derived expressions, it is found that these detectors are CFAR with respect to the scale parameter $\gamma$. The correctness of the derived expressions is also verified by MC simulations. Additionally, some analyses and comparisons of the CA, GO, SO and OS detectors are given. These analyses have some guiding significance for the practical use of these detectors.