Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy
Abstract
:1. Introduction
1.1. Related Works
1.2. Motivation
- (1)
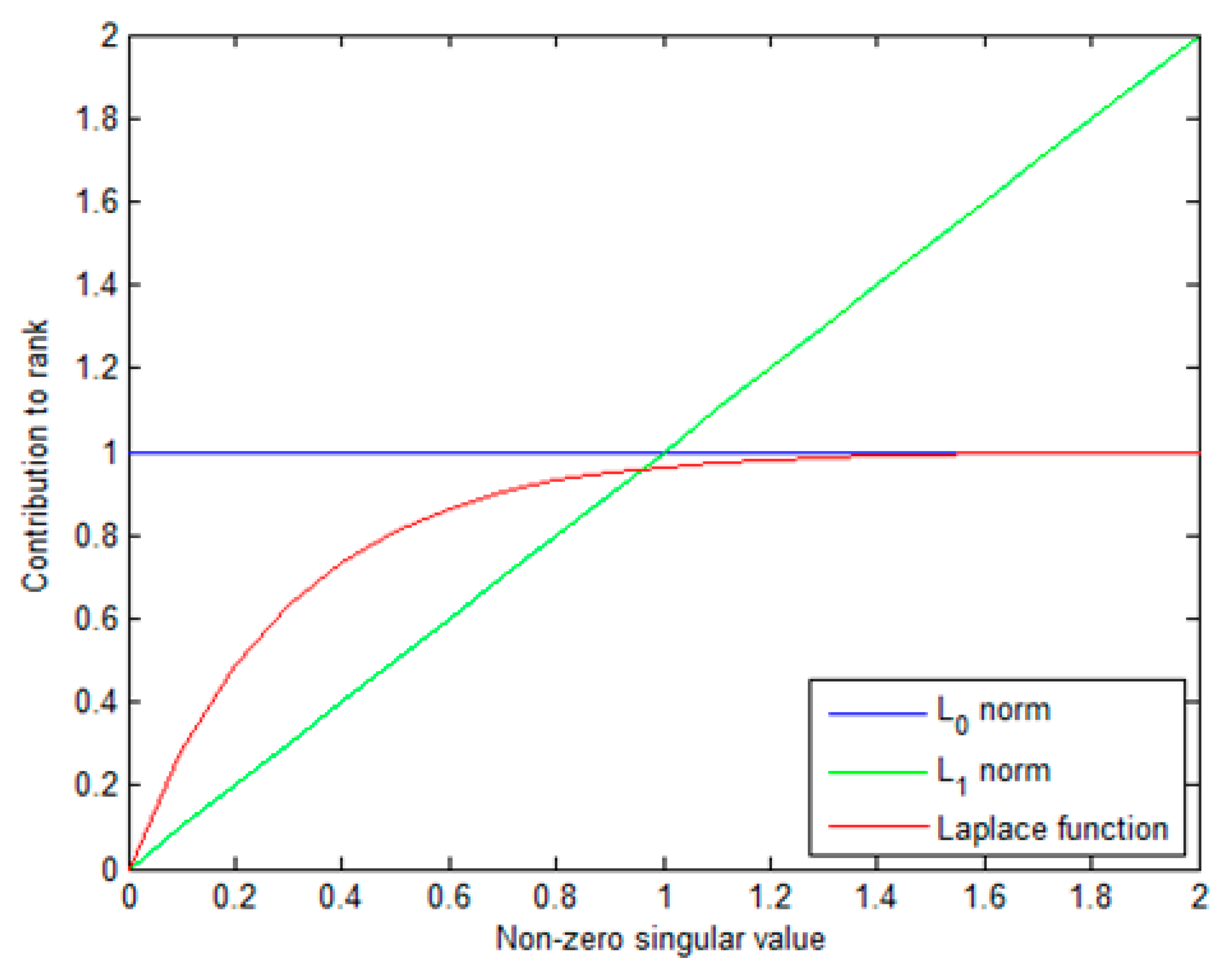
- First, to more appropriately characterize the low-rank property of background tensor, we apply a non-convex tensor rank surrogate via Laplace function to infrared small target detection. The non-convex surrogate can adaptively assign different weights to singular values and can approximate -norm better. The advantages of the method lead to a more robust target background separation performance.
- (2)
- Second, by introducing a novel local contrast energy feature into IPT model, the proposed model, which takes advantages of IPT model and traditional local contrast detection method, can suppress the complex background and preserve the dim small target better.
- (3)
- Third, considering that residual strong edge interferences are linearly structured sparse, we add a structured sparse item utilizing the norm constraint to IPT model, which can reduce false alarm caused by structured sparse interference sources.
- (4)
- Fourth, an optimization way via alternating direction method of multipliers (ADMM) is designed to solve the non-convex model accurately and efficiently.
2. Preliminaries
2.1. Mathematical Symbols and Definitions
| Algorithm 1 A fast t-SVD. |
| Input:; |
| Output: t-SVD components of ; |
| 1. Compute ; |
| 2. Compute frontal slices of from |
| fordo |
| end for |
| for do |
| ; |
| ; |
| ; |
| end for |
| 3. Compute , , ; |
2.2. Infrared Patch-Tensor Model
3. Proposed Method
3.1. The Nonconvex Surrogate of Tensor Rank
| Algorithm 2 Each iteration solution of optimization problem in Equation (16). |
| Input:, , , ; |
| Output:,; |
| 1. Compute ; |
| 2. Compute each frontal slice of by |
| fordo |
| 1: ; |
| 2: can be obtained by Equation (18); |
| 3: ; |
| end for |
| for do |
| ; |
| end for |
| 3. Compute; |
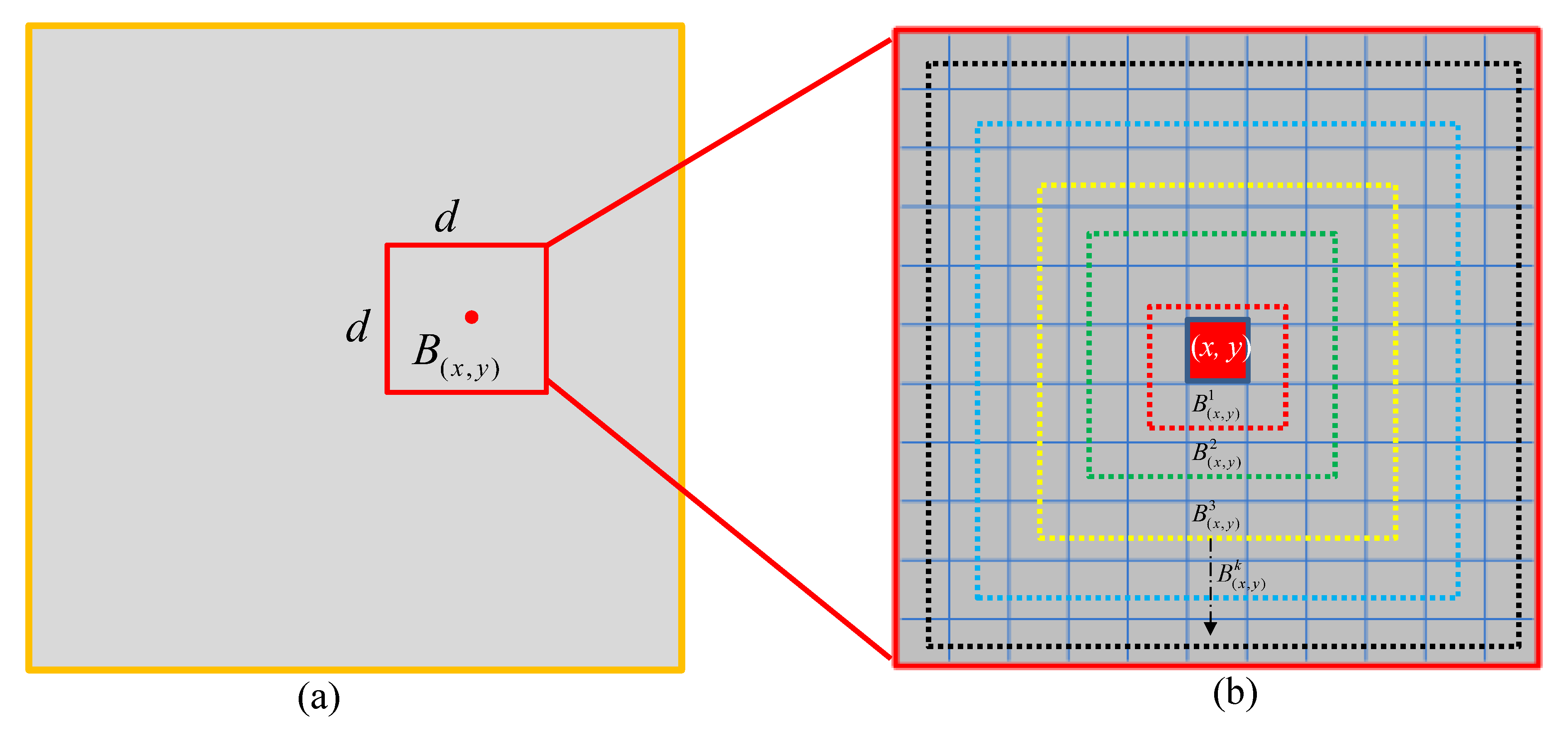
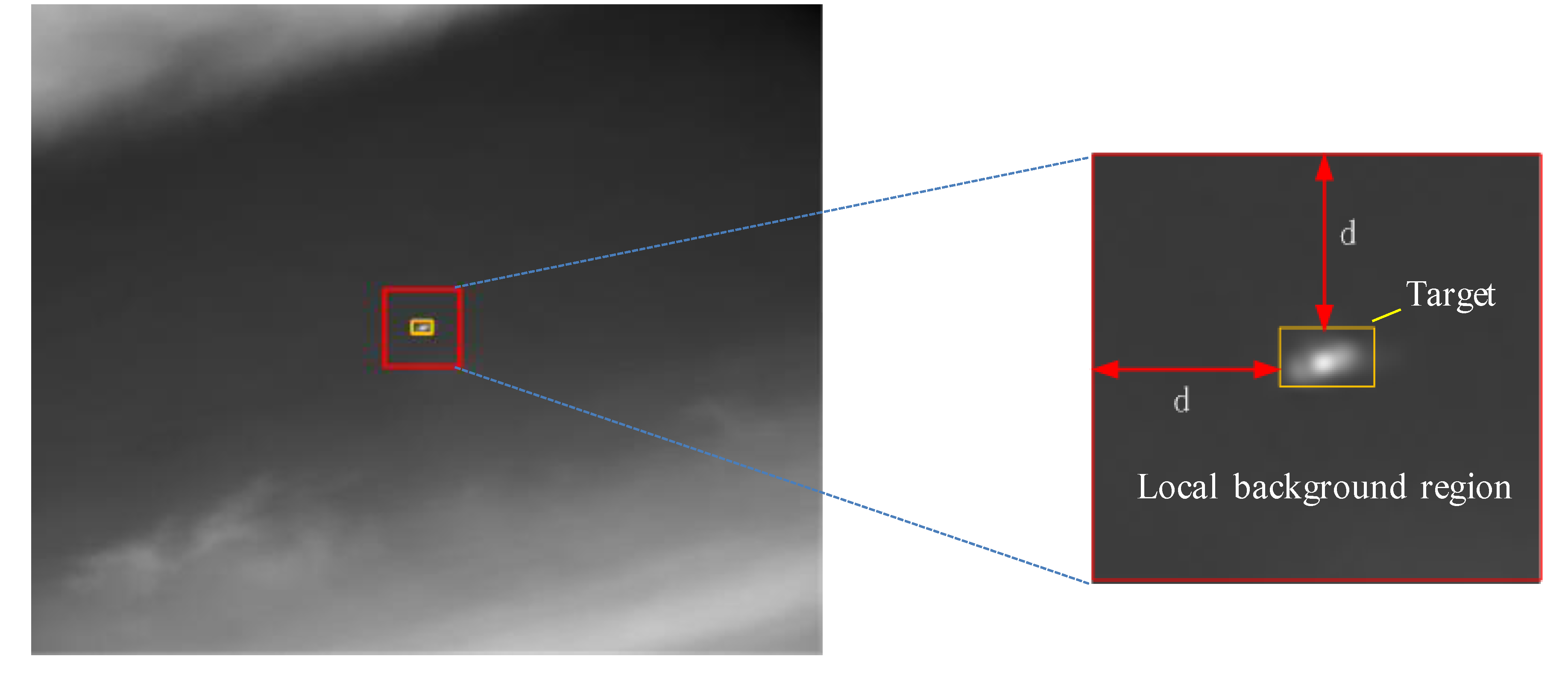
3.2. Local Prior Weight Map
3.3. Structured Sparse Regularization
3.4. The Proposed NTRS Model
3.5. Solution of NTRS Model
| Algorithm 3 ADMM for solving the proposed NTRS model. |
| Input: Original patch-image , , , ; |
| Initialize:, = 0, , , , , , , ; |
| While not converged do |
| 1: Fix the others and update by Algorithm 2; |
| 2: Fix the others and update by |
| ; |
| 3: Update via |
| ; |
| 4: Update via |
| ; |
| 5: Update by |
| ; |
| ; |
| 6: Update by |
| ; |
| 7: Inspect the stop conditions |
| or ; |
| 8: Update |
| ; |
| End while |
| Output:, , |
3.6. Target Detection
- (1)
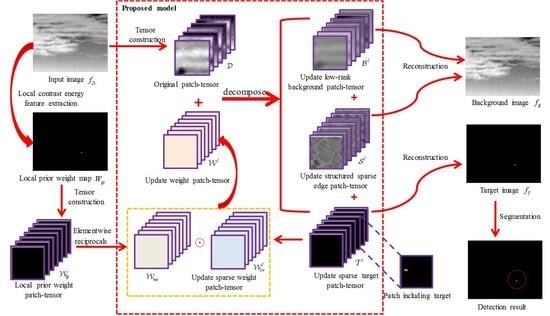
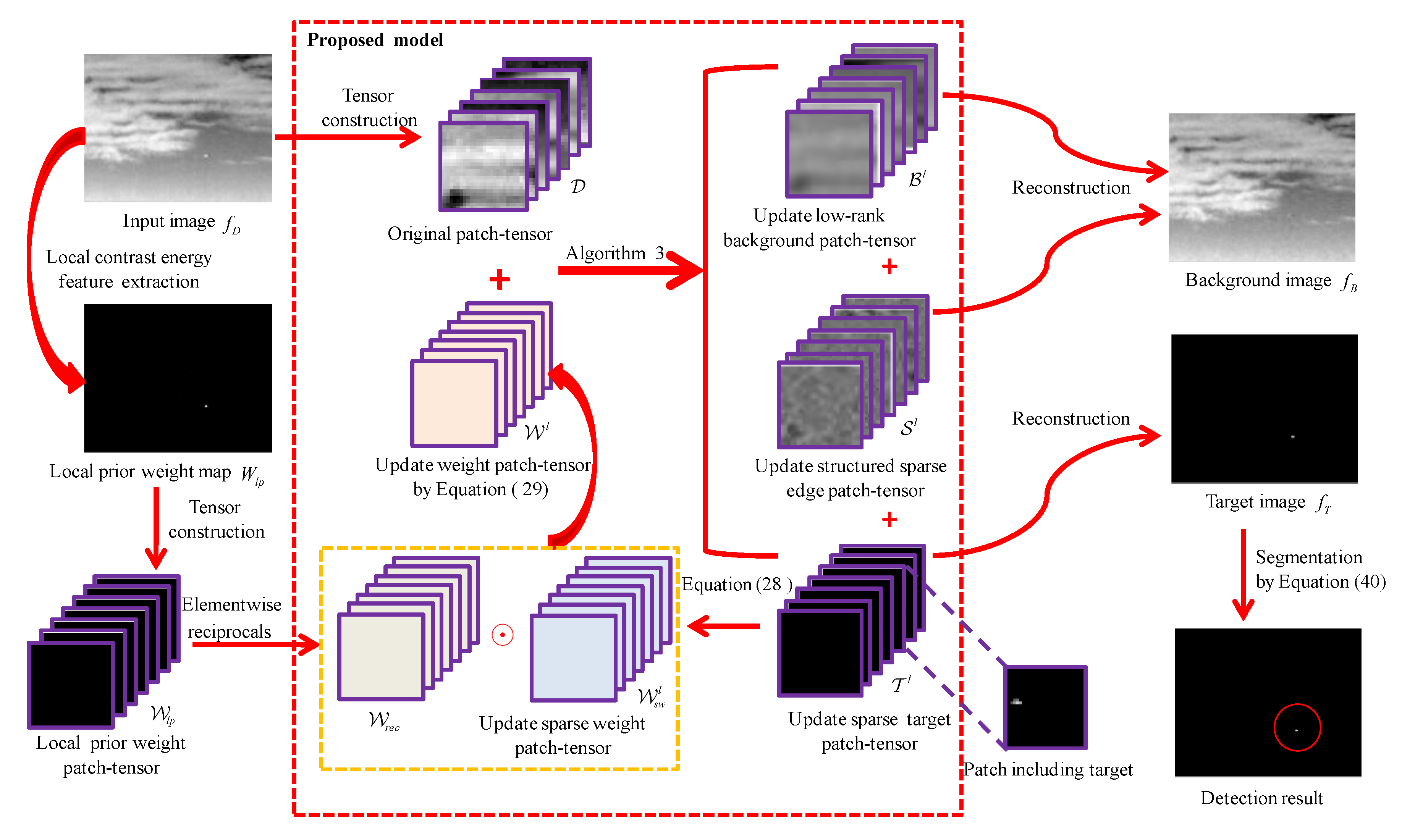
- Local prior map generation. For an input infrared image , its local prior weight map is calculated via Equation (25).
- (2)
- Patch-tensor construction. Original patch-tensor can be constructed by stacking image patches which are obtained via sliding a window of size over the input image, as shown in Figure 2. In the same way, the local prior weight patch-tensor can be constructed from local prior weight map.
- (3)
- Background–target–edge separation. By Algorithm 3, an original infrared patch-tensor can be decomposed into three patch-tensor components: the low rank background , the sparse target , and the structured sparse edge .
- (4)
- Image reconstruction. The two-dimensional image can be reconstructed by the inverse operation of patch-tensor construction [42]. Considering that structured edges are also background, we first sum and as the final background patch-tensor . Then, the target image and the background image are reconstructed from target patch-tensor and background patch-tensor , respectively. For the overlapped positions, one-dimensional median filter can be used to determine the values.
- (5)
- Target detection. Considering that the pixels of the true targets have higher grayscale in the reconstructed target image [70], small targets can be extracted via a simple adaptive threshold segmentation algorithm. The threshold is as follows:where and are the standard deviation and mean of the reconstructed target image , respectively. is an empirical coefficient to compromise false alarm rate and detection probability.
4. Experimental Results and Analysis
4.1. Experimental Preparation
4.2. Evaluation Metrics
4.3. Parameter Analysis
4.3.1. Patch Size
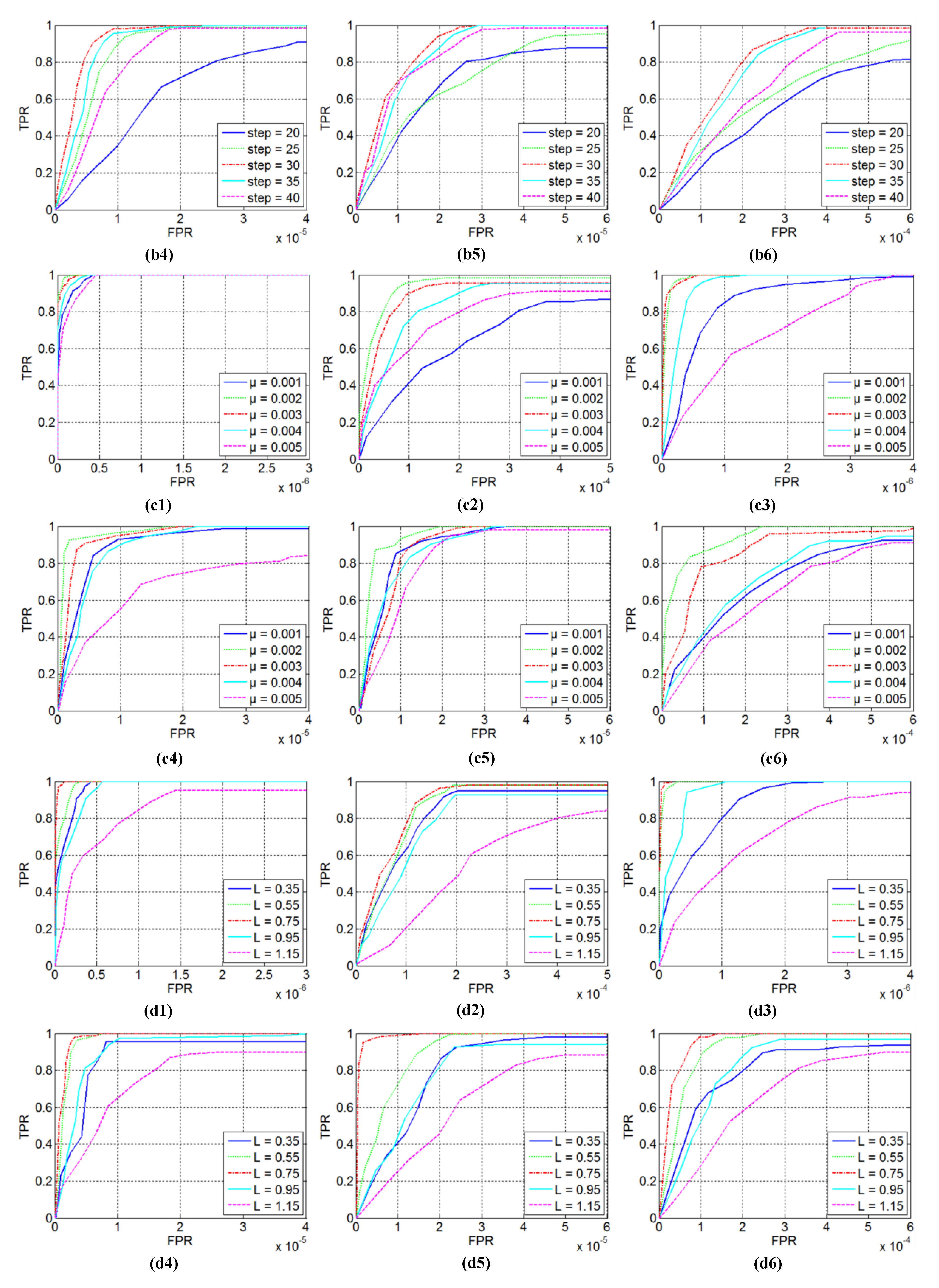
4.3.2. Sliding Step
4.3.3. Penalty Factor
4.3.4. Compromising Parameters and
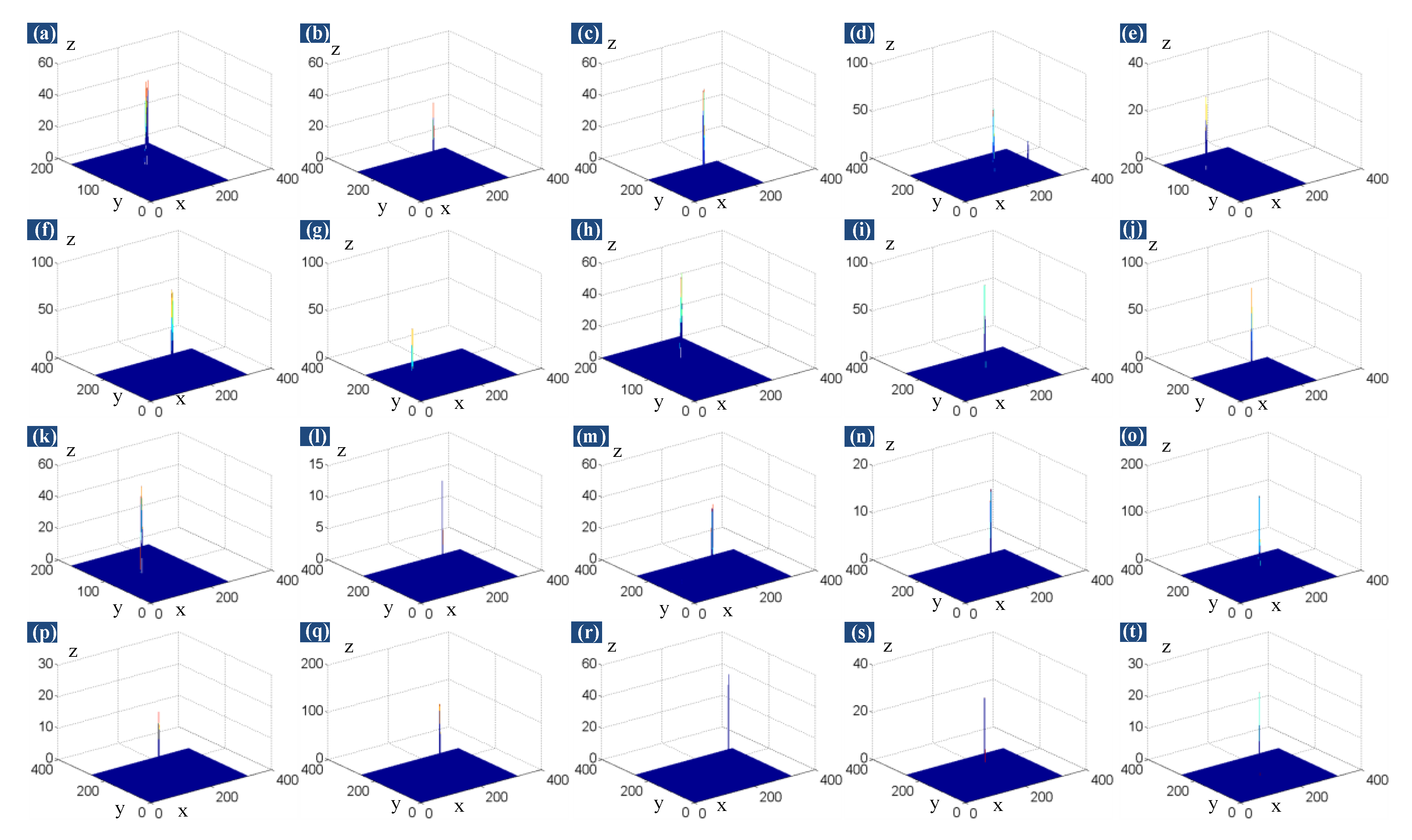
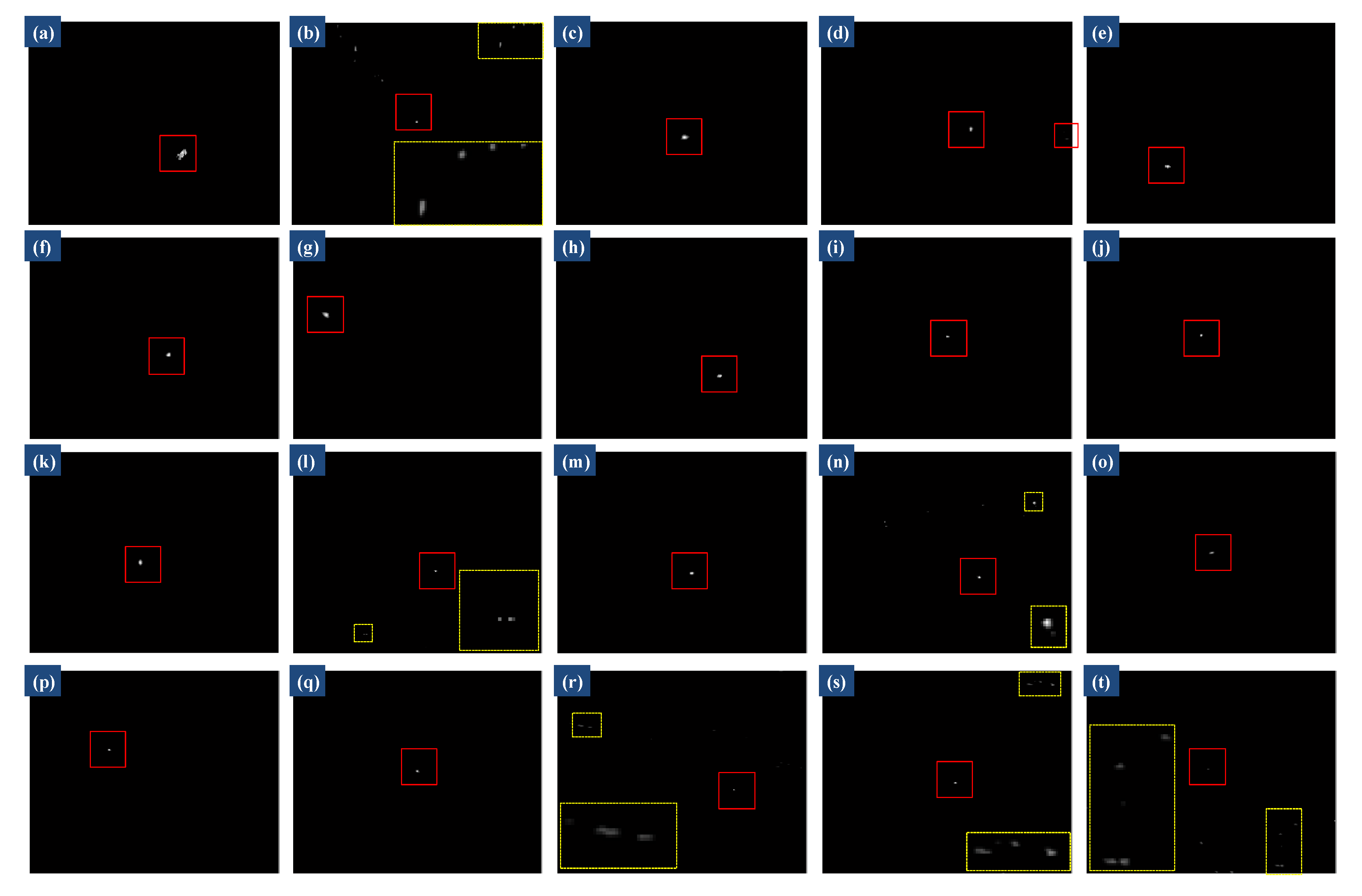
4.4. Qualitative Evaluation
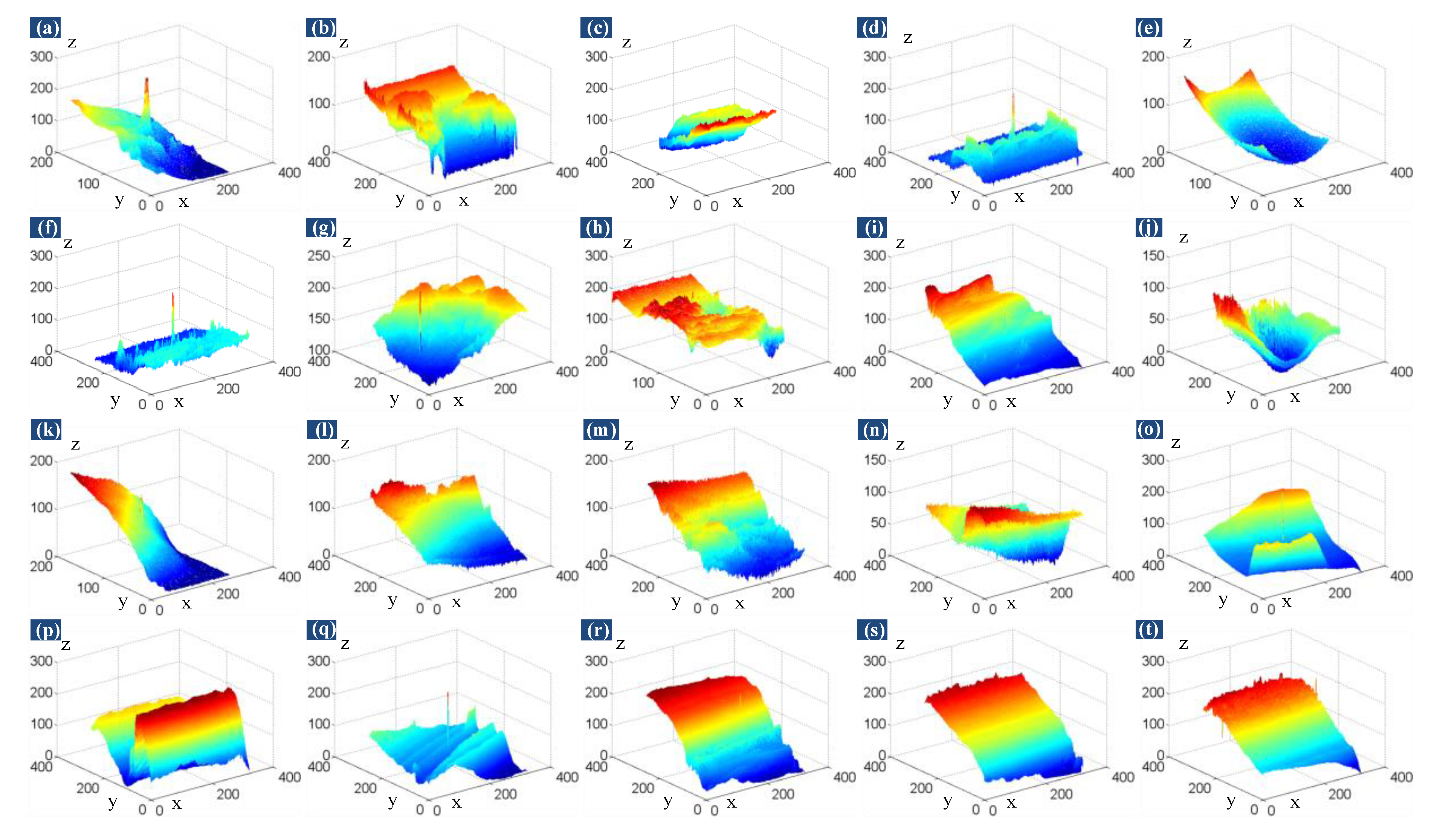
4.4.1. Robustness to Various Scenes
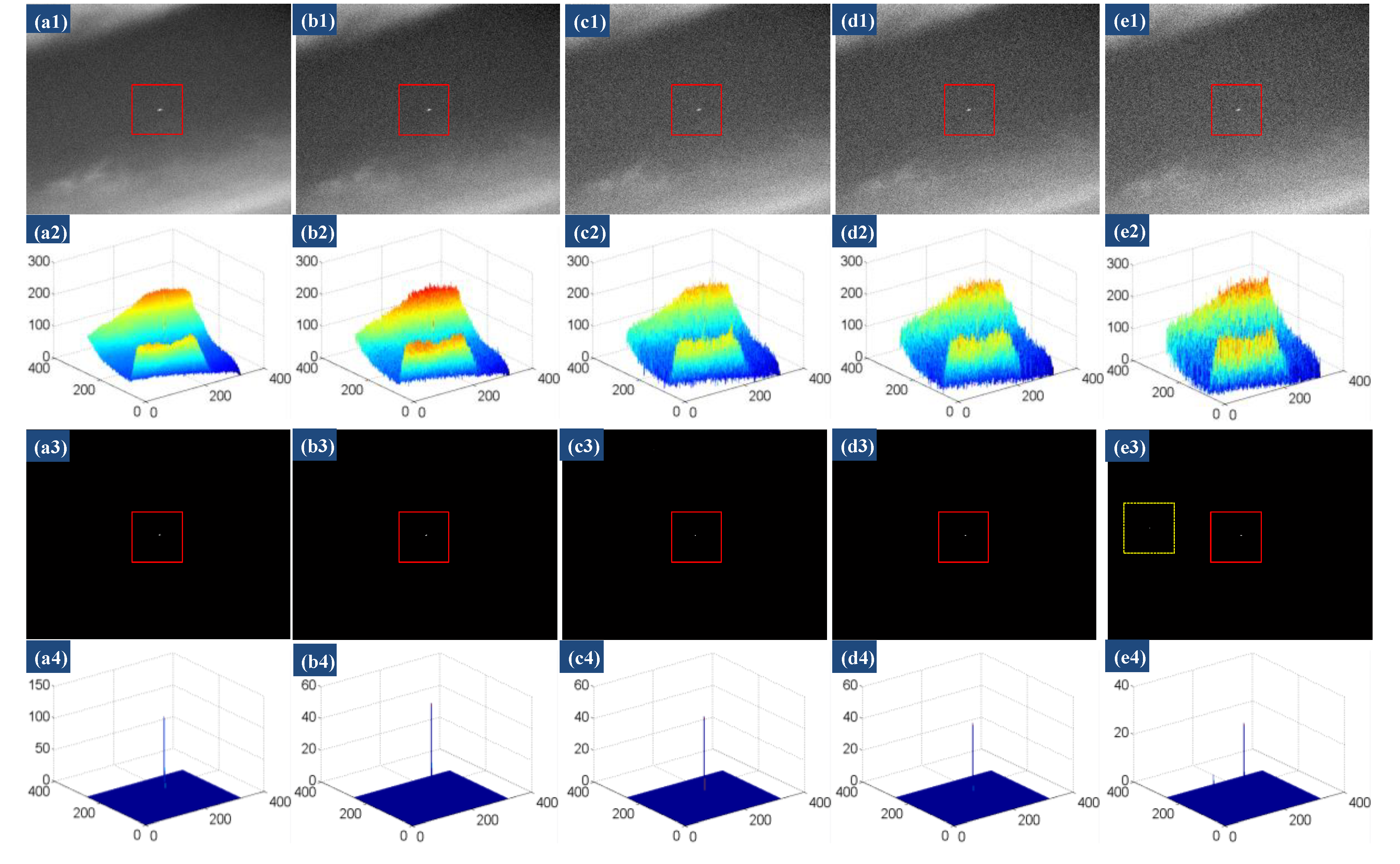
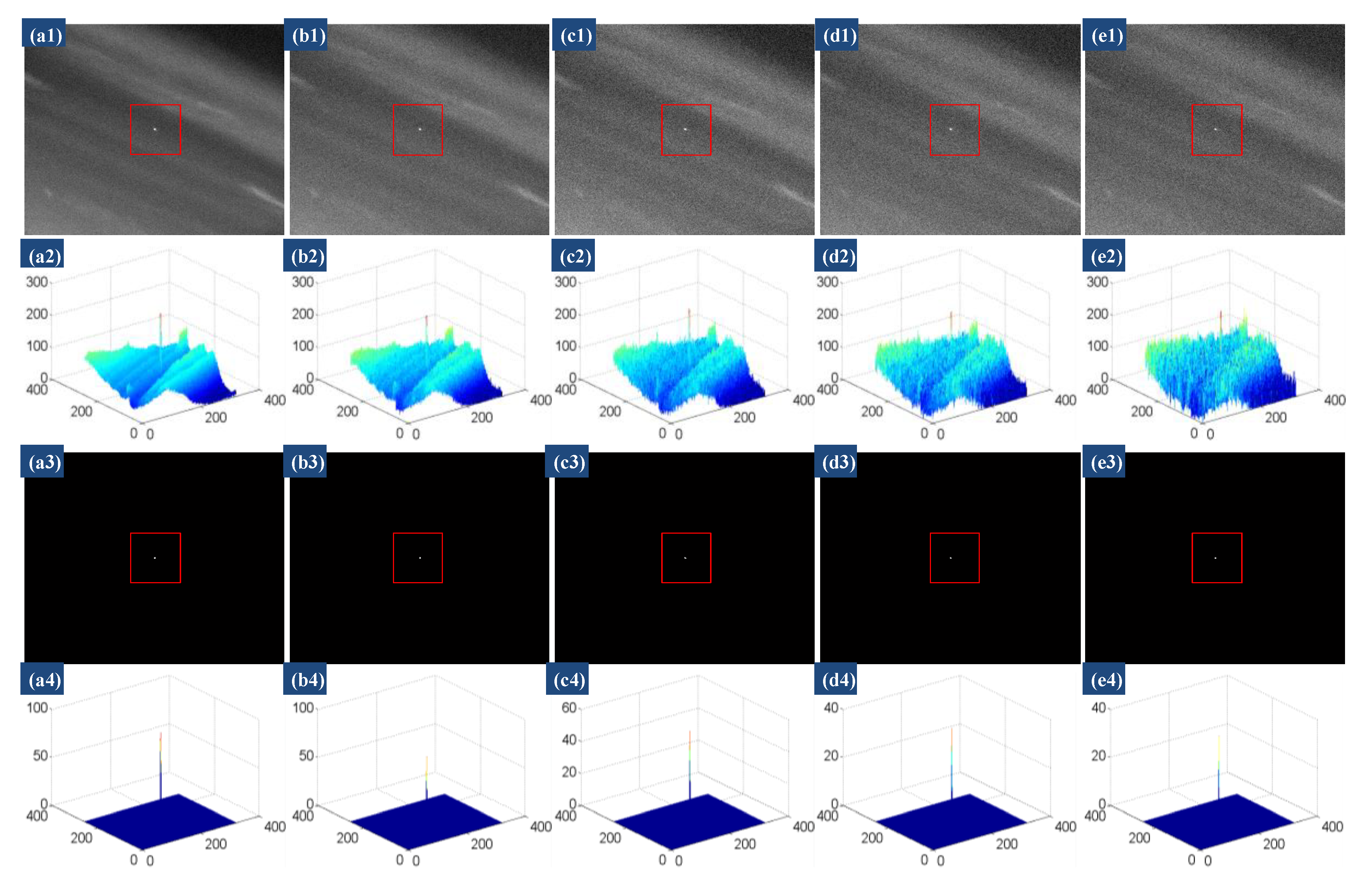
4.4.2. Anti-Noise Performance
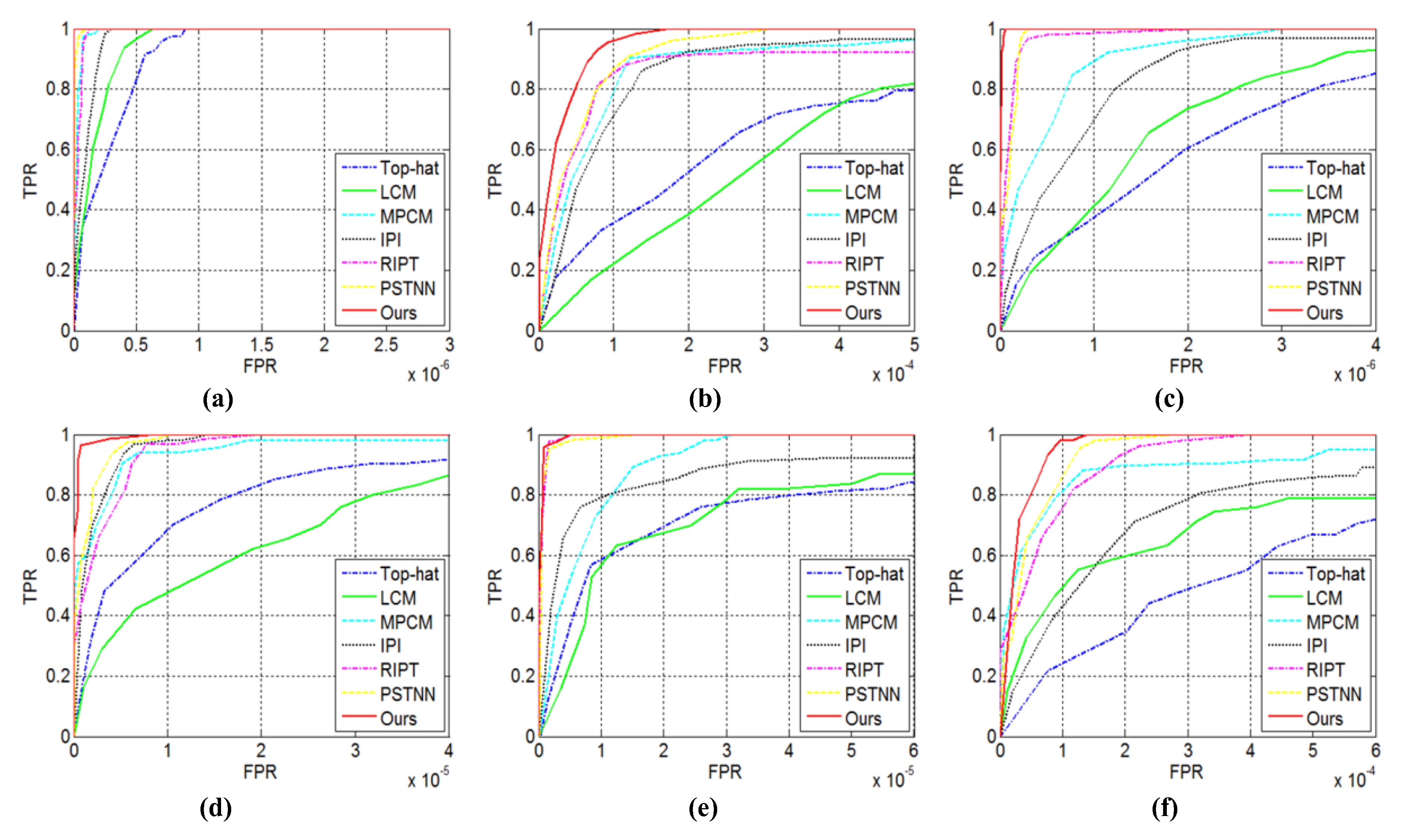
4.5. Quantitative Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, S.Q.; Liu, Y.H.; He, Y.M.; Zhang, T.F.; Peng, Z.M. Structure-Adaptive Clutter Suppression for Infrared Small Target Detection: Chain-Growth Filtering. Remote Sens. 2020, 12, 47. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.Y.; Peng, Z.M.; Kong, D.H.; Zhang, P.; He, Y.M. Infrared dim target detection based on total variation regularization and principal component pursuit. Image Vis. Comput. 2017, 63, 1–9. [Google Scholar] [CrossRef]
- Wang, X.Y.; Peng, Z.M.; Kong, D.H.; He, Y.M. Infrared Dim and Small Target Detection Based on Stable Multisubspace Learning in Heterogeneous Scene. IEEE Trans. Geosci. Remote. 2017, 55, 5481–5493. [Google Scholar] [CrossRef]
- Huang, S.Q.; Peng, Z.m.; Wang, Z.R.; Wang, X.Y.; Li, M.H. Infrared Small Target Detection by Density Peaks Searching and Maximum-Gray Region Growing. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1919–1923. [Google Scholar] [CrossRef]
- Zhang, T.F.; Wu, H.; Liu, Y.; Peng, L.B.; Yang, C.P.; Peng, Z.M. Infrared Small Target Detection Based on Non-Convex Optimization with Lp-Norm Constraint. Remote Sens. 2019, 11, 559. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.M.; Zhang, Q.H.; Wang, J.R.; Zhang, Q.P. Dim target detection based on nonlinear multifeature fusion by Karhunen-Loeve transform. Opt. Eng. 2004, 43, 2954–2958. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Li, M.H.; Peng, Z.M.; Liu, X.R. Investigating Detectability of Infrared Radiation Based on Image Evaluation for Engine Flame. Entropy 2019, 21, 946. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.D.; Peng, Z.M. Infrared Small Target Detection Based on Partial Sum of the Tensor Nuclear Norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.Q.; Li, X.R.; Zhao, L.Y. Infrared small target detection via modified random walks. Remote Sens. 2018, 10, 2004. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.T.; You, X.G.; Li, H. Multiscale patch-based contrast measure for small infrared target detection. Pattern Recogn. 2016, 58, 216–226. [Google Scholar] [CrossRef]
- Qi, H.; Mo, B.; Liu, F.; He, Y.; Liu, S.D. Small infrared target detection utilizing local region similarity difference map. Infrared Phys. Technol. 2015, 71, 131–139. [Google Scholar] [CrossRef]
- Reed, I.S.; Gagliardi, R.M.; Stotts, L.B. Optical moving target detection with 3-D matched filter. IEEE Trans. Aerosp. Electorn. Syst. 2002, 24, 327–336. [Google Scholar] [CrossRef]
- Wang, G.; Inigo, R.M.; Mcvey, E.S. A pipeline algorithm for detection and tracking of pixel-sized target trajectories. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 1 October 1990; pp. 167–178. [Google Scholar]
- Modestino, J.W. Spatiotemporal multiscan adaptive matched filtering. In Signal and Data Processing of Small Targets; International Society for Optics and Photonics: Bellingham, WA, USA, 1995. [Google Scholar]
- Tonissen, S.M.; Evans, R.J. Performance of dynamic programming techniques for Track-Before-Detect. IEEE Trans. Aerosp. Electorn. Syst. 1996, 32, 1440–1451. [Google Scholar] [CrossRef]
- Gao, C.Q.; Zhang, T.Q.; Li, Q. Small infrared target detection using sparse ring representation. IEEE Aerosp. Electron. Syst. Mag. 2012, 27, 21–30. [Google Scholar]
- Gao, C.Q.; Wang, L.; Xiao, Y.X.; Zhao, Q.; Meng, D.Y. Infrared small-dim target detection based on Markov random field guided noise modeling. Pattern Recogn. 2018, 76, 463–475. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Yuan, D.; Chen, H. Infrared small target detection based on local intensity and gradient properties. Infrared Phys. Technol. 2018, 89, 88–96. [Google Scholar] [CrossRef]
- Wang, X.Y.; Peng, Z.M.; Zhang, P.; He, Y.M. Infrared Small Target Detection via Nonnegativity-Constrained Variational Mode Decomposition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1700–1704. [Google Scholar] [CrossRef]
- Liu, D.P.; Cao, L.; Li, Z.Z.; Liu, T.M.; Che, P. Infrared Small Target Detection Based on Flux Density and Direction Diversity in Gradient Vector Field. IEEE J-Stars. 2018, 11, 2528–2554. [Google Scholar] [CrossRef]
- Peng, L.B.; Zhang, T.F.; Liu, Y.H.; Li, M.H.; Peng, Z.M. Infrared Dim Target Detection Using Shearlet’s Kurtosis Maximization under Non-Uniform Background. Symmetry 2019, 11, 723. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.B.; Zhang, T.F.; Huang, S.Q.; Pu, T.; Liu, Y.H.; Lv, Y.X.; Zheng, Y.C.; Peng, Z.M. Infrared Small Target Detection Based on Multi-directional Multi-scale High Boost Response. Opt. Rev. 2019, 26, 568–582. [Google Scholar] [CrossRef]
- Dai, Y.M.; Wu, Y.Q. Reweighted Infrared Patch-Tensor Model with Both Nonlocal and Local Priors for Single-Frame Small Target Detection. IEEE J-Stars. 2017, 10, 3752–3767. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhao, M.; Deng, X.; Li, L.; Li, L.; Zhang, W. Infrared Small Target Detection Using Local and Nonlocal Spatial Information. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 3677–3689. [Google Scholar] [CrossRef]
- Deshpande, S.D.; Er, M.H.; Venkateswarlu, R.; Chan, P. Max-mean and max-median filters for detection of small targets. In Proceedings of the Signal and Data Processing of Small Targets, Denver, CO, USA, 18–23 July 1999; pp. 74–84. [Google Scholar]
- Hadhoud, M.M.; Thomas, D.W. The two-dimensional adaptive LMS (TDLMS) algorithm. IEEE Trans. Circuits Syst. 1988, 35, 485–494. [Google Scholar] [CrossRef]
- Tom, V.T.; Peli, T.; Leung, M.; Bondaryk, J.E. Morphology-based algorithm for point target detection in infrared backgrounds. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 22 October 1993; pp. 2–12. [Google Scholar]
- Bae, T.W.; Zhang, F.; Kweon, I.S. Edge directional 2D LMS filter for infrared small target detection. Infrared Phys. Technol. 2012, 55, 137–145. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, R.M.; Yang, J. Small target detection using two-dimensional least mean square (TDLMS) filter based on neighborhood analysis. Int. J. Infrared Milli. 2008, 29, 188–200. [Google Scholar] [CrossRef]
- Ye, Z.; Ruan, Y.; Wang, J.; Zou, Y. Detection algorithm of weak infrared point targets under complicated background of sea and sky. Infrared Millimeter Terahertz Waves. 2000, 19, 121–124. [Google Scholar]
- Gu, Y.F.; Wang, C.; Liu, B.X.; Zhang, Y. A kernel-based nonparametric regression method for clutter removal in infrared small-target detection applications. IEEE Trans. Geosci. Remote Sens. Lett. 2010, 7, 469–473. [Google Scholar] [CrossRef]
- Wang, H.; Yang, F.; Zhang, C.; Ren, M. Infrared Small Target Detection Based on Patch Image Model with Local and Global Analysis. Int. J. Image Graph. 2018, 18, 1850002. [Google Scholar] [CrossRef]
- Kim, S.; Yang, Y.; Lee, J.; Park, Y. Small target detection utilizing robust methods of the human visual system for IRST. Infrared Milli. Terahertz Waves 2009, 30, 994–1011. [Google Scholar] [CrossRef]
- Chen, C.P.; Li, H.; Wei, Y.T.; Xia, T.; Tang, Y.Y. A local contrast method for small infrared target detection. IEEE Trans. Geosci. Remote Sens. 2013, 52, 574–581. [Google Scholar] [CrossRef]
- Shi, Y.F.; Wei, Y.T.; Yao, H.; Pan, D.H.; Xiao, G.R. High-Boost-Based Multiscale Local Contrast Measure for Infrared Small Target Detection. IEEE Geosci. Remote Sens. Lett. 2018, 15, 33–37. [Google Scholar] [CrossRef]
- Du, P.; Hamdulla, A. Infrared Small Target Detection Using Homogeneity-Weighted Local Contrast Measure. IEEE Geosci. Remote Sens. Lett. 2019. [Google Scholar] [CrossRef]
- Bai, X.Z.; Bi, Y.G. Derivative entropy-based contrast measure for infrared small-target detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2452–2466. [Google Scholar] [CrossRef]
- Gao, C.Q.; Meng, D.Y.; Yang, Y.; Wang, Y.T.; Zhou, X.F.; Hauptmann, A.G. Infrared Patch-Image Model for Small Target Detection in a Single Image. IEEE Trans. Image Process. 2013, 22, 4996–5009. [Google Scholar] [CrossRef]
- Dai, Y.M.; Wu, Y.Q.; Song, Y. Infrared small target and background separation via column-wise weighted robust principal component analysis. Infrared Phys. Technol. 2016, 77, 421–430. [Google Scholar] [CrossRef]
- Dai, Y.M.; Wu, Y.Q.; Song, Y.; Guo, J. Non-negative infrared patch-image model: Robust target-background separation via partial sum minimization of singular values. Infrared Phys. Technol. 2017, 81, 182–194. [Google Scholar] [CrossRef]
- Guo, J.; Wu, Y.Q.; Dai, Y.M. Small target detection based on reweighted infrared patch-image model. IET Image Process. 2018, 12, 70–79. [Google Scholar] [CrossRef]
- Zhang, L.D.; Peng, L.B.; Zhang, T.F.; Cao, S.Y.; Peng, Z.M. Infrared Small Target Detection via Non-Convex Rank Approximation Minimization Joint l2,1 Norm. Remote Sens. 2018, 10, 1821. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Yang, J.G.; Long, Y.L.; Shang, Z.R.; An, W. Infrared Patch-Tensor Model with Weighted Tensor Nuclear Norm for Small Target Detection in a Single Frame. IEEE Access 2018, 6, 76140–76152. [Google Scholar] [CrossRef]
- Goldfarb, D.; Qin, Z.W. Robust Low-Rank Tensor Recovery: Models and Algorithms. Siam J. Matrix Anal. Appl. 2014, 35, 225–253. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.H.; Zhao, X.L.; Ji, T.Y.; Miao, J.Q.; Ma, T.H. Laplace function based nonconvex surrogate for low-rank tensor completion. Signal Process. Image Commun. 2019, 73, 62–69. [Google Scholar] [CrossRef]
- Romera-Paredes, B.; Pontil, M. A new convex relaxation for tensor completion. In Proceedings of the Advances in Neural Information Processing Systems, Harrahs and Harveys, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 2967–2975. [Google Scholar]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Semerci, O.; Hao, N.; Kilmer, M.E.; Miller, E.L. Tensor-based formulation and nuclear norm regularization for multienergy computed tomography. IEEE Trans. Image Process. 2014, 23, 1678–1693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.Y.; Ding, Q.H.; Luo, H.B.; Hui, B.; Chang, Z.; Zhang, J.C. Infrared small target detection based on an image-patch tensor model. Infrared Phys. Technol. 2019, 99, 55–63. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar] [CrossRef] [Green Version]
- Kilmer, M.E.; Martin, C.D. Factorization strategies for third-order tensors. Linear Algebra Appl. 2011, 435, 641–658. [Google Scholar] [CrossRef] [Green Version]
- Martin, C.D.; Shafer, R.; LaRue, B. An order-p tensor factorization with applications in imaging. SIAM J. Sci. Comput. 2013, 35, A474–A490. [Google Scholar] [CrossRef]
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis with A New Tensor Nuclear Norm. IEEE Trans. Pattern Anal. Mach. Intell. 2019. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.M.; Aeron, S.C. Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Carroll, J.D.; Chang, J.-J. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Oh, T.H.; Tai, Y.W.; Bazin, J.C.; Kim, H.; Kweon, I.S. Partial sum minimization of singular values in robust PCA: Algorithm and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 744–758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, T.-X.; Huang, T.-Z.; Zhao, X.-L.; Deng, L.-J. A novel nonconvex approach to recover the low-tubal-rank tensor data: When t-SVD meets PSSV. arXiv 2018, arXiv:1712.05870v2 [cs.NA]. [Google Scholar]
- Chen, Y.; Guo, Y.; Wang, Y.; Wang, D.; Peng, C.; He, G. Denoising of hyperspectral images using nonconvex low rank matrix approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5366–5380. [Google Scholar] [CrossRef]
- Benedek, C.; Descombes, X.; Zerubia, J. Building Development Monitoring in Multitemporal Remotely Sensed Image Pairs with Stochastic Birth-Death Dynamics. IEEE Trans. Pattern Anal. 2012, 34, 33–50. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted l1 Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Gu, S.H.; Zhang, L.; Zuo, W.M.; Feng, X.C. Weighted Nuclear Norm Minimization with Application to Image Denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Suo, J.; Dai, Q.; Xu, W. Reweighted low-rank matrix recovery and its application in image restoration. IEEE Trans. Cybern. 2014, 44, 2418–2430. [Google Scholar] [CrossRef]
- Lu, C.Y.; Tang, J.H.; Yan, S.C.; Lin, Z.C. Nonconvex Nonsmooth Low Rank Minimization via Iteratively Reweighted Nuclear Norm. IEEE Trans. Image Process. 2016, 25, 829–839. [Google Scholar] [CrossRef] [Green Version]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-Rank matrices. arXiv 2010, arXiv:1009.5055v1. [Google Scholar]
- Bouwmans, T.; Javed, S.; Zhang, H.Y.; Lin, Z.C.; Otazo, R. On the Applications of Robust PCA in Image and Video Processing. Proc. IEEE. 2018, 106, 1427–1457. [Google Scholar] [CrossRef] [Green Version]
- Guan, X.W.; Peng, Z.M.; Huang, S.Q.; Chen, Y.P. Gaussian Scale-Space Enhanced Local Contrast Measure for Small Infrared Target Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 327–331. [Google Scholar] [CrossRef]
- Lin, Z.; Ganesh, A.; Wright, J.; Wu, L.; Chen, M.; Ma, Y. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix. In Proceedings of the CAMSAP 2009, Aruba, Dutch Antilles, 13–16 December 2009; pp. 1–18. [Google Scholar]






| Sequence (Seq) | Length | Image Size | Target and Background Description |
|---|---|---|---|
| Sequence 1 (Scene o) | 180 | 320 × 256 | Target lies in flat area between two complex clouds, moving fast with changing shape, brightness |
| Sequence 2 (Scene p) | 168 | 320 × 256 | Target appears near the cloud edge, with very bright cloud and banded cloud, very dim tiny |
| Sequence 3 (Scene q) | 191 | 320 × 256 | Target is above the complex structure cloud, moving fast with changing size |
| Sequence 4 (Scene r) | 210 | 320 × 256 | Target is submerged in heavy cloud, with banded cloud, small size, low contrast |
| Sequence 5 (Scene s) | 233 | 320 × 256 | Background includes sky and ground, with heavy cloud, target with small size and low contrast |
| Sequence 6 (Scene t) | 292 | 320 × 256 | Target closes to ground, with a large number of ground highlight interferences, very dim |
| Method | Parameters |
|---|---|
| Top-hat | Structure size: 5 × 5, shape: disk |
| LCM | Largest scale: , size of u: 3 × 3, 5 × 5, 7 × 7 |
| MPCM | |
| IPI | Sliding step: 10, patch size: 50 × 50, , |
| RIPT | Sliding step: 10, patch size: 30 × 30, , , , |
| PSTNN | Sliding step: 40, patch size: 40 × 40, , |
| Ours | Sliding step: 30, patch size: 40 × 40, , , , |
| Method | 32nd Frame of Sequence 1 GSCR BSF | 18th Frame of Sequence 2 GSCR BSF | 58th Frame of Sequence 3 GSCR BSF | 103rd Frame of Sequence 4 GSCR BSF | 29th Frame of Sequence 5 GSCR BSF | 203rd Frame of Sequence 6 GSCR BSF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Top-hat | 10.89 | 12.31 | 139.62 | 6.98 | 23.72 | 18.38 | 179.28 | 140.14 | 27.39 | 29.18 | 9.05 | 15.16 |
| LCM | 13.82 | 0.42 | 3.09 | 0.61 | 24.89 | 0.74 | 15.98 | 0.82 | 4.84 | 0.73 | 5.38 | 0.80 |
| MPCM | 31.41 | 1.67 | 1693.7 | 47.35 | 20.12 | 0.46 | 2996.3 | 328.60 | 88.12 | 17.03 | 131.79 | 36.92 |
| IPI | 3957.3 | 90734.1 | 1729.7 | 10865.3 | 1034.1 | 33076.2 | INF | INF | — | — | 2087.2 | 86371.2 |
| RIPT | INF | INF | — | — | INF | INF | INF | INF | INF | INF | INF | INF |
| PSTNN | INF | INF | INF | INF | INF | INF | INF | INF | INF | INF | 3482.6 | 55673.7 |
| Ours | INF | INF | INF | INF | INF | INF | INF | INF | INF | INF | INF | INF |
| Method | Sequence 1 | Sequence 2 | Sequence 3 | Sequence 4 | Sequence 5 | Sequence 6 |
|---|---|---|---|---|---|---|
| Top-hat | 999999.7425 | 794181.6994 | 852337.9990 | 916660.2614 | 840634.2914 | 719838.1942 |
| LCM | 999999.8425 | 814156.2798 | 931285.3525 | 864024.5811 | 866948.3188 | 787920.5486 |
| MPCM | 999999.9723 | 964616.2269 | 999999.5500 | 980992.2208 | 999993.0149 | 948777.5151 |
| IPI | 999999.9095 | 963380.2816 | 968361.9116 | 999998.1042 | 922509.7606 | 890273.9153 |
| RIPT | 999999.9678 | 922475.7108 | 999999.8932 | 999997.4886 | 999999.4593 | 999936.6724 |
| PSTNN | 999999.9931 | 999949.1340 | 999999.9091 | 999998.7491 | 999999.2596 | 999955.1185 |
| Ours | 1000000.0 | 999973.0608 | 999999.9917 | 999999.7070 | 999999.6314 | 999971.1846 |
| Method | Sequence 1 | Sequence 2 | Sequence 3 | Sequence 4 | Sequence 5 | Sequence 6 |
|---|---|---|---|---|---|---|
| Top-hat | 0.0806 | 0.0840 | 0.0814 | 0.0841 | 0.0864 | 0.0817 |
| LCM | 0.2536 | 0.2521 | 0.2562 | 0.2550 | 0.2528 | 0.2539 |
| MPCM | 0.2920 | 0.2989 | 0.2976 | 0.2928 | 0.2997 | 0.2901 |
| IPI | 24.8471 | 26.3660 | 23.5119 | 22.6283 | 8.1903 | 17.2996 |
| RIPT | 2.9696 | 1.2252 | 4.4051 | 1.8489 | 1.8196 | 1.7307 |
| PSTNN | 0.1474 | 0.6687 | 0.3471 | 0.6511 | 0.6148 | 0.5380 |
| Ours | 0.2838 | 0.3614 | 0.3111 | 0.3997 | 0.3680 | 0.3257 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Zhang, L.; Huang, S.; Peng, Z. Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy. Remote Sens. 2020, 12, 1520. https://doi.org/10.3390/rs12091520
Guan X, Zhang L, Huang S, Peng Z. Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy. Remote Sensing. 2020; 12(9):1520. https://doi.org/10.3390/rs12091520
Chicago/Turabian StyleGuan, Xuewei, Landan Zhang, Suqi Huang, and Zhenming Peng. 2020. "Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy" Remote Sensing 12, no. 9: 1520. https://doi.org/10.3390/rs12091520
APA StyleGuan, X., Zhang, L., Huang, S., & Peng, Z. (2020). Infrared Small Target Detection via Non-Convex Tensor Rank Surrogate Joint Local Contrast Energy. Remote Sensing, 12(9), 1520. https://doi.org/10.3390/rs12091520