1. Introduction
Spectral emissivity (SE) is an intrinsic material property, defined as the ratio (0–1) of the electromagnetic radiation emitted by an object at a particular wavelength to that emitted at the same wavelength by a perfect blackbody at the same thermodynamic temperature [
1]. SE values range from 0 to 1 emissivity units, albeit when averaged across the mid-wave infrared (MWIR) or long-wave infrared (LWIR) atmospheric windows most natural materials have an SE higher than 0.4 and 0.6 respectively. SE information is essential for the derivation of land surface temperature (LST), an Essential Climate Variable (ECV) important to the understanding and modelling of many Earth system processes from local to global scales [
2,
3].
LST retrieval algorithms primarily use remotely sensed observations of electromagnetic radiation in the long-wave infrared (LWIR; 8–14 μm) part of the thermal infrared atmospheric window. Some LST algorithms do make use of the mid-wave infrared (MWIR; 3–5 μm) atmospheric window, though these are less common because daytime MWIR measurements are a mixture of thermally emitted and solar reflected radiation [
3]. Usually the specific emissivity information required for use in LST retrieval algorithms is the SE integrated over the spectral response function of each of the spectral measurement channels considered in the algorithm [
4], though for convenience we still refer herein to SE since typically it is by knowing this that the band-integrated spectral integrated emissivity values are determined.
However, errors in emissivity typically result in significant LST biases. For example, for typical Earth surface conditions, SE uncertainties of 0.01 deliver typical uncertainties of around 0.6 K in the retrieved LST [
5]. Given this and recent experimental studies into angular and structural emissivity dependence [
6,
7], accurate knowledge of SE has been identified as one of the greatest challenges to retrieving sufficiently precise LST to support a wider range of applications [
8].
Remotely sensed LST algorithms typically require either (i) knowledge of the SE or its spectral integral in advance, as with widely used split-window algorithms (for example [
9]) or (ii) estimate SE or its spectral integral as part of the retrieval process, as with the Temperature Emissivity Separation (TES) algorithm [
10]. Laboratory measurements of SE, typically made using Fourier transform infrared (FTIR) spectrometer setups, are commonly used in both approaches, either when deriving the split-window coefficients [
11], for calibration of satellite or airborne sensors [
12] or for ground-truthing of the LST and SE outputs [
13,
14,
15].
Interest in SE measurements has increased in recent years, largely due to advances in thermal remote sensing and a concerted effort to reduce LST retrieval uncertainty following the classification of LST as an ECV. Campaigns such as Fiducial Reference Measurements for validation of Surface Temperature from Satellites (FRM4STS) have focused on such efforts [
16,
17]. Laboratory measurements of SE are generally considered to be the “truth” in such work, either for measurement of samples that can be transported without modifying the sample and its emissivity or for evaluating the accuracy of field methodologies on appropriate samples [
18]. One key advantage of laboratory SE measurements is the highly controlled conditions under which measurements can be made compared to typical field measurement conditions, and potentially the higher spectral resolution often possible with laboratory setups [
19]. Laboratory SE measurements are therefore commonly used as reference measurements when comparing them to those derived using field, airborne or satellite observations [
20,
21,
22].
Given the importance of SE information, multiple laboratories have now developed capabilities for determining SE from thermally emitted or reflected infrared radiation measurements of target samples. Whilst the former “thermal emission” approach is used in for example the SLUM (Spectral Library of impervious Urban Materials) library of Kotthaus et al. [
23], the method requires that the samples be heated to well above room temperature, which for some materials is not always possible and which can introduce issues with regards to sample temperature homogeneity when the sample is removed from the heat source to be measured. The latter “reflected radiation” approach instead illuminates a room temperature sample with infrared radiation and measures how much of the radiation is reflected, with SE then determined through use of Kirchhoff’s Law [
24]. Key advantages of this approach are that no artificial heating of the samples is required, so all types of sample are analysable, and sample temperature inhomogeneity is not an issue. The approach has been widely applied to provide much of the SE data populating the most commonly used online spectral emissivity libraries, such as the ECOSTRESS (ECOsystem Spaceborne Thermal Radiometer Experiment on a Space Station)—formerly ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer)—spectral library [
25]. SE data from the ECOSTRESS spectral library are used within the TES algorithm to provide the spectra required to derive some of the algorithm coefficients [
26].
However, the quality of laboratory SE measurements is not always apparent, and there are relatively few reflectance standards readily available for use in the MWIR and LWIR spectral regions with which to assess this, unlike in the near-infrared (NIR) or shortwave infrared (SWIR) [
27]. SE quality metrics for an individual laboratory’s SE measurements have often been provided as uncertainty values based on repeated measurements of the sample with the same equipment (for example [
28]), but comparisons of laboratory SE measurements derived for the same samples but with different equipment and laboratory setups are rare [
27,
29]. Here we redressed this gap through a “Round-Robin” study involving seven international laboratories all measuring the same set of reference samples whose SE they determined using their own equipment and measurement protocols. The differing SE measurements were intercompared and their inconsistencies explored to understand the impact that any identified differences in SE would have on remotely sensed LST determination.
The lead investigators of this “Round-Robin” study are based at the National Centre for Earth Observation (NCEO) in King’s College London (KCL), and their SE measurement setup shown in
Figure 1 uses a very similar set of equipment to that used in the Department of Earth Systems Analysis at the University of Twente (UT-ITC) and detailed in [
27]. SE measurements of the target sample are inferred from reflected infrared radiation measurements made by a Bruker VERTEX 70 spectrometer and application of Kirchhoff’s Law, with the sample positioned under a port of a diffuse highly reflective gold-coated integrating sphere and illuminated by intense radiation coming from an external mid-infrared (MIR) source (
Figure 1). Hecker et al. [
27] describe two measurement approaches to derive SE from these types of reflectance measurements—the substitution and comparative calibration methods that are described in detail below.
The substitution method of SE derivation uses a material of known emissivity (in this case a Labsphere Infragold™ plate) as a reference sample, and this is first placed under the sample port (e.g., of the integrating sphere of
Figure 1) and a “reference measurement” made. The reference sample is then replaced by the target sample and the “sample measurement” made. Spectral reflectance is then calculated through the ratio of these two measurements. In the comparative calibration method of SE derivation, the sample and reference samples are mounted simultaneously (e.g., through multiple ports or use of the internal sphere wall as for the reference), their measurements made consecutively (e.g., through use of an internal rotating mirror), with the sample spectral reflectance again calculated through their ratio. Theoretically, the comparative method should provide some benefit since it avoids a known limitation in the substitution method (the so-called “substitution error”), where changes in the total internal sphere reflectance between measurements of the reference and the sample cause underestimation of sample reflectances (and thus overestimation of emissivity) as discussed in [
30]. Hardy and Pineo [
31] determined that the substitution error could be as much as 25% for low reflectance samples and 12% for samples with medium reflectance. Corrections have been developed [
32,
33] but even these are known to include errors of up to 1% from approximations in the calculations. However using both the substitution and comparative methods with the setup at UT-ITC, Hecker et al. [
27] observed differences between the SEs derived, with those calculated using the substitution method in closer agreement with other spectra, thus questioning the assumption that the comparative method provided improved results. They attributed these differences to variations in the measurement geometries between the reference and sample measurements made using the comparative method. The measurement setup at the KCL laboratory has been designed to attempt to overcome this issue, and design specifications were to have as identical a path length as possible between the sample and reference measurement when using the comparative method. Within the current work we will therefore also assess the relative performance of the KCL setup when performing SE retrieval with these two different measurement approaches.
Our objectives are therefore threefold: (i) investigate the consistency of SE measurements derived from measurements made in different international laboratories through a Round Robin intercomparison study using reference samples, (ii) evaluate the substitution and comparative calibration methods of SE measurement using the setup shown in
Figure 1, and (iii) assess the impact that any SE differences and uncertainties stemming from the results of (i) and (ii) have on typical satellite LST retrievals.
4. Discussion
Absolute differences observed between the different measurements were larger than anticipated with no clear cause. The derived emissivity does not correspond to different spectrometer types as may be expected: DLR and CSIRO’s measurements were both made on setups based on a Bruker VERTEX 80v FTIR spectrometer, albeit with different spheres, however there were large differences between these measurements for all three samples over the full wavelength range. Furthermore, the measured absolute differences cannot be solely attributed to the use of the reference standard, although results from
Section 3.3 indicate that the uncertainty in reference standard calibration is a key factor in the SE uncertainty. The contribution to uncertainty from reference calibration is particularly pertinent given that Labsphere Infragold standards can no longer be bought with NIST traceability calibration certificates. Differences in the absolute reflectance of the reference standards could be due to different coatings but could also result from physical damage or degradation from humidity absorption. To reduce uncertainty regarding the latter, laboratories should ensure regular calibration of their reference standards to monitor for drift.
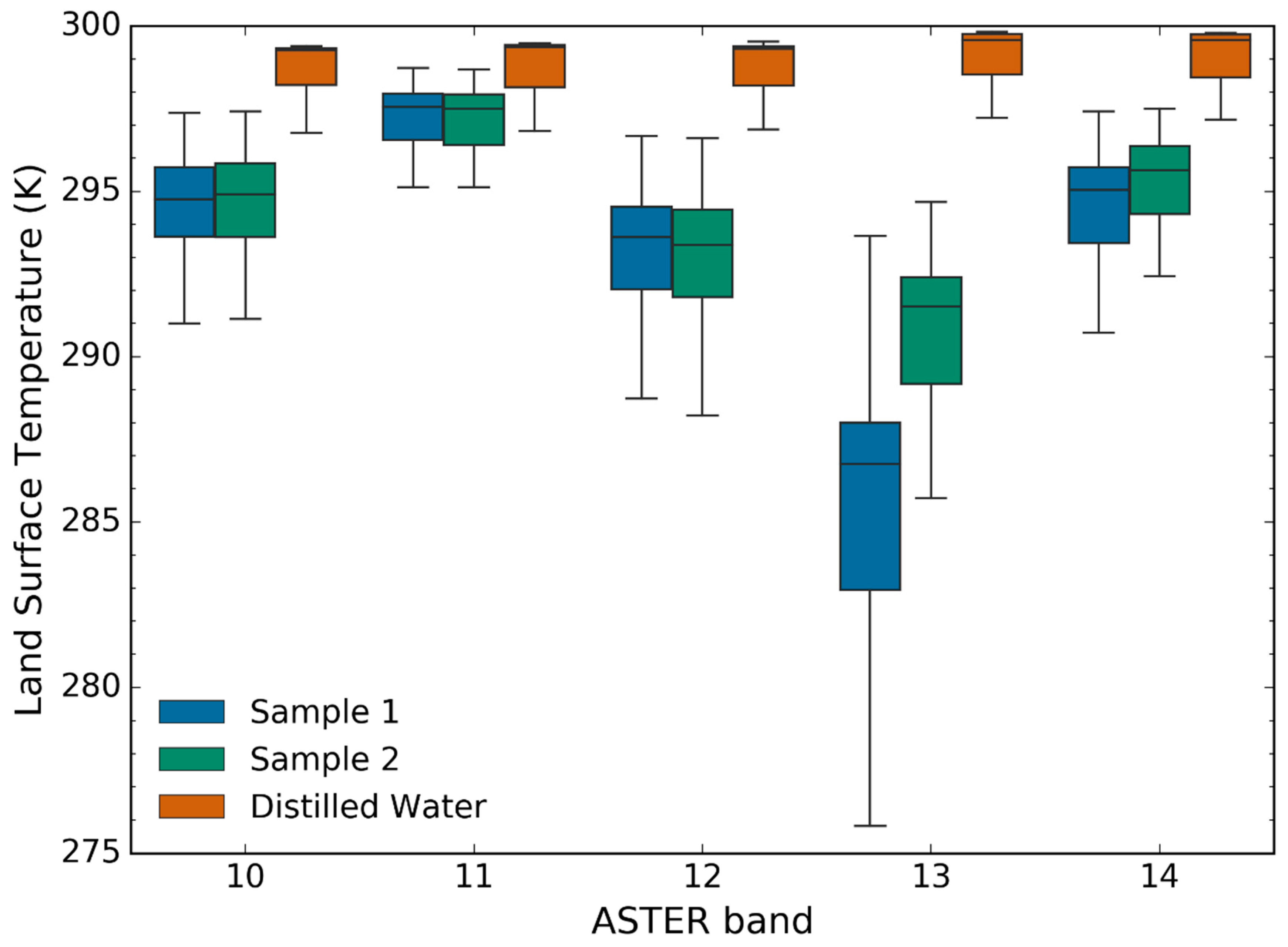
Results from all three samples considered indicated that three of the four CSIRO measurements made using the VERTEX 80 had a consistent negative bias, with the measurement made with the reference target in the lower port and the sample in the top port (CSIRO BG-B_S-T) the only one in agreement with the others. Given the similarity in the spectral shapes measured by this setup and those measured at other laboratories for all three samples, this could suggest that CSIRO may need to re-characterise their reflectance standards for the other three configurations used with the VERTEX 80v spectrometer. However, these differences may also be due to the different optical path lengths of the sample beam with each permutation, or to directional reflectance effects of the sample at the different incident angles of each permutation. Further investigation is recommended if CSIRO wish to use any of the three biased configurations (e.g., to measure liquid samples, which is not currently possible with the sample in top port configuration). Removing these three measurements from the analysis reduces standard deviations to ±0.089 (14.69%), ±0.038 (5.16%) and ±0.008 (<1%) for Sample 1, Sample 2 and distilled water respectively across the 2.5–14 μm wavelength range. Furthermore, the impacts on LST are reduced considerably without these measurements, with the range of the LSTs calculated using distilled water spectra convolved to the ASTER TIR bands reduced to <0.45 K in all bands.
Differences were also observed between measurements made on the KCL setup with the reference target in different positions. Possible causes for these differences at KCL are (i) differences in the path lengths for each measurement setup that remain unaccounted for as discussed in Hecker et al. [
27], (ii) insufficient correction for the substitution error in the substitution method, (iii) differences in reflective properties of the reflectance targets (being flat and curved respectively for the substitution and comparative methods) and (iv) incorrect characterization of the reference target spectral reflectance (the Infragold reference panel and sphere wall for the substitution and comparative methods respectively). In terms of the latter possible cause, it was identified that scaling the provided absolute spectral reflectance of the internal wall of the KCL integrating sphere (which is used as the reference target during the comparative method) by a factor of 0.87 (so that
0.84) brought the derived SE very close to that derived using the substitution method (which used the Infragold reference panel as the reference) for all three samples, as shown over the LWIR region in
Figure 14. However, the reflectance of the internal wall coating should be much higher than this given the material type and the fact that both this system and the Infragold target used as the reference target for the substitution method are new. Note that it is not physically possible for the quoted spectral reflectance of the Infragold reference panel to be higher by this amount as this would result in emissivities above
. Evaluating the performance of the two methods provides mixed results. While measurements derived using the comparative method of calibration were found to be closer to the mean for all samples, KCL’s distilled water emissivity measurements retrieved using the substitution method of calibration were observed to be closer to the ECOSTRESS spectral library spectrum than those derived using the comparative method. This could indicate that the mean may have been negatively skewed by the afore-mentioned bias in the CSIRO measurements. Discounting the three negatively biased measurements from CSIRO from the analysis supports this: KCL’s measurements derived using the substitution method were in good agreement (<0.01) with the recalculated mean over 2.5–14 μm for all three samples while KCL’s measurements derived using the comparative method were in poorer agreement, with differences of up to 0.04 across 2.5–14 μm. Based on these results, further investigation should be conducted to determine the cause of the differences between the measurements from KCL and to determine an optimal approach.
The increased variability in the MWIR than LWIR observed is likely due to the increased atmospheric effects in this region, with the DLR measurements of Samples 1 and 2 clearly impacted in the CO
2 region (
Figure 4). An alternate explanation for the reduced variability in the LWIR for both artificial samples could be because this is an area of high emissivity (and thus low reflectance), which Hecker et al. [
27] observed to be areas of better agreement in their intercomparison of emissivity spectra from different laboratories.
This latter interpretation could also be why the distilled water measurements (with uniformly high emissivity) had reduced variability compared to the artificial sample SE measurements (which had variable emissivities between 0 and 1). However, it is more likely that the increased variability of the SE measurements of the artificial samples was due to the composition of these samples and their interaction with different setups. Tsilingiris [
50] provide a transmittance spectrum for polyethylene (PE), and considering this against the measured spectra of Samples 1 and 2 in
Figure 4, it is clear that variability amongst the different measurements was lower in the regions where PE had a low transmittance (3.5 μm, 6.9 μm and 13.8 μm). In all other spectral regions, the PE formed a multilayer system, which is potentially sensitive to directional illumination characteristics. Differences in the incident angles upon the samples within the different measurement setups could therefore at least partly explain the SE variations seen. Given that Sobrino and Cuenca [
51] observed that emissivities in field measurements tended to decrease with increases in the observation angle, results from this study indicate that future work should be conducted to explore whether emissivities from DHR setups in the laboratory similarly correlate with the incident angle. Materials with expected directional behaviour should in particular be considered.
The observed spectral shifts between different measurements of the specular sample also raise interesting questions about the impact of incident angles on SE measurements. While this may not be an issue for non-specular samples without coating (and therefore for most natural samples), these discrepancies indicate that further work should be conducted to confirm and investigate the impact of the incident angle on the spectral stability and absolute emissivity. Spectral shifts of the magnitude observed in this study will have more implications when working with data from hyperspectral rather than multispectral thermal imagers. Conversely airborne hyperspectral instruments such as NASA-JPL’s airborne Hyperspectral Thermal Emission Spectrometer (HyTES) sensor have so many narrowband (18 nm) spectral channels between 7.5 and 12 µm that TES and spectral smoothness approaches can be applied, which reduce the need to prescribe emissivity in advance [
52,
53]. However, such TES approaches often rely on laboratory emissivity spectra to derive empirical relationships used within the algorithm, and so their accuracy is still important even though for each hyperspectral image pixel the emissivity is directly retrieved [
10]. Such wavelength shifts may also have implications for use of spectral emissivity features in, e.g., mineral identification studies [
54], and also may affect in situ LST measurements given that radiometers commonly used in LST validation studies are affected—such as the Heitronics KT15.85 IIP radiometer with a spectral range of 9.6–11.5 μm [
16,
55].
Consideration of how the uncertainty of individual SE measurements translates into retrieved LSTs in
Section 3.4 indicates the importance of reducing uncertainties in laboratory SE measurements to improve remotely sensed LST estimates. While it must be acknowledged that the artificial samples are not representative of many land surfaces, with most natural surface less reflective in the LWIR, similar samples may be observed in remote sensing of urban areas (e.g., for urban heat island monitoring) or monitoring of plastic pollution in water [
7,
56,
57].
5. Summary and Conclusions
Surface spectral emissivity data collected with twelve different laboratory spectrometer measurement setups made at seven different laboratories were compared over the MWIR and LWIR spectral ranges in a Round-Robin intercomparison exercise. All measurements were based on the principle of illuminating the sample with an intense source of infrared radiation, measuring the reflected signal, and converting this to an emissivity spectrum using Kirchhoff’s Law. Three different samples were used for the exercise. The first two were artificial samples constructed from gold and aluminium sheets each laminated in PE films that had Lambertian and specular characteristics respectively and with widely varying emissivity features across the 2.5–14 μm spectral range. The third sample was distilled water, which has a relatively flat emissivity spectrum close to unity.
Comparing the measurements from the different laboratories we found that the inter-setup variability of the SE measurements was larger than anticipated, with differences in magnitude and spectral shape. Standard deviations of ±0.092 (15.98%) and ±0.054 (7.56%) were identified across the 2.5–14 μm spectral range for Samples 1 and 2 respectively. Repeated measurements using the same measurement setup and protocol at different times confirmed that observed SE differences were not attributable to changes in the sample properties over the course of the study but were rather due to the different setups and measurement procedures used in the various laboratories. Variability was greater in the MWIR rather than LWIR spectral region, likely due to differing efficiencies of atmospheric purging, which impact this region more. SE differences across the LWIR atmospheric window (8–14 μm), which is the most important for the remote sensing of LST, were ± 0.046 and ± 0.037 respectively for Samples 1 and 2, and most of the Sample 2 SE measurements were within 0.02 of the mean. The greater variability for the specular sample (Sample 1) over this region was attributed to spectral shifts, with differences between identification of spectral maxima and minima of up to 0.09 μm between different laboratories and up to 0.13 μm between different positional permutations on one setup were observed in the 9.8–11 μm spectral range in particular. Investigation indicated potential causes of these spectral shifts to be different sample orientations during measurements or differences in the incident angles within the different measurement setups. The latter cause was also identified as a potential cause of the absolute emissivity differences. Further investigation is therefore recommended into the impact of directional effects in laboratory measurements of emissivity (particularly for materials with known directional behaviour) given recent advances into understanding the angular dependence of emissivity for field and satellite measurements [
6,
58].
Use of different reference standards was found to contribute to the observed SE differences between different laboratory measurements but not to be the sole factor. Nonetheless, the differences observed from use of a different reference standard suggest that uncertainty in the reference standard calibration is a key factor in emissivity uncertainty in laboratory measurements. Regular calibration of the reference standards is recommended to reduce this uncertainty.
SE variability was comparatively lower for distilled water than for the artificial samples, with a mean emissivity of 0.962 ± 0.028 determined over the 2.5–14 μm spectral range. These uncertainties are larger than those observed in other studies but standard deviations were reduced to 0.008 when discounting measurements from one laboratory with a consistent negative bias (likely indicating inaccurate calibration of their reference standard). Other contributions to the SE differences included the method of calibration to reflectance, different incident angles and the placement of the sample and reference standards within the same setup. Regarding the setup at KCL, the primary laboratory used in this study, the measurements indicate that the comparative method of calibration was closer to the mean of all measurements. However consideration of the distilled water suggested instead improved performance using the substitution method and therefore further investigation is recommended.
The impact of the determined spectral emissivity differences on LST retrieval was evaluated by considering a typical mid-latitude summer scene with the surface emissivities set to the sample emissivities convolved to the ASTER TIR bands. With Sample 2 (the diffuse sample) considered more representative of natural surfaces than Sample 1, use of the three samples in this simulation provided LST error estimates over diffuse surfaces, over an extreme case of 100% specular surfaces and over water bodies. Calculated LSTs using the convolved artificial sample emissivities ranged by over 3.5 K in each band, with a maximum difference of 17.8 K (Sample 1, Band 13). The range of the LSTs calculated using distilled water spectra convolved to the ASTER TIR bands (and thus an error estimate for retrieval of LST over water bodies) was lower, but still around 2.5 K. The variability of the artificial samples and the distilled water emissivities measured at different laboratories would therefore result in uncertainties in LST estimates that exceeded the target accuracy requirements for satellite observations of land surface temperature, even without considering contributions from atmospheric effects.
Overall, our findings highlight the need for the infrared spectroscopic community to work towards standardized and interlaboratory comparable results, with regular calibration of reflectance standards and the laboratory setup against SI traceable standards.