Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments
Abstract
:1. Introduction
2. Structure and Methods
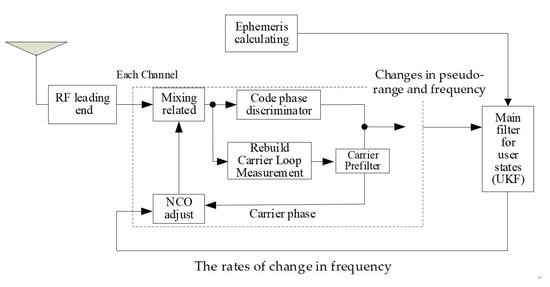
2.1. Tracking Loop Structure
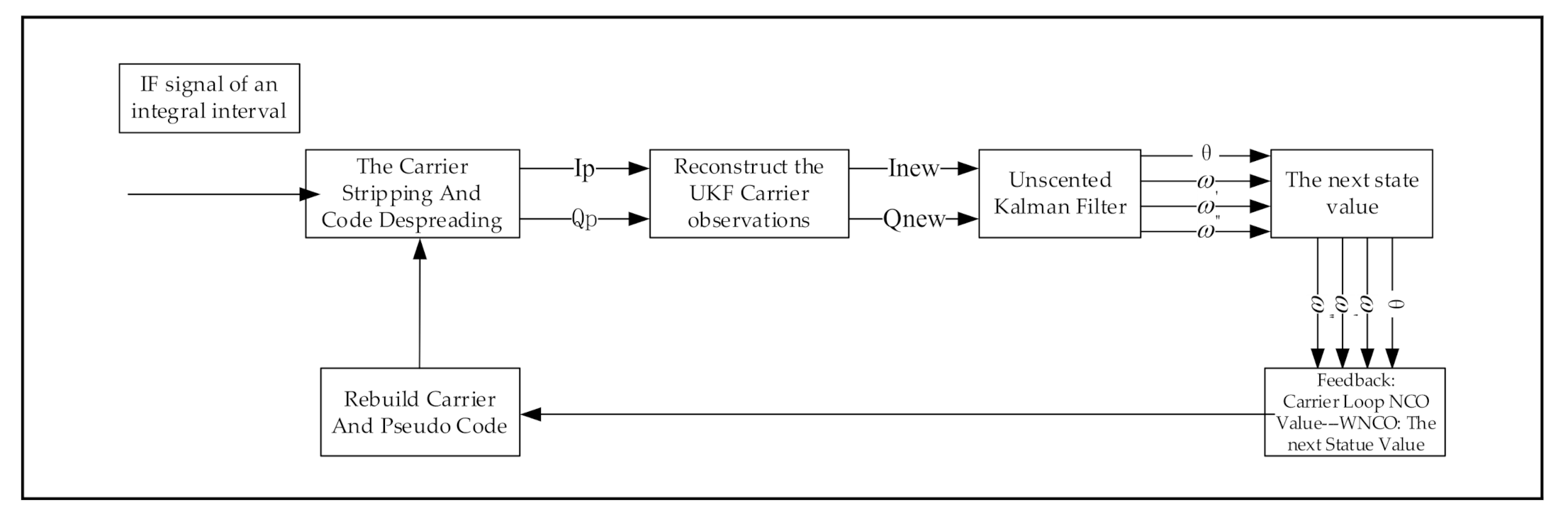
2.2. Cascading Tracking Methods
3. Results
3.1. GPS Signal Source Used
3.2. Results Analysis
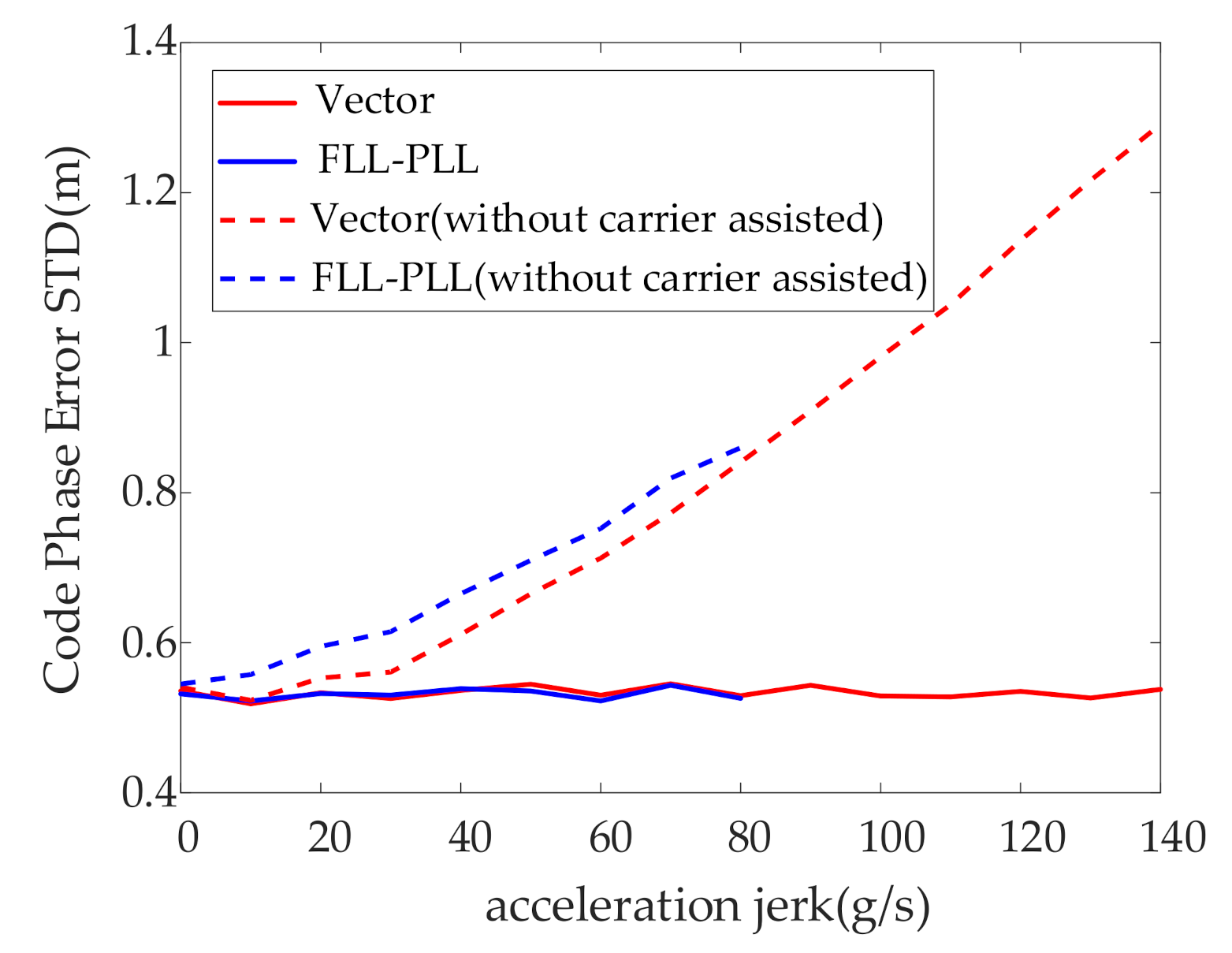
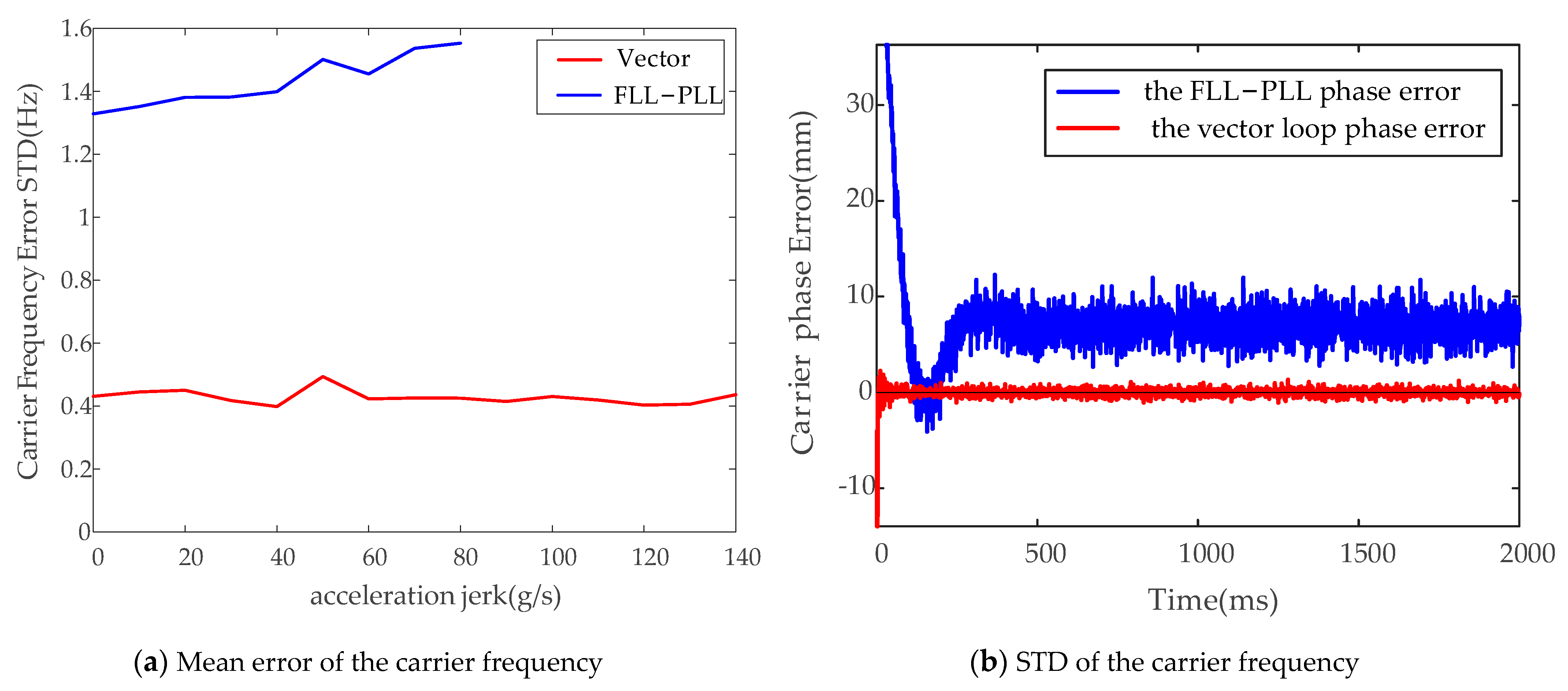
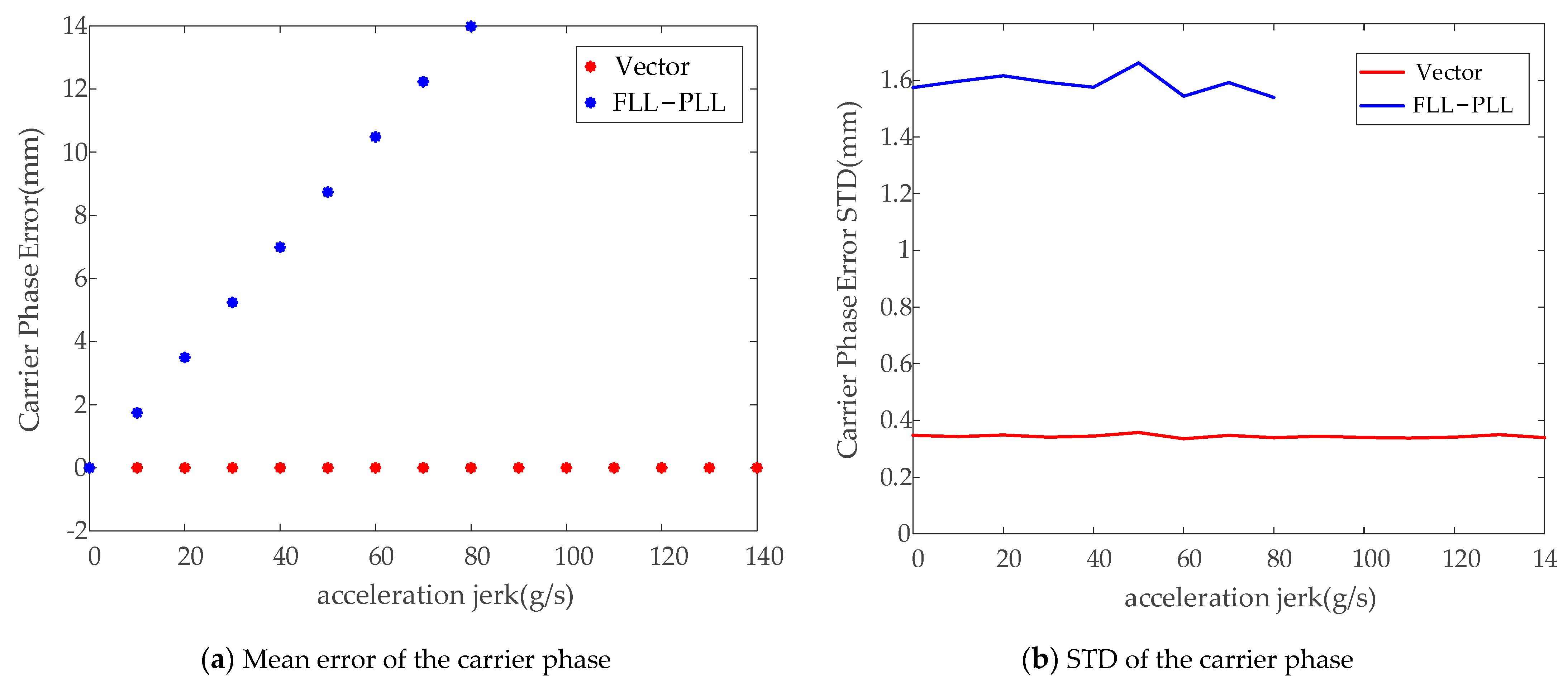
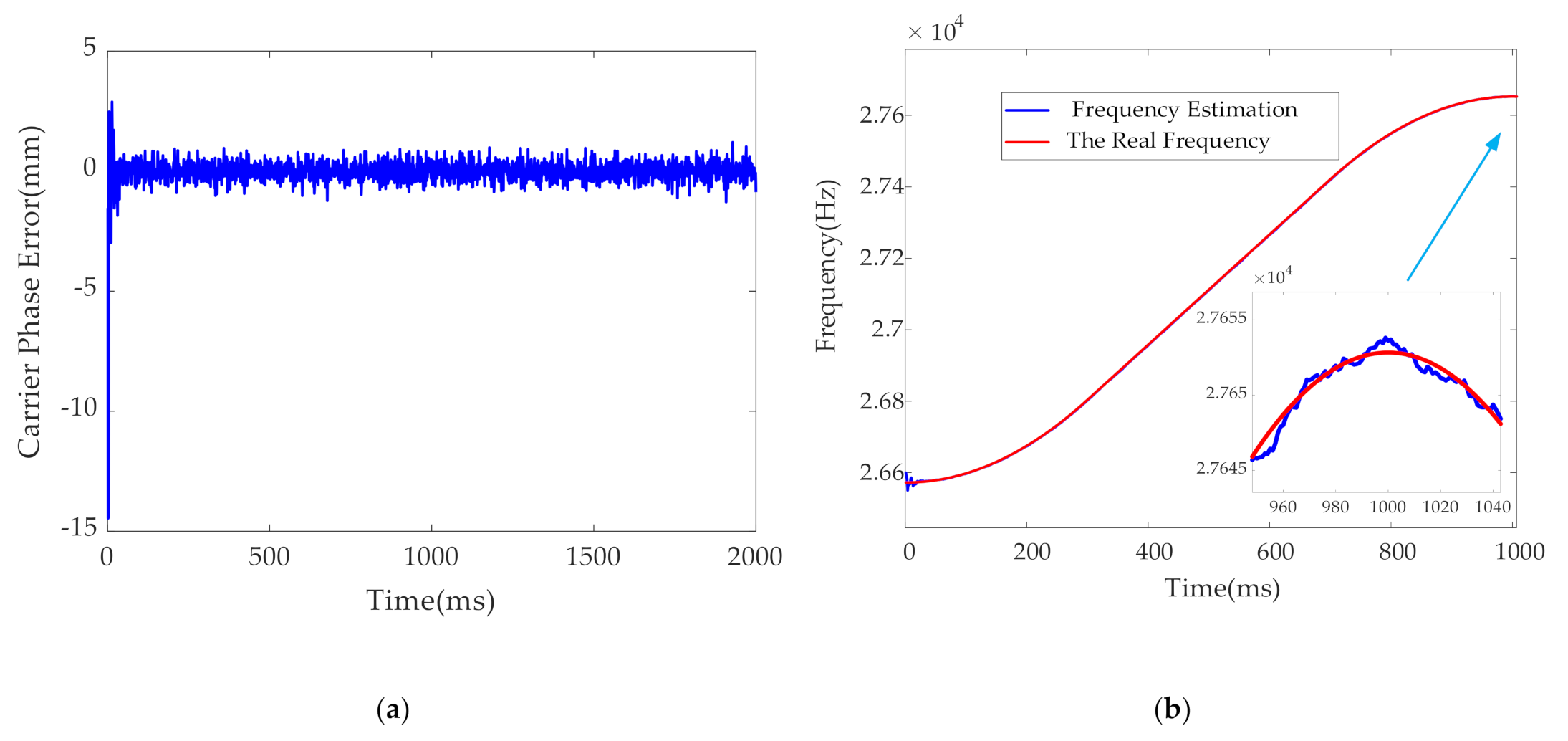
3.2.1. Simulation and Analysis of High Dynamic Signal
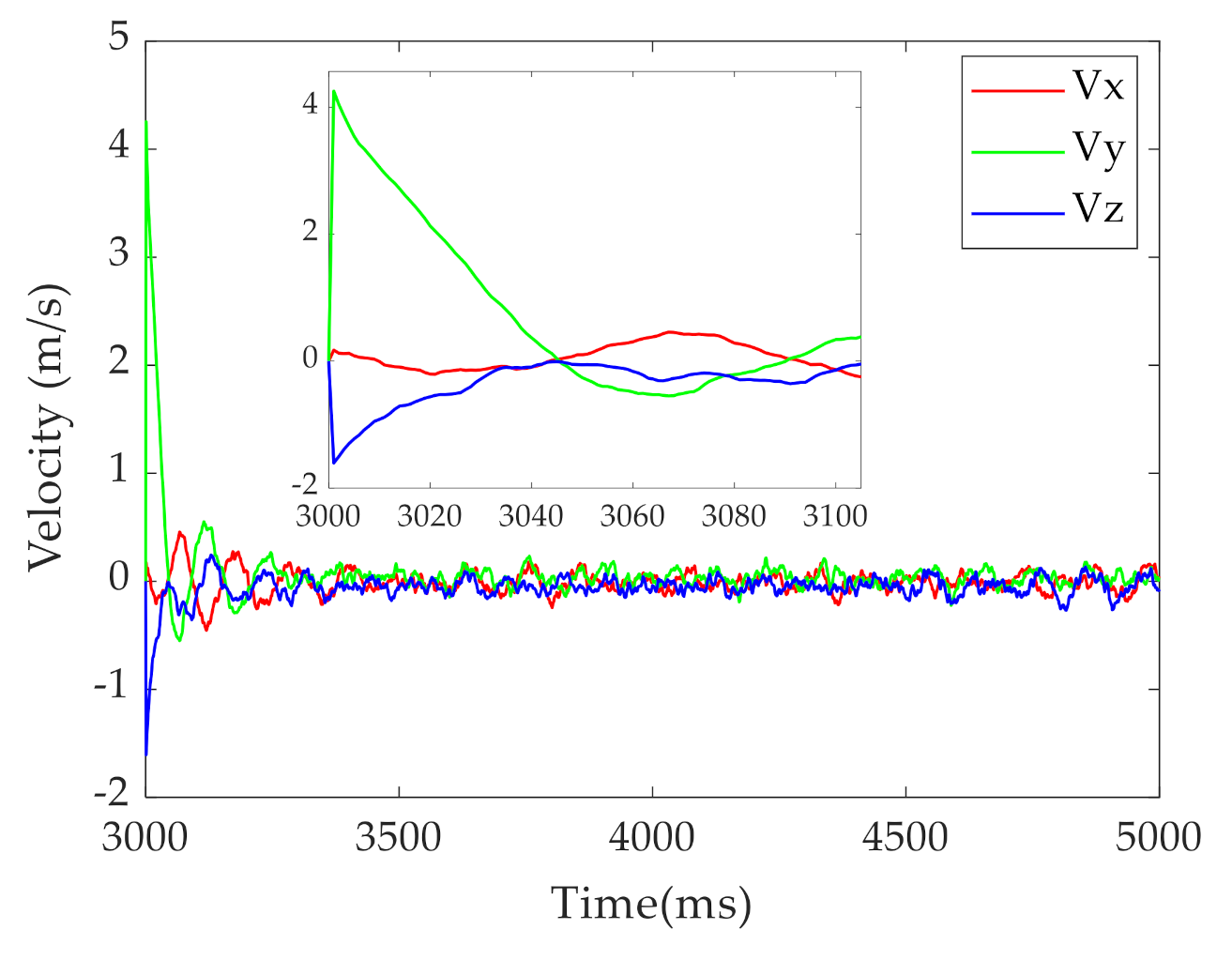
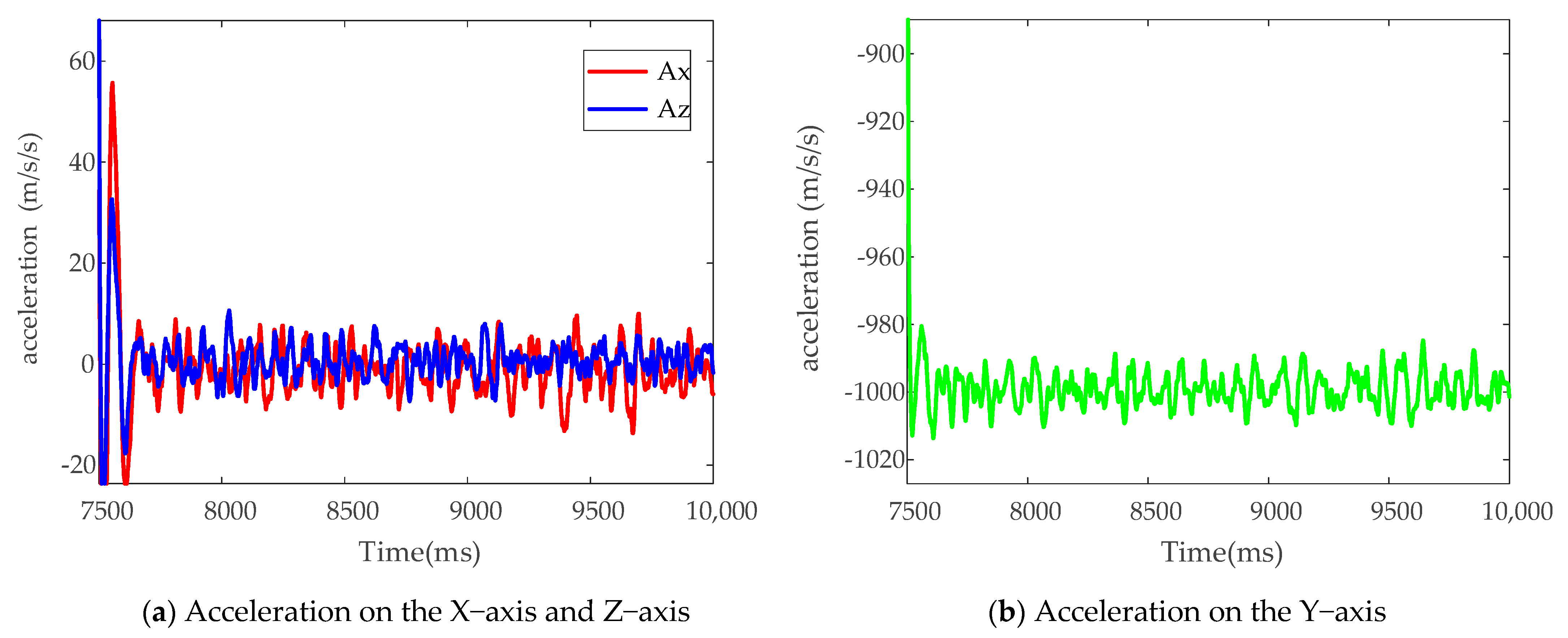
3.2.2. Signal Analysis Based on the Simulator
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krasner, N.F. GPS Receiver and Method for Processing GPS Signals. U.S. Patent 56,637,34A, 14 July 1998. Available online: https://patentimages.storage.googleapis.com/9a/19/7f/30ba615e98c917/US5663734.pdf (accessed on 15 May 2021).
- Hu, H.; Xu, L. GPS Carrier Tracking Research and Simulation. In Proceedings of the 2008 International Symposium on Information Science and Engineering, Shanghai, China, 20–22 December 2008; Volume 1, pp. 414–416. [Google Scholar]
- Hurd, W.J.; Statman, J.I.; Vilnrotter, V.A. High Dynamic GPS Receiver Using Maximum Likelihood Estimationand Frequency Tracking. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 425–437. [Google Scholar] [CrossRef]
- Won, J.-H.; Pany, T.; Eissfeller, B. Iterative Maximum Likelihood Estimators for High-Dynamic GNSS Signal Tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2875–2893. [Google Scholar] [CrossRef]
- Yan, K.; Ziedan, N.I.; Zhang, H.; Guo, W.; Niu, X.; Liu, J. Weak GPS Signal Tracking Using FFT Discriminator in Open Loop Receiver. GPS Solut. 2016, 20, 225–237. [Google Scholar] [CrossRef]
- Mosavi, M.; Shokhmzan, Z. Spoofing Mitigation of GPS Receiver Using Least Mean Squares-Based Adaptive Filter. Iran. J. Electr. Electron. Eng. 2015, 11, 1–11. [Google Scholar]
- Miao, Z.; Lv, Y.; Xu, D.; Shen, F.; Pang, S. Analysis of a Variational Bayesian Adaptive Cubature Kalman Filter Tracking Loop for High Dynamic Conditions. GPS Solut. 2017, 21, 111–122. [Google Scholar] [CrossRef]
- Zeng, C.; Li, W. Application of Extended Kalman Filter for Tracking High Dynamic GPS Signal. In Proceedings of the 2016 IEEE International Conference on Signal and Image Processing (ICSIP), Beijing, China, 13–15 August 2016; pp. 503–507. [Google Scholar]
- Spilker, J.J., Jr.; Axelrad, P.; Parkinson, B.W.; Enge, P. (Eds.) Global Positioning System: Theory and Applications, Volume I; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1996. [Google Scholar]
- Zhao, S.; Akos, D. An Open Source GPS/GNSS Vector Tracking Loop—Implementation, Filter Tuning, and Results. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 1293–1305. [Google Scholar]
- Amani, E. Scalar and Vector Tracking Algorithms with Fault Detection and Exclusion for GNSS Receivers: Design and Performance Evaluation. Ph.D. Thesis, Université Paris-Est, Paris, France, 2017. [Google Scholar]
- Lashley, M.; Bevly, D.M. Performance Comparison of Deep Integration and Tight Coupling. Navig. J. Inst. Navig. 2013, 60, 159–178. [Google Scholar] [CrossRef]
- Bye, C.T.; Schipper, B.W.; Vallot, L.C. GPS/IMU Clock Synchronization Particularly for Deep Integration Vector Tracking Loop. U.S. Patent 711,708,6B2 9 September 2003. Available online: https://patentimages.storage.googleapis.com/79/ab/b8/56fa2ac5af7274/US7117086.pdf (accessed on 3 October 2006).
- Lashley, M.; Bevly, D.M.; Hung, J.Y. Performance Analysis of Vector Tracking Algorithms for Weak GPS Signals in High Dynamics. IEEE J. Sel. Top. Signal Process. 2009, 3, 661–673. [Google Scholar] [CrossRef]
- Benson, D. Interference Benefits of a Vector Delay Lock Loop (VDLL) GPS Receiver. In Proceedings of the 63rd Annual Meeting of The Institute of Navigation, Cambridge, MA, USA, 25 April 2007; pp. 749–756. [Google Scholar]
- Petovello, M.G.; Lachapelle, G. Comparison of Vector-Based Software Receiver Implementations With Application to Ultra-Tight GPS/INS Integration. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation, Fort Worth, TX, USA, 29 September 2006; pp. 1790–1799. [Google Scholar]
- Marcal, J.; Nunes, F.; Sousa, F.M.G. Performance of a Scintillation Robust Vector Tracking for Gnss Carrier Phase Signals. In Proceedings of the 2016 8th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 14–16 December 2016; pp. 1–8. [Google Scholar]
- Lin, T.; O’Driscoll, C.; Lachapelle, G. Development of a Context-Aware Vector-Based High-Sensitivity GNSS Software Receiver. In Proceedings of the 2011 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 24–26 January 2011; pp. 1043–1055. [Google Scholar]
- Hsu, L.-T.; Jan, S.-S.; Groves, P.D.; Kubo, N. Multipath Mitigation and NLOS Detection Using Vector Tracking in Urban Environments. GPS Solut. 2015, 19, 249–262. [Google Scholar] [CrossRef]
- Chen, X.; Wang, W.; Meng, W.; Zhang, Z. A Novel UKF Based Scheme for GPS Signal Tracking in High Dynamic Environment. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010; pp. 202–206. [Google Scholar]
- Tu, Z.; Lu, T.; Chen, Q. A Novel Carrier Loop Based on Unscented Kalman Filter Methods for Tracking High Dynamic GPS Signals. In Proceedings of the 2018 IEEE 18th International Conference on Communication Technology (ICCT), Chongqing, China, 8–11 October 2018; pp. 1007–1012. [Google Scholar]
- Zhu, Z. Research on Key Techniques of Vector Tracking for Satellite Navigation. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2011. [Google Scholar]







| Time: (ms) | 0~300 | 300~700 | 700~1000 |
|---|---|---|---|
| Initial velocity: (m/s) | 5060 | ||
| Initial acceleration: (g) | 0 | ||
| Acceleration jerk: (g/s) | 100 | 0 | −100 |
| Time (unit: ms) | 0–1000 | 1000–2000 | after 2000 ms |
|---|---|---|---|
| Velocity (unit: m/s) | 5000 | vary with the acceleration and acceleration jerk | |
| Acceleration (unit: g) | 0 | vary with the acceleration jerk | −100/−80/−60/−40/−20 |
| acceleration jerk(unit: g/s) | 0 | −100/−80/−60/−40/−20 | 0 |
| Acceleration (g) | −20 | −40 | −60 | −80 | −100 |
|---|---|---|---|---|---|
| Carrier phase tracking error of vector tracking structure (STD, unit: mm) | 0.57 | 0.55 | 0.52 | 0.51 | 0.52 |
| Carrier phase tracking error of second-order frequency locked loop assisted third-order phase locked loop (STD, unit: mm) | 3.50 | 3.56 | 3.71 | The lock has been lost in the variable acceleration section | The lock has been lost in the variable acceleration section |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Z.; Lou, Y.; Guo, W.; Song, W.; Wang, Y. Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments. Remote Sens. 2021, 13, 2000. https://doi.org/10.3390/rs13102000
Tu Z, Lou Y, Guo W, Song W, Wang Y. Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments. Remote Sensing. 2021; 13(10):2000. https://doi.org/10.3390/rs13102000
Chicago/Turabian StyleTu, Zhiyong, Yidong Lou, Wenfei Guo, Weiwei Song, and Yusheng Wang. 2021. "Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments" Remote Sensing 13, no. 10: 2000. https://doi.org/10.3390/rs13102000
APA StyleTu, Z., Lou, Y., Guo, W., Song, W., & Wang, Y. (2021). Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments. Remote Sensing, 13(10), 2000. https://doi.org/10.3390/rs13102000