1. Introduction
Snow cover is a crucial component of the climate system, with its high albedo allowing up to 90% of incoming solar radiation to be reflected. Snow is also an important insulator, and in cold climates such as those found in the high latitude regions, it protects underlying soil and vegetation from frost damage. However, past and present changes in the global climate have been producing pronounced effects in the polar regions, as increasing temperatures lead to loss of snow, glacier and sea ice cover which in turn reduce the surface albedo and increase absorption of solar radiation, producing even greater warming [
1]. The Svalbard archipelago, located in the High Arctic, is heavily glaciated and glaciers alone make up 57% of the total land area of Svalbard [
2]. However, as a result of a warming climate, the spatiotemporal characteristics of seasonal snow cover on Svalbard have undergone significant changes in the past two decades, with large parts of the archipelago exhibiting trends of earlier spring snowmelt and disappearance [
3,
4]. Projected changes in climate, as outlined in a recent report on the future climate of Svalbard, indicate that by 2100, increases of 3–4 °C and 6–8 °C in the mean annual temperature can be expected for the west coast and northeastern regions respectively, compared with the 1961–1990 average [
5]. Such marked warming will inevitably lead to significant impacts across the cryosphere, hydrosphere and biosphere, as changes in snow and ice cover affect timing and intensity of surface runoff and water storage and availability. On average, predictions for Svalbard indicate more than doubling of the snow-free season length and total runoff from glaciers and seasonal snow between 1957–2018 and 2019–60 for a RCP4.5 emission scenario [
6]. Snowpack water content is an important component of the hydrological cycle; therefore, snow cover mapping is useful in both assessing water resources and for calibration of hydrological models [
7,
8,
9] through data assimilation [
10]. Up-to-date, detailed information on snow cover and conditions is also an important element for forecasting of natural hazards such as avalanches, slush flows and snowmelt floods, all of which may occur more frequently in a warming climate. Knowledge of snow water equivalent (SWE) in mountain catchments is also crucial to the hydropower industry, especially for management of seasonal water resources. Operational daily maps of simulated snow conditions have already existed for 15 years for mainland Norway. However, there is an absence of detailed, spatiotemporal information of snow conditions on Svalbard, despite the obvious relevance and need for such information in, for example, natural hazard forecasting on Svalbard and planning of outdoor and tourism activities.
The evolution of snow parameters can be simulated continuously in space and time through utilization of snow models. These require a surface meteorological forcing, which is either obtained from output of regional climate/numerical weather prediction models or reanalysis datasets for large-scale modelling. The evolution of the seasonal snowpack over land in Svalbard is dominated by snow accumulation during autumn and winter and subsequent melting during late spring and summer. Snow accumulation and spring maximum snow depth is mostly determined by cumulative precipitation in the form of snow during autumn and winter, while snowmelt depends on land-atmosphere interactions that can be estimated using simple melt-air temperature relationships such as the positive-degree day model, or more sophisticated models that solve the surface energy balance. Snow models therefore represent a valuable tool for filling spatial and temporal gaps in observational datasets. Moreover, they can simulate snow over longer time-periods and larger spatial domains than observational datasets. Essential to snow model calibration and validation is the use of in situ and/or remote sensing snow products, estimates of SWE, snow depth, density, temperature and water content. However, measuring snow parameters traditionally by means of in situ observations provide only point measurements and is limited in spatial coverage. Furthermore, the installation and maintenance of networks of meteorological instruments is often challenging in high mountain and remote terrain environments.
Remote sensing of snow cover provides a means of observing snow cover over large spatial areas that cannot be fulfilled by in situ observations alone and has been well-reviewed in recent years [
11,
12]. Optical sensors make detection of snow possible by utilizing the reflectance characteristics of snow at different wavelengths. Snow is distinguishable from other types of surface cover due to its high reflectance properties at visible wavelengths, low reflectance in the near infrared band and shortwave infrared wavelengths [
13]. Several generations of optical sensors have now been acquiring data globally for several decades; the Moderate Resolution Imaging Spectroradiometer (MODIS) onboard the Terra and Aqua satellites has been acquiring optical images since 2000, from which the Normalized Difference Snow Index (NDSI) can be derived [
14] as well as fractional snow cover [
15]. Recently, a 20-year MODIS snow cover fraction (SCF) dataset for Svalbard based on the NASA MOD10A1-product [
16] at 500 m spatial resolution has been produced and investigated [
4]. Other spaceborne optical sensors include the Advanced Very High-Resolution Radiometer (AVHRR) instrument, which has flown onboard polar orbiting satellites since the late 1970s and provides observations for monitoring snow cover extent (SCE). The instrument has approximately 1 km spatial resolution, but only data at a reduced effective resolution of approximately 4 km is permanently archived and available with global area coverage (GAC). Meanwhile, newer more sophisticated optical sensors on board the Sentinel-2 A and B satellites have been delivering data over Svalbard since 2016 at a nominal 10 m pixel spacing. Since the launch of the Sentinel-2B satellite in 2017, daily coverage of Svalbard has also been possible, therefore providing unrivalled opportunities to study snow cover changes in Svalbard at high temporal and spatial resolution. A recent study has begun to address the similarities and differences in fractional snow cover retrievals using three optical sensors at different resolution and extracted using retrieval algorithms for a study site in northwest Svalbard [
17]. The remote sensing observations were further validated by very high-resolution terrestrial photography. Even though the study area and time period were limited in extent, the results nevertheless indicate that there exist discrepancies when comparing observations from lower and higher resolution sensors, as well as the methods used to retrieve them. Furthermore, compiling long term climate records and linking observations to climatic variations by combining data from different sensors that cover different time periods inevitably becomes challenging due to mixed-pixel problems creating biases in fractional snow cover estimates when aggregated over large areas [
18].
Despite the existence of multiple optical satellite datasets and snow model datasets, there is an obvious lack of continuity and consistency with respect to spatial resolution and periods of data coverage. Moreover, few attempts have been made that demonstrate how current-day, high resolution remote sensing datasets can be used to reconstruct and upscale snow cover observations of the earlier, low resolution datasets that often provide long time periods of data coverage. This is especially true for the high latitude Svalbard archipelago, where changes in seasonal snow are occurring faster than snow-covered areas at lower latitudes. Furthermore, studies of snow cover to date have often only utilized either remote sensing or modelling and there is therefore a need for large scale comparisons between different resolution sensors and models as well as evaluating the relative strengths and weaknesses of each dataset. Therefore, the objective of this study is to demonstrate the similarities and differences of snow cover observations made using remote sensing datasets and snow models, and how these differences can affect the extraction of derived parameters linked to the dynamical processes such as snow melt and disappearance. We examine snow cover fraction derived using the AVHRR dataset at 4 km resolution and Sentinel-2 observations produced at 20 m resolution and how they compare with the recently published MODIS SCF dataset for Svalbard at 500 m resolution [
4]. In addition, two independent snow models developed by the University of Uppsala (Energy balance—snow and firn model; EBFM) and the Norwegian Water Resources and Energy Directorate (seNorge) that provide estimates of SWE and fractional snow-covered area, are used to derive snow cover extent maps. These are compared with the snow cover extent derived from binarization of the MODIS SCF maps to examine the temporal and spatial differences in snow cover. The area of study for this work is defined by the overlapping area common to all datasets available. For this work, we have therefore carried out the data analysis for the Nordenskiöld Land region in the central part of Svalbard.
An overview of the study area will be presented in
Section 2 together with a description of the remote sensing and snow model datasets and an outline of the data processing and analysis methods used to perform the comparisons between the datasets. The results of the comparisons as well as a quantitative evaluation of the consistency between the datasets are presented in
Section 3. In
Section 4, a discussion of the main results is made in the context of current knowledge and earlier studies of relevance. A summary of the primary findings of this study, as well as suggestions for further work is given in the conclusion, in
Section 5.
3. Results
In this section, we present the results of the data processing and analysis outlined in
Section 2. This section is divided into five subsections, which describe the different aspects of the data comparisons made. In
Section 3.1, a description of the general relationship between the datasets is made, while in
Section 3.2, we present a more specific comparisons of the geographical and altitudinal differences between the datasets.
Section 3.3 is dedicated to the results of the normalization, or correction of the snow cover time series using the results of
Section 3.1, and in
Section 3.4, we quantify the effect of the corrections on derived estimates of first snow-free day, compared with the original time series. A quantitative evaluation of the differences between the datasets, before and after corrections is made in
Section 3.5.
3.1. General Relationship between the Datasets
In this section, a comparison of the snow cover fraction time series is made for each dataset, with respect to the MODIS SCF time series. These comparisons are made using the SCF which is obtained by averaging the snow cover products over the study area.
Figure 3 shows the time series of the land-averaged snow cover fraction for all datasets used in this study. There is some overlap between datasets: for example, between MODIS, AVHRR and the EBFM dataset, from 2000–2019, and from 2013–2015, there is overlap between MODIS, AVHRR, EBFM and the seNorge datasets. In the final four years of the period (2016–2019), there is overlap between MODIS, seNorge, EBFM and Sentinel-2. There is good agreement in the SCF minimum values for MODIS, AVHRR and EBFM for the first five years of the period, though with AVHRR exhibiting greater and more frequent fluctuations in SCF during the summer minimum compared with MODIS and EBFM. From 2006 onwards the fluctuations in SCF derived from AVHRR during the minimum period become more pronounced; moreover, the SCF values during this period also tend to be some tens of percent greater compared with MODIS. It may also be noticed that in spring the MODIS SCF begins to fall slightly earlier compared with AVHRR and EBFM, while the increase in SCF at the end of the summer is somewhat misleading due to the different periods of coverage of the dataset, with the two remote sensing datasets ending at either September 30 (AVHRR) or October 31 (MODIS). The alternative snow model dataset, seNorge provides SCF from 2013 until 2019 inclusive. Here it can be seen that like AVHRR, there are large fluctuations in the land-averaged SCF during the period where SCF is at a minimum. These fluctuations can also be several tens of percent in magnitude. The curves in 2014 and 2015 display these large variations in the seNorge SCF quite clearly. Moreover, the lowest SCF reached in the seNorge dataset is some 20% lower than those exhibited by the MODIS and Sentinel-2 datasets. In general, the Sentinel-2 snow cover fraction follows closely the temporal variations of the MODIS estimates, though in 2016 and 2018 the Sentinel-2 SCF appears to fall marginally earlier than MODIS in the spring.
Figure 4 is a representation of the data shown in
Figure 3, as a scatter plot. Here the SCF values from each dataset were plotted against the MODIS SCF, with the time series separated into two periods corresponding to data from 1 March–31 August (blue) and from 1 September–31 October (coral), or until the end of the dataset being compared. This was done to separate snow cover estimates made during the spring melt period and those from autumn snow onset. In all but the case of the Sentinel-2 dataset, the lower resolution data from AVHRR and the snow models were plotted on the x-axis, with MODIS along the y-axis. Since the Sentinel-2 data are at higher resolution than the MODIS dataset, these were plotted along the y-axis to derive the relation that transforms the lower resolution dataset to the SCF estimates of the higher resolution sensor. Since this study endeavors to examine the differences in timing of snow disappearance between the datasets, the most critical period for dataset correction is the snow melt period. As such, the function used to transform the datasets is obtained by fitting a cubic spline function to the pairs of data obtained only in the period from 1 March–31 August (blue datapoints) to derive the general relationship with the MODIS values; this is displayed by the light blue curves. The number of scatter points in each plot reflects the size of the dataset, with the AVHRR and EBFM datasets being the largest with respectively 16 and 20 full years of data that overlap with MODIS. Of all four datasets being compared against MODIS, there is poorest agreement with the AVHRR dataset, in terms of magnitude. This is especially true when the land-averaged MODIS SCF lies the range 30–60%, with the corresponding AVHRR SCF being on average 20% greater than MODIS. On the other hand, the land-averaged SCF obtained from Sentinel-2 generally agrees well with MODIS at low (<25%) and high (>90%) snow cover fractions. At all other snow cover fractions, the Sentinel-2 snow cover fraction is in general lower than MODIS and can reach up to nearly 10% lower than MODIS. For the seNorge dataset there is generally a good but non-linear correlation with the MODIS values, when considering only the SCF data from between 1 March–31 August. There is clearly a large spread in values for SCF obtained in the period 1 September–31October, but for the melt period of interest the land-averaged SCF derived from seNorge is of the order 5–10% greater than MODIS when MODIS SCF is >30%. For the EBFM dataset, shown in
Figure 4d the relationship between the MODIS SCF and the model-derived SCF is similar to that of seNorge snow model, but the EBFM estimates can be on average up to 15% greater than MODIS for the period between 1 March–31 August, as indicated by the largest offset between the fitted spline (light blue curve) and the equality line (dark blue, dashed) while EBFM estimates of SCF obtained from after September 1 which corresponds to the start of the hydrological year, are consistently lower than MODIS.
3.2. Geographical and Elevation Differences
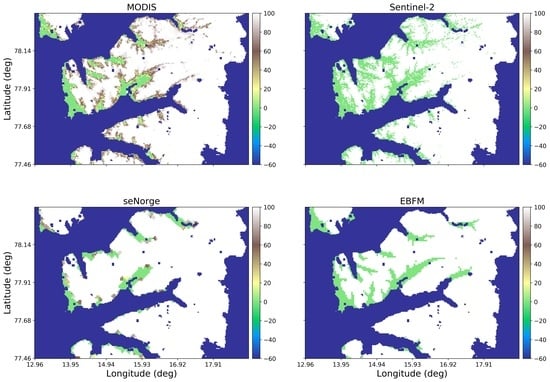
The difference in annual number of days with snow cover derived from each of the data products and that obtained from MODIS was mapped. To make this geographical comparison, a binary snow map was first obtained. For the fractional snow cover products SCF was thresholded at 50%, where SCF below the threshold is defined as “no snow” and SCF greater than the threshold, “snow”. Hence, for each pixel in the grid, the number of days the pixel was classified as snow covered/not-snow covered during each year of data coverage using the datasets was calculated. The difference in number of days with snow cover between AVHRR/Sentinel-2 and MODIS, and the two snow model datasets and MODIS was then calculated. For the remote sensing datasets, the difference in number of days with snow applies only to the part of the year outside of the polar night period. For the AVHRR dataset, this is the difference in number of days with snow between 1 March and 30 September, while for Sentinel 2 it is restricted to only the period 15 April–15 September. Since the two snow models produce SWE and SCF for the entire year, the full period of MODIS coverage from 1 March–31 October is used in the comparisons.
In
Figure 5, the mean difference in number of days with snow derived for each of the datasets is shown. The mean difference was calculated per pixel by averaging the difference in number of days with snow over all the years in each dataset. Since the difference is calculated by subtracting the MODIS number of days with snow from the AVHRR number of days with snow, positive numbers indicate a greater number of days with snow per year on average with respect to MODIS and negative numbers indicate fewer days with snow per year on average, compared with MODIS. In the case of the AVHRR dataset, it has already been shown in
Figure 4a that snow cover fraction is on average for the study area, always greater than that estimated using the MODIS instrument, for the period of data cover 2000–2015.
Figure 5a illustrates this pattern geographically, where there are large areas of blue (positive difference in number of days with snow) that correspond to low-lying valleys. Areas with light yellow tone indicate where the number of days with snow each year estimated by AVHRR and MODIS are roughly the same (zero difference). Since the AVHRR data were georeferenced to the MODIS grid, the downscaling from 4 km to 500 m pixel spacing is also clear from the square-like edges of blue areas. Areas where the difference in number of days with snow cover estimated by AVHRR was less than MODIS, indicated by the dark red areas, can also very likely be attributed to the resolution differences.
For Sentinel-2 data on the other hand, which have much higher spatial resolution than MODIS, the difference in mean number of days with snow for the period 2016–2019, shown in
Figure 5b is close to zero or below zero across the area of study, as exhibited by the prevalence of yellow and orange. This implies that MODIS always estimates a greater number of days with snow per year than Sentinel-2, with greatest differences on mountain slopes.
Figure 5b would suggest that MODIS estimates greater than 60 days more with snow in these areas, compared to Sentinel-2.
The comparison of mean days with snow cover between MODIS and the two models, seNorge and EBFM is shown in
Figure 5c,d respectively. The geographical distribution and magnitude of the differences are quite different; for the seNorge snow cover area dataset, the snow model estimates on average fewer days with snow cover per year in the low-lying valleys and around all coastal areas, when compared with MODIS. On the other hand, blue areas corresponding to the highest elevation mountain zones indicate that the seNorge estimates on average a greater number of days with snow in these areas compared to the MODIS dataset. For the EBFM dataset shown in
Figure 5d, there is also a tendency toward moderate to large underestimation in mean number of days with snow cover per year for the valley areas when compared with MODIS, as shown by the light yellow, orange and red regions. However, different to the seNorge dataset, EBFM tends to produce larger underestimation in number of days with snow in the inland parts of the valleys, whereas the largest underestimations for the valley areas in the seNorge dataset tends to be situated closer to the coastal areas. In addition, the EBFM dataset also transitions to greater number of days with snow cover compared to MODIS in the mountainous regions in the northern and eastern part of the study area but begins at much lower elevations than for the seNorge dataset. This is especially noticeable for the mountain slopes that are also located along coastal areas.
These elevation-dependent differences in the mean number of days with snow per year, between the different remote sensing and snow model datasets, and MODIS, is illustrated in
Figure 6. This figure was produced by averaging the mean differences in number of days with snow (
Figure 5) over all elevation zones at intervals of 200 m between 0 and 1200 m.a.s.l. using a high resolution (20 m) Digital Elevation Model (DEM). Here, the x-axis of
Figure 6 represents the middle point of each elevation interval.
Figure 6 therefore demonstrates that the degree of overestimation in mean number of days with snow by AVHRR in the low altitude areas (0–200 m.a.s.l.) is in fact only of the order of 10 days on average for the whole area of interest. The magnitude of underestimation in mean number of days with snow estimated by AVHRR with respect to MODIS increases with elevation, with the data suggesting underestimations of approximately 40 days or more for all altitudes intervals above 600 m.a.s.l. As shown in
Figure 5b, Sentinel-2 data exhibit of the order 10–15 fewer days with snow on average compared to MODIS at all elevations, though at the lowest altitudes the difference is only 5 days.
Common to both snow models, there is a relatively large underestimation in mean number of days with snow at elevations between 0–200 m.a.s.l. when compared with the MODIS dataset. The mean number of days with snow is on average of the order of 25 days less than MODIS in this elevation zone for the EBFM and seNorge datasets. However, the elevation distributions are noticeably different for the two snow models at elevations above 400 m.a.s.l. While the seNorge dataset exhibits a negative difference in mean number of days with snow compared with MODIS on average (15–20 days) for the whole region at all elevations >200 m.a.s.l., EBFM estimates on average 10–20 days greater snow cover per year compared with MODIS when averaged over all the elevation intervals above 400 m.a.s.l., with largest differences present at elevations between 600–1000 m.a.s.l. This pattern was also described earlier for the geographical distribution of the differences shown in
Figure 5d.
3.3. Correction of the Datasets
The Sentinel-2 dataset, with the highest spatial resolution of all the datasets but relatively small temporal period of coverage, was used to adjust the lower-resolution MODIS SCF time series by applying the obtained spline fit (
Figure 4b) to the MODIS time series. With the adjusted MODIS time series, spline fits to the three remaining datasets were subsequently updated and applied to the respective time series to obtain a final corrected SCF for the three remaining lower resolution datasets (AVHRR, seNorge and EBFM). The objective of this procedure was to normalize the snow cover observations from each dataset to a baseline in order to achieve better consistency between the products. The final corrected SCF time series and the corresponding spline fits associated with these are presented in
Figure 7a–d. While there remains a degree of spread in the land-averaged SCF values, the corrected time series are on average much closer to the MODIS values, as exhibited by the final spline fits which lie close to the equality line (dark blue, dashed). In particular, the relationship between the corrected datapoints and the MODIS datasets for the melt period between 1 March–31 August is more linear compared with their original time series. This is true for all datasets.
3.4. Estimation of First Snow-Free Day (FSFD)
The SCF time series produced using the different datasets were used to extract estimates of the first snow-free day, which is taken to be the point at which the SCF first falls below 50%. FSFD was estimated using the uncorrected and corrected land-averaged SCF time series for each dataset and compared with the FSFD values produced using the corresponding MODIS time series. These are shown in
Figure 8a,b. Qualitatively speaking, the FSFD estimates made using the uncorrected datasets lie much further from the MODIS estimates (
Figure 8a) compared with those made using the corrected SCF time series, as shown in
Figure 8b. Significant improvements in the estimates of FSFD occur following correction of the SCF time series, which before the dataset was corrected, were up to 15 days greater than the corresponding MODIS FSFD estimates. Following correction of all datasets, FSFD estimates obtained from AVHRR, seNorge and EBFM all lie close to the MODIS FSFD estimates, with the corrected FSFD occurring within approximately 5 days later or earlier than MODIS. This is as expected since the spline fit made to the corrected datasets, shown in
Figure 6, all closely follow the line which indicates where the two datasets would be equal.
In the case of the AVHRR dataset, the entire 34-year time series of snow cover extent maps for 1982–2015 are used to first extract the land-averaged SCF which is then corrected using the updated spline fits. By estimating FSFD for the entire 34–year period, decadal trends in FSFD have also been calculated using both the original uncorrected AVHRR SCF time series. This has allowed us to examine differences in FSFD trends when the data had not been upscaled using the fitted spline function. For the two corrected SCF time series corresponding to the snow models, only estimates of FSFD were made and compared with MODIS, since the temporal period of coverage of each dataset was not long enough to obtain meaningful estimates of decadal trends.
For the FSFD estimates extracted using the original AVHRR time series from 1982–2015, shown in
Figure 9, FSFD occurs later compared with those extracted from the corrected time series. The offset between the two linear trend lines is approximately 15 days, indicating that using the original AVHRR SCF time series results in FSFD estimates that are later by on average 2 weeks when compared with the FSFD estimates extracted from the corrected time series. Moreover, the slope of the linear trend line is also smaller, with a decadal trend in FSFD of −3.36 days/decade (
p = 0.08) for the uncorrected time series, while the decadal trend in FSFD estimated with the corrected AVHRR SCF time series is −2.81 days/decade (
p = 0.01). Hence, not only does the decadal trend in FSFD derived from the corrected time series become significant at the 95% confidence level, but the advance in FSFD is >0.5 days/decade slower than that suggested by the original AVHRR dataset.
3.5. Evaluation Metrics
To evaluate the effect of the corrections on each dataset, four metrics were selected for evaluation using both the uncorrected and corrected datasets, following the approach of recent similar studies that compare snow cover retrievals from lower and higher resolution datasets [
17,
30,
31]. We have first calculated the mean error, which indicates the bias of the dataset being evaluated. This was done firstly using Sentinel-2 as a baseline for the MODIS snow cover dataset and subsequently for the AVHRR, seNorge and EBFM datasets with MODIS as the baseline dataset. We have therefore implicitly assumed that Sentinel-2 is more accurate than MODIS and that MODIS is more accurate than AVHRR and the two snow models for the purpose of this evaluation. The root mean-squared error (RMSE) was also calculated, as well as the Spearman rank correlation coefficient. The Spearman rank correlation coefficient was chosen over the Pearson correlation coefficient since it is known to be more appropriate for non-linear relationships between datasets. For both the uncorrected and corrected datasets, each of the four metrics was calculated for two cases: firstly, using the period from 1 March–31 August and second, the period from 1 September–31 October as a basis for the calculations.
Table 2 summarizes the RMSE, mean error (bias) and Spearman correlation coefficient for the AVHRR, seNorge and EBFM datasets for the main period of interest (1 March –31 August) as well as the autumn data acquired after 1 September, which are stated in italic. The upper section presents the metrics calculated using the uncorrected SCF time series, while the lower section of
Table 2 displays the same metrics calculated following correction of the datasets. Sentinel-2 was used as a baseline for obtaining the spline model with which corrections to the MODIS time series was made and we show only the metrics that were calculated for the datasets sharing the same (MODIS) baseline.
Firstly, comparison of the metrics calculated for the spring (1 March–31 August) and autumn (1 September–31 October) data reinforces the patterns described by the scatter plots shown in
Figure 3. For all three datasets, there is greater spread in the data acquired after 1 September, as indicated by the larger RMSE values; the mean error is also greater and in the case of the snow models, of the opposite polarity compared with the spring data. Comparison of the metrics calculated before and after corrections were made to the time series shows an obvious improvement and reduction in the RMSE and mean error. Greatest changes in RMSE occur in the correction of the AVHRR time series, resulting in RMSE being nearly halved, from 11.22 to 5.95%. The mean error is also reduced from 7.85% to 0.39%, indicating that the positive bias, or overestimate becomes almost minimal following correction of the dataset. This is indeed reflected by the scatter plot in
Figure 6a. The Spearman correlation coefficient was only marginally increased by correcting the time series and this is not surprising since there was qualitatively a good and non-linear correlation between AVHRR and MODIS before corrections were made. For the MODIS dataset itself, the corrections made to the time series using the relationship with Sentinel-2 also resulted in a small reduction in RMSE (not shown), as well as removal of the positive bias of 2.8% which was present in the uncorrected time series. The Spearman correlation coefficient of 0.97 remained unchanged. For the two snow models, the corrections made using the spline fits also resulted in a reduction in the RMSE by between 2–2.5% while the slight positive biases in both uncorrected datasets were reduced to almost zero. For the seNorge snow model, the Spearman correlation coefficient increased from 0.85 to 0.90 while for the EBFM dataset there was no change.
5. Conclusions
Accurate maps of snow cover and characterization of the dynamic processes are critical in applications such as calibration of hydrological models and climate predictions, and especially so in regions where seasonal snow cover is responding rapidly to ongoing changes in climate. This study has investigated the similarities and differences between snow cover observations over Nordenskiöld Land in Svalbard, obtained by three optical remote sensing datasets and two snow models. The purpose of this work was to attempt to use high spatial resolution snow cover observations to make corrections to earlier, lower spatial resolution snow cover products to reconstruct long term snow cover datasets at both high spatial and temporal resolution. To achieve this, relationships between the higher and lower resolution datasets were obtained for the land-averaged snow cover fraction over the study area. Sentinel-2, with its high spatial resolution, was first utilised to adjust the moderate resolution MODIS dataset, which had excellent temporal overlap with the AVHRR dataset as well as the two snow models. This adjusted MODIS dataset was subsequently used to correct the lower resolution datasets and estimates of the timing of snow disappearance were made. For all the uncorrected datasets, estimates of FSFD were found to be later than MODIS FSFD by 10–15 days. Following correction of these datasets to the higher resolution of the MODIS dataset, FSFD estimates were significantly improved and varied by up to ±5 days from the MODIS estimates. Furthermore, the decadal advance in FSFD estimated from the uncorrected 34-year AVHRR time series were found to be 0.5 days/decade greater than the decadal trend in FSFD following correction of the AVHRR time series, indicating that interpretation of lower resolution datasets requires some care when put in the context of climate-related change.
This work has demonstrated that there is potential to improve the consistency in snow cover observations made using earlier generation remote sensing instruments which have lower resolution than current day sensors that have comparatively high temporal and spatial resolution. Specifically, we have presented a method to implement relatively simple corrections to land-averaged snow cover fraction estimated by different remote sensing datasets and snow models. This approach has been shown to produce significant updates in estimates of snow disappearance timing and decadal trends in this parameter. However, since this study has focused on improving the consistency between snow cover observations at a land-averaged scale, further work is required to upscale lower resolution snow cover datasets at the pixel level and reconcile the associated geographical and elevation dependent differences in snow cover made by remote sensing and snow model datasets, as was highlighted in this study. Ultimately, it would be desirable to reproduce older snow cover maps at the high resolution of the newest sensors. This could for example be achieved by establishing a statistical average of the snow cover distribution at high spatial resolution, given a land-averaged snow cover fraction obtained from a lower resolution dataset.