Snow Phenology and Hydrologic Timing in the Yukon River Basin, AK, USA
Abstract
1. Introduction
2. Materials and Methods
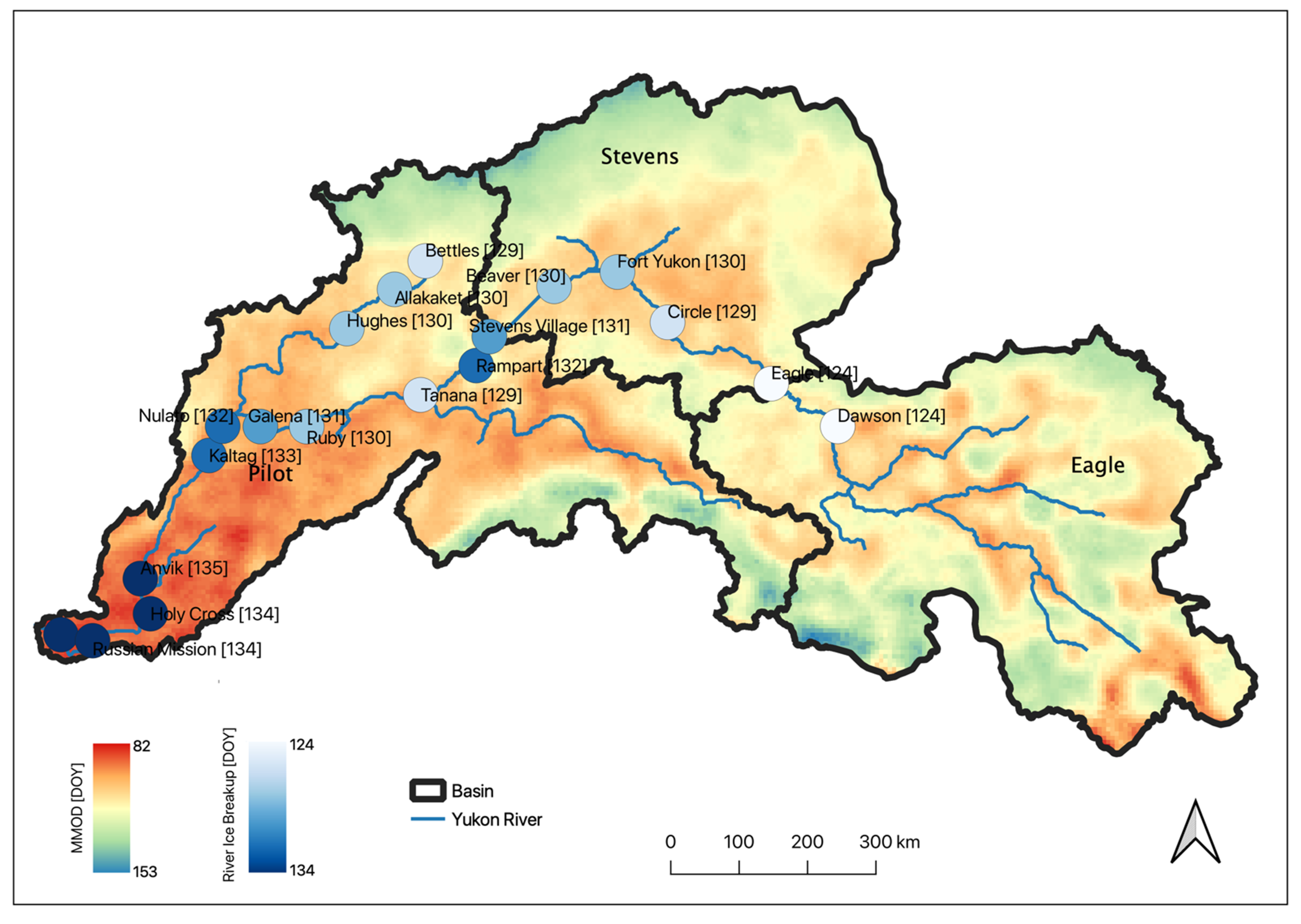
2.1. Study Domain
2.2. Passive Microwave Satellite Record 1988–2016
2.3. Other Ancillary Datasets
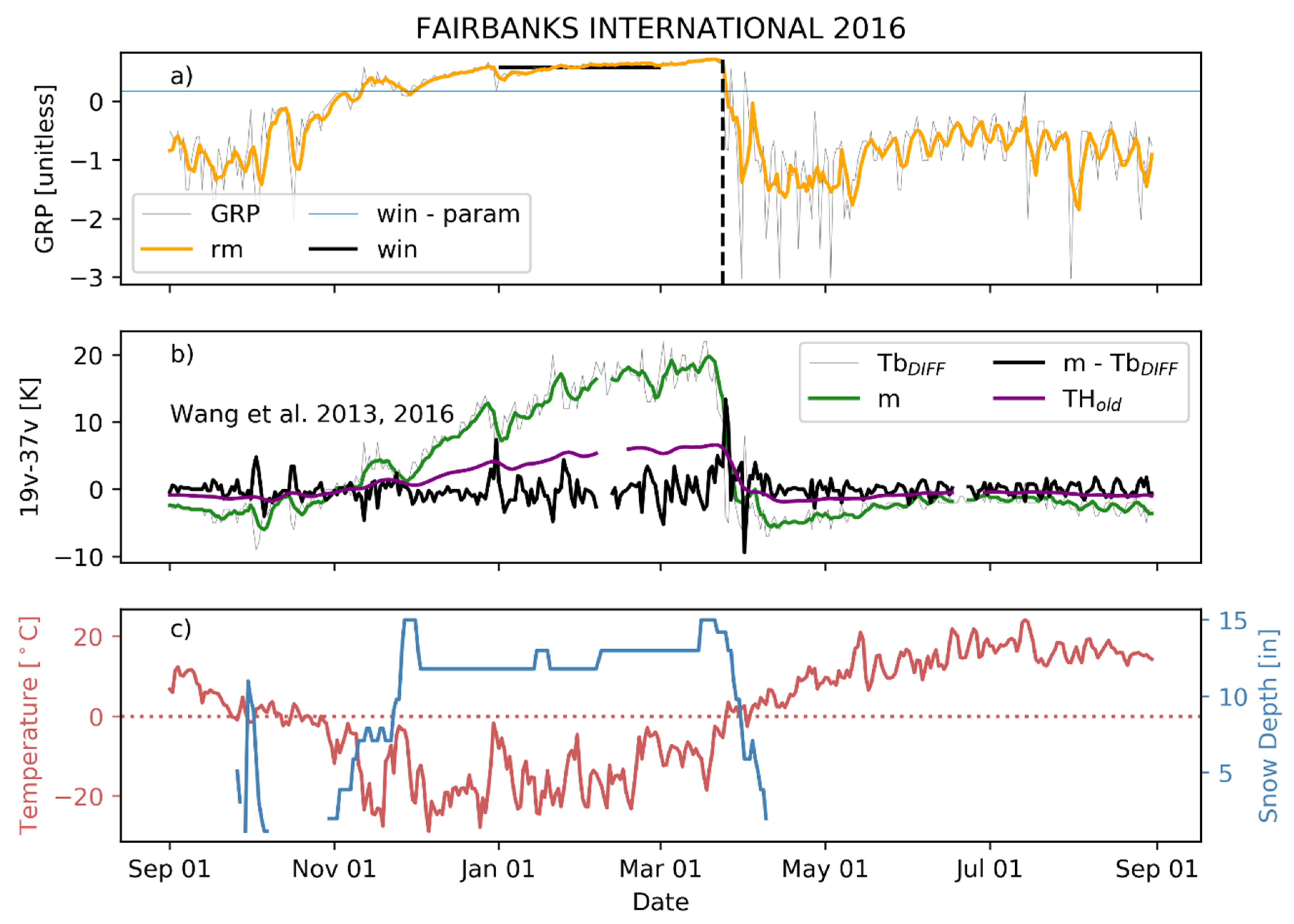
2.4. Deriving MMOD
2.5. MMOD Validation and Evaluation
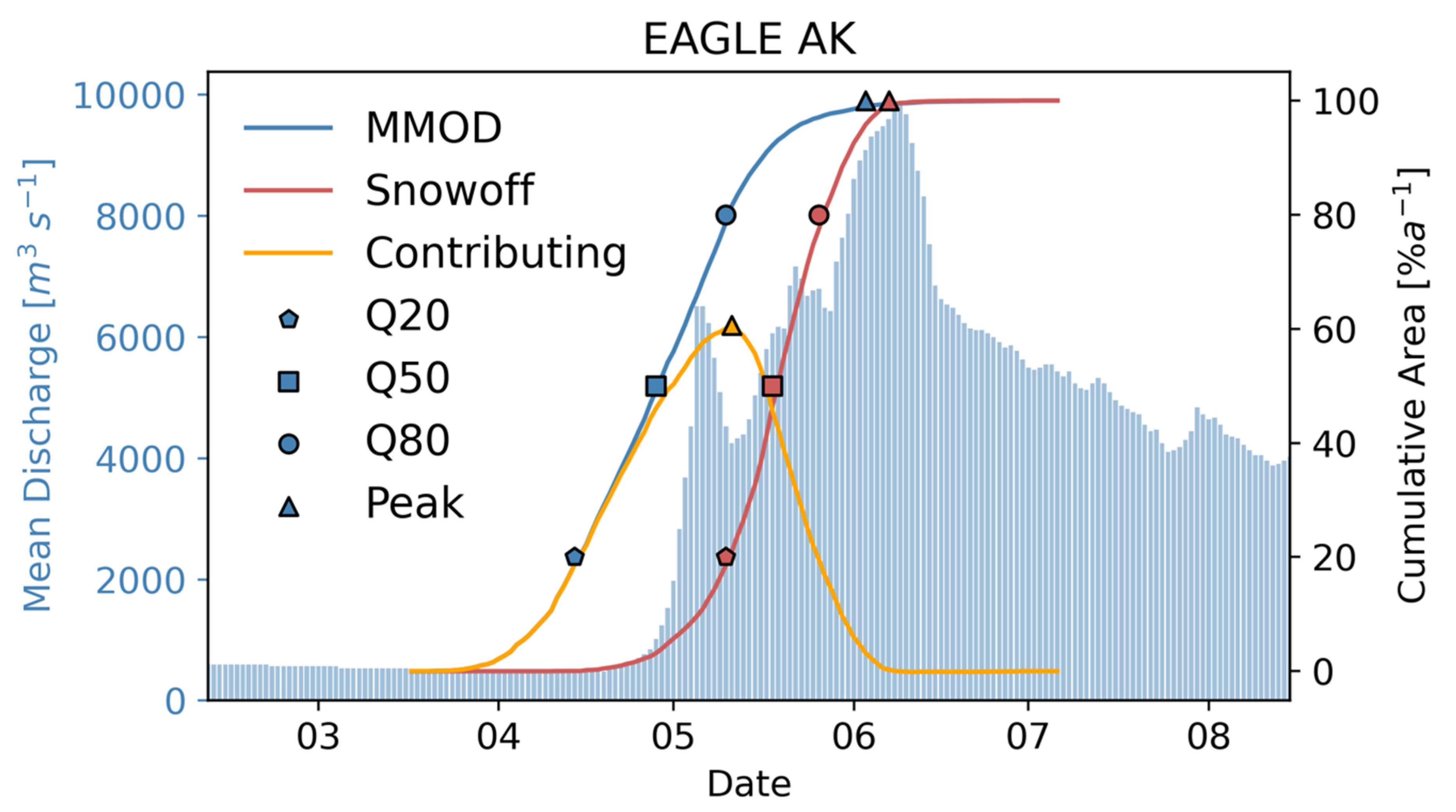
2.6. Snow and Streamflow Indices in the Yukon River Basin
2.7. Snow and River Ice Breakup in the Yukon River Basin
3. Results
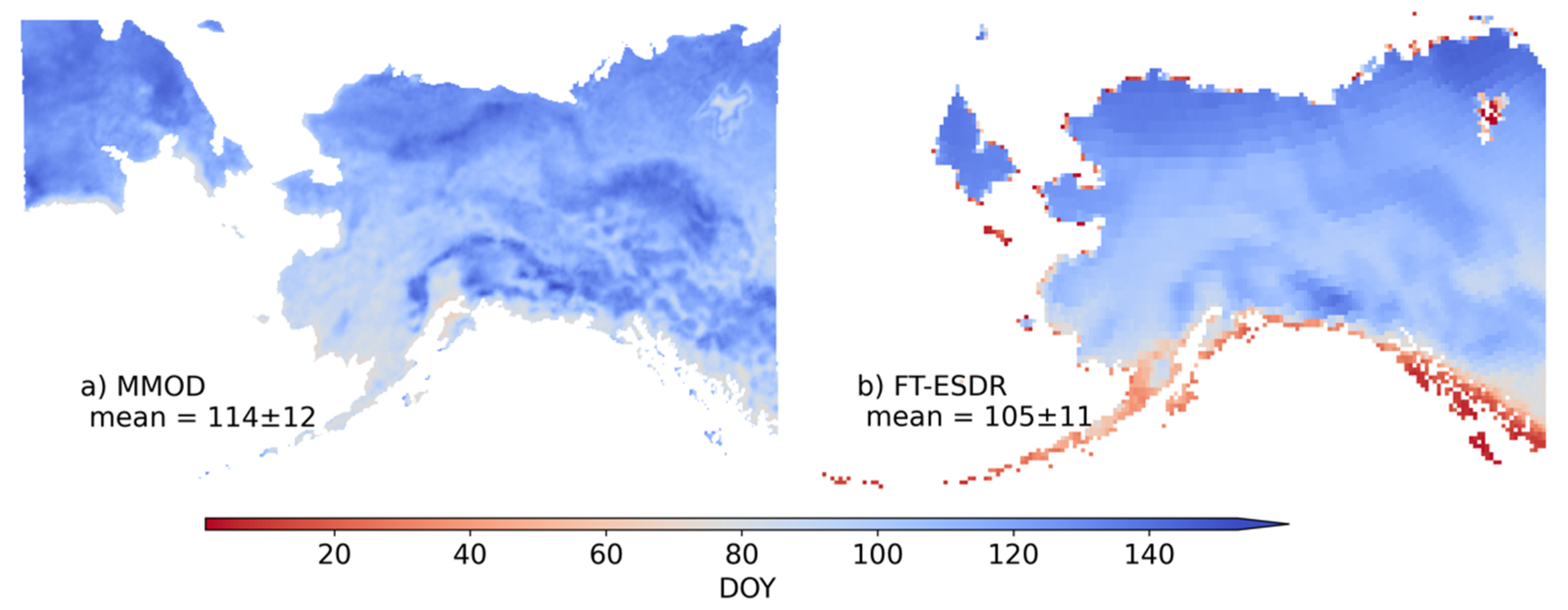
3.1. MMOD Classification Accuracy
3.2. Snow Metric Distribution in the YRB
3.3. Streamflow and River Ice Breakup
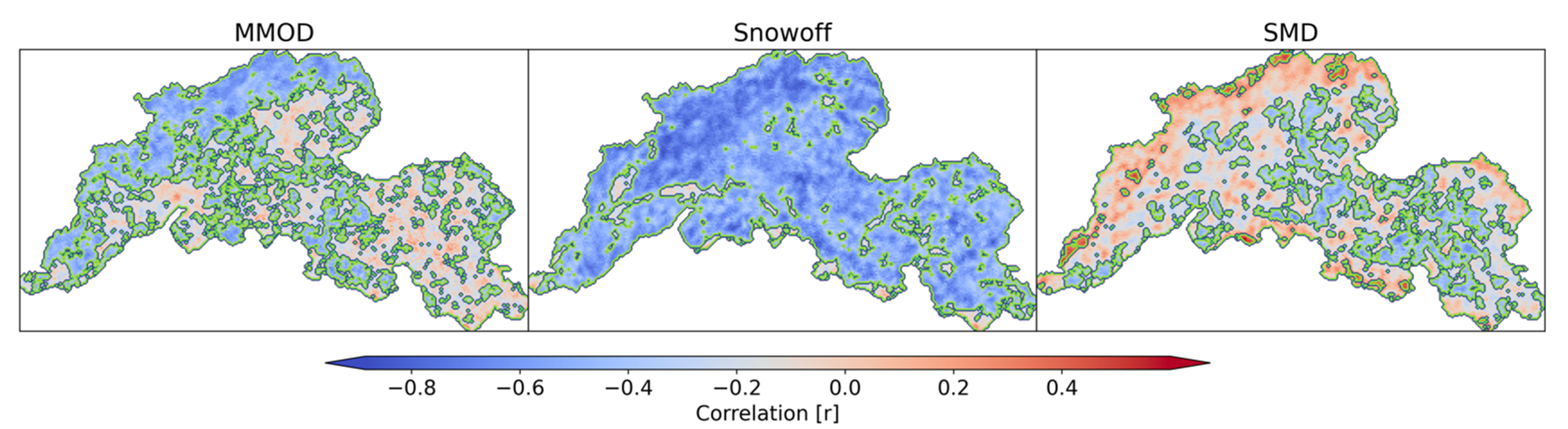
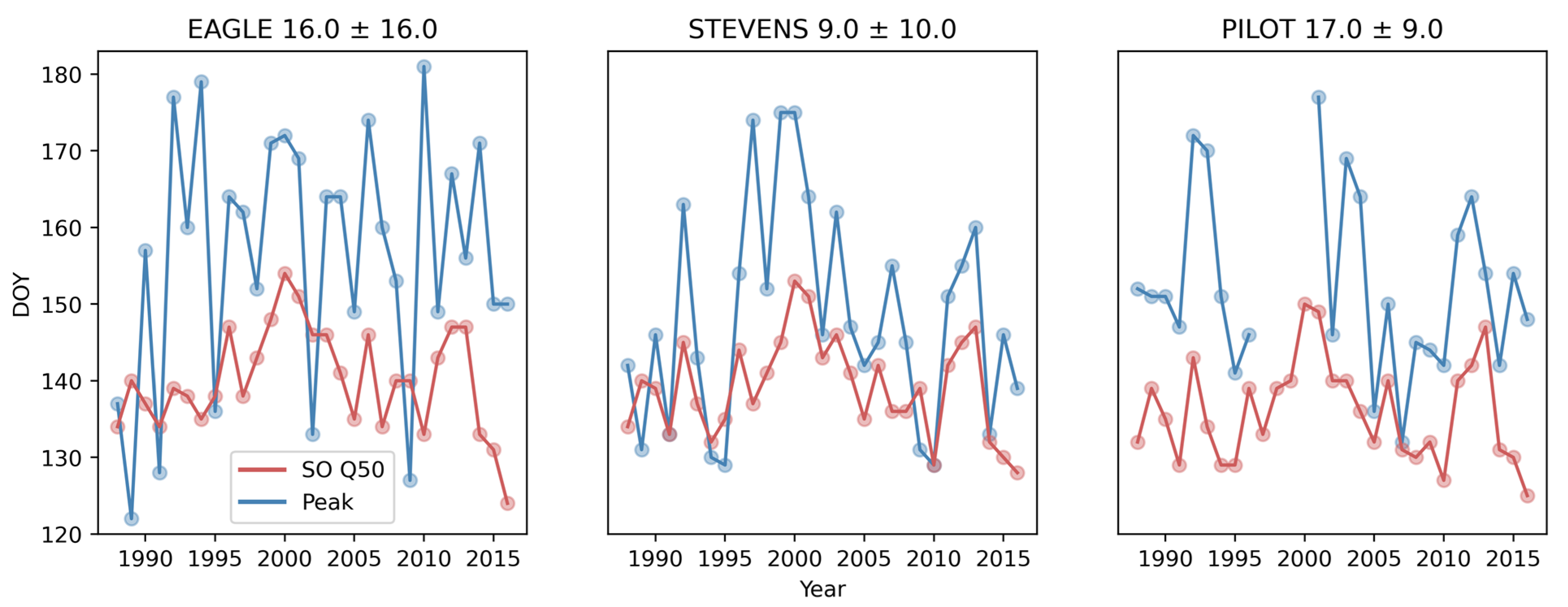
3.3.1. Interaction between Snow Metrics and Discharge in the YRB
3.3.2. Interaction between Snow Metrics and River Ice Breakup in the YRB
4. Discussion
4.1. MMOD Algorithm Performance
4.2. Changes in Snowmelt Properties
4.3. Snow and Hydrologic Interactions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Name | Period of Record | Latitude | Longitude | FW [%] | FF [%] | |
|---|---|---|---|---|---|---|
| Start | End | |||||
| ANCHOR RIVER DIVIDE | 2007 | 2020 | 59.86 | −151.32 | 23.17 | 20 |
| BETTLES FIELD | 2011 | 2020 | 66.92 | −151.53 | 0.81 | 19 |
| COLDFOOT | 2003 | 2020 | 67.25 | −150.18 | 0.60 | 15 |
| FAIRBANKS F.O. | 2011 | 2020 | 64.85 | −147.80 | 1.11 | 11 |
| GRANITE CRK | 2003 | 2020 | 63.94 | −145.40 | 1.83 | 37 |
| GRANDVIEW | 2003 | 2020 | 60.61 | −149.06 | 8.70 | 48 |
| INDEPENDENCE MINE | 2007 | 2020 | 61.79 | −149.28 | 3.79 | 0 |
| KENAI MOOSE PENS | 2003 | 2020 | 60.73 | −150.48 | 31.02 | 45 |
| LITTLE CHENA RIDGE | 2003 | 2020 | 65.12 | −146.73 | 0.34 | 14 |
| MONUMENT CREEK | 2003 | 2020 | 65.08 | −145.87 | 0.26 | 3 |
| MUNSON RIDGE | 2003 | 2020 | 64.85 | −146.21 | 0.22 | 4 |
| MT. RYAN | 2003 | 2020 | 65.25 | −146.15 | 0.30 | 5 |
| POINT MACKENZIE | 2003 | 2015 | 61.39 | −150.03 | 17.84 | 33 |
| MAY CREEK | 2009 | 2020 | 61.35 | −142.71 | 4.05 | 55 |
| SUMMIT CREEK | 2003 | 2020 | 60.62 | −149.53 | 7.28 | 31 |
| SUSITNA VALLEY HIGH | 2003 | 2020 | 62.13 | −150.04 | 2.34 | 34 |
| TEUCHET CREEK | 2003 | 2020 | 64.95 | −145.52 | 0.23 | 29 |
| TOKOSITNA VALLEY | 2007 | 2020 | 62.63 | −150.78 | 3.35 | 35 |
| TURNAGAIN PASS | 2003 | 2020 | 60.78 | −149.18 | 10.37 | 24 |
| UPPER TSAINA RIVER | 2009 | 2020 | 61.19 | −145.65 | 5.59 | 4 |
Appendix B
| Location | Longitude [dd] | Latitude [dd] | Start | End | Obs | Basin |
|---|---|---|---|---|---|---|
| Koyukuk River at Allakaket | −152.64 | 66.57 | 1988 | 2017 | 28 | Pilot |
| Koyukuk River at Bettles | −151.51 | 66.93 | 1988 | 2017 | 30 | Pilot |
| Koyukuk River at Hughes | −154.26 | 66.05 | 1988 | 2017 | 25 | Pilot |
| Yukon River at Anvik | −160.19 | 62.66 | 1988 | 2017 | 28 | Pilot |
| Yukon River at Beaver | −147.39 | 66.36 | 1997 | 2017 | 21 | Stevens |
| Yukon River at Circle | −144.06 | 65.83 | 1988 | 2017 | 29 | Stevens |
| Yukon River at Dawson | −139.43 | 64.07 | 1988 | 2017 | 30 | Eagle |
| Yukon River at Eagle | −141.33 | 64.79 | 1988 | 2017 | 30 | Eagle |
| Yukon River at Fort Yukon | −145.28 | 66.56 | 1988 | 2017 | 29 | Stevens |
| Yukon River at Galena | −156.9 | 64.74 | 1988 | 2017 | 30 | Pilot |
| Yukon River at Holy Cross | −159.77 | 62.21 | 1988 | 2017 | 28 | Pilot |
| Yukon River at Kaltag | −158.73 | 64.33 | 1988 | 2017 | 27 | Pilot |
| Yukon River at Marshall | −162.09 | 61.88 | 1988 | 2017 | 21 | Pilot |
| Yukon River at Nulato | −158.1 | 64.72 | 1997 | 2017 | 21 | Pilot |
| Yukon River at Rampart | −150.17 | 65.51 | 1996 | 2017 | 20 | Pilot |
| Yukon River at Ruby | −155.48 | 64.74 | 1988 | 2017 | 30 | Pilot |
| Yukon River at Russian Mission | −161.32 | 61.78 | 1988 | 2017 | 28 | Pilot |
| Yukon River at Stevens Village | −149.72 | 65.88 | 1998 | 2017 | 18 | Stevens |
| Yukon River at Tanana | −152.07 | 65.17 | 1988 | 2017 | 28 | Pilot |
Appendix C
| Snow Variable | Meanr | Minr | Maxr | Significant Variables | Basin |
|---|---|---|---|---|---|
| Contribution Peak | 0.565 | 0.55 | 0.58 | [’Peak’, ’Q20 ’] | PILOT |
| MMOD Q50 | 0.41 | 0.4 | 0.42 | [’Peak’, ’Q20 ’] | PILOT |
| MMOD Q80 | 0.49 | 0.4 | 0.58 | [’Peak’, ’Q20 ’] | PILOT |
| SO Q20 | 0.5 | 0.48 | 0.52 | [’Peak’, ’Q20 ’] | PILOT |
| SO Q50 | 0.59 | 0.55 | 0.63 | [’Peak’, ’Q20 ’] | PILOT |
| SO Q80 | 0.47 | 0.47 | 0.47 | [’Peak’] | PILOT |
| Contribution Peak | 0.655 | 0.64 | 0.67 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| MMOD Peak | 0.455 | 0.4 | 0.51 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| MMOD Q20 | 0.39 | 0.37 | 0.41 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| MMOD Q50 | 0.58 | 0.58 | 0.58 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| MMOD Q80 | 0.68 | 0.65 | 0.71 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| SO Peak | 0.475 | 0.38 | 0.57 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| SO Q20 | 0.675 | 0.67 | 0.68 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| SO Q50 | 0.675 | 0.64 | 0.71 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| SO Q80 | 0.59 | 0.52 | 0.66 | [’Peak’, ’Q20 ’] | STEVENS VILLAGE |
| Contribution Peak | 0.6 | 0.6 | 0.6 | [’Q20 ’] | EAGLE |
| MMOD Q20 | 0.5 | 0.5 | 0.5 | [’Q20 ’] | EAGLE |
| MMOD Q50 | 0.48 | 0.48 | 0.48 | [’Q20 ’] | EAGLE |
| MMOD Q80 | 0.47 | 0.47 | 0.47 | [’Q20 ’] | EAGLE |
| SO Q20 | 0.61 | 0.61 | 0.61 | [’Q20 ’] | EAGLE |
| SO Q50 | 0.49 | 0.49 | 0.49 | [’Q20 ’] | EAGLE |
| SO Q80 | 0.46 | 0.46 | 0.46 | [’Q20 ’] | EAGLE |
Appendix D
| Station | Metric | Cor | Pval | Nobs | Meansnow | Meanri | Dif |
|---|---|---|---|---|---|---|---|
| Koyukuk River at Allakaket | mmod | 0.6 | 0.001 | 26 | 112.50 | 130.19 | −17.69 |
| Koyukuk River at Bettles | mmod | 0.42 | 0.023 | 29 | 109.72 | 129.38 | −19.66 |
| Koyukuk River at Hughes | mmod | 0.36 | 0.085 | 24 | 106.67 | 130.08 | −23.42 |
| Yukon River at Anvik | mmod | 0.42 | 0.035 | 25 | 91.92 | 135.00 | −43.08 |
| Yukon River at Beaver | mmod | 0.75 | 0 | 20 | 108.20 | 130.10 | −21.90 |
| Yukon River at Circle | mmod | 0.12 | 0.559 | 28 | 111.00 | 128.71 | −17.71 |
| Yukon River at Dawson | mmod | 0.4 | 0.034 | 29 | 110.48 | 123.97 | −13.48 |
| Yukon River at Eagle | mmod | 0.45 | 0.014 | 29 | 111.83 | 123.66 | −11.83 |
| Yukon River at Fort Yukon | mmod | 0.15 | 0.457 | 28 | 105.00 | 129.50 | −24.50 |
| Yukon River at Galena | mmod | 0.41 | 0.029 | 29 | 101.79 | 131.34 | −29.55 |
| Yukon River at Holy Cross | mmod | 0.46 | 0.018 | 26 | 91.73 | 134.27 | −42.54 |
| Yukon River at Kaltag | mmod | 0.17 | 0.396 | 26 | 94.00 | 133.31 | −39.31 |
| Yukon River at Marshall | mmod | 0.34 | 0.141 | 20 | 91.40 | 134.45 | −43.05 |
| Yukon River at Nulato | mmod | 0.62 | 0.004 | 20 | 98.85 | 132.35 | −33.50 |
| Yukon River at Rampart | mmod | 0.36 | 0.125 | 19 | 112.89 | 131.79 | −18.89 |
| Yukon River at Ruby | mmod | 0.48 | 0.019 | 24 | 97.38 | 130.04 | −32.67 |
| Yukon River at Russian Mission | mmod | 0.25 | 0.214 | 26 | 85.42 | 134.12 | −48.69 |
| Yukon River at Stevens Village | mmod | 0.32 | 0.217 | 17 | 111.94 | 130.88 | −18.94 |
| Yukon River at Tanana | mmod | 0.11 | 0.596 | 25 | 102.60 | 128.88 | −26.28 |
| Koyukuk River at Allakaket | smd | −0.02 | 0.929 | 26 | 22.88 | 130.19 | −107.31 |
| Koyukuk River at Bettles | smd | 0.18 | 0.346 | 29 | 24.86 | 129.38 | −104.52 |
| Koyukuk River at Hughes | smd | −0.03 | 0.881 | 24 | 24.96 | 130.08 | −105.13 |
| Yukon River at Anvik | smd | 0.18 | 0.384 | 25 | 33.88 | 135.00 | −101.12 |
| Yukon River at Beaver | smd | −0.25 | 0.292 | 20 | 22.35 | 130.10 | −107.75 |
| Yukon River at Circle | smd | 0.42 | 0.024 | 28 | 22.25 | 128.71 | −106.46 |
| Yukon River at Dawson | smd | −0.15 | 0.43 | 29 | 21.76 | 123.97 | −102.21 |
| Yukon River at Eagle | smd | 0.05 | 0.792 | 29 | 22.31 | 123.66 | −101.34 |
| Yukon River at Fort Yukon | smd | 0.16 | 0.424 | 28 | 24.36 | 129.50 | −105.14 |
| Yukon River at Galena | smd | −0.21 | 0.279 | 29 | 27.69 | 131.34 | −103.66 |
| Yukon River at Holy Cross | smd | 0.4 | 0.042 | 26 | 33.73 | 134.27 | −100.54 |
| Yukon River at Kaltag | smd | 0.36 | 0.07 | 26 | 34.27 | 133.31 | −99.04 |
| Yukon River at Marshall | smd | 0.16 | 0.51 | 20 | 35.55 | 134.45 | −98.90 |
| Yukon River at Nulato | smd | −0.05 | 0.82 | 20 | 33.35 | 132.35 | −99.00 |
| Yukon River at Rampart | smd | 0.21 | 0.381 | 19 | 21.21 | 131.79 | −110.58 |
| Yukon River at Ruby | smd | 0.01 | 0.973 | 24 | 29.29 | 130.04 | −100.75 |
| Yukon River at Russian Mission | smd | 0.52 | 0.007 | 26 | 40.38 | 134.12 | −93.73 |
| Yukon River at Stevens Village | smd | 0.17 | 0.511 | 17 | 21.41 | 130.88 | −109.47 |
| Yukon River at Tanana | smd | −0.08 | 0.696 | 25 | 24.96 | 128.88 | −103.92 |
| Koyukuk River at Allakaket | snowoff | 0.78 | 0 | 26 | 134.08 | 130.19 | 3.88 |
| Koyukuk River at Bettles | snowoff | 0.7 | 0 | 29 | 134.66 | 129.38 | 5.28 |
| Koyukuk River at Hughes | snowoff | 0.48 | 0.018 | 24 | 131.38 | 130.08 | 1.29 |
| Yukon River at Anvik | snowoff | 0.7 | 0 | 25 | 125.40 | 135.00 | −9.60 |
| Yukon River at Beaver | snowoff | 0.81 | 0 | 20 | 130.20 | 130.10 | 0.10 |
| Yukon River at Circle | snowoff | 0.63 | 0 | 28 | 131.43 | 128.71 | 2.71 |
| Yukon River at Dawson | snowoff | 0.5 | 0.006 | 29 | 131.69 | 123.97 | 7.72 |
| Yukon River at Eagle | snowoff | 0.63 | 0 | 29 | 135.14 | 123.66 | 11.48 |
| Yukon River at Fort Yukon | snowoff | 0.34 | 0.08 | 28 | 130.93 | 129.50 | 1.43 |
| Yukon River at Galena | snowoff | 0.42 | 0.025 | 29 | 129.07 | 131.34 | −2.28 |
| Yukon River at Holy Cross | snowoff | 0.64 | 0 | 26 | 125.04 | 134.27 | −9.23 |
| Yukon River at Kaltag | snowoff | 0.54 | 0.005 | 26 | 127.85 | 133.31 | −5.46 |
| Yukon River at Marshall | snowoff | 0.39 | 0.093 | 20 | 126.00 | 134.45 | −8.45 |
| Yukon River at Nulato | snowoff | 0.73 | 0 | 20 | 133.75 | 132.35 | 1.40 |
| Yukon River at Rampart | snowoff | 0.59 | 0.008 | 19 | 135.05 | 131.79 | 3.26 |
| Yukon River at Ruby | snowoff | 0.54 | 0.007 | 24 | 127.25 | 130.04 | −2.79 |
| Yukon River at Russian Mission | snowoff | 0.46 | 0.017 | 26 | 125.81 | 134.12 | −8.31 |
| Yukon River at Stevens Village | snowoff | 0.73 | 0.001 | 17 | 132.00 | 130.88 | 1.12 |
| Yukon River at Tanana | snowoff | 0.5 | 0.011 | 25 | 124.48 | 128.88 | −4.40 |
Appendix E
| Abbreviation | Description |
|---|---|
| MMOD | Main Melt Onset Date |
| SMD | Snow Melt Duration |
| SO | Snowoff Date |
| PMW | Passive Microwave |
| MMODPMW | MMOD derived from passive microwave observations |
| SMDPMW | SMD derived from passive microwave observations |
| SOPMW | SO derived from passive microwave observations |
| RIB | River ice breakup date |
| LWC | Liquid water content |
| Tb | Brightness temperature |
| GRP | Gradient Ratio Polarization |
| YRB | Yukon River Basin |
| DMSP | Defense Meteorological Satellite Program |
| NOAA | National Oceanic and Atmospheric Administration |
| SSM/I | Special Sensor Microwave/Imager |
| km | Kilometer |
| Ghz | Gigahertz |
| H | Horizontal |
| V | Vertical |
| MEaSUREs | Making Earth Data Systems Data Records for Use in Research |
| WY | Water year |
| FW | Fractional water |
| SNOTEL | Snow Telemetry |
| MMODT | MMOD detected from SNOTEL temperature |
| MMODSWE | MMOD detected from SNOTEL SWE |
| FT | Freeze/Thaw |
| GRDC | Global Runoff Database Centre |
| Q | Quantiles |
| DOY | Day of year |
| GLIMS | Global Land Ice Measurements from Space |
| JJA | June July August |
| AMSR | Advanced Microwave Scanning Radiometer |
| SNAP | Scenarios Network for Alaska and Arctic Planning |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| FF | Fractional Forest |
| Q20MMOD | MMOD Q20 |
| Q20Flow | Quantile derived from streamflow |
| Q20SO | SO Q20 |
References
- Barnhart, T.B.; Molotch, N.P.; Livneh, B.; Harpold, A.A.; Knowles, J.F.; Schneider, D. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 2016, 43, 8006–8016. [Google Scholar] [CrossRef]
- Clow, D.W. Changes in the timing of snowmelt and streamflow in Colorado: A response to recent warming. J. Clim. 2010, 23, 2293–2306. [Google Scholar] [CrossRef]
- Pederson, G.T.; Gray, S.T.; Ault, T.; Marsh, W.; Fagre, D.B.; Bunn, A.G.; Woodhouse, C.A.; Graumlich, L.J. Climatic controls on the snowmelt hydrology of the northern Rocky Mountains. J. Clim. 2011, 24, 1666–1687. [Google Scholar] [CrossRef]
- Adam, J.; Hamlet, A.; Lettenmaier, D. Implications of global climate change for snowmelt hydrology in the twenty-first century. Hydrol. Process. 2009, 23, 962–972. [Google Scholar] [CrossRef]
- Musselman, K.N.; Clark, M.P.; Liu, C.; Ikeda, K.; Rasmussen, R. Slower snowmelt in a warmer world. Nat. Clim. Chang. 2017, 7, 214–220. [Google Scholar] [CrossRef]
- Beltaos, S.; Prowse, T. River-ice hydrology in a shrinking cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Lesack, L.F.W.; Marsh, P.; Hicks, F.E.; Forbes, D.L. Local spring warming drives earlier river-ice breakup in a large Arctic Delta. Geophys. Res. Lett. 2014, 41, 1560–1566. [Google Scholar] [CrossRef]
- Semmens, K.A.; Ramage, J.M. Recent changes in spring snowmelt timing in the Yukon River basin detected by passive microwave satellite data. Cryosph. 2013, 7, 905–916. [Google Scholar] [CrossRef]
- Cold, H.S.; Brinkman, T.J.; Brown, C.L.; Hollingsworth, T.N.; Brown, D.R.N.; Heeringa, K.M. Assessing vulnerability of subsistence travel to effects of environmental change in interior Alaska. Ecol. Soc. 2020, 25. [Google Scholar] [CrossRef]
- Brown, D.R.N.; Brinkman, T.J.; Bolton, W.R.; Brown, C.L.; Cold, H.S.; Hollingsworth, T.N.; Verbyla, D.L. Implications of climate variability and changing seasonal hydrology for subarctic riverbank erosion. Clim. Change 2020. [Google Scholar] [CrossRef]
- Rokaya, P.; Budhathoki, S.; Lindenschmidt, K.E. Trends in the Timing and Magnitude of Ice-Jam Floods in Canada. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Callaghan, T.V.; Johansson, M.; Brown, R.D.; Groisman, P.Y.; Labba, N.; Radionov, V.; Barry, R.G.; Bulygina, O.N.; Essery, R.L.H.; Frolov, D.M.; et al. The Changing Face of Arctic Snow Cover: A Synthesis of Observed and Projected Changes. Ambio 2012, 17–31. [Google Scholar] [CrossRef]
- Serreze, M.C.; Barry, R.G. Process and impacts of Arctic amplification: A research synthesis. Glob. Planet. Change 2011, 77, 85–96. [Google Scholar] [CrossRef]
- Bieniek, P.A.; Walsh, J.E.; Thoman, R.L.; Bhatt, U.S. Using climate divisions to analyze variations and trends in Alaska temperature and precipitation. J. Clim. 2014, 27, 2800–2818. [Google Scholar] [CrossRef]
- Boelman, N.T.; Liston, G.E.; Gurarie, E.; Meddens, A.J.H.; Mahoney, P.J.; Kirchner, P.B.; Bohrer, G.; Brinkman, T.J.; Cosgrove, C.L.; Eitel, J.U.H.; et al. Integrating snow science and wildlife ecology in Arctic-boreal North America. Environ. Res. Lett. 2019, 14. [Google Scholar] [CrossRef]
- Naderpour, R.; Houtz, D.; Schwank, M. Snow wetness retrieved from close-range L-band radiometry in the western Greenland ablation zone. J. Glaciol. 2021, 67, 27–38. [Google Scholar] [CrossRef]
- Houtz, D.; Mätzler, C.; Naderpour, R.; Schwank, M.; Steffen, K. Quantifying Surface Melt and Liquid Water on the Greenland Ice Sheet using L-band Radiometry. Remote Sens. Environ. 2021, 256. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Jones, L.A.; Kim, Y.; Glassy, J.; Watts, J.D. A global satellite environmental data record derived from AMSR-E and AMSR2 microwave Earth observations. Earth Syst. Sci. Data 2017, 9, 791–808. [Google Scholar] [CrossRef]
- Tedesco, M.; Derksen, C.; Deems, J.S.; Foster, J.L. Remote sensing of snow depth and snow water equivalent. Remote Sens. Cryosph. 2015, 73–98. [Google Scholar] [CrossRef]
- Tedesco, M.; Miller, J. Observations and statistical analysis of combined active-passive microwave space-borne data and snow depth at large spatial scales. Remote Sens. Environ. 2007, 111, 382–397. [Google Scholar] [CrossRef]
- Ramage, J.M.; Isacks, B.L. Determination of melt-onset and refreeze timing on southeast Alaskan icefields using SSM/I diurnal amplitude variations. Ann. Glaciol. 2002, 34, 391–398. [Google Scholar] [CrossRef]
- Wang, L.; Toose, P.; Brown, R.; Derksen, C. Frequency and distribution of winter melt events from passive microwave satellite data in the pan-Arctic, 1988-2013. Cryosphere 2016, 10, 2589–2602. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Glassy, J.; Du, J. An extended global Earth system data record on daily landscape freeze – thaw status determined from satellite passive microwave remote sensing. Earch Syst. Sci. Data 2017, 9, 133–147. [Google Scholar] [CrossRef]
- Pan, C.G.; Kirchner, P.B.; Kimball, J.S.; Kim, Y.; Du, J. Rain-on-snow events in Alaska, their frequency and distribution from satellite observations. Environ. Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Pan, C.G.; Kimball, J.S.; Munkhjargal, M.; Robinson, N.P.; Tijdeman, E.; Menzel, L.; Kirchner, P.B. Role of Surface Melt and Icing Events in Livestock Mortality across Mongolia’s Semi-Arid Landscape. Remote Sens. 2019, 11, 2392. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Koskinen, J.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Lindsay, C.; Zhu, J.; Miller, A.E.; Kirchner, P.; Wilson, T.L. Deriving snow cover metrics for Alaska from MODIS. Remote Sens. 2015, 7, 12961–12985. [Google Scholar] [CrossRef]
- Pan, C.G.; Kirchner, P.B.; Kimball, J.S.; Du, J. A Long-Term Passive Microwave Snowoff Record for the Alaska Region 1988 – 2016. Remote Sens. 2020, 12, 153. [Google Scholar] [CrossRef]
- Steiner, N.; Tedesco, M. A wavelet melt detection algorithm applied to enhanced-resolution scatterometer data over Antarctica (2000-2009). Cryosphere 2014, 8, 25–40. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Robinson, D.A.; Derksen, C. New satellite climate data records indicate strong coupling between recent frozen season changes and snow cover over high northern latitudes. Environ. Res. Lett. 2015, 10, 1–10. [Google Scholar] [CrossRef]
- Rawlins, M.A.; McDonald, K.C.; Frolking, S.; Lammers, R.B.; Fahnestock, M.; Kimball, J.S.; Vörösmarty, C.J. Remote sensing of snow thaw at the pan-Arctic scale using the SeaWinds scatterometer. J. Hydrol. 2005, 312, 294–311. [Google Scholar] [CrossRef]
- Brabets, T.P.; Wang, B.; Meade, R.H. Environmental and hydrologic overview of the Yukon River basin, Alaska and Canada. USGS Water-Resources Investig. Rep. 2000, 99, 1–114. [Google Scholar]
- Brodzik, M.J.; Long, D.G.; Harman, A.; Page, A.; Armstong, R. Updated 2020. MEaSUREs Calibrated Enhanced-Resolution Passive Microwave Daily EASE-Grid 2.0 Brightness Temperature ESDR, Version 1. Available online: https://nsidc.org/data/nsidc-0630/versions/1 (accessed on 30 August 2020).
- Long, D.G.; Brodzik, M.J. Optimum Image Formation for Spaceborne Microwave Radiometer Products. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2763–2779. [Google Scholar] [CrossRef] [PubMed]
- Brodzik, M.; Long, D.; Hardman, M. Best Practices in Crafting the Calibrated, Enhanced-Resolution Passive-Microwave EASE-Grid 2.0 Brightness Temperature Earth System Data Record. Remote Sens. 2018, 10, 1793. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Jones, L.A.; Watts, J.D. Implementation of satellite based fractional water cover indices in the pan-Arctic region using AMSR-E and MODIS. Remote Sens. Environ. 2016, 184, 469–481. [Google Scholar] [CrossRef]
- Carroll, M.; Townshend, J.; Hansen, M.; DiMiceli, C.; Sohlberg, R.; Wurster, K. MODIS Vegetative Cover Conversion and Vegetation Continuous Fields BT - Land Remote Sensing and Global Environmental Change: NASA’s Earth Observing System and the Science of ASTER and MODIS. In Remote Sensing and Digital Image Processing; Ramachandran, B., Justice, C.O., Abrams, M.J., Eds.; Springer: New York, NY, USA, 2011; pp. 725–745. ISBN 978-1-4419-6749-7. [Google Scholar]
- Cai, L.; Alexeev, V.A.; Arp, C.D.; Jones, B.M.; Liljedahl, A.K.; Gädeke, A. The polar WRF downscaled historical and projected twenty-first century climate for the coast and foothills of arctic alaska. Front. Earth Sci. 2018, 5, 1–15. [Google Scholar] [CrossRef]
- Dolant, C.; Langlois, A.; Montpetit, B.; Brucker, L.; Roy, A.; Royer, A. Development of a rain-on-snow detection algorithm using passive microwave radiometry. Hydrol. Process. 2016, 30, 3184–3196. [Google Scholar] [CrossRef]
- Wang, L.; Derksen, C.; Brown, R.; Markus, T. Recent changes in pan-Arctic melt onset from satellite passive microwave measurements. Geophys. Res. Lett. 2013, 40, 522–528. [Google Scholar] [CrossRef]
- Wang, K.; Jafarov, E.; Overeem, I.; Romanovsky, V.; Schaefer, K.; Clow, G.; Urban, F.; Cable, W.; Piper, M.; Schwalm, C.; et al. A synthesis dataset of permafrost-affected soil thermal conditions for Alaska, USA. Earth Syst. Sci. Data 2018, 10, 2311–2328. [Google Scholar] [CrossRef]
- Chen, X.; Liu, L.; Bartsch, A. Detecting soil freeze/thaw onsets in Alaska using SMAP and ASCAT data. Remote Sens. Environ. 2019, 220, 59–70. [Google Scholar] [CrossRef]
- Walsh, J.E.; Bieniek, P.A.; Brettschneider, B.; Euskirchen, E.S.; Lader, R.; Thoman, R.L. The exceptionally warm winter of 2015/16 in Alaska. J. Clim. 2017, 30, 2069–2088. [Google Scholar] [CrossRef]
- Musselman, K.N.; Lehner, F.; Ikeda, K.; Clark, M.P.; Prein, A.F.; Liu, C.; Barlage, M.; Rasmussen, R. Projected increases and shifts in rain-on-snow flood risk over western North America. Nat. Clim. Chang. 2018, 8. [Google Scholar] [CrossRef]
- Wu, X.; Che, T.; Li, X.; Wang, N.; Yang, X. Slower Snowmelt in Spring Along With Climate Warming Across the Northern Hemisphere. Geophys. Res. Lett. 2018, 45, 12,331–12,339. [Google Scholar] [CrossRef]
- Scalzitti, J.; Strong, C.; Kochanski, A. Climate change impact on the roles of temperature and precipitation in western U.S. snowpack variability. Geophys. Res. Lett. 2016, 43, 5361–5369. [Google Scholar] [CrossRef]
- Wang, L.; Derksen, C.; Brown, R. Detection of pan-Arctic terrestrial snowmelt from QuikSCAT, 2000-2005. Remote Sens. Environ. 2008, 112, 3794–3805. [Google Scholar] [CrossRef]
- Derksen, C.; Brown, R. Spring snow cover extent reductions in the 2008-2012 period exceeding climate model projections. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Dolant, C.; Langlois, A.; Brucker, L.; Royer, A.; Roy, A.; Montpetit, B. Meteorological inventory of rain-on-snow events in the Canadian Arctic Archipelago and satellite detection assessment using passive microwave data. Phys. Geogr. 2017, 3646, 1–17. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in snowmelt runoff timing using a ‘business as usual’ climate change scenario. Clim. Change 2004, 62, 217–232. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Smith, L.C. Spatial and temporal patterns in Arctic river ice breakup observed with MODIS and AVHRR time series. Remote Sens. Environ. 2004, 93, 328–338. [Google Scholar] [CrossRef]
- Bormann, K.J.; Brown, R.D.; Derksen, C.; Painter, T.H. Estimating snow-cover trends from space. Nat. Clim. Chang. 2018, 8, 924–928. [Google Scholar] [CrossRef]
- Park, H.; Yoshikawa, Y.; Oshima, K.; Kim, Y.; Ngo-Duc, T.; Kimball, J.S.; Yang, D. Quantification of warming climate-induced changes in terrestrial Arctic river ice thickness and phenology. J. Clim. 2016, 29, 1733–1754. [Google Scholar] [CrossRef]
- Bieniek, P.A.; Bhatt, U.S.; Rundquist, L.A.; Lindsey, S.D.; Zhang, X.; Thoman, R.L. Large-scale climate controls of interior Alaska river ice breakup. J. Clim. 2011, 24, 286–297. [Google Scholar] [CrossRef]



| Dataset | Spatial Resolution | Period of Record | Use | Reference/Source |
|---|---|---|---|---|
| PMW | 6.25 km | 1988–2016 | MMOD | Brodzik et al. 2018 |
| Snowoff | 6.25 km | 1988–2016 | SO, SMD Analysis | Pan et al. 2020 |
| FW | 6.25 km | 2003–2015 | MMOD/Validation | Du et al. 2017 |
| FF | 250 m | 2011 | Validation | Carroll et al. 2011 |
| WRF Reanalysis | 20 km | 1988–2015 | Climate Analysis | SNAP UAF |
| SNOTEL | in situ | 2004–2016 | Validation | NRCS |
| Streamflow | in situ | 1988–2016 | Streamflow Analysis | GRDC |
| River Ice Observations | in situ | 1988–2016 | RIB Analysis | NWS |
| Snow Variables | Correlation [r] | Significant Variables | Basin | ||
|---|---|---|---|---|---|
| Mean | Minimum | Maximum | |||
| MMOD Q20 | 0.5 | 0.5 | 0.5 | [’Q20 ’] | EAGLE |
| SO Q20 | 0.61 | 0.61 | 0.61 | [’Q20 ’] | EAGLE |
| Contribution Peak | 0.6 | 0.6 | 0.6 | [’Q20 ’] | EAGLE |
| MMOD Q80 | 0.68 | 0.65 | 0.71 | [’Peak’, ’Q20’] | STEVENS VILLAGE |
| SO Q50 | 0.675 | 0.64 | 0.71 | [’Peak’, ’Q20’] | STEVENS VILLAGE |
| SO Q80 | 0.59 | 0.52 | 0.66 | [’Peak’, ’Q20’] | STEVENS VILLAGE |
| MMOD Q50 | 0.41 | 0.4 | 0.42 | [’Peak’, ’Q20’] | PILOT |
| MMOD Q80 | 0.49 | 0.4 | 0.58 | [’Peak’, ’Q20’] | PILOT |
| SO Q20 | 0.5 | 0.48 | 0.52 | [’Peak’, ’Q20’] | PILOT |
| SO Q50 | 0.59 | 0.55 | 0.63 | [’Peak’, ’Q20’] | PILOT |
| Station | Metric | Correlation [r] | Pvalue | Observations | Snow Metric [DOY] | Observed RIB [DOY] | Difference [Days] |
|---|---|---|---|---|---|---|---|
| Allakaket | mmod | 0.6 | 0.001 | 26 | 112.5 | 130.19 | −17.69 |
| Beaver | mmod | 0.75 | 0 | 20 | 108.2 | 130.1 | −21.9 |
| Nulato | mmod | 0.62 | 0.004 | 20 | 98.85 | 132.35 | −33.5 |
| Beaver | snowoff | 0.81 | 0 | 20 | 130.2 | 130.1 | 0.1 |
| Circle | snowoff | 0.63 | 0 | 28 | 131.43 | 128.71 | 2.71 |
| Eagle | snowoff | 0.63 | 0 | 29 | 135.14 | 123.66 | 11.48 |
| Holy Cross | snowoff | 0.64 | 0 | 26 | 125.04 | 134.27 | −9.23 |
| Russian Mission | smd | 0.52 | 0.007 | 26 | 40.38 | 134.12 | −93.73 |
| Circle | smd | 0.42 | 0.024 | 28 | 22.25 | 128.71 | −106.46 |
| Holy Cross | smd | 0.4 | 0.042 | 26 | 33.73 | 134.27 | −100.54 |
| Kaltag | smd | 0.36 | 0.07 | 26 | 34.27 | 133.31 | −99.04 |
| Snow Metric | Basin | Correlation [r] | Pvalue | Observations | Mean RIB [DOY] | Mean Snow Metric [DOY] |
|---|---|---|---|---|---|---|
| mmodq20 | Bettles | 0.77 | 0 | 29 | 129 | 121 |
| mmodq20 | Galena | 0.48 | 0.008 | 29 | 131 | 102 |
| mmodq50 | Allakaket | 0.79 | 0 | 26 | 130 | 122 |
| mmodq50 | Eagle | 0.37 | 0.051 | 29 | 124 | 115 |
| Contribution Peak | Allakaket | 0.78 | 0 | 26 | 130 | 133 |
| Contribution Peak | Bettles | 0.75 | 0 | 29 | 129 | 139 |
| Contribution Peak | Dawson | 0.5 | 0.005 | 29 | 124 | 128 |
| Contribution Peak | Eagle | 0.43 | 0.021 | 29 | 124 | 128 |
| Contribution Peak | Hughes | 0.81 | 0 | 24 | 130 | 131 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, C.G.; Kirchner, P.B.; Kimball, J.S.; Du, J.; Rawlins, M.A. Snow Phenology and Hydrologic Timing in the Yukon River Basin, AK, USA. Remote Sens. 2021, 13, 2284. https://doi.org/10.3390/rs13122284
Pan CG, Kirchner PB, Kimball JS, Du J, Rawlins MA. Snow Phenology and Hydrologic Timing in the Yukon River Basin, AK, USA. Remote Sensing. 2021; 13(12):2284. https://doi.org/10.3390/rs13122284
Chicago/Turabian StylePan, Caleb G., Peter B. Kirchner, John S. Kimball, Jinyang Du, and Michael A. Rawlins. 2021. "Snow Phenology and Hydrologic Timing in the Yukon River Basin, AK, USA" Remote Sensing 13, no. 12: 2284. https://doi.org/10.3390/rs13122284
APA StylePan, C. G., Kirchner, P. B., Kimball, J. S., Du, J., & Rawlins, M. A. (2021). Snow Phenology and Hydrologic Timing in the Yukon River Basin, AK, USA. Remote Sensing, 13(12), 2284. https://doi.org/10.3390/rs13122284






