Global Sensitivity Analysis for Canopy Reflectance and Vegetation Indices of Mangroves
Abstract
:1. Introduction
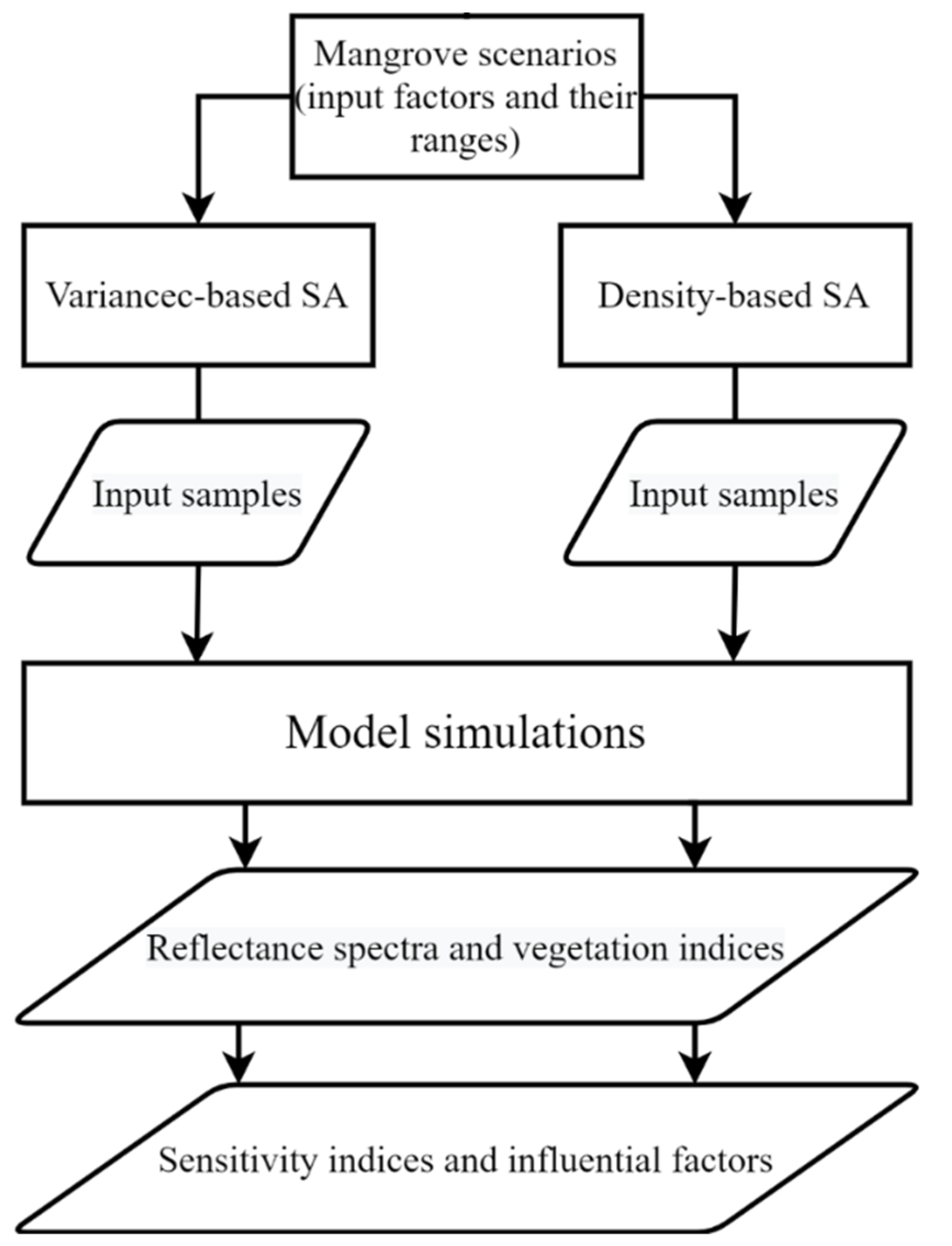
2. Methodology
2.1. Overview
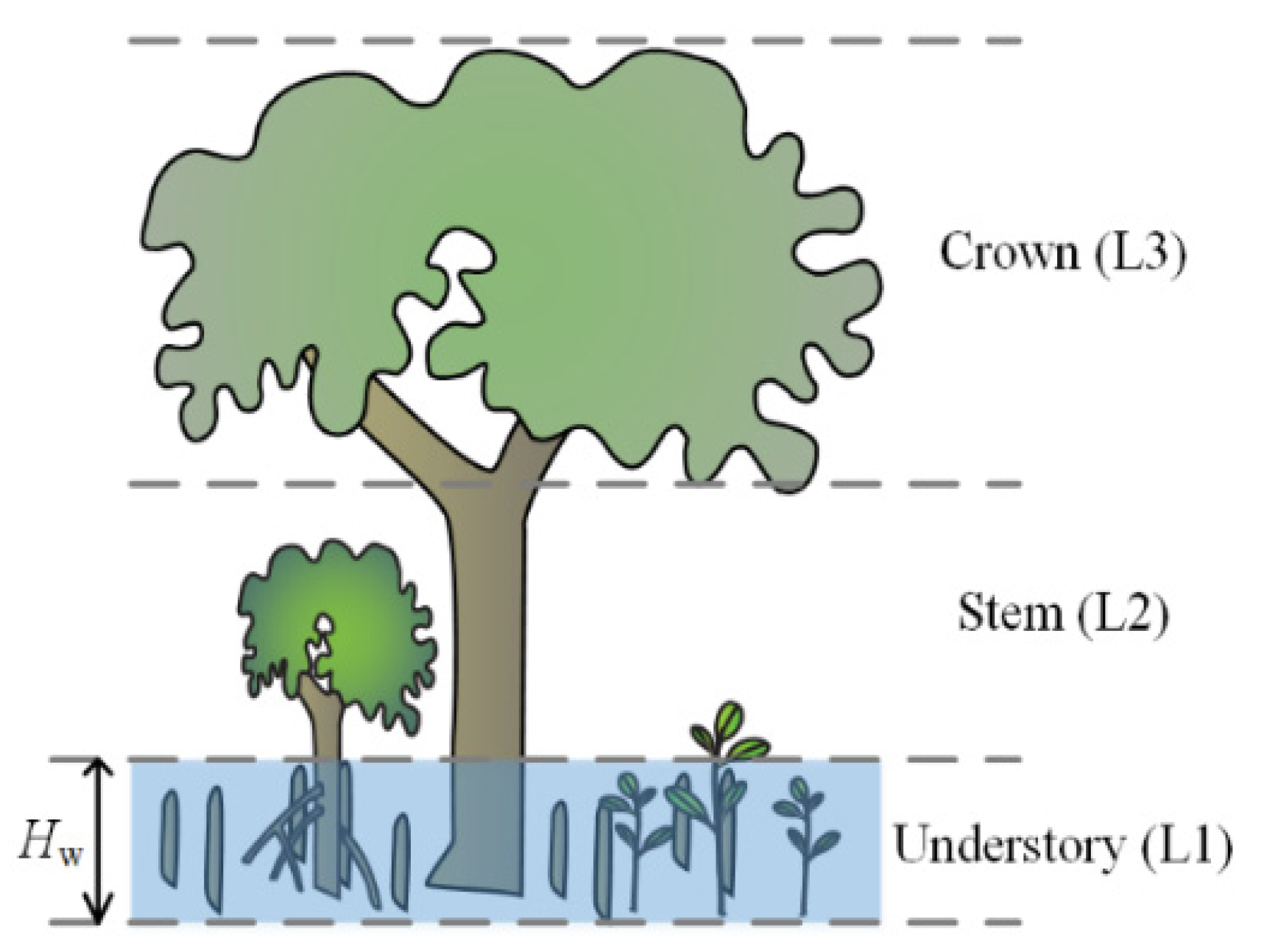
2.2. Canopy Reflectance Model of Mangroves
2.3. Mangrove Scenarios
2.3.1. Factors, Their Ranges and Distributions
2.3.2. Correlated PAI(3) and fCv(3)
2.4. Vegetation Indices
2.5. Sensitivity Analysis Methods
2.5.1. Variance-Based Sensitivity Analysis
2.5.2. Density-Based Sensitivity Analysis
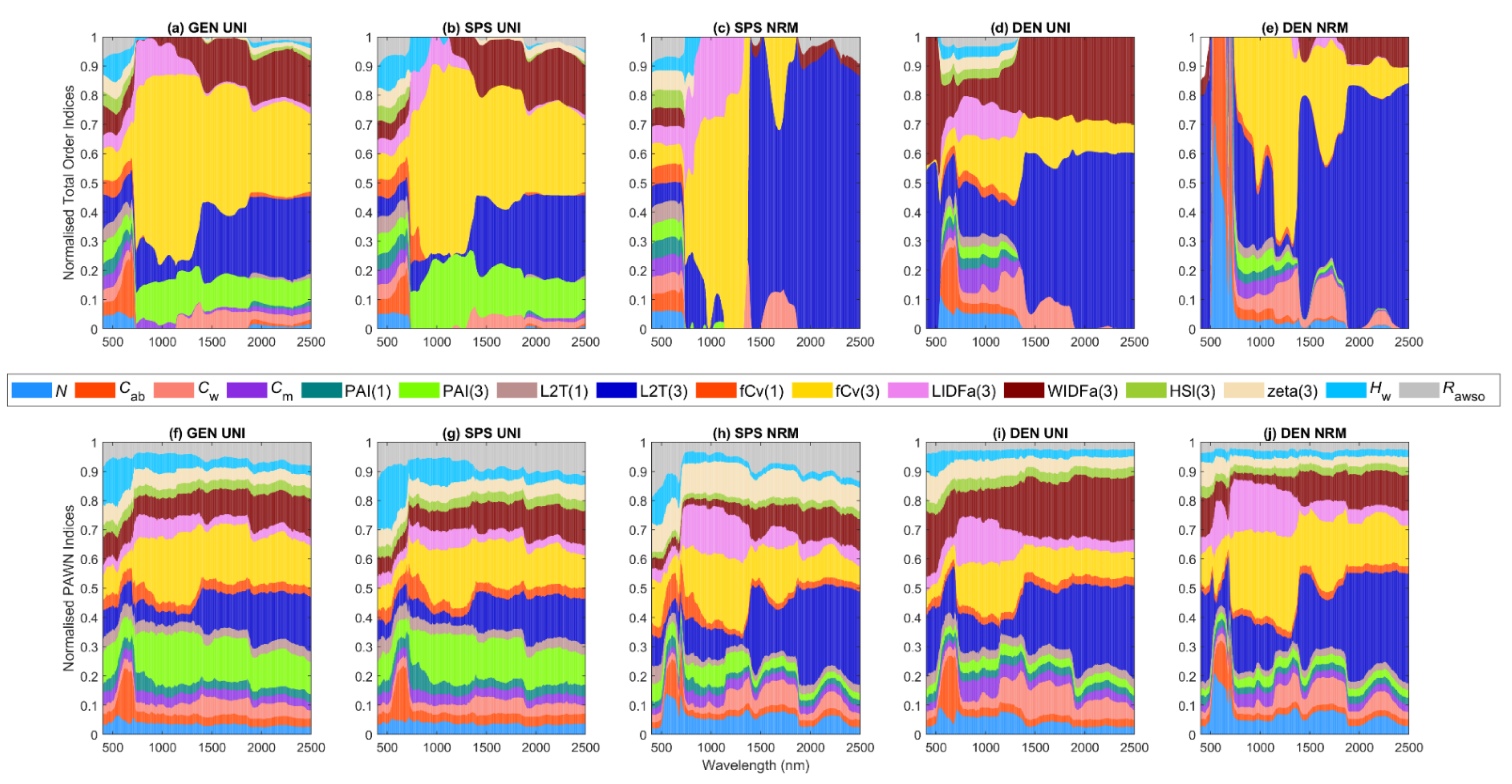
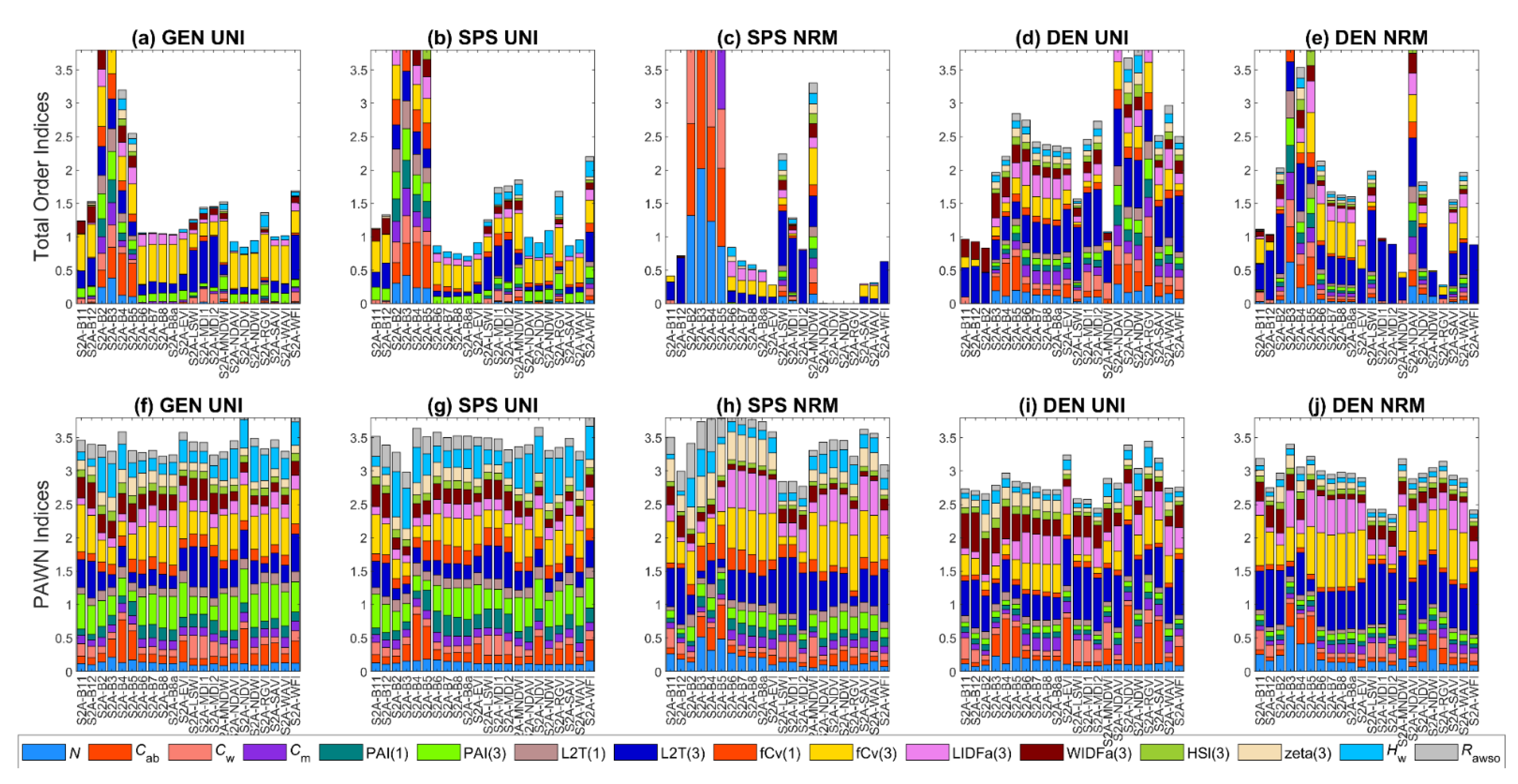
3. Results
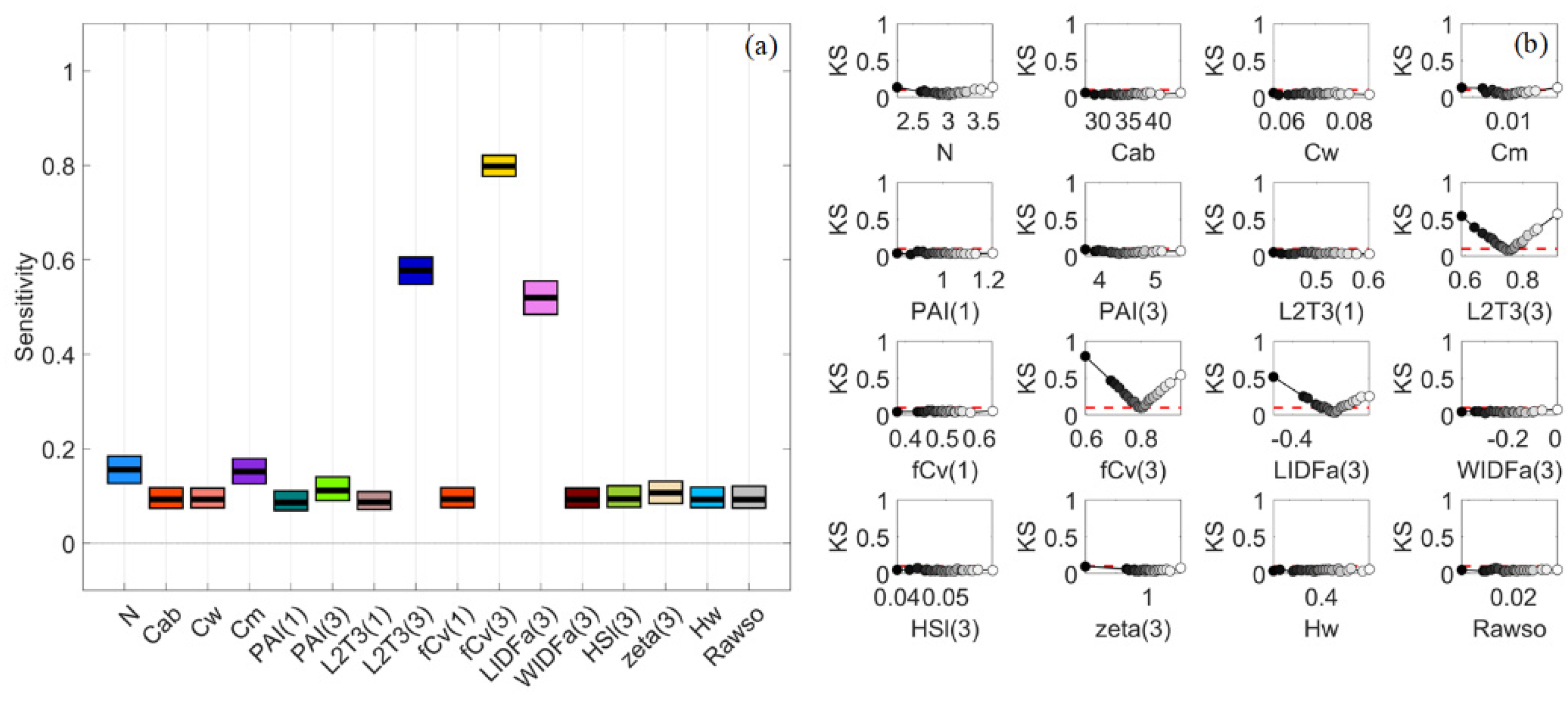
3.1. General Scenario
3.2. Sparse Mangroves—Uniform Input Probability Distributions
3.3. Sparse Mangroves—Normal Input Probability Distributions
3.4. Dense Mangroves—Uniform Input Probability Distributions
3.5. Dense Mangroves—Normal Input Probability Distributions
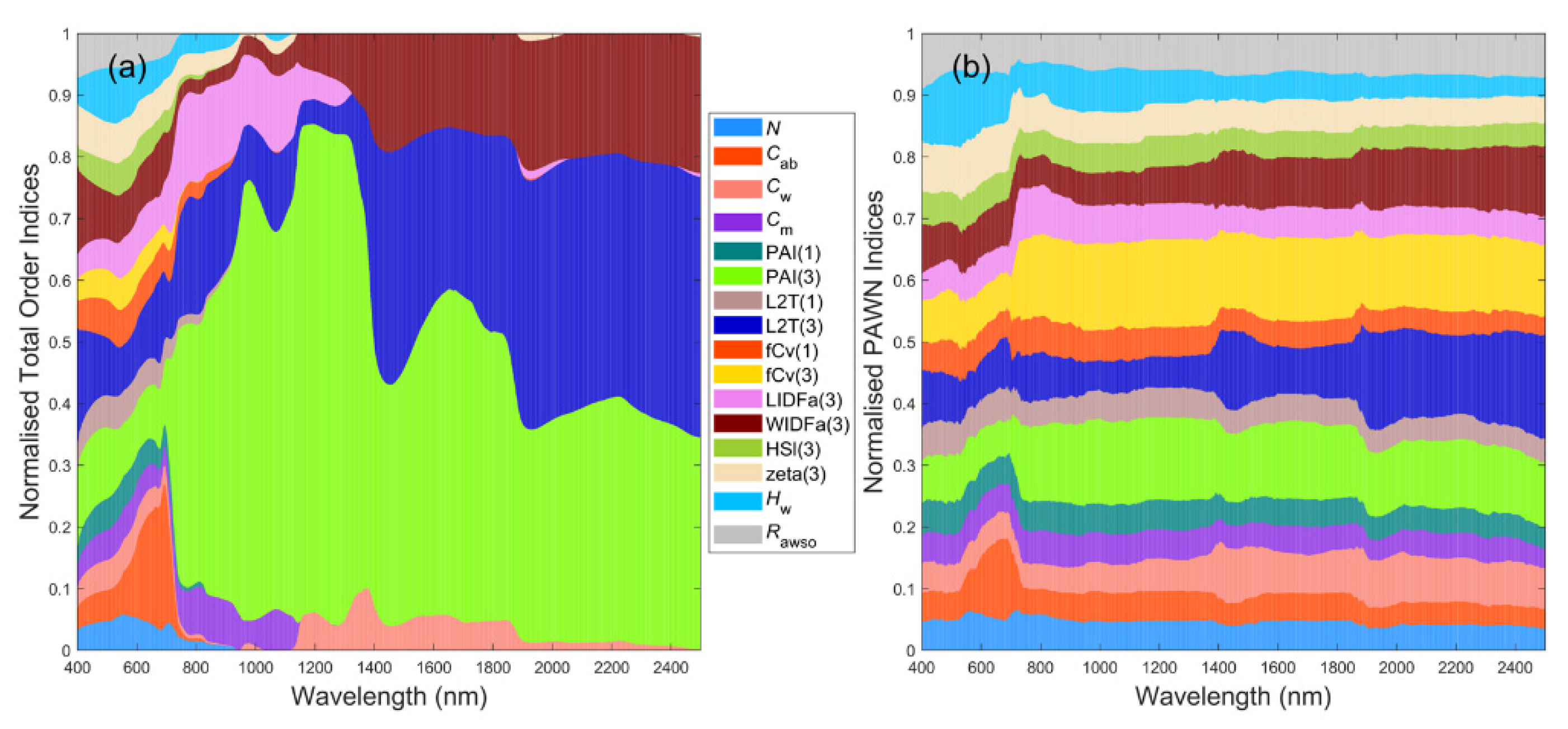
3.6. General Scenario with Correlated PAI(3) and fCv(3)
3.7. A Brief Summary
4. Discussion
4.1. Global Sensitivity Analysis Methods and Interpretations of the Results
4.2. Differences between Sparse and Dense Mangrove Canopies
4.3. Potential Limitations and Suggestions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kamal, M.; Phinn, S. Hyperspectral data for mangrove species mapping: A comparison of pixel-based and object-based approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef] [Green Version]
- Kovacs, J.M.; Wang, J.; Flores-Verdugo, F. Mapping mangrove leaf area index at the species level using IKONOS and LAI-2000 sensors for the Agua Brava Lagoon, Mexican Pacific. Estuar. Coast. Shelf Sci. 2005, 62, 377–384. [Google Scholar] [CrossRef]
- Heenkenda, M.K.; Maier, S.W.; Joyce, K.E. Estimating Mangrove Biophysical Variables Using WorldView-2 Satellite Data: Rapid Creek, Northern Territory, Australia. J. Imaging 2016, 2, 24. [Google Scholar] [CrossRef] [Green Version]
- Jia, M.; Wang, Z.; Wang, C.; Mao, D.; Zhang, Y. A new vegetation index to detect periodically submerged Mangrove forest using single-tide Sentinel-2 imagery. Remote Sens. 2019, 11, 2043. [Google Scholar] [CrossRef] [Green Version]
- Widlowski, J.-L.; Côté, J.-F.; Béland, M. Abstract tree crowns in 3D radiative transfer models: Impact on simulated open-canopy reflectances. Remote Sens. Environ. 2014, 142, 155–175. [Google Scholar] [CrossRef]
- Cárdenas, N.Y.; Joyce, K.E.; Maier, S.W. Monitoring mangrove forests: Are we taking full advantage of technology? Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. Sensitivity analysis of environmental models: A systematic review with practical workflow. Environ. Model. Softw. 2016, 79, 214–232. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canpioes. Ph.D. Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1998. [Google Scholar]
- Verhoef, W.; Bach, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.-S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Campbell, G. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, W.; Zhou, D.; Gong, H. Sensitivity analysis of vegetation reflectance to biochemical and biophysical variables at leaf, canopy, and regional scales. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4014–4024. [Google Scholar] [CrossRef]
- Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Global sensitivity analysis of the spectral radiance of a soil–vegetation system. Remote Sens. Environ. 2014, 145, 131–144. [Google Scholar] [CrossRef]
- Villa, P.; Mousivand, A.; Bresciani, M. Aquatic vegetation indices assessment through radiative transfer modeling and linear mixture simulation. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 113–127. [Google Scholar] [CrossRef]
- Zhou, G.; Ma, Z.; Sathyendranath, S.; Platt, T.; Jiang, C.; Sun, K. Canopy Reflectance Modeling of Aquatic Vegetation for Algorithm Development: Global Sensitivity Analysis. Remote Sens. 2018, 10, 837. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Niu, C.; Xu, W.; Yang, W.; Wang, J.; Zhao, H. Canopy modeling of aquatic vegetation: A radiative transfer approach. Remote Sens. Environ. 2015, 163, 186–205. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A simple and efficient method for global sensitivity analysis based on cumulative distribution functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Borgonovo, E.; Tarantola, S. Moment independent and variance-based sensitivity analysis with correlations: An application to the stability of a chemical reactor. Int. J. Chem. Kinet. 2008, 40, 687–698. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Niu, C. Canopy Reflectance Modelling for Mapping Coastal Wetland Vegetation of South East Queensland, Australia. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2021. [Google Scholar]
- Kearney, M.S.; Stutzer, D.; Turpie, K.; Stevenson, J.C. The effects of tidal inundation on the reflectance characteristics of coastal marsh vegetation. J. Coast. Res. 2009, 25, 1177–1186. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Kamal, M.; Phinn, S.; Johansen, K. Assessment of multi-resolution image data for mangrove leaf area index mapping. Remote Sens. Environ. 2016, 176, 242–254. [Google Scholar] [CrossRef]
- Noacco, V.; Sarrazin, F.; Pianosi, F.; Wagener, T. Matlab/R workflows to assess critical choices in Global Sensitivity Analysis using the SAFE toolbox. MethodsX 2019, 6, 2258–2280. [Google Scholar] [CrossRef]
- Henrich, V.; Götze, E.; Jung, A.; Sandow, C.; Thürkow, D.; Gläßer, C. Development of an Online indices-database: Motivation, concept and implementation. In Proceedings of the 6th EARSeL Imaging Spectroscopy SIG Workshop Innovative Tool for Scientific and Commercial Environment Applications, Tel Aviv, Israel, 16–18 March 2009. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the vernal advancement and retrogradation (green wave effect) of natural vegetation. In NASA/GSFCT Type III Final Report; Greenbelt, MD, USA, 1974. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.V.; Van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Villa, P.; Laini, A.; Bresciani, M.; Bolpagni, R. A remote sensing approach to monitor the conservation status of lacustrine Phragmites australis beds. Wetl. Ecol. Manag. 2013, 21, 399–416. [Google Scholar] [CrossRef]
- Nuarsa, I.W.; Nishio, F.; Hongo, C. Spectral characteristics and mapping of rice plants using multi-temporal Landsat data. J. Agric. Sci. 2011, 3, 54. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the Performance of Sentinel-2, Landsat 8 and Pléiades-1 in Mapping Mangrove Extent and Species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Xiao, X.; Boles, S.; Liu, J.; Zhuang, D.; Frolking, S.; Li, C.; Salas, W.; Moore, B. Mapping paddy rice agriculture in southern China using multi-temporal MODIS images. Remote Sens. Environ. 2005, 95, 480–492. [Google Scholar] [CrossRef]
- Tarantola, S.; Becker, W. SIMLAB Software for Uncertainty and Sensitivity Analysis. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Sarrazin, F.; Pianosi, F.; Wagener, T. An Introduction to the SAFE Matlab Toolbox With Practical Examples and Guidelines. In Sensitivity Analysis in Earth Observation Modelling; Petropoulos, G., Srivastava, P.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 363–378. [Google Scholar]
- Vanuytrecht, E.; Raes, D.; Willems, P. Global sensitivity analysis of yield output from the water productivity model. Environ. Model. Softw. 2014, 51, 323–332. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S. Inversion of the PROSPECT+ SAIL canopy reflectance model from AVIRIS equivalent spectra: Theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Morcillo-Pallarés, P.; Rivera-Caicedo, J.P.; Belda, S.; De Grave, C.; Burriel, H.; Moreno, J.; Verrelst, J. Quantifying the Robustness of Vegetation Indices through Global Sensitivity Analysis of Homogeneous and Forest Leaf-Canopy Radiative Transfer Models. Remote Sens. 2019, 11, 2418. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Treitz, P.M.; Chen, D.; Quan, C.; Shi, L.; Li, X. Mapping mangrove forests using multi-tidal remotely-sensed data and a decision-tree-based procedure. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 201–214. [Google Scholar] [CrossRef]
- Malenovský, Z.; Martin, E.; Homolová, L.; Gastellu-Etchegorry, J.-P.; Zurita-Milla, R.; Schaepman, M.E.; Pokorný, R.; Clevers, J.G.; Cudlín, P. Influence of woody elements of a Norway spruce canopy on nadir reflectance simulated by the DART model at very high spatial resolution. Remote Sens. Environ. 2008, 112, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Zheng, G.; Eitel, J.U.; Magney, T.S.; Moskal, L.M. Determining woody-to-total area ratio using terrestrial laser scanning (TLS). Agric. For. Meteorol. 2016, 228, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Strahler, A.; Schaaf, C.; Jupp, D.; Schaefer, M.; Olofsson, P. Seasonal change of leaf and woody area profiles in a midlatitude deciduous forest canopy from classified dual-wavelength terrestrial lidar point clouds. Agric. For. Meteorol. 2018, 262, 279–297. [Google Scholar] [CrossRef]
- Bailey, B.N.; Mahaffee, W.F. Rapid measurement of the three-dimensional distribution of leaf orientation and the leaf angle probability density function using terrestrial LiDAR scanning. Remote Sens. Environ. 2017, 194, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Vicari, M.B.; Pisek, J.; Disney, M. New estimates of leaf angle distribution from terrestrial LiDAR: Comparison with measured and modelled estimates from nine broadleaf tree species. Agric. For. Meteorol. 2019, 264, 322–333. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Li, L.; Zhang, W.; Mu, X.; Yan, G. Estimating Leaf Angle Distribution From Smartphone Photographs. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1190–1194. [Google Scholar] [CrossRef]
- Yan, G.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. CAN_EYE V6.4.91 User Manual; INRA-UMR: Avignon, France, 2017. [Google Scholar]



| Factors | Unit | Definitions | General Uniform | Sparse Uniform | Sparse Normal | Dense Uniform | Dense Normal | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Mean | STD | Min | Max | Mean | STD | |||
| Leaf | ||||||||||||
| N | - | Leaf structural properties | 1 | 4 | 1 | 4 | 3 | 0.3 | 1 | 4 | 3 | 0.3 |
| Cab | μg∙cm−2 | Leaf chlorophyll content | 0 | 100 | 0 | 100 | 35 | 3.5 | 0 | 100 | 35 | 3.5 |
| Cw | μg∙cm−2 | Leaf water content | 0 | 0.2 | 0 | 0.2 | 0.07 | 0.007 | 0 | 0.2 | 0.07 | 0.007 |
| Cm | g∙cm−2 | Leaf dry matter content | 0 | 0.05 | 0 | 0.05 | 0.01 | 0.001 | 0 | 0.05 | 0.01 | 0.001 |
| Canopy | ||||||||||||
| PAI(1) | - | Plant area index (PAI) of Layer 1 (L1, understory) | 0 | 3 | 0 | 3 | 1 | 0.1 | 0 | 3 | 1 | 0.1 |
| PAI(3) | - | PAI of Layer 3 (L3, crown) | 0 | 6 | 0 | 3 | 2 | 0.2 | 3 | 6 | 4.5 | 0.45 |
| L2T(1) | - | Leaf-to-total area ratio of L1 | 0 | 1 | 0 | 1 | 0.5 | 0.05 | 0 | 1 | 0.5 | 0.05 |
| L2T(3) | - | Leaf-to-total area ratio of L3 | 0 | 1 | 0 | 1 | 0.75 | 0.075 | 0 | 1 | 0.75 | 0.075 |
| fCv(1) | - | Fractional cover of L1 | 0 | 1 | 0 | 1 | 0.5 | 0.05 | 0 | 1 | 0.5 | 0.05 |
| fCv(3) | - | Fractional cover of L3 | 0 | 1 | 0 | 0.7 | 0.3 | 0.03 | 0.5 | 1 | 0.8 | 0.08 |
| LIDFa(3) | - | Leaf inclination distribution function parameter a of L3 a | −1 | 1 | −1 | 1 | −0.2 | 0.1 | −1 | 1 | −0.2 | 0.1 |
| WIDFa(3) | - | Wood inclination distribution function parameter a of L3 | −1 | 1 | −1 | 1 | −0.2 | 0.1 | −1 | 1 | −0.2 | 0.1 |
| HSl(3) | - | Hot spot size parameter of L3 | 0 | 0.1 | 0 | 0.1 | 0.05 | 0.005 | 0 | 0.1 | 0.05 | 0.005 |
| zeta(3) | - | Tree shape factor of L3 | 0 | 2 | 0 | 2 | 1 | 0.1 | 0 | 2 | 1 | 0.1 |
| Other | ||||||||||||
| Hw | m | Water depth | 0 | 2 | 0 | 2 | 0.4 | 0.04 | 0 | 2 | 0.4 | 0.04 |
| Raw_so | - | Bidirectional reflectance of water surface | 0 | 0.03 | 0 | 0.03 | 0.02 | 0.002 | 0 | 0.03 | 0.02 | 0.002 |
| Indices | Descriptions | References |
|---|---|---|
| NDVI | Normalised Difference Vegetation Index | [34] |
| SAVI | Soil Adjusted Vegetation Index (L: 0–1) | [39] |
| EVI | Enhanced Vegetation Index (G = 2.5, L = 1, C1 = 6, C2 = 7.5) | [35] |
| NDWI | Normalised Difference Water Index | [40] |
| MNDWI | Modified Normalised Difference Water Index | [41] |
| NDAVI | Normalised Difference Aquatic Vegetation Index | [36] |
| WAVI | Water Adjusted Vegetation Index (L: 0–1) | [21] |
| WFI | Wetland Forest Index | [38] |
| MDI1 MDI2 | Mangrove Discrimination Index using SWIR 1 or SWIR2 | [38] |
| LSWI | Land Surface Water Index | [42] |
| RGVI | Rice Growth Vegetation Index | [37] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, C.; Phinn, S.; Roelfsema, C. Global Sensitivity Analysis for Canopy Reflectance and Vegetation Indices of Mangroves. Remote Sens. 2021, 13, 2617. https://doi.org/10.3390/rs13132617
Niu C, Phinn S, Roelfsema C. Global Sensitivity Analysis for Canopy Reflectance and Vegetation Indices of Mangroves. Remote Sensing. 2021; 13(13):2617. https://doi.org/10.3390/rs13132617
Chicago/Turabian StyleNiu, Chunyue, Stuart Phinn, and Chris Roelfsema. 2021. "Global Sensitivity Analysis for Canopy Reflectance and Vegetation Indices of Mangroves" Remote Sensing 13, no. 13: 2617. https://doi.org/10.3390/rs13132617
APA StyleNiu, C., Phinn, S., & Roelfsema, C. (2021). Global Sensitivity Analysis for Canopy Reflectance and Vegetation Indices of Mangroves. Remote Sensing, 13(13), 2617. https://doi.org/10.3390/rs13132617








