New Forest Aboveground Biomass Maps of China Integrating Multiple Datasets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field AGB Data
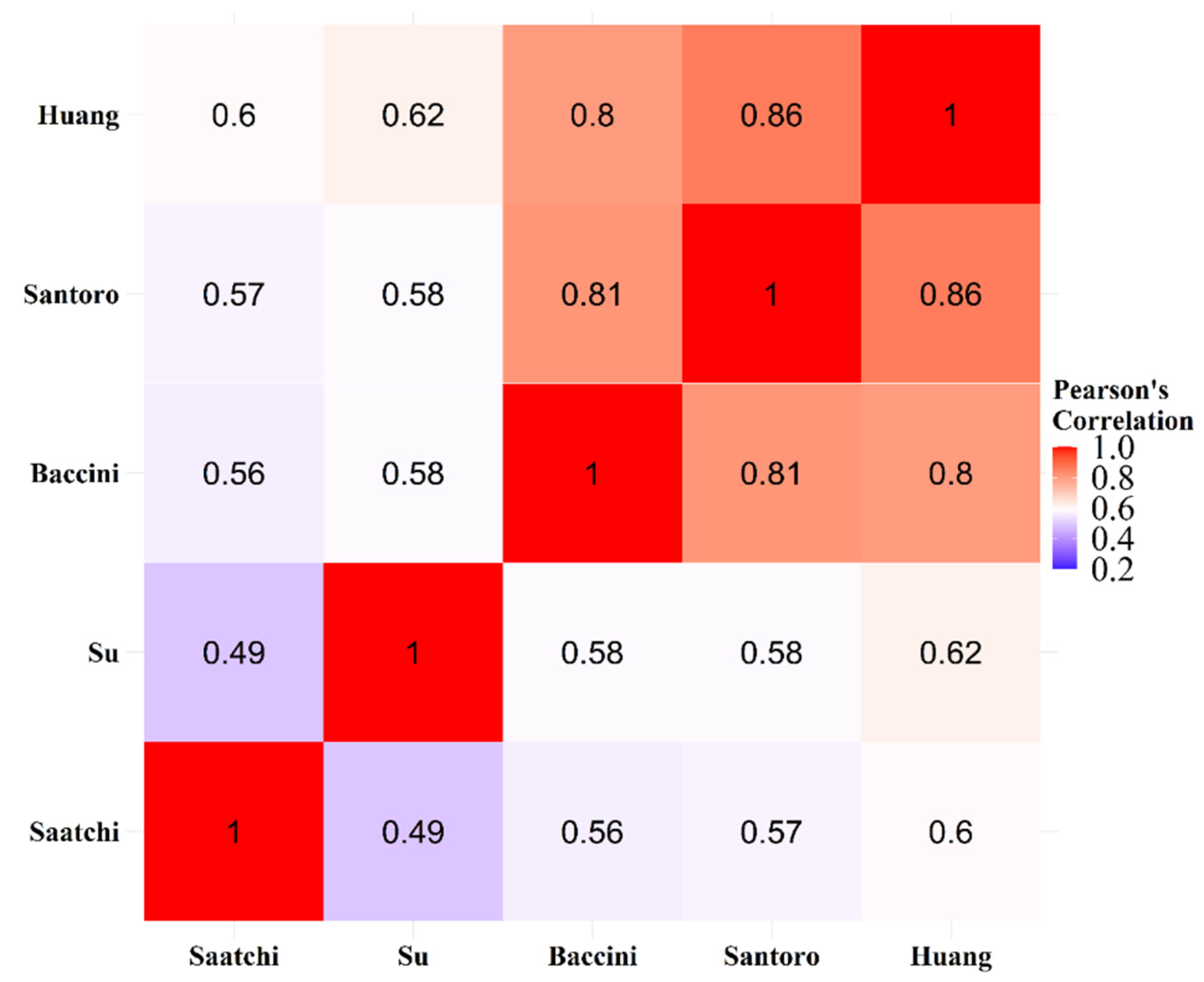
2.2. AGB Maps
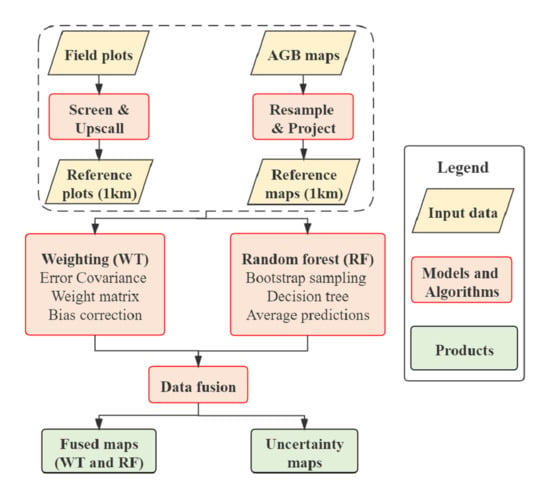
2.3. AGB Estimation Method
2.3.1. AGB Estimation the Using Weighting Technique
2.3.2. AGB Estimation the Using Random Forest Regression Method
2.4. Model Evaluation
3. Results
3.1. Performance of the Two Hybrid Products
3.2. Evaluation of the Two Hybrid Products over China
3.3. Uncertainties of the Two Hybrid Products
4. Discussion
4.1. AGB Estimation in China’s Forests
4.2. Limitations of the Present Study
- Temporal and spatial mismatch
- 2.
- Impact of different definitions of forest
4.3. Implications for National C Budgets
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, F.; Hu, H.; Sun, W.; Zhu, J.; Liu, G.; Zhou, W.; Zhang, Q.; Shi, P.; Liu, X.; Wu, X.; et al. Effects of national ecological restoration projects on carbon sequestration in China from 2001 to 2010. Proc. Natl. Acad. Sci. USA 2018, 115, 4039–4044. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Guo, Z.; Piao, S.; Chen, A. Terrestrial vegetation carbon sinks in China, 1981–2000. Sci. China Earth Sci. 2007, 50, 1341–1350. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef]
- Zhang, C.; Ju, W.; Chen, J.M.; Zan, M.; Li, D.; Zhou, Y.; Wang, X. China’s forest biomass carbon sink based on seven inventories from 1973 to 2008. Clim. Chang. 2013, 118, 933–948. [Google Scholar] [CrossRef]
- Guo, Z.; Hu, H.; Li, P.; Li, N.; Fang, J. Spatio-temporal changes in biomass carbon sinks in China’s forests from 1977 to 2008. Sci. China Life Sci. 2013, 56, 661–671. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Chen, J.M.; Zhou, L.; Ju, W.; Zhang, H.; Machida, T.; Ciais, P.; Peters, W.; Wang, H.; Chen, B.; et al. A comprehensive estimate of recent carbon sinks in China using both top-down and bottom-up approaches. Sci. Rep. 2016, 6, 22130. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S. Climate change, human impacts, and carbon sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, Z.; Fang, J.; Pan, Y.; Birdsey, R. Inventory-based estimates of forest biomass carbon stocks in China: A comparison of three methods. For. Ecol. Manag. 2010, 259, 1225–1231. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, J.; Zhao, N.; Liu, Y.; Wang, Y.; Wilson, J.P.; Yue, T. Estimation of China’s forest stand biomass carbon sequestration based on the continuous biomass expansion factor model and seven forest inventories from 1977 to 2013. For. Ecol. Manag. 2019, 448, 528–534. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping global forest aboveground biomass with spaceborne LiDAR, optical imagery, and forest inventory data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Margolis, H.; Montesano, P.l.; Sun, G.Q.; Cook, B.; Corp, L.; Andersen, H.; deJong, B.; Pellat, F.P.; Fickel, T.; et al. Lidar-based estimates of aboveground biomass in the continental US and Mexico using ground, airborne, and satellite observations. Remote Sens. Environ. 2017, 188, 127–140. [Google Scholar] [CrossRef] [Green Version]
- Cartus, O.; Santoro, M. Exploring combinations of multi-temporal and multi-frequency radar backscatter observations to estimate above-ground biomass of tropical forest. Remote Sens. Environ. 2019, 232, 111313. [Google Scholar] [CrossRef]
- Bloom, A.A.; Exbrayat, J.F.; van der Velde, I.R.; Feng, L.; Williams, M. The decadal state of the terrestrial carbon cycle: Global retrievals of terrestrial carbon allocation, pools, and residence times. Proc. Natl. Acad. Sci. USA 2016, 113, 1285–1290. [Google Scholar] [CrossRef] [Green Version]
- Xue, B.-L.; Guo, Q.; Hu, T.; Wang, G.; Wang, Y.; Tao, S.; Su, Y.; Liu, J.; Zhao, X. Evaluation of modeled global vegetation carbon dynamics: Analysis based on global carbon flux and above-ground biomass data. Ecol. Model. 2017, 355, 84–96. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Ciais, P.; Santoro, M.; Huang, Y.; Li, W.; Wang, Y.; Bastos, A.; Goll, D.; Arneth, A.; Anthoni, P.; et al. Comparison of forest above-ground biomass from dynamic global vegetation models with spatially explicit remotely sensed observation-based estimates. Glob. Chang. Biol. 2020, 26, 3997–4012. [Google Scholar] [CrossRef] [PubMed]
- Requena Suarez, D.; Rozendaal, D.M.A.; De Sy, V.; Phillips, O.L.; Alvarez-Davila, E.; Anderson-Teixeira, K.; Araujo-Murakami, A.; Arroyo, L.; Baker, T.R.; Bongers, F.; et al. Estimating aboveground net biomass change for tropical and subtropical forests: Refinement of IPCC default rates using forest plot data. Glob. Chang. Biol. 2019, 25, 3609–3624. [Google Scholar] [CrossRef] [PubMed]
- Berenguer, E.; Ferreira, J.; Gardner, T.A.; Aragao, L.E.; De Camargo, P.B.; Cerri, C.E.; Durigan, M.; Cosme De Oliveira Junior, R.; Vieira, I.C.; Barlow, J. A large-scale field assessment of carbon stocks in human-modified tropical forests. Glob. Chang. Biol. 2014, 20, 3713–3726. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Wang, S.; Guo, Z.; Xu, B.; Fang, J. The stage-classified matrix models project a significant increase in biomass carbon stocks in China’s forests between 2005 and 2050. Sci. Rep. 2015, 5, 11203. [Google Scholar] [CrossRef] [Green Version]
- Piao, S.; Sitch, S.; Ciais, P.; Friedlingstein, P.; Peylin, P.; Wang, X.; Ahlstrom, A.; Anav, A.; Canadell, J.G.; Cong, N.; et al. Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends. Glob. Chang. Biol. 2013, 19, 2117–2132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, X.; Yan, M.; van der Tol, C.; Li, Z.; Su, Z.; Chen, E.; Li, X.; Li, L.; Wang, X.; Pan, X. Modeling forest above-ground biomass dynamics using multi-source data and incorporated models: A case study over the qilian mountains. Agric. For. Meteorol. 2017, 246, 1–14. [Google Scholar] [CrossRef]
- Yue, T.; Wang, Y.; Du, Z.; Zhao, M.; Zhang, L.; Zhao, N.; Lu, M.; Larocque, G.R.; Wilson, J.P. Analysing the uncertainty of estimating forest carbon stocks in China. Biogeosciences 2016, 13, 3991–4004. [Google Scholar] [CrossRef] [Green Version]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Balsamo, G.; Agusti-Panareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Blyth, E.; Bousserez, N.; Boussetta, S.; Brown, A.; et al. Satellite and in situ observations for advancing global earth surface modelling: A review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef] [Green Version]
- Quegan, S.; Toan, L.T.; Chave, J.; Dall, J.; Exbrayat, J.F.; Minh, D.H.T.; Lomas, M.; D’Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; van Leeuwen, W.; Miura, T.; Glenn, E. MODIS vegetation indices. In Land Remote Sensing and Global Environmental Change; Springer: New York, NY, USA, 2010; pp. 579–602. [Google Scholar]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: Status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef] [Green Version]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A Pathfinder Mission for Global-Scale Monitoring of the Environment. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3307–3316. [Google Scholar] [CrossRef]
- Dalponte, M.; Jucker, T.; Liu, S.C.; Frizzera, L.; Gianelle, D. Characterizing forest carbon dynamics using multi-temporal lidar data. Remote Sens. Environ. 2019, 224, 412–420. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M. Biomass estimation from simulated GEDI, ICESat-2 and NISAR across environmental gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef] [Green Version]
- Réjou-Méchain, M.; Barbier, N.; Couteron, P.; Ploton, P.; Vincent, G.; Herold, M.; Mermoz, S.; Saatchi, S.S.; Chave, J.; de Boissieu, F.; et al. Upscaling forest biomass from field to satellite measurements: Sources of errors and ways to reduce them. Surv. Geophys. 2019, 40, 881–911. [Google Scholar] [CrossRef]
- Rodriguez-Veiga, P.; Quegan, S.; Carreiras, J.; Persson, H.J.; Fransson, J.E.S.; Hoscilo, A.; Ziółkowski, D.; Stereńczak, K.; Lohberger, S.; Stängel, M.; et al. Forest biomass retrieval approaches from earth observation in different biomes. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 53–68. [Google Scholar] [CrossRef]
- Avitabile, V.; Camia, A. An assessment of forest biomass maps in Europe using harmonized national statistics and inventory plots. For. Ecol. Manag. 2018, 409, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Mitchard, E.T.; Feldpausch, T.R.; Brienen, R.J.; Lopez-Gonzalez, G.; Monteagudo, A.; Baker, T.R.; Lewis, S.L.; Lloyd, J.; Quesada, C.A.; Gloor, M.; et al. Markedly divergent estimates of Amazon forest carbon density from ground plots and satellites. Glob. Ecol. Biogeogr. 2014, 23, 935–946. [Google Scholar] [CrossRef]
- Li, Y.; Sulla-Menashe, D.; Motesharrei, S.; Song, X.-P.; Kalnay, E.; Ying, Q.; Li, S.; Ma, Z. Inconsistent estimates of forest cover change in China between 2000 and 2013 from multiple datasets: Differences in parameters, spatial resolution, and definitions. Sci. Rep. 2017, 7, 8748. [Google Scholar] [CrossRef] [Green Version]
- Chave, J.; Davies, S.J.; Phillips, O.L.; Lewis, S.L.; Sist, P.; Schepaschenko, D.; Armston, J.; Baker, T.R.; Coomes, D.; Disney, M.; et al. Ground data are essential for biomass remote sensing missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Rodriguez-Veiga, P.; Saatchi, S.S.; Wheeler, J.; Tansey, K.; Balzter, H. Methodology for regional to global mapping of aboveground forest biomass. In Earth Observation for Land and Emergency Monitoring; Balzter, H., Ed.; John Wiley & Sons: West Sussex, UK, 2017; pp. 7–32. [Google Scholar]
- Zhang, Y.; Liang, S.; Yang, L. A review of regional and global gridded forest biomass datasets. Remote Sens. 2019, 11, 2744. [Google Scholar] [CrossRef] [Green Version]
- Abbas, S.; Wong, M.S.; Wu, J.; Shahzad, N.; Muhammad Irteza, S. Approaches of Satellite Remote Sensing for the Assessment of Above-Ground Biomass across Tropical Forests: Pan-tropical to National Scales. Remote Sens. 2020, 12, 3351. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zhou, X.; Ouyang, Z.; Avitabile, V.; Qi, J.; Chen, J.; Giannico, V. Estimating aboveground biomass in subtropical forests of China by integrating multisource remote sensing and ground data. Remote Sens. Environ. 2019, 232, 111341. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scholze, M.; Buchwitz, M.; Dorigo, W.; Guanter, L.; Quegan, S. Reviews and syntheses: Systematic earth observations for use in terrestrial carbon cycle data assimilation systems. Biogeosciences 2017, 14, 3401–3429. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Liang, S. Fusion of Multiple Gridded Biomass Datasets for Generating a Global Forest Aboveground Biomass Map. Remote Sens. 2020, 12, 2559. [Google Scholar] [CrossRef]
- Bishop, C.H.; Abramowitz, G. Climate model dependence and the replicate Earth paradigm. Clim. Dyn. 2013, 41, 885–900. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, G.; Bishop, C.H. Climate model dependence and the ensemble dependence transformation of CMIP projections. J. Clim. 2015, 28, 2332–2348. [Google Scholar] [CrossRef]
- Hobeichi, S.; Abramowitz, G.; Evans, J.; Ukkola, A. Derived Optimal Linear Combination Evapotranspiration (DOLCE): A global gridded synthesis ET estimate. Hydrol. Earth Syst. Sci. 2018, 22, 1317–1336. [Google Scholar] [CrossRef] [Green Version]
- Hobeichi, S.; Abramowitz, G.; Evans, J.; Beck, H.E. Linear Optimal Runoff Aggregate (LORA): A global gridded synthesis runoff product. Hydrol. Earth Syst. Sci. 2019, 23, 851–870. [Google Scholar] [CrossRef] [Green Version]
- Hobeichi, S.; Abramowitz, G.; Evans, J. Conserving Land–Atmosphere Synthesis Suite (CLASS). J. Clim. 2020, 33, 1821–1844. [Google Scholar] [CrossRef]
- Ge, Y.; Avitabile, V.; Heuvelink, G.B.M.; Wang, J.; Herold, M. Fusion of pan-tropical biomass maps using weighted averaging and regional calibration data. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 13–24. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and limitations of Landsat and land cover data for aboveground woody biomass estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, X.; Zhao, X.; Bai, Y.; Tang, Z.; Wang, W.; Zhao, Y.; Wan, H.; Xie, Z.; Shi, X.; Wu, B.; et al. Carbon pools in China’s terrestrial ecosystems: New estimates based on an intensive field survey. Proc. Natl. Acad. Sci. USA 2018, 115, 4021–4026. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Sun, S.; Yong, S.; Zhou, Z.; Wang, R. Vegetation map of the People’s Republic of China (1:1000000); Geology Publishing House: Beijing, China, 2007. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, B.-J.; Liu, G.-H.; Lü, Y.-H.; Chen, L.-D.; Ma, K.-M. Ecoregions and ecosystem management in China. Int. J. Sustain. Dev. World Ecol. 2004, 11, 397–409. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [Green Version]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.; Avitabilie, V.; Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Rodríguez Veiga, P.; et al. The global forest above-ground biomass pool for 2010 estimated from high-resolution satellite observations. Earth Syst. Sci. Data Discuss. 2020, 2020, 1–38. [Google Scholar]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of multi-resource remotely sensed data and allometric models for forest aboveground biomass estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Quegan, S.; Le Toan, T.; Ho Tong Minh, D.; Saatchi, S.S.; Carvalhais, N.; Reichstein, M.; Scipal, K. Coverage of high biomass forests by the ESA BIOMASS mission under defense restrictions. Remote Sens. Environ. 2017, 196, 154–162. [Google Scholar] [CrossRef]
- Baccini, A.; Walker, W.; Carvalho, L.; Farina, M.; Sulla-Menashe, D.; Houghton, R.A. Tropical forests are a net carbon source based on aboveground measurements of gain and loss. Science 2017, 358, 230–234. [Google Scholar] [CrossRef] [Green Version]
- Mitchard, E.T.; Saatchi, S.S.; Baccini, A.; Asner, G.P.; Goetz, S.J.; Harris, N.L.; Brown, S. Uncertainty in the spatial distribution of tropical forest biomass: A comparison of pan-tropical maps. Carbon Balance Manag. 2013, 8, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Kuang, W.; Zhang, Z.; Xu, X.; Qin, Y.; Ning, J.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; et al. Spatiotemporal characteristics, patterns, and causes of land-use changes in China since the late 1980s. J. Geogr. Sci. 2014, 24, 195–210. [Google Scholar] [CrossRef]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Yu, G.; He, N.; Wang, Q.; Gao, Y.; Wen, D.; Li, S.; Niu, S.; Ge, J. Carbon storage in China’s terrestrial ecosystems: A synthesis. Sci. Rep. 2018, 8, 2806. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. Research Pathways of Forest Above-Ground Biomass Estimation Based on SAR Backscatter and Interferometric SAR Observations. Remote Sens. 2018, 10, 608. [Google Scholar] [CrossRef] [Green Version]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W.; et al. The importance of consistent global forest aboveground biomass product validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E.; Næsset, E.; Saatchi, S.S.; Liknes, G.C.; Walters, B.F.; Chen, Q. Local validation of global biomass maps. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101931. [Google Scholar] [CrossRef]
- Neeti, N.; Kennedy, R. Comparison of national level biomass maps for conterminous US: Understanding pattern and causes of differences. Carbon Balance Manag. 2016, 11, 19. [Google Scholar] [CrossRef] [Green Version]
- Blackard, J.; Finco, M.; Helmer, E.; Holden, G.; Hoppus, M.; Jacobs, D.; Lister, A.; Moisen, G.; Nelson, M.; Riemann, R. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar]
- Sexton, J.O.; Noojipady, P.; Song, X.-P.; Feng, M.; Song, D.-X.; Kim, D.-H.; Anand, A.; Huang, C.; Channan, S.; Pimm, S.L.; et al. Conservation policy and the measurement of forests. Nat. Clim. Chang. 2015, 6, 192–196. [Google Scholar] [CrossRef]
- Tang, H.; Song, X.-P.; Zhao, F.A.; Strahler, A.H.; Schaaf, C.L.; Goetz, S.; Huang, C.; Hansen, M.C.; Dubayah, R. Definition and measurement of tree cover: A comparative analysis of field-, lidar- and landsat-based tree cover estimations in the Sierra national forests, USA. Agric. For. Meteorol. 2019, 268, 258–268. [Google Scholar] [CrossRef]
- Schepaschenko, D.; Chave, J.; Phillips, O.L.; Lewis, S.L.; Davies, S.J.; Rejou-Mechain, M.; Sist, P.; Scipal, K.; Perger, C.; Herault, B.; et al. The Forest Observation System, building a global reference dataset for remote sensing of forest biomass. Sci. Data 2019, 6, 198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clark, D.A.; Asao, S.; Fisher, R.; Reed, S.; Reich, P.B.; Ryan, M.G.; Wood, T.E.; Yang, X. Reviews and syntheses: Field data to benchmark the carbon cycle models for tropical forests. Biogeosciences 2017, 14, 4663–4690. [Google Scholar] [CrossRef] [Green Version]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Shaffer, S.; Veilleux, L.; Chakraborty, M.; Misra, T.; Bhan, R.; Sagi, V.R.; Satish, R. The NASA-ISRO SAR mission-An international space partnership for science and societal benefit. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 1610–1613. [Google Scholar]
- Du, J.; Shi, J.; Sun, R. The development of HJ SAR soil moisture retrieval algorithm. Int. J. Remote Sens. 2010, 31, 3691–3705. [Google Scholar] [CrossRef]
- Bird, R.; Whittaker, P.; Stern, B.; Angli, N.; Cohen, M.; Guida, R. NovaSAR-S: A low cost approach to SAR applications. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 84–87. [Google Scholar]
- Ningthoujam, R.; Balzter, H.; Tansey, K.; Morrison, K.; Johnson, S.; Gerard, F.; George, C.; Malhi, Y.; Burbidge, G.; Doody, S.; et al. Airborne S-Band SAR for Forest Biophysical Retrieval in Temperate Mixed Forests of the UK. Remote Sens. 2016, 8, 609. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.Y.; van Dijk, A.I.J.M.; de Jeu, R.A.M.; Canadell, J.G.; McCabe, M.F.; Evans, J.P.; Wang, G.J. Recent reversal in loss of global terrestrial biomass. Nat. Clim. Chang. 2015, 5, 470–474. [Google Scholar] [CrossRef]
- Fan, L.; Wigneron, J.P.; Ciais, P.; Chave, J.; Brandt, M.; Fensholt, R.; Saatchi, S.S.; Bastos, A.; Al-Yaari, A.; Hufkens, K.; et al. Satellite-observed pantropical carbon dynamics. Nat. Plants 2019, 5, 944–951. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Fan, L.; Ciais, P.; Bastos, A.; Brandt, M.; Chave, J.; Saatchi, S.; Baccini, A.; Fensholt, R. Tropical forests did not recover from the strong 2015–2016 El Niño event. Sci. Adv. 2020, 6, eaay4603. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Lei, X.; Liu, C.; Huang, H.; Zhou, C.; Peng, C. Re-estimating the changes and ranges of forest biomass carbon in China during the past 40 years. For. Ecosyst. 2019, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Ploton, P.; Mortier, F.; Réjou-Méchain, M.; Barbier, N.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial validation reveals poor predictive performance of large-scale ecological mapping models. Nat. Commun. 2020, 11, 4540. [Google Scholar] [CrossRef] [PubMed]







| Region | Participating Products | Sample Number | num.tree | mtry |
|---|---|---|---|---|
| A | All | 257 | 150 | 3 |
| B | All | 205 | 100 | 3 |
| C | All | 297 | 100 | 3 |
| D | All | 533 | 100 | 3 |
| E | Saatchi and Su | 270 | 10 | 2 |
| Region | WT | RF | Saatchi | Su | Baccini | Santoro | Huang |
|---|---|---|---|---|---|---|---|
| A | 92.77 ± 10.12 | 94.9 ± 42.42 | 90.13 | 86.11 | 64.95 | 61.65 | 51.16 |
| B | 122.34 ± 41.93 | 71.03 ± 18.22 | 97.87 | 141.23 | 65.47 | 46.13 | 34.12 |
| C | 53 ± 28.04 | 69.35 ± 18.34 | 86.61 | 97.53 | 52.97 | 30.63 | 37.12 |
| D | 75.81 ± 21.7 | 92.97 ± 18.35 | 114.78 | 129.67 | 123.68 | 54.26 | 47.48 |
| E | 139.57 ± 22.51 | 131.41 ± 44.45 | 177.78 | 202.99 | 127.89 | 93.47 | 63.67 |
| China | 92.29 ± 21.14 | 96.64 ± 28.43 | 116.58 | 130.67 | 101.06 | 60.31 | 49.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Z.; Hobeichi, S.; Wang, Y.-P.; Tang, X.; Abramowitz, G.; Chen, Y.; Cao, N.; Yu, M.; Huang, H.; Zhou, G.; et al. New Forest Aboveground Biomass Maps of China Integrating Multiple Datasets. Remote Sens. 2021, 13, 2892. https://doi.org/10.3390/rs13152892
Chang Z, Hobeichi S, Wang Y-P, Tang X, Abramowitz G, Chen Y, Cao N, Yu M, Huang H, Zhou G, et al. New Forest Aboveground Biomass Maps of China Integrating Multiple Datasets. Remote Sensing. 2021; 13(15):2892. https://doi.org/10.3390/rs13152892
Chicago/Turabian StyleChang, Zhongbing, Sanaa Hobeichi, Ying-Ping Wang, Xuli Tang, Gab Abramowitz, Yang Chen, Nannan Cao, Mengxiao Yu, Huabing Huang, Guoyi Zhou, and et al. 2021. "New Forest Aboveground Biomass Maps of China Integrating Multiple Datasets" Remote Sensing 13, no. 15: 2892. https://doi.org/10.3390/rs13152892
APA StyleChang, Z., Hobeichi, S., Wang, Y.-P., Tang, X., Abramowitz, G., Chen, Y., Cao, N., Yu, M., Huang, H., Zhou, G., Wang, G., Ma, K., Du, S., Li, S., Han, S., Ma, Y., Wigneron, J.-P., Fan, L., Saatchi, S. S., & Yan, J. (2021). New Forest Aboveground Biomass Maps of China Integrating Multiple Datasets. Remote Sensing, 13(15), 2892. https://doi.org/10.3390/rs13152892