Interseismic Slip and Coupling along the Haiyuan Fault Zone Constrained by InSAR and GPS Measurements
Abstract
:1. Introduction
2. Interseismic Deformation
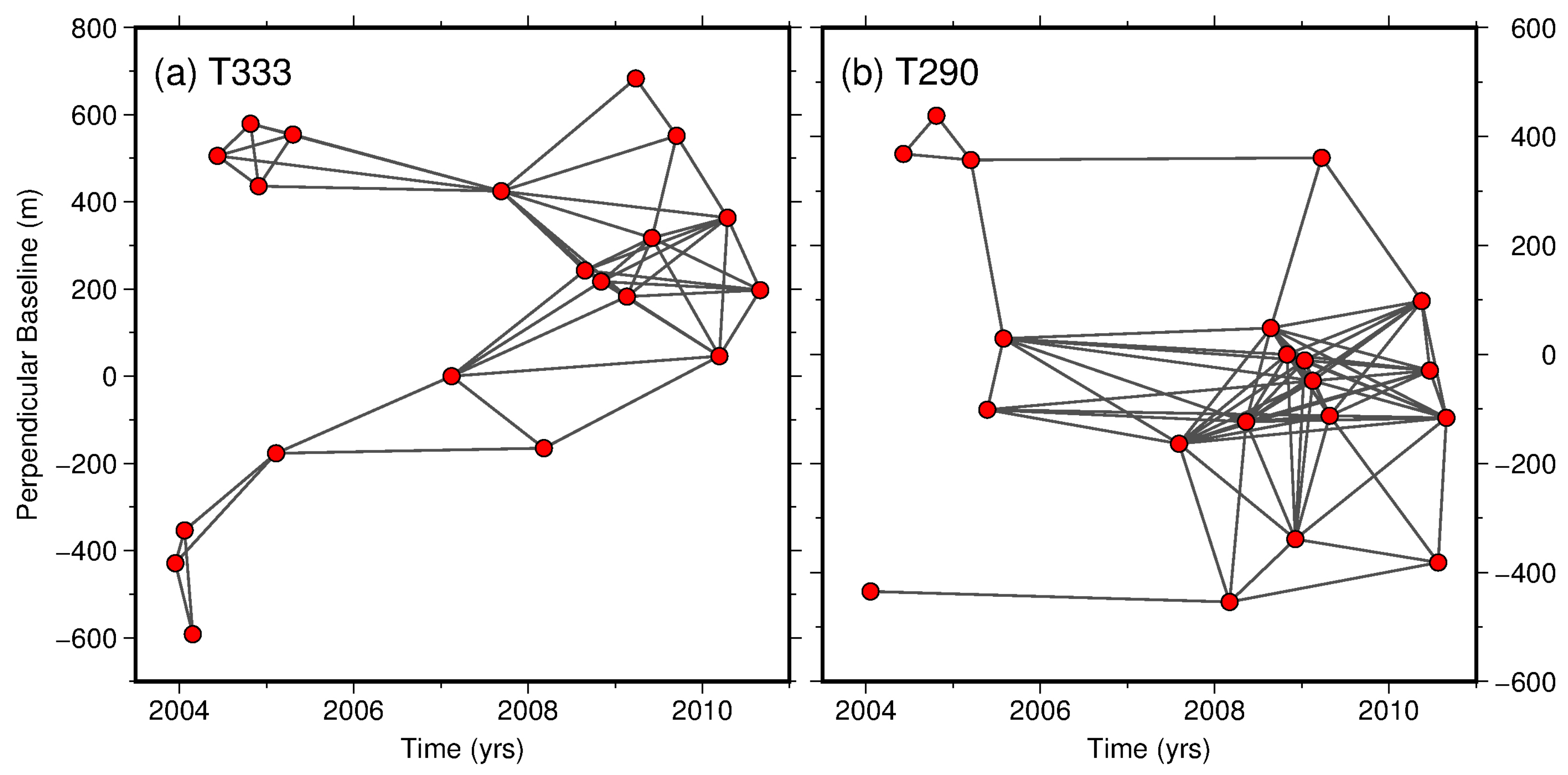
2.1. Data and Processing Method
2.2. InSAR Deformation Rate Field Analysis
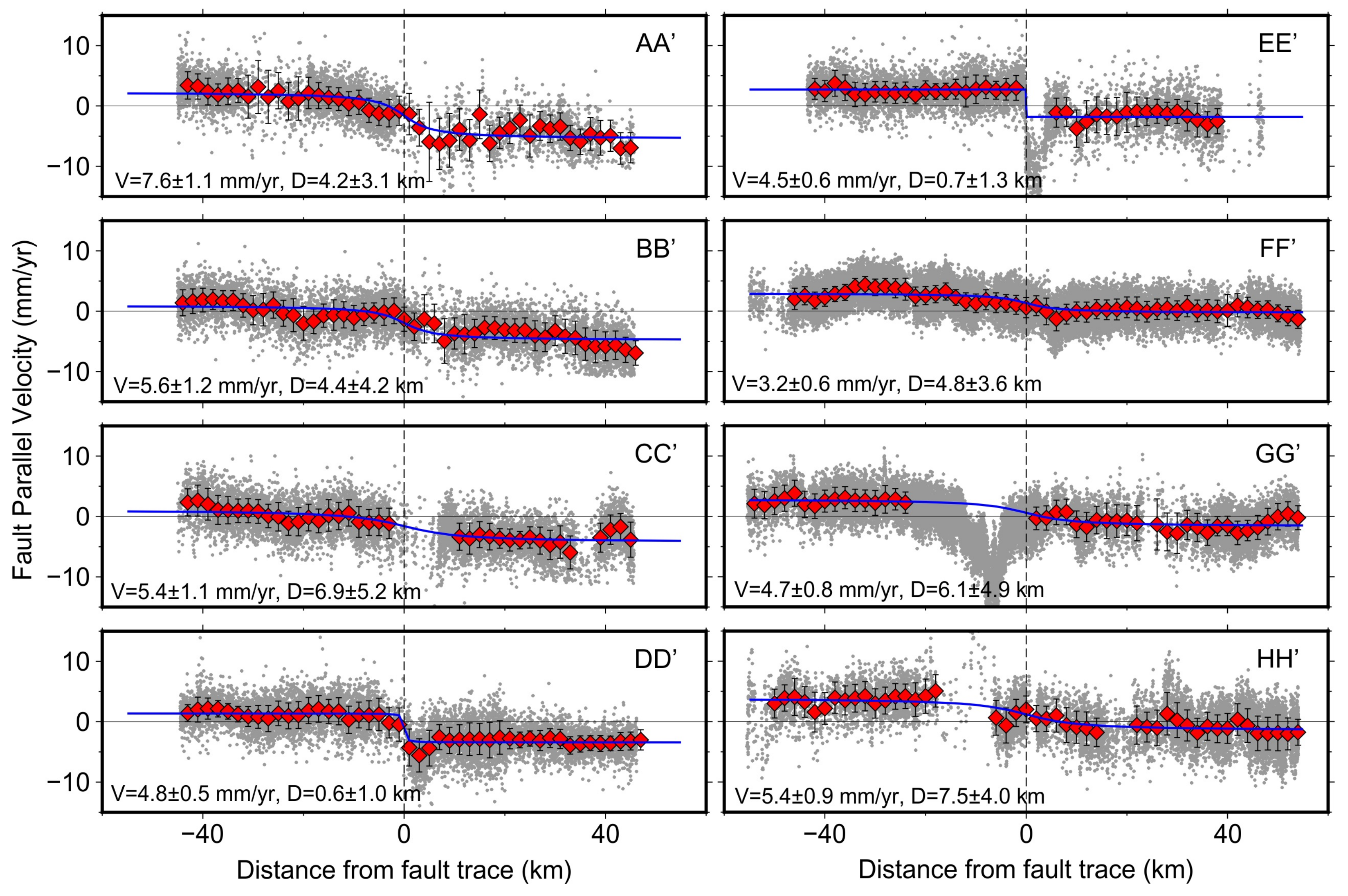
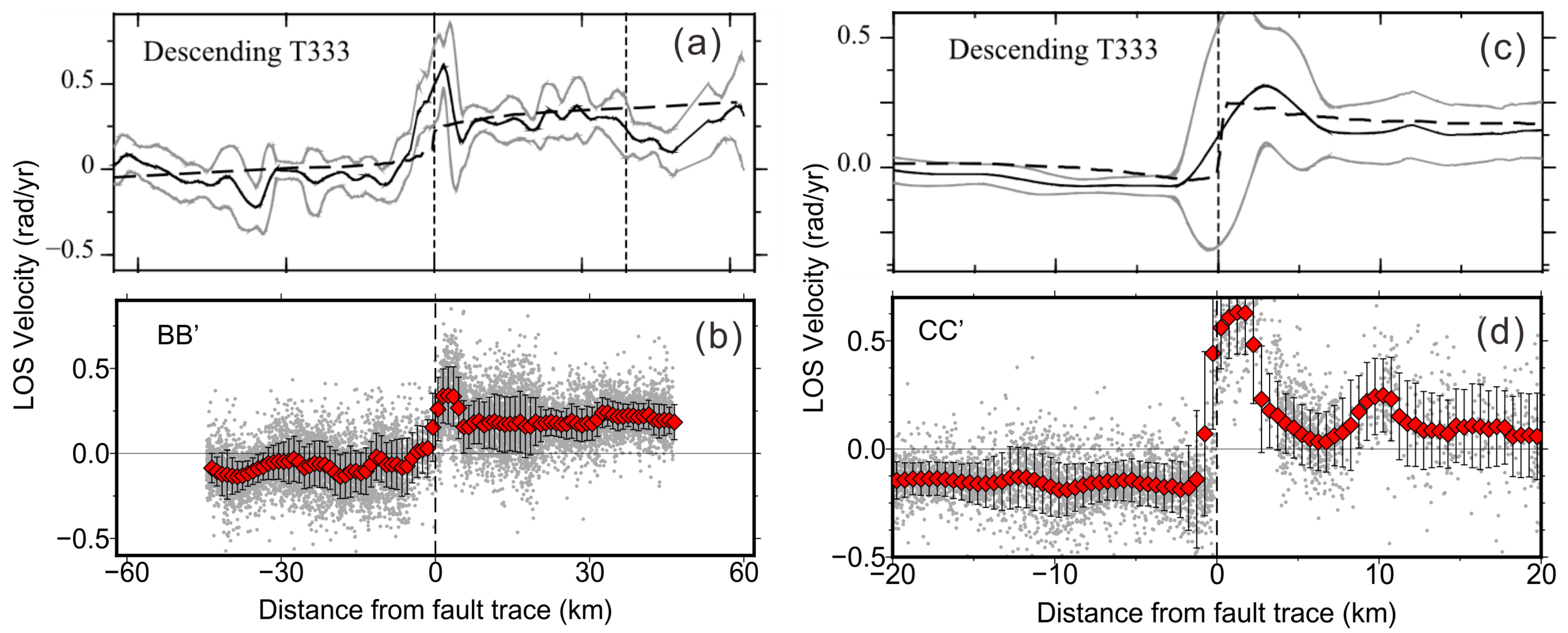
2.3. Deformation Profile Fitting Using the Screw Dislocation Model
3. Inversion Based on the Three-Dimensional Elastic Block Model
3.1. Inversion Method and Block Model Establishment
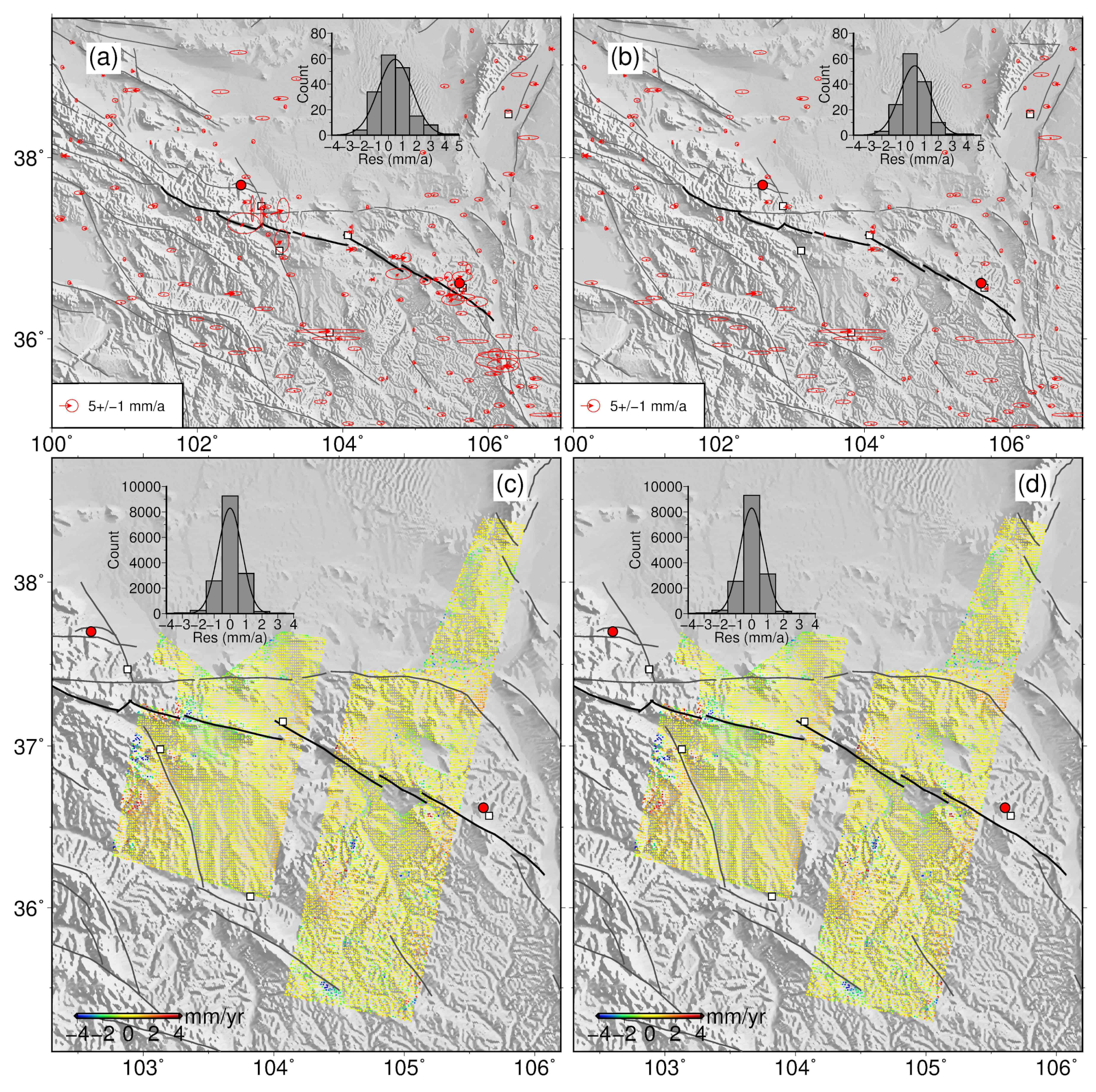
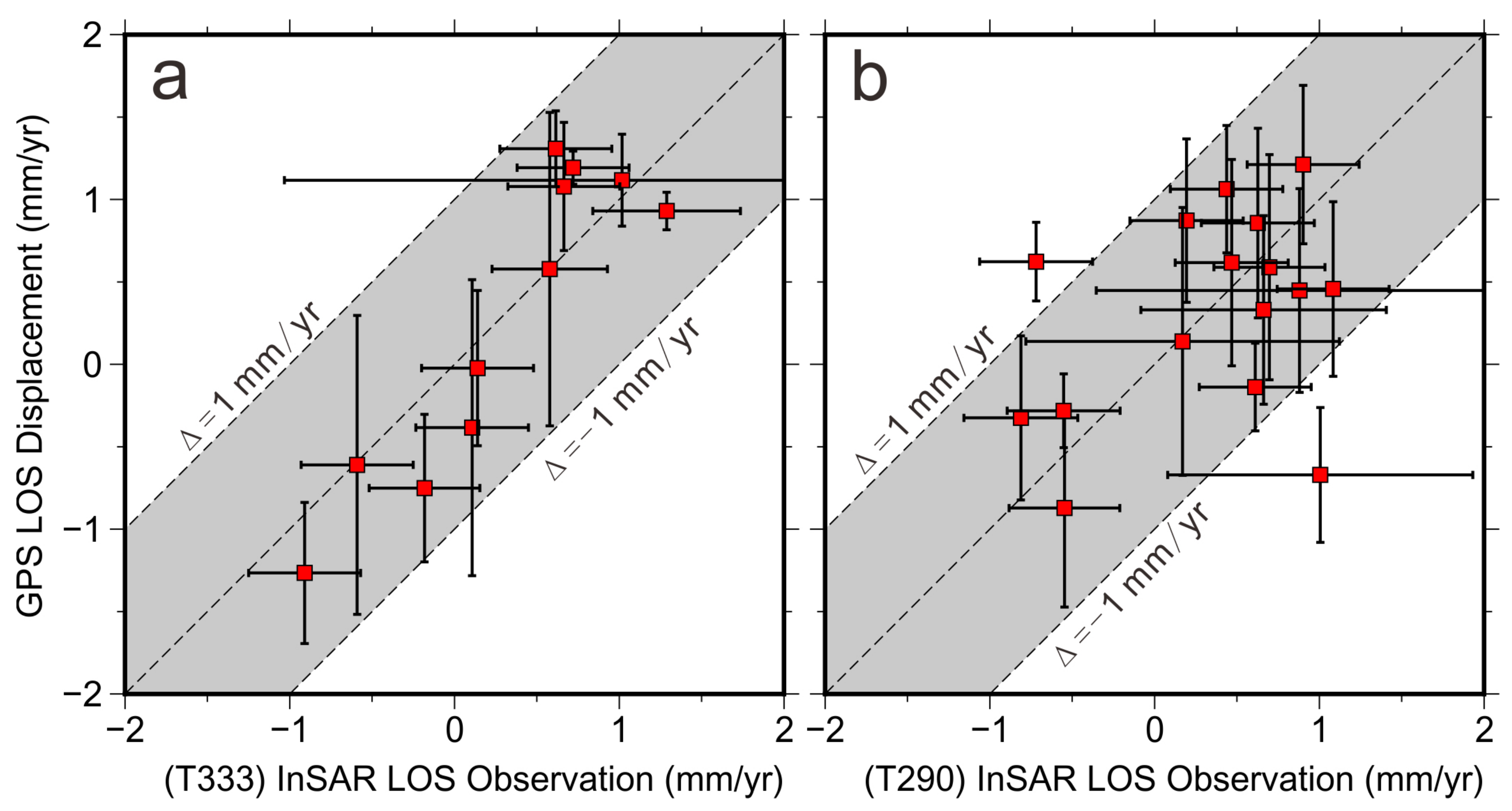
3.2. Inversion Constrainted by GPS and InSAR Alone and Jointly
3.2.1. Individual Inversion from GPS Data Only
3.2.2. Joint Inversion of GPS and InSAR Data
3.3. Comparison of Inversion Results of Different Data Combinations
4. Discussion
4.1. Comparison with Existing InSAR Results
4.2. Comparison with Previous Geological and GPS Results
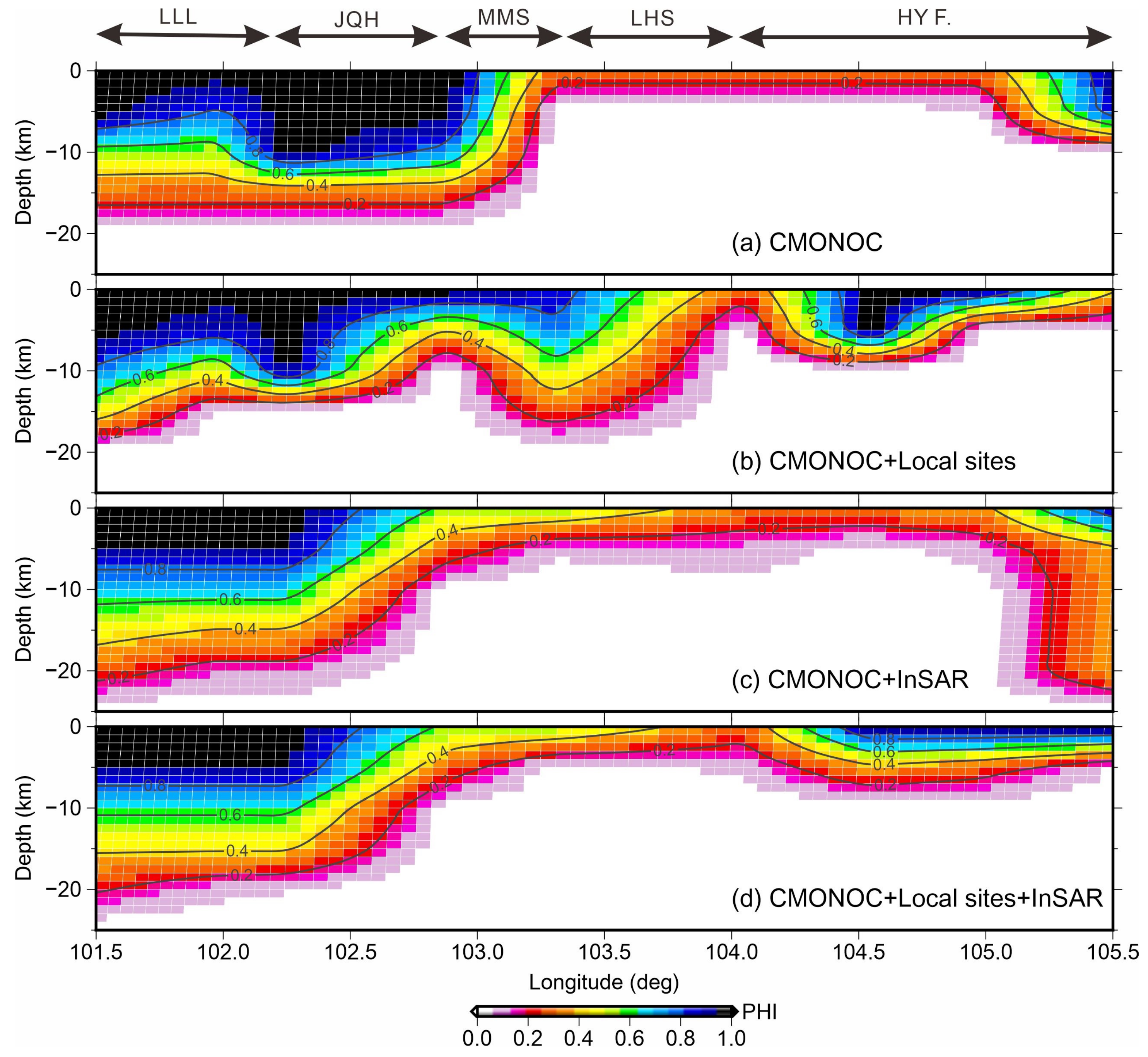
4.3. Constraint Effects of Different InSAR and GPS Datasets on Interseismic Inversion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaudemer, Y.; Tapponnier, P.; Meyer, B.; Peltzer, G.; Shunmin, G.; Zhitai, C.; Huagung, D.; Cifuentes, I. Partitioning of crustal slip between linked, active faults in the eastern Qilian Shan, and evidence for a major seismic gap, the ‘Tianzhu gap’, on the western Haiyuan Fault, Gansu (China). Geophys. J. Int. 1995, 120, 599–645. [Google Scholar] [CrossRef] [Green Version]
- Jing, L.-Z.; Klinger, Y.; Xu, X.; Lasserre, C.; Chen, G.; Chen, W.; Tapponnier, P.; Zhang, B. Millennial recurrence of large earthquakes on the Haiyuan fault near Songshan, Gansu Province, China. Bull. Seismol. Soc. Am. 2007, 97, 14–34. [Google Scholar]
- Lasserre, C.; Morel, P.H.; Gaudemer, Y.; Tapponnier, P.; Ryerson, F.; King, G.; Métivier, F.; Kasser, M.; Kashgarian, M.; Liu, B.; et al. Postglacial left slip rate and past occurrence of M⩾8 earthquakes on the western Haiyuan fault, Gansu, China. J. Geophys. Res. Solid Earth 1999, 104, 17633–17651. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, P.; Yin, J.; Min, W. Late Quaternary left-lateral slip rate of the Haiyuan fault, northeastern margin of the Tibetan Plateau. Tectonics 2009, 28. [Google Scholar] [CrossRef]
- Zhang, P.; Molnar, P.; Burchfiel, B.C.; Royden, L.; Wang, Y.; Deng, Q.; Song, F.; Zhang, W.; Jiao, D. Bounds on the Holocene slip rate of the Haiyuan fault, north-central China. Quat. Res. 1988, 30, 151–164. [Google Scholar]
- Burchfiel, B.; Zhang, P.; Wang, Y.; Zhang, W.; Song, F.; Deng, Q.; Molnar, P.; Royden, L. Geology of the Haiyuan fault zone, Ningxia-Hui Autonomous Region, China, and its relation to the evolution of the northeastern margin of the Tibetan Plateau. Tectonics 1991, 10, 1091–1110. [Google Scholar] [CrossRef]
- Zheng, W.; Zhang, P.; He, W.; Yuan, D.; Shao, Y.; Zheng, D.; Ge, W.; Min, W. Transformation of displacement between strike-slip and crustal shortening in the northern margin of the Tibetan Plateau: Evidence from decadal GPS measurements and late Quaternary slip rates on faults. Tectonophysics 2013, 584, 267–280. [Google Scholar] [CrossRef]
- Gan, W.; Zhang, P.; Shen, Z.K.; Niu, Z.; Wang, M.; Wan, Y.; Zhou, D.; Cheng, J. Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Thatcher, W. Microplate model for the present-day deformation of Tibet. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Duvall, A.R.; Clark, M.K. Dissipation of fast strike-slip faulting within and beyond northeastern Tibet. Geology 2010, 38, 223–226. [Google Scholar] [CrossRef]
- Cui, D.; Wang, Q.; Hu, Y.; Wang, W.; Zhu, G. Inversion of GPS data for slip rates and locking depths of the Haiyuan fault. Acta Seismol. Sin. 2009, 31, 516–525. [Google Scholar]
- Le Béon, M.; Klinger, Y.; Al-Qaryouti, M.; Mériaux, A.S.; Finkel, R.C.; Elias, A.; Mayyas, O.; Ryerson, F.J.; Tapponnier, P. Early Holocene and Late Pleistocene slip rates of the southern Dead Sea Fault determined from 10Be cosmogenic dating of offset alluvial deposits. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Papanikolaou, I.D.; Roberts, G.P.; Michetti, A.M. Fault scarps and deformation rates in Lazio–Abruzzo, Central Italy: Comparison between geological fault slip-rate and GPS data. Tectonophysics 2005, 408, 147–176. [Google Scholar] [CrossRef]
- Cowgill, E.; Gold, R.D.; Chen, X.; Wang, X.-F.; Arrowsmith, J.R.; Southon, J. Low Quaternary slip rate reconciles geodetic and geologic rates along the Altyn Tagh fault, northwestern Tibet. Geology 2009, 37, 647–650. [Google Scholar] [CrossRef]
- Qiao, X.; Zhou, Y. Geodetic imaging of shallow creep along the Xianshuihe fault and its frictional properties. Earth Planet. Sci. Lett. 2021, 567, 117001. [Google Scholar] [CrossRef]
- Li, Y.; Shan, X.; Qu, C.; Wang, Z. Fault locking and slip rate deficit of the Haiyuan-Liupanshan fault zone in the northeastern margin of the Tibetan Plateau. J. Geodyn. 2016, 102, 47–57. [Google Scholar] [CrossRef]
- Hao, M.; Li, Y.; Qin, S. Spatial and temporal distribution of slip rate deficit across Haiyuan-Liupan Shan fault zone constrained by GPS data. Seismol. Geol. 2017, 39, 471–484. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Cavalié, O.; Lasserre, C.; Doin, M.P.; Peltzer, G.; Sun, J.; Xu, X.; Shen, Z.K. Measurement of interseismic strain across the Haiyuan fault (Gansu, China), by InSAR. Earth Planet. Sci. Lett. 2008, 275, 246–257. [Google Scholar] [CrossRef]
- Jolivet, R.; Lasserre, C.; Doin, M.P.; Guillaso, S.; Peltzer, G.; Dailu, R.; Sun, J.; Shen, Z.K.; Xu, X. Shallow creep on the Haiyuan fault (Gansu, China) revealed by SAR interferometry. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Jolivet, R.; Lasserre, C.; Doin, M.P.; Peltzer, G.; Avouac, J.P.; Sun, J.; Dailu, R. Spatio-temporal evolution of aseismic slip along the Haiyuan fault, China: Implications for fault frictional properties. Earth Planet. Sci. Lett. 2013, 377, 23–33. [Google Scholar] [CrossRef]
- Daout, S.; Jolivet, R.; Lasserre, C.; Doin, M.P.; Barbot, S.; Tapponnier, P.; Peltzer, G.; Socquet, A.; Sun, J. Along-strike variations of the partitioning of convergence across the Haiyuan fault system detected by InSAR. Geophys. Suppl. Mon. Not. R. Astron. Soc. 2016, 205, 536–547. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Multibaseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Hooper, A.J. Persistent Scatter Radar Interferometry for Crustal Deformation Studies and Modeling of Volcanic Deformation; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Zhang, P.Z.; Shen, Z.; Wang, M.; Gan, W.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.; Sun, J.; Wu, J.; et al. Continuous deformation of the Tibetan Plateau from global positioning system data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Savage, J.C. A dislocation model of strain accumulation and release at a subduction zone. J. Geophys. Res. Solid Earth 1983, 88, 4984–4996. [Google Scholar] [CrossRef]
- Scholz, C.H. Earthquakes and friction laws. Nature 1998, 391, 37–42. [Google Scholar] [CrossRef]
- Matsu’ura, M.; Jackson, D.D.; Cheng, A. Dislocation model for aseismic crustal deformation at Hollister, California. J. Geophys. Res. Solid Earth 1986, 91, 12661–12674. [Google Scholar] [CrossRef]
- McCaffrey, R.; Stein, S.; Freymueller, J. Crustal block rotations and plate coupling. Plate Bound. Zones Geodyn. Ser 2002, 30, 101–122. [Google Scholar]
- McCaffrey, R.; Qamar, A.I.; King, R.W.; Wells, R.; Khazaradze, G.; Williams, C.A.; Stevens, C.W.; Vollick, J.J.; Zwick, P.C. Fault locking, block rotation and crustal deformation in the Pacific Northwest. Geophys. J. Int. 2007, 169, 1315–1340. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar] [CrossRef]
- Wang, W.; Qiao, X.; Yang, S.; Wang, D. Present-day velocity field and block kinematics of Tibetan Plateau from GPS measurements. Geophys. J. Int. 2017, 208, 1088–1102. [Google Scholar] [CrossRef]
- Deng, Q. Chinese Active Tectonic Map; Seismological Press: Beijing, China, 2007. [Google Scholar]
- Li, Y.; Shan, X.; Qu, C.; Zhang, Y.; Song, X.; Jiang, Y.; Zhang, G.; Nocquet, J.M.; Gong, W.; Gan, W.; et al. Elastic block and strain modeling of GPS data around the Haiyuan-Liupanshan fault, northeastern Tibetan Plateau. J. Asian Earth Sci. 2017, 150, 87–97. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; McClusky, S. GAMIT Reference Manual, Release 10.4; Massachusetts Institute of Technology: Cambridge, UK, 2010. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Liu, B.; Lu, T.; Yuan, D.; Liu, J.; Liu, X. Study on the segmentation of Laohushan fault zone. Northwest. Seismol. J. 1994, 16, 66–72. [Google Scholar]
- Song, X.; Jiang, Y.; Shan, X.; Gong, W.; Qu, C. A fine velocity and strain rate field of present-day crustal motion of the Northeastern Tibetan Plateau inverted jointly by InSAR and GPS. Remote Sens. 2019, 11, 435. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, X.; Qu, C.; Shan, X.; Zhao, D.; Liu, L. Interseismic Slip and Coupling along the Haiyuan Fault Zone Constrained by InSAR and GPS Measurements. Remote Sens. 2021, 13, 3333. https://doi.org/10.3390/rs13163333
Qiao X, Qu C, Shan X, Zhao D, Liu L. Interseismic Slip and Coupling along the Haiyuan Fault Zone Constrained by InSAR and GPS Measurements. Remote Sensing. 2021; 13(16):3333. https://doi.org/10.3390/rs13163333
Chicago/Turabian StyleQiao, Xin, Chunyan Qu, Xinjian Shan, Dezheng Zhao, and Lian Liu. 2021. "Interseismic Slip and Coupling along the Haiyuan Fault Zone Constrained by InSAR and GPS Measurements" Remote Sensing 13, no. 16: 3333. https://doi.org/10.3390/rs13163333
APA StyleQiao, X., Qu, C., Shan, X., Zhao, D., & Liu, L. (2021). Interseismic Slip and Coupling along the Haiyuan Fault Zone Constrained by InSAR and GPS Measurements. Remote Sensing, 13(16), 3333. https://doi.org/10.3390/rs13163333