Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake
Abstract
1. Introduction
2. Materials and Methods
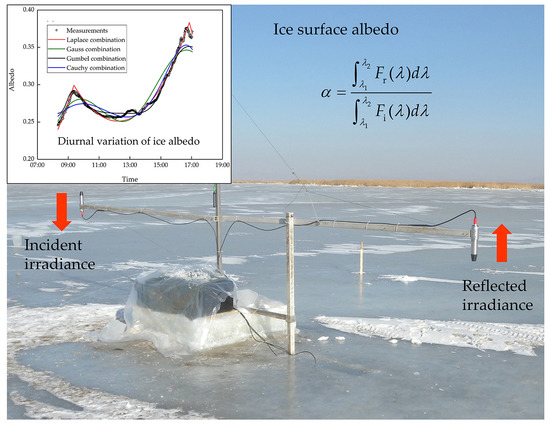
2.1. Field Observation
2.2. Simulation for Diurnal Cycle of Ice Albedo on Sunny Days
3. Results
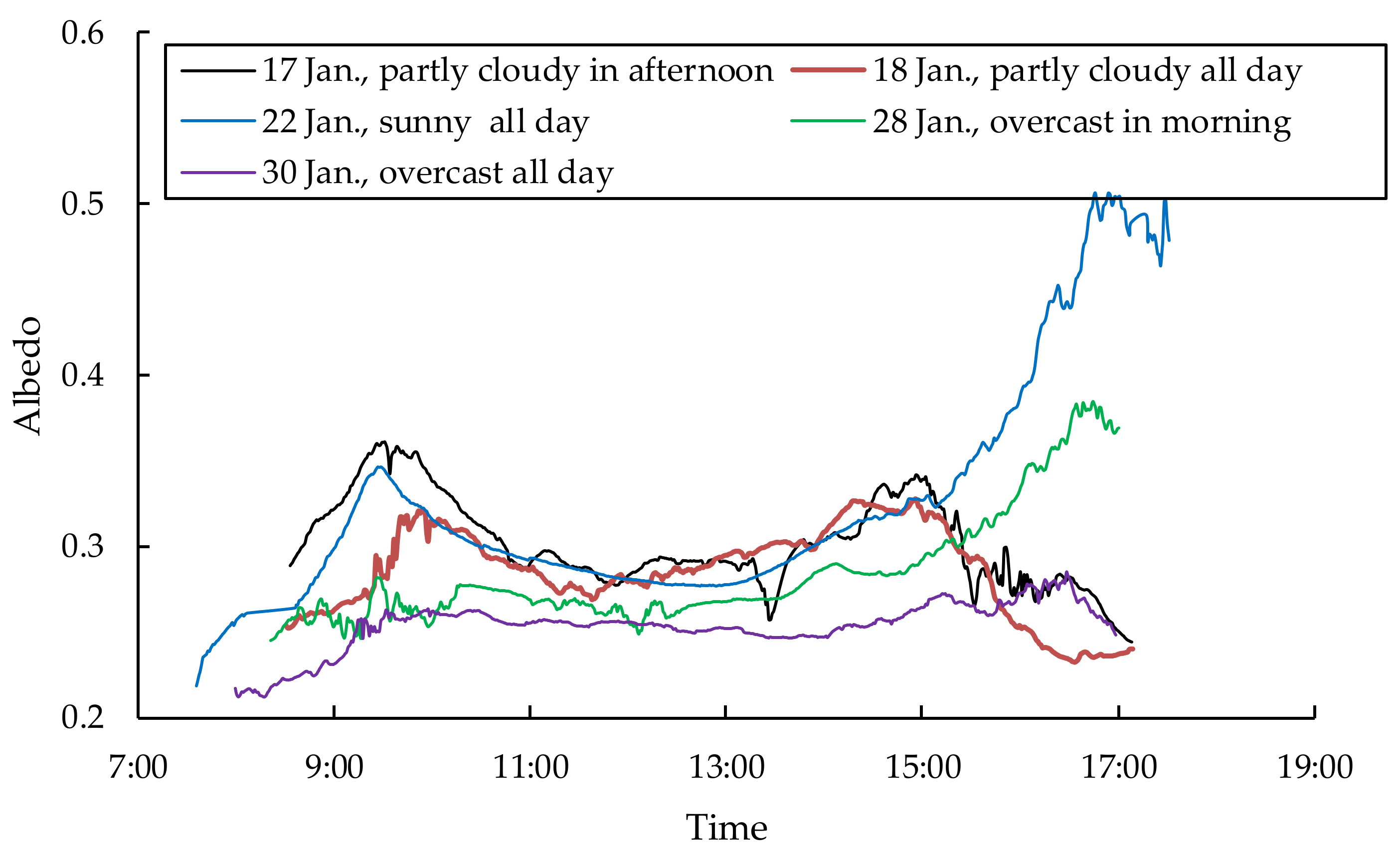
3.1. Diurnal Variation of Lake Ice Albedo
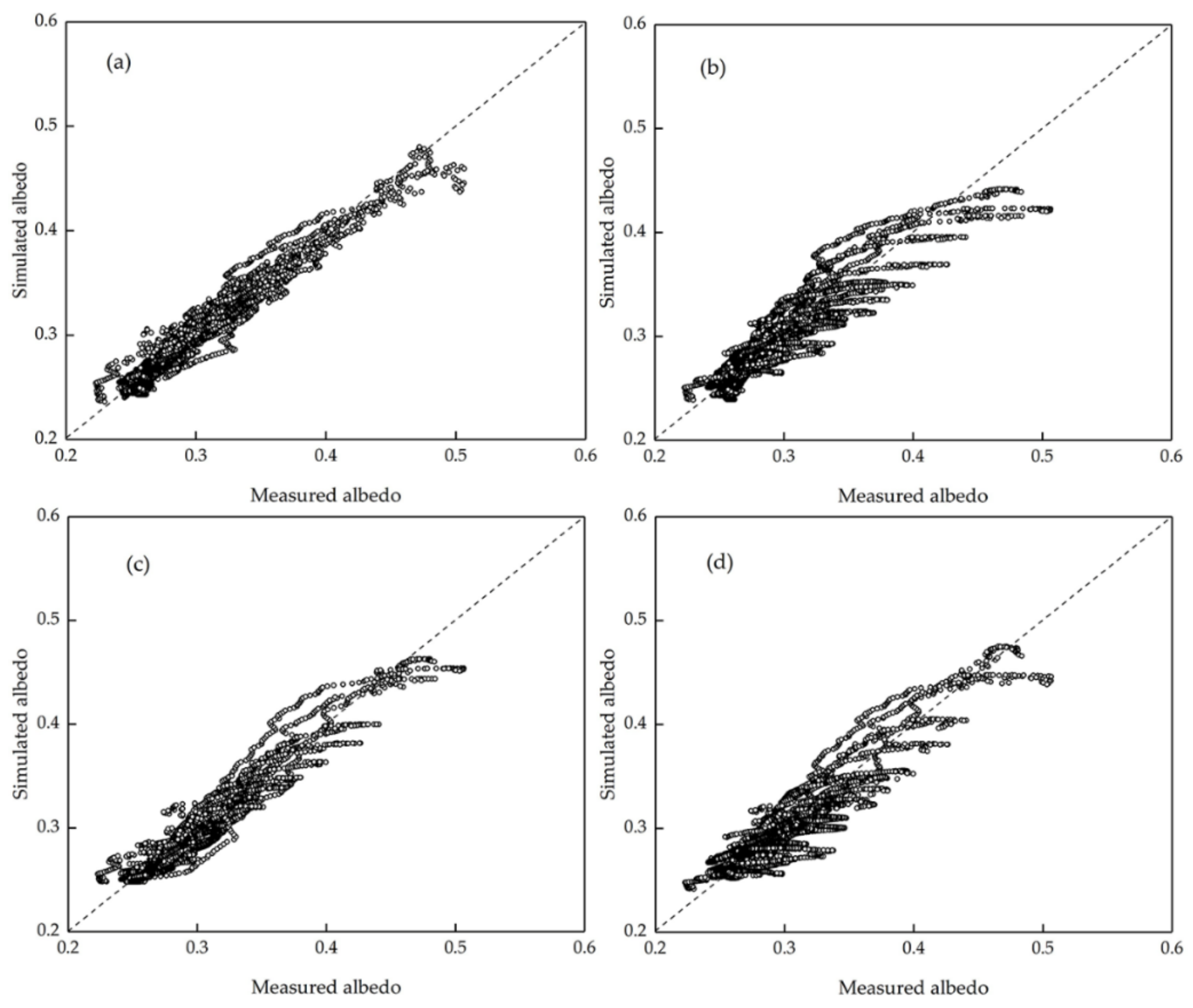
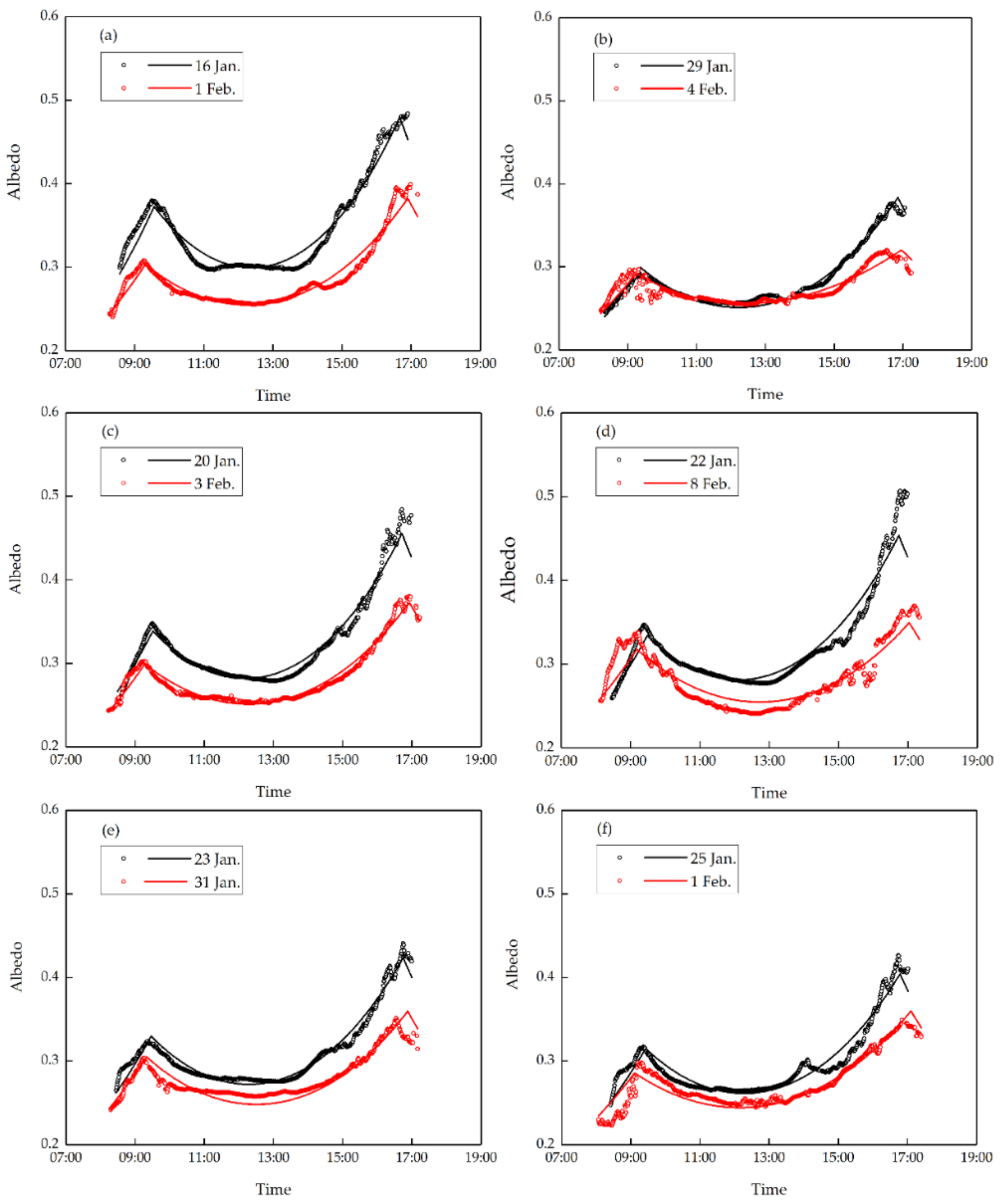
3.2. Simulating the Diurnal Cycle of Lake Ice Albedo on a Sunny Day
4. Discussion
4.1. Comparisons with the Diurnal Cycle of Ice Albedo in Melt Period
4.2. On the Statistical Models
4.3. Effect of Clouds on Ice Surface Albedo and Solar Radiation
4.4. Effect of Atmospheric Deposition on Ice Surface Albedo
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Surdu, C.M.; Duguay, C.R.; Pour, H.K.; Brown, L.C. Ice freeze-up and break-up detection of shallow lakes in Northern Alaska with spaceborne SAR. Remote Sens. 2015, 7, 6133–6159. [Google Scholar] [CrossRef]
- Song, S.; Li, C.; Shi, X.; Zhao, S.; Tian, W.; Li, Z.; Bai, Y.; Cao, X.; Wang, Q.; Huotari, J.; et al. Under-ice metabolism in a shallow lake in a cold and arid climate. Freshw. Biol. 2019, 64, 1710–1720. [Google Scholar] [CrossRef]
- Mironov, D.; Terzhevik, A.; Kirillin, G.; Jonas, T.; Malm, J.; Farmer, D. Radiatively driven convection in ice-covered lakes: Observations, scaling, and a mixed layer model. J. Geophys. Res. Ocean. 2002, 107, 3032. [Google Scholar] [CrossRef]
- Terzhevik, A.; Golosov, S.; Palshin, N.; Mitrokhov, A.; Zdorovennov, R.; Zdorovennova, G.; Kirillin, G.; Shipunova, E.; Zverev, I. Some features of the thermal and dissolved oxygen structure in boreal, shallow ice-covered Lake Vendyurskoe, Russia. Aquat. Ecol. 2009, 43, 617–627. [Google Scholar] [CrossRef]
- Yang, F.; Li, C.; Leppäranta, M.; Shi, X.; Zhao, S.; Zhang, C. Notable increases in nutrient concentrations in a shallow lake during seasonal ice growth. Water Sci. Technol. 2016, 74, 2773–2783. [Google Scholar] [CrossRef]
- Sun, C.; Li, C.; Liu, J.; Shi, X.; Zhao, S.; Wu, Y.; Tian, W. First-principles study on the migration of heavy metal ions in ice-water medium from Ulansuhai Lake. Water 2018, 10, 1149. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Anderson, B.; Zhang, S.; Shi, X.; Zhao, S. A modified QWASI model for fate and transport modeling of mercury between the water-ice-sediment in Lake Ulansuhai. Chemosphere 2017, 176, 117–124. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, M.; Cui, L.; Pan, X.; Liu, W.; Li, W.; Lei, Y. Winter decomposition of emergent macrophytes affects water quality under ice in a temperate shallow lake. Water 2020, 12, 2640. [Google Scholar] [CrossRef]
- Petrov, M.P.; Sutyrin, G.G. Diurnal cycle of convection in an ice-covered lake. Meteorol. Gidrolog. 1984, 1, 91–98. [Google Scholar]
- Pushistov, P.Y.; Ievlev, K.V. Numerical eddy-resolving model of nonstationary penetrative convection in spring solar heating of ice-covered lakes. Bull. Inst. Comput. Math. Math. Geophys. 2000, 5, 55–63. [Google Scholar]
- Bolsenga, S.J. Total albedo of Great Lakes ice. Water Resour. Res. 1969, 5, 1132–1133. [Google Scholar] [CrossRef]
- Dahlback, A.; Gelsor, N.; Stamnes, J.; Gjessing, Y. UV measurements in the 3000–5000 m altitude region in Tibet. J. Geophys. Res. 2007, 112, D09308. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, N.; Pu, J.; He, J.; Chen, L. Variations of albedo and spectral reflectance on Qiyi Glacier in Qilian Mountains during the ablation season. Sci. Cold Arid Reg. 2009, 1, 59–70. [Google Scholar]
- Wang, X.; Zender, C.S. Arctic and Antarctic diurnal and seasonal variations of snow albedo from multiyear Baseline Surface Radiation Network measurements. J. Geophys. Res. Earth Surf. 2011, 116, F03008. [Google Scholar] [CrossRef]
- Yao, T.; Zhang, Q. Study on land-surface albedo over different types of underlying surfaces in North China. Acta Phys. Sin. 2014, 63, 089201. (In Chinese) [Google Scholar] [CrossRef]
- Norsang, G.; Jin, Y.; Tsoja, W.; Zhou, Y.; Sunam, B.; Denggua, T. Ground-based measurements of global solar radiation and UV radition in Tibet. Spectrosc. Spectr. Anal. 2019, 39, 1683–1688. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, L.; Li, R.; Yao, J.; Sun, L.; Qiao, Y.; Jiao, K. The characteristics of surface albedo in permafrost regions of northern Tibetan plateau. J. Glaciol. Geocryol. 2010, 32, 480–488. (In Chinese) [Google Scholar]
- Sun, J.; Hu, Z.; Xun, X.; Peng, W.; Lv, B.; Xu, L. Albedo characteristics in different underlying surfaces in mid- and upper-reaches of HEIFE and its impact factor analysis. Plateau Meteorol. 2011, 30, 607–613. (In Chinese) [Google Scholar]
- Pirazzini, R. Challenges in snow and ice albedo parameterizations. Geophysica 2009, 45, 41–62. [Google Scholar]
- Pirazzini, R.; Vihma, T.; Granskog, M.A.; Cheng, B. Surface albedo measurements over sea ice in the Baltic Sea during the spring snowmelt period. Ann. Glaciol. 2006, 44, 7–14. [Google Scholar] [CrossRef]
- Jakkila, J.; Leppäranta, M.; Kawamura, T.; Shirasawa, K.; Salonen, K. Radiation transfer and heat budget during the ice season in Lake Pääjärvi, Finland. Aquat. Ecol. 2009, 43, 681–692. [Google Scholar] [CrossRef]
- Zdorovennova, G.; Palshin, N.; Efremova, T.; Zdorovennov, R.; Gavrilenko, G.; Volkov, S.; Bogdanov, S.; Terzhevik, A. Albedo of a small ice-covered boreal lake: Daily, meso-scale and interannual variability on the background of regional climate. Geosciences 2018, 8, 206. [Google Scholar] [CrossRef]
- Bolsenga, S.J.; Greene, G.M. Techniques to measure the spectral reflectance of ice. Proc. SPIE 1984, 489, 384–391. [Google Scholar] [CrossRef]
- Minnis, P.; Mayor, S.; Smith, W.L.; Young, D. Asymmetry in the diurnal variation of surface albedo. IEEE Trans. Geosci. Remote Sens. 1997, 35, 879–891. [Google Scholar] [CrossRef]
- Duguay, C.R.; Flato, G.M.; Jeffries, M.O.; Menard, P.; Morris, K.; Rouse, W.R. Ice-cover variability on shallow lakes at high latitudes: Model simulations and observations. Hydrol. Process. 2003, 17, 3465–3483. [Google Scholar] [CrossRef]
- Yang, Y.; Leppäranta, M.; Cheng, B.; Li, Z. Numerical modelling of snow and ice thicknesses in Lake Vanajavesi, Finland. Tellus Ser. A Dyn. Meteorol. Oceanol. 2012, 64, 17202. [Google Scholar] [CrossRef]
- Robinson, A.L.; Ariano, S.S.; Brown, L.C. The Influence of snow and ice albedo towards improved lake ice simulations. Hydrology 2021, 8, 11. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, S.; Jia, Y.; Zeng, Q.; Feng, D.; Lei, G. Spatial and temporal variations in waterbird communities and its implications for ecosystem management in a large temperate arid wetland of northwest P.R. China. Avian Biol. Res. 2017, 10, 119–128. [Google Scholar] [CrossRef]
- Sun, B.; Li, C.; Zhu, D. Changes of Wuliangsuhai Lake in past 150 years based on 3S technology. In Proceedings of the 2011 International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 24–26 June 2011. [Google Scholar]
- Lu, P.; Cao, X.; Li, G.; Huang, W.; Leppäranta, M.; Arvola, L.; Huotari, J.; Li, Z. Mass and heat balance of a lake ice cover in the central Asian arid climate zone. Water 2020, 12, 2888. [Google Scholar] [CrossRef]
- Chen, J.; Zuo, H.; Wang, Y.; Ren, P.; Wan, W.; Dong, L.; Wang, X. Parameterization scheme about albedo changing with solar altitude angle over different underlying surface in arid areas of Northwest China. Plateau Meteorol. 2014, 33, 80–88. (In Chinese) [Google Scholar] [CrossRef]
- Wen, L.; Lv, S.; Chen, S.; Meng, X.; Li, S.; Ao, Y. Observation study on diurnal asymmetry in surface albedo of oasis in arid region. Acta Energ. Sol. Sin. 2009, 30, 953–956. (In Chinese) [Google Scholar] [CrossRef]
- Bertilsson, S.; Burgin, A.; Carey, C.; Fey, S.; Grossart, H.P.; Grubisic, L.M.; Jones, I.D.; Kirillin, G.; Lennon, J.T.; Shade, A.; et al. The under-ice microbiome of seasonally frozen lakes. Limnol. Oceanogr. 2013, 58, 1998–2012. [Google Scholar] [CrossRef]
- Yu, Q.; Liu, S.; Li, H.; Zhang, Q. Formula derivation and application of solar elevation angle. J. Henan Univ. Eng. 2017, 29, 77–80. (In Chinese) [Google Scholar] [CrossRef]
- Strnad, F.; Moravec, V.; Markonis, Y.; Máca, P.; Masner, J.; Stočes, M.; Hanel, M. An index-flood statistical model for hydrological drought assessment. Water 2020, 12, 1213. [Google Scholar] [CrossRef]
- Gonzalez Cruz, M.; Hernandez, E.A.; Uddameri, V. Climatic influences on agricultural drought risks using semiparametric Kernel density estimation. Water 2020, 12, 2813. [Google Scholar] [CrossRef]
- Gargano, R.; Tricarico, C.; Granata, F.; Santopietro, S.; de Marinis, G. Probabilistic models for the peak residential water demand. Water 2017, 9, 417. [Google Scholar] [CrossRef]
- Heo, J.H.; Ahn, H.; Shin, J.Y.; Kjeldsen, T.R.; Jeong, C. Probability distributions for a quantile mapping technique for a bias correction of precipitation data: A case study to precipitation data under climate change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, W.; Yao, J.; Wang, W. Variation of cloud fraction and its relationship with solar radiation over semi-arid region. J. Arid Meteorol. 2015, 33, 684–693. (In Chinese) [Google Scholar] [CrossRef]
- Ashton, G.D.; Kennedy, J.F. Ripples on underside of river ice covers. J. Hydraul. Eng. ASCE 1972, 98, 1603–1624. [Google Scholar]
- Sarangi, C.; Qian, Y.; Rittger, K.; Leung, L.R.; Chand, D.; Bormann, K.J.; Painter, T.H. Dust dominates high-altitude snow darkening and melt over high-mountain Asia. Nat. Clim. Chang. 2020, 10, 1045–1051. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, S. Research progress of light-absorbing impurities in glaciers of the Tibetan Plateau and its surroundings. Chin. Sci. Bull. 2017, 62, 4151–4162. [Google Scholar] [CrossRef][Green Version]
- Xu, Z.; Yang, Y.; Sun, Z.; Li, Z.; Cao, W.; Ye, H. In situ measurement of the solar radiance distribution within sea ice in Liaodong Bay, China. Cold Reg. Sci. Tech. 2012, 71, 23–33. [Google Scholar] [CrossRef]
- Lang, J.; Lyu, S.; Li, Z.; Ma, Y.; Su, D. An investigation of ice surface albedo and its influence on the high-altitude lakes of the Tibetan Plateau. Remote Sens. 2018, 10, 218. [Google Scholar] [CrossRef]
- Beres, N.D.; Lapuerta, M.; Cereceda-Balic, F.; Moosmüller, H. Snow surface albedo sensitivity to black carbon: Radiative transfer modelling. Atmosphere 2020, 11, 1077. [Google Scholar] [CrossRef]
- Beres, N.D.; Sengupta, D.; Samburova, V.; Khlystov, A.Y.; Moosmüller, H. Deposition of brown carbon onto snow: Changes in snow optical and radiative properties. Atmos. Chem. Phys. 2020, 20, 6095–6114. [Google Scholar] [CrossRef]
- Qian, Y.; Yasunari, T.J.; Doherty, S.J.; Flanner, M.G.; Lau, W.K.M.; Ming, J.; Wang, H.; Wang, M.; Warren, S.G.; Zhang, R. Light-absorbing particles in snow and ice: Measurement and modeling of climatic and hydrological impact. Adv. Atmos. Sci. 2015, 32, 64–91. [Google Scholar] [CrossRef]
- Moosmüller, H.; Engelbrecht, J.P.; Skiba, M.; Frey, G.; Chakrabarty, R.K.; Arnott, W.P. Single scattering albedo of fine mineral dust aerosols controlled by iron concentration. J. Geophys. Res. Atmos. 2012, 117, D11210. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, G.; Deng, Y.; Li, Z.; Li, G.; Guo, W. Investigation on ice crystal, density and sediment content in ice at different positions in Bayannaoer Section of the Yellow River. Yellow River 2018, 40, 44–48. (In Chinese) [Google Scholar] [CrossRef]
- Azzoni, R.S.; Senese, A.; Zerboni, A.; Maugeri, M.; Smiraglia, C.; Diolaiuti, G.A. Estimating ice albedo from fine debris cover quantified by a semi-automatic method: The case study of Forni Glacier, Italian Alps. Cryosphere 2016, 10, 665–679. [Google Scholar] [CrossRef]
- Constantin, J.G.; Ruiz, L.; Villarosa, G.; Outes, V.; Bajano, F.; He, C.; Bajano, H.; Dawidowski, L. Measurements and modeling of snow albedo at Alerce Glacier, Argentina: Effects of volcanic ash, snow grain size and cloudiness. Cryosphere 2020, 14, 4581–4601. [Google Scholar] [CrossRef]




| Model | L1 | M1 | N1 | R2 | L2 | M2 | N2 | R2 |
|---|---|---|---|---|---|---|---|---|
| Laplace | −93.589 | 56.939 | −8.094 | 0.998 | −93.589 | 56.939 | −8.094 | 0.998 |
| Gauss | −43.254 | 26.555 | −3.769 | 0.998 | −49.789 | 30.606 | −4.357 | 0.998 |
| Gumbel | −6.245 | 3.998 | −0.586 | 0.790 | −43.199 | 26.151 | −3.761 | 0.998 |
| Cauchy | −136.430 | 82.683 | −11.859 | 0.998 | −137.250 | 82.281 | −11.932 | 0.998 |
| Date | Sunrise | Solar Noon | Sunset |
|---|---|---|---|
| 17 January | 08:06 | 12:55 | 17:44 |
| 18 January | 08:06 | 12:55 | 17:45 |
| 22 January | 08:03 | 12:56 | 17:50 |
| 28 January | 07:59 | 12:58 | 17:57 |
| 30 January | 07:57 | 12:58 | 17:59 |
| Date | Average Albedo | Weighted Average Albedo | ||
|---|---|---|---|---|
| Sunrise–Sunset | 11:00–14:00 | Sunrise–Sunset | 11:00–14:00 | |
| 17 January | 0.302 | 0.289 | 0.303 | 0.289 |
| 18 January | 0.286 | 0.288 | 0.294 | 0.289 |
| 22 January | 0.324 | 0.285 | 0.320 | 0.285 |
| 28 January | 0.285 | 0.267 | 0.283 | 0.268 |
| 30 January | 0.254 | 0.253 | 0.256 | 0.253 |
| Model | r | RMSE | MAE | Mean ± Std. |
|---|---|---|---|---|
| Laplace | 0.990 | 0.0049 | 0.0038 | −0.0004 ± 0.0049 |
| Gauss | 0.952 | 0.0108 | 0.0089 | 0.0004 ± 0.0108 |
| Gumbel | 0.979 | 0.0070 | 0.0050 | −0.0001 ± 0.0070 |
| Cauchy | 0.971 | 0.0084 | 0.0079 | −0.0003 ± 0.0084 |
| Model | r | RMSE | MAE | Mean ± Std. |
|---|---|---|---|---|
| Laplace | 0.972 | 0.0106 | 0.0080 | −0.0001 ± 0.0106 |
| Gauss | 0.931 | 0.0164 | 0.0124 | −0.0003 ± 0.0164 |
| Gumbel | 0.970 | 0.0112 | 0.0075 | −0.0023 ± 0.0110 |
| Cauchy | 0.940 | 0.0154 | 0.0112 | −0.0009 ± 0.0154 |
| Date | r | RMSE | MAE | Mean ± Std. | a1 | a2 |
|---|---|---|---|---|---|---|
| 16 January | 0.976 | 0.0115 | 0.0094 | 0.0004 ± 0.0111 | 0.1014 | 0.1458 |
| 20 January | 0.984 | 0.0089 | 0.0068 | 0.0006 ± 0.0090 | 0.0938 | 0.1449 |
| 22 January | 0.959 | 0.0155 | 0.0098 | 0.0008 ± 0.0154 | 0.0936 | 0.1472 |
| 23 January | 0.985 | 0.0074 | 0.006 | 0.0004 ± 0.0074 | 0.0949 | 0.1377 |
| 25 January | 0.967 | 0.0103 | 0.0083 | 0.0001 ± 0.0103 | 0.0921 | 0.1338 |
| 29 January | 0.990 | 0.0049 | 0.0038 | −0.0004 ± 0.0049 | 0.0903 | 0.1315 |
| 31 January | 0.926 | 0.0093 | 0.0071 | −0.0011 ± 0.0094 | 0.0961 | 0.1232 |
| 1 February | 0.971 | 0.0084 | 0.006 | 0.0001 ± 0.0085 | 0.0942 | 0.1342 |
| 3 February | 0.984 | 0.0059 | 0.0048 | 0.0005 ± 0.0059 | 0.0946 | 0.1329 |
| 4 February | 0.916 | 0.0075 | 0.0052 | 0.0002 ± 0.0076 | 0.0779 | 0.1816 |
| 8 February | 0.919 | 0.0141 | 0.0117 | 0.0007 ± 0.0140 | 0.1088 | 0.1261 |
| 11 February | 0.942 | 0.0101 | 0.0074 | 0.0000 ± 0.0102 | 0.0956 | 0.1373 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Wang, Q.; Tang, M.; Lu, P.; Li, G.; Leppäranta, M.; Huotari, J.; Arvola, L.; Shi, L. Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake. Remote Sens. 2021, 13, 3334. https://doi.org/10.3390/rs13163334
Li Z, Wang Q, Tang M, Lu P, Li G, Leppäranta M, Huotari J, Arvola L, Shi L. Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake. Remote Sensing. 2021; 13(16):3334. https://doi.org/10.3390/rs13163334
Chicago/Turabian StyleLi, Zhijun, Qingkai Wang, Mingguang Tang, Peng Lu, Guoyu Li, Matti Leppäranta, Jussi Huotari, Lauri Arvola, and Lijuan Shi. 2021. "Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake" Remote Sensing 13, no. 16: 3334. https://doi.org/10.3390/rs13163334
APA StyleLi, Z., Wang, Q., Tang, M., Lu, P., Li, G., Leppäranta, M., Huotari, J., Arvola, L., & Shi, L. (2021). Diurnal Cycle Model of Lake Ice Surface Albedo: A Case Study of Wuliangsuhai Lake. Remote Sensing, 13(16), 3334. https://doi.org/10.3390/rs13163334