Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China
Abstract
:1. Introduction
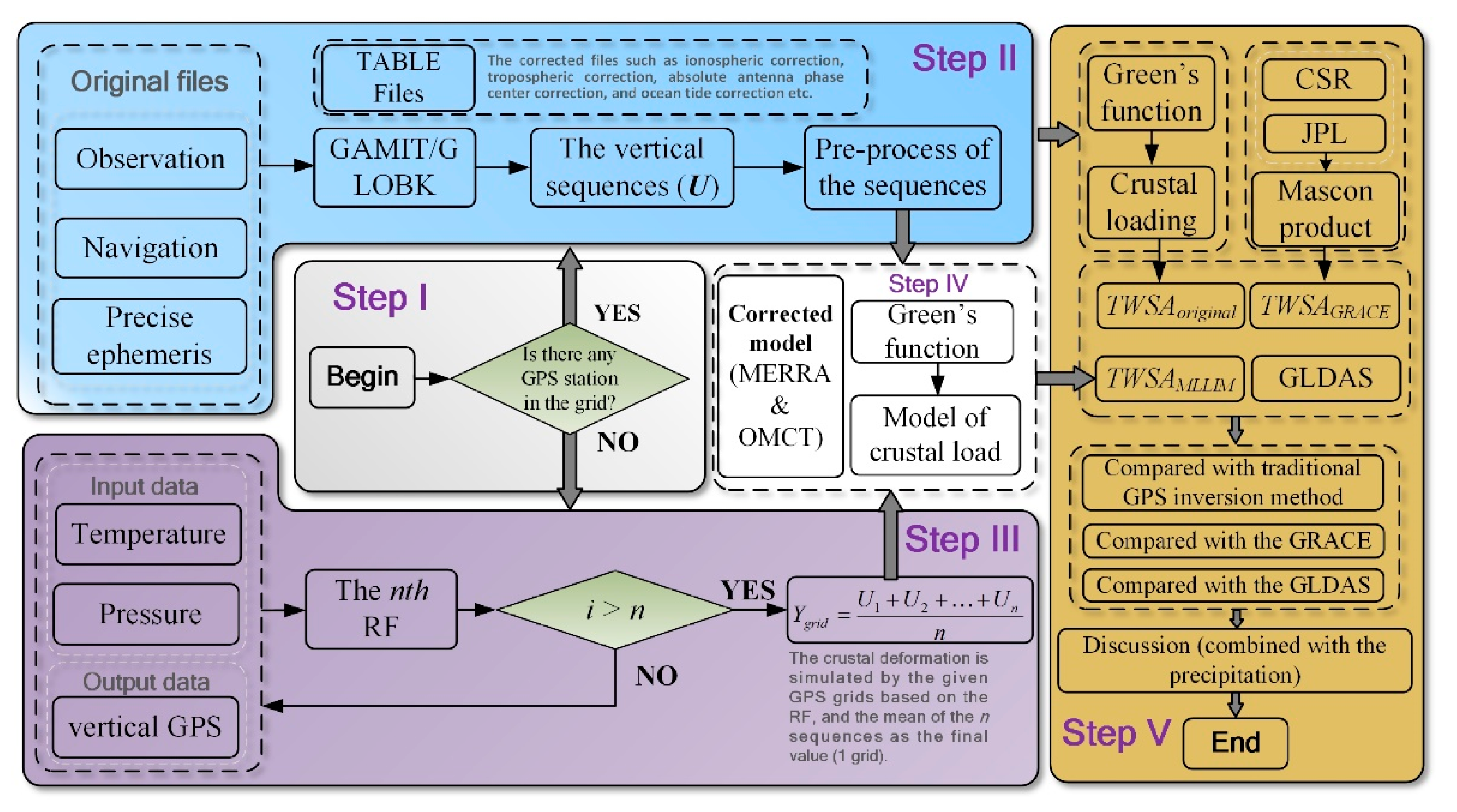
2. Materials and Methods
2.1. Materials
2.1.1. GPS Solutions
2.1.2. GRACE Solutions
2.1.3. Products of GLDAS and ERA 5
2.2. Methods
2.2.1. Random Forest
2.2.2. Inversion of TWSA Using Crustal Load–Deformation
2.2.3. Construction of the MLLIM
2.3. Evaluation Index
3. Results
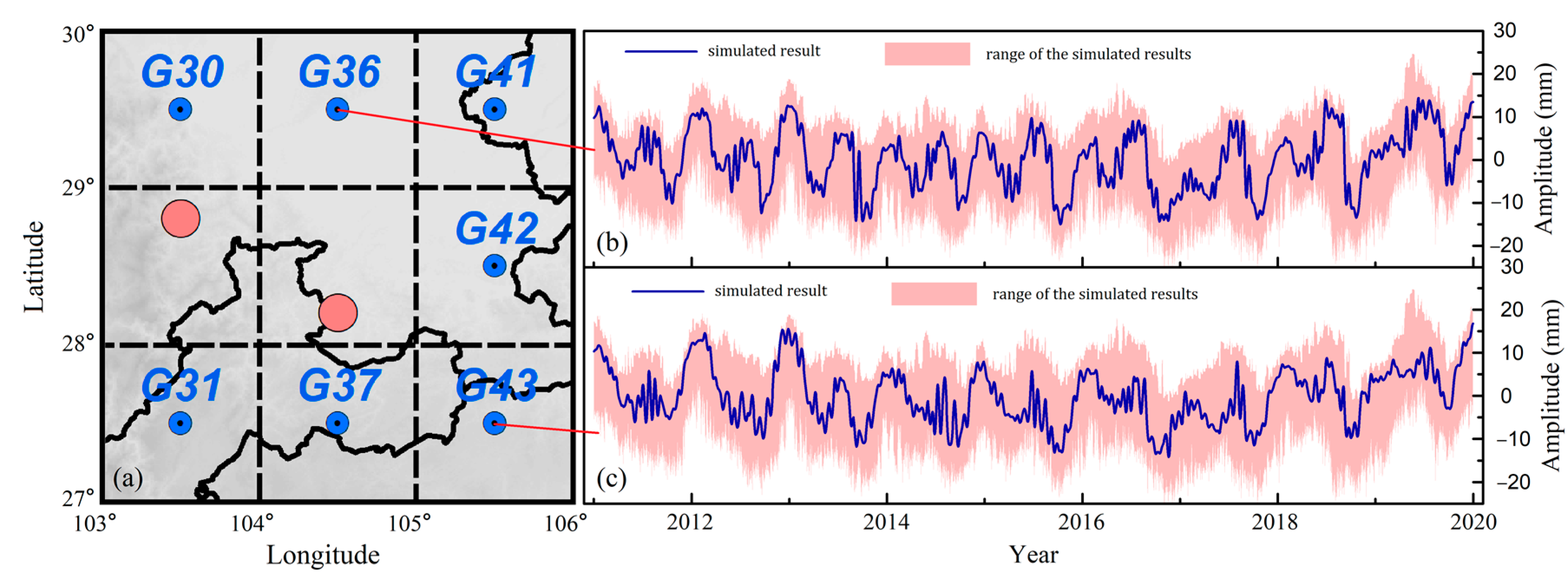
3.1. Inversion of the TWSA Based on the MLLIM
3.2. Comparison with Traditional Method of GPS Inversion
3.3. Comparison with GRACE
3.4. Comparison with the GLDAS Solutions
4. Discussion
5. Conclusions
- (1)
- To increase the inverted accuracy for TWSA, the MLLIM is constructed using RF and the crustal load model. To simulate the crustal displacement in unobserved grids, the sequences of temperature and atmospheric pressure are used as the input data, and the GPS vertical sequence is used as the output data. Thus, the unobserved grids’ crustal deformation can be simulated based on the MLLIM. Furthermore, all the corrected crustal sequences are employed as the input data for the crustal load model; specifically, the corrected sequences include the GPS vertical sequences and the simulated sequences.
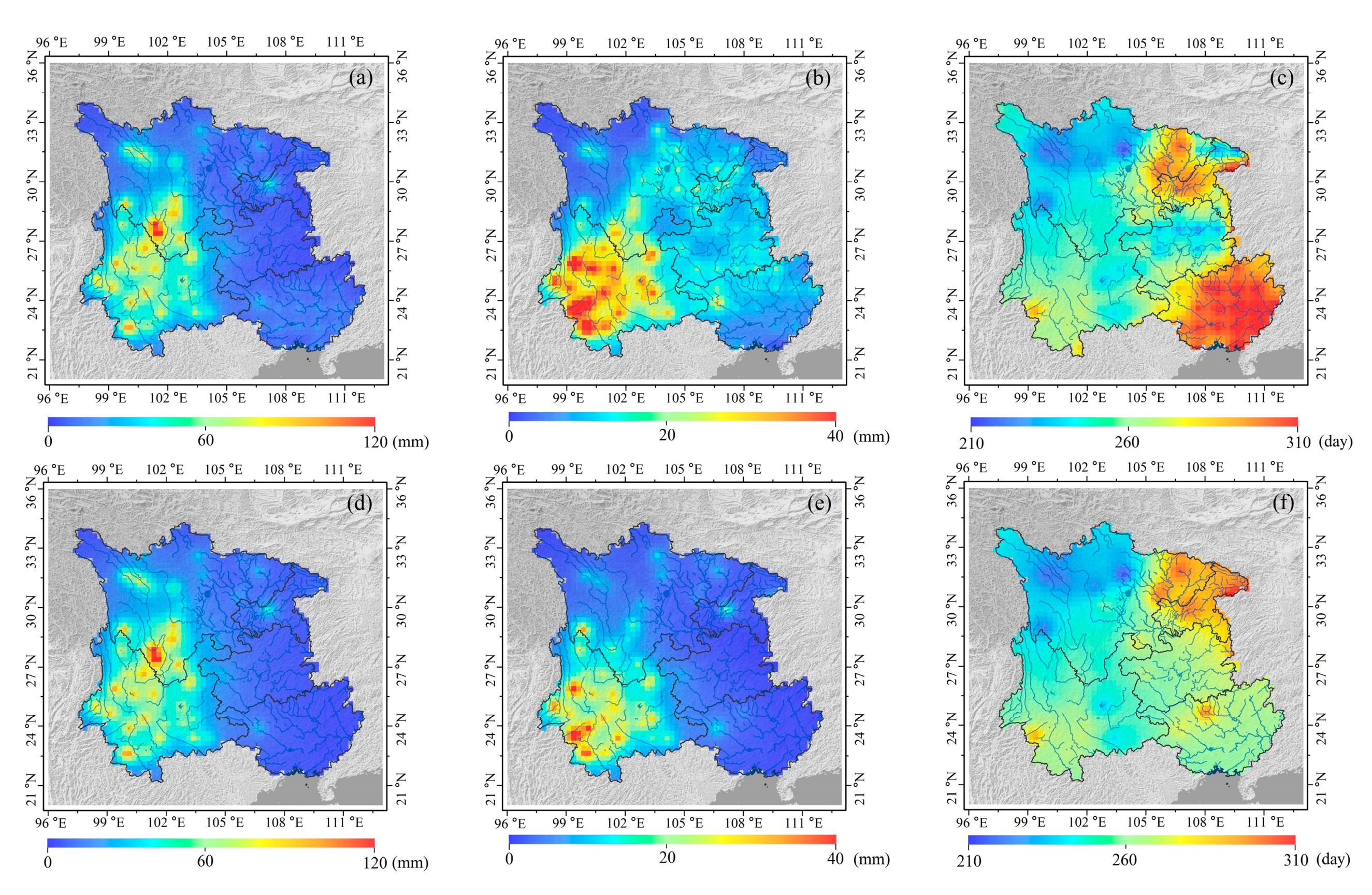
- (2)
- To verify the reliability of the MLLIM, the results of traditional GPS inverted method (without adding the simulated crustal deformation), GRACE, and GLDAS are used to compare with the TWSA based on the MLLIM. The compared results show that this inverted method can detect the raised region of annual amplitude in Yunnan, central Sichuan, and Guangxi provinces, and is consistent with the results of GRACE Mascon and GLDAS. However, the traditional GPS inverted method loses this characteristic signals due to the fitting of inversion (Figure 8d–f). From the comparison with GRACE, the values of PCC with GRACE and GRACE-FO equal 0.91 and 0.88, and the values of R2 equal 0.76 and 0.65, respectively. The MLLIM improves PCC and R2 by 7.98% and 9.30% than traditional method, respectively. From the comparison with GLDAS, the values of PCC and R2 equal 0.79 and 0.64, respectively, it improves PCC and R2 by 9.72% and 6.67% compared with the traditional method, respectively. On the whole, compared with the traditional GPS inverted method, the MLLIM effectively improves the accuracy of TWSA inversion.
- (3)
- The data of precipitation is combined to analyze the relationship between the TWSA and the rainfall. We apply the MLLIM to derive the TWSA in the five provinces, and the results indicate that the precipitation in Yunnan and Guangxi is significantly higher than other provinces. Meanwhile, the spatial distribution characteristics of TWSA is consistent with the precipitation in southwest China. From the comparison with GRACE and GLDAS solutions, the maximum PCC values equal 0.86 and 0.94, respectively. The above conclusions show that the TWSA can be inverted accurately based on the MLLIM in the region where the distribution of GPS stations is uneven.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, A.; Scanlon, B.; Aghakouchak, A.; Zhang, Z. Using GRACE satellite gravimetry for assessing Large-Scale hydrologic extremes. Remote Sens. 2017, 9, 1287. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Xu, B.; Yin, S.; Han, Y.; Zhang, X.; Dai, Z. Water resources utilization and protection in the coal mining area of northern China. Sci. Rep. 2019, 9, 1214. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Ning, L.; Wang, Q.; Chen, J.; Wan, L.; Hong, S. Vulnerability of and risk to water resources in arid and semi-arid regions of west China under a scenario of climate change. Clim. Chang. 2017, 144, 549–563. [Google Scholar] [CrossRef]
- Wu, T.; Zheng, W.; Yin, W.; Zhang, H. Spatiotemporal characteristics of drought and driving factors based on the GRACE-derived total storage deficit index: A case study in southwest China. Remote Sens. 2021, 13, 79–98. [Google Scholar] [CrossRef]
- Ma, S.; Wu, Q.; Wang, J.; Zhang, S. Temporal evolution of regional drought detected from GRACE TWSA and CCI SM in Yunnan Province, China. Remote Sens. 2017, 9, 1124. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S. Statistical downscaling of GRACE-derived groundwater storage using ET data in the North China Plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987. [Google Scholar] [CrossRef]
- Zheng, W.; Xu, Z.; Zhong, M.; Yun, M. Efficient accuracy improvement of GRACE global gravitational field recovery using a new inter-satellite range interpolation method. J. Geodyn. 2012, 53, 1–7. [Google Scholar] [CrossRef]
- Zhong, B.; Li, X.; Chen, J.; Li, Q.; Liu, T. Surface mass variations from GPS and GRACE/GFO: A case study in southwest China. Remote Sens. 2020, 12, 1835–1846. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Jiao, J.J. Evaluation of groundwater storage variations in northern China using GRACE data. Geofluids 2017, 2017, 8254824. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Zhong, M.; Mao, Y.; Ji, B. Evaluation of Evapotranspiration for Exorheic Catchments of China during the GRACE Era: From a Water Balance Perspective. Remote Sens. 2020, 12, 511. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Han, S.C.; Zheng, W.; Yeo, I.Y.; Ghobadi-Far, K. Improved water storage estimates within the North China Plain by assimilating GRACE data into the CABLE model. J. Hydrol. 2020, 590, 125348. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Enzminger, T.L.; Small, E.E.; Borsa, A.A. Accuracy of snow water equivalent estimated from GPS vertical displacements: A synthetic loading case study for western U.S. mountains. Water Resour. Res. 2018, 54, 581–599. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Sasgen, I.; Konrad, H.; Helm, V.; Grosfeld, K. High-resolution mass tends of the antarctic ice sheet through a spectral combination of satellite gravimetry and radar altimetry observations. Remote Sens. 2019, 11, 144. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wang, W.; Zhang, C.; Wen, H.; Zhong, Y.; Zhu, Y.; Li, Z. Bridging terrestrial water storage anomaly during GRACE/GRACE-FO gap using SSA method: A case study in China. Sensors 2019, 19, 4144–4161. [Google Scholar] [CrossRef] [Green Version]
- Tangdamrongsub, N.; Šprlák, M. The assessment of hydrologic- and flood-induced land deformation in data-sparse regions using GRACE/GRACE-FO data assimilation. Remote Sens. 2021, 13, 235. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J. Seasonal and long-term vertical deformation in the Nepal Himalaya constrained by GPS and GRACE measurements. J. Geophys. Res. Solid Earth 2012, 117, 487–497. [Google Scholar] [CrossRef]
- He, M.; Shen, W.; Pan, Y.; Chen, R.; Guo, G. Temporal–Spatial surface seasonal mass changes and vertical crustal deformation in south china block from GPS and GRACE measurements. Sensors 2017, 18, 99. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Khan, S.A.; Dam, T.V.; Liu, L.; Angelen, J.V.; Van, D.; Meertens, C.M. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res. Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef] [Green Version]
- Dagan, G. Solute transport in heterogeneous porous formations. Water Resour. Res. 2004, 55, 671–682. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Argus, D.F.; Fu, Y.; Landerer, F.W. Seasonal variation in total water storage in California inferred from GPS observations of vertical land motion. Geophys. Res. Lett. 2014, 41, 1971–1980. [Google Scholar] [CrossRef]
- Martens, H.R.; Rivera, L.; Simons, M. LoadDef: A python-based toolkit to model elastic deformation caused by surface mass loading on spherically symmetric bodies. Earth Space Sci. 2019, 6, 311–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adusumilli, S.; Borsa, A.A.; Fish, M.A.; McMillan, H.K.; Silverii, F. A decade of water storage changes across the contiguous united states from GPS and satellite gravity. Geophys. Res. Lett. 2019, 46, 13006–13015. [Google Scholar] [CrossRef]
- Xiong, W.; Chen, W.; Zhao, B.; Wen, Y.; Liu, G.; Nie, Z.; Qiao, X.; Xu, C.J.P. Insight into the 2016 menyuan M w 5.9 earthquake with InSAR: A blind reverse event promoted by historical earthquakes. Pure Appl. Geophys. 2018, 176, 577–591. [Google Scholar] [CrossRef]
- Drewes, H. Combination of VLBI, SLR and GPS determined station velocities for actual plate kinematic and crustal deformation models. In Proceedings of the Geodesy on the Move, Berlin, Germany, 12 March 1998; pp. 377–382. [Google Scholar]
- Gautam, P.K.; Gahalaut, V.K.; Prajapati, S.K.; Kumar, N.; Yadav, R.K.; Rana, N.; Dabral, C.P. Continuous GPS measurements of crustal deformation in Garhwal-Kumaun Himalaya. Quat. Int. 2017, 462, 124–129. [Google Scholar] [CrossRef]
- Liu, R.; Li, J.; Fok, H.; Shum, C.K.; Li, Z. Earth surface deformation in the North China Plain detected by joint analysis of GRACE and GPS data. Sensors 2014, 14, 19861–19876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H. Feature extraction algorithm using a correlation coefficient combined with the VMD and its application to the GPS and GRACE. IEEE Access 2021, 9, 17507–17519. [Google Scholar] [CrossRef]
- Ding, Y.H.; Huang, D.F.; Shi, Y.L.; Jiang, Z.S.; Chen, T. Determination of vertical surface displacements in Sichuan using GPS and GRACE measurements. Chin. J. Geophy. 2018, 061, 4777–4788. [Google Scholar]
- He, S.; Gu, Y.; Fan, D.; Zhao, H.; Zheng, R. Seasonal variation of terrestrial water storage in Yunnan province inferred from GPS vertical observations. Acta Geod. Cartogr. Sin. 2018, 47, 332–340. [Google Scholar]
- Martens, H.R.; Argus, D.F.; Norberg, C.; Blewitt, G.; Herring, T.A.; Moore, A.W.; Hammond, W.C.; Kreemer, C. Atmospheric pressure loading in GPS positions: Dependency on GPS processing methods and effect on assessment of seasonal deformation in the contiguous USA and Alaska. J. Geod. 2020, 94, 115. [Google Scholar] [CrossRef]
- Fu, Y.; Argus, D.F.; Freymueller, J.T.; Heflin, M.B. Horizontal motion in elastic response to seasonal loading of rain water in the Amazon Basin and monsoon water in Southeast Asia observed by GPS and inferred from GRACE. Geophys. Res. Lett. 2013, 40, 6048–6053. [Google Scholar] [CrossRef]
- Jiang, Z.; Hsu, Y.-J.; Yuan, L.; Cheng, S.; Li, Q.; Li, M. Estimation of daily hydrological mass changes using continuous GNSS measurements in mainland China. J. Hydrol. 2021, 598, 126349. [Google Scholar] [CrossRef]
- Tregoning, P.; van Dam, T. Atmospheric pressure loading corrections applied to GPS data at the observation level. Geophys. Res. Lett. 2005, 32, L22310. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Xin, S.; Williams, S.D.P.; Jiang, W. Comparing non-tidal ocean loading around the southern north sea with subdaily GPS/GLONASS data. J. Geophys.Res. Solid Earth 2021, 126, e2020JB020685. [Google Scholar] [CrossRef]
- Heki, K. Dense gps array as a new sensor of seasonal changes of surface loads. State Planet Front. Chall. Geophys. 2004, 150, 177–196. [Google Scholar]
- Fu, Y.; Argus, D.F.; Landerer, F.W. GPS as an independent measurement to estimate terrestrial water storage variations in Washington and Oregon. J. Geophys. Res. Solid Earth 2015, 120, 552–566. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Mcclusky, S.C. GAMIT Reference Manual GPS Analysis at MIT Release 10.3; Department of Earth, Atmospheric, Massachusetts Institute of Technology: Cambridge, MA, USA, 2006; p. 182. [Google Scholar]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys.Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Breiman. Random forests. Mach Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.J.; Friedman, J.H. The elements of statistical learning: Springer. Elements 2009, 1, 267–268. [Google Scholar]
- Wang, X.; Chen, L.; Ai, Y.; Xu, T.; Jiang, M.; Yuan, L.; Gao, Y. Crustal structure and deformation beneath eastern and northeastern Tibet revealed by P-wave receiver functions. Earth Planet. Sci. Lett. 2018, 497, 69–79. [Google Scholar] [CrossRef]
- Tesmer, V.; Steigenberger, P.; Dam, T.V.; Mayer-Guerr, T. Vertical deformations from homogeneously processed GRACE and global GPS long-term series. J. Geod. 2011, 85, 291–310. [Google Scholar] [CrossRef]
- Wang, H.; Xiang, L.; Jia, L.; Jiang, L.; Wang, Z.; Hu, B.; Gao, P. Load love numbers and Green’s functions for elastic earth models PREM, iasp91, ak135, and modified models with refined crustal structure from Crust 2.0. Comput. Geosci. 2012, 49, 190–199. [Google Scholar] [CrossRef]
- Wang, Z.; Ou, J. Determining the ridge parameter in a ridge estimation using L-curve method. Editor. Board Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 235–238. [Google Scholar]
- Argus, D. Sustained water changes in California during drought and heavy precipitation inferred from GPS, InSAR, and GRACE. In Proceedings of the Agu Fall Meeting, San Francisco, UCA, USA, 18 December 2015; pp. 14–18. [Google Scholar]
- Jin, S.; Zhang, T. Terrestrial water storage anomalies associated with drought in southwestern USA from GPS observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]
- Davis, J.L. Climate-driven deformation of the solid Earth from GRACE and GPS. Geophys. Res. Lett. 2004, 31, L24605. [Google Scholar] [CrossRef] [Green Version]
- Nahmani, S.; Bock, O.; Bouin, M.N.; Santamaría-Gómez, A.; Boy, J.P.; Collilieux, X.; Métivier, L.; Panet, I.; Genthon, P.; Linage, C.d. Hydrological deformation induced by the west African Monsoon: Comparison of GPS, GRACE and loading models. J. Geophys. Res. Atmos. 2012, 117, 0148–0227. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Dam, T.V.; Sneeuw, N.; Collilieux, X.; Weigelt, M.; Rebischung, P. Singular spectrum analysis for modeling seasonal signals from GPS time series. J. Geodyn. 2013, 72, 25–35. [Google Scholar] [CrossRef]
- Ji, L.; Senay, G.B.; Verdin, J.P. Evaluation of the global land data assimilation system (GLDAS) air temperature data products. J. Hydrometeorol. 2015, 16, 150731131106004. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, L.; Zhou, T.; Liu, J. The Asian subtropical westerly jet stream in CRA-40, ERA5, and CFSR reanalysis data: Comparative assessment. J. Meteorol. Res. 2021, 35, 46–63. [Google Scholar] [CrossRef]
- Borsa, A.A.; Agnew, D.C.; Cayan, D.R. Ongoing drought-induced uplift in the western United States. Science 2014, 345, 1587–1590. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE) aguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Heinzl, H.; Mittlbock, M. Pseudo R-squared measures for poisson regression models with over- or underdispersion. Comput. Stat. Data Anal. 2003, 44, 253–271. [Google Scholar]
- Fok, H.S.; Liu, Y. An improved GPS-inferred seasonal terrestrial water storage using terrain-corrected vertical crustal displacements constrained by GRACE. Remote Sens. 2019, 11, 1433. [Google Scholar] [CrossRef] [Green Version]
- Mangiarotti, S.; Cazenave, A.; Soudarin, L.; Crétaux, J. Annual vertical crustal motions predicted from surface mass redistribution and observed by space geodesy. J. Geophys. Res. Solid Earth 2001, 106, 4277–4291. [Google Scholar] [CrossRef]
- Nordman, M.; Kinen, J.; Virtanen, H.; Johansson, J.M.; Bilker-Koivula, M.; Virtanen, J. Crustal loading in vertical GPS time series in Fennoscandia. J. Geodyn. 2009, 48, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Gladkikh, V.; Tenzer, R.; Denys, P. Crustal deformation due to atmospheric pressure loading in new Zealand. J. Geod. Sci. 2011, 1, 271–279. [Google Scholar] [CrossRef]
- Petrov, L. The international mass loading service. Physics 2015, 02, 79–83. [Google Scholar]
- Bogusz, J.; Klos, A. On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut. 2016, 20, 655–664. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H.; Yang, S.; Su, K. Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China. Remote Sens. 2021, 13, 3358. https://doi.org/10.3390/rs13173358
Shen Y, Zheng W, Yin W, Xu A, Zhu H, Yang S, Su K. Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China. Remote Sensing. 2021; 13(17):3358. https://doi.org/10.3390/rs13173358
Chicago/Turabian StyleShen, Yifan, Wei Zheng, Wenjie Yin, Aigong Xu, Huizhong Zhu, Shuai Yang, and Kai Su. 2021. "Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China" Remote Sensing 13, no. 17: 3358. https://doi.org/10.3390/rs13173358
APA StyleShen, Y., Zheng, W., Yin, W., Xu, A., Zhu, H., Yang, S., & Su, K. (2021). Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China. Remote Sensing, 13(17), 3358. https://doi.org/10.3390/rs13173358





