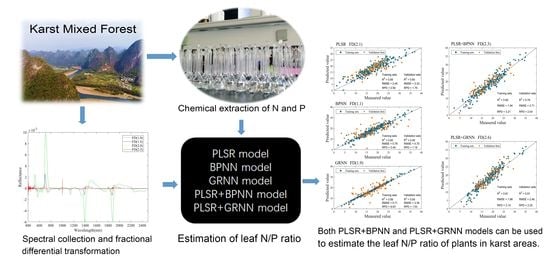
Using Field Spectroradiometer to Estimate the Leaf N/P Ratio of Mixed Forest in a Karst Area of Southern China: A Combined Model to Overcome Overfitting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.3. Methodology
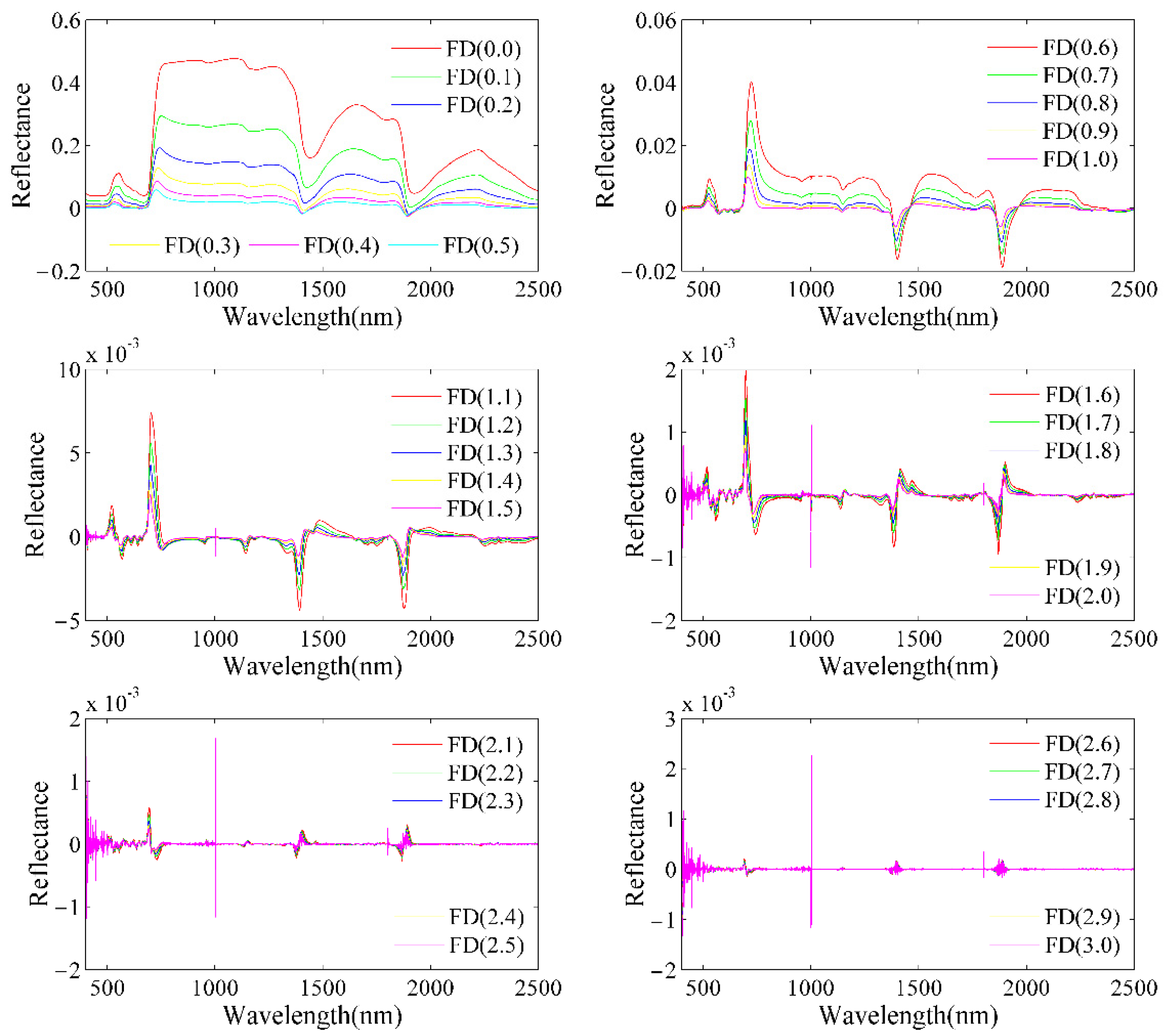
2.3.1. Fractional Differentiation (FD)
2.3.2. Partial Least Squares Regression (PLSR)
2.3.3. Back Propagation Neural Network (BPNN)
2.3.4. Generalized Regression Neural Network (GRNN)
2.3.5. Combined Models, Sample Segmentation, and Accuracy Assessment
3. Results
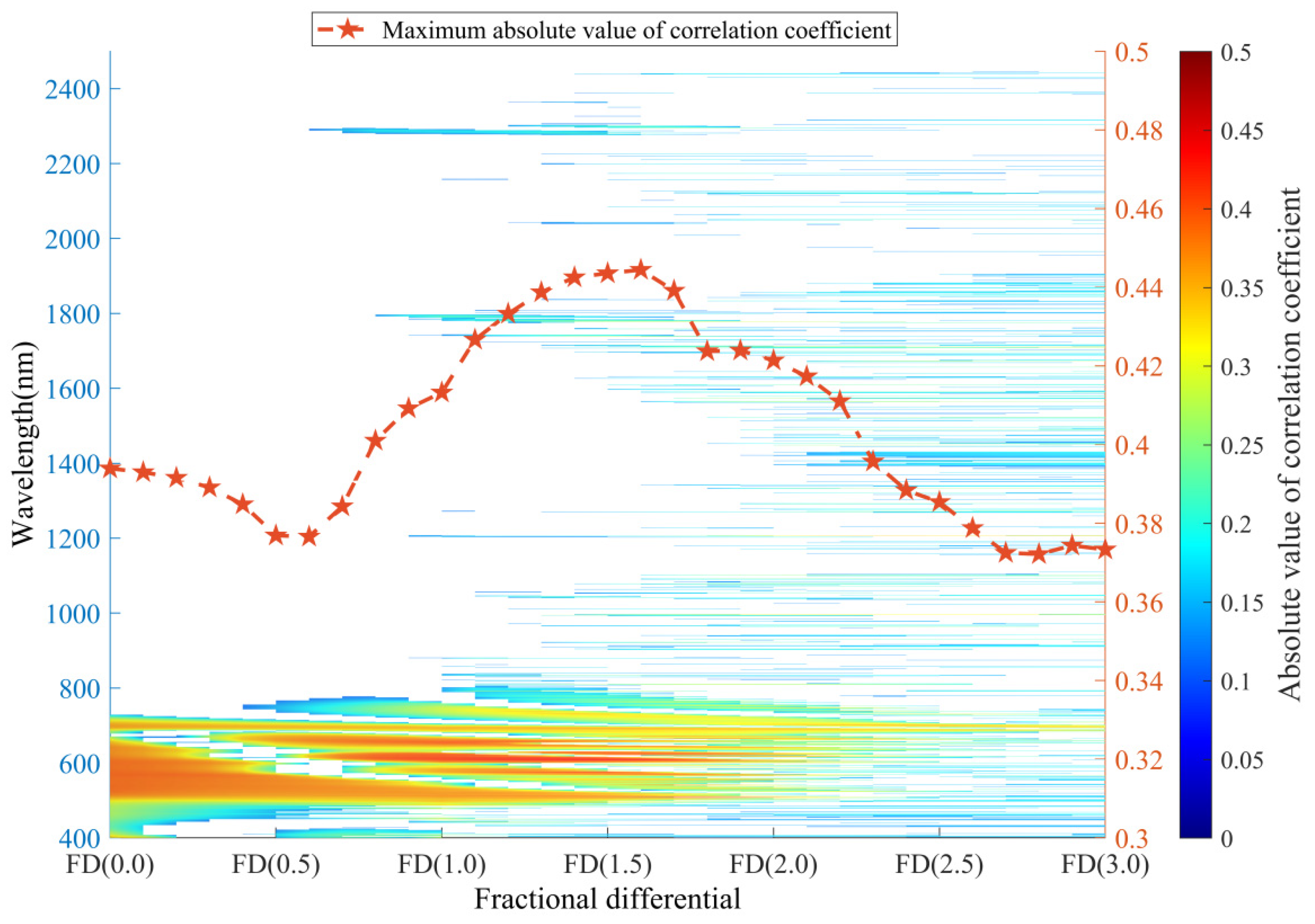
3.1. Leaf N/P Ratio, Fractional Differentiation of Reflectance, and Their Correlation
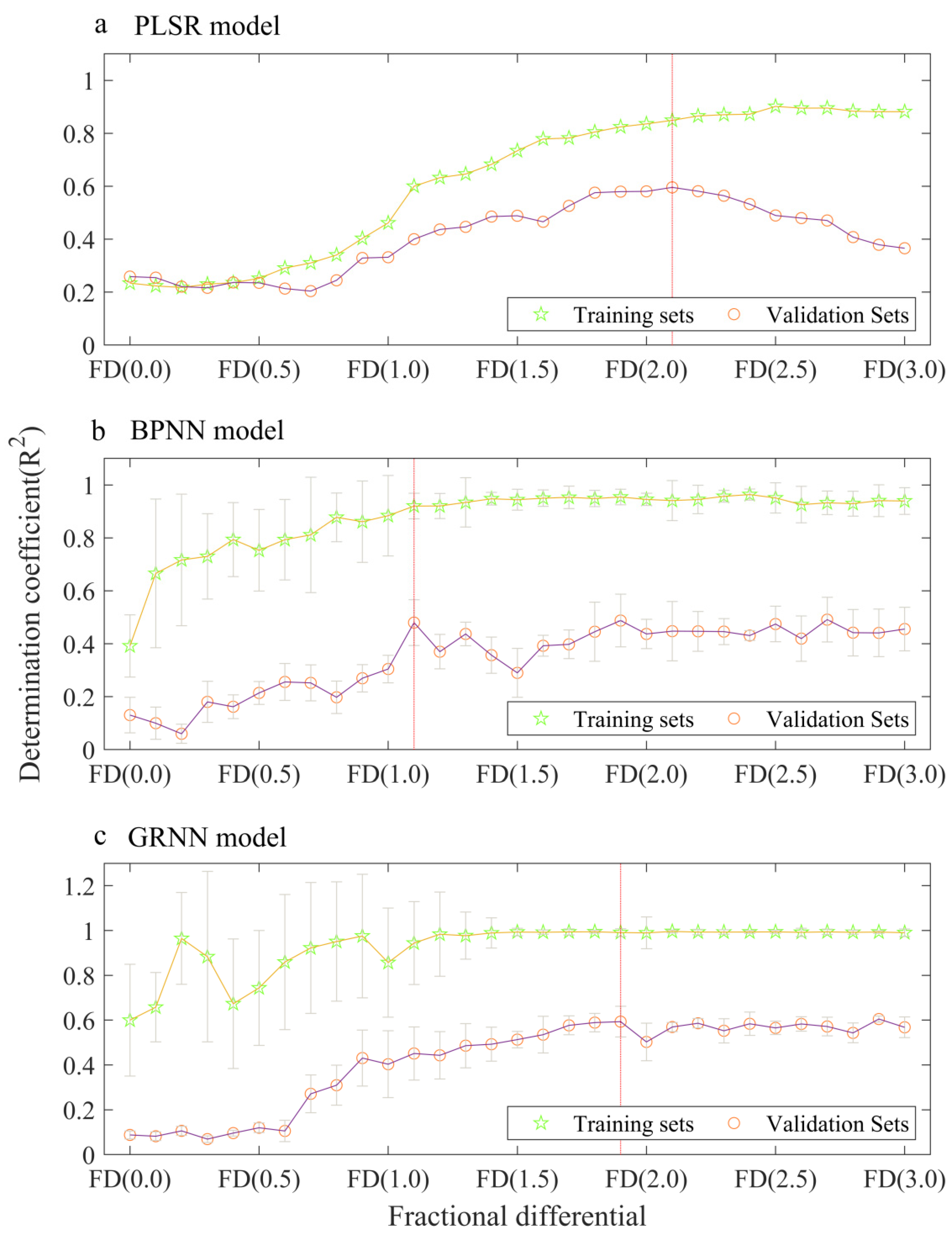
3.2. Performance of a Single Model Using Fractional Differentiation of Reflectance
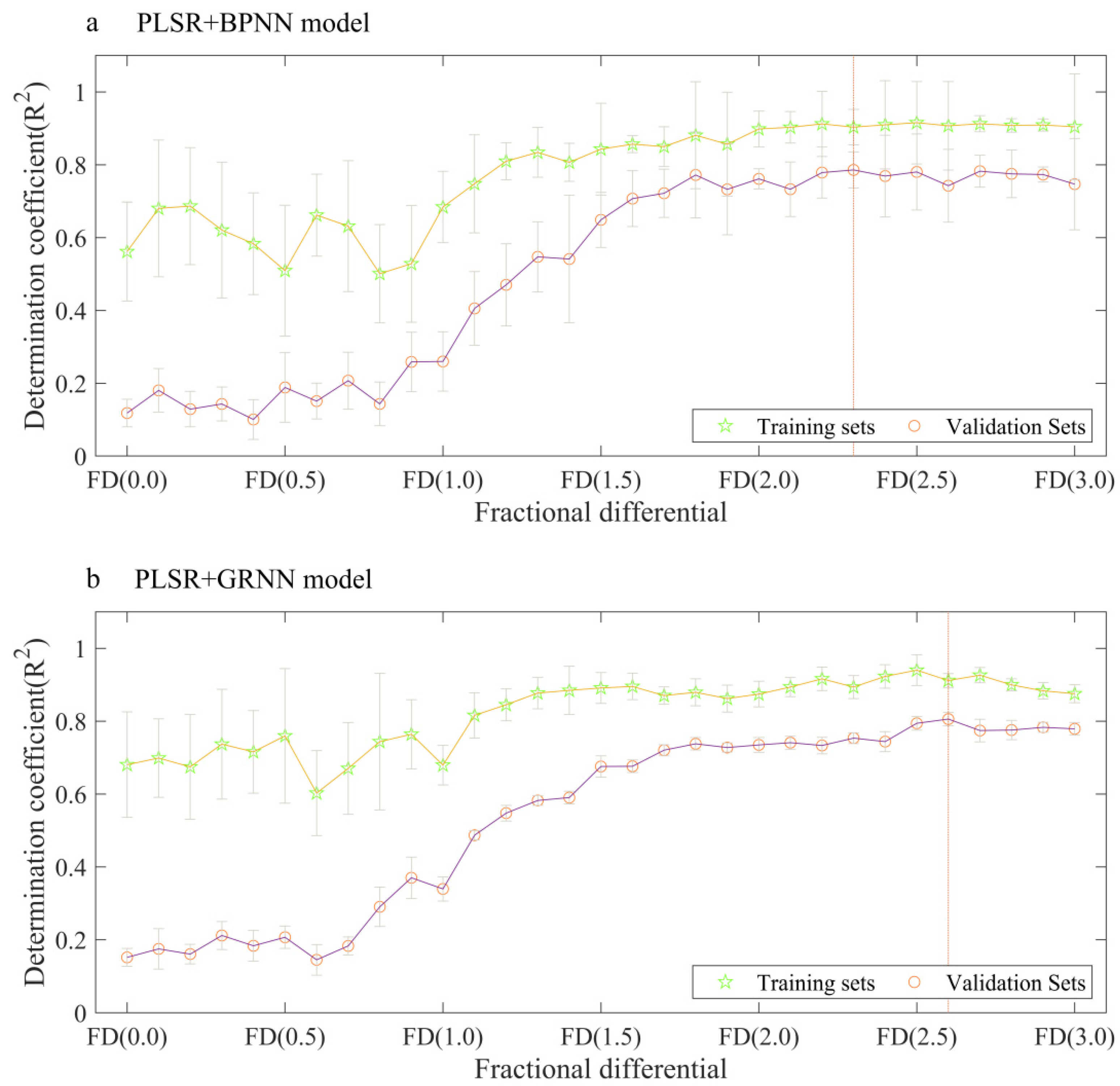
3.3. Performance of Combined Models Using Fractional Differentiation of Reflectance
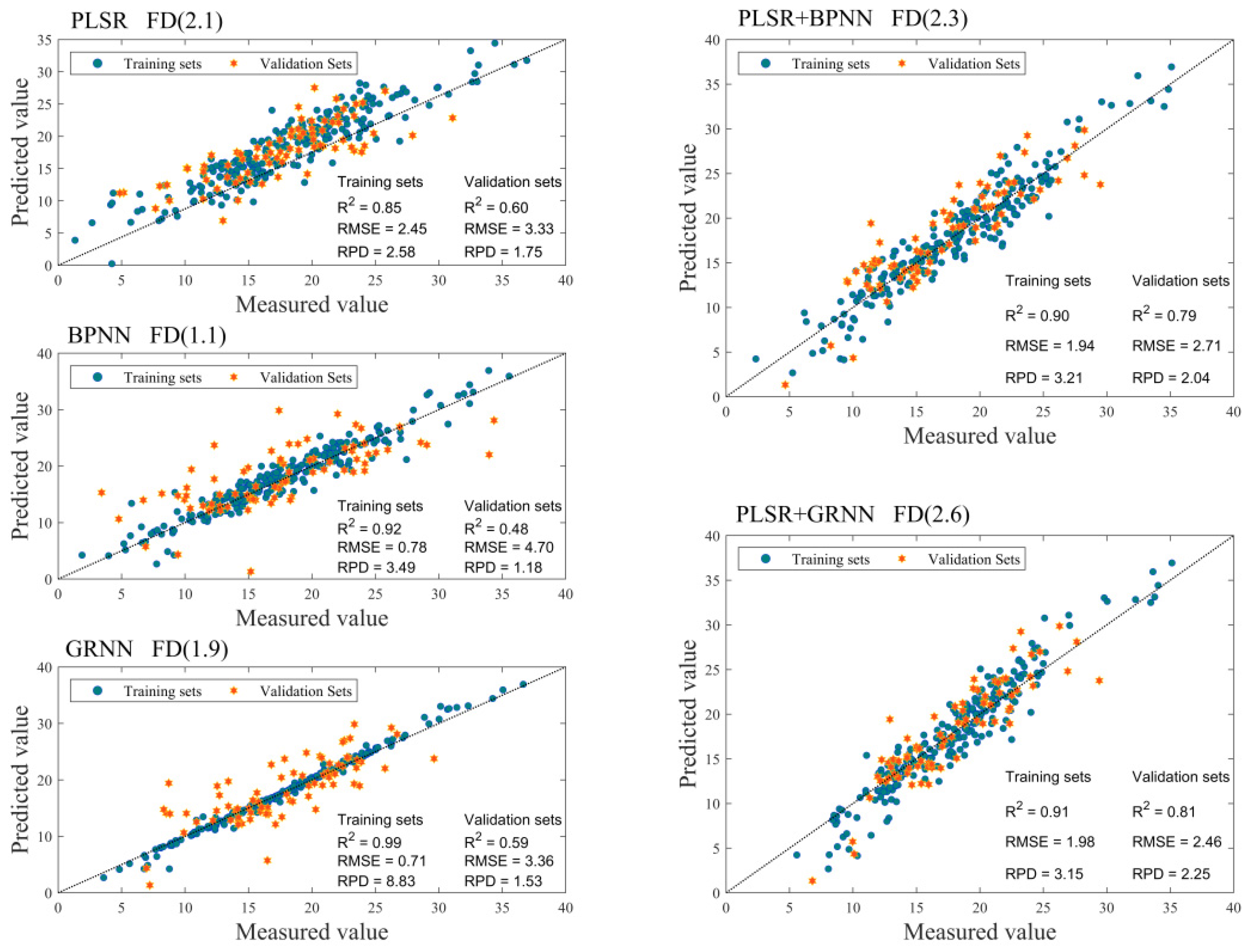
3.4. Model Comparison and Optimal Model Selection
3.5. Advantages of Fractional Differentiation
4. Discussion
4.1. Distribution of Sensitive Wavelengths
4.2. Control Overfitting
4.3. Application for Mixed Forest
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vrede, T.; Dobberfuhl, D.R.; Kooijman, S.A.L.M.; Elser, J.J. Fundamental connections among organism C: N: P stoichiometry, macromolecular composition, and growth. Ecology 2004, 85, 1217–1229. [Google Scholar] [CrossRef] [Green Version]
- Elser, J.J.; Sterner, R.W.; Gorokhova, E.; Fagan, W.F.; Markow, T.A.; Cotner, J.B.; Harrison, J.F.; Hobbie, S.E.; Odell, G.M.; Weider, L.W. Biological stoichiometry from genes to ecosystems. Ecol. Lett. 2000, 3, 540–550. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Gou, X.; Zhang, F.; Bian, R.; Yin, D. Spatial patterns in the C: N: P stoichiometry in Qinghai spruce and the soil across the Qilian Mountains, China. Catena 2020, 196, 104814. [Google Scholar] [CrossRef]
- Elser, J.J.; Fagan, W.F.; Kerkhoff, A.J.; Swenson, N.G.; Enquist, B.J. Biological stoichiometry of plant production: Metabolism, scaling and ecological response to global change. New Phytol. 2010, 186, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Batterman, S.A.; Wurzburger, N.; Hedin, L.O.; Austin, A. Nitrogen and phosphorus interact to control tropical symbiotic N2 fixation: A test inInga punctata. J. Ecol. 2013, 101, 1400–1408. [Google Scholar] [CrossRef]
- Koerselman, W.; Meuleman, A.M.F. The Vegetation N: P Ratio: A New Tool to Detect the Nature of Nutrient Limitation. J. Appl. Ecol. 1996, 33, 1441–1450. [Google Scholar] [CrossRef]
- Gusewell, S. Variation in nitrogen and phosphorus concentrations of wetland plants. Perspect. Plant Ecol. Evol. Syst. 2002, 5, 37–61. [Google Scholar] [CrossRef]
- Cui, L.; Dou, Z.; Liu, Z.; Zuo, X.; Lei, Y.; Li, J.; Zhao, X.; Zhai, X.; Pan, X.; Li, W. Hyperspectral inversion of phragmites communis carbon, nitrogen, and phosphorus stoichiometry using three models. Remote Sens. 2020, 12, 1998. [Google Scholar] [CrossRef]
- Rei, S.; Quan, W. Towards a Universal Hyperspectral Index to Assess Chlorophyll Content in Deciduous Forests. Remote Sens. 2017, 9, 191. [Google Scholar]
- Zhao, H.S.; Zhu, X.C.; Li, C.; Wei, Y.; Zhao, G.X.; Jiang, Y.M. Improving the accuracy of the hyperspectral model for apple canopy water content prediction using the equidistant sampling method. Sci. Rep. 2017, 7, 11192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamashita, H.; Sonobe, R.; Hirono, Y.; Morita, A.; Ikka, T. Dissection of hyperspectral reflectance to estimate nitrogen and chlorophyll contents in tea leaves based on machine learning algorithms. Sci. Rep. 2020, 10, 17360. [Google Scholar] [CrossRef]
- Barnaby, J.Y.; Huggins, T.D.; Lee, H.; McClung, A.M.; Pinson, S.R.M.; Oh, M.; Bauchan, G.R.; Tarpley, L.; Lee, K.; Kim, M.S.; et al. Vis/NIR hyperspectral imaging distinguishes sub-population, production environment, and physicochemical grain properties in rice. Sci. Rep. 2020, 10, 9284. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Al-Suhaibani, N.; Alotaibi, M.; Hassan, W.; Elsayed, S.; Tahir, M.U.; Mohamed, A.I.; Schmidhalter, U. Estimating growth and photosynthetic properties of wheat grown in simulated saline field conditions using hyperspectral reflectance sensing and multivariate analysis. Sci. Rep. 2019, 9, 16473. [Google Scholar] [CrossRef]
- Meacham-Hensold, K.; Montes, C.M.; Wu, J.; Guan, K.; Fu, P.; Ainsworth, E.A.; Pederson, T.; Moore, C.E.; Brown, K.L.; Raines, C.; et al. High-throughput field phenotyping using hyperspectral reflectance and partial least squares regression (PLSR) reveals genetic modifications to photosynthetic capacity. Remote Sens. Environ. 2019, 231, 111176. [Google Scholar] [CrossRef] [PubMed]
- Sonobe, R.; Hirono, Y.; Oi, A. Non-destructive detection of tea leaf chlorophyll content using hyperspectral reflectance and machine learning algorithms. Plants 2020, 9, 368. [Google Scholar] [CrossRef] [Green Version]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A.G.; Féret, J.-B.; Jacquemoud, S.; Ustin, S.L. Deriving leaf mass per area (LMA) from foliar reflectance across a variety of plant species using continuous wavelet analysis. ISPRS J. Photogramm. Remote Sens. 2014, 87, 28–38. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Doktor, D.; Lausch, A.; Spengler, D.; Thurner, M. Extraction of plant physiological status from hyperspectral signatures using machine learning methods. Remote Sens. 2014, 6, 12247–12274. [Google Scholar] [CrossRef] [Green Version]
- Oh, K.; Chung, Y.C.; Kim, K.W.; Kim, W.S.; Oh, I.S. Classification and visualization of Alzheimer’s disease using volumetric convolutional neural network and transfer learning. Sci. Rep. 2019, 9, 18150. [Google Scholar] [CrossRef]
- Gansfort, B.; Traunspurger, W. Environmental factors and river network position allow prediction of benthic community assemblies: A model of nematode metacommunities. Sci. Rep. 2019, 9, 14716. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, D.; Bandyopadhyay, S.; Sinha, D. A scoring scheme for online feature selection: Simulating model performance without retraining. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 405–414. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhou, H.; Cheng, J. The fisher-markov selector: Fast selecting maximally separable feature subset for multiclass classification with applications to high-dimensional data. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1217–1233. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef]
- Dou, Z.; Li, Y.; Cui, L.; Pan, X.; Ma, Q.; Huang, Y.; Lei, Y.; Li, J.; Zhao, X.; Li, W. Hyperspectral inversion of Suaeda salsa bi omass under different types of human activity in Liaohe Estuary wetland in north-eastern China. MAR Freshw. Res. 2020, 71, 482–492. [Google Scholar] [CrossRef]
- Guo, C.; Guo, X. Estimating leaf chlorophyll and nitrogen content of wetland emergent plants using hyperspectral data in the visible domain. Spectrosc. Lett. 2015, 49, 180–187. [Google Scholar] [CrossRef]
- Peuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Benkhettou, N.; Brito da Cruz, A.M.C.; Torres, D.F.M. A fractional calculus on arbitrary time scales: Fractional differentiation and fractional integration. Sig. Process. 2015, 107, 230–237. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Liu, J.; Liang, T.; Hou, M.; Ge, J.; Feng, Q.; Wu, C.; Li, W. Mapping the forage nitrogen-phosphorus ratio based on Sentinel-2 MSI data and a random forest algorithm in an alpine grassland ecosystem of the Tibetan Plateau. Remote Sens. 2020, 12, 2929. [Google Scholar] [CrossRef]
- Yuan, D. World correlation of karst ecosystem: Objectives and implementation plan. China Adv. Earth Sci. 2001, 4, 461–466. (In Chinese) [Google Scholar]
- Luo, Z.; Tang, S.; Jiang, Z.; Chen, J.; Fang, H.; Li, C. Conservation of terrestrial vertebrates in a global hotspot of karst area in southwestern China. Sci. Rep. 2016, 6, 25717. [Google Scholar] [CrossRef] [Green Version]
- Orme, C.D.; Davies, R.G.; Burgess, M.; Eigenbrod, F.; Pickup, N.; Olson, V.A.; Webster, A.J.; Ding, T.S.; Rasmussen, P.C.; Ridgely, R.S.; et al. Global hotspots of species richness are not congruent with endemism or threat. Nature 2005, 436, 1016–1019. [Google Scholar] [CrossRef]
- Zeng, F.; Peng, W.; Song, T.; Wang, K.; Wu, H.; Song, X.; Zeng, Z. Changes in vegetation after 22 years’ natural restoration in the karst disturbed area in northwestern Guangxi, China. Acta Ecol. Sin. 2007, 27, 5110–5119. [Google Scholar] [CrossRef]
- SU, Z.; LI, X. The types of natural vegetation in karst region of Guangxi and its classified system. Guihaia 2003, 23, 289–293. [Google Scholar]
- Shimadzu, S.; Seo, M.; Terashima, I.; Yamori, W. Whole irradiated plant leaves showed faster photosynthetic induction than individually irradiated leaves via improved stomatal opening. Front. Plant Sci. 2019, 10, 1512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richard, H.L.; Donald, L.S. Soil Science of America and American Society of Agronomy. In Methods of Soil Analysis. Part 3. Chemical Methods; Soil Science Society of America: Madison, WI, USA, 1996; pp. 1085–1121. [Google Scholar]
- Bao, S.D. Soil and Agricultural Chemistry Analysis; Agriculture Publication: Beijing, China, 2000; pp. 71–79. [Google Scholar]
- Kharintsev, S.S.; Salakhov, M. A simple method to extract spectral parameters using fractional derivative spectrometry. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2004, 60, 2125–2133. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Li, S.; Liu, H. Composite learning sliding mode synchronization of chaotic fractional-order neural networks. J. Adv. Res. 2020, 25, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Stathakis, D. How many hidden layers and nodes? Int. J. Remote Sens. 2009, 30, 2133–2147. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [Green Version]
- Lotfinejad, M.; Hafezi, R.; Khanali, M.; Hosseini, S.; Mehrpooya, M.; Shamshirband, S. A comparative assessment of predicting daily solar radiation using bat neural network (BNN), generalized regression neural network (GRNN), and neuro-fuzzy (NF) system: A case study. Energies 2018, 11, 1188. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.-W.; Laird, D.A.; Mausbach, M.J.; Hurburgh, C.R. Near-infrared reflectance spectroscopy–principal components regression analyses of soil properties. Soil Sci. Soc. Am. J. 2001, 65, 480–490. [Google Scholar] [CrossRef] [Green Version]
- Reich, P.B.; Oleksyn, J. Global patterns of plant leaf N and P in relation to temperature and latitude. Proc. Natl. Acad. Sci. USA 2004, 101, 11001–11006. [Google Scholar] [CrossRef] [Green Version]
- Han, W.; Fang, J.; Guo, D.; Zhang, Y. Leaf nitrogen and phosphorus stoichiometry across 753 terrestrial plant species in China. New Phytol. 2005, 168, 377–385. [Google Scholar] [CrossRef] [PubMed]
- Elser, J.J.; Fagan, W.F.; Denno, R.F.; Dobberfuhl, D.R.; Folarin, A.; Huberty, A.; Interlandi, S.; Kilham, S.S.; McCauley, E.; Schulz, K.L. Nutritional constraints in terrestrial and freshwater food webs. Nature 2000, 408, 578–580. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Li, Q.; Tu, C.; Cao, J. Carbon, nitrogen and phosphorus stoichiometry of typical plants in karst area of Maocun, Guilin. Guangxi Zhiwu/Guihaia 2015, 35, 493–555. [Google Scholar]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Xu, X.; Yang, G.; Yang, X.; Li, Z.; Feng, H.; Xu, B.; Zhao, X. Monitoring ratio of carbon to nitrogen (C/N) in wheat and barley leaves by using spectral slope features with branch-and-bound algorithm. Sci. Rep. 2018, 8, 10034. [Google Scholar] [CrossRef]
- Li, R.; Wang, S.; Du Xuelian, Y.G. Relationship among leaf anatomical characters and foliarδ~ (13) C values of six woody species for karst rocky desertification areas. China Sci. Silvae Sin. 2008, 44, 29–34. [Google Scholar]
- Liu, X.; Guanter, L.; Liu, L.; Damm, A.; Malenovský, Z.; Rascher, U.; Peng, D.; Du, S.; Gastellu-Etchegorry, J.-P. Downscaling of solar-induced chlorophyll fluorescence from canopy level to photosystem level using a random forest model. Remote Sens. Environ. 2018, 231, 110772. [Google Scholar] [CrossRef]
- Jay, S.; Maupas, F.; Bendoula, R.; Gorretta, N. Retrieving LAI, chlorophyll and nitrogen contents in sugar beet crops from multi-angular optical remote sensing: Comparison of vegetation indices and PROSAIL inversion for field phenotyping. Field Crop. Res. 2017, 210, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Han, X. Nonnegative principal component analysis for cancer molecular pattern discovery. IEEE/ACM Trans. Comput. Biol. Bioinform. 2010, 7, 537–549. [Google Scholar] [PubMed]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global data sets of vegetation leaf area index (LAI) 3g and fraction of photosynthetically active radiation (FPAR) 3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI 3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
- Camino, C.; Gonzalez-Dugo, V.; Hernandez, P.; Zarco-Tejada, P.J. Radiative transfer Vcmax estimation from hyperspectral imagery and SIF retrievals to assess photosynthetic performance in rainfed and irrigated plant phenotyping trials. Remote Sens. Environ. 2019, 231, 111186. [Google Scholar] [CrossRef]
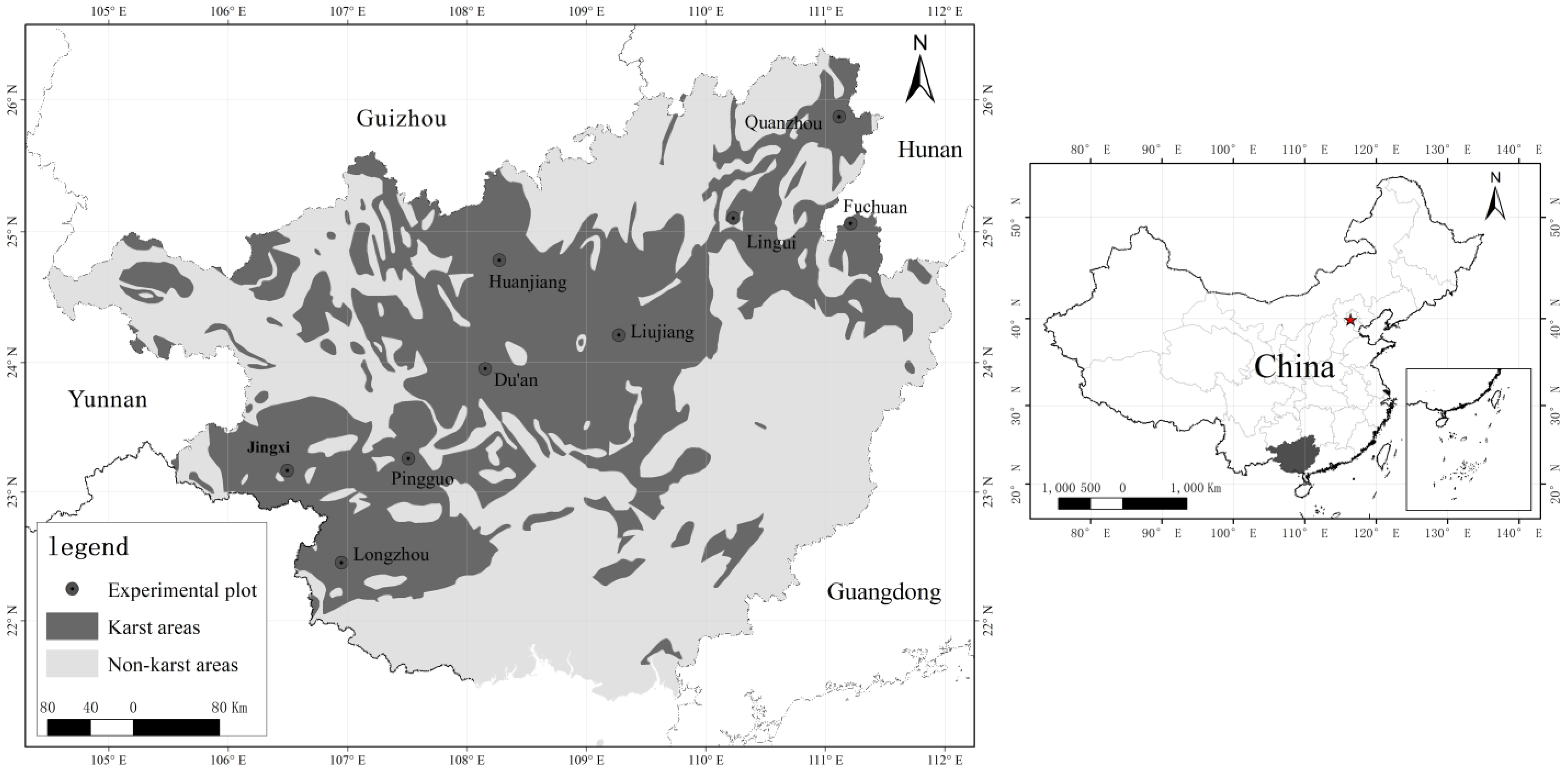

| No. | Name of the Experimental Plot | Successional Stages of the Plant Community | Name of Dominant Species | Average Annual Temperature | Average Annual Rainfall |
|---|---|---|---|---|---|
| 1 | Jingxi | Secondary forest | Cladrastis platycarpa (Maxim.) Makino, Bruguiera gymnorhiza (L.) Lam., Buddleja officinalis, Abelia biflora Turcz. | 21.68 | 1621.92 |
| 2 | Longzhou | Primary forest | Canthium dicoccum, Memecylon scutellatum, Pistacia weinmanniifolia, Boniodendron minus, Excentrodendron hsienmu | 23.28 | 1272.72 |
| 3 | Pingguo | Shrubs | Rhus chinensis Mill., Cipadessa baccifera (Roth.) Miq., Vitex negundo L., Alchornea trewioides | 22.03 | 1328.63 |
| 4 | Du’an | Shrubs | Psidium guajava, Vitis heyneana, Buddleja officinalis, Serissa japonica | 22.03 | 1733.37 |
| 5 | Huanjiang | Secondary forest | Solanum indicum L., Ficus tinctoria Forst. F. subsp. gibbosa (Bl.) Corner, Albizia lebbeck (Linn.) Benth., Vitex negundo L. | 22.50 | 1392.50 |
| 6 | Liujiang | Secondary forest | Alchornea trewioides, Litsea glutinosa, Maclura cochinchinensis, Vitex negundo L. | 21.57 | 1433.62 |
| 7 | Lingui | Scrubs | Bauhinia championii, Zanthoxylum bungeanum, Sageretia thea, Rosa cymosa | 21.56 | 1891.94 |
| 8 | Quanzhou | Scrubs | Paliurus ramosissimus, Ilex corallina var. loeseneri, Bauhinia championii, Sageretia thea | 21.65 | 1529.96 |
| 9 | Fuchuan | Secondary forest | Albizia kalkora, Pistacia chinensis Bunge, Sapium sebiferum (L.) Roxb., Vitex negundo L. | 19.47 | 1685.97 |
| Samples | Number | Mean | Standard Deviation | Coefficient of Variation (%) |
|---|---|---|---|---|
| Total samples | 301 | 17.97 | 6.05 | 33.68 |
| Training sets | 225 | 17.93 | 6.23 | 34.75 |
| Validation sets | 76 | 18.08 | 5.53 | 30.57 |
| Model | Orders | Training Sets R2 | Training Sets p | Training Sets RMSE | Training Sets RPD | Validation Sets R2 | Validation Sets p | Validation Sets RMSE | Validation Sets RPD |
|---|---|---|---|---|---|---|---|---|---|
| PLSR | FD (0.0) | 0.23 | 0.00 | 5.51 | 1.15 | 0.26 | 0.00 | 4.51 | 1.16 |
| FD (1.0) | 0.46 | 0.00 | 4.62 | 1.37 | 0.33 | 0.00 | 4.37 | 1.19 | |
| FD (2.0) | 0.84 | 0.00 | 2.55 | 2.47 | 0.58 | 0.00 | 3.40 | 1.53 | |
| FD (3.0) | 0.88 | 0.00 | 2.17 | 2.91 | 0.37 | 0.00 | 4.32 | 1.20 | |
| FD (2.1) | 0.85 | 0.00 | 2.45 | 2.58 | 0.60 | 0.00 | 3.33 | 1.57 | |
| BPNN | FD (0.0) | 0.39 | 0.00 | 5.96 | 1.05 | 0.13 | 0.00 | 8.12 | 0.68 |
| FD (1.0) | 0.88 | 0.00 | 2.25 | 2.77 | 0.30 | 0.00 | 5.33 | 1.04 | |
| FD (2.0) | 0.95 | 0.00 | 1.59 | 3.91 | 0.44 | 0.00 | 5.03 | 1.10 | |
| FD (3.0) | 0.94 | 0.00 | 1.63 | 3.83 | 0.46 | 0.00 | 4.32 | 1.28 | |
| FD (1.1) | 0.92 | 0.00 | 1.78 | 3.49 | 0.48 | 0.00 | 4.70 | 1.18 | |
| GRNN | FD (0.0) | 0.60 | 0.00 | 4.43 | 1.41 | 0.09 | 0.01 | 5.38 | 1.03 |
| FD (1.0) | 0.86 | 0.00 | 3.27 | 1.91 | 0.40 | 0.00 | 4.37 | 1.26 | |
| FD (2.0) | 0.99 | 0.00 | 0.86 | 7.20 | 0.50 | 0.00 | 4.33 | 1.28 | |
| FD (3.0) | 0.99 | 0.00 | 0.83 | 7.54 | 0.57 | 0.00 | 3.69 | 1.50 | |
| FD (1.9) | 0.99 | 0.00 | 0.71 | 8.83 | 0.59 | 0.00 | 3.61 | 1.53 | |
| PLSR+BPNN | FD (0.0) | 0.56 | 0.00 | 4.13 | 1.51 | 0.12 | 0.00 | 5.67 | 0.98 |
| FD (1.0) | 0.68 | 0.00 | 3.54 | 1.76 | 0.26 | 0.00 | 5.08 | 1.09 | |
| FD (2.0) | 0.90 | 0.00 | 2.00 | 3.11 | 0.76 | 0.00 | 2.78 | 1.99 | |
| FD (3.0) | 0.90 | 0.00 | 2.03 | 3.07 | 0.75 | 0.00 | 3.01 | 1.84 | |
| FD (2.3) | 0.90 | 0.00 | 1.94 | 3.21 | 0.79 | 0.00 | 2.71 | 2.04 | |
| PLSR+GRNN | FD (0.0) | 0.68 | 0.00 | 3.95 | 1.58 | 0.80 | 0.00 | 5.08 | 1.09 |
| FD (1.0) | 0.68 | 0.00 | 3.87 | 1.61 | 0.80 | 0.00 | 4.49 | 1.23 | |
| FD (2.0) | 0.87 | 0.00 | 2.44 | 2.56 | 0.80 | 0.00 | 2.86 | 1.93 | |
| FD (3.0) | 0.88 | 0.00 | 2.36 | 2.64 | 0.80 | 0.00 | 2.67 | 2.07 | |
| FD (2.6) | 0.91 | 0.00 | 1.98 | 3.15 | 0.81 | 0.00 | 2.46 | 2.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Li, Y.; Wang, J.; Yao, Y.; Yu, L.; Gu, D.; Ni, L. Using Field Spectroradiometer to Estimate the Leaf N/P Ratio of Mixed Forest in a Karst Area of Southern China: A Combined Model to Overcome Overfitting. Remote Sens. 2021, 13, 3368. https://doi.org/10.3390/rs13173368
He W, Li Y, Wang J, Yao Y, Yu L, Gu D, Ni L. Using Field Spectroradiometer to Estimate the Leaf N/P Ratio of Mixed Forest in a Karst Area of Southern China: A Combined Model to Overcome Overfitting. Remote Sensing. 2021; 13(17):3368. https://doi.org/10.3390/rs13173368
Chicago/Turabian StyleHe, Wen, Yanqiong Li, Jinye Wang, Yuefeng Yao, Ling Yu, Daxing Gu, and Longkang Ni. 2021. "Using Field Spectroradiometer to Estimate the Leaf N/P Ratio of Mixed Forest in a Karst Area of Southern China: A Combined Model to Overcome Overfitting" Remote Sensing 13, no. 17: 3368. https://doi.org/10.3390/rs13173368
APA StyleHe, W., Li, Y., Wang, J., Yao, Y., Yu, L., Gu, D., & Ni, L. (2021). Using Field Spectroradiometer to Estimate the Leaf N/P Ratio of Mixed Forest in a Karst Area of Southern China: A Combined Model to Overcome Overfitting. Remote Sensing, 13(17), 3368. https://doi.org/10.3390/rs13173368