Densely Connected Pyramidal Dilated Convolutional Network for Hyperspectral Image Classification
Abstract
:1. Introduction
2. Related Work
2.1. Residual Network Structure
2.2. Pyramidal Network Structure
2.3. Dilated Convolution
3. Materials and Methods
3.1. Densely Connected Network Structure
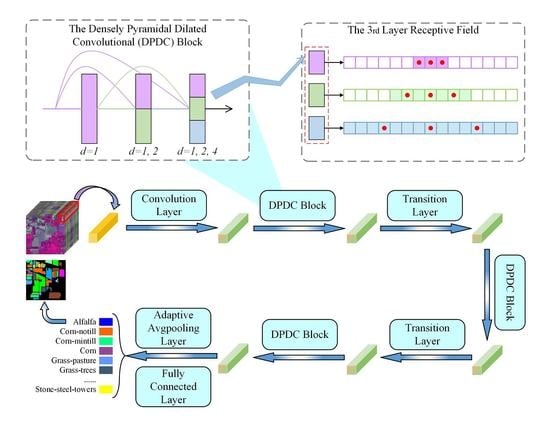
3.2. Densely Pyramidal Dilated Convolutional Block
3.3. Receptive Field
3.4. PDCNet Model
4. Experiments
4.1. Description of HSI Datasets
4.2. Setting of Experimental Parameters
4.3. Influence of Parameters
4.4. Ablation Experiments
4.5. Classification Results
4.5.1. Classification Results (IP Dataset)
4.5.2. Classification Results (UP Dataset)
4.5.3. Classification Results (SV Dataset)
4.6. Comparison with Other Segmentation Method
5. Discussion
5.1. Influence of Training Samples
5.2. Analysis of Running Time and Number of Network Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shabbir, S.; Ahmad, M. Hyperspectral image classification–traditional to deep models: A survey for future prospects. arXiv 2021, arXiv:2101.06116. [Google Scholar]
- Han, Y.; Li, J.; Zhang, Y.; Hong, Z.; Wang, J. Sea ice detection based on an improved similarity measurement method using hyperspectral data. Sensors 2017, 17, 1124. [Google Scholar] [CrossRef] [Green Version]
- Stuart, M.B.; McGonigle, A.J.; Willmott, J.R. Hyperspectral imaging in environmental monitoring: A review of recent developments and technological advances in compact field deployable systems. Sensors 2019, 19, 3071. [Google Scholar] [CrossRef] [Green Version]
- Garzon-Lopez, C.X.; Lasso, E. Species classification in a tropical alpine ecosystem using UAV-Borne RGB and hyperspectral imagery. Drones 2020, 4, 69. [Google Scholar] [CrossRef]
- Borana, S.; Yadav, S.; Parihar, S. Hyperspectral data analysis for arid vegetation species: Smart & sustainable growth. In Proceedings of the 2019 International Conference on Computing, Communication, and Intelligent Systems (ICCCIS), Greater Noida, India, 18–19 October 2019; pp. 495–500. [Google Scholar]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual spectral–spatial attention network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 449–462. [Google Scholar] [CrossRef]
- Meng, Z.; Jiao, L.; Liang, M.; Zhao, F. A lightweight spectral-spatial convolution module for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Signoroni, A.; Savardi, M.; Baronio, A.; Benini, S. Deep learning meets hyperspectral image analysis: A multidisciplinary review. J. Imaging 2019, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Okwuashi, O.; Ndehedehe, C.E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Sabat-Tomala, A.; Raczko, E.; Zagajewski, B. Comparison of support vector machine and random forest algorithms for invasive and expansive species classification using airborne hyperspectral data. Remote Sens. 2020, 12, 516. [Google Scholar] [CrossRef] [Green Version]
- Wang, A.; Wang, Y.; Chen, Y. Hyperspectral image classification based on convolutional neural network and random forest. Remote Sens. Lett. 2019, 10, 1086–1094. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Cariou, C.; Le Moan, S.; Chehdi, K. Improving k-nearest neighbor approaches for density-based pixel clustering in hyperspectral remote sensing images. Remote Sens. 2020, 12, 3745. [Google Scholar] [CrossRef]
- Tu, B.; Wang, J.; Kang, X.; Zhang, G.; Ou, X.; Guo, L. KNN-based representation of superpixels for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4032–4047. [Google Scholar] [CrossRef]
- Su, H.; Yu, Y.; Wu, Z.; Du, Q. Random subspace-based k-nearest class collaborative representation for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6840–6853. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Li, J.; Plaza, A. Active learning with convolutional neural networks for hyperspectral image classification using a new bayesian approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised hyperspectral image classification based on generative adversarial networks. IEEE Geosci. Remote Sens. Lett. 2017, 15, 212–216. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Wang, H.; Tao, C.; Qi, J.; Li, H.; Tang, Y. Semi-supervised variational generative adversarial networks for hyperspectral image classification. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019; pp. 9792–9794. [Google Scholar]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Sun, Y.; Jiang, K.; Li, C.; Jiao, L.; Zhou, H. Spatial sequential recurrent neural network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4141–4155. [Google Scholar] [CrossRef] [Green Version]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded recurrent neural networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Liang, M.; Chen, H.; Yang, S.; Liu, H.; Cao, X. Deep fully convolutional network-based spatial distribution prediction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5585–5599. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Li, Y.; Du, Q.; Xi, B.; Hu, J. Classification of hyperspectral imagery using a new fully convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 292–296. [Google Scholar] [CrossRef]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–spatial exploration for hyperspectral image classification via the fusion of fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- Xu, H.; Yao, W.; Cheng, L.; Li, B. Multiple spectral resolution 3D convolutional neural network for hyperspectral image classification. Remote Sens. 2021, 13, 1248. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W. Hyperspectral image classification based on multi-Scale residual network with attention mechanism. Remote Sens. 2021, 13, 335. [Google Scholar] [CrossRef]
- Rao, M.; Tang, P.; Zhang, Z. A developed siamese CNN with 3D adaptive spatial-spectral pyramid pooling for hyperspectral image classification. Remote Sens. 2020, 12, 1964. [Google Scholar] [CrossRef]
- Miclea, A.V.; Terebes, R.; Meza, S. One dimensional convolutional neural networks and local binary patterns for hyperspectral image classification. In Proceedings of the 2020 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 21–23 May 2020; pp. 1–6. [Google Scholar]
- Cao, X.; Yao, J.; Xu, Z.; Meng, D. Hyperspectral image classification with convolutional neural network and active learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4604–4616. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-branch multi-attention mechanism network for hyperspectral image classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of hyperspectral image based on double-branch dual-attention mechanism network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhong, Z.; Li, J.; Ma, L.; Jiang, H.; Zhao, H. Deep residual networks for hyperspectral image classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1824–1827. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Meng, Z.; Li, L.; Tang, X.; Feng, Z.; Jiao, L.; Liang, M. Multipath residual network for spectral-spatial hyperspectral image classification. Remote Sens. 2019, 11, 1896. [Google Scholar] [CrossRef] [Green Version]
- Han, D.; Kim, J.; Kim, J. Deep pyramidal residual networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5927–5935. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Meng, Z.; Li, L.; Jiao, L.; Feng, Z.; Tang, X.; Liang, M. Fully dense multiscale fusion network for hyperspectral image classification. Remote Sens. 2019, 11, 2718. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Meng, Z.; Jiao, L.; Liang, M.; Zhao, F. Hyperspectral image classification with mixed link networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2494–2507. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep&dense convolutional neural network for hyperspectral image classification. Remote Sens. 2018, 10, 1454. [Google Scholar]
- Nalepa, J.; Antoniak, M.; Myller, M.; Lorenzo, P.R.; Marcinkiewicz, M. Towards resource-frugal deep convolutional neural networks for hyperspectral image segmentation. Microprocess. Microsyst. 2020, 73, 102994. [Google Scholar] [CrossRef]
- Fu, P.; Sun, X.; Sun, Q. Hyperspectral image segmentation via frequency-based similarity for mixed noise estimation. Remote Sens. 2017, 9, 1237. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zheng, X.; Lu, X. A supervised segmentation network for hyperspectral image classification. IEEE Trans. Image Process 2021, 30, 2810–2825. [Google Scholar] [CrossRef]
- Si, Y.; Gong, D.; Guo, Y.; Zhu, X.; Huang, Q.; Evans, J.; He, S.; Sun, Y. An Advanced Spectral–Spatial Classification Framework for Hyperspectral Imagery Based on DeepLab v3+. Appl. Sci. 2021, 11, 5703. [Google Scholar] [CrossRef]
- Takahashi, N.; Mitsufuji, Y. Densely connected multidilated convolutional networks for dense prediction tasks. arXiv 2020, arXiv:2011.11844. [Google Scholar]
- Meng, Z.; Zhao, F.; Liang, M.; Xie, W. Deep Residual Involution Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3055. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Ge, Z.; Zhang, Y.; Fu, P. Double-Branch Network with Pyramidal Convolution and Iterative Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1403. [Google Scholar] [CrossRef]
- Gong, H.; Li, Q.; Li, C.; Dai, H.; He, Z.; Wang, W.; Li, H.; Han, F.; Tuniyazi, A.; Mu, T. Multiscale Information Fusion for Hyperspectral Image Classification Based on Hybrid 2D-3D CNN. Remote Sens. 2021, 13, 2268. [Google Scholar] [CrossRef]
- Li, C.; Qiu, Z.; Cao, X.; Chen, Z.; Gao, H.; Hua, Z. Hybrid Dilated Convolution with Multi-Scale Residual Fusion Network for Hyperspectral Image Classification. Micromachines 2021, 12, 545. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Chen, Z.; Li, C. Hierarchical Shrinkage Multi-Scale Network for Hyperspectral Image Classification with Hierarchical Feature Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5760–5772. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]













| Number | Class | Train Samples | Test Samples | Total Samples |
|---|---|---|---|---|
| 1 | Alfalfa | 7 | 39 | 46 |
| 2 | Corn-notill | 214 | 1214 | 1428 |
| 3 | Corn-mintill | 125 | 705 | 830 |
| 4 | Corn | 36 | 201 | 237 |
| 5 | Grass-pasture | 72 | 411 | 483 |
| 6 | Grass-trees | 110 | 620 | 730 |
| 7 | Grass-pasture-mowed | 4 | 24 | 28 |
| 8 | Hay-windrowed | 72 | 406 | 478 |
| 9 | Oats | 3 | 17 | 20 |
| 10 | Soybean-notill | 146 | 826 | 972 |
| 11 | Soybean-mintill | 368 | 2087 | 2455 |
| 12 | Soybean-clean | 89 | 504 | 593 |
| 13 | Wheat | 31 | 174 | 205 |
| 14 | Woods | 190 | 1075 | 1265 |
| 15 | Buildings-grass-trees-drivers | 58 | 328 | 386 |
| 16 | Stone-steel-towers | 14 | 79 | 93 |
| Sum | 1539 | 8710 | 10,249 |
| Number | Class | Train Samples | Test Samples | Total Samples |
|---|---|---|---|---|
| 1 | Asphalt | 332 | 6299 | 6631 |
| 2 | Meadows | 932 | 17,717 | 18,649 |
| 3 | Gravel | 105 | 1994 | 2099 |
| 4 | Trees | 153 | 2911 | 3064 |
| 5 | Painted metal sheets | 67 | 1278 | 1345 |
| 6 | Bare Soil | 251 | 4778 | 5029 |
| 7 | Bitumen | 67 | 1263 | 1330 |
| 8 | Self-Blocking Bricks | 184 | 3498 | 3682 |
| 9 | Shadows | 47 | 900 | 947 |
| Sum | 2138 | 40,638 | 42,776 |
| Number | Class | Train Samples | Test Samples | Total Samples |
|---|---|---|---|---|
| 1 | Brocoli_green_weeds_1 | 40 | 1969 | 2009 |
| 2 | Brocoli_green_weeds_2 | 75 | 3651 | 3726 |
| 3 | Fallow | 40 | 1936 | 1976 |
| 4 | Fallow_rough_plow | 28 | 1366 | 1394 |
| 5 | Fallow_smooth | 54 | 2624 | 2678 |
| 6 | Stubble | 79 | 3880 | 3959 |
| 7 | Celery | 72 | 3507 | 3579 |
| 8 | Grapes_untrained | 225 | 11,046 | 11,271 |
| 9 | Soil_vinyard_develop | 124 | 6079 | 6203 |
| 10 | Corn_senesced_green_weeds | 66 | 3212 | 3278 |
| 11 | Lettuce_romaine_4wk | 21 | 1047 | 1068 |
| 12 | Lettuce_romaine_5wk | 39 | 1888 | 1927 |
| 13 | Lettuce_romiane_6wk | 18 | 898 | 916 |
| 14 | Lettuce_romiane_7wk | 21 | 1049 | 1070 |
| 15 | Vinyard_untrained | 145 | 7123 | 7268 |
| 16 | Vinyard_vertical_trellis | 36 | 1771 | 1807 |
| Sum | 1083 | 53,046 | 54,129 |
| Datasets | 40 | 46 | 52 | 58 | 64 |
|---|---|---|---|---|---|
| IP | 99.43 ± 0.28 | 99.39 ± 0.28 | 99.43 ± 0.20 | 99.39 ± 0.21 | 99.40 ± 0.22 |
| UP | 99.78 ± 0.02 | 99.80 ± 0.05 | 99.82 ± 0.06 | 99.81 ± 0.03 | 99.78 ± 0.07 |
| SV | 99.12 ± 0.25 | 99.09 ± 0.23 | 99.15 ± 0.13 | 99.05 ± 0.29 | 98.93 ± 0.24 |
| Datasets | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| IP | 99.44 ± 0.20 | 99.43 ± 0.20 | 99.34 ± 0.23 | 99.45 ± 0.25 | 99.41 ± 0.24 |
| UP | 99.78 ± 0.01 | 99.82 ± 0.06 | 99.76 ± 0.03 | 99.77 ± 0.05 | 99.78 ± 0.04 |
| SV | 99.18 ± 0.17 | 99.15 ± 0.13 | 99.06 ± 0.25 | 99.02 ± 0.21 | 98.96 ± 0.15 |
| Datasets | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| IP | 99.40 ± 0.19 | 99.47 ± 0.17 | 99.43 ± 0.20 | 99.44 ± 0.20 | 99.42 ± 0.21 |
| UP | 99.73 ± 0.09 | 99.81 ± 0.02 | 99.82 ± 0.06 | 99.78 ± 0.04 | 99.71 ± 0.06 |
| SV | 98.97 ± 0.22 | 99.14 ± 0.25 | 99.15 ± 0.13 | 98.95 ± 0.34 | 98.88 ± 0.28 |
| Datasets | 9 | 11 | 13 | 15 | 17 |
|---|---|---|---|---|---|
| IP | 99.36 ± 0.09 | 99.43 ± 0.20 | 99.50 ± 0.18 | 99.38 ± 0.10 | 99.46 ± 0.06 |
| UP | 99.74 ± 0.10 | 99.82 ± 0.06 | 99.80 ± 0.05 | 99.74 ± 0.05 | 99.71 ± 0.07 |
| SV | 98.53 ± 0.13 | 99.15 ± 0.13 | 99.29 ± 0.21 | 99.45 ± 0.15 | 99.67 ± 0.12 |
| Class | SVM | 3-D CNN | FDMFN | PresNet | DenseNet | PDCNet |
|---|---|---|---|---|---|---|
| 1 | 66.15 ± 8.17 | 95.90 ± 1.26 | 88.21 ± 13.63 | 95.90 ± 3.08 | 96.92 ± 2.99 | 97.95 ± 1.92 |
| 2 | 81.55 ± 2.35 | 96.06 ± 0.79 | 97.50 ± 0.80 | 98.93 ± 0.35 | 99.32 ± 0.30 | 99.34 ± 0.32 |
| 3 | 76.83 ± 3.44 | 95.73 ± 1.26 | 97.44 ± 1.22 | 98.66 ± 0.98 | 99.57 ± 0.29 | 99.46 ± 0.57 |
| 4 | 70.33 ± 4.14 | 94.26 ± 4.66 | 96.64 ± 2.70 | 97.13 ± 3.28 | 97.43 ± 2.60 | 99.11 ± 1.34 |
| 5 | 92.55 ± 2.56 | 96.74 ± 1.16 | 98.59 ± 0.90 | 98.93 ± 0.91 | 99.32 ± 0.64 | 99.07 ± 1.03 |
| 6 | 96.75 ± 0.70 | 99.29 ± 0.28 | 99.52 ± 0.35 | 99.52 ± 0.51 | 99.55 ± 0.26 | 99.71 ± 0.26 |
| 7 | 80.83 ± 5.65 | 97.50 ± 3.33 | 93.33 ± 6.77 | 96.67 ± 4.86 | 97.50 ± 5.00 | 96.67 ± 3.12 |
| 8 | 98.33 ± 0.57 | 100.00 ± 0.0 | 100.00 ± 0.0 | 99.95 ± 0.10 | 100.00 ± 0.0 | 100.00 ± 0.0 |
| 9 | 63.53 ± 12.0 | 87.06 ± 5.76 | 91.76 ± 16.5 | 98.82 ± 2.35 | 95.29 ± 4.40 | 98.82 ± 2.35 |
| 10 | 77.74 ± 4.91 | 94.49 ± 1.94 | 97.57 ± 1.16 | 96.89 ± 1.37 | 98.13 ± 2.11 | 98.59 ± 1.39 |
| 11 | 84.32 ± 2.52 | 98.06 ± 0.69 | 99.32 ± 0.35 | 99.29 ± 0.54 | 98.76 ± 0.94 | 99.75 ± 0.19 |
| 12 | 80.83 ± 3.73 | 96.67 ± 1.24 | 97.75 ± 1.24 | 96.88 ± 1.16 | 99.05 ± 0.70 | 98.93 ± 0.69 |
| 13 | 96.32 ± 2.04 | 99.31 ± 0.67 | 99.77 ± 0.46 | 99.66 ± 0.46 | 100.00 ± 0.0 | 99.66 ± 0.46 |
| 14 | 94.42 ± 1.16 | 99.13 ± 0.62 | 99.65 ± 0.23 | 99.74 ± 0.27 | 99.70 ± 0.24 | 100.00 ± 0.0 |
| 15 | 67.52 ± 3.90 | 96.01 ± 4.80 | 96.50 ± 4.23 | 96.79 ± 3.01 | 99.64 ± 0.48 | 99.70 ± 0.46 |
| 16 | 92.66 ± 0.51 | 98.48 ± 1.86 | 99.24 ± 0.62 | 98.99 ± 0.51 | 97.72 ± 1.24 | 97.72 ± 0.95 |
| OA (%) | 84.54 ± 0.48 | 97.25 ± 0.09 | 98.47 ± 0.28 | 98.74 ± 0.26 | 99.12 ± 0.45 | 99.47 ± 0.17 |
| AA (%) | 82.54 ± 1.07 | 96.54 ± 0.40 | 97.05 ± 1.50 | 98.30 ± 0.50 | 98.62 ± 0.49 | 99.03 ± 0.31 |
| Kappa (%) | 82.39 ± 0.55 | 96.87 ± 0.10 | 98.25 ± 0.32 | 98.57 ± 0.30 | 99.00 ± 0.51 | 99.39 ± 0.20 |
| Class | SVM | 3-D CNN | FDMFN | PresNet | DenseNet | PDCNet |
|---|---|---|---|---|---|---|
| 1 | 92.98 ± 0.76 | 98.44 ± 1.00 | 99.38 ± 0.23 | 99.36 ± 0.14 | 99.77 ± 0.14 | 99.69 ± 0.31 |
| 2 | 97.33 ± 0.21 | 99.71 ± 0.15 | 99.90 ± 0.06 | 99.88 ± 0.08 | 99.96 ± 0.03 | 99.99 ± 0.01 |
| 3 | 76.97 ± 2.25 | 90.73 ± 2.91 | 95.74 ± 2.42 | 95.70 ± 2.67 | 98.35 ± 0.75 | 99.82 ± 0.13 |
| 4 | 87.15 ± 1.93 | 97.62 ± 0.89 | 98.83 ± 0.38 | 98.52 ± 0.59 | 98.91 ± 0.37 | 98.89 ± 0.52 |
| 5 | 99.31 ± 0.09 | 99.66 ± 0.36 | 99.92 ± 0.09 | 100.00 ± 0.0 | 99.84 ± 0.13 | 99.83 ± 0.10 |
| 6 | 77.14 ± 1.28 | 98.64 ± 1.74 | 98.86 ± 1.45 | 99.88 ± 0.15 | 99.99 ± 0.02 | 99.99 ± 0.01 |
| 7 | 58.04 ± 5.75 | 92.29 ± 3.89 | 98.15 ± 1.52 | 97.31 ± 2.00 | 99.76 ± 0.40 | 99.87 ± 0.15 |
| 8 | 85.25 ± 1.59 | 96.62 ± 1.81 | 99.11 ± 0.24 | 98.81 ± 0.86 | 99.78 ± 0.33 | 99.89 ± 0.19 |
| 9 | 99.84 ± 0.15 | 98.60 ± 0.62 | 99.64 ± 0.20 | 99.93 ± 0.13 | 99.02 ± 0.68 | 99.07 ± 0.74 |
| OA (%) | 90.67 ± 0.16 | 98.26 ± 0.79 | 99.28 ± 0.17 | 99.33 ± 0.09 | 99.73 ± 0.02 | 99.82 ± 0.06 |
| AA (%) | 86.00 ± 0.79 | 96.92 ± 1.22 | 98.84 ± 0.33 | 98.82 ± 0.24 | 99.49 ± 0.06 | 99.67 ± 0.08 |
| Kappa (%) | 87.26 ± 0.22 | 97.70 ± 1.04 | 99.05 ± 0.23 | 99.11 ± 0.12 | 99.65 ± 0.03 | 99.76 ± 0.07 |
| Class | SVM | 3-D CNN | FDMFN | PresNet | DenseNet | PDCNet |
|---|---|---|---|---|---|---|
| 1 | 98.32 ± 0.64 | 99.22 ± 0.90 | 99.57 ± 0.67 | 99.80 ± 0.22 | 84.33 ± 13.24 | 100.00 ± 0.0 |
| 2 | 99.67 ± 0.31 | 99.78 ± 0.18 | 99.96 ± 0.04 | 99.75 ± 0.48 | 99.98 ± 0.03 | 100.00 ± 0.0 |
| 3 | 96.55 ± 4.33 | 97.96 ± 2.10 | 99.73 ± 0.39 | 99.71 ± 0.24 | 99.12 ± 1.68 | 99.98 ± 0.04 |
| 4 | 99.18 ± 0.31 | 99.33 ± 0.50 | 99.50 ± 0.56 | 99.33 ± 0.29 | 99.41 ± 0.69 | 99.37 ± 0.55 |
| 5 | 98.31 ± 0.97 | 97.26 ± 0.93 | 99.71 ± 0.26 | 99.66 ± 0.22 | 99.64 ± 0.26 | 99.70 ± 0.35 |
| 6 | 99.61 ± 0.18 | 99.92 ± 0.11 | 99.99 ± 0.01 | 100.00 ± 0.0 | 100.00 ± 0.0 | 100.00 ± 0.0 |
| 7 | 99.44 ± 0.28 | 99.41 ± 0.25 | 99.94 ± 0.13 | 99.90 ± 0.10 | 99.97 ± 0.03 | 99.99 ± 0.01 |
| 8 | 86.92 ± 1.67 | 88.68 ± 1.25 | 93.05 ± 1.07 | 95.07 ± 0.31 | 96.15 ± 1.70 | 97.62 ± 0.62 |
| 9 | 99.04 ± 0.82 | 99.38 ± 0.46 | 100.00 ± 0.0 | 99.89 ± 0.13 | 99.69 ± 0.55 | 100.00 ± 0.0 |
| 10 | 94.24 ± 0.73 | 96.37 ± 1.72 | 98.64 ± 0.96 | 98.85 ± 0.92 | 99.59 ± 0.41 | 99.68 ± 0.36 |
| 11 | 94.01 ± 3.98 | 97.25 ± 1.77 | 99.69 ± 0.35 | 98.93 ± 1.06 | 99.64 ± 0.36 | 99.90 ± 0.15 |
| 12 | 99.51 ± 0.41 | 99.59 ± 0.35 | 99.99 ± 0.02 | 99.99 ± 0.02 | 100.00 ± 0.0 | 100.00 ± 0.0 |
| 13 | 98.37 ± 0.58 | 99.35 ± 0.46 | 99.93 ± 0.09 | 100.00 ± 0.0 | 100.00 ± 0.0 | 100.00 ± 0.0 |
| 14 | 91.08 ± 2.20 | 97.16 ± 1.65 | 99.81 ± 0.13 | 99.92 ± 0.11 | 99.56 ± 0.74 | 99.96 ± 0.05 |
| 15 | 61.00 ± 2.57 | 77.19 ± 3.89 | 94.61 ± 1.09 | 95.58 ± 1.22 | 97.42 ± 1.81 | 98.03 ± 0.90 |
| 16 | 98.05 ± 0.98 | 97.38 ± 1.02 | 98.45 ± 0.70 | 99.00 ± 0.64 | 99.67 ± 0.28 | 99.74 ± 0.23 |
| OA (%) | 90.66 ± 0.50 | 93.75 ± 0.78 | 97.62 ± 0.19 | 98.16 ± 0.15 | 98.12 ± 0.78 | 99.18 ± 0.17 |
| AA (%) | 94.58 ± 0.62 | 96.58 ± 0.41 | 98.91 ± 0.05 | 99.09 ± 0.13 | 98.39 ± 1.04 | 99.62 ± 0.07 |
| Kappa (%) | 89.59 ± 0.55 | 93.03 ± 0.87 | 97.35 ± 0.21 | 97.96 ± 0.17 | 97.90 ± 0.87 | 99.08 ± 0.19 |
| Class | KSC (5%) | UP (5%) | ||
|---|---|---|---|---|
| DeepLab v3+ | PDCNet | DeepLab v3+ | PDCNet | |
| 1 | 98.89 | 100.0 | 99.19 | 99.69 |
| 2 | 100.0 | 95.84 | 99.48 | 99.99 |
| 3 | 97.98 | 97.53 | 99.30 | 99.82 |
| 4 | 99.13 | 88.79 | 97.53 | 98.89 |
| 5 | 96.20 | 90.20 | 99.92 | 99.83 |
| 6 | 100.0 | 98.06 | 99.79 | 99.99 |
| 7 | 100.0 | 92.20 | 98.90 | 99.87 |
| 8 | 91.42 | 98.98 | 96.91 | 99.89 |
| 9 | 100.0 | 100.0 | 99.78 | 99.07 |
| 10 | 99.47 | 99.53 | / | / |
| 11 | 98.74 | 99.65 | / | / |
| 12 | 97.88 | 99.54 | / | / |
| 13 | 100.0 | 100.0 | / | / |
| OA (%) | 98.47 | 98.40 | 99.10 | 99.82 |
| AA (%) | 98.44 | 96.95 | 98.98 | 99.67 |
| Kappa (%) | 98.29 | 98.22 | 98.81 | 99.76 |
| Dataset | Training Samples | SVM | 3-D CNN | FDMFN | PresNet | DenseNet | PDCNet |
|---|---|---|---|---|---|---|---|
| IP | 12.0% | 83.19 ± 0.60 | 95.98 ± 0.23 | 97.60 ± 0.35 | 98.38 ± 0.27 | 98.91 ± 0.27 | 99.17 ± 0.19 |
| 13.0% | 83.88 ± 0.58 | 96.63 ± 0.09 | 98.04 ± 0.33 | 98.56 ± 0.31 | 98.95 ± 0.28 | 99.22 ± 0.34 | |
| 14.0% | 84.27 ± 0.59 | 96.95 ± 0.09 | 98.30 ± 0.36 | 98.58 ± 0.45 | 99.03 ± 0.33 | 99.34 ± 0.20 | |
| 15.0% | 84.54 ± 0.48 | 97.25 ± 0.09 | 98.47 ± 0.28 | 98.74 ± 0.26 | 99.12 ± 0.45 | 99.43 ± 0.20 | |
| 16.0% | 84.82 ± 0.65 | 97.76 ± 0.26 | 98.70 ± 0.34 | 99.05 ± 0.24 | 99.36 ± 0.20 | 99.50 ± 0.19 | |
| UP | 4.00% | 90.32 ± 0.16 | 96.84 ± 1.86 | 98.82 ± 0.24 | 98.80 ± 0.26 | 99.57 ± 0.07 | 99.60 ± 0.06 |
| 5.00% | 90.67 ± 0.16 | 98.26 ± 0.79 | 99.28 ± 0.17 | 99.33 ± 0.09 | 99.73 ± 0.02 | 99.82 ± 0.06 | |
| 6.00% | 90.85 ± 0.16 | 98.58 ± 0.65 | 99.54 ± 0.12 | 99.49 ± 0.21 | 99.75 ± 0.07 | 99.85 ± 0.03 | |
| 7.00% | 90.95 ± 0.14 | 98.75 ± 0.43 | 99.61 ± 0.08 | 99.62 ± 0.19 | 99.79 ± 0.03 | 99.89 ± 0.04 | |
| 8.00% | 91.05 ± 0.11 | 98.79 ± 0.57 | 99.65 ± 0.10 | 99.65 ± 0.15 | 99.77 ± 0.16 | 99.88 ± 0.05 | |
| SV | 2.00% | 90.66 ± 0.50 | 93.75 ± 0.78 | 97.62 ± 0.19 | 98.16 ± 0.15 | 98.12 ± 0.78 | 99.15 ± 0.13 |
| 3.00% | 91.35 ± 0.23 | 94.46 ± 0.50 | 97.98 ± 0.49 | 98.09 ± 0.32 | 97.98 ± 0.90 | 99.18 ± 0.33 | |
| 4.00% | 91.90 ± 0.22 | 95.91 ± 0.40 | 98.98 ± 0.14 | 99.42 ± 0.12 | 99.48 ± 0.20 | 99.75 ± 0.07 | |
| 5.00% | 92.12 ± 0.18 | 96.59 ± 0.50 | 99.27 ± 0.15 | 99.48 ± 0.18 | 99.64 ± 0.10 | 99.86 ± 0.07 | |
| 6.00% | 92.36 ± 0.14 | 96.71 ± 0.27 | 99.36 ± 0.13 | 99.57 ± 0.19 | 99.66 ± 0.15 | 99.88 ± 0.05 |
| Dataset | Method | Training Time (s) | Testing Time (s) | Total Params (M) |
|---|---|---|---|---|
| IP | SVM | 16.562 | 5.270 | / |
| 3-D CNN | 77.328 | 4.313 | 0.101 | |
| FDMFN | 45.623 | 2.177 | 0.139 | |
| PresNet | 77.152 | 3.975 | 1.126 | |
| DenseNet | 108.55 | 5.229 | 4.749 | |
| PDCNet | 180.27 | 3.578 | 1.020 | |
| UP | SVM | 12.294 | 12.575 | / |
| 3-D CNN | 63.365 | 22.895 | 0.050 | |
| FDMFN | 53.930 | 15.485 | 0.137 | |
| PresNet | 96.108 | 34.141 | 1.110 | |
| DenseNet | 138.71 | 47.872 | 4.651 | |
| PDCNet | 234.46 | 29.790 | 0.927 | |
| SV | SVM | 6.967 | 9.888 | / |
| 3-D CNN | 53.659 | 22.261 | 0.103 | |
| FDMFN | 32.264 | 11.695 | 0.139 | |
| PresNet | 54.216 | 21.372 | 1.127 | |
| DenseNet | 75.681 | 28.788 | 4.753 | |
| PDCNet | 125.25 | 19.043 | 1.024 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Zhang, J.; Meng, Z.; Liu, H. Densely Connected Pyramidal Dilated Convolutional Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3396. https://doi.org/10.3390/rs13173396
Zhao F, Zhang J, Meng Z, Liu H. Densely Connected Pyramidal Dilated Convolutional Network for Hyperspectral Image Classification. Remote Sensing. 2021; 13(17):3396. https://doi.org/10.3390/rs13173396
Chicago/Turabian StyleZhao, Feng, Junjie Zhang, Zhe Meng, and Hanqiang Liu. 2021. "Densely Connected Pyramidal Dilated Convolutional Network for Hyperspectral Image Classification" Remote Sensing 13, no. 17: 3396. https://doi.org/10.3390/rs13173396
APA StyleZhao, F., Zhang, J., Meng, Z., & Liu, H. (2021). Densely Connected Pyramidal Dilated Convolutional Network for Hyperspectral Image Classification. Remote Sensing, 13(17), 3396. https://doi.org/10.3390/rs13173396