Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data

Abstract

Linear discriminant analysis (LDA) is a mathematically robust multivariate data analysis approach that is sometimes used for surface oil slick signature classification. Our goal is to rank the effectiveness of LDAs to differentiate oil spills from look-alike slicks. We explored multiple combinations of (i) variables (size information, Meteorological-Oceanographic (metoc), geo-location parameters) and (ii) data transformations (non-transformed, cube root, log₁₀). Active and passive satellite-based measurements of RADARSAT, QuikSCAT, AVHRR, SeaWiFS, and MODIS were used. Results from two experiments are reported and discussed: (i) an investigation of 60 combinations of several attributes subjected to the same data transformation and (ii) a survey of 54 other data combinations of three selected variables subjected to different data transformations. In Experiment 1, the best discrimination was reached using ten cube-transformed attributes: ~85% overall accuracy using six pieces of size information, three metoc variables, and one geo-location parameter. In Experiment 2, two combinations of three variables tied as the most effective: ~81% of overall accuracy using area (log transformed), length-to-width ratio (log- or cube-transformed), and number of feature parts (non-transformed). After verifying the classification accuracy of 114 algorithms by comparing with expert interpretations, we concluded that applying different data transformations and accounting for metoc and geo-location attributes optimizes the accuracies of binary classifiers (oil spill vs. look-alike slicks) using the simple LDA technique.

1. Introduction

The sea-surface signature of mineral oil contamination (“oil slicks”) can be the result of natural causes seeping out of the sea floor (“oil seeps”) or being spilled through human intervention (“oil spills”). Petroleum pollution in both coastal and open-ocean waters is of great ecological concern [1,2]. Oil-related incidents usually draw media attention and public awareness, leading the oil and gas industry to enforce rigorous safety protocols and invest in contingency plans, as well as causing political conflicts, economic issues, ecological problems, and scientific concerns [3,4]. A recent catastrophic oil spillage, unprecedented in the last decades, occurred at the end of 2019 when an unknown source caused a myriad of massive oil slicks along Brazil’s shoreline [5].

Remote sensing can help the detection of severe events, including the recent Brazilian case [6], or in the relatively frequent minor oil slicks observed at the ocean surface; satellite data can be useful in hindcast oil-slick models [7]. Satellite-based oil pollution monitoring has been extensively employed in recent times, and among the space-borne sensors widely used to study mineral oil floating on the surface of the ocean are the Advanced Very High-Resolution Radiometer (AVHRR [8]), Sea-Viewing Wide Field-of-View Sensor (SeaWiFS [9]), Moderate Resolution Imaging Spectroradiometer (MODIS [10]), and Synthetic Aperture Radar (SAR [11]). Although SAR is considered the most well-suited tool for oil surveillance, partly because of immunity to the surface being hidden by clouds and not needing solar illumination to provide the signal, there is a crucial issue: the ambiguity of oil signatures in the radar backscatter [12]. Other environmental phenomena also produce the same signal as oil in SAR imagery—biogenic films, algal blooms, upwelling, low winds, rain cells, and others [13]. These oil-free false targets are often called “look-alike slicks”.

The remote sensing community has long invested effort to improve understanding of the oil signature in SAR measurements, a process often referred to as image segmentation [14,15]. This mostly consists of identifying smooth sea surface regions with reduced radar backscattering signals, thus delineating the shape of potential oil features [16]. Following SAR image segmentation, another major task is in developing algorithms for the discrimination between possible causes of the signals—oil slicks vs. look-alike slicks [17]. Some researchers have focused on obtaining information about automatic [18] or semi-automatic approaches [19], while others rely on human interpretation [20] to identify oil in SAR imagery. Most of these discrimination algorithms involve complex machine learning techniques, e.g., the Mahalanobis classifier [21], artificial neural networks [22], fuzzy logic [23], decision trees [24], among others; Al-Ruzouq et al. [25] reviews the most frequently used machine learning techniques used for oil slick detection. These methods also use many complicated attributes; Espedal and Johannessen [26] and Stathakis et al. [27] provide an extensive compilation of frequently used attributes. Polarimetric SAR attributes (scattering matrices) have also been investigated [28]. A series of review papers have described the processes for the detection of marine oil slicks, e.g., [29,30,31,32].

Linear discriminant analysis (LDA) is a simple supervised classification technique that can be applied to satellite measurements for classifying oil slicks [33]. Even though LDA is a mathematically robust multivariate data analysis approach, it is seldom published in the scientific literature for oil slick classification [33]. Mattson et al. [34] used LDAs to classify six different infrared spectral patterns of 194 petroleum pollutant samples. The main conclusion of their analysis was that LDAs did not reach a satisfactory classification success rate; however, the LDA performance was positive after postulating it with decision trees. Xu et al. [35] compared the use of penalized LDAs with six other techniques for the classification of 198 targets (spills and look-alikes) identified in 93 satellite images. These authors confirmed that LDAs were effective with 81% to 87% success rates depending on the choice of accuracy metric; but three other methods were more effective. In an attempt to use LDAs, among three other techniques for detecting oil spills, Liu et al. [36] explored three different marine radar images to build a semi-automatic adaptive thresholding detection method. Their LDAs were capable of flagging about 80% of the spills visually identified by human interpretation, with LDAs being the second-best technique. Exploiting 267 targets (spills and look-alikes) observed in 198 SAR images, Cao et al. [37] compared four techniques, including LDA, to train active learning methods to use fewer samples to accomplish effective oil slick classification. They found LDAs as the third best technique reducing the number of utilized samples. The conclusions presented in the few papers using LDAs in classification problems are that there is room for improvement. In the Methods section below, we give more details about LDAs.

A recent research topic is the use of LDAs to differentiate between oil categories: oil seeps vs. oil spills [33]. An aspect of the seep-spill LDA investigation is that easily identified variables (e.g., area and perimeter) resulted in successful classification rates of ~70% [38,39,40]. The positive results of the seep-spill LDA studies, combined with the simplicity and power of the linear analyses to classify oil slicks identified in satellite imagery, form the justifications to retain this linear classification technique in the research reported here, where we study the classification between oil spills and look-alike slicks. While LDAs were applied to remotely sensed features obtained with the Canadian RADARSAT-2 to classify seeps and spills in Gulf of Mexico waters [41], here LDAs are applied to features retrieved in images of the Canadian RADARSAT-1 to distinguish the presence of mineral oil on the sea-surface from other petroleum-free features off the Brazilian coast [42].

Our overall objective here is to rank algorithms applied to many satellite-derived parameters in various data combinations with simple data transformations, according to their success in oil-slick classification. Two experiments to assess the classification of oil spills from look-alike slicks were designed to fulfill our two objectives to rank several combinations of (i) variables and (ii) data transformations using satellite-derived measurements (microwave, infrared, and visible):

• Exclusion or inclusion of specific types of data (Experiment 1); and
• Data transformations applied to the attributes (Experiment 2).

Besides ranking the algorithms and to find the best binary classifiers, our research also seeks to provide improved baseline information for future analyses to discriminate sea-surface features identifiable in SAR imagery. The research reported here introduces five innovations (referred to as “developments”):

• Implementation of stringent knowledge-driven filters;
• Use of simple morphological characteristics (or simply “size information”);
• Exploration of several combinations of Meteorological-Oceanographic parameters (collectively referred to as “metoc variables”);
• Assess the value of the including geo-location parameters (“geo-loc”);
• Application of different data transformations to the attributes in the same analysis.

Following the introduction and statement of objectives given in Section 1, information about the study area and the satellite-based datasets are found in Section 2; the methods are given in Section 3; results are presented in Section 4; important remarks are reported in Section 5 in the discussion of the major findings; and the paper concludes with a summary of our results and some recommendations for future work in Section 6.

2. Study Area and Data

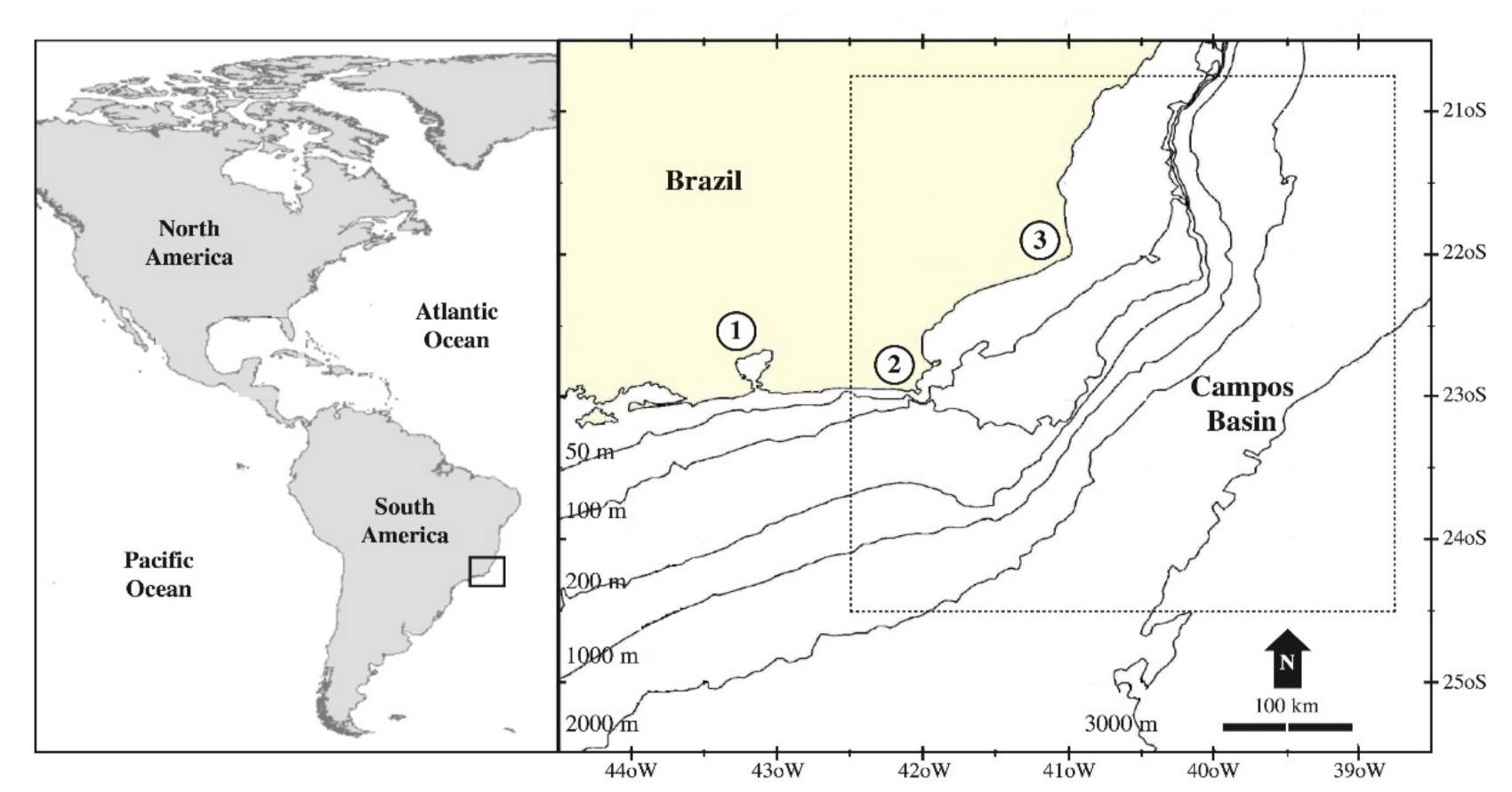
2.1. Study Region

Our area of interest is the Campos Basin offshore of the southeast coast of Brazil (Figure 1). The relevance of this region to the Brazilian economy is due to its numerous offshore oil and gas exploration and production facilities—in 2020, 38 operational fields represented ~25% of the country’s fossil fuel supply with 989,949 barrels of oil equivalent [43].

The Campos Basin has very dynamic meteorological and oceanographic conditions throughout the year: during the austral summer, constant northeasterly winds support upwelling events that drop the surface water temperature and increase the primary biological production, but in the winter months, strong southwesterly winds tend to roughen the sea and primary biological production is reduced [44,45]. These phenomena are not confined to the offshore region between the Cabo de São Tomé and Cabo Frio, near Guanabara Bay, but that is where they are most frequently observed (Figure 1).

2.2. Database

A tabular remote sensing dataset, including microwave, infrared, and visible satellite measurements, was exploited here. This dataset was first utilized by Bentz [46], and later explored by Moutinho [47] and Carvalho et al. [42]. An important characteristic of this dataset for our study is the classification of oil spills vs. look-alikes based on expert interpretation. We use these interpretations as the basis for assessing the LDA accuracies.

The original dataset contained 779 individual polygons that were identified in 402 scenes of the Canadian RADARSAT-1 taken between July of 2001 and June of 2003. These 8-bit, HH polarized, C-band SAR images are from different beam modes [48,49]: ScanSAR Narrow (incident angles: 20 to 46) and Extended Low (incident angles: 10 to 23). Their data were re-sampled to ground resolutions of 100 m [46]. The borders of all observed features with low-backscatter radar signal, i.e., oil and non-oil, were delimited using a multiple resolution segmentation approach [50]. 358 spills are associated with oil samples from identified exploration or production facilities and ship-spills; confirmed spills but from unknown origins are referred to as orphan-spills. 421 look-alike slicks are sea-surface expressions of five different environmental phenomena: biogenic films, algal blooms, upwelling, low wind conditions, and convective rain cells.

Each polygon was described using 34 main descriptive characteristics divided into six attribute types:

• Two textural (i.e., contrast and entropy of the pixels within the features);
• Four related to SAR-signatures (e.g., standard deviation and mean ratios between the pixel values inside and outside of the targets);
• Three scene-related (e.g., quantity of identified features pre-SAR image);
• Nine pieces of size information (e.g., area and perimeter);
• Four metoc variables—cloud cover information, wind speed (WND), sea-surface temperature (SST), and chlorophyll-a concentration (CHL)); and
• Twelve geo-loc parameters (e.g., bathymetry (BAT) and distance to coastline (CST) calculated to the feature centroid).

The textural and SAR-signature attributes were calculated from uncalibrated SAR measurements, i.e., digital numbers (DNs [51]). Metoc measurements were retrieved from auxiliary environmental Earth-Observation System (EOS) satellites: WND from SeaWinds scatterometer onboard the Quick Scatterometer (QuikSCAT [52]), SST from AVHRR on the National Oceanic and Atmospheric Administration (NOAA) satellites [53,54], and CHL from SeaWiFS on the OrbView-2 satellite [55] or MODIS on the Terra satellite [56]. Additionally, ancillary WND, SST, and CHL maps, derived from measurements from these sensors, were also utilized by the experts to assist their binary classifications.

All algorithms evaluated here use part of the data records and some of the attributes contained in the “original dataset” [46]. The subset of the database analyzed here is defined after the discussion of our research strategy and data mining.

3. Methods

A pair of methodological steps was performed: research strategy and data mining exercises (Figure 2). These evolved from prior analyses using LDAs to: (i) differentiate oil spills from oil seeps in RADARSAT-2 images off the Gulf of Mexico coast (Campeche Bay, Mexico) proposed by Carvalho [33] and further developed by Carvalho et al. [38,39,40]; and (ii) distinguish oil spills from look-alike slicks observed in RADARSAT-1 scenes off the coast of Brazil (Campos Basin) [42].

We explored many data combinations: 60 combinations of variables (Experiment 1) and 54 combinations of data transformations (Experiment 2). In practice, each combination was considered as an individual “LDA algorithm”. The data combinations in our algorithms are different to those explored in earlier studies, but are similar in number of combinations in three other papers, i.e., 32 [39] + 61 [40] + 39 [42] = 132. Of the combinations analyzed here (60 + 54 = 114), only nine have been previously investigated, but were modified as discussed below.

3.1. Research Strategy

This section has three parts describing the data filtering, the removal or inclusion of data (Experiment 1), and the consideration of various data transformations in the same analysis (Experiment 2).

3.1.1. Data-Filtering Scheme

The first development is that we removed samples based on the likelihood of them being outliers. Because of a common issue faced in data classification problems, i.e., to define a good collection of instances with representative characteristics of each class [57,58], the proposed filtering was based on local, historical, and empirical knowledge. As a result, we designed quality control tests to remove samples that include values of any variables that are unlikely to contribute to the oil spill vs. look-alike classification. The number of instances in the experiments was determined by this filtering.

3.1.2. Data Information: Removal or Inclusion

This section presents the different ways the attributes were combined to verify the consequences of removal or inclusion of data. These actions assisted in the ranking of the different combinations of variables, which is our first objective.

Of the six attribute types in the original dataset, three were not considered: textural, SAR-signature, and scene-related information (Section 2.2). In the original dataset, texture and SAR-signature had not been converted to backscatter coefficients (sigma-, beta-, or gamma-naught [59]) making it impossible to compare time series of images, but instead, they had been registered in uncalibrated DN values, therefore permitting only relative comparisons within individual scenes. Scene parameters (i.e., number of identified features per scene, sum of the areas of all features within each SAR image, etc.) cannot contribute to a classification scheme, as these are functions of the SAR swath width and not of the slicks. We thus utilized variables from the remaining three attribute types: size information, metoc variables, and geo-loc parameters (Section 2.2). Within these attribute types, we explored three subdivisions: “Size Plus Metoc Set” (Figure 3A: blue panel); “Size Set” (Figure 3B: green panel); and “Metoc Set” (Figure 3C: gray panel). These subdivisions, which were analyzed in conjunction with geo-loc parameters (white circles in Figure 3), are further discussed below.

3.1.2.1. Size Information

The second development here is the independent use of simple size information. Besides the nine geometry, shape, and dimensions characteristics—area, perimeter, shape index (SHP = (perimeter/4).(area^1/2)), compact index (CMP = (4.π.area)/(perimeter²)), asymmetry (ASY = 1 − (ratio between feature’s length and width)), aspect ratio (LtoW = length/width), density (DEN), curvature (CUR), and number of parts of each feature (NUM)—we also explored two other morphologic variables: perimeter-to-area ratio (PtoA), and fractal index (FRA = 2.ln(perimeter/4)/ln(area)). However, several of these eleven attributes are correlated: area with perimeter, CMP with SHP and DEN, LtoW with ASY, and PtoA with CUR [38,39,40,42]. The FRA and NUM variables did not correlate with any other attribute. The choice of uncorrelated attributes is given below (Section 3.2.2). Because the five correlated characteristics (i.e., perimeter, SHP, DEN, ASY, and CUR) led to no LDA classification improvements [42], they are not pursued here. Thus, we use the six uncorrelated variables to define the Size Set; in Figure 3 they are represented by yellow circles:

• area;
• CMP;
• LtoW;
• PtoA;
• FRA; and
• NUM.

3.1.2.2. Metoc Variables

Of the four metoc variables (clouds, WND, SST, and CHL), only cloud cover information was discretely registered as the absence (0) or presence (1) of clouds within the polygons, and is not explored further here due to its binary character. The third development explored three different combinations of metoc variables to quantify their influence (individual and combined) on the algorithm’s accuracy. In Figure 3, black circles correspond to the three combinations defining the Metoc Set:

• WND, SST, and CHL;
• WND; and
• SST and CHL.

3.1.2.3. Geo-Location Parameters

The fourth development is the use of geo-loc parameters. Because most geo-location attributes are site-specific (e.g., distance to petroleum platforms or to underwater pipelines) we only considered two of them:

• bathymetry (BAT); and
• distance to coastline (CST).

In Figure 3, these parameters are shown by white circles. One should note that even though they are considered independently, they are always analyzed together with size information and/or metoc variables.

3.1.2.4. Data Transformations

The application of data transformations to the attributes prior to using them in the machine learning methods is, in principle, capable of improving algorithm classification accuracy [35]. Carvalho et al. [39] tested the LDA performance with data from eight non-linear transformations, and based on their results, we analyzed the data without any transformation (i.e., “non-transformed set”) and with two data transformations:

• cube root; and
• logarithm base 10 (log₁₀).

It should be noted that the FRA variable contains negative values and cannot be subjected to logarithmic transformation.

3.1.2.5. Data Combinations

Eleven variables were carried forward in our study: six pieces of size information (Section 3.1.2.1), three metoc variables (Section 3.1.2.2), and two geo-loc parameters (Section 3.1.2.3). These resulted in nine data combinations of the Size Plus Metoc Set subdivision with and without geo-loc (Figure 3A), three Size Set combinations with and without geo-loc (Figure 3B), and eight Metoc Set combinations with and without geo-loc (Figure 3C). The three attribute-type subdivisions when analyzed with or without geo-loc parameters formed 20 different data combinations. Each of these combinations was analyzed three times—in which all variables were subjected to the same data transformation: non-transformed, cube root, or log₁₀ (Section 3.1.2.4). In the first experiment (denoted as “Data-Information Experiment”) we compared the performance of as many as 60 LDAs (20 × 3). This collection of LDAs was implemented to reach our first objective (Experiment 1) and differ from those proposed in the section to follow to attain our second objective (Experiment 2).

Three of the 39 combinations investigated by Carvalho et al. [42], indicated in Figure 3 by the # symbol, are also evaluated here: (i) all-size information plus all-metoc variables; (ii) all-size information; and (iii) all-metoc variables. However, Carvalho et al. [42] did not include any geo-location data, but all variables were also subjected to the same data transformations as those used in this experiment. This resulted in nine combinations (3 × 3) in common with their study, but here, these combinations are treated differently due to two of the five developments: the elimination of some samples and the analysis including geo-loc parameters.

3.1.3. Combined Use of Several Data Transformations in the Same Analysis

The fifth development of this research in relation to any other published binary classification studies (to our knowledge), is that we verified the influence of applying different data transformations to the attributes in the same analysis, i.e., our second objective. Three selected variables were each subjected to different transformations.

Table 1. The 27 possible data combinations of three variables (Var.) each of which are subjected to three data transformations in the same analysis: none, cube root, or log₁₀. Two distinct assemblages were used in the “Data-Transformation Experiment” to address the second objective—establish the best combination of data transformation for the discrimination of oil spills from look-alike slicks. Baseline combinations with the same transformation are given in the first row. “Metoc Assemblage”: wind speed (WND), sea-surface temperature (SST), and chlorophyll-a concentration (CHL). “Size Assemblage”: area, aspect ratio (length-to-width ratio: LtoW), and number of parts of each feature (NUM)—see also Figure 4 in Carvalho et al. [42]. See also Section 3.1.3.

Var. 1	Var. 2	Var. 3	Var. 1	Var. 2	Var. 3	Var. 1	Var. 2	Var. 3
None	None	None	Cube	Cube	Cube	log10	log10	log10
None	None	Cube	Cube	Cube	None	log10	log10	None
None	Cube	Cube	Cube	None	None	log10	None	None
None	Cube	None	Cube	None	Cube	log10	None	log10
None	None	log10	Cube	Cube	log10	log10	log10	Cube
None	log10	log10	Cube	log10	log10	log10	Cube	Cube
None	log10	None	Cube	log10	Cube	log10	Cube	log10
None	Cube	log10	Cube	None	log10	log10	None	Cube
None	log10	Cube	Cube	log10	None	log10	Cube	None

depicts the 27 possible combinations and its pool of 27 different LDAs—3 variables vs. 3 transformations. LDAs were implemented in two distinct assemblages of variables:

• “Metoc Assemblage”: WND, SST, and CHL; and
• “Size Assemblage”: area, LtoW, and NUM.

These two assemblages resulted in another series of 54 LDAs (27 × 2) that are used in the second experiment, referred to as the “Data-Transformation Experiment”. Regarding the “Assemblage” nomenclature, the reader should not get confused with the terms using “Set” previously defined in Section 3.1.2: Size Set and Metoc Set.

While the Size Assemblage was chosen based on inspection of the dendrograms identifying uncorrelated variables (see Figure 4 in Carvalho et al. [42]), the Metoc Assemblage verifies if we can exclude the use of SAR data and solely use measurements from environmental EOSs sensors. One should note that even though the Metoc Assemblage has the same metoc variables as those from the first Metoc Set, the attributes of this assemblage are subjected to different transformations instead of the same transformation as in the set.

3.2. Data Mining Exercises

This section has three parts describing the selection of attributes, the LDA algorithms, and the evaluation of the algorithm accuracy. An open-access software package was used: Paleontological Statistics (PAST [60]).

3.2.1. Attribute-Selection Approach

Rooted tree dendrograms (Unweighted Pair Group Method with Arithmetic mean: UPGMA [61]) were used to assess the level of correlation among variables. The threshold for uncorrelated attributes using dendrograms is user-defined, and two of the most common approaches have been separately applied here:

• In Experiment 1, an across-dendrogram numeric threshold (phenon line [62]) was used to identify groups of correlated variables from which one attribute is selected per group. This used a fixed Pearson’s r correlation coefficient (0.3 > r > −0.3 [63]); and
• In Experiment 2, a visual identification of correlated groups of variables, from which one attribute is manually selected for each group.

3.2.2. Linear Discriminant Analysis (LDA)

In addition to being used to reduce the dimensionality of data classification analyses, LDAs can be used as a classification technique [64]. In our analyses we explore conventional LDAs, but many other LDA variants exist: global-local LDA [65], probabilistic LDA [66], dual-space LDA [67], null-space LDA [68], penalized LDA [69], among others. While Tharwat et al. [70] and Legendre and Legendre [71] discuss these linear analyses in a wider context, a summary of the main benefits and weaknesses of conventional LDAs is given below:

• Advantages: LDA is a supervised classification method that uses the observed values (attribute magnitudes) of the data (samples) to determine the location of a specific boundary (a linear discriminant axis) between each group (in our case, oil and look-alikes). The LDA general concept is to use the data according to two criteria: (i) maximization of the distance between the average value of each group; and (ii) minimization of the scatter within each group. The ratio of these two criteria, mean squared differences to sum of the variances, is projected onto a line (the linear discriminant axis), providing the ability to linearly separate the groups of samples. This projected lower-dimensional space inherently preserves the group discriminatory information, if one exists. A covariance matrix is calculated for each group along with a within-group scatter matrix to create what is called a discriminant function [72]. Numerically, this function, which corresponds to the dependent variable (DF(X)), is the sum of the product of the independent variables’ values (X_n) with a calculated independent variables’ weight (W_n); a constant offset may apply (C): DF(X) = (X₁W₁ + X₂W₂ + … + X_nW_n) − C [73].
• Disadvantages: LDA outcomes tend to support good classification decisions, but there are limitations. The number of variables must not exceed the number of samples [74]. LDAs are restricted to linearly separable groups. In addition, the variables used should have as small a correlation as possible [75]. This was accomplished through the pre-selection of attributes. Another aspect to consider is that the dataset must include a binary labeling that can be used to assess the LDA performance [76]: the accuracies of our supervised learning method were verified against the baseline of the experts’ classifications.

3.2.3. Classification-Accuracy Assessment

The outcomes of the LDA algorithms (“predicted classes”) were assessed by comparison with the baseline interpretation of experts (“true classes”) with all samples used as the training-set. We choose to work with five straightforward evaluators obtained from 2-by-2 confusion matrices [77] (Figure 4: Panel 1). Because the standalone use of the common performance metric, i.e., overall accuracy (ratio of all correct decisions to all possible outcomes), can be misleading, four additional metrics were used: sensitivity, specificity, positive- and negative-predictive values [78]. Different nomenclatures are found in the literature for these metrics, for instance: “recall” rather than sensitivity, “precision” instead of positive-predictive value, etc. [79]. These four performance metrics play equally important roles alongside the overall accuracy in measuring the success of binary classification algorithms. While sensitivity and specificity indicate the amount of previously known features correctly identified by the LDAs (the predicted classes), the positive- and negative-predictive values report how many of the features predicted by the LDA match the a priori knowledge (the true classes). Figure 4 illustrates the domains of these metrics:

• Panel 1: Diagonal analysis produces the overall accuracy;
• Panel 2: Horizontal analysis provides the sensitivities and specificities (the producer’s accuracy), and their complements (false negatives and false positives: Type I error or omission error); and
• Panel 3: Vertical analysis gives the positive- and negative-predictive values (the user’s accuracy) and their counterparts (inverse of the positive- and inverse of negative-predictive values: Type II error or commission error).

The classification-accuracy assessment using these three 2-by-2 matrix domains (diagonal, horizontal, and vertical) differs from other published investigations exploring oil-slick LDA classifiers, which do not report their accuracies in such a succinct manner as we do here. Some papers ignore the vertical-analysis metrics (e.g., [35]) or even both, horizontal and vertical (e.g., [34,36]).

Algorithms were deemed “void” if an evaluator was below 60%. Another reason to void the algorithms was due to unbalanced classification rates, i.e., algorithms correctly identifying 30% or more of one class than another; see Section 4.1 for the balance sampling percentages of the database analyzed here.

Because of the generation of multiple 2-by-2-tables (60 + 54 = 114), the five performance metrics are given in a compact confusion matrix form. This compact structure is shown in Figure 4 (Panel 4) and displays: the five metrics; the number of correctly identified oil spills and look-alikes (A and D, respectively); and the quantity of all correct classifications (A + D). This simple configuration enables us to construct a single table accounting for all 60 combinations (Experiment 1), and two other tables with 27 combinations each (Experiment 2).

4. Results

This section follows the research strategy (Figure 2). Throughout this section we list 15 important “remarks” that are revisited in the discussion section.

4.1. Data-Filtering Scheme

In the first part of our research (Figure 2) we indicated the number of instances utilized in the 114 LDA algorithms. The outcomes of the knowledge-driven filters are summarized in

Table 2. Summary of the data-filtering scheme showing the number of eliminated records. Wind speed (WND) filter: <3 m/s and >6 m/s. Sea surface temperature (SST) filter: <11 °C. Transcription errors (typo) filter. The statistics of all removed samples, of the original dataset instances [46], and of the analyzed database are also given. See also Section 4.1.

Class/Category	Orginal Dataset		WND Filter			SST Filter	Typo Filter	All Filters	Analyzed Database
			<3 m/s	>6 m/s	Both
Formation Tests	65	(8.3%)	0	−10	−10	0	−3	−13	52	(9.3%)
Accidental Discards	149	(19.1%)	−2	−19	−21	0	−3	−24	125	(22.3%)
Ship-Spills	76	(9.9%)	−1	−13	−14	0	0	−14	62	(11.1%)
Orphan-Spills	68	(8.7%)	−4	−20	−24	0	−2	−26	42	(7.5%)
Oil Spills	358	(46.0%)	−7	−62	−69	0	−8	−77	281	(50.2%)
Biogenic Films	203	(26.1%)	−40	−1	−41	−4	0	−45	158	(28.2%)
Algal Blooms	61	(7.8%)	−18	0	−18	0	0	−18	43	(7.7%)
Upwelling	27	(3.5%)	−2	−5	−7	0	−1	−8	19	(3.4%)
Low Wind	51	(6.5%)	−38	0	−38	0	−1	−39	12	(2.1%)
Rain Cells	79	(10.1%)	0	−26	−26	−6	0	−32	47	(8.4%)
Slick-Alikes	421	(54.0%)	−98	−32	−130	−10	−2	−142	279	(49.8%)
Class/Category	Orginal Dataset		WND filter			SST filter	Typo filter	All Filters	Analyzed Database
			<3 m/s	>6 m/s	Both
All Features	779		−105	−94	−199	−10	−10	−219	560
	100.0%		−13.5%	−12.0%	−25.5%	−1.3%	−1.3%	−28.1%	71.9%

. Ten samples (eight spills and two look-alikes) were identified as having transcription errors, thus removing 1.3% of the original dataset (Table 2). Apart from these, only the WND and SST variables presented unexpected values, and their removal is summarized below:

• WND Filter: The SAR-detection ability to identify sea-surface features relies on reduced radar backscatter from the sea-surface, which is dependent on the local wind field [80]. However, the wind limits (lower and upper) to identify sea-surface features in SAR images are not agreed upon by the remote sensing community [81,82,83]. Weak wind conditions (<3 m/s) may prevent correct classification of features as the ambient water around them is also smooth [81]. Even though some authors have pointed out that oil slicks can be observed in ~10 m/s or higher winds (e.g., [82]), others have found the upper wind limit is ~6 m/s (e.g., [83]). To eliminate unwanted wind influence on our classifiers, samples having wind speed <3 m/s and >6 m/s were not considered. WND filtering removed 199 features (69 spills and 130 look-alikes) that represent 25.5% of the original dataset (Table 2). A primary concern about the WND variable is the ground resolution disparity between the QuikSCAT wind data and the SAR pixel: ~25 km vs. ~100 m. Although we used the wind information already included in the original dataset [46], finer wind measurements could produce different outcomes. The reader is referred to Remark 5 below, where we discuss the WND variable impact on the LDA classification decision.
• SST Filter: The upwelled cold water that usually surfaces in the Campos Basin region comes from the South Atlantic Central Water and has temperatures between 6 °C and 20 °C [84]. However, an analysis of all AVHRR images from the year 2001 in this basin, 176 cloud-free scenes, did not indicate SSTs <11 °C even in the coldest core of the upwelling between Cabo de São Tomé and Cabo Frio [45]. Thus, all samples with SSTs <11 °C were removed prior to the analysis. This SST filtering did not remove any spill samples but eliminated 10 look-alike slicks amounting to 1.3% of the original dataset (Table 2). The ground resolution discrepancy between the AVHRR SSTs and SAR measurements is not as marked as that with the wind, but may also be a matter to bear in mind: ~1 km vs. ~100 m. As this filter only removed 10 look-alikes (Table 2), it is most likely that it did not exert as much influence as the WND filter on the analysis. Even though our choice of 11 °C was based on an earlier analysis, other SST thresholds could influence the LDA outcomes.

These filters removed 21.5% of the oil spills (77) and 33.7% of the look-alike slicks (142) from our analyses (Table 2), resulting in ~28% fewer instances (219) being analyzed in relation to the 779 samples in the original dataset [46]. Consequently, the database analyzed here has 560 records. Since all LDAs were evaluated using the same collection of samples, the discretization resolution of our analyses is 0.18%, i.e., one misclassified feature (1/560).

While the original dataset had a somewhat unbalanced sampling percentage, 46% (358 spills) and 54% (421 look-alikes), the filtered database used here has fortuitously a well-balanced sampling: 50.2% (281 spills) and 49.8% (279 look-alikes); Table 2. This balance increased the chances of reaching good predictability levels among the five performance metrics, thus enabling a more meaningful comparison of the performance of the LDA algorithms.

The data-filtering scheme determined the most effective combination of samples by considering the magnitudes of all selected variables, thus adequately accomplishing its goal of establishing a collection of samples using a conservative approach to reduce the chances of incorrect classification in the two experiments presented below. Other factors influencing the delineation of oil-slick features in the SAR signal include oil type (light or heavy oil), slick age (time in the sea-surface since its release), acquisition geometry (incident angle), among others [85,86]. However, these were not stored as separate attributes in the dataset to allow their implementation as filters.

4.2. Experiment 1: Data Information

Sixty data combinations were analyzed in the second part of our research (Figure 2). The UPGMA dendrograms revealed that the bulk of these combinations had variables correlated at levels practically within the similarity threshold of 0.3 > r > −0.3. The LDA outcomes are presented in

Table 3. Classification accuracy from testing 60 LDA algorithms to determine the best combination of variables—first objective, i.e., “Data-Information Experiment”. Inclusive hierarchy runs from 1 to 60 and is divided in three color-coded blocks: (A) Size Plus Metoc Set (blue: 1–29) (B) Size Set (green: 25–36) and Metoc Set (gray: 37–60), all of which were analyzed with or without at least one geo-location parameter and were subjected to the same data transformation (Transf.): none, cube root, or log₁₀. A ranking within attribute-type subdivisions is also provided between parentheses: 1–27 (Size Plus Metoc Set: blue), 1–9 (Size Set: green), and 1–24 (Metoc Set: gray). Blocks match the three attribute-type subdivisions (Figure 3). Size information: area, compact index (CMP: (4.π.area)/(perimeter²)), aspect ratio (length-to-width ratio: LtoW), perimeter-to-area ratio (PtoA), fractal index (FRA: 2.ln(perimeter/4)/ln(area)), and number of parts of each feature (NUM). Meteorological-Oceanographic (metoc) variables: wind speed (WND), sea surface temperature (SST), and chlorophyll-a concentration (CHL). Geo-location (geo-loc) parameters: bathymetry (BAT) and distance to coastline (CST). Variables not used are indicated with a dot. # indicates combinations previously investigated [42]. $ indicates hierarchies out of order. * indicates unbalanced identification rate: algorithms correctly identifying 30% or more oil spills than look-alike slicks. ! indicates void algorithms: at least one performance metric below 60%, i.e., specificity. For the interpretation of thick table lines see Section 4.2. Detailed statistical information is found in Figure 4.

(A)
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
	1	(1)	Size	WND	SST	CHL	BAT	.	Cube	251	89.3%	223	79.9%	474	84.6%
											81.8%		88.1%
	2	(2)	Size	WND	SST	CHL	BAT	.	log10	251	89.3%	221	79.2%	472	84.3%
											81.2%		88.0%
	3	(3)	Size	WND	SST	CHL	.	CST	Cube	250	89.0%	222	79.6%	472	84.3%
											81.4%		87.7%
	4	(4)	Size	WND	SST	CHL	.	CST	None	245	87.2%	226	81.0%	471	84.1%
											82.2%		86.3%
	5	(5)	Size	WND	SST	CHL	.	CST	log10	250	89.0%	221	79.2%	471	84.1%
											81.2%		87.7%
#	6	(6)	Size	WND	SST	CHL	.	.	None	244	86.8%	226	81.0%	470	83.9%
											82.2%		85.9%
#	7	(7)	Size	WND	SST	CHL	.	.	Cube	250	89.0%	220	78.9%	470	83.9%
											80.9%		87.6%
	8	(8)	Size	WND	.	.	BAT	.	log10	247	87.9%	223	79.9%	470	83.9%
											81.5%		86.8%
	9	(9)	Size	WND	SST	CHL	BAT	.	None	243	86.5%	226	81.0%	469	83.8%
											82.1%		85.6%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
	10	(10)	Size	WND	.	.	.	CST	Cube	247	87.9%	220	78.9%	467	83.4%
											80.7%		86.6%
	11	(11)	Size	WND	.	.	.	CST	None	239	85.1%	227	81.4%	466	83.2%
											82.1%		84.4%
	12	(12)	Size	WND	.	.	.	CST	log10	247	87.9%	219	78.5%	466	83.2%
											80.5%		86.6%
	13	(13)	Size	WND	.	.	.	.	Cube	242	86.1%	223	79.9%	465	83.0%
											81.2%		85.1%
	14	(14)	Size	WND	.	.	BAT	.	Cube	243	86.5%	222	79.6%	465	83.0%
											81.0%		85.4%
	15	(15)	Size	.	SST	CHL	BAT	.	Cube	250	89.0%	215	77.1%	465	83.0%
											79.6%		87.4%
	16	(16)	Size	WND	.	.	.	.	None	237	84.3%	226	81.0%	463	82.7%
											81.7%		83.7%
	17	(17)	Size	WND	.	.	BAT	.	None	237	84.3%	226	81.0%	463	82.7%
											81.7%		83.7%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
#	18	(18)	Size	WND	SST	CHL	.	.	log10	244	86.8%	218	78.1%	462	82.5%
											80.0%		85.5%
	19	(19)	Size	.	SST	CHL	.	.	None	246	87.5%	216	77.4%	462	82.5%
											79.6%		86.1%
	20	(20)	Size	.	SST	CHL	.	CST	Cube	250	89.0%	212	76.0%	462	82.5%
											78.9%		87.2%
	21	(21)	Size	.	SST	CHL	.	.	log10	246	87.5%	214	76.7%	460	82.1%
											79.1%		85.9%
	22	(22)	Size	.	SST	CHL	.	.	Cube	245	87.2%	213	76.3%	458	81.8%
											78.8%		85.5%
	23	(23)	Size	.	SST	CHL	.	CST	None	244	86.8%	214	76.7%	458	81.8%
											79.0%		85.3%
	24	(24)	Size	.	SST	CHL	BAT	.	None	243	86.5%	215	77.1%	458	81.8%
											79.2%		85.0%
$	26	(25)	Size	.	SST	CHL	BAT	.	log10	247	87.9%	209	74.9%	456	81.4%
											77.9%		86.0%
$	27	(26)	Size	WND	.	.	.	.	log10	240	85.4%	216	77.4%	456	81.4%
											79.2%		84.0%
$	29	(27)	Size	.	SST	CHL	.	CST	log10	248	88.3%	206	73.8%	454	81.1%
											77.3%		86.2%
(B)
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
$	25	(1)	Size	.	.	.	BAT	.	Cube	245	87.2%	211	75.6%	456	81.4%
											78.3%		85.4%
$	28	(2)	Size	.	.	.	BAT	.	log10	245	87.2%	210	75.3%	455	81.3%
											78.0%		85.4%
	30	(3)	Size	.	.	.	.	CST	Cube	248	88.3%	205	73.5%	453	80.9%
											77.0%		86.1%
#	31	(4)	Size	.	.	.	.	.	log10	237	84.3%	215	77.1%	452	80.7%
											78.7%		83.0%
	32	(5)	Size	.	.	.	.	CST	log10	245	87.2%	205	73.5%	450	80.4%
											76.8%		85.1%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
	33	(6)	Size	.	.	.	BAT	.	None	240	85.4%	207	74.2%	447	79.8%
											76.9%		83.5%
#	34	(7)	Size	.	.	.	.	.	None	233	82.9%	213	76.3%	446	79.6%
											77.9%		81.6%
#	35	(8)	Size	.	.	.	.	.	Cube	233	82.9%	213	76.3%	446	79.6%
											77.9%		81.6%
	36	(9)	Size	.	.	.	.	CST	None	241	85.8%	203	72.8%	444	79.3%
											76.0%		83.5%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
	37	(1)	.	WND	SST	CHL	BAT	.	log10	220	78.3%	199	71.3%	419	74.8%
											73.3%		76.5%
	38	(2)	.	WND	SST	CHL	.	CST	log10	219	77.9%	199	71.3%	418	74.6%
											73.2%		76.2%
#	39	(3)	.	WND	SST	CHL	.	.	Cube	217	77.2%	200	71.7%	417	74.5%
											73.3%		75.8%
	40	(4)	.	WND	SST	CHL	.	CST	Cube	217	77.2%	200	71.7%	417	74.5%
											73.3%		75.8%
#	41	(5)	.	WND	SST	CHL	.	.	log10	217	77.2%	199	71.3%	416	74.3%
											73.1%		75.7%
	42	(6)	.	WND	SST	CHL	BAT	.	Cube	216	76.9%	198	71.0%	414	73.9%
											72.7%		75.3%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
	43	(7)	.	WND	.	.	.	CST	Cube	215	76.5%	198	71.0%	413	73.8%
											72.6%		75.0%
	44	(8)	.	WND	SST	CHL	BAT	.	None	209	74.4%	204	73.1%	413	73.8%
											73.6%		73.9%
	45	(9)	.	WND	.	.	BAT	.	log10	214	76.2%	198	71.0%	412	73.6%
											72.5%		74.7%
	46	(10)	.	WND	SST	CHL	.	CST	None	210	74.7%	202	72.4%	412	73.6%
											73.2%		74.0%
#	47	(11)	.	WND	SST	CHL	.	.	None	208	74.0%	203	72.8%	411	73.4%
											73.2%		73.6%
	48	(12)	.	WND	.	.	.	CST	log10	217	77.2%	193	69.2%	410	73.2%
											71.6%		75.1%
	49	(13)	.	WND	.	.	BAT	.	Cube	211	75.1%	197	70.6%	408	72.9%
											72.0%		73.8%
	50	(14)	.	WND	.	.	.	CST	None	208	74.0%	198	71.0%	406	72.5%
											72.0%		73.1%
	51	(15)	.	WND	.	.	BAT	.	None	204	72.6%	197	70.6%	401	71.6%
											71.3%		71.9%
Hierarchy		(Rank)	Size	Metoc			Geo-Loc		Transf.	Oil Spills		Slick-Alikes		All Features
*!	52	(16)	.	.	SST	CHL	BAT	.	Cube	223	79.4%	152	54.5%	375	67.0%
											63.7%		72.4%
*!	53	(17)	.	.	SST	CHL	.	.	Cube	221	78.6%	153	54.8%	374	66.8%
											63.7%		71.8%
*!	54	(18)	.	.	SST	CHL	BAT	.	log10	209	74.4%	162	58.1%	371	66.3%
											64.1%		69.2%
*!	55	(19)	.	.	SST	CHL	.	CST	log10	210	74.7%	159	57.0%	369	65.9%
											63.6%		69.1%
*!	56	(20)	.	.	SST	CHL	.	CST	Cube	216	76.9%	153	54.8%	369	65.9%
											63.2%		70.2%
*!	57	(21)	.	.	SST	CHL	.	.	None	212	75.4%	151	54.1%	363	64.8%
											62.4%		68.6%
*!	58	(22)	.	.	SST	CHL	.	CST	None	211	75.1%	148	53.0%	359	64.1%
											61.7%		67.9%
*!	59	(23)	.	.	SST	CHL	.	.	log10	197	70.1%	158	56.6%	355	63.4%
											61.9%		65.3%
*!	60	(24)	.	.	SST	CHL	BAT	.	None	206	73.3%	145	52.0%	351	62.7%
											60.6%		65.9%

A,B.

The best classification accuracy had an overall accuracy of 84.6%, in which 474 samples were correctly identified: 251 oil spills and 223 look-alike slicks. This was achieved with good levels of other performance metrics (sensitivity (89.3%), specificity (79.9%), positive- (81.8%), and negative-predictive (88.1%) values), and was identified from a combination of ten cube-transformed attributes: six pieces of size information (area, CMP, LtoW, PtoA, FRA, and NUM) plus the three metoc variables (WND, SST, and CHL), with one geo-location parameter (BAT). In contrast, the poorest classification accuracy resulted from a combination of three non-transformed variables (SST, CHL, and BAT): 62.7%—351 successful predictions (206 oil spills and 145 look-alikes). The classification accuracy difference between the poorest and the best classifier is ~22% (123 samples). However, the result of the poorest classifier was considered void because its specificity was below 60% and it had an unbalanced identification rate (Section 3.2.3). Consequently, the lowest “valid” classification accuracy was reached with only two non-transformed variables: WND and BAT. The performance metrics were ~70%—sensitivity (72.6%), specificity (70.6%), positive- (71.3%), and negative-predictive (71.9%) values. Its overall accuracy (71.6%—401 good decisions: 204 oil spills and 197 look-alikes) is 13% (73 samples) lower than the best of all classifications.

An inclusive hierarchy based on the classifier’s overall accuracies is provided in Table 3A,B: running from 1 to 60. These are assembled into “hierarchy blocks”, color-coded as in Figure 3. All combinations are grouped in three major blocks corresponding to the three proposed attribute-type subdivisions with and without one of the two geo-loc parameters: size information plus metoc variables (1 to 29: blue), Size Set (25 to 36: green), and Metoc Set (37 to 60: gray)—in Table 3A,B. See Remark 1 below. The averaged values per block are presented in

Table 4. Averaged overall accuracies of Experiment 1 (Data Information). Three hierarchy blocks and their respective subgroups (as color-coded in Table 3A,B): size information plus Meteorological-Oceanographic (metoc) variables (blue: 1–29), “Size Set” (green: 25–36), and “Metoc Set” (gray: 37–60), all of which were analyzed with or without at least one geo-location (geo-loc) parameter and were subjected to the same data transformations. Averaged number of correctly classified samples is provided in parentheses. Blocks match the proposed attribute-type subdivisions (Figure 3). + indicates the range of accuracies (and samples) in these blocks. * indicates unbalanced identification rate: algorithms correctly identifying 30% or more oil spills than look-alike slicks. ! indicates void algorithms: at least one performance metric below 60%, i.e., specificity. See also Section 4.2.

Blocks	Subdivisions	Percentages	(Samples)	Subgroups		Percentages	(Samples)
Top- Blue (1–29)	Size Plus Metoc Set	83.0%	(465)	Top Group	WND, SST, and CHL	84.1%	(471)
				Middle Group	WND	83.0%	(465)
		3.6%	(20) +	Bottom Group	SST and CHL	81.9%	(459)
Middle- Green (25–36)	Size Set	80.3%	(450)	First Group	log10 or cube root	80.9%	(453)
		2.1%	(12) +	Second Group	Original set	79.6%	(446)
Bottom- Gray (37–60)	Metoc Set	70.5%	(395)	Top Group	WND, SST, and CHL	74.4%	(417)
				Middle Group	WND	73.1%	(410)
		12.1%	(68) +	Bottom Group	SST and CHL	65.2%	(365) *!

. Each of these color-coded blocks was also ranked within attribute-type subdivisions. These define the “subdivision ranks” which are given in parentheses in Table 3A,B: 1–27 (Size Plus Metoc Set: blue), 1–9 (Size Set: green), and 1–24 (Metoc Set: gray). Each major block was further divided in “subgroups” (Table 3A,B), based on the characteristics of the variables. The averaged subgroup information is also given in Table 4. See Remark 2 below.

The thick lines in the table show a subtle characteristic displayed in Table 3A,B that link combinations with equal overall accuracies. See Remark 3 below. Even though the hierarchy blocks and subdivision ranks are interchangeably used when we refer to blocks, hierarchies run from 1 through 60, whereas references to ranks match the attribute-type subdivision count given above. A series of findings apparent in Table 3A,B and Table 4 is discussed by subdivision rank below.

4.2.1. Size Plus Metoc Set, with or without Geo-Location (Blue: 1–27)

Within this top hierarchy block, three subgroups are identified. The top ranked nine combinations are primarily formed by the combinations of the Size Plus Metoc Set. As stated above, the best accuracy is 84.6%. The middle group has eight combinations predominantly based on size plus WND combinations. The lowest subgroup has ten combinations mostly formed by size plus SST and CHL combinations. More details are given in Remark 3 below.

Although the difference between the best and worst classification rate is 3.6% (20 samples; Table 4), there is a demonstrable synergy in combining different attributes: firstly, the six pieces of size information plus the three metoc variables (size + WND, SST, and CHL) out-performed size with only one metoc (size + WND), and secondly, size + WND surpassed size plus the other two metoc (size + SST and CHL). Regarding the use of geo-location parameters, when either of them was included, there was a gain in accuracy. In this hierarchy block, there was no improvement of the data-transformed combinations over the non-transformed set.

4.2.2. Size Set, with or without Geo-Location (Green: 1–9)

There are two subgroups in the middle hierarchy block. The first has five combinations, all of which were transformed: cube root or log₁₀. The best combination was the six size plus BAT cube transformed: 81.4% (456 samples correctly classified; Table 3B). The second subgroup has four combinations (ranks 6–9) and most of them are non-transformed combinations: size with and without geo-loc. The exception was a cube-transformed combination (rank 8: size without geo-loc) that was not within the first subgroup, but in the second.

While the averaged overall accuracy of the first group was ~81% (453 samples), the second group average was ~80% (446 samples); Table 4. The inclusion of geo-loc parameters promoted an improvement of the classification accuracies. The difference between the most and least accurate classification in this block is 2.1% (12 samples; Table 4), but data-transformed combinations have better outcomes than those without transformation—indeed this is the basis for the formation of groups in this block.

4.2.3. Metoc Set, with or without Geo-Location (Gray: 1–24)

The lowest hierarchy block has three subgroups. The top subgroup has six combinations using all three metoc variables (with and without one geo-loc) that have been transformed: cube root or log₁₀. The most successful combination in this block has three metoc variables with log transformed BAT: 74.8% (419 samples). The middle subgroup has nine combinations (ranks 7–15) that include the three non-transformed combinations of three metoc variables (with and without one geo-loc), and the six combinations only using WND plus either of the geo-loc parameters. The lowest subgroup has nine combinations (ranks 16–24) using SST and CHL, with or without geo-loc. However, they were all considered void for the two reasons given in Section 3.2.3: (i) their specificity was below 60% (Table 3B); and (ii) they had unbalanced classification rates.

The averaged overall accuracies of these groups are ~74%, ~73%, and ~65%, respectively with the number of samples correctly identified per group being 417, 410, and 365 (Table 4). The highest and lowest classification rate had a difference of 12.1% (68 samples). There was an evident synergy in using all metoc variables together, as they improved the ability of the classifier to discriminate oil spills from look-alike slicks. Likewise, the sole use of WND (with any geo-loc) produced better classifiers than those using the other two metoc variables, i.e., SST and CHL (with or without geo-loc). The use of geo-loc parameters improved the classification accuracy. There was a clear dependence on the use of data transformations in the top and middle groups, with the absence of transformations producing the least accurate classifications.

4.2.4. Comparative Classification Accuracy

In this section we compare the results of nine data combinations that have been analyzed by Carvalho et al. [42] that are indicated in Figure 3.

Table 5. Classification accuracy comparisons between our results (see the # symbol in Figure 3 and Table 3A,B) and those in Carvalho et al. [42]—see their Table 7. Attribute-type subdivision (Section 3.1.2): size information plus Meteorological-Oceanographic (metoc) variables, “Size Set”, and “Metoc Set”. In both studies, variables have been subjected to the same data transformation (Transf.). Herein, combinations were analyzed with or without at least one geo-location (geo-loc) parameter: bathymetry (BAT) or distance to coastline (CST). Overall accuracies are shown in bold font. A pair of differences in percentages (Diff.) are reported: (i) this study compared to Carvalho et al. [42]; and (ii) present study: with minus without geo-loc. A local order is provided per subdivision. The hierarchy (shown in parentheses) has been taken from Table 3A,B and Table 7 in Carvalho et al. [42]. * indicates the best accuracy within subdivisions. See also Section 4.2.4.

		Carvalho et al. [42]		This Paper (without Geo-Loc)			This Paper (with Geo-Loc)
Sub Division	Transf.	Overall	Order	Overall	Order	Diff. i	Overall	Order	Diff. ii	Geo- Loc
		Accuracy	(Hierarchy)	Accuracy	(Hierarchy)		Accuracy	(Hierarchy)
Size Plus Metoc Set	None	83.1%	2 (5)	83.9%	* 1 (6)	0.8%	84.1%	3 (4)	0.2%	CST
	Cube Root	83.7%	* 1 (2)	83.9%	2 (7)	0.2%	84.6%	* 1 (1)	0.7%	BAT
	log10	83.0%	3 (7)	82.5%	3 (18)	−0.5%	84.3%	2 (2)	1.8%	BAT
Size Set	None	79.1%	* 1 (19)	79.6%	2 (34)	0.5%	79.8%	3 (33)	0.2%	BAT
	Cube Root	78.9%	2 (21)	79.6%	3 (35)	0.7%	81.4%	* 1 (25)	1.8%	BAT
	log10	78.0%	3 (24)	80.7%	* 1 (31)	2.7%	81.3%	2 (28)	0.6%	BAT
Metoc Set	None	76.9%	2 (27)	73.4%	3 (47)	−3.5%	73.8%	3 (44)	0.4%	BAT
	Cube Root	77.1%	* 1 (26)	74.5%	* 1 (39)	−2.6%	74.5%	2 (40)	0.0%	CST
	log10	76.7%	3 (29)	74.3%	2 (41)	−2.4%	74.8%	* 1 (37)	0.5%	BAT

shows the main classification accuracy differences extracted from Table 3A,B and Table 7 in Carvalho et al. [42]; see Remark 4 below. Two differences in percentages (Diff.) are reported in Table 5, comparing (i) our results with those of Carvalho et al. [42] and (ii) the inclusion of geo-loc parameters. These are described below:

• Comparisons with Earlier Results ofCarvalho et al. [42]: Although the classification accuracy is improved compared with earlier results by using subdivision of the Size Plus Metoc Set in nearly all combinations, there was one exception: log₁₀ without geo-loc (82.5% − 83.0% = −0.5%). Likewise, all accuracies of the Size Set increased (log₁₀ transformation without geo-loc: 80.7% − 78.0% = 2.7%). On the contrary, all combinations of the Metoc Set showed decreased accuracy, and this was independent of the inclusion of geo-loc (no transformation and no geo-loc: 73.4% − 76.9% = −3.5%). See Remark 5 below. Table 5 contains a local ordering of the three data transformations of each attribute-type subdivision. This ordering confirmed that there was no clear consistency to show which data transformation was best; in Table 5, asterisks indicate best accuracies per subdivision. An example of the lack of consistency is seen in the subdivisions of the Size Set that indicated different best transformations in each study: the overall accuracy without any transformation (79.1%) reported by Carvalho et al. [42] surpassed the application of transformations, while here, the most successful transformation without geo-loc was log₁₀ (80.7%), but the best outcome including a geo-loc parameter (BAT) was with the cube-transformed combination (81.4%). See Remark 6 below.
• Including Geo-Location: In nearly all cases, combinations including at least one geo-location parameter had better performance than those without; the exception being the Metoc Set cube-transformed that remained the same with or without geo-loc: 74.5%. The largest overall accuracy increases when geo-loc parameters were considered was ~2%: the Size Set combination with cube root transformation (from 79.6% to 81.4%) and the Size Plus Metoc Set combination with log₁₀ transformation (from 82.5% to 84.3%). See Remark 7 below. In the combinations including geo-loc, BAT was preferable to CST. In only two of nine cases CST achieved superior accuracy. Indeed, among the combinations, the best classifier (cube transformed Size Plus Metoc Set) was improved by ~1% with the use of BAT: from 83.9% to 84.6% (Table 3 and Table 5). See Remark 8 below.

4.3. Experiment 2: Data Transformation

Fifty-four data combinations were considered in the third part of our research (Figure 2). The analyses of the UPGMA dendrograms showed that the correlation of these combinations of variables were within the recommended similarity threshold: 0.3 > r > −0.3. Table 6 and Table 7 condense the classifications of the two distinct assemblages: Metoc Assemblage and Size Assemblage; each of which having 3 variables subjected to 3 transformations—27 LDAs each. See Remark 9 below. These Results are presented below.

4.3.1. Metoc Assemblage (WND, SST, and CHL) with Different Data Transformations

Unlike the 27 combinations of the Size Assemblage (see below: Section 4.3.2), those with variables from the Metoc Assemblage did not form identifiable blocks (Table 6). Additionally, there was no combination being deemed void in the Metoc Assemblage (Table 3 and Table 7). See Remark 10 below.

Table 6. Classification accuracy hierarchy of the 27 algorithms using three variables subjected to different data transformations in the same analysis—Meteorological-Oceanographic data (metoc: “Metoc Assemblage”—wind speed (WND), sea surface temperature (SST), and chlorophyll-a concentration (CHL)). Bold font indicates baseline combinations with the same transformation. For the interpretation of thick table lines see Section 4.3.1. Detailed statistical information is found in Figure 4. See also Table 1 and Table 7, and Section 4.3: Experiment 2 (Data-Transformation).

Hierarchy	WND	SST	CHL	Oil Spills		Slick-Alikes		All Features
1	None	Cube	log10	214	76.2%	205	73.5%	419	74.8%
					74.3%		75.4%
2	None	None	log10	215	76.5%	203	72.8%	418	74.6%
					73.9%		75.5%
3	None	log10	log10	213	75.8%	205	73.5%	418	74.6%
					74.2%		75.1%
4	log10	None	log10	218	77.6%	200	71.7%	418	74.6%
					73.4%		76.0%
5	log10	None	Cube	219	77.9%	199	71.3%	418	74.6%
					73.2%		76.2%
6	Cube	Cube	log10	218	77.6%	200	71.7%	418	74.6%
					73.4%		76.0%
7	Cube	Cube	Cube	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
8	Cube	log10	log10	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
9	Cube	log10	Cube	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
10	log10	Cube	log10	218	77.6%	199	71.3%	417	74.5%
					73.2%		76.0%
11	log10	log10	log10	217	77.2%	199	71.3%	416	74.3%
					73.1%		75.7%
12	log10	None	None	216	76.9%	200	71.7%	416	74.3%
					73.2%		75.5%
13	log10	Cube	Cube	218	77.6%	198	71.0%	416	74.3%
					72.9%		75.9%
14	Cube	None	log10	216	76.9%	200	71.7%	416	74.3%
					73.2%		75.5%
15	Cube	None	Cube	216	76.9%	199	71.3%	415	74.1%
					73.0%		75.4%
16	log10	Cube	None	214	76.2%	201	72.0%	415	74.1%
					73.3%		75.0%
17	None	log10	Cube	214	76.2%	201	72.0%	415	74.1%
					73.3%		75.0%
18	Cube	None	None	213	75.8%	201	72.0%	414	73.9%
					73.2%		74.7%
19	None	None	Cube	213	75.8%	201	72.0%	414	73.9%
					73.2%		74.7%
20	None	Cube	Cube	214	76.2%	200	71.7%	414	73.9%
					73.0%		74.9%
21	log10	log10	Cube	218	77.6%	196	70.3%	414	73.9%
					72.4%		75.7%
22	Cube	Cube	None	212	75.4%	201	72.0%	413	73.8%
					73.1%		74.4%
23	Cube	log10	None	211	75.1%	201	72.0%	412	73.6%
					73.0%		74.2%
24	None	None	None	208	74.0%	203	72.8%	411	73.4%
					73.2%		73.6%
25	None	Cube	None	209	74.4%	202	72.4%	411	73.4%
					73.1%		73.7%
26	None	log10	None	209	74.4%	202	72.4%	411	73.4%
					73.1%		73.7%
27	log10	log10	None	213	75.8%	198	71.0%	411	73.4%
					72.4%		74.4%

Table 6. Classification accuracy hierarchy of the 27 algorithms using three variables subjected to different data transformations in the same analysis—Meteorological-Oceanographic data (metoc: “Metoc Assemblage”—wind speed (WND), sea surface temperature (SST), and chlorophyll-a concentration (CHL)). Bold font indicates baseline combinations with the same transformation. For the interpretation of thick table lines see Section 4.3.1. Detailed statistical information is found in Figure 4. See also Table 1 and Table 7, and Section 4.3: Experiment 2 (Data-Transformation).

Hierarchy	WND	SST	CHL	Oil Spills		Slick-Alikes		All Features
1	None	Cube	log10	214	76.2%	205	73.5%	419	74.8%
					74.3%		75.4%
2	None	None	log10	215	76.5%	203	72.8%	418	74.6%
					73.9%		75.5%
3	None	log10	log10	213	75.8%	205	73.5%	418	74.6%
					74.2%		75.1%
4	log10	None	log10	218	77.6%	200	71.7%	418	74.6%
					73.4%		76.0%
5	log10	None	Cube	219	77.9%	199	71.3%	418	74.6%
					73.2%		76.2%
6	Cube	Cube	log10	218	77.6%	200	71.7%	418	74.6%
					73.4%		76.0%
7	Cube	Cube	Cube	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
8	Cube	log10	log10	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
9	Cube	log10	Cube	217	77.2%	200	71.7%	417	74.5%
					73.3%		75.8%
10	log10	Cube	log10	218	77.6%	199	71.3%	417	74.5%
					73.2%		76.0%
11	log10	log10	log10	217	77.2%	199	71.3%	416	74.3%
					73.1%		75.7%
12	log10	None	None	216	76.9%	200	71.7%	416	74.3%
					73.2%		75.5%
13	log10	Cube	Cube	218	77.6%	198	71.0%	416	74.3%
					72.9%		75.9%
14	Cube	None	log10	216	76.9%	200	71.7%	416	74.3%
					73.2%		75.5%
15	Cube	None	Cube	216	76.9%	199	71.3%	415	74.1%
					73.0%		75.4%
16	log10	Cube	None	214	76.2%	201	72.0%	415	74.1%
					73.3%		75.0%
17	None	log10	Cube	214	76.2%	201	72.0%	415	74.1%
					73.3%		75.0%
18	Cube	None	None	213	75.8%	201	72.0%	414	73.9%
					73.2%		74.7%
19	None	None	Cube	213	75.8%	201	72.0%	414	73.9%
					73.2%		74.7%
20	None	Cube	Cube	214	76.2%	200	71.7%	414	73.9%
					73.0%		74.9%
21	log10	log10	Cube	218	77.6%	196	70.3%	414	73.9%
					72.4%		75.7%
22	Cube	Cube	None	212	75.4%	201	72.0%	413	73.8%
					73.1%		74.4%
23	Cube	log10	None	211	75.1%	201	72.0%	412	73.6%
					73.0%		74.2%
24	None	None	None	208	74.0%	203	72.8%	411	73.4%
					73.2%		73.6%
25	None	Cube	None	209	74.4%	202	72.4%	411	73.4%
					73.1%		73.7%
26	None	log10	None	209	74.4%	202	72.4%	411	73.4%
					73.1%		73.7%
27	log10	log10	None	213	75.8%	198	71.0%	411	73.4%
					72.4%		74.4%

The minimum (73.4%) and maximum (74.8%) overall accuracy rate difference was only 1.4% (8 samples; Table 6). Within this classification range, there were six values that had many combinations with similar performance, 73.4% to 74.6%, these are delineated in Table 6 by thick lines. A characteristic of most of them is that they did not correctly identify the same samples; this is apparent in Table 6 in the number of correctly classified oil spills and look-alike slicks—for instance, hierarchies 19, 20, and 21 all identified 414 samples (73.9%) but their classifications per class varied: spill (213, 214, and 218 samples, respectively) and look-alikes (201, 200, and 196, respectively). See Remark 11 below.

If we consider the baseline combinations with the three variables subjected to the same transformation (bold font in Table 1 and Table 6), the cube root (74.5%) surpassed the log-transformed (74.3%), as well as the non-transformed (73.4%). These are hierarchies 7, 11, and 24, in Table 6. Note that the non-transformed version was worse by ~1% compared to the two with a transformation.

4.3.2. Size Assemblage (Area, LtoW, and NUM) with Different Data Transformations

The key outcomes of the 27 LDAs of the Size Assemblage (Table 7) are as follows: (i) two combinations reached best classification accuracy (80.9%): area (log₁₀) and NUM (non-transformed) with LtoW (either log- or cube-transformed) (see Remark 12 below); (ii) the poorest combination was area (without transformation), LtoW (without transformation), and NUM (log₁₀ transformed)—67.0%. Nonetheless, this was considered void because specificity <60% and unbalanced identification rate differing by >30% (see Remark 13 below); and (iii) the lowest valid classification accuracy was reached with area (cube transformed), LtoW (log₁₀ transformed), and NUM (log₁₀ transformed): 76.1%.

A remarkable accuracy improvement was observed from worst to best classifiers with different data transformations: 13.9% (78 samples; Table 7). Considering the baseline combinations with the three variables subjected to the same transformation (bold font in Table 1 and Table 7), the log-transformed (78.6%) surpassed the cube-transformed (77.3%), and the non-transformed (70.2%; void). These are hierarchies 10, 14, and 20, in Table 7. The non-transformed version was poorer by >7% and voided. See Remark 14 below.

The 27 combinations within the Size Assemblage were divided into three major blocks mostly guided by a specific attribute: area (Table 7). A secondary group, apparent in these blocks, is controlled by another variable: NUM—these are shown in Table 7 by thick lines. In the blocks guided by the area variable, the application of the log transformation forms the top block, followed by combinations subjected to the cube transformation, and lastly by non-transformed versions. On the other hand, the groups controlled by the NUM variable had the non-transformed assemblage being more accurate than those with the application of cube root and log transformations. See Remark 15 below.

5. Discussion

Other than the oil-slick classification studies described in Carvalho et al. [38,39,40,42], involving LDA algorithms to discriminate surface ocean slicks detected in RADARSAT measurements, there are few publications in the literature (to our knowledge) classifying satellite-detected features using LDAs in a similar fashion as reported here. Most papers using LDAs to classify oil slicks differ from our research in that: (i) they were only successful once LDAs were postulated with another machine learning technique (e.g., [34]), while we reached successful discriminations solely based on the use of conventional LDAs; (ii) they fail to report essential accuracy metrics (e.g., [35]), thus ignoring the importance of reporting a full algorithm’s accuracy assessment in a more efficient and effective manner; (iii) they explored marine radar images (e.g., [36]), rather than SAR satellite imagery. A pair of other characteristics set our study apart from these earlier investigations: the pre-selection of specific data (Experiment 1) and combination of attributes subjected to several data transformations in the same algorithm form (Experiment 2). In addition, of the 114 LDA algorithms tested here, only nine have been previously examined, with these being modified here. The remainder of this section discusses the 15 remarks previously introduced in the results section.

Table 7. Classification accuracy hierarchy of the 27 algorithms using three attributes subjected to different data transformations in the same analysis—morphological characteristics (“Size Assemblage”: area, aspect ratio (length-to-width ratio: LtoW), and number of parts of each feature (NUM)). The explanation of the hierarchy blocks: 1–6, 7–18, and 19–27 is given in the text. * indicates unbalanced identification rate: algorithms correctly identifying 30% or more oil spills than look-alike slicks. ! indicates void algorithms: at least one performance metric below 60%, i.e., specificity. Bold font indicates baseline combinations with the same transformation. For the interpretation of thick table lines see Section 4.3.2. Detailed statistical information is found in Figure 4. See also Table 1 and Table 6, and Section 4.3: Experiment 2 (Data-Transformation).

Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
	1	log10	log10	None	250	89.0%	203	72.8%	453	80.9%
						76.7%		86.8%
	2	log10	Cube	None	251	89.3%	202	72.4%	453	80.9%
						76.5%		87.1%
	3	log10	None	None	250	89.0%	201	72.0%	451	80.5%
						76.2%		86.6%
	4	log10	log10	Cube	247	87.9%	200	71.7%	447	79.8%
						75.8%		85.5%
	5	log10	None	Cube	246	87.5%	199	71.3%	445	79.5%
						75.5%		85.0%
	6	log10	Cube	Cube	246	87.5%	199	71.3%	445	79.5%
						75.5%		85.0%
Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
*	7	Cube	None	None	269	95.7%	175	62.7%	444	79.3%
						72.1%		93.6%
*	8	Cube	log10	None	266	94.7%	175	62.7%	441	78.8%
						71.9%		92.1%
*	9	Cube	Cube	None	267	95.0%	174	62.4%	441	78.8%
						71.8%		92.6%
	10	log10	log10	log10	239	85.1%	201	72.0%	440	78.6%
						75.4%		82.7%
	11	log10	None	log10	240	85.4%	198	71.0%	438	78.2%
						74.8%		82.8%
	12	log10	Cube	log10	239	85.1%	199	71.3%	438	78.2%
						74.9%		82.6%
*	13	Cube	log10	Cube	251	89.3%	183	65.6%	434	77.5%
						72.3%		85.9%
*	14	Cube	Cube	Cube	251	89.3%	182	65.2%	433	77.3%
						72.1%		85.8%
*	15	Cube	None	Cube	250	89.0%	181	64.9%	431	77.0%
						71.8%		85.4%
	16	Cube	None	log10	243	86.5%	188	67.4%	431	77.0%
						72.8%		83.2%
	17	Cube	Cube	log10	241	85.8%	185	66.3%	426	76.1%
						71.9%		82.2%
	18	Cube	log10	log10	242	86.1%	184	65.9%	426	76.1%
						71.8%		82.5%
Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
*!	19	None	log10	None	246	87.5%	149	53.4%	395	70.5%
						65.4%		81.0%
*!	20	None	None	None	247	87.9%	146	52.3%	393	70.2%
						65.0%		81.1%
*!	21	None	Cube	None	247	87.9%	146	52.3%	393	70.2%
						65.0%		81.1%
*!	22	None	log10	Cube	230	81.9%	158	56.6%	388	69.3%
						65.5%		75.6%
*!	23	None	None	Cube	234	83.3%	153	54.8%	387	69.1%
						65.0%		76.5%
*!	24	None	Cube	Cube	230	81.9%	157	56.3%	387	69.1%
						65.3%		75.5%
*!	25	None	log10	log10	221	78.6%	158	56.6%	379	67.7%
						64.6%		72.5%
*!	26	None	Cube	log10	219	77.9%	160	57.3%	379	67.7%
						64.8%		72.1%
*!	27	None	None	log10	219	77.9%	156	55.9%	375	67.0%
						64.0%		71.6%

Table 7. Classification accuracy hierarchy of the 27 algorithms using three attributes subjected to different data transformations in the same analysis—morphological characteristics (“Size Assemblage”: area, aspect ratio (length-to-width ratio: LtoW), and number of parts of each feature (NUM)). The explanation of the hierarchy blocks: 1–6, 7–18, and 19–27 is given in the text. * indicates unbalanced identification rate: algorithms correctly identifying 30% or more oil spills than look-alike slicks. ! indicates void algorithms: at least one performance metric below 60%, i.e., specificity. Bold font indicates baseline combinations with the same transformation. For the interpretation of thick table lines see Section 4.3.2. Detailed statistical information is found in Figure 4. See also Table 1 and Table 6, and Section 4.3: Experiment 2 (Data-Transformation).

Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
	1	log10	log10	None	250	89.0%	203	72.8%	453	80.9%
						76.7%		86.8%
	2	log10	Cube	None	251	89.3%	202	72.4%	453	80.9%
						76.5%		87.1%
	3	log10	None	None	250	89.0%	201	72.0%	451	80.5%
						76.2%		86.6%
	4	log10	log10	Cube	247	87.9%	200	71.7%	447	79.8%
						75.8%		85.5%
	5	log10	None	Cube	246	87.5%	199	71.3%	445	79.5%
						75.5%		85.0%
	6	log10	Cube	Cube	246	87.5%	199	71.3%	445	79.5%
						75.5%		85.0%
Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
*	7	Cube	None	None	269	95.7%	175	62.7%	444	79.3%
						72.1%		93.6%
*	8	Cube	log10	None	266	94.7%	175	62.7%	441	78.8%
						71.9%		92.1%
*	9	Cube	Cube	None	267	95.0%	174	62.4%	441	78.8%
						71.8%		92.6%
	10	log10	log10	log10	239	85.1%	201	72.0%	440	78.6%
						75.4%		82.7%
	11	log10	None	log10	240	85.4%	198	71.0%	438	78.2%
						74.8%		82.8%
	12	log10	Cube	log10	239	85.1%	199	71.3%	438	78.2%
						74.9%		82.6%
*	13	Cube	log10	Cube	251	89.3%	183	65.6%	434	77.5%
						72.3%		85.9%
*	14	Cube	Cube	Cube	251	89.3%	182	65.2%	433	77.3%
						72.1%		85.8%
*	15	Cube	None	Cube	250	89.0%	181	64.9%	431	77.0%
						71.8%		85.4%
	16	Cube	None	log10	243	86.5%	188	67.4%	431	77.0%
						72.8%		83.2%
	17	Cube	Cube	log10	241	85.8%	185	66.3%	426	76.1%
						71.9%		82.2%
	18	Cube	log10	log10	242	86.1%	184	65.9%	426	76.1%
						71.8%		82.5%
Hierarchy		Area	LtoW	NUM	Oil Spills		Slick-Alikes		All Features
*!	19	None	log10	None	246	87.5%	149	53.4%	395	70.5%
						65.4%		81.0%
*!	20	None	None	None	247	87.9%	146	52.3%	393	70.2%
						65.0%		81.1%
*!	21	None	Cube	None	247	87.9%	146	52.3%	393	70.2%
						65.0%		81.1%
*!	22	None	log10	Cube	230	81.9%	158	56.6%	388	69.3%
						65.5%		75.6%
*!	23	None	None	Cube	234	83.3%	153	54.8%	387	69.1%
						65.0%		76.5%
*!	24	None	Cube	Cube	230	81.9%	157	56.3%	387	69.1%
						65.3%		75.5%
*!	25	None	log10	log10	221	78.6%	158	56.6%	379	67.7%
						64.6%		72.5%
*!	26	None	Cube	log10	219	77.9%	160	57.3%	379	67.7%
						64.8%		72.1%
*!	27	None	None	log10	219	77.9%	156	55.9%	375	67.0%
						64.0%		71.6%

5.1. Data-Information Experiment

• Remark 1: Considering the hierarchy blocks, when variables from Size Plus Metoc Set were combined, the algorithms were more accurate than those using variables from one type alone. Additionally, when comparing the sole use of size information, the classification accuracies were superior to those using only the metoc variables. A corresponding hierarchical pattern was also observed among the 61 data combinations reported in Carvalho et al. [40]. The hierarchy block formation was only disrupted by two combinations of the Size Set (hierarchies 25 and 28: green group) that were more accurate than a few combinations of the Size Plus Metoc Set (hierarchies 26, 27, and 29: blue group).
• Remark 2: Regarding the subgroups, it is noteworthy that some data combinations achieve classifications better than others (Table 3A,B). Table 4 shows the top-blue (Size Plus Metoc Set) and middle-green (Size Set) blocks have an average difference of ~1% between each of their groups: ~84% to ~80%. The differences between the middle-green and lowest-gray (Metoc Set) blocks were greater, as were those within the groups in the last block.
• Remark 3: Of the many combinations that had the same overall accuracies (to the number of decimal places indicated), most of them did not correctly identify the same samples—this is seen in Table 3A,B: the number of correctly classified oil spills and look-alike slicks. Only hierarchies 34 and 35 (79.6%—Size Set without geo-loc: non-transformed and cube root, respectively) and hierarchies 39 and 40 (74.5%—Metoc Set with and without CST, both cube-transformed) identified the same samples.

5.1.1. Comparative Classification Accuracy

• Remark 4: Although nearly all accuracies were improved in the Size Plus Metoc Set and Size Set subdivisions described by Carvalho et al. [42], the same did not hold for the Metoc Set subdivision that had its overall accuracies reduced (Table 5). While the largest improvements were ~3% in two log-transformed Size Set combinations: without geo-loc (from 78.0% to 80.7%) and with geo-loc (from 78.0% to 81.3%), the best of all combinations (cube transformed Size Plus Metoc Set) had its accuracy increased by ~1% by the inclusion of one geo-loc parameter (BAT): from 83.7% to 84.6% (Table 5). These improvements demonstrate the success of the removal of samples that are unlikely to contribute to the classification and the addition of geo-loc attributes.

5.1.2. Comparisons with Earlier Results

• Remark 5: The Metoc Set combinations did not produce high-ranking accuracies in comparison with the earlier results of Carvalho et al. [42] (Table 5). This may be due to many records having been removed based on the WND thresholds: lower (<3 m/s: 105 samples) and upper (>6 m/s: 94 samples)—i.e., 25.5% of the original dataset (Table 2), even though the exclusion of these cases was based on physical reasoning.
• Remark 6: There was not a clear pattern to indicate which data transformation was best. The non-transformed set and log₁₀ had only two cases each as the best combination among the nine compared, and the cube-transformed combinations were more accurate in five cases (Table 5).

5.1.3. Geo-Location Inclusion

• Remark 7: Two geo-loc parameters available in the original dataset were studied here, but they were not considered together because they are highly correlated. The inclusion of geo-loc parameters results in improved accuracies (Table 5).
• Remark 8: Combinations using Bathymetry (BAT, ranging from 5 m to ~4 km) tended to have improved accuracies compared to those using the distance to coastline (CST, 186 m to ~435 km); Table 5.

5.2. Data-Transformation Experiment

• Remark 9: The investigation of two assemblages of only three variables subjected to three data transformations indicated that the Metoc Assemblage did not show an advantage of using the different transformations, however, the results of using different data transformations within the variables of the Size Assemblage were promising; see below Remarks 12 and 15, and Future Work Recommendations.

5.2.1. Metoc Assemblage: WND, SST, and CHL

• Remark 10: There was a lack of hierarchy blocks in the Metoc Assemblage subjected to different transformations. This may be due to the relatively small range among the analyzed features (WND (3 to 6 m/s), SST (11.44 to 29.43 °C), and CHL (0.003 and 9.7 mg/m³)).
• Remark 11: Even though there was a span of 1.4% (8 samples) between the best and worst accuracy among the 27 combinations of the Metoc Assemblage, if we compare the baseline combinations of three pieces of metoc variables with the same transformation (shown in bold in Table 6), we notice that subjecting variables to different data transformations in the same analysis slightly improved the accuracies of the LDA algorithms.

5.2.2. Size Assemblage: Area, LtoW, and NUM

• Remark 12: The use of three pieces of size information subjected to different transformations (i.e., the two combinations that tied with 80.9%—area (log₁₀), LtoW (log- or cube-transformed), and NUM (non-transformed); hierarchies 1 and 2 in Table 7) reached an equivalent accuracy to the best combination of six pieces of size information log-transformed without geo-loc or metoc (80.7%; hierarchy 31 in Table 3B). Clearly, the combination of various attributes subjected to several data transformations in the same analysis, can lead to improving the LDA algorithm accuracy.
• Remark 13: The combinations using non-transformed areas were void—hierarchies 19 to 27 in Table 7. The lack of data transformation may also be negatively influencing other combinations of variables using the non-transformed area, for example, those among the 60 depicted in Figure 3, and presented in Table 3A,B. As such, other variables may also be suffering from using non-transformed areas, and this should be further investigated. See also Remark 15 below.
• Remark 14: The best of the three baseline combinations of three pieces of size information with the same transformation (shown in bold font in Table 1 and Table 7) was subjected to log₁₀—78.6% (hierarchy 10 in Table 7). However, nine other combinations were better, the best being 80.9% (hierarchies 1 and 2 in Table 7). This improvement of 2.3% is another indication that the combined use of attributes subjected to different data transformations improves the LDA classification accuracy.
• Remark 15: Considering the major hierarchy blocks and secondary groups, among the 27 combinations that use three pieces of size information with three data transformations (Table 7), one reason is given for this ranking: among the 560 analyzed features, areas have a large range of continuous values (from oil spills with 0.45 km² to look-alikes with 8177.24 km² cause by upwelling events), whereas the NUM variable with its discrete values had features with only 1 part up to look-alike slicks with 24 different parts caused by biogenic films.

6. Summary and Conclusions

We report on successful differentiation of oil spills from look-alike slicks using simple, linear discriminant analyses (LDAs) of satellite-based information (RADARSAT-1, QuikSCAT, AVHRR, SeaWiFS, and MODIS) from the Campos Basin, Brazil (Figure 1). A series of effective classification algorithms was produced based on the combination of characteristics of three attribute types: (i) morphological characteristics (size information: area, compact index (CMP), aspect ratio (length-to-width ratio: LtoW), perimeter-to-area ratio (PtoA), fractal index (FRA), and number of feature’s parts (NUM)); (ii) Meteorological-Oceanographic (metoc) variables (wind speed (WND), sea-surface temperature (SST), and chlorophyll-a concentration (CHL)); and (iii) geo-location (geo-loc) parameters (bathymetry (BAT) and distance to coastline (CST)). Two data transformations were considered in addition to non-transformed: cube root and log₁₀. The quantitative accuracy of 114 LDA algorithms was evaluated and ranked with five performance metrics: overall accuracy, sensitivity, specificity, positive-, and negative-predictive values (Figure 4). This study was built upon the ability to distinguish sea-surface features in SAR images using LDAs—oil spills vs. look-alike slicks [42], as well as oil spills vs. oil seeps [38,39,40]—and included developments beyond past research [33,34,35,36,37]. Our two objectives have been achieved through two separate experiments (Figure 2):

6.1. Objective 1

The “Data-Information Experiment” sought the most effective combination of variables among 60 combinations (Figure 3). Three proposed attribute-type subdivisions were hierarchized in major blocks: “Size Plus Metoc Set”, “Size Set”, and “Metoc Set” (Table 3A,B). These were considered with or without at least one geo-loc parameter and all variables were subjected to the same data transformations. The best accuracies were reached with all variables from each subdivision. Each block was further stratified in subgroups related to the variable’s characteristics (Table 4). Bathymetry (BAT) was generally better than distance to coastline (CST). The main developments used here—sample removal (data filter) and inclusion of geo-loc information—improved classification accuracy (Table 5). The main results regarding the LDA accuracies (Table 3A,B) are summarized as:

• if all variables are available, the best accuracy is 84.6% (hierarchy 1; cube-transformed);
• without geo-loc parameters, the best accuracy is 83.9% (hierarchy 6; non-transformed);
• if Oceanographic data are not available, the best accuracy is 83.9% (hierarchy 8; log-transformed);
• if Meteorological data are unavailable, the best accuracy is 83.0% (hierarchy 15; cube-transformed);
• if only size information is given, the best accuracy is 80.7% (hierarchy 31; log-transformed);
• without size information, the best accuracy is 74.8% (hierarchy 37; log-transformed);
• if only Meteorological data and geo-loc are used, the best accuracy is 73.8% (hierarchy 43; cube-transformed); and
• if only Oceanographic data are accounted for (with or without geo-loc), the results are considered void (hierarchies 52–60).

6.2. Objective 2

The “Data-Transformation Experiment” sought the most effective combination of data transformations to improve accuracy. This experiment is a development over published binary classification papers, as here we combined variables undergoing different data transformations in the same analysis. Two distinct assemblages of 27 data combinations each with three variables were tested with three data transformations (Table 1). In the first assemblage (“Metoc Assemblage”: WND, SST, and CHL—Table 6), there was no noteworthy classification improvement as revealed by the small range of ~1.5% (8 samples) from its best (74.8%) to worst (73.4%) overall accuracies. On the contrary, the second assemblage (“Size Assemblage”: area, LtoW, and NUM—Table 7) showed accuracy improvements from different transformations—the best (80.9%) to worst (67.0%) accuracy had a remarkable difference of ~14.0% (78 samples). Two combinations subjected to three transformations tied as the most effective LDA—80.9% (453 samples): area (log₁₀), LtoW (log- or cube-transformed), and NUM (non-transformed). These two best combinations of three variables vs. three transformations were superior to the best baseline combination with the same transformation applied to all variables—78.6% (440 samples): area (log₁₀), LtoW (log₁₀), and NUM (log₁₀); Table 1 and Table 7. Moreover, they achieved a comparable outcome to the best combination using the six pieces of size information (without metoc or geo-loc) all being subjected to log₁₀ transformation (80.7%; 452 samples). The framework of combining different data transformations in the same classification algorithm simplifies and optimizes the LDA classification as fewer attributes were used to reach the same result.

6.3. Future Work Recommendations

Future work could apply other linear and non-linear methods (e.g., decision tree, random forest, support vector machine, artificial neural network) to guide the development of improved classifiers. A continuation of this research could include a larger collection of variables being subjected to different data transformations in the same classification algorithm, as it would be interesting to investigate if the behavior observed in the Data-Transformation Experiment also occurs with other attributes, i.e., testing different data transformations on a greater number of variables. For instance, what would happen if in the best Size Set combinations that accounts for six variables (without metoc or geo-loc) all of which were subjected to log₁₀ (i.e., 80.7%; 452 samples; hierarchy 31 in Table 3A,B) had been subjected to different transformations?