Assessing the Impacts of Rising Sea Level on Coastal Morpho-Dynamics with Automated High-Frequency Shoreline Mapping Using Multi-Sensor Optical Satellites
Abstract
:1. Introduction
1.1. Sea Level Rise (SLR) and Shoreline Dynamics
1.2. Shoreline Detection
1.3. Satellite Derived Shorelines
1.4. Malaysia: Sea-Level Rise and Coastal Vulnerability
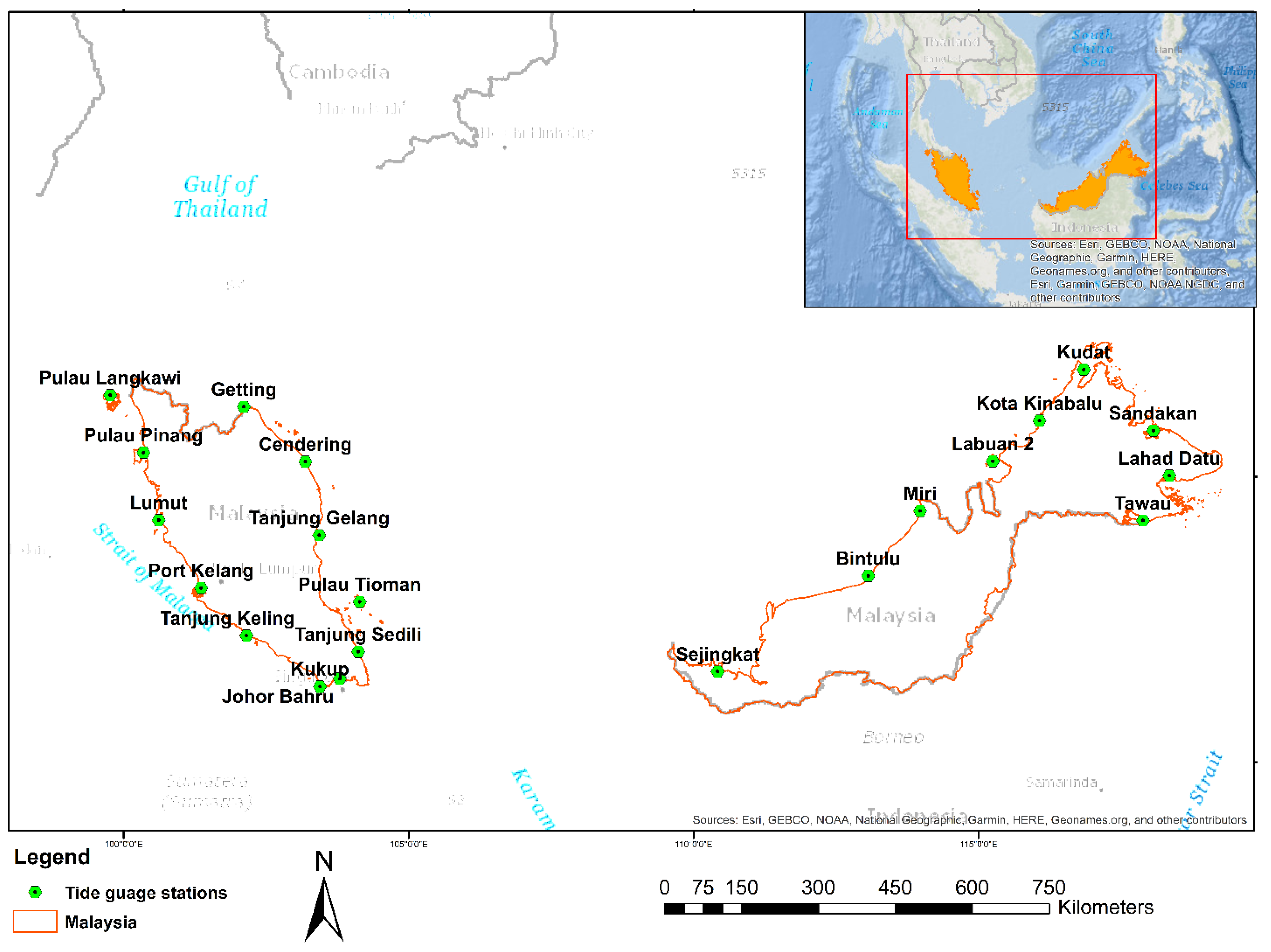
2. Study Area and Data Used
3. Methodology
3.1. Estimation of Sea-Level Trend
3.2. Shoreline Extraction
3.2.1. Data Acquisition
3.2.2. Data Preprocessing
3.2.3. Shoreline Detection
3.2.4. Tidal Correction
3.3. Shoreline Analysis
4. Results
5. Discussion
5.1. High-Frequency Sampling and Automatic Extraction with GEE
5.2. SLR and Shoreline Dynamics
5.3. Other Processes Responsible for Shifting Shorelines
5.4. Future Impact of Rising Sea Level
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vitousek, P.M.; Mooney, H.A.; Lubchenco, J.; Melillo, J.M. Human domination of earth’s ecosystems. Science 1997, 277, 494. [Google Scholar] [CrossRef] [Green Version]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef] [PubMed]
- Cabezas-Rabadan, C.; Pardo-Pascual, J.E.; Palomar-Vazquez, J.; Fernandez-Sarria, A. Characterizing beach changes using high-frequency Sentinel-2 derived shorelines on the Valencian coast (Spanish Mediterranean). Sci. Total Environ. 2019, 691, 216–231. [Google Scholar] [CrossRef] [PubMed]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A google earth engine-enabled python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Mills, A.K.; Ruggiero, P.; Bolte, J.P.; Serafin, K.A.; Lipiec, E. Quantifying uncertainty in exposure to coastal hazards associated with both climate change and adaptation strategies: A U.S. pacific northwest alternative coastal futures analysis. Water 2021, 13, 545. [Google Scholar] [CrossRef]
- Anfuso, G.; Postacchini, M.; Di Luccio, D.; Benassai, G. Coastal sensitivity/vulnerability characterization and adaptation strategies: A review. J. Mar. Sci. Eng. 2021, 9, 72. [Google Scholar] [CrossRef]
- Le Cozannet, G.; Garcin, M.; Yates, M.; Idier, D.; Meyssignac, B. Approaches to evaluate the recent impacts of sea-level rise on shoreline changes. Earth-Sci. Rev. 2014, 138, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Anzidei, M.; Scicchitano, G.; Scardino, G.; Bignami, C.; Tolomei, C.; Vecchio, A.; Serpelloni, E.; De Santis, V.; Monaco, C.; Milella, M.; et al. Relative sea-level rise scenario for 2100 along the coast of south eastern sicily (Italy) by InSAR data, satellite images and high-resolution topography. Remote Sens. 2021, 13, 1108. [Google Scholar] [CrossRef]
- Di Stefano, A.; De Pietro, R.; Monaco, C.; Zanini, A. Anthropogenic influence on coastal evolution: A case history from the Catania Gulf shoreline (eastern Sicily, Italy). Ocean. Coast. Manag. 2013, 80, 133–148. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef] [Green Version]
- Mengel, M.; Levermann, A.; Frieler, K.; Robinson, A.; Marzeion, B.; Winkelmann, R. Future sea level rise constrained by observations and long-term commitment. Proc. Natl. Acad. Sci. USA 2016, 113, 2597–2602. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; Deconto, R.M.; Ghosh, T.; et al. Sea level rise and implications for low-lying islands, coasts and communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; IPCC: Geneva, Switzerland, 2019; In Press. [Google Scholar]
- Rahmstorf, S.J.S. A semi-empirical approach to projecting future sea-level rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [Green Version]
- Horton, R.; Herweijer, C.; Rosenzweig, C.; Liu, J.; Gornitz, V.; Ruane, A.C. Sea level rise projections for current generation CGCMs based on the semi-empirical method. Geophys. Res. Lett. 2008, 35, 2. [Google Scholar] [CrossRef]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Gomez, N.; Clark, P.U.J.S. The sea-level fingerprint of West Antarctic collapse. Science 2009, 323, 753. [Google Scholar] [CrossRef]
- Peltier, W. Global glacial isostatic adjustment and modern instrumental records of relative sea level history. In International Geophysics; Elsevier: Amsterdam, The Netherlands, 2001; Volume 75, pp. 65–95. [Google Scholar]
- Ezer, T.; Corlett, W.B. Analysis of relative sea level variations and trends in the Chesapeake Bay: Is there evidence for acceleration in sea level rise? In Proceedings of the OCEANS 2012 MTS/IEEE Harnessing the Power of the Ocean, Virginia, VA, USA, 14–19 October 2012. [Google Scholar]
- Werner, A.D.; Simmons, C.T.J.G. Impact of sea-level rise on sea water intrusion in coastal aquifers. Groundwater 2009, 47, 197–204. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef] [Green Version]
- Cazenave, A.; Llovel, W. Contemporary sea level rise. Annu. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef] [Green Version]
- Ranjbar, A.; Cherubini, C.; Saber, A. Investigation of transient sea level rise impacts on water quality of unconfined shallow coastal aquifers. Int. J. Environ. Sci. Technol. 2020, 17, 2607–2622. [Google Scholar] [CrossRef]
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.; Nunn, P. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013; p. 1137. [Google Scholar]
- Gutierrez, B.T.; Plant, N.G.; Thieler, E.R. A Bayesian network to predict coastal vulnerability to sea level rise. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Adebisi, N.; Balogun, A.-L.; Min, T.H.; Tella, A. Advances in estimating Sea Level Rise: A review of tide gauge, satellite altimetry and spatial data science approaches. Ocean. Coast. Manag. 2021, 208, 105632. [Google Scholar] [CrossRef]
- Webb, A.P.; Kench, P.S. The dynamic response of reef islands to sea-level rise: Evidence from multi-decadal analysis of island change in the Central Pacific. Glob. Planet. Chang. 2010, 72, 234–246. [Google Scholar] [CrossRef]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A. Shoreline detection using optical remote sensing: A review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef] [Green Version]
- Ribas, F.; Simarro, G.; Arriaga, J.; Luque, P. Automatic shoreline detection from video images by combining information from different methods. Remote Sens. 2020, 12, 3717. [Google Scholar] [CrossRef]
- Jóia Santos, C.; Andriolo, U.; Ferreira, J.C. Shoreline response to a sandy nourishment in a wave-dominated coast using video monitoring. Water 2020, 12, 1632. [Google Scholar] [CrossRef]
- Valentini, N.; Saponieri, A.; Molfetta, M.G.; Damiani, L. New algorithms for shoreline monitoring from coastal video systems. Earth Sci. Inform. 2017, 10, 495–506. [Google Scholar] [CrossRef]
- Vélez-Nicolás, M.; García-López, S.; Barbero, L.; Ruiz-Ortiz, V.; Sánchez-Bellón, Á. Applications of unmanned aerial systems (UASs) in hydrology: A review. Remote Sens. 2021, 13, 1359. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Li, J.; Roy, D.P. A global analysis of sentinel-2A, sentinel-2B and landsat-8 data revisit intervals and implications for terrestrial monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, D.; Sesli, F.A. Shoreline change analysis of the Kizilirmak Lagoon Series. Ocean. Coast. Manag. 2015, 118, 290–308. [Google Scholar] [CrossRef]
- Sekovski, I.; Stecchi, F.; Mancini, F.; Del Rio, L. Image classification methods applied to shoreline extraction on very high-resolution multispectral imagery. Int. J. Remote Sens. 2014, 35, 3556–3578. [Google Scholar] [CrossRef]
- Aedla, R.; Dwarakish, G.S.; Reddy, D.V. Automatic Shoreline Detection and Change Detection Analysis of Netravati-GurpurRivermouth Using Histogram Equalization and Adaptive Thresholding Techniques. Aquat. Procedia 2015, 4, 563–570. [Google Scholar] [CrossRef]
- Ghoneim, E.; Mashaly, J.; Gamble, D.; Halls, J.; AbuBakr, M. Nile Delta exhibited a spatial reversal in the rates of shoreline retreat on the Rosetta promontory comparing pre- and post-beach protection. Geomorphology 2015, 228, 1–14. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Sherman, D.J.; Wu, Q.; Su, H. Algorithmic foundation and software tools for extracting shoreline features from remote sensing imagery and LiDAR data. J. Geogr. Inf. Syst. 2011, 3, 99. [Google Scholar] [CrossRef] [Green Version]
- García-Rubio, G.; Huntley, D.; Russell, P. Evaluating shoreline identification using optical satellite images. Mar. Geol. 2015, 359, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Elnabwy, M.T.; Elbeltagi, E.; El Banna, M.M.; Elshikh, M.M.Y.; Motawa, I.; Kaloop, M.R. An approach based on landsat images for shoreline monitoring to support integrated coastal management—A case study, ezbet elborg, nile delta, egypt. ISPRS Int. J. Geo-Inf. 2020, 9, 199. [Google Scholar] [CrossRef] [Green Version]
- Foody, G. Pattern recognition and classification of remotely sensed images by artificial neural networks. In Ecological Informatics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 459–477. [Google Scholar]
- Tsekouras, G.E.; Trygonis, V.; Maniatopoulos, A.; Rigos, A.; Chatzipavlis, A.; Tsimikas, J.; Mitianoudis, N.; Velegrakis, A.F. A Hermite neural network incorporating artificial bee colony optimization to model shoreline realignment at a reef-fronted beach. Neurocomputing 2018, 280, 32–45. [Google Scholar] [CrossRef]
- Kerh, T.; Lu, H.; Saunders, R. Construct. Architect. Eng. Shoreline change estimation from survey image coordinates and neural network approximation. Int. J. Civil Struct. Construct. Architect. Eng. 2014, 8, 372–377. [Google Scholar]
- Nazeer, M.; Waqas, M.; Shahzad, M.I.; Zia, I.; Wu, W. Coastline vulnerability assessment through landsat and cubesats in a coastal mega city. Remote Sens. 2020, 12, 749. [Google Scholar] [CrossRef] [Green Version]
- Balogun, A.-L.; Adebisi, N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble Ocean-Atmospheric processes on models’ accuracy. Geomat. Nat. Hazards Risk 2021, 12, 653–674. [Google Scholar] [CrossRef]
- Adebisi, N.; Balogun, A.-L. A deep-learning model for national scale modelling and mapping of Sea level rise in Malaysia: The past, present, and future. Geocarto Int. 2021, 1–23. [Google Scholar] [CrossRef]
- Foo, W.Y.; Teh, H.M.; Babatunde, A.-L. Morphodynamics of the teluk nipah shorelines. J. Eng. 2020, 4, 29–40. [Google Scholar]
- Ehsan, S.; Ara Begum, R.; Ghani Md Nor, N.; Nizam Abdul Maulud, K. Current and potential impacts of sea level rise in the coastal areas of Malaysia. IOP Conf. Ser. Earth Environ. Sci. 2019, 228, 012023. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google earth engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Hwang, C.; Khalid, N.F.; Tugi, A.; Omar, K.M. Contemporary sea level rise rates around Malaysia: Altimeter data optimization for assessing coastal impact. J. Asian Earth Sci. 2018, 166, 247–259. [Google Scholar] [CrossRef]
- USGS. Landsat collection 1 level 1 product definition. In United States Geological Survey, 1st ed.; 2017. Available online: https://prd-wret.s3.us-west-2.amazonaws.com/assets/palladium/production/atoms/files/LSDS-1656_%20Landsat_Collection1_L1_Product_Definition-v2.pdf (accessed on 1 May 2021).
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Din, A.H.M.; Hamid, A.I.A.; Yazid, N.M.; Tugi, A.; Khalid, N.F.; Omar, K.M.; Ahmad, A.J.J.T. Malaysian sea water level pattern derived from 19 years tidal data. J. Teknol. 2017, 79, 5. [Google Scholar]
- Holland, P.W.; Welsch, R.E. Robust regression using iteratively reweighted least-squares. Commun. Stat.-Theory Methods 1977, 6, 813–827. [Google Scholar] [CrossRef]
- Wicaksono, A.; Wicaksono, P.; Khakhim, N.; Mohammad, N.; Farda, M.A.M.J.G.I. Tidal correction effects analysis on shoreline mapping in Jepara Regency. Geosp. Inf. 2018, 2, 2. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F.; Cancet, M.; Guillot, A.; Picot, N. FES 2014, a new tidal model—Validation results and perspectives for improvements. In Proceedings of the ESA living planet symposium, Prague, Czech Republic, 9–13 May 2016; pp. 9–13. [Google Scholar]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; US Geological Survey: Reston, VA, USA, 2018.
- Berman, J.J. Understanding your data. In Data Simplification; Berman, J.J., Ed.; Morgan Kaufmann: Boston, MA, USA, 2016; pp. 135–187. [Google Scholar]
- Church, J.A.; Clark, P.U.; Cazenave, A.; Gregory, J.M.; Jevrejeva, S.; Levermann, A.; Merrifield, M.A.; Milne, G.A.; Nerem, R.S.; Nunn, P.D. Sea Level Change; PM Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]










| Category | Data | Format | Source | Purpose |
|---|---|---|---|---|
| Sea Level | Tide gauge | csv | PSMSL | For estimating sea-level trend |
| Satellite altimetry | Netcdf | CMEMS | ||
| Shoreline | Optical satellites: Landsat, Sentinel | GeoTIFF | GEE | For assessing shoreline dynamics |
| Elevation | SRTM digital elevation model | GeoTIFF | GEE | For estimating the beach slope required for tidal correction |
| Oceanic Tide Model | FES2014 | Netcdf | Archiving, Validation and Interpretation of Satellite Oceanographic data (AVISO) | For estimating tide level required for tidal correction |
| Satellite Mission | Pixel Size of Required Bands | Periodicity (Days) | GEE Collections |
|---|---|---|---|
| Landsat 5 (TM) | 30 m R, G, B, NIR, SWIR1 bands | 16 | LANDSAT/LT05/C01/T1_TOA |
| Landsat 7 (ETM+) | 30 m R, G, B, NIR, SWIR1 bands + 15 m panchromatic band | 16 | LANDSAT/LE07/C01/T1_RT_TOA |
| Landsat 8 (OLI) | 30 m R, G, B, NIR, SWIR1 bands + 15 m panchromatic band | 16 | LANDSAT/LC08/C01/T1_RT_TOA |
| Sentinel-2 | 10 m R, G, B, NIR + 20 m SWIR1 | 5 | COPERNICUS/S2 |
| Transect ID | TCD (m) | Length (m) | SCE (m) | NSM (m) | EPR (m/y) | LRR (m/y) | WLR (m/y) |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 139.69 | 72.36 | 4.24 | 0.14 | 1.58 | 1.66 |
| 2 | 200 | 86.88 | 79.38 | −6.2 | −0.2 | 1.19 | 1.3 |
| 3 | 300 | 97.37 | 61.87 | −1.92 | −0.06 | 0.96 | 1.09 |
| 4 | 400 | 111.26 | 35.49 | −25.07 | −0.83 | −0.13 | −0.13 |
| 5 | 500 | 174.30 | 91.89 | −43.36 | −1.43 | −1.37 | −1.36 |
| 6 | 600 | 121.59 | 89.55 | −43.39 | −1.44 | 0.48 | 1.02 |
| 7 | 700 | 55.76 | 50.23 | −22.95 | −0.76 | 0.09 | 0.22 |
| 8 | 800 | 40.66 | 39.65 | −26.95 | −0.89 | −0.15 | −0.12 |
| 9 | 900 | 58.57 | 50.37 | −25.32 | −0.84 | −0.31 | −0.28 |
| 10 | 1000 | 84.49 | 46.37 | −32.36 | −1.07 | −0.02 | 0.03 |
| 11 | 1100 | 118.66 | 39.21 | −14.15 | −0.47 | 0.22 | 0.27 |
| 12 | 1200 | 172.65 | 40.05 | −21.61 | −0.71 | −0.02 | 0.06 |
| 13 | 1300 | 263.21 | 77.31 | −49.29 | −1.63 | 0.05 | 0.18 |
| 14 | 1400 | 308.90 | 54.18 | 6.88 | 0.23 | −0.14 | −0.26 |
| Mean | 59.14 | −21.53 | −0.71 | −0.23 | −0.30 |
| Stations | Relative Sea Level (mm/y) | Absolute Sea Level (mm/y) | SCE (m) | NSM (m) | EPR (m/y) | LRR (m/y) | Shoreline Change Pattern | Correlation of Mean Annual Shoreline and Absolute Sea-Level Change |
|---|---|---|---|---|---|---|---|---|
| Pulau Langkawi | 3.98 2.28 | 2.78 1.30 | 45.11 | −12.28 | −0.21 | −0.41 | Erosion | 0.23 |
| Pulau Pinang | 4.44 2.48 | 3.47 1.36 | 34.37 | −2.26 | −0.42 | −0.24 | Erosion | 0.43 |
| Lumut | 3.76 2.04 | 3.89 1.42 | 63.53 | 5.37 | 0.03 | 0.1 | Accretion | 0.13 |
| Port Kelang | 3.85 2.47 | 3.81 1.53 | 60.75 | −8.17 | −0.75 | −0.2 | Erosion | 0.32 |
| Tanjung Keling | 3.08 2.07 | 3.91 1.33 | 41.78 | −4.49 | −0.18 | −0.23 | Erosion | 0.12 |
| Kukup | 5.91 1.85 | 2.63 1.22 | 52.05 | 2.30 | 0.94 | 0.09 | Accretion | 0.05 |
| Johor Bahru | 4.52 1.99 | 2.95 1.15 | 29.44 | −20.64 | −0.15 | −0.24 | Erosion | 0.36 |
| Getting | 3.22 1.14 | 3.58 0.92 | 19.6 | 0.06 | −0.29 | −0.33 | Erosion | 0.26 |
| Cendering | 3.63 1.55 | 3.86 0.89 | 56.35 | 2.06 | 0.17 | 0.31 | Accretion | 0.12 |
| Tanjung Gelang | 3.96 1.34 | 3.76 0.86 | 25.54 | −17.81 | 0.03 | −0.36 | Erosion | 0.16 |
| Pulau Tioman | 3.36 1.60 | 3.72 0.85 | 53.88 | −19.08 | −0.17 | −0.44 | Erosion | 0.06 |
| Tanjung Sedili | 2.47 1.62 | 3.38 0.97 | 31.9 | −3.75 | −0.67 | −0.32 | Erosion | 0.54 |
| Sandakan | 3.81 2.46 | 4.03 1.75 | 50.91 | 0.61 | 0.05 | 0.2 | Accretion | 0.08 |
| Bintulu | 2.86 1.76 | 3.58 1.23 | 26.2 | −12.37 | −0.57 | −0.19 | Erosion | 0.34 |
| Kota Kinabalu | 4.31 2.00 | 4.04 1.63 | 45.83 | −7.75 | −0.12 | −0.37 | Erosion | 0.23 |
| Lahad Datu | 2.97 3.03 | 4.46 2.13 | 53.59 | 15.20 | 0.38 | 0.15 | Accretion | 0.02 |
| Tawau | 3.83 2.82 | 4.09 2.17 | 53.8 | −2.28 | −0.46 | −0.36 | Erosion | 0.16 |
| Kudat | 2.81 2.78 | 4.20 1.6 | 48.92 | −12.08 | 0.2 | −0.41 | Erosion | 0.10 |
| Labuan 2 | 3.24 2.57 | 3.79 1.44 | 30.61 | −19.84 | −0.38 | −0.42 | Erosion | 0.32 |
| Sejingkat | −3.99 5.80 | 4.11 0.98 | 32.42 | −17.90 | −0.74 | −0.41 | Erosion | 0.17 |
| Miri | 10.51 2.39 | 3.99 1.34 | 24.7 | −7.15 | −0.24 | −0.40 | Erosion | 0.42 |
| Transect ID | TCD | Length (m) | SCE (m) | NSM (m) | EPR (m/y) | LRR (m/y) | WLR (m/y) |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 139.6885251 | 13.63 | −2.2 | −0.07 | −0.16 | −0.16 |
| 2 | 200 | 86.88467384 | 25.75 | 2.96 | 0.1 | −0.02 | −0.02 |
| 3 | 300 | 97.36654348 | 24.42 | 11.26 | 0.37 | 0.38 | 0.38 |
| 4 | 400 | 111.264345 | 23.42 | −17.34 | −0.58 | −0.63 | −0.63 |
| 5 | 500 | 174.2997707 | 76.64 | −48.69 | −1.62 | −2.26 | −2.26 |
| 6 | 600 | 121.5914144 | 40.36 | −31.05 | −1.03 | −1.36 | −1.36 |
| 7 | 700 | 55.76084843 | 25.35 | −22.11 | −0.73 | −0.85 | −0.85 |
| 8 | 800 | 40.65624084 | 24.91 | −21.74 | −0.72 | −0.9 | −0.9 |
| 9 | 900 | 58.57434371 | 32.65 | −24.35 | −0.81 | −1.06 | −1.06 |
| 10 | 1000 | 84.49062081 | 29.02 | −18.32 | −0.61 | −0.84 | −0.84 |
| 11 | 1100 | 118.6596668 | 20.12 | −9.05 | −0.3 | −0.51 | −0.51 |
| 12 | 1200 | 172.6533679 | 32.53 | −16.94 | −0.56 | −0.7 | −0.7 |
| 13 | 1300 | 263.2099826 | 43.55 | −34.83 | −1.16 | −1.38 | −1.38 |
| 14 | 1400 | 308.8970508 | 2.85 | −2.85 | −0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adebisi, N.; Balogun, A.-L.; Mahdianpari, M.; Min, T.H. Assessing the Impacts of Rising Sea Level on Coastal Morpho-Dynamics with Automated High-Frequency Shoreline Mapping Using Multi-Sensor Optical Satellites. Remote Sens. 2021, 13, 3587. https://doi.org/10.3390/rs13183587
Adebisi N, Balogun A-L, Mahdianpari M, Min TH. Assessing the Impacts of Rising Sea Level on Coastal Morpho-Dynamics with Automated High-Frequency Shoreline Mapping Using Multi-Sensor Optical Satellites. Remote Sensing. 2021; 13(18):3587. https://doi.org/10.3390/rs13183587
Chicago/Turabian StyleAdebisi, Naheem, Abdul-Lateef Balogun, Masoud Mahdianpari, and Teh Hee Min. 2021. "Assessing the Impacts of Rising Sea Level on Coastal Morpho-Dynamics with Automated High-Frequency Shoreline Mapping Using Multi-Sensor Optical Satellites" Remote Sensing 13, no. 18: 3587. https://doi.org/10.3390/rs13183587
APA StyleAdebisi, N., Balogun, A.-L., Mahdianpari, M., & Min, T. H. (2021). Assessing the Impacts of Rising Sea Level on Coastal Morpho-Dynamics with Automated High-Frequency Shoreline Mapping Using Multi-Sensor Optical Satellites. Remote Sensing, 13(18), 3587. https://doi.org/10.3390/rs13183587







