Delineating Functional Urban Areas Using a Multi-Step Analysis of Artificial Light-at-Night Data

Abstract

A functional urban area (FUA) is a geographic entity that consists of a densely inhabited city and a less densely populated commuting zone, both highly integrated through labor markets. The delineation of FUAs is important for comparative urban studies and it is commonly performed using census data and data on commuting flows. However, at the national scale, censuses and commuting surveys are performed at low frequency, and, on the global scale, consistent and comparable data are difficult to obtain overall. In this paper, we suggest and test a novel approach based on artificial light at night (ALAN) satellite data to delineate FUAs. As ALAN is emitted by illumination of thoroughfare roads, frequented by commuters, and by buildings surrounding roads, ALAN data can be used, as we hypothesize, for the identification of FUAs. However, as individual FUAs differ by their ALAN emissions, different ALAN thresholds are needed to delineate different FUAs, even those in the same country. To determine such differential thresholds, we use a multi-step approach. First, we analyze the ALAN flux distribution and determine the most frequent ALAN value observed in each FUA. Next, we adjust this value for the FUA’s compactness, and run regressions, in which the estimated ALAN threshold is the dependent variable. In these models, we use several readily available, or easy-to-calculate, characteristics of FUA cores, such as latitude, proximity to the nearest major city, population density, and population density gradient, as predictors. At the next step, we use the estimated models to define optimal ALAN thresholds for individual FUAs, and then compare the boundaries of FUAs, estimated by modelling, with commuting-based delineations. To measure the degree of correspondence between the commuting-based and model-predicted FUAs’ boundaries, we use the Jaccard index, which compares the size of the intersection with the size of the union of each pair of delineations. We apply the proposed approach to two European countries—France and Spain—which host 82 and 72 FUAs, respectively. As our analysis shows, ALAN thresholds, estimated by modelling, fit FUAs’ commuting boundaries with an accuracy of up to 75–100%, being, on the average, higher for large and densely-populated FUAs, than for small, low-density ones. We validate the estimated models by applying them to another European country—Austria—which demonstrates the prediction accuracy of 47–57%, depending on the model type used.

1. Introduction

More than 50% of the world’s population currently resides in urban areas, and this share is expected to increase to 70% by 2050 [1]. Due to a significant concentration of production factors, urban areas produce approximately 80% of the global GDP [2]. This makes spatial dynamics of urban areas to be important for policy-makers and researchers alike. Decision-makers can devise informed development policies, while in the research community, this information can be used to monitor the process of urban growth and the forces behind it [3,4,5], to assess the impact of urbanization on agriculture and natural landscapes [6], on biodiversity [7], on land surface temperature [8], and other socioeconomic and physical phenomena.

Urban growth is characterized by two distinctive components—physical growth and functional change. The former group of attributes reflect changes in impervious surfaces and built-up characteristics, such as building density, building volumes [9,10], as well as population size and density of individual urban settlements [11,12,13]. Concurrently, functional attributes of urban growth reflect factor mobility, associated with various economic activities, such as commuting, commerce, industrial production and services [14]. Such exchanges are especially intense between urban cores, where a large share of production factors is concentrated, and their surrounding areas. Functionally-integrated clusters, representing geographic entities that consist of a densely inhabited city and a less densely populated commuting zone, both highly integrated through labor markets, are commonly referred to as functional urban areas or FUAs [15]. A FUA is conceptually different from an urban agglomeration, which is commonly defined as a major city surrounded by an adjacent hinterland [16]. The major difference between the two is commuting, which is crucial for delineating FUAs, but is not a prime consideration for the definition of urban agglomerations.

According to the mainstream approach adopted by the European Union (EU) and the Organization for Economic Co-operation and Development (OECD), the boundaries of FUAs are defined in three consecutive steps. First, urban cores are identified as contiguities of high-density grid cells with population density of at least 1500 residents per km² and the total population in the contiguous cells of at least 50,000 residents. Second, local administrative units (LAUs) with at least 50% of their residents living inside the urban core are identified. At the final step, the commuting zone, comprising LAUs, which have at least 15% of their residents employed in the core city, is determined. Together with the central city, these administrative units are assumed to form a single FUA [17].

However, commuting data, needed to perform such delineations, are laborious to collect and are infrequent and sporadic even in developed countries [18]. In addition, different countries and regions report communing data with different frequencies, and sometime collect them using different definitions and methodologies [18]. As a result, comparable cross-country estimates of FUA boundaries cannot always be obtained.

As artificial light-at-night (ALAN) data are freely available globally and provide a seamless global coverage, the idea of using them for the identification of human activities was investigated in several studies (see inter alia [19,20,21]). In previous studies, ALAN data were used in health geography [22,23,24,25,26,27], for the analysis of economic performance of countries and regions [28,29,30,31], and in population density research [20,32,33,34,35,36]. The use of such data in the studies of light pollution and its ecological effects is also common [24,37,38,39,40].

In recent years there have been attempts to use ALAN data for the identification of urban areas [20,21,41,42,43,44,45,46,47]. In one such study, Imhoff et al. [41] examined frequency-based ALAN thresholds for three large metropolitan areas in the U.S.—Miami, Chicago and Sacramento. After the authors analyzed the frequencies of differently lit pixels in the ALAN images, they determined that pixels present with 85%, 89% and 94% frequencies, occupy the areas of approximately same size, such as those reported in the Census for the corresponding metropolitan entities.

In another study, Sutton et al. [20] investigated 2000 cities across the globe, and compared their actual boundaries with those produced by three different frequency-based ALAN thresholds—40%, 80% and 90%. As the study revealed, pixels in the ALAN image, observed with a frequency of 80% or more, correspond to the actual municipal boundaries best, reaching a correlation level of about 68%.

In a separate study, Henderson et al. [21] examined frequency- and intensity-based ALAN thresholds that match the boundaries of San Francisco, Beijing and Lhasa. As the authors of this study have found, the optimal ALAN frequency-based thresholds that produce the total lit area comparable in size to the Landsat data-derived urban delineations, reach 88% for Lhasa, 97% for Beijing, and 92% for San Francisco, with the corresponding ALAN flux being equal to 19, 30 and 51 digital numbers (DN), respectively. However, the spatial correspondence between metropolitan boundaries, determined using ALAN thresholds, and actual metropolitan delineations was found to be relatively low, not exceeding 8–44%.

It should also be noted that the aforementioned studies focus on the identification of built-up urban contiguities, while, to the best of our knowledge, only one study by Bosker et al. [18] analyzed functional urban delineations based on commuting flows. The authors of this analysis compared varying percentiles of ALAN intensities, reported by the VIIRS/DNB satellite’s sensor for 2015, with commuting delineations in Malaysia. As this study revealed, the best fit of ~40% is observed when 7% commuting frequency delineations are compared with delineations based on the 25th percentile of ALAN intensities.

A possible reason for such a low fit of less than 40% is that FUAs even in the same country differ by the amount of ALAN they emit. As a result, different ALAN thresholds must be used for the delineation of FUA boundaries in different parts of the urban system. In Figure 1, we illustrate this point using two FUAs in France, as an example. As evidenced by this figure, the ALAN threshold of 0.71 nW/cm²/sr fits reasonably well the boundaries of the Paris FUA, but the same threshold fits rather poorly the much smaller Chateauroux FUA, ALAN flux at which boundary does not exceed 0.15 nW/cm²/sr.

Considering that ALAN emissions from different FUAs vary substantially, it is thus important to establish varying ALAN thresholds, which would fit individual FUAs. This task can be performed for each FUA separately. However, in order to be practical, the approach needs to be sufficiently general, to enable its application to different FUAs, both for countries and regions with well-established commuting data and for other locations with unavailable or sparsely available commuting information. In this paper, we develop such an approach and test it against actual FUA delineations.

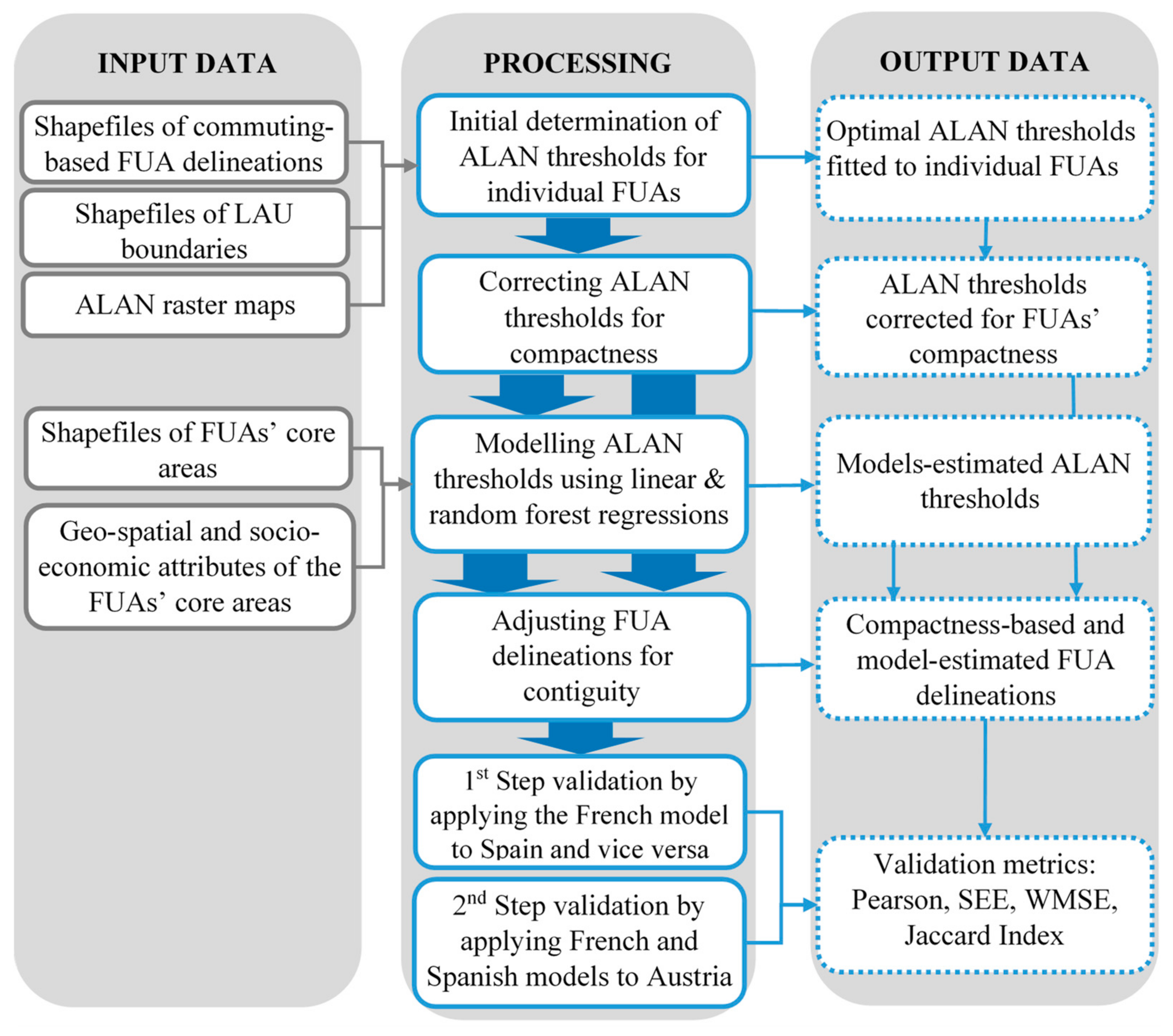
2. Materials and Methods

2.1. Study Phases

The proposed approach is implemented in several steps, as detailed in Figure 2. The data sources and analysis stages are described in the subsections below.

2.2. Data Sources

Data for the present study were drawn from the following four main sources:

(1)

The ALAN raster maps of France and Spain (see Figure 3), used in the study for model training and validation, and ALAN raster for Austria, used for additional validation of the models’ performance, were clipped from 2015 radiance-calibrated ALAN image downloaded from the VIIRS/SNPP website [48]. The ALAN data used in the study are free of background noise, solar and lunar contamination, and also free from data degraded by cloud cover, and features unrelated to electric lighting (e.g., fires, flares, volcanoes) [49]. In addition, the data underwent an outlier removal procedure, applied to abnormally high radiance pixels that occur infrequently over a year [49]. The image in question is the closest temporal match for other data sources used in the analysis, specifically for the FUA delineations, available for 2011 only (Figure 4). Although ALAN images are available today from the VIIRS-SNPP website on a monthly basis, and, since 2018, as daily composites [50], we opted to use an annual composite image, so as to minimize disturbances resulting from ALAN seasonal fluctuations and weather conditions, such as, e.g., cloud cover, which are often present in monthly and daily composites [50]. The subject image is of a ~500 × 500 m spatial resolution and reports the summarized intensity of nighttime light in nW/cm²/sr for different wavelengths in the 500–900 ηm diapason [46]. In the image, ALAN levels vary from 0 to 4187 nW/cm²/sr for France, and from 0 to 550 nW/cm²/sr for Spain (see Figure 3 and

Table 1. Descriptive statistics of the research variables.

Variable	Minimum	Maximum	Mean	SD
France (82 FUAs)
Latitude of the FUA core’s centroid (dd)	42.757	51.001	47.137	2.366
Population density of the FUA core (persons per km2)	89.529	2586.130	470.764	382.596
Population density decline gradient a	1.110	15.409	3.986	2.224
Distance to the nearest major city (dd) a	0.000	5.900	1.781	1.359
Average ALAN level (nW/cm2/sr)	0.649	20.411	3.640	3.614
Spain (72 FUAs)
Latitude of the FUA core centroid (dd)	36.110	43.561	40.093	2.381
Population density of the FUA core (persons per km2)	20.554	3485.360	831.839	794.144
Population density decline gradient b	0.926	16.232	4.863	3.724
Distance to the nearest major city (dd)	0.000	5.120	2.202	1.542
ALAN averaged level (nW/cm2/sr)	0.745	23.129	6.442	4.583

Notes: ^a Calculated as straight line distance between a FUA core’s centroid and centroid of the closest FUA with 1.5M+ residents; ^b Calculated as the ratio between the population density of the FUA core and that of the core’s buffer with a 5 km width for small FUAs (less than 100,000 residents), a 15 km buffer for medium-size FUAs (100,000–250,000 residents), and a 25 km buffer for large FUAs (over 250,000 residents).

).

(2)

Boundaries of FUAs and their cores (see Figure 4) were obtained as shapefiles from the OECD website [51]. These shapefiles are generated using GeoStat grids, based on 2011 commuting data reported in national censuses [51].

(3)

The latitudes of the FUA cores’ centroids and distances to the closest major city, used to explain the variance of the optimal ALAN thresholds, were calculated using the above FUA cores’ shapefiles by applying ArcGIS−10.x software tools.

(4)

Population density of the FUA cores, and population densities of their 5–15–25 km buffers, also used as explanatory variables for the estimation of the optimal ALAN thresholds, were calculated using 1 × 1 km population grids obtained from the LandScan database for 2011 [52].

2.3. Initial Determination of the ALAN Thresholds

For the sake of simplicity, let’s assume that the nighttime light source of highest intensity is located at the center of a FUA, and light intensities drop monotonically and uniformly towards the FUA’s periphery (see Figure 5).

Such an assumption might be fully plausible for compact and monocentric urban areas (Figure 6). Under these conditions, the territorial footprint of the FUA’s ALAN emissions follows a perfect circle, and the most frequently observed (i.e., modal) ALAN values are found at the FUA’s outer boundary (Figure 5a). These modal values are also the dimmest ones, and, as such, they effectively define the FUA’s outer boundary (Figure 5b).

If the above assumptions are upheld, the analysis of the frequency distribution of the observed ALAN values can help to identify the ALAN level, which coincides best with the FUA’s boundary. In particular, the researcher needs to choose the modal ALAN value, for which ALAN intensity is expected to be close to zero (Figure 5b).

2.4. Correction for Compactness

The above assumption of monotonic and concentric distribution of ALAN emissions (Figure 5) is upheld only if the boundaries of FUAs that are circularly shaped. However, if a FUA’s shape is not circular, using the modal ALAN value as a delineation threshold would underestimate the actual area of the FUA. Figure A1 in Appendix A, which reports different FUAs’ footprints, helps to illustrate this point. As this figure shows, the more distant the shape of a FUA from a perfect circle, the brighter ALAN values emerge as the most frequent. For such non-circular FUAs, it is thus necessary to correct for compactness, so as to account for a FUA’s shape deviation from a perfect circle.

To perform such a correction, we first estimate the FUA’s compactness (c), calculating it as the ratio between the area of a FUA and the area of its bounding circle [53,54]:

$$c_{FUA}=\frac{S_{FUA}}{S_{BC}}$$

(1)

where S_FUA = area of a FUA; S_BC = area of the bounding circle, calculated using the Minimum Bounding Geometry tool in the ArcGIS software.

Next, to represent FUAs, which deviate from circular shapes, we model them as ellipses of the same compactness:

$$c_{El}=\frac{S_{El}}{S_{BC}}=\frac{\pi ab}{\pi a^2}=\frac{b}{a}=c_{FUA}$$

(2)

where S_El = area of an ellipse with semi-axes a and b (a > b).

At the next step, to correct the initially estimated ALAN threshold (see Section 2.3) for a FUA’s compactness, we calculate the radius of the circle, r, which has the maximal intersection with ellipse, C_El. As shown in Box A1 in Appendix A, this radius is equal to:

$$r=\sqrt{ab}$$

(3)

Lastly, we estimate the percentile of the ALAN value distribution, p*, corrected for compactness (see Box A1 in the Appendix A for the justification):

$$p^{*}=\frac{2}{\pi }arcsin\left(\frac{1-c}{1+c}\right)$$

(4)

According to (4), for compact shapes, which are close to a circle, i.e., for which c → 1, the optimal ALAN threshold percentile (p*) tends to the dimmest ALAN value (p* → 0), while for prolongated shapes with c → 0, p* → 100, that is, the optimal ALAN threshold will tend to the highest ALAN percentile (see Figure 7).

2.5. Regression Modelling

After the optimal ALAN threshold is identified for each FUA by determining the modal ALAN value (see Section 2.3), and corrected for compactness (Section 2.4), we link the estimated threshold values to several explanatory variables, characterizing the FUA cores, so as to determine these variables’ load on the optimal ALAN threshold value. To model these relationships, the following generic regression equation is used:

$$ALA{N}_i=b_0+b_1*La{t}_i+b_2*D_i+b_3*P{D}_i+b_4*PD{D}_i+{\epsilon }_i$$

(5)

where ALAN_i is the optimal ALAN threshold for FUA i (nW/cm²/sr); Lat_i is latitude of the FUA core’s centroid (decimal degrees, dd); D_i is distance to the nearest major city, calculated between a given FUA core’s centroid and the centroid of the nearest FUA with more than 1.5M residents (dd); PD is population density of the FUA core (persons per km²); PDD is population density decline gradient, calculated as the ratio between the FUA core’s population density and population density in the FUA core’s buffer with a 5 km width for small FUAs (under 100,000 residents), a 15 km width for mid-sized FUAs (100,000–250,000 residents), and a 25 km width for large FUAs (over 250,000 residents); b₀..b₄—regression coefficients, and ε is a random error term.

The predictors used in the model are expected to contribute to the ALAN threshold’s variance due to varying reasons. In particular, population density is known to be closely associated with ALAN flux (see inter alia [33,35,55]). Concurrently, population density gradient might capture changes in the pattern of population density around the FUA core. Concurrently, distance to the nearest major city is likely to show how local development patterns are modulated by proximity to major urban concentrations [55]. In addition, as population concentrations in high latitudes often require more artificial illumination, especially during long winters [40], FUA’s latitude is also included into the model as a potential predictor.

In the analysis, we tested different functional forms of the models, and determined that the logarithmic transformation of the PD and PDD variables provides the best results, by improving the regression fit substantially (p < 0.05). The initial analysis was performed in the IBM SPSSv.25 software using its multiple regression module. To ensure the normality distribution of the dependent variable, ALAN_i, we applied Box-Cox transformation procedure, to redefine the ALAN thresholds [56].

In addition to ordinary least square regressions (OLS), we also tested “random forest” regressions. Such regressions imply building an ensemble of “decision trees”, each of which “voting” for a certain level of the dependent variable, with subsequent averaging of the estimates across all the decision trees [57]. In the present analysis, we implemented a standard realization of the “random forest” regression (the TreeBagger module) in the MATLAB v.R2020x software [58]. During the estimation procedure, two parameters were a matter of choice—the number of independent variables used for the individual decision tree construction and the number of decision trees that comprise the forest. To ensure the comparability of the results, we used all independent variables, covered by the analysis, for the decision trees’ construction, and defined number of trees to be equal to 100, which is usually considered to be a reasonable number for reaching a generalization error convergence (see for example [57,59]). Each decision tree was built for 80% of randomly selected observations.

2.6. Adjustment for Contiguity

When the analysis is performed, any given ALAN threshold level might identify several clusters of identically lit pixels, some of which might be related to a given FUA, while other pixels might be located elsewhere. Therefore, to identify the ALAN pixels relevant to a given FUA, the following analytical procedure was implemented. First, for each FUA, we identified pixels that overlap the FUA’s core area, considering the core boundary information as an initial input (see Section 2.2: Data Sources). Next, for each pixel selected thereby, we analyzed all the pixels in its surroundings. If the ALAN value of a neighboring pixel was lower or equal to that of the pixel under analysis but greater than the ALAN threshold identified for the FUA (see Section 2.3 and Section 2.4), the pixel in question was considered to be a part of the FUA analyzed. We have continued this procedure as long as all the pixels, which satisfy the above criteria, maintained a spatial contiguity. Then, for each FUA, we selected local administrative areas (LAUs), most of which area (that is, >50%) is occupied by the pixels identified thereby. These LAUs were considered to be a part of a given FUA (the MATLAB code for contiguity adjustment can be obtained from the authors upon request).

2.7. Initial Validation

To assess the performance of the estimated models (see Section 2.5), we analyzed the degree of correspondence between the empirically determined (see Section 2.4) and model-predicted ALAN thresholds adjusted for contiguity (see Section 2.6). To this end, the model estimated for France was used to predict the ALAN thresholds for individual FUAs in Spain and vice versa. In order to assess the extent to which the empirically determined and model-predicted ALAN thresholds coincide, we used different metrics, including Pearson correlation coefficients, standard error of the estimates (SEE), and weighted mean squared errors (WMSE).

Next, we compared the FUAs’ delineations, either empirically determined using the modal ALAN values (see Section 2.4) and adjusted for contiguity (see Section 2.6), or model-predicted (see Section 2.5), with commuting-based FUAs’ delineations (see Section 2.2). To perform such a comparison, we used the Jaccard Index (JI), which estimates the share of intersection within the union of the two sets relative to these shapes’ union [60]:

$$JI\left(FU{A}_C,FU{A}_T\right)=\frac{\left|FU{A}_C\cap FU{A}_T\right|}{\left|FU{A}_C\cup FU{A}_T\right|}$$

(6)

where FUA_C = the set of local autonomous units (LAUs) forming a FUA defined by commuting, and FUA_T = set of LAUs within either an empirically determined or model-predicted FUA boundary. The value of the index in question ranges from zero, when no intersection between the two sets is present, to one, when the two sets completely coincide and their intersection is equal to their union [60].

2.8. Second-Step Validation

For an additional validation, we applied the models estimated for France and Spain to FUAs in another European country—Austria (Figure 8).

Although Austria differs from the two other countries under analysis in terms of size, urbanization level, topography, and FUAs’ location, it was chosen for an additional model validation, to demonstrate that the estimated models perform reasonably well even in this specific case. As all FUAs in this country are located apart from each other (see Figure 8), this country is considered particularly suitable for the intended validation.

The validation procedure was carried out in the following four steps. First, we determined the optimal ALAN thresholds for each FUA empirically (see Section 2.3 and Section 2.4). Second, we used the ALAN-threshold identification models, estimated for France and Spain (see Section 2.5), to predict optimal ALAN thresholds for FUAs in Austria, using relevant input variables (see Section 2.2 and Section 2.5), and, then, adjusted these estimates for contiguity (see Section 2.6). Considering that FUAs in Austria are located in close proximity to international borders, the input information was not limited to the areas inside Austria only. For instance, population density-decline gradient and distance to the closest major city were calculated regardless of the state borders. Third, we assessed the correspondence between the empirically determined and models-predicted ALAN thresholds using Pearson correlation coefficients, SEE, and WMSE. Finally, we compared delineations, based on model-predicted ALAN thresholds, with commuting-based delineations, while expanding the study area by a 50-km buffer around the Austrian border, to cover the parts of FUAs located outside Austria and potentially extending into neighboring countries. As in the previous stage of the analysis (Section 2.7), the comparison of the shapes was performed using JI.

3. Results

3.1. Optimal ALAN Thresholds

The descriptive statistics of the ALAN thresholds, estimated by the multi-step approach described in Section 2.1, are reported in

Table 2. Descriptive statistics of the identified ALAN thresholds.

Country/Variable	Minimum	Maximum	Mean	SD
France (Number of FUAs = 82)
• ALAN percentile (0–100)	13.610	45.290	25.623	6.533
• ALAN threshold (nW/cm2/sr)	0.150	9.910	0.664	1.218
Spain (Number of FUAs = 72)
• ALAN percentile (0–100)	12.660	46.460	29.355	7.279
• ALAN threshold (nW/cm2/sr)	0.130	8.230	1.026	1.518

, separately for France and Spain, both as ALAN percentiles and actual ALAN levels in nW/cm²/sr. As evidenced by this table, the optimal ALAN thresholds identified for individual FUAs appear to vary widely, ranging from 0.15 to 9.91 nW/cm²/sr for France, and from 0.13 to 8.23 nW/cm²/sr for Spain.

The most frequent (i.e., modal) ALAN values for all FUAs under analysis are reported in Figure 9, separately for France and Spain. In both countries, the modal ALAN values are not identical to the dimmest ones, thus pointing out that the “circularity” assumption (see Section 2.3) is violated. The bottom sub-figures report ALAN thresholds, corrected for compactness using the approach described in Section 2.4. As it can be seen from the comparison of the upper and bottom diagrams, modal ALAN thresholds, corrected for compactness are closer to the dimmest ALAN values than before the correction (especially for France), albeit differences in distributions are still valid.

3.2. Explaining the Variance of the Observed ALAN Thresholds

In

Table 3. Factors affecting ALAN threshold values estimated for individual FUAs (Method—OLS; Dependent variable—ALAN optimal threshold level, Box-Cox transformed with α = −0.55).

Predictor	Model 1 (France)			Model 2 (Spain)
	B a	Beta b	t c	B a	Beta b	t c
(Constant)	−11.192	-	−8.466 *	−11.846	-	−8.090 *
Latitude (dd)	0.106	0.246	4.209 *	0.140	0.278	3.909 *
Population density of the FUA core, persons per km2 (ln)	1.151	0.751	11.143 *	1.158	1.114	13.124 *
Population density gradient (ln)	−1.369	−0.685	−10.349 *	−1.209	−0.724	−7.977 *
Distance to the nearest major city (dd)	−0.137	−0.183	−3.035 *	−0.147	−0.190	−2.945 *
N of obs.	82			72
R2	0.739			0.740
r	0.866			0.812
SEE	0.533			0.629
WMSE	4.521			2.718
F	54.43 *			46.304 *

Notes: ^a unstandardized regression coefficients; ^b standardized regression coefficients; ^c t-statistic and its significance level; SEE = standard error of the estimates; WMSE = weighted mean squared error; F = F-statistics; * 0.01 significance level.

, we report the results of OLS analysis, linking individually determined optimal ALAN thresholds with geographic and socio-economic attributes of the FUAs’ core areas. As evidenced by Table 3, the predictors used in the analysis help to explain ~74% of the ALAN threshold variance (R² = 0.739–0.740). Characteristically, in both models, significant predictors are nearly identical and exhibit the same signs: population density (+); population density gradient (−); latitude (+), and distance to the nearest major city (−) (p < 0.01).

As random forest regressions do not provide explicit estimates of the explanatory variables’ coefficients, we do not report these models here, but should remark that these estimates in terms of correlation with the actual ALAN threshold levels are similar to the OLS estimates reported in Table 3 (r = 0.856 for France and r = 0.883 for Spain, as opposed to r = 0.866 for France and r = 0.812 for Spain in the OLS models), while in terms of SEE they are poorer (SEE = 0.913 for France and SEE = 0.817 for Spain in comparison to SEE = 0.533 for France and SEE = 0.629 for Spain; see Table 3).

However, in terms of WMSE, random forest regressions are much better (WMSE = 0.945 for France and WMSE = 0.545 for Spain in comparison to WMSE = 4.521 for France and WMSE = 2.718 for Spain in the OLS models; see Table 3). Considering this result, we use the ALAN threshold estimates, produced by the random forest regressions, in the following analysis.

3.3. Model Cross-Validation

In Figure 10, we report the correspondence between the empirically determined and model-predicted ALAN thresholds. For this analysis, the model estimated for France (see Table 3) is applied to FUAs in Spain and vice versa. As evidenced by this figure, the estimates are fairly congruent, with r > 0.819.

3.4. Model-Estimated vs. Commuting-Based FUAs’ Delineations

Figure 11 shows several most successful examples of FUAs’ delineations, generated by the proposed approach. Concurrently, in Figure 12, we report actual FUA delineations and model estimates for all FUAs in continental France and Spain. In addition, in

Table 4. Values of the Jaccard index (JI) calculated for FUAs of different size and population density.

FUA Type	N. of Obs.	Delineations Derived from Compactness-Based ALAN Thresholds		Delineations Derived from Model-Based ALAN Thresholds
		Mean	SD	Mean	SD
All FUAs under analysis	154	0.342	0.158	0.351	0.150
FUAs in:
• France	82	0.304	0.116	0.326	0.124
• Spain	72	0.385	0.186	0.378	0.171
FUAs by class:
• 1&2 (Smallest)	93	0.327	0.154	0.335	0.152
• 3 (Medium)	55	0.351	0.154	0.361	0.138
• 4 (Largest)	6	0.499	0.187	0.507	0.134
Population density in the FUA core, people per km2 (ln)
• ≤5	18	0.235	0.097	0.349	0.139
• >5	136	0.356	0.159	0.351	0.151
• >6.5	48	0.440	0.177	0.424	0.174
• >7.5	12	0.551	0.190	0.487	0.204
Population density in the core’s buffer zone, people per km2 (ln)
• ≤5	101	0.313	0.137	0.340	0.135
• >5	53	0.398	0.180	0.372	0.174
• >6	11	0.525	0.220	0.469	0.235
• >6.3	4	0.638	0.277	0.557	0.299
Ratio between population density in the core and the core’s buffer zone
• ≤2	25	0.303	0.151	0.319	0.157
• >2	129	0.350	0.159	0.357	0.148
• >5	43	0.363	0.153	0.357	0.155
• >10	11	0.467	0.184	0.458	0.197

, we report the degree of correspondence between the model-estimated and commuting-based delineations, assessed using JI.

As can be seen in Table 4, the calculated JI values range between 0.30 and 0.64, being higher for large FUAs (JI = 0.499–0.507) than for small FUAs (JI = 0.33–0.34). For densely populated FUAs, the match between the commuting-based and ALAN-based delineations is especially high, reaching 0.557–0.638, or 56–64% (see Table 4). [The JI values for all the French and Spanish FUAs are reported in Figure A2 in Appendix A].

3.5. Second-Step Validation

In

Table 5. Individually fitted vs. model-estimated ALAN thresholds for FUAs in Austria.

FUA	ALAN Threshold, nW/cm2/sr
	Individually Fitted	Estimated Using the “French” Model	Estimated Using the “Spanish” Model
Vienna	0.34	0.65	1.56
Graz	0.23	0.48	1.05
Linz	0.24	0.49	1.04
Salzburg	0.27	0.49	1.08
Innsbruck	0.26	0.30	0.78
Klagenfurt	0.17	0.30	0.72
Performance indicators (in relation to individually fitted ALAN threshold)
r	-	0.783	0.771
SEE	-	0.216	0.819
WMSE	-	0.711	10.102

, we report ALAN threshold values for FUAs in Austria, calculated using the ‘French’ and ‘Spanish’ models (Table 3), and compared to individually fitted ALAN thresholds. As evidenced by this table, the ALAN thresholds, estimated using the French and Spanish models, correspond to the individually fitted ALAN thresholds quite well, with r > 0.77 and SEE < 0.82. Yet, in terms of WMSE, the French model performs poorer in comparison to the Spanish model (WMSE = 0.711 vs. WMSE = 10.102, respectively). In Figure 13, we report FUAs’ delineations obtained by averaging the estimates obtained using the French and Spanish models (see Table 3).

4. Discussion and Conclusions

The delineation of geographic boundaries of FUAs is important for comparative urban studies. However, using commuting data for this task is not always feasible due to difficulties in data collection. In the present study, we suggested and tested an approach, based on the analysis of ALAN data. As ALAN is emitted from roads, frequented by commuters, and by buildings surrounding roads, ALAN emissions can be used, as we hypothesize, for the identification of FUAs.

We verify this hypothesis using data on commuting-based delineations available for France and Spain, applying a multi-step approach. First, we fit the ALAN threshold for each individual FUA, using the modal value of the ALAN frequency distribution. Next, we explain this threshold by a multiple regression analysis, using several characteristics of the FUAs’ cores, such as latitude of the core’s centroid, distance to the closest major city, population density, and density decline gradient. Although the boundaries of the FUA core areas used as an initial input are not generated by the analysis per se, such boundaries, if not a priori available, can be identified easily using Global Human Settlement [61] or LandScan [52] as contiguities of densely populated grids. Lastly, we cross-validate the obtained models for three European countries.

As our analysis indicates, the degree of correspondence between the individually fitted and model-predicted ALAN thresholds is relatively high (r > 0.819), with Jaccard Index values reaching up to 75% for France and up to 100% for Spain.

Our results are more robust than those obtained by Bosker and colleagues [18] for FUAs in Indonesia, according to which the correspondence between ALAN-based and 15% commuting-based FUA delineations did not exceed 28%. We explain the improvement, obtained in the present study, by the use of individually-fitted ALAN thresholds, based on the analysis of modal values, corrected for compactness.

To the best of our knowledge, this study is the first that estimates the optimal ALAN thresholds that approximate the boundaries of individual FUAs, using readily available, or easy-to-compute, characteristics of the FUAs’ cores, such as latitude of the core’s centroid, distance to the closest major city, population density and population density decline gradient, combined with ALAN flux data.

The proposed modelling approach might be useful for FUA delineations in countries and regions, for which commuting data are unavailable, as well as for places, in which commuting data are not updated on a regular basis, and for a comparative analysis of countries and regions, which use different commuting-assessment procedures. Using our modeling approach, FUAs’ boundaries can be determined in the following steps. First, the boundaries of FUAs’ cores should be identified. If such boundaries are not readily available, they can be determined as contiguities of high-density grid cells, using input sources, such as Global Human Settlement [61] or LandScan [52] grids. The procedure might follow the algorithm described in Dijkstra et al. (2019): Grid cells with population density of at least 1500 residents per km² are identified. Afterward, the grid cells identified thereby are grouped into contiguous area with a total population of at least 50,000 residents. For such areas, the development and locational characteristics are identified next, including the latitude of the contiguity’s centroid, distance to the closest major city, population density and population density decline gradient (see Section 2.5). These characteristics of the core areas are then used as predictors in the ALAN-threshold estimation models, reported in Section 2.5 for either France or Spain, or both, to obtain the optimal ALAN threshold estimates for each individual FUA. Finally, a VIIRS-DNB raster is used, to select pixels, corresponding to the estimated ALAN threshold, and to identify LAUs associated with such pixels’ contiguities, as detailed in Section 2.6.

The present study has several limitations. While for some FUAs, our estimates are quite accurate, reaching the levels of accuracy of 74–100%, for other, typically smaller FUAs, our estimations are less accurate. We assume that the reason might be that commuting-based boundaries rely mainly on work-related commuting, while omitting other human flows, such as travels for leisure, services, and social activities. In contrast, the suggested ALAN approach captures human activities at large. In addition, the ALAN-based approach might omit areas occupied by functions that operate mainly at daytime and emit much less light at night. For smaller FUAs, this source of error might by more pronounced than for large FUAs, where many functions operate around the clock. Another possible reason for a relatively low correspondence between some commuting- and ALAN-based delineations might be due to the fact that many FUAs are not monocentric, or might have a shape which is far from circular or elliptic, which we considered for modelling. For such cases, further studies might be needed to reflect more complex situations, in which FUA is either polycentric, or adjacent to other FUAs and their boundaries overlap or merge.

It should also be noted that in this study, we investigated the performance of the proposed method by applying it to three well-developed countries in Europe—France, Spain, and Austria. Yet, question remains about the models’ applicability to countries outside Europe and to countries in mid-latitudes, and, especially, to less-developed countries. We expect that applying the models to such countries might result in the overestimation of the optimal ALAN thresholds and thus in the underestimation of the commuting extent (the evidence for this conclusion is provided in [21]). Therefore, a follow-up investigation of the applicability of the proposed models to less developed countries and regions might be needed. Additionally, we need to acknowledge that a temporal mismatch between ALAN and actual FUAs’ delineation exists. Whether it might affect the results of the analysis should be clarified in future studies, after newer commuting data become available.