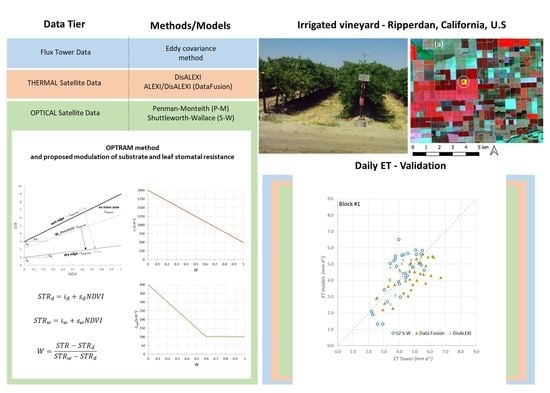
Determining Evapotranspiration by Using Combination Equation Models with Sentinel-2 Data and Comparison with Thermal-Based Energy Balance in a California Irrigated Vineyard
Abstract
:1. Introduction
- (a)
- reflectance and vegetation index (VI) based-methods: crop coefficient and canopy parameters, such as hemispherical albedo and leaf area index LAI, are obtained by means of different analytics from reflectance or vegetation indices. These parameters are the basic inputs for the application of the widely used FAO-56 approach [3] for determining crop evapotranspiration, either by the direct calculation of the combination equation of Penman–Monteith or by using the crop coefficient and reference evapotranspiration. These methods are already implemented in operational applications for irrigation management [4] and are evolving toward the more explicit definition of the canopy conductance [5,6];
- (b)
- thermal-based energy balance models: land surface temperature is the main input for estimating sensible heat flux and then latent heat flux as a residual term of the surface energy balance. Significant advancements have been made from the first contextual approaches using soil–vegetation–transfer models [7] to one-source models i.e., SEBAL [8], SEBS [9] and METRIC [10], and two-source models, such as TSEB [11] and ALEXI [12]. Thermal-based models have been intensively applied by using observation data from Landsat [13], which is, at the present moment, the only operational platform with medium resolution acquisitions in the thermal infrared (100 m), which are resampled to 30 m with a revisit time of 8 to 16 days depending on the site;
- (c)
- EO-driven soil water balance models: these are simulation models of water balance using EO-based input data related to crop development [14,15]. These models produce a continuous spatially distributed output, the quality of which strongly depends on the availability of reliable soil physical and hydraulic properties, as well as precipitation/irrigation inputs [16].
2. Theory
2.1. The Sparse Canopy Combination Equation
- -
- the substrate resistance rss, which regulates the evaporation from the soil and has been considered to vary between 500 (wet soil) and 2000 sm−1 (dry soil) [22];
- -
- the bulk boundary layer resistance:
- -
- And the bulk stomatal canopy resistance, rsc, already defined in Equation (5).
2.2. Linking Substrate and Canopy Resistance with SWIR Observations in the OPTRAM Approach
2.3. Thermal-Based Energy Balance Models
3. Study Area Description and Datasets Developed in the Context of GRAPEX
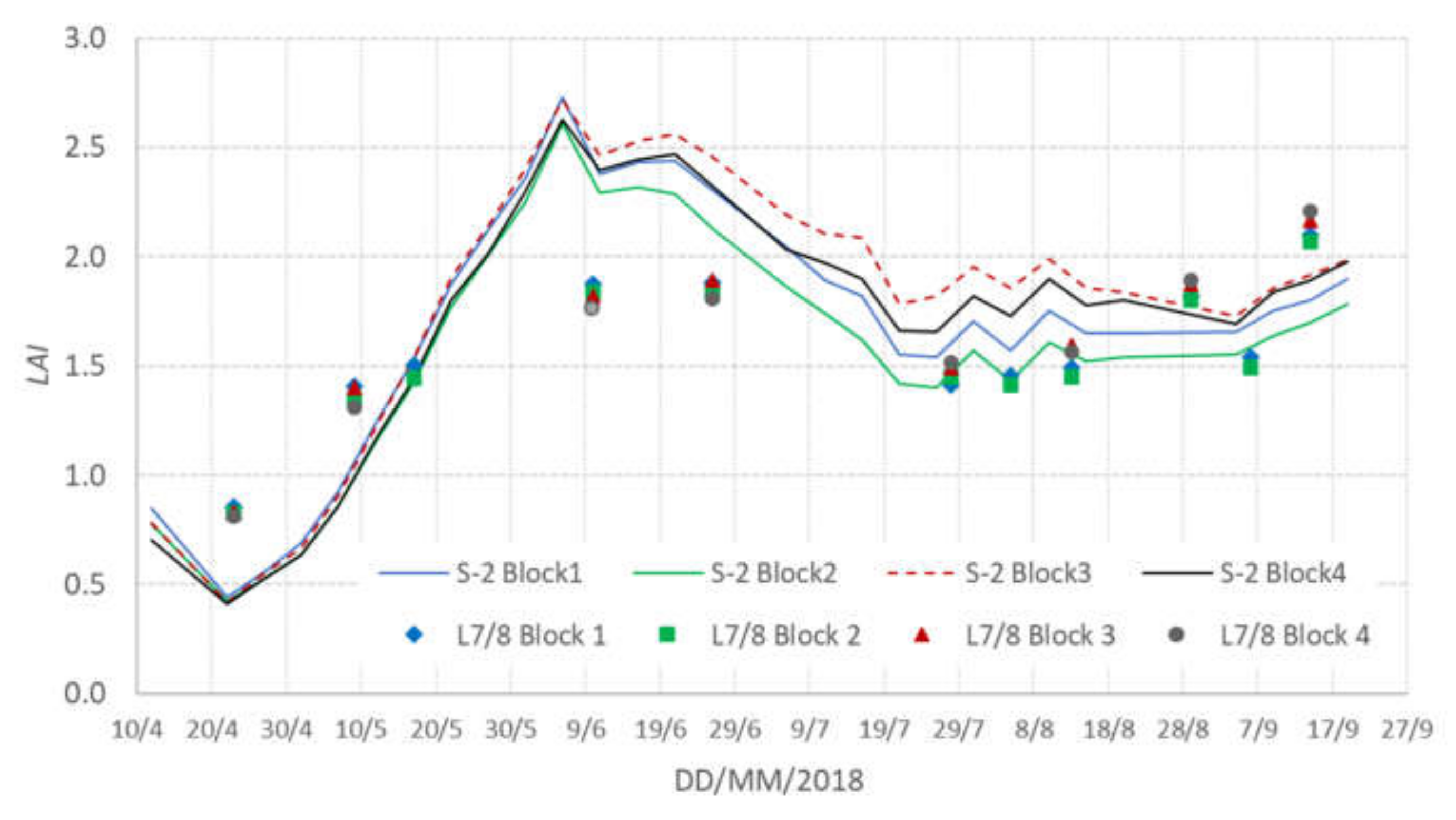
4. Description of the Sentinel-2 and Landsat-7–8 Datasets and Derived Products
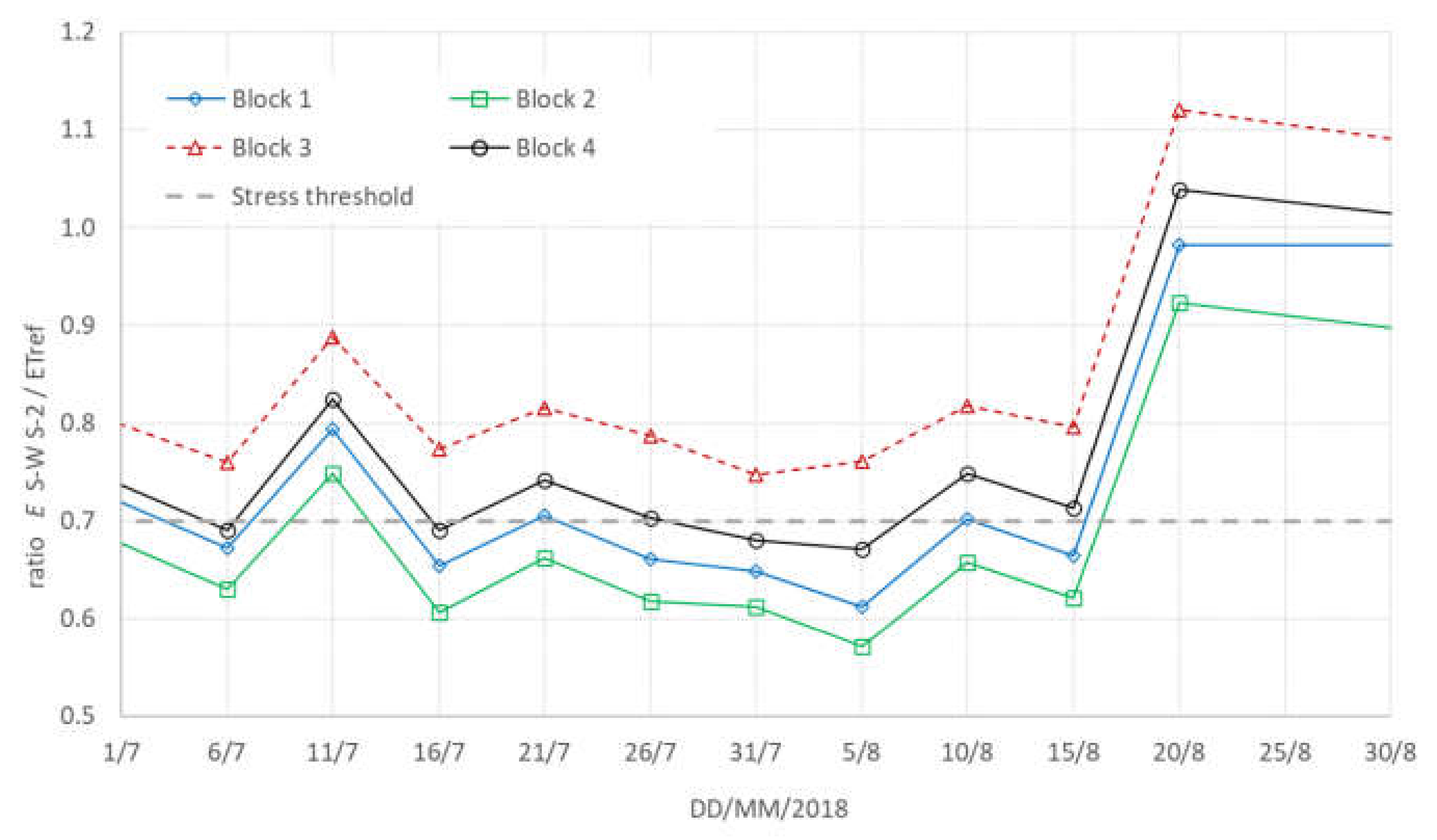
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

References
- Vuolo, F.; Essl, L.; Atzberger, C. Costs and benefits of satellite-based tools for irrigation management. Front. Environ. Sci. 2015, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Vuolo, F.; D’Urso, G.; De Michele, C.; Bianchi, B.; Cutting, M. Satellite-based irrigation advisory services: A common tool for different experiences from Europe to Australia. Agric. Water Manag. 2015, 147, 82–95. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M.; Ab, W. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 2008. [Google Scholar]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.M.; Liu, J. Evolution of evapotranspiration models using thermal and shortwave remote sensing data. Remote Sens. Environ. 2020, 237, 111594. [Google Scholar] [CrossRef]
- García-Gutiérrez, V.; Stöckle, C.; Gil, P.M.; Meza, F.J. Evaluation of Penman–Monteith Model Based on Sentinel-2 Data for the Estimation of Actual Evapotranspiration in Vineyards. Remote Sens. 2021, 13, 478. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A method to make use of thermal infrared temperature and NDVI measurements to infer surface soil water content and fractional vegetation cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL)—1. Formulation. J. Hydrol. 1998, 213, 198–212. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Anderson, M.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- D’Urso, G.; Menenti, M.; Santini, A. Regional application of one-dimensional water flow models for irrigation management. Agric. Water Manag. 1999, 40, 291–302. [Google Scholar] [CrossRef]
- Boegh, E.; Thorsen, M.; Butts, M.; Hansen, S.; Christiansen, J.; Abrahamsen, P.; Hasager, C.B.; Jensen, N.; van der Keur, P.; Refsgaard, J.C.; et al. Incorporating remote sensing data in physically based distributed agro-hydrological modelling. J. Hydrol. 2004, 287, 279–299. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating evapotranspiration of an apple orchard using a remote sensing-based soil water balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef] [Green Version]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. A data fusion approach for mapping daily evapotranspiration at field scale. Water Resour. Res. 2013, 49, 4672–4686. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.; Gao, F.; Hain, C.; Kustas, W. Mapping daily evapotranspiration at field scales over rainfed and irrigated agricultural areas using remote sensing data fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Alsina, M.M.; Hain, C.R.; Alfieri, J.G.; Prueger, J.H.; Gao, F.; McKee, L.G.; Sanchez, L.A. Using High-Spatiotemporal Thermal Satellite ET Retrievals for Operational Water Use and Stress Monitoring in a California Vineyard. Remote Sens. 2019, 11, 2124. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Anderson, M.C.; Gao, F.; Wardlow, B.; Hain, C.R.; Otkin, J.A.; Alfieri, J.; Yang, Y.; Sun, L.; Dulaney, W. Field-scale mapping of evaporative stress indicators of crop yield: An application over Mead, NE, USA. Remote Sens. Environ. 2018, 210, 387–402. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling High-Resolution Actual Evapotranspiration through Sentinel-2 and Sentinel-3 Data Fusion. Remote Sens. 2020, 12, 1433. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse-crops—An energy combination theory. Quart. J. R. Meteor. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Chapter 13: Steady state heat balance. In Principles of Environmental Physics, 3rd ed.; Academic Press: Burlington, VT, USA, 2008; pp. 250–255. [Google Scholar]
- Brutsaert, W. Evaporation into the Atmosphere; Springer: Geneva, Switzerland, 1982. [Google Scholar]
- Mahrt, L.; Ek, M. The influence of atmospheric stability on potential evaporation. J. Appl. Meteor. 1984, 23, 222–234. [Google Scholar] [CrossRef] [Green Version]
- Szeicz, G.; Long, I.F. Surface Resistance of Crop Canopies. Water Resour. Res. 1969, 5, 622–633. [Google Scholar] [CrossRef]
- Spank, U.; Köstner, B.; Moderow, U.; Grunwald, T.; Bernhofer, C. Surface Conductance of Five Different Crops Based on 10 Years of Eddy-Covariance Measurements. Meteorol. Z. 2016, 25, 251–266. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Kanga, S.; Tonga, L.; Dua, T.; Haoa, X.; Zhao, P. Comparison of several surface resistance models for estimating crop evapotranspiration over the entire growing season in arid regions. Agric. Forest Meteor. 2015, 208, 1–15. [Google Scholar] [CrossRef]
- Chávez, J.L.; López-Urrea, R. One-step approach for estimating maize actual water use: Part I. Modeling a variable surface resistance. Irrig. Sci. 2019, 3, 123–137. [Google Scholar] [CrossRef]
- Körner, C. Leaf diffusive conductance in the major vegetation types of the globe. In Ecophysiology of Photosynthesis; Springer: Berlin/Heidelberg, Germany, 1994; Volume 100, pp. 463–490. [Google Scholar]
- Kelliher, F.; Leuning, R.; Raupach, M.; Schulze, E.-D. Maximum conductances for evaporation from global vegetation types. Agric. For. Meteorol. 1995, 73, 1–16. [Google Scholar] [CrossRef]
- Leuning, R.; Zhang, Y.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Möller, M.; Alchanatis, V.; Cohen, Y.; Meron, M.; Tsipris, J.; Naor, A.; Ostrovsky, V.; Sprintsin, M.; Cohen, S. Use of thermal and visible imagery for estimating crop water status of irrigated grapevine. J. Exp. Bot. 2007, 58, 827–838. [Google Scholar] [CrossRef] [Green Version]
- Amazirh, A.; Er-Raki, S.; Chehbouni, A.; Rivalland, V.; Diarra, A.; Khabba, S.; Ezzahar, J.; Merlin, O. Modified Penman–Monteith equation for monitoring evapotranspiration of wheat crop: Relationship between the surface resistance and remotely sensed stress index. Biosyst. Eng. 2017, 164, 68–84. [Google Scholar] [CrossRef]
- Autovino, D.; Minacapilli, M.; Provenzano, G. Modelling bulk surface resistance by MODIS data and assessment of MOD16A2 evapotranspiration product in an irrigation district of Southern Italy. Agric. Water Manag. 2016, 167, 86–94. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound.-Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Verhoef, A.; McNaughton, K.G.; Jacobs, A.F.G. A parameterization of momentum roughness length and displacement height for a wide range of canopy densities. Hydrol. Earth Syst. Sci. 1997, 1, 81–91. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete-Echeverría, C. Latent heat flux over Cabernet Sauvignon vineyard using the Shuttleworth and Wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Jones, S.B.; Philpot, W.D. A linear physically-based model for remote sensing of soil moisture using short wave infrared bands. Remote Sens. Environ. 2015, 164, 66–76. [Google Scholar] [CrossRef]
- Van Keulen, H.; Seligman, N.G. Simulation of Water Use; Nitrogen and Growth of a Spring Wheat Crop; Simulation Monograph; Pudoc: Wageningen, The Netherlands, 1997. [Google Scholar]
- Feddes, R.; Kabat, P.; Van Bakel, P.; Bronswijk, J.; Halbertsma, J. Modelling soil water dynamics in the unsaturated zone—State of the art. J. Hydrol. 1988, 100, 69–111. [Google Scholar] [CrossRef] [Green Version]
- Choi, M.; Kustas, W.P.; Anderson, M.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, U.S.) during SMACEX. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A Two-Source Energy Balance Approach Using Directional Radiometric Temperature Observations for Sparse Canopy Covered Surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Cammalleri, C.; Ciraolo, G.; La Loggia, G.; Maltese, A. Daily evapotranspiration assessment by means of residual surface energy balance modeling: A critical analysis under a wide range of water availability. J. Hydrol. 2012, 452-453, 119–129. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Torn, R.D.; Kustas, W.P.; Basara, J.B. A multi-scale remote sensing model for disaggregating regional fluxes to micrometeorological scales. J. Hydrometeorol. 2004, 5, 343–363. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- USDA. GRAPEX. Available online: https://www.ars.usda.gov/northeast-area/beltsville-md-barc/beltsville-agricultural-research-center/hydrology-and-remote-sensing-laboratory/docs/grapex/grapex-home/ (accessed on 16 September 2021).
- Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Knipper, K.; Torres-Rua, A.; Parry, C.K.; Nieto, H.; Agam, N.; White, A.; Gao, F.; et al. The Grape Remote sensing Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX). Bull. Am. Meteorol. Soc. 2018, 99, 1791–1812. [Google Scholar] [CrossRef] [Green Version]
- Xia, T.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Gao, F.; McKee, L.; Prueger, J.H.; Geli, H.M.E.; Neale, C.M.U.; Sanchez, L.; et al. Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one- and two-source modeling schemes. Hydrol. Earth Syst. Sci. 2016, 20, 1523–1545. [Google Scholar] [CrossRef] [Green Version]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.M.; Prueger, J.H.; et al. Evaluation of TSEB turbulent fluxes using different methods for the retrieval of soil and canopy component temperatures from UAV thermal and multispectral imagery. Irrig. Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Prueger, J.H.; Hain, C.R.; Gao, F.; Yang, Y.; McKee, L.G.; Nieto, H.; et al. Evapotranspiration estimates derived using thermal-based satellite remote sensing and data fusion for irrigation management in California vineyards. Irrig. Sci. 2019, 37, 431–449. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; McKee, L.M.; Prueger, J.H.; Hipps, L.E. Micro-scale spatial variability in soil heat flux (SHF) in a wine-grape vineyard. Irrig. Sci. 2019, 37, 253–268. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Kustas, W.P.; Prueger, J.H.; McKee, L.G.; Hipps, L.E.; Gao, F. A multi-year inter-comparison of micrometeorological observations at adjacent vineyards in California’s central valley during GRAPEX. Irrig. Sci. 2019, 37, 345–357. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. Chapter 15: The Light Environment of Plant Canopies. In An Introduction to Environmental Biophysics, 2nd ed.; Springer: New York, NY, USA, 1998; pp. 247–278. [Google Scholar]
- Menenti, M.; Bastiaanssen, W.G.M.; van Eick, D. Determinantion of surface hemispherical reflectance with Thematic Mapper data. Remote Sens. Environ. 1989, 28, 327–337. [Google Scholar] [CrossRef]
- Anderson, M.C.; Gao, F.; Kustas, W.P.; Wang, Y. Simple method for retrieving leaf area index from Landsat using MODIS leaf area index products as reference. J. Appl. Remote Sens. 2012, 6, 063554. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. Sentinel-2 ToolBox Level 2 Products: LAI, FAPAR, FCOVER, Version 1.1; European Space Agency: Noordwijk, The Netherlands, 2016; Available online: https://step.esa.int/docs/extra/ATBD_S2ToolBox_L2B_V1.1.pdf (accessed on 16 September 2021).
- Pasqualotto, N.; D’Urso, G.; Bolognesi, S.F.; Belfiore, O.R.; Van Wittenberghe, S.; Delegido, J.; Pezzola, A.; Winschel, C.; Moreno, J. Retrieval of Evapotranspiration from Sentinel-2: Comparison of Vegetation Indices, Semi-Empirical Models and SNAP Biophysical Processor Approach. Agronomy 2019, 9, 663. [Google Scholar] [CrossRef] [Green Version]
- Ambrosone, M.; Matese, A.; Di Gennaro, S.F.; Gioli, B.; Tudoroiu, M.; Genesio, L.; Miglietta, F.; Baronti, S.; Maienza, A.; Ungaro, F.; et al. Retrieving soil moisture in rainfed and irrigated fields using Sentinel-2 observations and a modified OPTRAM approach. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102113. [Google Scholar] [CrossRef]
















| Block #1 | Block #2 | Block #3 | Block #4 | |
|---|---|---|---|---|
| cumulated IRR (mm) | 302.8 | 293.5 | 308.2 | 348.2 |
| averaged IRR (mm/d) | 1.79 | 1.74 | 1.82 | 2.06 |
| cumulated E (mm) | 680.3 | 669.2 | 775.2 | 755.4 |
| averaged E (mm/d) | 4.03 | 3.96 | 4.59 | 4.47 |
| min E (mm/d) | 1.34 | 1.46 | 1.51 | 1.35 |
| max E (mm/d) | 6.85 | 6.16 | 8.41 | 6.61 |
| 26 June 2018 | 14 September 2018 | |||
|---|---|---|---|---|
| Block | Landsat-8 | Sentinel-2 | Landsat-8 | Sentinel-2 |
| 1 | 1.89 | 2.26 | 2.11 | 1.75 |
| 2 | 1.81 | 2.15 | 2.08 | 1.70 |
| 3 | 1.90 | 2.39 | 2.18 | 1.86 |
| 4 | 1.81 | 2.33 | 2.21 | 1.88 |
| Flux Tower Meteorological Data | CFSR Meteorological Data | |||
|---|---|---|---|---|
| P-M S-2 | S-W S-2 | P-M S-2 | S-W S-2 | |
| Pearson coeff. | 0.798 | 0.743 | 0.759 | 0.703 |
| Determ. coeff. R2 | 0.638 | 0.551 | 0.577 | 0.494 |
| RMSE | 1.016 | 1.037 | 1.390 | 1.801 |
| MAE | 0.850 | 0.815 | 1.147 | 1.520 |
| slope | 0.871 | 1.015 | 0.904 | 1.096 |
| F | 2576.9 | 2237.2 | 1090.4 | 914.2 |
| degr. freed. | 111 | 111 | 111 | 111 |
| Block #1 | S-W S-2 | S-W S-2 CFSR | Data Fusion | DisALEXI | Block #2 | S-W S-2 | S-W S-2 CFSR | Data Fusion | DisAlexi |
|---|---|---|---|---|---|---|---|---|---|
| Pearson | 0.706 | 0.667 | 0.753 | 0.773 | Pearson | 0.756 | 0.746 | 0.816 | 0.753 |
| R2 | 0.498 | 0.445 | 0.567 | 0.597 | R2 | 0.572 | 0.557 | 0.666 | 0.568 |
| RMSE | 1.036 | 1.818 | 1.017 | 0.631 | RMSE | 0.871 | 1.558 | 0.995 | 0.582 |
| MAE | 0.816 | 1.553 | 0.823 | 0.523 | MAE | 0.675 | 1.328 | 0.828 | 0.530 |
| Slope | 1.069 | 1.125 | 1.158 | 1.069 | slope | 1.021 | 1.068 | 1.182 | 1.081 |
| F | 578.0 | 208.9 | 1101.1 | 1031.3 | F | 674.2 | 235.7 | 1603.4 | 1012.8 |
| degr. freed. | 28 | 28 | 27 | 16 | degr. freed. | 28 | 28 | 27 | 16 |
| Block #3 | S-W S-2 | S-W S-2 CFSR | Data fusion | DisALEXI | Block #4 | S-W S-2 | S-W S-2 CFSR | Data fusion | DisALEXI |
| Pearson | 0.718 | 0.635 | 0.810 | 0.834 | Pearson | 0.801 | 0.770 | 0.859 | 0.824 |
| R2 | 0.515 | 0.403 | 0.657 | 0.695 | R2 | 0.641 | 0.593 | 0.738 | 0.679 |
| RMSE | 1.183 | 2.129 | 0.796 | 0.650 | RMSE | 0.951 | 1.729 | 0.683 | 0.766 |
| MAE | 0.919 | 1.828 | 0.641 | 0.437 | MAE | 0.744 | 1.444 | 0.531 | 0.462 |
| Slope | 1.002 | 1.078 | 1.014 | 0.966 | slope | 0.975 | 1.045 | 1.051 | 0.965 |
| F | 491.5 | 181.5 | 1084.0 | 1170.3 | F | 677.4 | 234.8 | 1684.6 | 1207.0 |
| degr. freed. | 28 | 28 | 27 | 16 | degr. freed. | 28 | 28 | 27 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Urso, G.; Bolognesi, S.F.; Kustas, W.P.; Knipper, K.R.; Anderson, M.C.; Alsina, M.M.; Hain, C.R.; Alfieri, J.G.; Prueger, J.H.; Gao, F.; et al. Determining Evapotranspiration by Using Combination Equation Models with Sentinel-2 Data and Comparison with Thermal-Based Energy Balance in a California Irrigated Vineyard. Remote Sens. 2021, 13, 3720. https://doi.org/10.3390/rs13183720
D’Urso G, Bolognesi SF, Kustas WP, Knipper KR, Anderson MC, Alsina MM, Hain CR, Alfieri JG, Prueger JH, Gao F, et al. Determining Evapotranspiration by Using Combination Equation Models with Sentinel-2 Data and Comparison with Thermal-Based Energy Balance in a California Irrigated Vineyard. Remote Sensing. 2021; 13(18):3720. https://doi.org/10.3390/rs13183720
Chicago/Turabian StyleD’Urso, Guido, Salvatore Falanga Bolognesi, William P. Kustas, Kyle R. Knipper, Martha C. Anderson, Maria M. Alsina, Christopher R. Hain, Joseph G. Alfieri, John H. Prueger, Feng Gao, and et al. 2021. "Determining Evapotranspiration by Using Combination Equation Models with Sentinel-2 Data and Comparison with Thermal-Based Energy Balance in a California Irrigated Vineyard" Remote Sensing 13, no. 18: 3720. https://doi.org/10.3390/rs13183720
APA StyleD’Urso, G., Bolognesi, S. F., Kustas, W. P., Knipper, K. R., Anderson, M. C., Alsina, M. M., Hain, C. R., Alfieri, J. G., Prueger, J. H., Gao, F., McKee, L. G., De Michele, C., McElrone, A. J., Bambach, N., Sanchez, L., & Belfiore, O. R. (2021). Determining Evapotranspiration by Using Combination Equation Models with Sentinel-2 Data and Comparison with Thermal-Based Energy Balance in a California Irrigated Vineyard. Remote Sensing, 13(18), 3720. https://doi.org/10.3390/rs13183720