Abstract
Global navigation satellite system signals are known to be an efficient tool to monitor the Earth ionosphere. We suggest Galileo E5 AltBOC phase and pseudorange observables—a single-frequency combination—to estimate the ionospheric total electron content (TEC). We performed a one-month campaign in September 2020 to compare the noise level for different TEC estimations based on single-frequency and dual-frequency data. Unlike GPS, GLONASS, or Galileo E5a and E5b single-frequency TEC estimations (involving signals with binary and quadrature phase-shift keying, such as BPSK and QPSK, or binary offset carrier (BOC) modulation), an extra wideband Galileo E5 AltBOC signal provided the smallest noise level, comparable to that of dual-frequency GPS. For elevation higher than 60 degrees, the 100 s root-mean-square (RMS) of TEC, an estimated TEC noise proxy, was as follows for different signals: ~0.05 TECU for Galileo E5 AltBOC, 0.09 TECU for GPS L5, ~0.1TECU for Galileo E5a/E5b BPSK, and 0.85 TECU for Galileo E1 CBOC. Dual-frequency phase combinations provided RMS values of 0.03 TECU for Galileo E1/E5, 0.03 and 0.07 TECU for GPS L1/L2 and L1/L5. At low elevations, E5 AltBOC provided at least twice less single-frequency TEC noise as compared with data obtained from E5a or E5b. The short dataset of our study could limit the obtained estimates; however, we expect that the AltBOC single-frequency TEC will still surpass the BPSK analogue in noise parameters when the solar cycle evolves and geomagnetic activity increases. Therefore, AltBOC signals could advance geoscience.
1. Introduction
Many scientific problems and practical applications (involving transionospheric propagation) require reliable monitoring of the ionospheric variability at different spatial and temporal scales. For some applications, engineers need 3D electron density distribution, but often they need only total electron content (TEC)—an integral parameter.
To estimate TEC, scientists have suggested radio beacons which provide data on the Faraday rotation of the signal polarization plane [1] or the signal phase and pseudorange (group delay) [2,3]. The first approach requires geomagnetic field data along the line of sight and linearly polarized signals. This makes the second approach more usable for low Earth orbit (LEO) [4], medium Earth orbit (MEO) [5], and geostationary Earth orbit (GEO) [6,7,8] satellite data. Global navigation satellite systems (GNSS)—such as GPS, GLONASS, Galileo and BeiDou—include MEO and GEO (BeiDou) satellites which provide global coverage of stable signals at multiple coherent operating frequencies. Thus, global navigation satellite system signals have become an efficient tool to monitor the Earth ionosphere.
GNSS TEC provides a basis for different techniques: GNSS radio tomography [9,10,11], GNSS radio interferometry of travelling ionospheric disturbances (TID) [12], ionosphere mapping [13,14], absolute TEC estimation [15], and ionospheric perturbation indices estimation [16,17,18]. Scientists use these techniques and data to study space weather, to create empirical or first principal ionospheric models [19,20], to estimate the quality of different models [21,22], and to update ionospheric models [23].
Most of the above studies involve dual-frequency phase and pseudorange observations. The dual-frequency approach exploits frequency dependence of the ionospheric delay. The single-frequency approach exploits opposite dependence of ionosphere effects on phase and pseudorange observations. For binary-phase shift keying (BPSK) and binary offset carrier (BOC) [24] modulation, noises of pseudorange observations exceed those of phase observations. This results in high amounts of noise in dual-frequency pseudorange TEC or single-frequency TEC. The high noise limits the applications of single-frequency TEC, though exceptions are some data from geostationary satellites [7] and from low-end GNSS receivers in legacy smartphones [25].
Satellites’ clock stability and the coherency of the two operating frequencies affect the dual-frequency TEC estimates. Thus, EGNOS dual-frequency phase TEC noises exceed those in GPS/GLONASS single-frequency TEC [6]. However, advances in GNSS signals have allowed the signal to noise ratio (SNR) to be increased and the noise in observables (and subsequently in TEC) to be decreased, mostly by implementing advanced signal coding. Among those advanced signal coding methods is AltBOC (alternative BOC), described in detail in [26]. The AltBOC signal features an extra wideband within twice a bandwidth of QPSK signals and provides a very steep autocorrelation function.
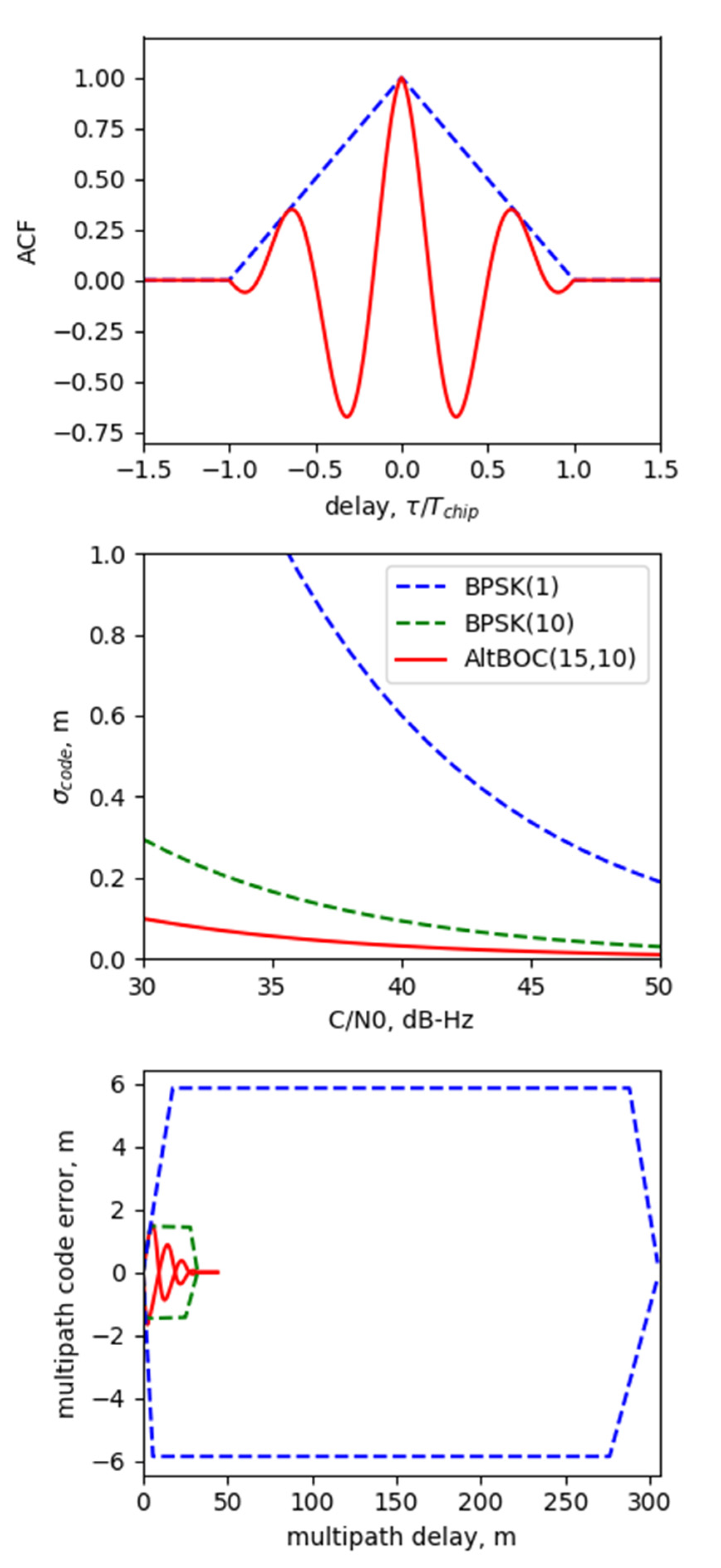
Following [27], we considered the properties of an AltBOC signal, which can affect noises in TEC estimates. The upper panel in Figure 1 shows autocorrelation functions of BPSK and AltBOC(15,10) signals. Integers (m,n) and (n) in brackets stand for multipliers for subcarrier frequency fs = m × f0 and chip rate frequency fchip = n × f0, with f0 = 1.023 MHz, a value typical for GNSS; Tchip is chip length. The main correlation peak of the AltBOC signal is steeper than the peak of the BPSK signal.
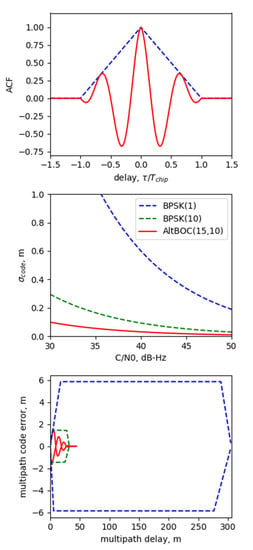
Figure 1.
Autocorrelation functions (top), pseudorange noises (middle) and code multipath envelopes (bottom) for BPSK and AltBOC signals. Blue lines stand for BPSK(1), the green line represents BPSK(10), and the red line is for AltBOC(15,10).
Because code tracking noise is inversely proportional to the steepness of the autocorrelation function, we expect a decrease in pseudorange noise for the AltBOC signal compared to the BPSK signal. The middle panel in Figure 1 shows pseudorange noise (σcode) vs. the carrier-to-noise ratio (C/N0) for AltBOC(15,10), BPSK(10) and BPSK(1) signals. For calculations we used the following parameters: a delay-locked loop filter bandwidth of 1Hz, delay-locked loop correlator spacing of 1/12 chips for BPSK(1) and 1/5 chips for BPSK(10) and AltBOC(15,10), and a correlation time of 20 ms for BPSK(1) and 100 ms for BPSK(10) and AltBOC(15,10).
The AltBOC signal outperforms both BPSK(1) and BPSK(10), with a noise below 5 cm down to a C/N0 of 35dB-Hz. The bottom panel in Figure 1 describes signals’ resistance against multipath (code multipath envelopes) for BPSK and AltBOC signals assuming an early-late power discriminator with the above-mentioned spacing and one reflected ray with a signal over multipath ratio SMR = 2.
The AltBOC modulation provides much higher multipath resistance compared to the BPSK(1) modulation. AltBOC signals surpass BPSK(10) signals for long delays to mitigate multipath, while the signals have comparable characteristics for short multipath delays. Such an improvement in both pseudorange noise and multipath resistance should improve noise in TEC estimates if they rely on pseudorange observables.
Recently, Galileo started to exploit extra wideband E5 AltBOC signals [26] available with modern geodetic receivers. The current article studies the potential of Galileo E5 AltBOC signals for TEC estimates. For that, we compare TEC noises when different observables are used, and analyze the rate of the TEC index deduced from AltBOC signals.
2. Galileo E5 AltBOC Signal
The Galileo satellites transmit E5 signals in the [1164–1215 MHz] band, which is the largest radionavigation satellite system (RNSS) band. It is also a highly protected aeronautical radio navigation services (ARNS) radio band, but it is not exclusive to RNSS. That means that Galileo E5 signals share this band with other GNSS signals, as well as with non-RNSS services. In particular, GPS L5 and L2C, QZSS L5S and L2, SBAS L5, IRNSS L5, BeiDou B2a/B2b, as well as future GLONASS L3 all fall within this band.
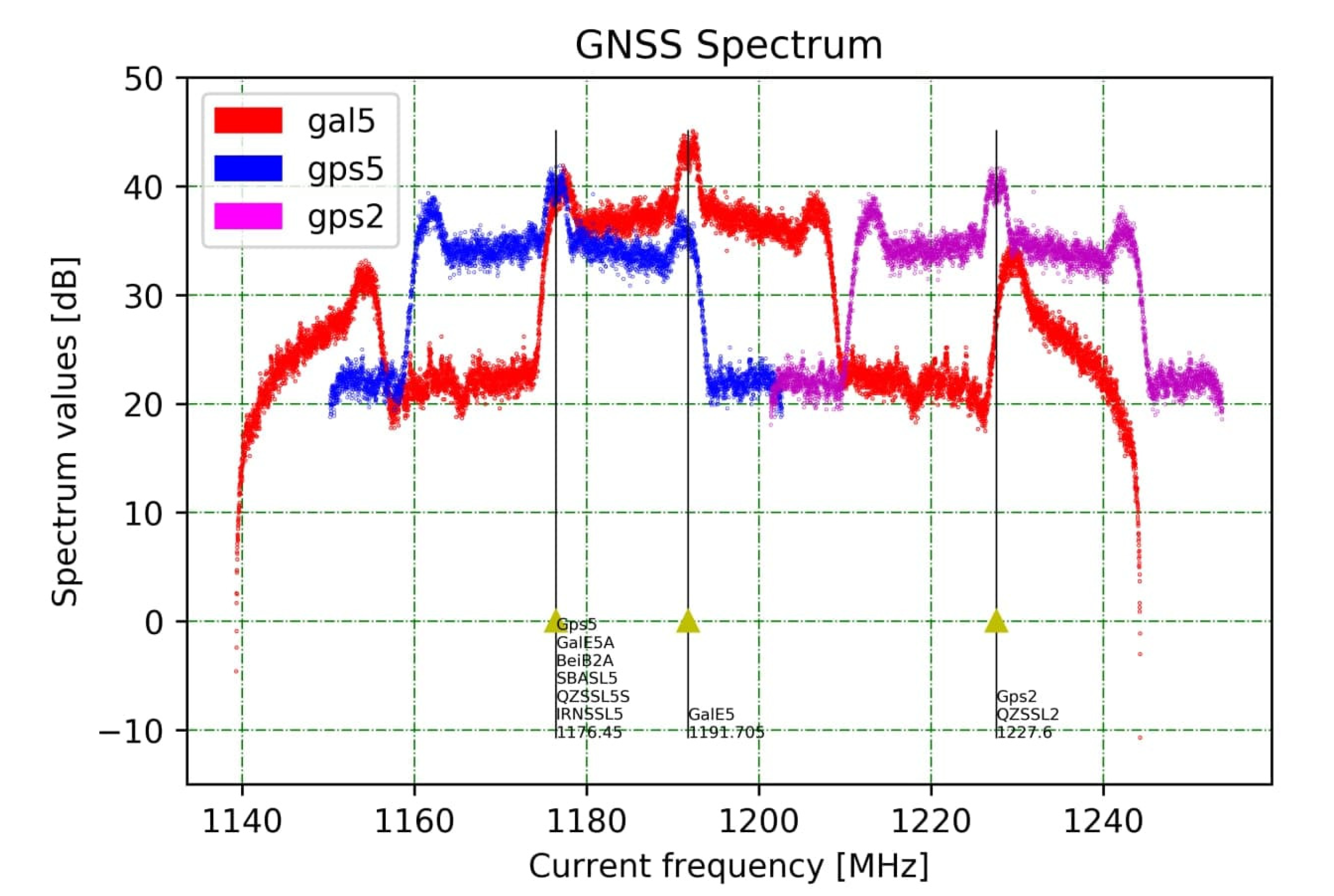
Figure 2 compares the spectrum of the Galileo E5 signal with the spectra of GPS L5 and L2C. These spectra were obtained from the MSU test site equipped with a JAVAD Delta3 receiver according to the procedure described in [28]. (Section 4 provides information about the MSU test site.) The Galileo E5a signal overlaps with the GPS L5 signal, which has similar signal characteristics (see Figure 2), as well as with the BeiDou B2a signal. The Galileo E5b signal does not interfere with any of the GPS signals, but it has the same frequency and modulation as the BeiDou B2b signal and is very close to the future GLONASS L3 signal. Figure 2 shows that the spectrum of the E5 AltBOC signal has twice a bandwidth compared to those of GPS L5 and L2C. That fact, together with the steeper autocorrelation function of the AltBOC modulated signal [29], should lead to significant improvements in positioning and multipath mitigation, and, thus, to a decrease in noise for single-frequency TEC estimation.
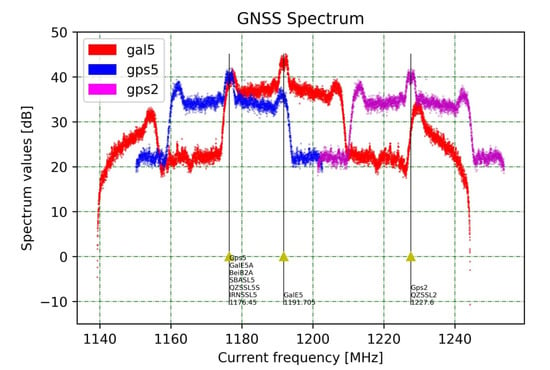
Figure 2.
Spectra of Galileo E5(E5a + E5b) (red line), GPS L5 (blue line) and L2C (purple line) signals.
Table 1 presents the details on the Galileo E5 signal [30]. The signal consists of 2 components—E5a and E5b, which are centered on 1176.45 MHz and 1207.14 MHz, correspondingly. The E5b and E5a signals are QPSK-modulated with 10230-chip long codes of 10.23 MHz. Both components include the data (nav) channel (I—in-phase) and the pilot channel (Q—quadra-phase) with equal powers. A receiver could treat both channels (data and pilot) as two independent BPSK-modulated signals.

Table 1.
Main characteristics of the Galileo E5 signal.
Being in adjacent bands, E5a and E5b signals are transmitted coherently using AltBOC(15,10) 8-PSK modulation [26] with the same filter and high-power amplifier (HPA) operating at saturation for higher efficiency. The whole Galileo E5 signal is thus an extra wideband signal (see Figure 2) that can be received either as a whole or separately.
When processing E5a and E5b signals simultaneously, the whole E5 band (51.15 MHz minimum bandwidth) should be downconverted through the same RF/IF chain. Extra wideband requires a rather high sampling rate, which GNSS receivers have not provided until recently, because it was hard to implement in hardware. However, such extra wideband receivers benefit from pseudorange measurements, which are the most resistant GNSS signals toward thermal noise, multipath and narrow-band interference [27,29,31]. In turn, these measurements should provide a low noise level for single-frequency TEC [31,32].
Processing E5a and E5b signals separately as two independent QPSK-coded signals does not require an extra-wide bandwidth receiver, thus reducing its complexity. This is exactly the way the majority of current-generation professional GNSS receivers operate. In this case, low-noise TEC estimates can be obtained only with dual-frequency E5a/E5b phase measurements, while range measurements contain significant noise due to narrower bandwidth and less sophisticated coding.
Note also that the minimal receiving power of both Galileo E5a and E5b signals exceeds those of the Galileo E1 signal by 2 dB [30]. Therefore, using E5a/E5b, we could assume a better performance (as compared with Galileo E1) in case of signal obstruction.
3. Ionospheric TEC Estimation with GNSS Signals
As mentioned above, TEC can be estimated using either dual- or single-frequency pseudorange and carrier phase measurements. In the first case, the linear combinations of phase (Li and Lj) or pseudorange (Pi and Pj) measurements at two frequencies fi and fj give the slant TEC estimate along the receiver–satellite line of sight via the following well-known relations [33]:
where K = 40.308 m3/s2, c is the speed of light in a vacuum, const represents undefined carrier-phase ambiguities, and DCB stands for the sum of differential code biases in satellites transmitting and receivers receiving chains. For Galileo, (Li, Lj) and (Pi, Pj) correspond to phase and code measurements for any pair of signals. Combination (2) proved to be very noisy compared to (1) when applied to BPSK- and BOC-coded signals. We used dual-frequency combination (1) as a reference in the comparative TEC noise analysis.
A single-frequency pseudorange / carrier phase combination for slant TEC estimation can be also constructed by exploiting the fact that ionospheric contribution enters phase and group refractivity index with the opposite sign [34]:
where the same notations apply and const once again stands for unknown carrier-phase ambiguities. When one uses combination (3), a significant noise appears when applied to BPSK- and BOC-coded signals due to pseudorange measurements. Moreover, like combination (1), it provides only relative estimates of slant TEC due to an unknown initial phase. This is the reason that single-frequency combination (3) is not widely applied in ionospheric studies. New extra wideband GNSS signals (i.e. Galileo E5 AltBOC) could resolve some issues arising with single-frequency combinations, especially the TEC noise problem: the wider spectral occupancy and steeper main peak of autocorrelation function of such signals results in lower noise and higher multipath robustness. Below, we provide the comparison of noise characteristics for slant TEC estimated via (3) with BPSK-, BOC- and AltBOC-coded signals, assuming dual-frequency combination (1) as a reference.
We corrected raw data to mitigate cycle slip effects. If two consecutive TEC values exceed (in absolute value) the previous values by more than 4 TECU, cycle slips occur. The TEC jump provides a correction constant for the TEC values after the slip.
Following [6], we used the TEC root-mean-square within 100 s (or 100 s TEC RMS) as a proxy for TEC noise throughout this work:
The 100 s interval was selected for two reasons: on the one hand, it is reasonably long enough to provide a statistically significant amount of TEC data, and on the other hand, it is reasonably short enough to limit the influence of the ionospheric variability (which usually has larger timescales) on the obtained results.
Note that assuming DCBs are known/calibrated carrier leveling or code smoothing procedures can be applied to (1) and (2), providing absolute values of TEC, while due to unknown phase ambiguities, single-frequency combination (3) seems to be suitable for monitoring TEC changes rather than absolute TEC values. Nevertheless, the approach for resolving unknown constants in (3), which is quite similar to DCB estimation [34], could be adopted, making single-frequency relative TEC estimates quite useful for applications that require absolute TEC data.
4. Experimental Setup
Currently, there are 24 Galileo satellites continuously transmitting wideband E5 AltBOC signals, which can be used to estimate the ionospheric TEC via single-frequency combination (3). The number of receiving sites capable of working with that type of signal is also increasing. To analyze the noise level of TEC estimation with E5 AltBOC signals, we performed a one-month campaign in September 2020. The test receiver MSU was located at the roof of the Faculty of Physics, Lomonosov Moscow State University, Russia. Table 2 shows the coordinates and technical characteristics of the receiver.

Table 2.
Characteristics of the MSU receiving site used for studying the TEC noise level.
We performed our campaign in the early ascending phase in solar cycle 25; the monthly average F10.7 was 71 s.f.u. The studied equinox period covers mostly undisturbed conditions, except 2 geomagnetic storms (Kp indices reached 50 on September 28, and 5+ on September 27). However, we do not expect significant effects on GNSS signals at mid-latitudes for these minor storms.
Experimental facilities included two receivers (Sigma and Delta3), but only one (Delta3) treated extra wideband E5 signals, while the other (Sigma) processed E5a/E5b signals separately. In the current study, we show only the Delta3 receiver data. However, both receivers used the same RingAnt antenna connected by a 20 m RG-8x cable through the Mini-Circuits ZB4PD1-2000-s splitter (6 dB loss). To adjust the input signal (which is split between two receivers), the chain included a 20 dB low-noise amplifier (LNA) with a bandpass of 1.1–1.65 GHz (see Figure 3). The amplifier resulted in comparatively high values of SNR for all GNSS signals observed at this site.

Figure 3.
Block diagram of the receivers’ installation at the MSU site.
Note also that the receiver is located in the Moscow urban area; 200 m to the north there is the 240-m-high main building of Lomonosov Moscow State University dominating the landsight from the receiving site. That may lead to additional errors due to multipath effects. To mitigate them, we excluded corresponding azimuthal directions from the analysis.
5. Experimental Results
This section considers an example of TEC data on 2 September 2020, statistical analysis of TEC observations based on different observables, and finally the application of single-frequency Galileo TEC for ROTI (rate of TEC index) calculations.
5.1. Galileo TEC Observations: Case Study on 2 September 2020
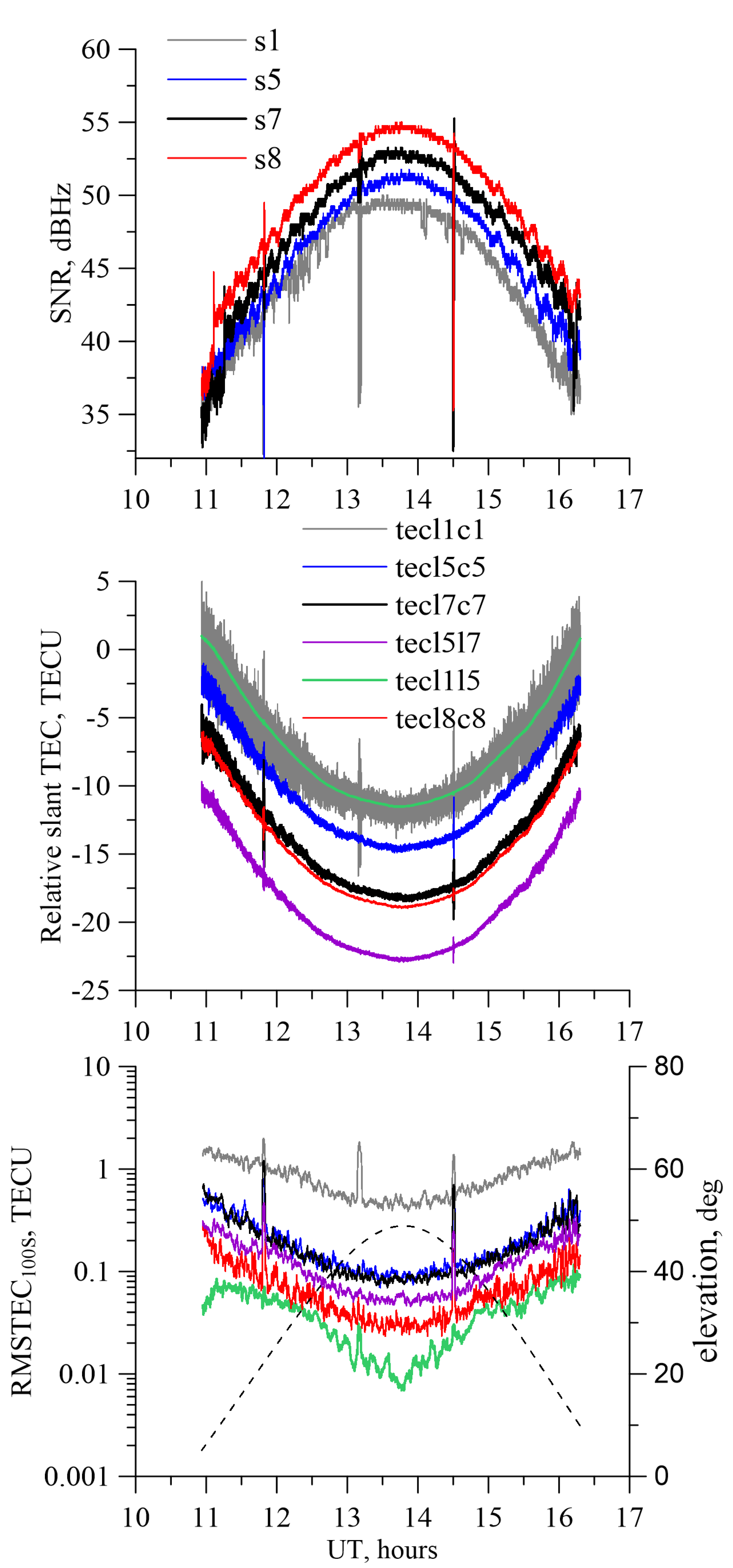
The top panel in Figure 4 shows an example of a signal strength observable (SNR) from the Galileo E11 satellite on 2 September 2020. The dynamics in SNR correspond to the dynamics in elevation, including low signal strength when the satellite rises above the horizon, maximal SNR at maximal elevation and then minimal SNR in the end of the pass. Sharp decreases in SNR correspond to multipath effects. The Galileo E5 signal strength (S8—see Table 1 for RINEX notations of the observables) exceeds the signal strength of the other signals, while the E1 signal features the smallest signal strength (S1). The E5b signal strength (S7) exceeds the E5a signal strength (S5).
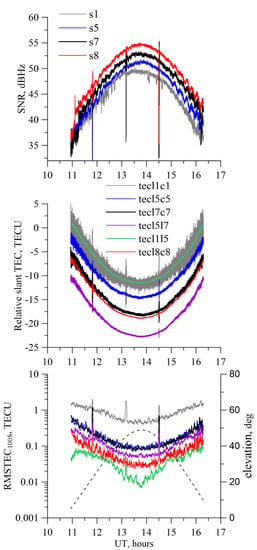
Figure 4.
SNR (top), slant TEC (middle) and RMSTEC100S (bottom) for the MSU-Galileo E11 pass on 2 September 2020. On the upper panel the grey, blue, black and red solid lines correspond to S1, S5, S7, S8 observables, correspondingly. On the middle and bottom panels, the grey, blue, black, purple, green, and red lines correspond to L1C1, L5C5, L7C7, L5L7, L1L5, L8C8 combinations, correspondingly. The dashed line in the bottom panel shows the satellite’s elevation dynamics.
The relative slant TEC (the middle panel in Figure 4) shows typical dynamics as well as corresponding dynamics with elevation, including higher TEC values at low elevations and minimal TEC values at high elevations. Decreases in SNR result in sharp variations in TEC data. It is evident that the single-frequency L1C1 TEC (from here on L stands for phase measurements, while C stands for code pseudorange measurements) combination provides the most noisy data, while single-frequency L8C8 and dual-frequency L1L5 combinations provide less noisy data.
The bottom panel in Figure 4 provides TEC noise estimates based on 100 s TEC RMS (RMSTEC100S). The noise of the L1L5 TEC combination varies from 0.01 to 0.1 TECU, depending on the elevation and SNR. The noise of the AltBOC single-frequency combination (L8C8) exceeds several times the noise of the L1L5 TEC combination, but at elevations higher than 20 degrees, it does not exceed 0.1 TECU. Other combinations demonstrate higher noises, even up to 1 TECU (L1C1).
5.2. Galileo TEC: Statistical Analysis
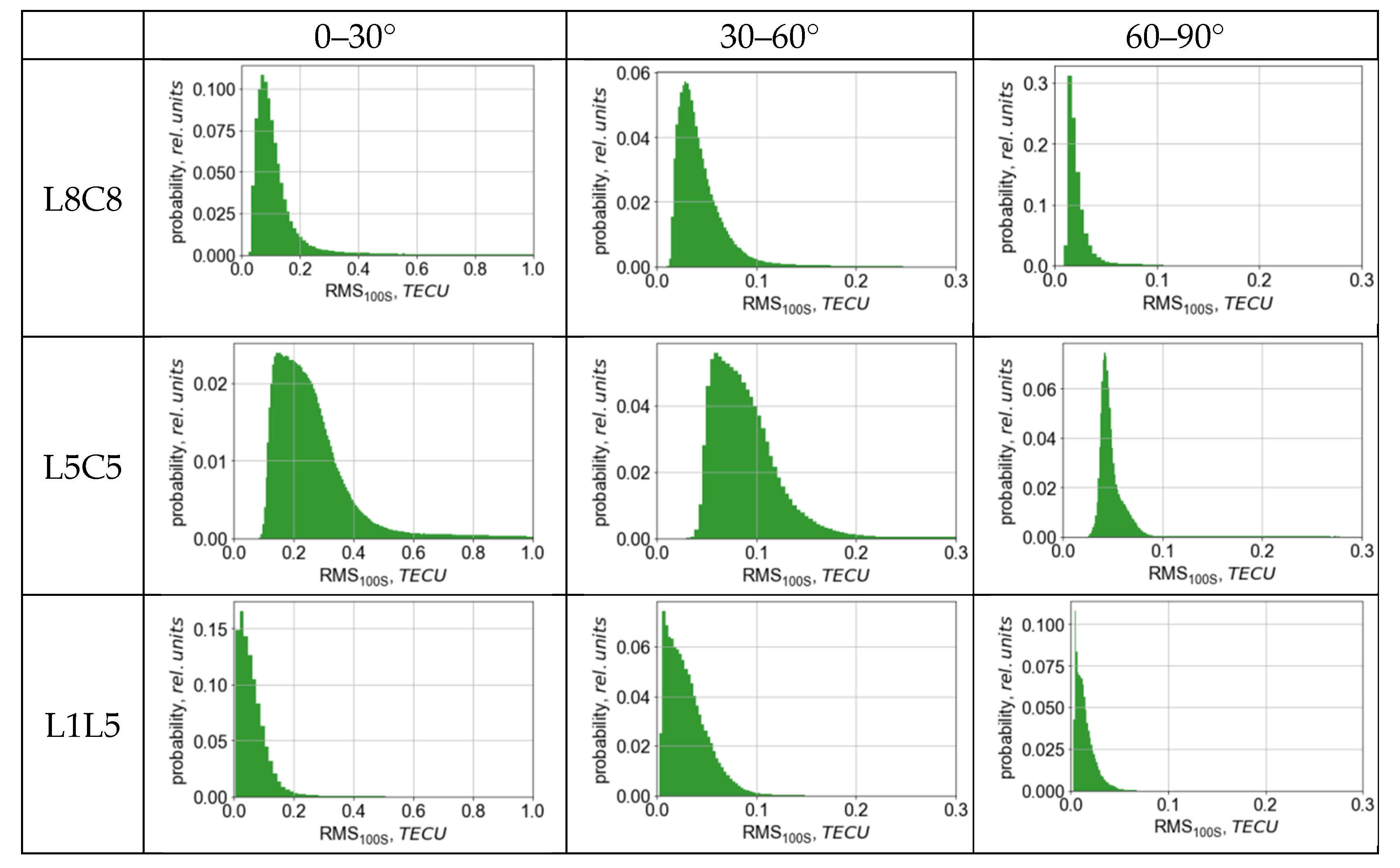
One single pass gives only a clue regarding the situation but provides unreliable evidence of AltBOC performance. Thus, we statistically analyzed the whole available one-month dataset, involving all time intervals and all Galileo satellites. The data were split into 3 sets, corresponding to low elevations (0–30°), medium elevations (30–60°), and high elevations (60–90°). For each set, we considered probability density functions of TEC RMS for two single-frequency (L8C8 and L5C5) combinations and one dual-frequency (L1L5) combination (see Figure 5).
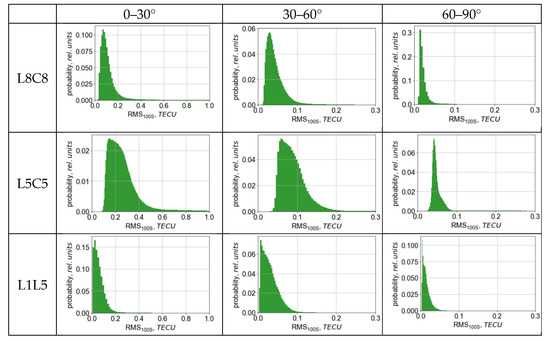
Figure 5.
Probability density functions of 100 s TEC RMS for L8C8 (top), L5C5 (middle), L1L5 (bottom) combinations at different elevations.
Both ionospheric irregularities and observables’ noises contribute to 100 s TEC RMS. The gap between the histogram and the zero value show the base noise level. L1L5 data features the smallest gap; calm conditions (when no ionospheric irregularities appear) correspond to zero TEC RMS values. Conversely, L8C8 and L5C5 data show no small 100 s TEC RMS values due to higher noises.
The higher the elevation, more narrow the distributions and the closer it becomes to the zero value. We expected this, because higher phase and pseudorange noise at low elevations should produce higher amounts of TEC noise. Even at 60–90° elevations, noise shifts the L8C8 TEC RMS distribution to higher values. However, the L8C8 TEC RMS distribution is shifted much less than the L5C5 distribution, especially at low elevations.
Table 3 summarizes the average TEC RMS for the whole observational dataset. Note that an increase in elevation decreases the TEC RMS by 7–10 times for combinations involving the AltBOC signal.

Table 3.
Average RMS (in TECU) for the whole campaign: Galileo.
The Galileo E5 AltBOC signal provides the smallest noise of single-frequency TEC (L8C8), which is comparable to that of the L1L5 dual-frequency combination. At low elevations, L1L5 and L8C8 TEC RMS are almost the same; at higher elevations, L8C8 TEC RMS exceeds L1L5 ones by 1.5 times. Other combinations feature ~1.5–20 times higher values of TEC noise against Galileo L8C8. The worst results correspond to the single-frequency L1C1 combination.
At low elevations, E5 AltBOC provides at least twice less noise as compared with E5a/E5b combinations (both single- and dual-frequency). The E5a/E5b dual-frequency combination provides almost no advantage over the single-frequency E5 AltBOC combination, probably due to the closeness of their frequencies. Nevertheless, the noise in single-frequency E5a or E5b combinations exceeds those of the dual-frequency E5a/E5b phase combination by ~1.5 times.
We also compared obtained Galileo TEC noise with those from GPS. Table 4 provides results on 100 s RMS for L1L5, L5C5 and L1L2 GPS TEC. Except at low elevations, the Galileo E5 AltBOC single-frequency combination features less noise as compared with the GPS L1L2 and L1L5 (and, of course, the GPS L5C5) combinations.

Table 4.
Average RMS (in TECU) for the whole campaign: GPS.
At high elevations, the 100 s single-frequency TEC root-mean-squares were (from low to high values): ~0.05 TECU for Galileo E5 AltBOC, 0.09 TECU for GPS L5, 0.1TECU for Galileo E5a/E5b BPSK, and 0.85 TECU for Galileo E1 CBOC. At the same elevations, dual-frequency combinations provided: 0.03 TECU for Galileo E1/E5 TEC, 0.03 TECU and 0.07 TECU for GPS L1L2 and L1L5. Therefore, the Galileo E5 AltBOC signal provided the smallest amount of noise for TEC among single-frequency combinations, which is comparable to that of the dual-frequency TEC of both GPS and Galileo.
5.3. Galileo Single-Frequency Data for ROTI Calculations
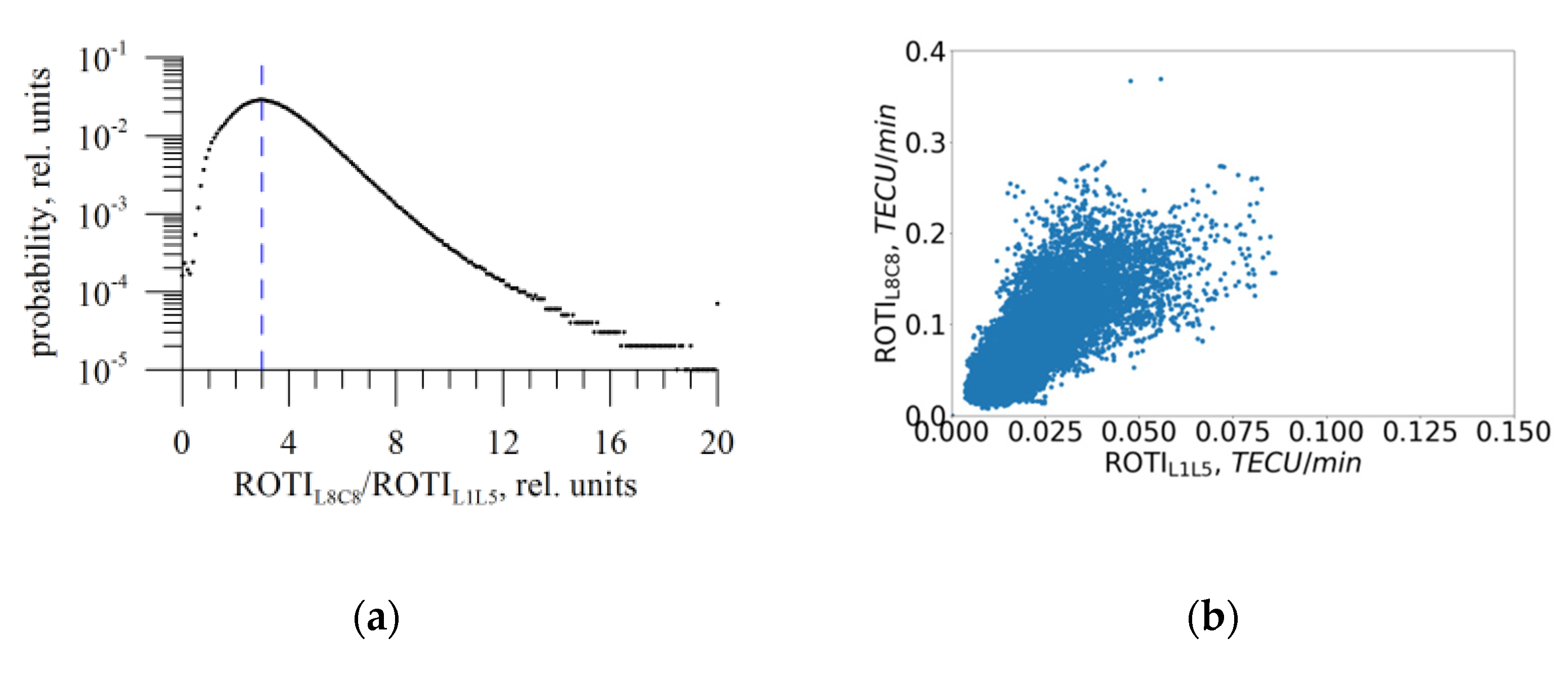
Many scientists use the ROTI index [16] to study small-scale ionospheric irregularities [35]. A higher noise level in the single-frequency TEC data (against dual-frequency data) results in higher ROTI values. However, we expect that such data could also be useful to estimate the effects of ionospheric irregularities. To estimate this, we analyzed ROTI quality from Galileo AltBOC data (L8C8) against ROTI quality from dual-frequency data (we chose L1L5 as a reference).
Figure 6 shows how the ROTI values from single-frequency Galileo AltBOC data (L8C8) corresponds to those from L1L5. We compare the data for the same satellite-receiver set, but for different observables. L1L5 provides a reference to find a discrepancy for AltBOC single-frequency data.
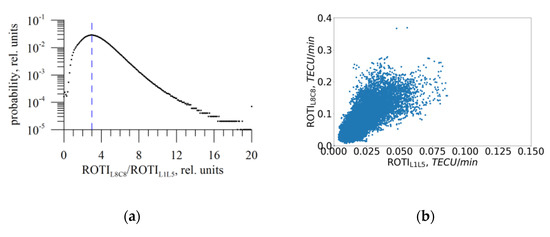
Figure 6.
ROTI quality from Galileo AltBOC data. (a) ROTIL8C8/ROTIL1L5; (b) ROTIL8C8 vs. ROTIL1L5.
We expect a noise-multiplying effect for ROTI. Figure 6a provides the ROTIL8C8-to-ROTIL1L5 ratio. ROTIL8C8 values 3 times (maximum of the distribution) exceed ROTIL1L5. Outliers in ROTI estimations provide an increase in distribution at 20 (we chose this value as a limit). ROTIL1L5 values could exceed ROTIL8C8 values due to L1/L5 noises.
Scattering diagrams (Figure 6b) also show (for low ROTI) a positive correlation between ROTIL8C8 and ROTIL1L5, but the coefficient between them differs from 1. This positive correlation gives hope that scientists could use the single-frequency AltBOC ROTI as an additional indicator for the ionosphere state.
6. Discussion and Conclusions
Different factors affect TEC measurements: the intrinsic thermal noise of the receiver, the stability of the disciplined oscillator, the coherence of the operating frequencies, multipath, etc. [36]. Increase in the satellite transmitter power [37], application of choke ring antennas, or advanced signal coding (providing a steeper and narrower main maximum of the autocorrelation function) could, to some extent, compensate for such negative factors.
Our results (involving Galileo as an example) show a one-order decrease in single-frequency TEC noises when a system uses AltBOC signals instead of BPSK signals. The estimated TEC noise proxies (for elevation higher 60 deg.)—100 s root-mean-square (RMS) of TEC—were: ~0.05 TECU for Galileo E5 AltBOC, 0.09 TECU for GPS L5, ~0.1TECU for Galileo E5a/E5b BPSK, and 0.85 TECU for Galileo E1 CBOC. Dual-frequency combinations provide RMS values of 0.03 TECU for Galileo E1E5 and 0.03/0.07 TECU for GPS L1L2/L1L5. At low elevations, E5 AltBOC provides at least twice less single-frequency TEC noise as compared with the data obtained from E5a or E5b.
The obtained results indicate that AltBOC signals level down the noise in TEC from a single-frequency phase-code combination to the noise in TEC from the reference phase dual-frequency signals encoded in BPSK.
Note that our comparison used data obtained simultaneously on the same receiver and antenna, which guarantees the same level of thermal noise. We installed a choke ring antenna, which itself suppresses multipath effects. We could expect that the single-frequency AltBOC TEC has even more of an advantage over single-frequency BPSK TEC when standard antennas are used, especially at low elevations. However, this requires a separate study.
The short dataset during mostly undisturbed geomagnetic conditions could limit obtained estimates. Mid-latitude observations also could limit our study, since no intense small-scale ionospheric irregularities (which appear at mid-latitudes usually during strong or severe storms [38]) affected the GNSS signals. It would be important for future studies to verify our results in the presence of small-scale irregularities at high-, mid- and low-latitudes under intense geomagnetic storms and plasma bubble conditions. We expect that, qualitatively, results will hold as the solar cycle evolves and geomagnetic activity increases, such that the AltBOC single-frequency TEC will still surpass BPSK analogue in noise parameters.
The obtained TEC noise estimates contain contributions from the intrinsic noise specific to each individual receiver. Therefore, we cannot consider the obtained estimates as universal estimates. However, we suppose similar features for other receivers: a fold reduction in TEC noise when using AltBOC signals could be expected, but the TEC noise level should agree with a receiver’s intrinsic and multipath noise. To verify, one can use the approach by Demyanov et al. [36].
We also analyzed the ROTI index based on single-frequency AltBOC TEC. The positive correlation observed with dual-frequency data gives hope that scientists could use the single-frequency AltBOC ROTI as an additional indicator for the state of the ionosphere.
Note that assuming DCBs are known/calibrated dual-frequency combinations together provide absolute values of TEC, while single-frequency combinations seem to be suitable for monitoring TEC changes rather than absolute TEC values. Nevertheless, the approach for resolving unknown constants through LxCx combinations, which is quite similar to DCB estimation [34], could be adopted, making this data quite useful for problems that require absolute TEC.
We expect similar features (a fold decrease in the single-frequency TEC noise) for BeiDou B2 AltBOC signals. Unfortunately, Galileo and BeiDou use AltBOC coding only on one operating frequency. We could also expect a decrease in dual-frequency TEC noise when both frequencies use AltBOC coding. That would make it possible to record TEC disturbances of low amplitude from such important events as, for example, the effects of artificial high-frequency heating [39], the response of the ionosphere to C-class solar flares [40] and low-magnitude earthquakes [41], which can produce effects at levels typical of the current GNSS TEC estimates. Therefore, AltBOC signals could advance geoscience.
Author Contributions
Conceptualization, A.M.P.; methodology, A.M.P., A.A.M., Y.V.Y.; software, A.A.M., A.M.V., Y.V.M.; validation, A.M.P., A.A.M., Y.V.Y.; formal analysis, A.A.M., Y.V.M.; investigation, A.M.P., A.A.M., Y.V.Y., Y.V.M.; data curation, Y.V.M., G.A.K.; writing—original draft preparation, A.M.P., A.A.M., Y.V.Y., Y.V.M.; writing—review and editing, A.M.P., A.A.M., Y.V.Y.; visualization, A.A.M.; supervision, A.M.P.; project administration, A.M.P.; funding acquisition, Y.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
Data processing and Galileo AltBOC signal property investigation performed under the Russian Science Foundation Grant No. 17-77-20005. Experimental Galileo data at the MSU test site were obtained with the support of the Russian Foundation for Basic Research (project #19-05-00941). The APC was funded by the above-mentioned foundations.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available by request from MSU and ISTP SB RAS.
Acknowledgments
The authors acknowledge V.V. Demyanov for the fruitful discussions, Javad GNSS for providing technical support under GNSS data acquisition, and the anonymous reviewers for their suggestions to improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Davies, K. Recent progress in satellite radio beacon studies with particular emphasis on the ATS-6 radio beacon experiment. Space Sci. Rev. 1980, 25, 357–430. [Google Scholar] [CrossRef]
- Aitchison, G.J.; Weekes, K. Some deductions of ionospheric information from the observations of emissions from satellite 1957-alpha-2.1. The theory of the analysis. J. Atmos. Terr. Phys. 1959, 144, 236–243. [Google Scholar] [CrossRef]
- Alpert, I.L. On Ionospheric Investigations by Coherent Radiowaves Emitted from Artificial Earth Satellites. Space Sci. Rev. 1976, 18, 551–602. [Google Scholar] [CrossRef]
- Bernhardt, P.A.; Siefring, C.L.; Galysh, I.J.; Koch, D.E. A new technique for absolute total electron content determination using the CITRIS instrument on STPSat1 and the CERTO beacons on COSMIC. Radio Sci. 2010, 45, RS3006. [Google Scholar] [CrossRef] [Green Version]
- Royden, H.N.; Miller, R.B.; Buennagel, L.A. Comparison NAVSTAR satellite L band ionospheric calibrations with Faraday rotation measurements. Radio Sci. 1984, 19, 798–804. [Google Scholar] [CrossRef]
- Kunitsyn, V.E.; Padokhin, A.M.; Kurbatov, G.A.; Yasyukevich, Y.V.; Morozov, Y.V. Ionospheric TEC estimation with the signals of various geostationary navigational satellites. GPS Solut. 2016, 20, 877–884. [Google Scholar] [CrossRef]
- Cooper, C.; Mitchell, C.N.; Wright, C.J.; Jackson, D.R.; Witvliet, B.A. Measurement of ionospheric total electron content using single-frequency geostationary satellite observations. Radio Sci. 2019, 54, 10–19. [Google Scholar] [CrossRef]
- Savastano, G.; Komjathy, A.; Shume, E.; Vergados, P.; Ravanelli, M.; Verkhoglyadova, O.; Meng, X.; Crespi, M. Advantages of Geostationary Satellites for Ionospheric Anomaly Studies: Ionospheric Plasma Depletion Following a Rocket Launch. Remote Sens. 2019, 11, 1734. [Google Scholar] [CrossRef] [Green Version]
- Bust, G.S.; Crowley, G.; Garner, T.W.; Gaussiran, T.L.; Meggs, R.W.; Mitchell, C.N.; Spencer, P.S.J.; Yin, P.; Zapfe, B. Four-dimensional GPS imaging of space weather storms. Space Weather 2007, 5, S02003. [Google Scholar] [CrossRef]
- Kunitsyn, V.E.; Nesterov, I.A.; Padokhin, A.M.; Tumanova, Y.S. Ionospheric radio tomography based on the GPS/GLONASS navigation systems. J. Commun. Technol. Electron. 2011, 56, 1269–1281. [Google Scholar] [CrossRef]
- Nesterov, I.A.; Kunitsyn, V.E. GNSS radio tomography of the ionosphere: The problem with essentially incomplete data. Adv. Space Res. 2011, 47, 1789–1803. [Google Scholar] [CrossRef]
- Afraimovich, E.L.; Palamartchouk, K.S.; Perevalova, N.P. Statistical Angle-of-arrival and Doppler Method for GPS radio interferometry of TIDs. Adv. Space Res. 2000, 26, 1001–1004. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geophys. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS derived ionospheric TEC measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Yasyukevich, Y.; Mylnikova, A.; Vesnin, A. GNSS-Based Non-Negative Absolute Ionosphere Total Electron Content, its Spatial Gradients, Time Derivatives and Differential Code Biases: Bounded-Variable Least-Squares and Taylor Series. Sensors 2020, 20, 5702. [Google Scholar] [CrossRef]
- Pi, X.; Mannucci, A.J.; Lindqwister, U.J.; Ho, C.M. Monitoring of global ionospheric irregularities using the worldwide GPS network. Geophys. Res. Lett. 1997, 24, 2283–2286. [Google Scholar] [CrossRef]
- Nesterov, I.A.; Andreeva, E.S.; Padokhin, A.M.; Tumanova, Y.S.; Nazarenko, M.O. Ionospheric perturbation indices based on the low- and high-orbiting satellite radio tomography data. GPS Solut. 2017, 21, 1679–1694. [Google Scholar] [CrossRef]
- Wilken, V.; Kriegel, M.; Jakowski, N.; Berdermann, J. An ionospheric index suitable for estimating the degree of ionospheric perturbations. J. Space Weather Space Clim. 2018, 8, A19. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, V.; Gefan, G.; Gorbachev, O. Global empirical modelling of the total electron content of the ionosphere for satellite radio navigation systems. J Atmos. Sol.-Terr. Phys. 2011, 73, 1703–1707. [Google Scholar] [CrossRef]
- Zhukov, A.V.; Yasyukevich, Y.V.; Bykov, A.E. GIMLi: Global Ionospheric total electron content model based on machine learning. GPS Solut. 2021, 25, 19. [Google Scholar] [CrossRef]
- Ephishov, I.I.; Baran, L.W.; Shagimuratov, I.I.; Yakimova, G.A. Comparison of total electron content obtained from GPS with IRI. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2000, 25, 339–342. [Google Scholar] [CrossRef]
- Feltens, J.; Angling, M.; Jackson-Booth, N.; Jakowski, N.; Hoque, M.; Hernández-Pajares, M.; Aragón-Àngel, A.; Orús, R.; Zandbergen, R. Comparative testing of four ionospheric models driven with GPS measurements. Radio Sci. 2011, 46, RS0D12. [Google Scholar] [CrossRef] [Green Version]
- Kotova, D.S.; Ovodenko, V.B.; Yasyukevich, Y.V.; Klimenko, M.V.; Ratovsky, K.G.; Mylnikova, A.A.; Andreeva, E.S.; Kozlovsky, A.E.; Korenkova, N.A.; Nesterov, I.A.; et al. Efficiency of updating the ionospheric models using total electron content at mid- and sub-auroral latitudes. GPS Solut. 2020, 24, 25. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J.B. Understand GPS/GNSS Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2017; p. 703. [Google Scholar]
- Hernández-Pajares, M.; Roma-Dollase, D.; Garcia-Fernàndez, M.; Orus-Perez, R.; García-Rigo, A. Precise Ionospheric Electron Content Monitoring from Single-Frequency GPS Receivers. GPS Solut. 2018, 22, 102. [Google Scholar] [CrossRef] [Green Version]
- Lestarquit, L.; Artaud, G.; Issler, J.-L. AltBOC for Dummies or Everything You Always Wanted to Know About AltBOC. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 961–970. [Google Scholar]
- Sleewaegen, J.M.; De Wilde, W.; Hollreiser, M. Galileo AltBOC Receiver. In Proceedings of the ION GNSS 2004, Rotterdam, The Netherlands, 16–19 May 2004. [Google Scholar]
- JAVAD GNSS Receiver External Interface Specification. Available online: http://download.javad.com/manuals/GREIS/GREIS_Reference_Guide.pdf (accessed on 22 August 2021).
- Silva, P.F.; Silva, J.S.; Peres, T.R.; Fernández, A.; Palomo, J.M.; Andreotti, M.; Hill, C.; Colomina, I.; Miranda, C.; Parés, M.E. Results of Galileo AltBOC for precise positioning. In Proceedings of the in 6th ESA Workshop on Satellite Navigation Technologies (Navitec 2012) & European Workshop on GNSS Signals and Signal Processing, Noordwijk, The Netherlands, 5–12 December 2012; pp. 1–9. [Google Scholar] [CrossRef]
- Galileo—Open Service—Signal in Space Interface Control Document (OS SIS ICD V1.3). Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo-OS-SIS-ICD.pdf (accessed on 22 August 2021).
- Diessongo, H.; Bock, H.; Schueler, T.; Junker, S.; Kiroe, A. Exploiting the Galileo E5 Wideband Signal for Improved Single-Frequency Precise Positioning. Inside GNSS 2012, 7, 64–73. [Google Scholar]
- Julien, O.; Macabiau, C.; Issler, J.-L. Ionospheric delay estimation strategies using Galileo E5 signals only. In Proceedings of the in GNSS 2009, 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation, Savannah, GA, USA, 22–25 September 2009; pp. 3128–3141. [Google Scholar]
- Hoffmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System: Theory and Practice, 5th ed.; Springer: New York, NY, USA, 2001; p. 313. [Google Scholar]
- Yasyukevich, Y.V.; Mylnikova, A.A.; Ivanov, V.B. Estimating the absolute total electron content based on single-frequency satellite radio navigation GPS/GLONASS data. Sol.-Terr. Phys. 2017, 3, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Basu, S.; Groves, K.M.; Quinn, J.M.; Doherty, P. A comparison of TEC fluctuations and scintillations at Ascension Island. J. Atmos. Sol.-Terr. Physics. 1999, 61, 1219–1226. [Google Scholar] [CrossRef]
- Demyanov, V.; Sergeeva, M.; Fedorov, M.; Ishina, T.; Gatica-Acevedo, V.J.; Cabral-Cano, E. Comparison of TEC Calculations Based on Trimble, Javad, Leica, and Septentrio GNSS Receiver Data. Remote Sens. 2020, 12, 3268. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Yasyukevich, A.S.; Astafyeva, E.I. How modernized and strengthened GPS signals enhance the system performance during solar radio bursts. GPS Solut. 2021, 25, 46. [Google Scholar] [CrossRef]
- Astafyeva, E.I.; Afraimovich, E.L.; Voeykov, S.V. Generation of secondary waves due to intensive large-scale AGW traveling. Adv. Space Res. 2008, 41, 1459–1462. [Google Scholar] [CrossRef]
- Kunitsyn, V.E.; Andreeva, E.S.; Frolov, V.L.; Komrakov, G.P.; Nazarenko, M.O.; Padokhin, A.M. Sounding of HF heating-induced artificial ionospheric disturbances by navigational satellite radio transmissions. Radio Sci. 2012, 47, RS0L15. [Google Scholar] [CrossRef]
- Yasyukevich, Y.V.; Voeykov, S.V.; Zhivetiev, I.V.; Kosogorov, E.A. Ionospheric response to solar flares of C and M classes in January–February 2010. Cosm. Res. 2013, 51, 114–123. [Google Scholar] [CrossRef]
- Perevalova, N.P.; Sankov, V.A.; Astafyeva, E.I.; Zhupityaeva, A.S. Threshold magnitude for Ionospheric TEC response to earthquakes. J. Atmos. Sol.-Terr. Phys. 2014, 108, 77–90. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).