Next Article in Journal
Synergistic Use of Sentinel-1 and Sentinel-2 to Map Natural Forest and Acacia Plantation and Stand Ages in North-Central Vietnam
Previous Article in Journal
Impact of COVID-19 Lockdown on the Fisheries Sector: A Case Study from Three Harbors in Western India
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 2
10.3390/rs13020184
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Impact of Monsoon-Transported Anthropogenic Aerosols and Sun-Glint on the Satellite-Derived Spectral Remote Sensing Reflectance in the Indian Ocean

by
Rongjie Liu
1,2,
Jie Zhang
1,
Tingwei Cui
3,4,* and
Haocheng Yu
5
1
First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China
2
Information Science and Technology, College Dalian Maritime University, Dalian 116026, China
3
Guangdong Province Key Laboratory for Climate Change and Natural Disaster Studies, Sun Yat-sen University, Zhuhai 519000, China
4
Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519000, China
5
College of Information Science and Engineering, Ocean University of China, Qingdao 266071, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(2), 184; https://doi.org/10.3390/rs13020184
Submission received: 2 December 2020 / Revised: 1 January 2021 / Accepted: 5 January 2021 / Published: 7 January 2021
(This article belongs to the Section Ocean Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Spectral remote sensing reflectance (Rrs(λ), sr−1) is one of the most important products of ocean color satellite missions, where accuracy is essential for retrieval of in-water, bio-optical, and biogeochemical properties. For the Indian Ocean (IO), where Rrs(λ) accuracy has not been well documented, the quality of Rrs(λ) products from Moderate Resolution Imaging Spectroradiometer onboard both Terra (MODIS-Terra) and Aqua (MODIS-Aqua), and Visible Infrared Imaging Radiometer Suite onboard the Suomi National Polar-Orbiting Partnership spacecraft (VIIRS-NPP), is evaluated and inter-compared based on a quality assurance (QA) system, which can objectively grade each individual Rrs(λ) spectrum, with 1 for a perfect spectrum and 0 for an unusable spectrum. Taking the whole year of 2016 as an example, spatiotemporal pattern of Rrs(λ) quality in the Indian Ocean is characterized for the first time, and the underlying factors are elucidated. Specifically, QA analysis of the monthly Rrs(λ) over the IO indicates good quality with the average scores of 0.93 ± 0.02, 0.92 ± 0.02 and 0.92 ± 0.02 for VIIRS-NPP, MODIS-Aqua, and MODIS-Terra, respectively. Low-quality (~0.7) data are mainly found in the Bengal Bay (BB) from January to March, which can be attributed to the imperfect atmospheric correction due to anthropogenic absorptive aerosols transported by the northeasterly winter monsoon. Moreover, low-quality (~0.74) data are also found in the clear oligotrophic gyre zone (OZ) of the south IO in the second half of the year, possibly due to residual sun-glint contributions. These findings highlight the effects of monsoon-transported anthropogenic aerosols, and imperfect sun-glint removal on the Rrs(λ) quality. Further studies are advocated to improve the sun-glint correction in the oligotrophic gyre zone and aerosol correction in the complex ocean–atmosphere environment.

Graphical Abstract

1. Introduction

Satellite ocean color remote sensing plays an unique and important role in the aquatic science researches of ocean biogeochemical cycles [1,2,3,4], water quality variability [5,6,7], and climate change [8,9,10], through providing long term, high-quality, and consistent data records in a large scale (globally or regionally).
As the most important ocean optical parameter derived from satellite ocean color observations, spectral remote sensing reflectance (Rrs(λ), sr−1) is key for retrieval of the in-water bio-optical and biogeochemical properties [11,12]. Uncertainties of satellite derived Rrs(λ) is thus of particular importance in terms of the spatial, temporal, and spectral distributions [13,14,15,16], which are usually derived through comparison with concurrent in situ observations based on vessels, buoys, and fixed offshore platforms, etc. Insights into Rrs(λ) uncertainties, mainly attributed to imperfect atmospheric correction and sensor calibration, have been gained for major ocean color missions of Sea-viewing Wide Field-of-view Sensor (SeaWiFS), Moderate Resolution Imaging Spectroradiometer (MODIS), Medium Resolution Imaging Spectrometer (MERIS), and Visible infrared Imaging Radiometer (VIIRS) from numerous dedicated validations based on in situ measurements in various parts of the global ocean. The 5% uncertainty in the blue bands over oligotrophic waters is usually used as the goal of ocean color sensors [13,14]. Bailey and Werdell [13] found that SeaWiFS data approached the target uncertainties of ±5% for clear water as defined prior to launch. It was also found that the goal of 5% uncertainty was reached for MERIS and MODIS-Aqua derived Rrs(λ) in the blue bands in clear waters [14,17]. Based on in situ-satellite matchups, Moore et al. [15] also found that the desired goal of 5% accuracy for SeaWiFS and MODIS-Aqua derived water-leaving radiance in blue bands in the open ocean had yet to be achieved. Buoy-based validation in the Mediterranean Sea showed that bluest band (Rrs(412)) of MERIS, SeaWiFS, and MODIS-Aqua had poor performance, with average relative percent difference of 60.2%, 20.6%, and 21.4% respectively [18]. Vessel-based validation in turbid waters along China coast showed that Rrs(λ) at the blue-green and green bands derived from MERIS, MODIS-Aqua, and SeaWiFS had the lowest uncertainties with a median of the absolute percentage difference of 15–27%, whereas the Rrs(λ) uncertainty at 412 nm is highest (47–62%) [19,20].
Most of the validation activities are dedicated to the Pacific and Atlantic Oceans [13,14,17,19,20,21,22]. While, to our best knowledge, there has been few dedicated studies on the Rrs(λ) validation in the Indian Ocean (IO), except a few studies on ocean optical classification. For example, Lee and Hu [23] showed that most of the IO waters were optically Case-1 water. Optical diversity analysis of the IO coastal regions using global SeaWiFS Rrs(λ) data also showed that most of the IO coastal waters were also Case-1 [24]. Recent study based on the monthly climatological datasets of Rrs(λ) identified eight optical classes of the coastal waters in the northern IO, among which classes 1–6 belong to Case-1 waters and 7–8 correspond to Case-2 waters [25]. More importantly, as the in situ measurements are sparse in space [17,18,21] and time [19,20], these validation results can hardly characterize the spatial and temporal distribution of Rrs(λ) data quality [14,26].
Recently, a novel Rrs(λ) quality assurance (QA) method was developed by Wei et al. [27], which can be used to objectively evaluate the quality of the Rrs(λ) spectrum for each valid pixel in a satellite image, yielding a quality score from 0 to 1 (hereafter termed QA). Compared to the in situ based validation, advantages of this method are at least two folds. Firstly, dependence of satellite validation on in situ measurements is avoided. Secondly, spatial pattern and temporal variability of Rrs(λ) quality can be revealed. The QA method has been successfully used in the validation of Rrs(λ) products [5,21,28] and has been adopted within NOAA Multi-Sensor Level-1 to Level- 2 (MSL12) ocean color data processing system [21].
The objective of this paper is to (1) characterize the data quality of Rrs(λ) products, especially the spatial pattern and temporal variability, of MODIS-Aqua, MODIS-Terra, and VIIRS-NPP in the IO based on the QA method, and (2) explore the factors influencing the spatiotemporal pattern of Rrs(λ) uncertainty in the IO, especially the monsoon-transported anthropogenic aerosol and sun-glint. This paper is arranged as follows. Section 2 describes the satellite and in situ data, as well as QA method. Validation results are presented in Section 3, followed by discussions in Section 4, and conclusions in Section 5.

2. Data and Methods

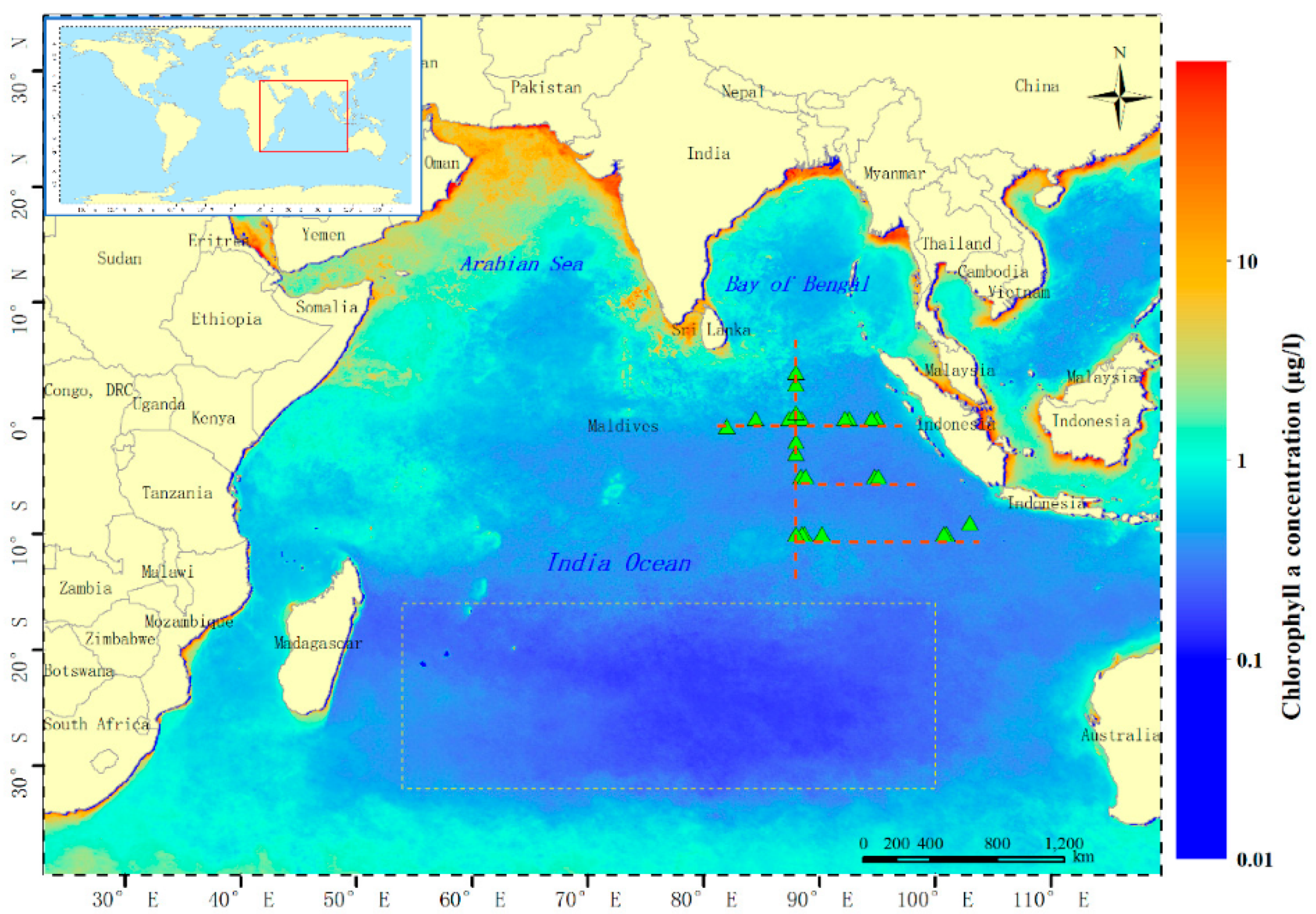
2.1. Study Area

The IO is bounded by Asia on the north, Africa on the west, Australia on the east, and the Southern Ocean on the south (Figure 1), with the average depth of 3741 m [29]. Due to the significant influence of wind, the IO can be subdivided into two general latitudinal climatic zones, which are the trade wind zone and monsoon zone [30]. The trade wind zone lies between 10° S and 30° S (the southern IO), with steady southeasterly trade wind throughout the year [30]. The monsoon zone extends north from latitude 10° S (the northern IO) with two contrasting monsoons, winter monsoon, and summer monsoon [31]. The summer monsoon, also known as the southwest monsoon, usually starts from May to September. During this period, winds are mainly southwesterly or westerly. The winter monsoon (also called the northeast monsoon) starts from October and continues until April. During this period, northeast winds are prevailing [32]. Hence, the IO is a dynamically complex and highly variable system, which in turn, results in substantial variations in marine biogeochemical and ecosystem responses [33,34].
The study area of this paper is shown in Figure 1.

2.2. In Situ Data

In situ Rrs(λ) at 21 stations were collected from a cruise in December 2016, including 4 transects of 0° S, 5° S, 10 ° S, and 88° E (Figure 1), using a well calibrated hyperspectral radiometric profiler (350–800 nm, Satlantic Inc., Richmond, BC, Canada). The Rrs(λ) was measured following the ocean optics protocols [35] under favorable weather conditions, with wave height of 0.7–2.4 m and wind speed of 1.8–10.5 m/s. The depths of the stations were 3600–4400 m, with transparency of 22–32 m.
The hyperspectral profiler data processing follows the National Aeronautics and Space Administration (NASA) ocean optics protocols [35]. Firstly, the spectral water-leaving radiance (Lw(λ)) was derived from measured profiles of upwelling radiance (Lu(λ,z)) propagated to just above the sea surface (0+), using the determined diffuse attenuation coefficient for the upwelling radiance, as well as the radiance transmittance [36]. Then Rrs(λ) was derived as the ratio of Lw(λ) to the measured Es(λ), and corrected for the bidirectional effects using the look-up table method [37]. The derived Rrs(λ) spectra are shown in Figure 2, with typical spectral characteristics of Case-1 clear oceanic waters [38]. The in situ Rrs(λ) spectra were used for the verification and comparison with the satellite derived Rrs(λ).

2.3. Satellite Data

The level 2 and level 3 Rrs(λ) products with the spatial resolution of 1 km and 4 km respectively, in 2016 of MODIS-Aqua and MODIS-Terra, and VIIRS-NPP were collected from National Aeronautics and Space Administration (NASA) Goddard Space Flight Center (GSFC) archives (https://oceancolor.nasa.gsfc.gov). The level 2 products were used to evaluate the consistency between satellite derived and in situ measured Rrs(λ). Due to effects of cloud, haze, sun glint, and other factors, valid MODIS observations over the oceans are only ~4.9% per day [39]. Therefore, level 3 monthly (rather than daily) products were used to characterize the spatiotemporal distribution of Rrs(λ) uncertainties by the QA method, due to its higher spatial coverage.
The level 2 Rrs(λ) products were processed with the atmospheric correction based on near infrared (NIR) iterative approach [40,41]. The level 3 Rrs(λ) products were generated from level 2 Rrs(λ) data using spatial and temporal binning algorithm [42]. The processing versions of the satellite data used in this paper were R2018 (Ocean Biology Processing Group (OBPG), 2018), the latest processing version. It is well known that MODIS-Terra suffers from uncertainties and instabilities, particularly the 412 nm band [43]. The improvement has been made by NASA through reprocessing based on improved calibration of the MODIS-Terra visible (VIS)–NIR bands [44,45]. For comparison, the MODIS Terra Rrs(λ) products of previous processing version R2014 were also validated (OBPG, 2014). The spatiotemporal match-up dataset of satellite and in situ measured Rrs(λ) was established according to the method of Cui et al. [19] with a spatial window of 3 × 3 pixels and a temporal window of 3 h. There were 4, 8, and 7 match-ups for MODIS-Aqua, MODIS-Terra and VIIRS-NPP, respectively.
The daily level 3 absorption aerosol optical depth (AAOD) products at 388 nm of Ozone Monitoring Instrument (OMI) onboard NASA’s Aura satellite in 2016 were also collected from NASA’s GSFC (http://disc.gsfc.nasa.gov/Aura/OMI/), for the mechanism analysis of Rrs(λ) uncertainties.

2.4. QA Method

In the QA system, the global ocean was clustered into 23 optical water types [24,46]. Each water type has an unique reference of the normalized Rrs(λ) spectrum (nRrs-ref(λ), dimensionless), with an upper and a lower bound obtained from a wide range of in situ measurements [24]. The target Rrs(λ) spectrum is compared with the reference spectrum and a score is assigned, with 1 for perfect Rrs(λ) spectrum and 0 for unusable Rrs(λ) spectrum.
There are several steps to perform QA method. Step 1 is to calculate nRrs(λ) for each pixel by dividing the spectrum by its root sum of squares. Step 2 is to assign a water type to the target Rrs(λ) by comparing it with the reference nRrs-ref(λ) spectra using a spectral angle mapper (SAM). Step 3 is to calculate the QA scores by comparing the target nRrs(λ) spectrum with the upper and lower boundaries of reference nRrs-ref(λ) spectrum. At each wavelength λi, once the target nRrs(λi) is found beyond either the upper or lower boundary of the reference nRrs-ref(λi) spectra, the score at this wavelength C(λi) will be assigned 0, otherwise 1. Moreover, the score of each spectrum (Ctot) is the arithmetic average of scores at each wavelength (C(λi)), varying from 0 to 1.
Ctot = (C(λ2) + C(λ2) + … + C(λN))/N
where N is the total number of wavelengths. A higher score indicates higher data quality [24].
To evaluate the quality of each sensor band in the IO, the percentage of pixels (P(λi)) with C(λi) of 1 over the study area for each band λi, is calculated as follows.
P(λi) = Nq(λi)/Ntotal
where Nq(λi) is the number of pixels with score of 1 for the whole study area and Ntotal is the number of total valid pixels of the study area. A subjective threshold of 0.75 is adopted, and if P(λi) < 0.75, the band λi is regarded as “low-quality” band.

3. Results

3.1. Validation Results

Level 3 monthly Rrs(λ) products of MODIS-Aqua, MODIS-Terra and VIIRS-NPP acquired in 2016 were evaluated using the QA method. Eight bands of MODIS Rrs(λ) were involved in the evaluation, including 412 nm, 443 nm, 488 nm, 531 nm, 547 nm, 555 nm, 667 nm, and 678 nm. Five bands of VIIRS-NPP Rrs(λ) were evaluated, including 410 nm, 443 nm, 486 nm, 551 nm, and 671 nm. Regional averaged scores of monthly Rrs(λ) of the three sensors are shown in Table 1.
(1)
MODIS-Aqua
From Table 1 and Figure 3, it is found that generally speaking, MODIS-Aqua level 3 Rrs(λ) monthly products have good quality, as indicated by the average score of 0.92 ± 0.12. Annual maximum (0.95) and minimum (0.88) of monthly scores are found in April and May, and September and October, respectively (Figure 4a). Spatially, low scores (warm colors in Figure 3) are mainly distributed in the BB, with average scores of 0.83 ± 0.18 (Table 1). Surprisingly, it is found that scores in clear waters of OZ (light blue pixels in Figure 3) are low in the second half of the year (average score of 0.86 vs. 0.97 in the first half of the year), although it is commonly recognized that atmospheric correction algorithms perform well in the oceanic waters [13,14,17,47,48]. Further quality check at all bands indicates that low QA score of a spectrum is mainly attributed to its performance in the blue bands (412 nm and 443 nm), as shown in Figure 5.
Furthermore, we extracted Rrs(λ) samples with low scores in the BB (<0.3) and oligotrophic gyre zone (<0.7), and found that there were defects in the Rrs(λ) spectra with low scores. The Rrs(λ) spectra from the BB at the blue bands are significantly underestimated, as indicated by negative values at 412 nm and 443 nm bands (Figure 6a). Rrs(λ) spectra samples from the OZ also show anomaly at 443 nm band, compared to the in situ measured Rrs(λ) (Figure 6b). The satellite derived Rrs(λ) have a small peak at 443 nm, while the in situ measured Rrs(λ) spectra do not show this feature.
(2)
MODIS-Terra
MODIS-Terra Rrs(λ) (R2018) shows comparable quality (average score of 0.92) with MODIS-AQUA. Similar seasonal variability and spatial pattern are also found (Figure 7), with the highest (0.95) and lowest (0.88) monthly scores in April and September, respectively (Figure 4d). Waters in the BB exhibit low scores of 0.84 ± 0.17 (Table 1, Figure 7). Scores in the OZ of the southern IO decrease from 0.98 in the first half of the year to 0.88 in the second half of the year, which is also due to the poor performance of blue bands (412 nm and 443 nm), as shown in Figure 5.
From comparison between Figure 7 and Figure 8, it can be found that the quality of MODIS-Terra Rrs(λ) has been improved by recent reprocessing through updating sensor calibration and vicarious calibration (OBPG, 2018), as indicated by the increase of scores from 0.81 (R2014) to 0.92 (R2018) (Figure 4c,d, Table 1). Moreover, the annually averaged high-score percentage P(λi) at bands of 412 nm, 443 nm, 488 nm, 531 nm, 547 nm, 555 nm, 667 nm, and 678 nm of MODIS-Terra (R2014) are 74.82%, 56.54%, 85.01%, 87.21%, 91.93%, 54.23%, 96.53%, and 95.92%, respectively, indicating that the lower scores of R2014 MODIS-Terra data are mainly caused by the imperfect Rrs(λ) data quality at bands of 412 nm, 443 nm, and 555 nm.
(3)
VIIRS-NPP
VIIRS-NPP Rrs(λ) products show the best data quality among the three satellite datasets, in terms of its highest average score (0.93), which is mainly attributed to the better performance in the BB with the average scores of 0.92 ± 0.12 (Table 1). Annual maxima (0.96) are found in February, March, and April, and minima (0.90) are in September and October (Figure 4b). Low quality pixels (with average scores of 0.88 ± 0.16, light blue colors in Figure 9) are mainly located in the OZ of the IO, especially from June to December, which is also attributed to the poor performance at blue bands (412 nm and 443 nm), as shown in Figure 5.

3.2. Mechanisms of Rrs(λ) Quality Spatiotemporal Distribution

Low quality Rrs(λ) products derived from MODIS-Aqua, MODIS-Terra, and VIIRS-NPP are all found in the BB of the northern IO and the OZ of the southern IO. Different driving mechanisms in these two regions are analyzed as follows.

3.2.1. Monsoon in the Northern IO

Results showed that the data quality of Rrs(λ) products in the northern IO (AS and BB) was significantly affected by the two contrasting monsoons, winter monsoon and summer monsoon.
In the winter monsoon, the lower scores are mainly found in the BB. Samples from the BB show that Rrs(λ) at the blue bands are significantly underestimated, as indicated by negative values at 412 nm and 443 nm bands (Figure 6a), which may be attributed to the increase of AAOD. During the winter monsoon, the northeast winds transport large amounts of anthropogenic aerosols, including high absorptive black carbon (BC) [49,50], brown carbon (BrC) [51,52] and dust [53], which are originated from the biomass or fossil fuel combustion, to the BB and offshore area of the AS [54,55]. Statistics from OMI AAOD show that the average AAOD at 388 nm of BB (0.053) in the winter monsoon increased by 26.43%, compared to that in the summer monsoon (0.042). Correlation analysis between the monthly AAOD and QA scores of MODIS-Aqua, MODIS-Terra and VIIRS-NPP in the BB during the winter monsoon show significant negative correlation (R = −0.82, p = 0.001; R = −0.80, p = 0.002; R = −0.72, p = 0.009) in the BB (Figure 10a). Taking February as an example, we analyzed the relationship between the daily AAOD and scores of MODIS-Aqua, MODIS-Terra, and VIIRS-NPP. For most pixels with scores <0.5, the AAODs are more than the annual averaged AAOD of 0.02 in the IO (Figure 10b–d). The satellite-observed radiance is a combination of aerosol radiance contribution and ocean radiance contribution. The presence of absorptive aerosols results in overestimation of aerosol contributions, which in turn leads to the underestimation of ocean contribution at shorter wavebands [56,57]. Therefore, the over-corrected aerosol contribution leads to the underestimation of Rrs(λ).
It is noted that although AS is also affected by the winter monsoon, the Rrs(λ) perform better than that in the BB during winter monsoon (Table 1). This may be attributed to the clearer atmosphere in the AS. Different from the BB, the average AAOD (0.02) in the AS decreased during the winter monsoon, compared to that of summer monsoon (0.04). Correspondingly, the average scores of MODIS-Terra, MODIS-Aqua, and VIIRS-NPP are 0.89, 0.89, and 0.92 respectively in the winter monsoon, and 0.82, 0.83, and 0.93 in the summer monsoon. Existing literatures also showed that the atmosphere over BB was more turbid than that of AS in the winter monsoon [58] and contained less absorptive aerosols than the BB [59]. Hence, the data quality of Rrs(λ) in the AS is better than that in the BB during the winter monsoon.
During the summer monsoon, the southwest wind prevails, which brings sea salt and mineral dust aerosols to the northern IO [29]. The sea salt contributes ~60% of the composite aerosol optical depth [60], which will be in favor of the accurate atmospheric correction [61] and thus higher Rrs(λ) data quality. However, the summer monsoon period is the main rainy season in the northern IO, leading to the low valid data coverage (Figure 4). The average valid data coverage of the three sensors in the BB and AS are only 52% and 48%, respectively, compared to 88% and 95% in the winter monsoon season. The lowest valid data coverage is only 12% in the AS (Figure 4). The low valid data coverage in summer results in loss of large amounts of high-score pixels in the south of AS and BB, leading to the decrease of the average scores, which amplifies the seasonal difference in Rrs(λ) data quality.

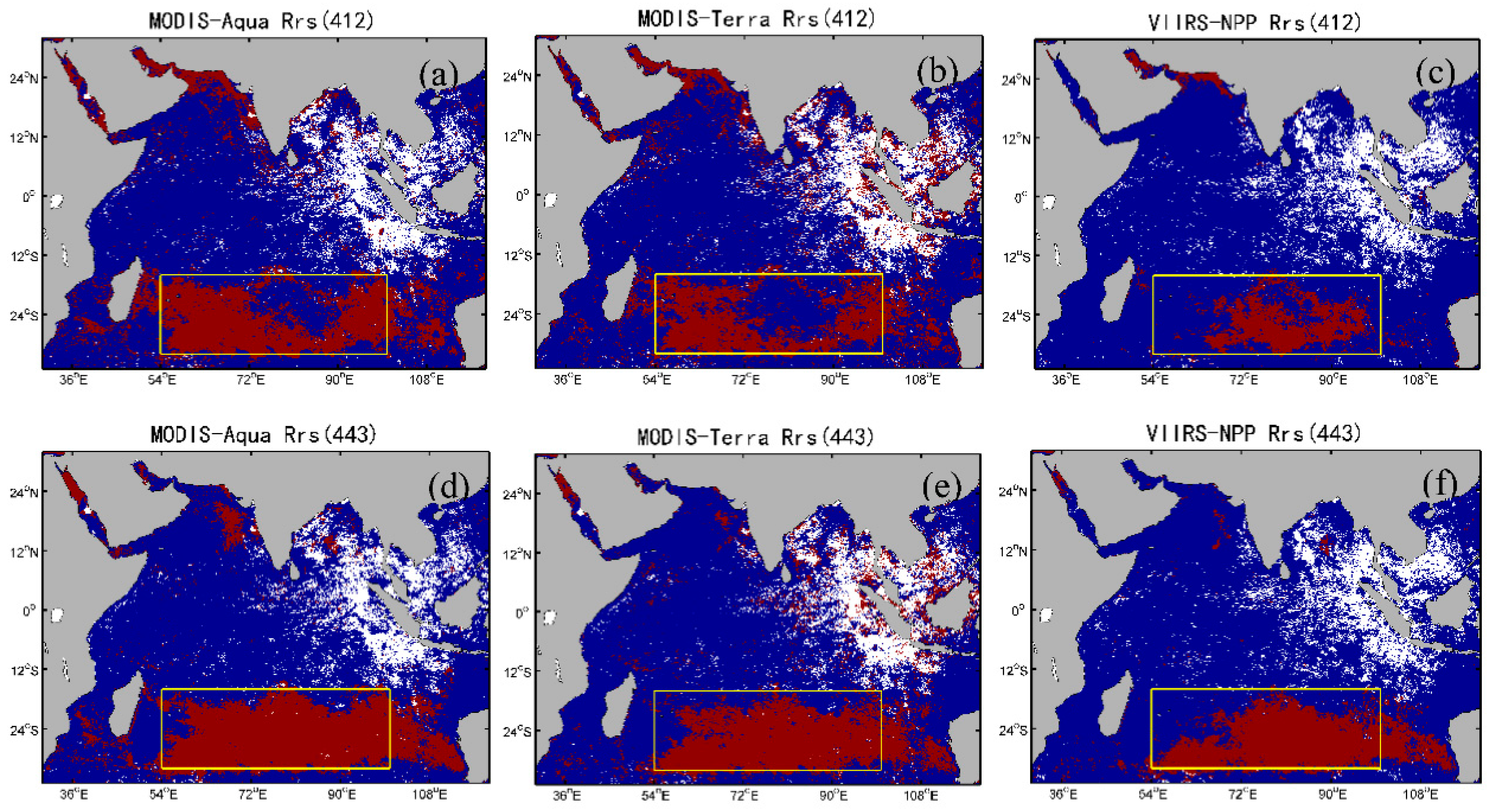
3.2.2. Sun Glint in the OZ

Low-quality Rrs(λ) in the clear OZ of the southern IO in the second half of the year may be attributed to the contamination by the residual sun-glint signals. For sensors without a tilting capacity (such as MODIS and VIIRS), the ocean color observations in the tropical and sub-tropical oceans are more likely affected by the sun-glint (e.g., the north and south Atlantic gyres, and the South Indian gyre) [62,63,64], which is the bright pattern of the specular reflection of the sun by the wavy sea surface [64,65]. Morel and Gentili [63] indicated that the residual sun-glint resulted in the anomaly of level 3 Rrs(λ) products in the sub-tropical oligotrophic gyres and sun-glint effect migrated with the sun declination course.
During MODIS and VIIRS images processing from level 1 to level 2 implemented by the NASA Ocean Biology Processing Group (OBPG), the pixels are flagged as “HIGLINT” and “MODGLINT” if the normalized sun-glint surface-reflected radiance (LGN) exceeds 0.005 sr−1 and 0.0001 sr−1, and then a glint correction [66] is applied according to the wind speed [67,68]. The pixels with a “HIGLINT” flag are masked out during the processing from level 2 to level 3, while those with a “MODGLINT” flag are reserved.
Taking VIIRS-NPP as an example, we counted the number of level 2 Rrs(λ) pixels with “MODGLINT” flag corresponding to each level 3 Rrs(λ) pixel. The average number of Rrs(λ) pixels with “MODGLINT” flag was significantly lower in the first half of the year (mainly austral autumn and winter) than that in the second half of the year (mainly austral spring and summer) (17.8 ± 5.3 vs. 29.1 ± 7.1), with maximum of 36.4 in December and minimum of 10.4 in June (Figure 11). Further analysis of VIIRS-NPP level 2 Rrs(λ) data with scores <0.5 show that the percentage (66.2%) of pixels with “MODGLINT” flag is about twice the pixels with no “MODGLINT” flag (33.8%). The statistics indicate the impact of residual sun-glint contamination. Hence, the development of advanced algorithm to remove residual sun-glint is still needed.

4. Discussion

4.1. QA Analysis

Except the dominant effects from monsoon and sun-glint, other potential factors affecting QA score are discussed in this section, including differences in band configurations between VIIRS and MODIS (5 bands vs. 8 bands) and level 3 product types (Daily vs. Monthly).

4.1.1. Bands Involved in QA Analysis

It is noted that the bands involved in QA analysis are different, with five bands for VIIRS and eight bands for MODIS. For the analysis of the effect of bands involved in QA analysis and fair quality comparison across sensors, bands of 531 nm, 547 nm, and 678 nm that VIIRS does not have are excluded from MODIS QA analysis. QA results for MODIS-Aqua, MODIS-Terra (R2018), and MODIS-Terra (R2014) are shown in Figure 12, based on Rrs(λ) spectra at the remaining 5 bands of 412 nm, 443 nm, 488 nm, 555 nm, and 667 nm, which are also close to the nominal wavelengths of VIIRS-NPP.
The 5-band based QA scores for MODIS-Aqua and MODIS-Terra (R2018) are almost identical with those of 8-band (Figure 12a,b), whereas large discrepancy is found for MODIS-Terra (R2014), whose 5-band based scores are significantly lower than those of 8-bands (Figure 12c). This phenomenon can be explained by results of score statistics at each band of MODIS-Terra (R2014). In the 5-band evaluation, three low quality bands of 412 nm, 443 nm, and 555 nm are involved (Figure 12c), accounting for 60% of numbers of all the involved bands and leading to a lower average score. Whereas bands of 531 nm, 547 nm, and 678 nm, which have good data quality and contribute to the higher average scores of the 8-band evaluation, are excluded from 5-band statistics. Different from MODIS-Terra (R2014), high QA scores for MODIS-Aqua and MODIS-Terra (R2018) are achieved at all the 8 band and, thus, excluding bands of 531 nm, 547 nm, and 678 nm would have little effect on the score statistics.
The above results have implications in the QA method application. First, for the comparison between QA results of the same sensor by the different researcher, it is suggested to pay attention to the consistency of bands involved in the QA analysis. The QA results may be quite different when different bands are selected. Second, from the in-water parameter retrieval point of view, it would be more practical and indicative to evaluate the QA score for a spectrum only based on bands, which are involved in a specific retrieval algorithm rather than full bands.

4.1.2. Daily vs. Monthly Products

Statistics show that the percentage of valid observations of level 3 daily products in the study area is less than 10% for all these sensors, which implies that the level 3 daily data is not qualified for characterizing the spatial distribution of Rrs(λ) quality. Therefore, the level 3 monthly products were adopted for QA analysis due to its higher spatial coverage (~91.7%). To explore the differences in scores between daily and monthly products, the level 3 daily products are also validated by QA method. The noticeable agreement between these scores can be found in terms of their close values and consistent trend, especially for VIIRS (Figure 13). It is also noted that scores of monthly products are higher than that of daily ones to some extent (~2%), which may be attributed to the data quality improvement through spatiotemporal binning, as well as the abnormal values removal [42].

4.2. Comparison between Results from In Situ-Based and QA Methods

To verify the QA method, we use both the in situ measured Rrs(λ) and QA method to evaluate the level 2 Rrs(λ) products simultaneously and compare the results. Compared with the in situ measured Rrs(λ), the median absolute percent difference (MPD) of MODIS-Aqua, MODIS-Terra and VIIRS-NPP derived Rrs(λ) are 8.4–15.2%, 8.9–15.7%, and 17.5–22.9% at bands of 412–555 (551) nm, respectively (Figure 14a–c). Correspondingly, the average validation scores by QA method are 0.92, 0.92, and 0.86, for MODIS-Aqua, MODIS-Terra and VIIRS-NPP, respectively. Validation results by in situ data and QA method show good consistency and a significant negative correlation (p = −1) (Figure 14d). The high score data has small MPD.

4.3. Implications

The in situ-based evaluation results may provide the valuable information about uncertainties at each band, with little clues of the rationality of the spectral shape, as shown in Figure 15. It is found that, Terra (R2014) Rrs(λ) at all bands except for 412 nm band agree well with the in situ data. Nevertheless, it is noted that due to the underestimation at 412 nm, Terra (R2014) fails to retrieve the actual spectral shape of in situ Rrs(λ). Different from the in situ-based validation method, the QA method can give the validation results based on the Rrs(λ) spectrum shape. Moreover, the QA scores for Terra (R2014) and Terra (R2018) are 0.67 and 1, respectively, which reveals the defects of Terra (R2014) Rrs(λ) spectrum. Therefore, it is necessary to involve the Rrs(λ) spectrum shape when the validation of Rrs(λ) is conducted, especially for the satellite ocean color algorithms based on the spectral shape, such as fluorescence line height (FLH) [69], maximum chlorophyll index (MCI) [70], and floating algae index (FAI) [71].
The potential negative effects of the low-quality Rrs(λ) at 412 nm and 443 nm in the OZ on the accuracy of ocean color products should be envisaged, especially for Chla [12,72] and colored dissolved organic matter (CDOM) [73], which are usually retrieved by algorithms using the above bands. Taking OC3 and OC4 algorithms as examples, Rrs(λ) quality degradation at 443 nm in the OZ may result in overestimation of Rrs(443)/Rrs(555) by 6.45%, 8.23%, and 16.93% for VIIRS-NPP, MODIS-Aqua, and MODIS-Terra, respectively. Accordingly, Chla would be underestimated by 16.12%, 16.39%, and 30.83% for VIIRS-NPP, MODIS-Aqua, and MODIS-Terra, respectively. As the Rrs(λ) quality degradation is significant in certain months, biased seasonality in the derived Chla would also probably occur in the OZ.
The same issue exists for the BB. In addition to the low Rrs(λ) quality in the winter monsoon, the low valid data coverage is another obstacle to characterize the seasonal pattern of ocean color parameters in this region. The lower Rrs(λ) data quality in the BB reveals that much more efforts are still required to improve the performance of atmospheric correction algorithms to address the influence of anthropogenic absorptive aerosols.

5. Conclusions

Satellite ocean color remote sensing plays an important role in the study of the Indian Ocean, which is a dynamically complex and highly variable system with complicated marine biogeochemical and ecological process. To facilitate quantitative satellite ocean color application in this area, taking the year of 2016 as an example, the spatial and temporal distribution of satellite-derived Rrs(λ) quality from MODIS-Aqua, MODIS-Terra, and VIIRS-NPP in the IO is characterized for the first time, using a recently developed quality assurance (QA) system.
QA analysis indicates that the satellite-derived Rrs(λ) products generally exhibit good quality, with the average scores of 0.93 ± 0.02, 0.92 ± 0.02, and 0.92 ± 0.02 for VIIRS-NPP, MODIS-Aqua, and MODIS-Terra, respectively. Low-score regions are mainly located in the BB and the OZ of the southern IO, due to the monsoon-transported anthropogenic absorptive aerosols and sun-glint contamination, respectively. As a result of the above effects, Rrs(λ) data quality shows clear seasonal pattern, with the highest quality (~0.95) in April and the lowest one in September (<0.90). Besides, quality of MODIS-Terra Rrs(λ) is found to be significantly improved after the latest reprocessing (R2018) through the calibration update, as indicated by an average QA score of 0.92 compared to 0.81 for previous (R2014) version.
These findings highlight the effects of monsoon-transported anthropogenic aerosols, imperfect sun-glint removal, and radiometric calibration on the Rrs(λ) quality. Further studies are advocated to improve the correction of sun-glint in the oligotrophic gyre and absorptive aerosol in the complex ocean–atmosphere environment.

Author Contributions

Conceptualization, R.L. and T.C.; methodology, R.L.; software, H.Y.; validation, R.L. and H.Y.; resources, J.Z.; writing—original draft preparation, R.L.; writing—review and editing, T.C.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Key R&D Program of China (Nos. 2017YFC1405105 and 2016YFA0600102), the National Natural Science Foundation of China (Nos. 41506204, 41876206, 41706209, and 61890964), the China–Korea joint ocean research project (PI-2019-1-01), the Global Change and Air-Sea Interaction Program (GASI-02-IND-STSaut, GASI-02-IND-STSwin), Guangdong Province Key Laboratory for Climate Change and Natural Disaster Studies (2020B1212060025), and the Dragon-4 project (32405).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://oceancolor.nasa.gsfc.gov.

Acknowledgments

The authors would like to thank the participants of the investigation voyages in the southern waters of the East IO in autumn 2016 for their dedication in in situ measurements and the three anonymous reviewers for providing helpful comments and suggestions to improve the manuscript. The authors would also like to thank NASA for the distribution of MODIS and VIIRS Rrs(λ) data, OMI and Aura science teams for their efforts in producing the OMI data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Ford, D.; Barciela, R. Global marine biogeochemical reanalyses assimilating two different sets of merged ocean colour products. Remote Sens. Environ. 2017, 203, 40–54. [Google Scholar] [CrossRef]
  2. Le, C.; Zhou, X.; Hu, C.; Lee, Z.; Li, L.; Stramski, D. A Color-Index-Based Empirical Algorithm for Determining Particulate Organic Carbon Concentration in the Ocean from Satellite Observations. J. Geophys. Res. Oceans 2018, 123, 7407–7419. [Google Scholar] [CrossRef]
  3. Li, J.; Yu, Q.; Tian, Y.Q.; Becker, B.L. Remote sensing estimation of colored dissolved organic matter (CDOM) in optically shallow waters. ISPRS J. Photogramm. Remote Sens. 2017, 128, 98–110. [Google Scholar] [CrossRef] [Green Version]
  4. Reygondeau, G.; Longhurst, A.R.; Martinez, E.; Beaugrand, G.; Antoine, D.; Maury, O. Dynamic biogeochemical provinces in the global ocean. Glob. Biogeochem. Cycles 2013, 27, 1046–1058. [Google Scholar] [CrossRef] [Green Version]
  5. Feng, L.; Hou, X.; Zheng, Y. Monitoring and understanding the water transparency changes of fifty large lakes on the Yangtze Plain based on long-term MODIS observations. Remote Sens. Environ. 2019, 221, 675–686. [Google Scholar] [CrossRef]
  6. Hakvoort, H.; De Haan, J.; Jordans, R.; Vos, R.; Peters, S.; Rijkeboer, M. Towards airborne remote sensing of water quality in The Netherlands—validation and error analysis. ISPRS J. Photogramm. Remote Sens. 2002, 57, 171–183. [Google Scholar] [CrossRef]
  7. Salama, M.S.; Verhoef, W. Two-stream remote sensing model for water quality mapping: 2SeaColor. Remote Sens. Environ. 2015, 157, 111–122. [Google Scholar] [CrossRef] [Green Version]
  8. Dutkiewicz, S.; Hickman, A.E.; Jahn, O.; Henson, S.; Beaulieu, C.; Monier, E. Ocean colour signature of climate change. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
  9. Montes-Hugo, M.; Doney, S.C.; Ducklow, H.W.; Fraser, W.; Martinson, D.; Stammerjohn, S.E.; Schofield, O. Recent changes in phytoplankton communities associated with rapid regional climate change along the western Antarctic Penin-sula. Science 2009, 323, 1470–1473. [Google Scholar] [CrossRef]
  10. Sathyendranath, S.; Brewin, R.J.; Jackson, T.; Mélin, F.; Platt, T. Ocean-colour products for climate-change studies: What are their ideal characteristics? Remote Sens. Environ. 2017, 203, 125–138. [Google Scholar] [CrossRef] [Green Version]
  11. Lee, Z.; Shang, S.; Wang, Y.; Wei, J.; Ishizaka, J. Nature of optical products inverted semianalytically from remote sensing reflectance of stratified waters. Limnol. Oceanogr. 2020, 65, 387–400. [Google Scholar] [CrossRef]
  12. O’Reilly, J.E.; Werdell, P.J. Chlorophyll algorithms for ocean color sensors—OC4, OC5; OC6. Remote Sens. Environ. 2019, 229, 32–47. [Google Scholar] [CrossRef]
  13. Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
  14. Hu, C.; Feng, L.; Lee, Z. Uncertainties of SeaWiFS and MODIS remote sensing reflectance: Implications from clear water measurements. Remote Sens. Environ. 2013, 133, 168–182. [Google Scholar] [CrossRef]
  15. Moore, T.S.; Campbell, J.W.; Feng, H. Characterizing the uncertainties in spectral remote sensing reflectance for SeaWiFS and MODIS-Aqua based on global in situ matchup data sets. Remote Sens. Environ. 2015, 159, 14–27. [Google Scholar] [CrossRef]
  16. Zibordi, G.; Mélin, F.; Berthon, J.-F. A Regional Assessment of OLCI Data Products. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1490–1494. [Google Scholar] [CrossRef]
  17. Mélin, F.; Sclep, G.; Jackson, T.; Sathyendranath, S. Uncertainty estimates of remote sensing reflectance derived from comparison of ocean color satellite data sets. Remote Sens. Environ. 2016, 177, 107–124. [Google Scholar] [CrossRef]
  18. Antoine, D.; D’Ortenzio, F.; Hooker, S.B.; Bécu, G.; Gentili, B.; Tailliez, D.; Scott, A.J. Assessment of uncertainty in the ocean reflectance determined by three satellite ocean color sensors (MERIS, SeaWiFS and MODIS-A) at an offshore site in the Mediterranean Sea (BOUSSOLE project). J. Geophys. Res. Space Phys. 2008, 113, 7. [Google Scholar] [CrossRef]
  19. Cui, T.; Zhang, J.; Groom, S.; Sun, L.; Smyth, T.; Sathyendranath, S. Validation of MERIS ocean-color products in the Bohai Sea: A case study for turbid coastal waters. Remote Sens. Environ. 2010, 114, 2326–2336. [Google Scholar] [CrossRef]
  20. Cui, T.; Zhang, J.; Tang, J.; Sathyendranath, S.; Groom, S.; Ma, Y.; Zhao, W.; Song, Q. Assessment of satellite ocean color products of MERIS, MODIS and SeaWiFS along the East China Coast (in the Yellow Sea and East China Sea). ISPRS J. Photogramm. Remote Sens. 2014, 87, 137–151. [Google Scholar] [CrossRef]
  21. Barnes, B.B.; Cannizzaro, J.P.; English, D.C.; Hu, C. Validation of VIIRS and MODIS reflectance data in coastal and ocean-ic waters: An assessment of methods. Remote Sens. Environ. 2019, 220, 110–123. [Google Scholar] [CrossRef] [Green Version]
  22. Qin, P.; Simis, S.; Tilstone, G. Radiometric validation of atmospheric correction for MERIS in the Baltic Sea based on continuous observations from ships and AERONET-OC. Remote Sens. Environ. 2017, 200, 263–280. [Google Scholar] [CrossRef] [Green Version]
  23. Lee, Z.; Hu, C. Global distribution of Case-1 waters: An analysis from SeaWiFS measurements. Remote Sens. Environ. 2006, 101, 270–276. [Google Scholar] [CrossRef]
  24. Mélin, F.; Vantrepotte, V. How optically diverse is the coastal ocean? Remote Sens. Environ. 2015, 160, 235–251. [Google Scholar] [CrossRef]
  25. Monolisha, S.; Platt, T.; Sathyendranath, S.; Jayasankar, J.; George, G.; Jackson, T. Optical Classification of the Coastal Waters of the Northern Indian Ocean. Front. Mar. Sci. 2018, 5, 87. [Google Scholar] [CrossRef] [Green Version]
  26. Liu, R.; Zhang, J.; Yao, H.; Cui, T.; Wang, N.; Zhang, Y.; Wu, L.; An, J. Hourly changes in sea surface salinity in coastal waters recorded by Geostationary Ocean Color Imager. Estuar. Coast. Shelf Sci. 2017, 196, 227–236. [Google Scholar] [CrossRef]
  27. Wei, J.; Lee, Z.; Shang, S. A system to measure the data quality of spectral remote-sensing reflectance of aquatic environ-ments. J. Geophys. Res. Oceans 2016, 121, 8189–8207. [Google Scholar]
  28. Shang, S.; Lee, Z.; Lin, G.; Hu, C.; Shi, L.; Zhang, Y.; Li, X.; Wu, J.; Yan, J. Sensing an intense phytoplankton bloom in the western Taiwan Strait from radiometric measurements on a UAV. Remote Sens. Environ. 2017, 198, 85–94. [Google Scholar] [CrossRef]
  29. Eakins, B.W.; Sharman, G.F. Volumes of the World’s Oceans from ETOPO1; NOAA National Geophysical Data Center: Boulder, CO, USA, 2010. [Google Scholar]
  30. Wincentsen, D.L. Encyclopedia of Global Warming and Climate Change. Ref. Rev. 2013, 27, 30. [Google Scholar] [CrossRef]
  31. Schott, F.A.; Xie, S.P.; McCreary, J.P., Jr. Indian Ocean circulation and climate variability. Rev. Geophys. 2009, 47, 245. [Google Scholar] [CrossRef]
  32. Li, F.; Ramanathan, V. Winter to summer monsoon variation of aerosol optical depth over the tropical Indian Ocean. J. Geophys. Res. Atmos. 2002, 107, AAC-2. [Google Scholar] [CrossRef]
  33. Levy, M.; Shankar, D.; Andre, J.M.; Shenoi, S.S.; Durand, F.; Montegut, C.D. Phytoplankton blooms in the Indian Ocean: Linking seacolor to near-surface ocean dynamics. J. Geophys. Res. 2007, 112, 4090. [Google Scholar] [CrossRef] [Green Version]
  34. Hood, R.R.; Wiggert, J.D.; Naqvi, S.W.A.; Brink, K.H.; Smith, S.L. Indian Ocean research: Opportunities and challenges. Sea Ice 2009, 185, 409–429. [Google Scholar] [CrossRef]
  35. Mueller, J.L. In-water radiometric profile measurements and data analysis protocols. In Ocean Optics Protocols for Satellite Ocean Color Sensor Validation; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003; Volume 4, pp. 7–20. [Google Scholar]
  36. Austin, R.W. Gulf of Mexico, ocean-color surface-truth measurements. Bound. Layer Meteorol. 1980, 18, 269–285. [Google Scholar] [CrossRef]
  37. Morel, A.; Antoine, D.; Gentili, B. Bidirectional reflectance of oceanic waters: Accounting for Raman emission and varying particle scattering phase function. Appl. Opt. 2002, 41, 6289–6306. [Google Scholar] [CrossRef]
  38. Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
  39. Feng, L.; Hu, C. Comparison of Valid Ocean Observations between MODIS Terra and Aqua Over the Global Oceans. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1575–1585. [Google Scholar] [CrossRef]
  40. Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef] [PubMed]
  41. Bailey, S.W.; Franz, B.A.; Werdell, P.J. Estimation of near-infrared water-leaving reflectance for satellite ocean color data processing. Opt. Express 2010, 18, 7521–7527. [Google Scholar] [CrossRef]
  42. Campbell, J.W.; Blaisdell, J.M.; Darzi, M. Level-3 Sea WiFS data products: Spatial and temporal binning algorithms. Oceanogr. Lit. Rev. 1996, 9, 952. [Google Scholar]
  43. Franz, B.A.; Kwiatowska, E.J.; Meister, G.; McClain, C.R. Moderate Resolution Imaging Spectroradiometer on Terra: Limitations for ocean color applications. J. Appl. Remote Sens. 2008, 2, 023525. [Google Scholar] [CrossRef]
  44. Meister, G.; Franz, B.A. Adjustments to the MODIS Terra radiometric calibration and polarization sensitivity in the 2010 reprocessing. Opt. Eng. Appl. 2011, 8153, 815308. [Google Scholar] [CrossRef] [Green Version]
  45. Li, J.; Hu, C.; Shen, Q.; Barnes, B.B.; Murch, B.; Feng, L. Recovering low quality modis-terra data over highly turbid wa-ters through noise reduction and regional vicarious calibration adjustment: A case study in taihu lake. Remote Sens. Environ. 2017, 197, 72–84. [Google Scholar] [CrossRef]
  46. Cui, T.; Zhang, J.; Wang, K.; Wei, J.; Mu, B.; Ma, Y.; Zhu, J.; Liu, R.; Chen, X. Remote sensing of chlorophyll a concentration in turbid coastal waters based on a global optical water classification system. ISPRS J. Photogramm. Remote Sens. 2020, 163, 187–201. [Google Scholar] [CrossRef]
  47. Liu, H.; Zhou, Q.; Li, Q.; Hu, S.; Shi, T.; Wu, G. Determining switching threshold for NIR-SWIR combined atmospheric correction algorithm of ocean color remote sensing. ISPRS J. Photogramm. Remote Sens. 2019, 153, 59–73. [Google Scholar] [CrossRef]
  48. Wang, M.; Shi, W. The NIR-SWIR combined atmospheric correction approach for MODIS ocean color data processing. Opt. Express 2007, 15, 15722–15733. [Google Scholar] [CrossRef] [Green Version]
  49. Meehl, G.A.; Arblaster, J.M.; Collins, W.D. Effects of Black Carbon Aerosols on the Indian Monsoon. J. Clim. 2008, 21, 2869–2882. [Google Scholar] [CrossRef] [Green Version]
  50. Budhavant, K.; Andersson, A.; Holmstrand, H.; Bikkina, P.; Bikkina, S.; Satheesh, S.K.; Gustafsson, Ö. Enhanced Light-Absorption of Black Carbon in Rainwater Compared With Aerosols Over the Northern Indian Ocean. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
  51. Srinivas, B.; Sarin, M.M. Light absorbing organic aerosols (brown carbon) over the tropical indian ocean: Impact of bio-mass burning emissions. Environ. Res. Lett. 2013, 8, 044042. [Google Scholar] [CrossRef] [Green Version]
  52. Laskin, A.; Laskin, J.; Nizkorodov, S.A. Chemistry of Atmospheric Brown Carbon. Chem. Rev. 2015, 115, 4335–4382. [Google Scholar] [CrossRef] [Green Version]
  53. Banerjee, P.; Satheesh, S.K.; Moorthy, K.K.; Nanjundiah, R.S.; Nair, V.S. Long-Range Transport of Mineral Dust to the Northeast Indian Ocean: Regional versus Remote Sources and the Implications. J. Clim. 2019, 32, 1525–1549. [Google Scholar] [CrossRef]
  54. Ramanathan, V.; Crutzen, P.J.; Lelieveld, J.; Mitra, A.P.; Althausen, D.; Anderson, L.M.; Andreae, M.O.; Cantrell, W.; Cass, G.R.; Chung, E.; et al. Indian Ocean Experiment: An integrated analysis of the climate forcing and effects of the great Indo-Asian haze. J. Geophys. Res. Space Phys. 2001, 106, 28371–28398. [Google Scholar] [CrossRef]
  55. Rajeev, K.; Ramanathan, V. The Indian ocean experiment: Aerosol forcing obtained from satellite data. Adv. Space Res. 2002, 29, 1731–1740. [Google Scholar] [CrossRef]
  56. Gordon, H.R.; Du, T.; Zhang, T. Remote sensing of ocean color and aerosol properties: Resolving the issue of aerosol absorption. Appl. Opt. 1997, 36, 8670–8684. [Google Scholar] [CrossRef]
  57. Moulin, C.; Gordon, H.R.; Banzon, V.F.; Evans, R.H. Assessment of Saharan dust absorption in the visible from SeaWiFS imagery. J. Geophys. Res. Space Phys. 2001, 106, 18239–18249. [Google Scholar] [CrossRef]
  58. Satheesh, S.K.; Moorthy, K.K.; Das, I. Aerosol spectral optical depths over the Bay of Bengal, Arabian Sea and Indian Ocean. Curr. Sci. 2001, 81, 1617–1625. [Google Scholar] [CrossRef]
  59. Satheesh, S.K. Radiative forcing by aerosols over Bay of Bengal region. Geophys. Res. Lett. 2002, 29, 2083. [Google Scholar] [CrossRef]
  60. Vinoj, V.; Satheesh, S.K. Measurements of aerosol optical depth over Arabian Sea during summer monsoon season. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
  61. Gordon, H.R. Atmospheric correction of ocean color imagery in the Earth Observing System era. J. Geophys. Res. Space Phys. 1997, 102, 17081–17106. [Google Scholar] [CrossRef]
  62. Barnes, B.B.; Hu, C. Dependence of satellite ocean color data products on viewing angles: A comparison between Sea-WiFS, MODIS, and VIIRS. Remote Sens. Environ. 2016, 175, 120–129. [Google Scholar] [CrossRef]
  63. Morel, A.; Gentili, B. Practical application of the “turbid water” flag in ocean color imagery: Interference with sun-glint contaminated pixels in open ocean. Remote Sens. Environ. 2008, 112, 934–938. [Google Scholar] [CrossRef]
  64. Steinmetz, F.; Deschamps, P.-Y.; Ramon, D. Atmospheric correction in presence of sun glint: Application to MERIS. Opt. Express 2011, 19, 9783–9800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  65. Gregg, W.W.; Conkright, M.E. Global seasonal climatologies of ocean chlorophyll: Blending in situ and satellite data for the Coastal Zone Color Scanner era. J. Geophys. Res. Space Phys. 2001, 106, 2499–2515. [Google Scholar] [CrossRef]
  66. Wang, M.; Bailey, S.W. Correction of Sun glint Contamination on the SeaWiFS Ocean and Atmosphere Products. Appl. Opt. 2001, 40, 4790–4798. [Google Scholar] [CrossRef] [PubMed]
  67. Harmel, T.; Chami, M. Estimation of the sunglint radiance field from optical satellite imagery over open ocean: Multidi-rectional approach and polarization aspects. J. Geophys. Res. Oceans 2013, 118, 76–90. [Google Scholar] [CrossRef] [Green Version]
  68. Kay, S.; Hedley, J.D.; Lavender, S. Sun glint correction of high and low spatial resolution images of aquatic scenes: A re-view of methods for visible and near-infrared wavelengths. Remote Sens. 2009, 1, 697–730. [Google Scholar] [CrossRef] [Green Version]
  69. Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
  70. Gower, J.F.R.; King, S.; Goncalves, P. Global monitoring of plankton blooms using MERIS MCI. Int. J. Remote Sens. 2008, 29, 6209–6216. [Google Scholar] [CrossRef]
  71. Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
  72. O’Reilly, J.E.; Maritorena, S.; O’brien, M.C.; Siegel, D.A.; Toole, D.; Menzies, D.; Chavez, F.P. SeaWiFS postlaunch cal-ibration and validation analyses, part 3. NASA Tech. Memo 2000, 206892, 3–8. [Google Scholar]
  73. Mannino, A.; Russ, M.E.; Hooker, S.B. Algorithm development and validation for satellite-derived distributions of DOC and CDOM in the U.S. Middle Atlantic Bight. J. Geophys. Res. Space Phys. 2008, 113, 7. [Google Scholar] [CrossRef]
Remotesensing 13 00184 g001 550
Figure 1. Study area and in situ Rrs(λ) measurement stations (green triangles) along four transects of 0°, 5° S, 10° S, and 88° E (red dashed lines). Annual average of the global chlorophyll a concentration from Moderate Resolution Imaging Spectroradiometer (MODIS)-Aqua in 2016 is overlaid on the map. The dotted rectangle outlines the oligotrophic gyre in the south Indian Ocean characterized by the extremely low chlorophyll a concentration (Chla) (typically ≤0.1 mg/m3).
Figure 1. Study area and in situ Rrs(λ) measurement stations (green triangles) along four transects of 0°, 5° S, 10° S, and 88° E (red dashed lines). Annual average of the global chlorophyll a concentration from Moderate Resolution Imaging Spectroradiometer (MODIS)-Aqua in 2016 is overlaid on the map. The dotted rectangle outlines the oligotrophic gyre in the south Indian Ocean characterized by the extremely low chlorophyll a concentration (Chla) (typically ≤0.1 mg/m3).
Remotesensing 13 00184 g001
Remotesensing 13 00184 g002 550
Figure 2. Measured Rrs(λ) spectra at 21 stations in the Indian Ocean (IO) from a cruise in December 2016.
Figure 2. Measured Rrs(λ) spectra at 21 stations in the Indian Ocean (IO) from a cruise in December 2016.
Remotesensing 13 00184 g002
Remotesensing 13 00184 g003 550
Figure 3. Monthly QA scores of MODIS–Aqua level 3 Rrs(λ) products from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Figure 3. Monthly QA scores of MODIS–Aqua level 3 Rrs(λ) products from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Remotesensing 13 00184 g003
Remotesensing 13 00184 g004 550
Figure 4. Monthly averaged scores (left y–axis, red squares) of MODIS–Aqua (a), VIIRS–NPP (b) and MODIS–Terra (c,d) level 3 Rrs(λ) products over the IO in 2016. The valid data coverage (open symbols, right y–axis) is overlaid. The low–quality bands (P(λi) < 75%) for each satellite dataset (if any) are also shown.
Figure 4. Monthly averaged scores (left y–axis, red squares) of MODIS–Aqua (a), VIIRS–NPP (b) and MODIS–Terra (c,d) level 3 Rrs(λ) products over the IO in 2016. The valid data coverage (open symbols, right y–axis) is overlaid. The low–quality bands (P(λi) < 75%) for each satellite dataset (if any) are also shown.
Remotesensing 13 00184 g004
Remotesensing 13 00184 g005 550
Figure 5. Rrs(λ) QA scores at blue bands (412 nm and 443 nm) of MODIS–Aqua (a,d), MODIS–Terra (b,e), and VIIRS–NPP (c,f) in October, 2016. The red color represents score of 0 (low–quality data) and blue color represents score of 1 (high quality data). The white color represents invalid pixels. The yellow rectangles roughly outline the location of the oligotrophic gyre zone in the southern Indian Ocean.
Figure 5. Rrs(λ) QA scores at blue bands (412 nm and 443 nm) of MODIS–Aqua (a,d), MODIS–Terra (b,e), and VIIRS–NPP (c,f) in October, 2016. The red color represents score of 0 (low–quality data) and blue color represents score of 1 (high quality data). The white color represents invalid pixels. The yellow rectangles roughly outline the location of the oligotrophic gyre zone in the southern Indian Ocean.
Remotesensing 13 00184 g005
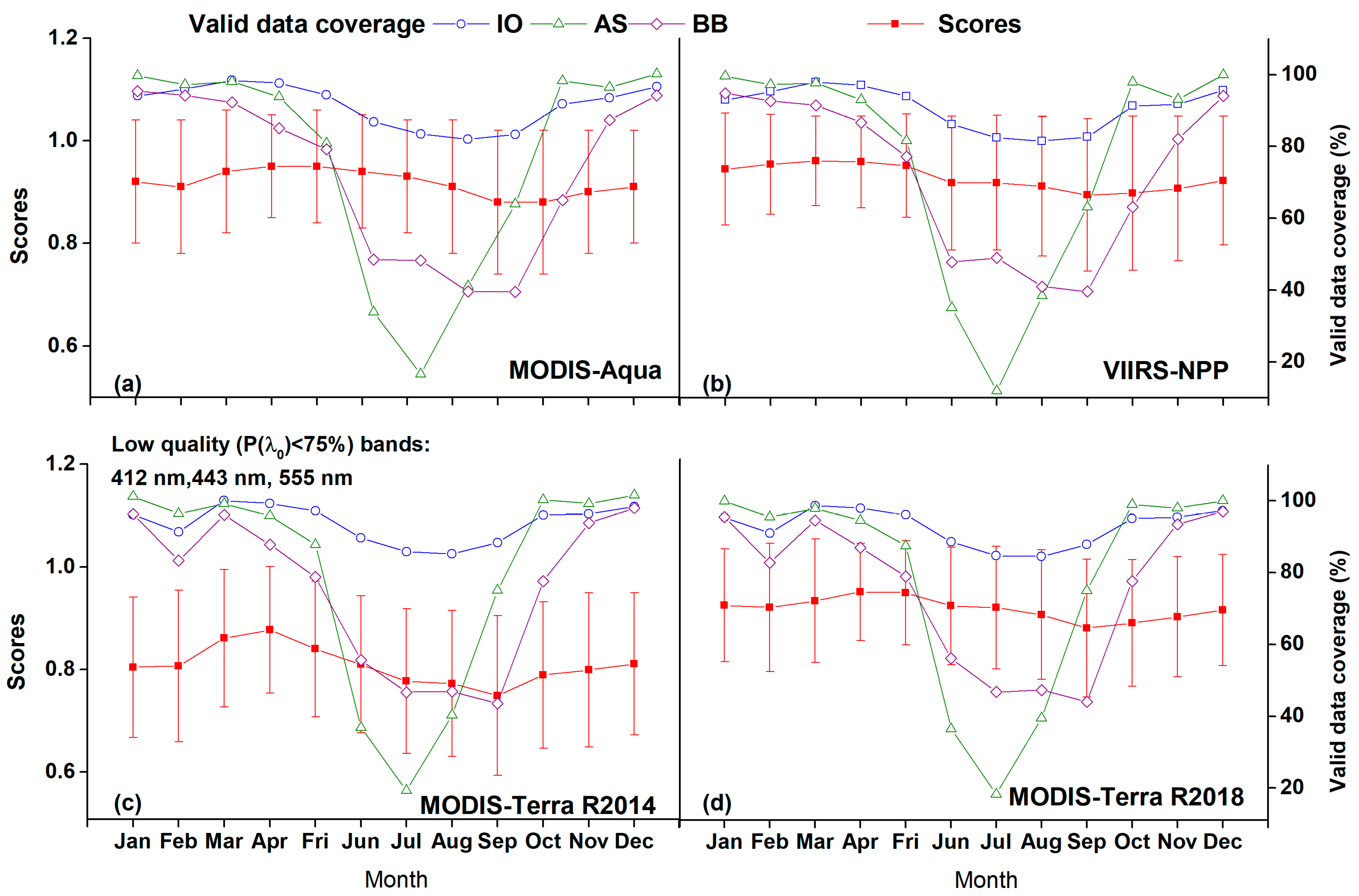
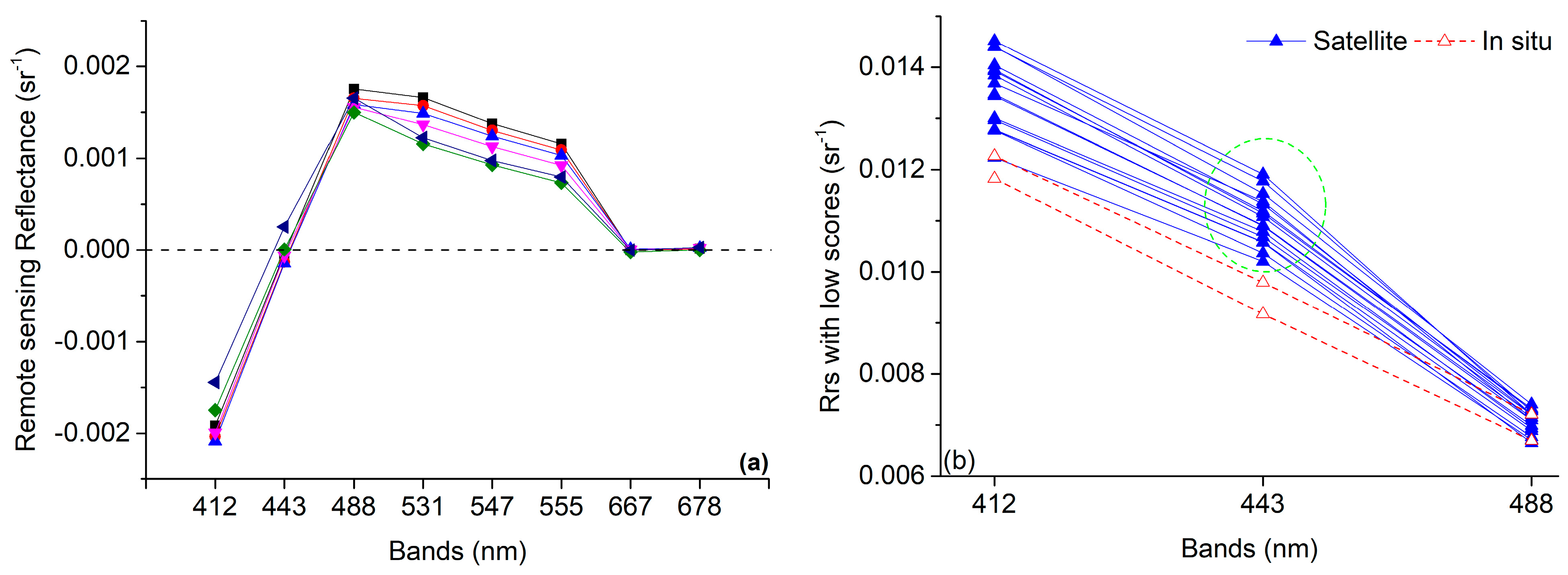
Remotesensing 13 00184 g006 550
Figure 6. Samples of low quality Rrs(λ) spectra derived from MODIS–Aqua, in the BB (scores < 0.3) characterized by negative values at 412 nm and 443 nm bands (a), and in the OZ (scores < 0.7) compared with in situ measured Rrs(λ) spectra (b).
Figure 6. Samples of low quality Rrs(λ) spectra derived from MODIS–Aqua, in the BB (scores < 0.3) characterized by negative values at 412 nm and 443 nm bands (a), and in the OZ (scores < 0.7) compared with in situ measured Rrs(λ) spectra (b).
Remotesensing 13 00184 g006
Remotesensing 13 00184 g007 550
Figure 7. Monthly QA scores of MODIS–Terra level 3 Rrs(λ) products (R2018) from January (a) to December (l) in 2016 in the IO. White color represents invalid pixels.
Figure 7. Monthly QA scores of MODIS–Terra level 3 Rrs(λ) products (R2018) from January (a) to December (l) in 2016 in the IO. White color represents invalid pixels.
Remotesensing 13 00184 g007
Remotesensing 13 00184 g008 550
Figure 8. Monthly QA scores of MODIS–Terra level 3 Rrs(λ) products (R2014) from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Figure 8. Monthly QA scores of MODIS–Terra level 3 Rrs(λ) products (R2014) from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Remotesensing 13 00184 g008
Remotesensing 13 00184 g009 550
Figure 9. QA Scores of VIIRS–NPP level 3 Rrs(λ) monthly products from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Figure 9. QA Scores of VIIRS–NPP level 3 Rrs(λ) monthly products from January (a) to December (l) in 2016 in the IO. The white color represents invalid pixels.
Remotesensing 13 00184 g009
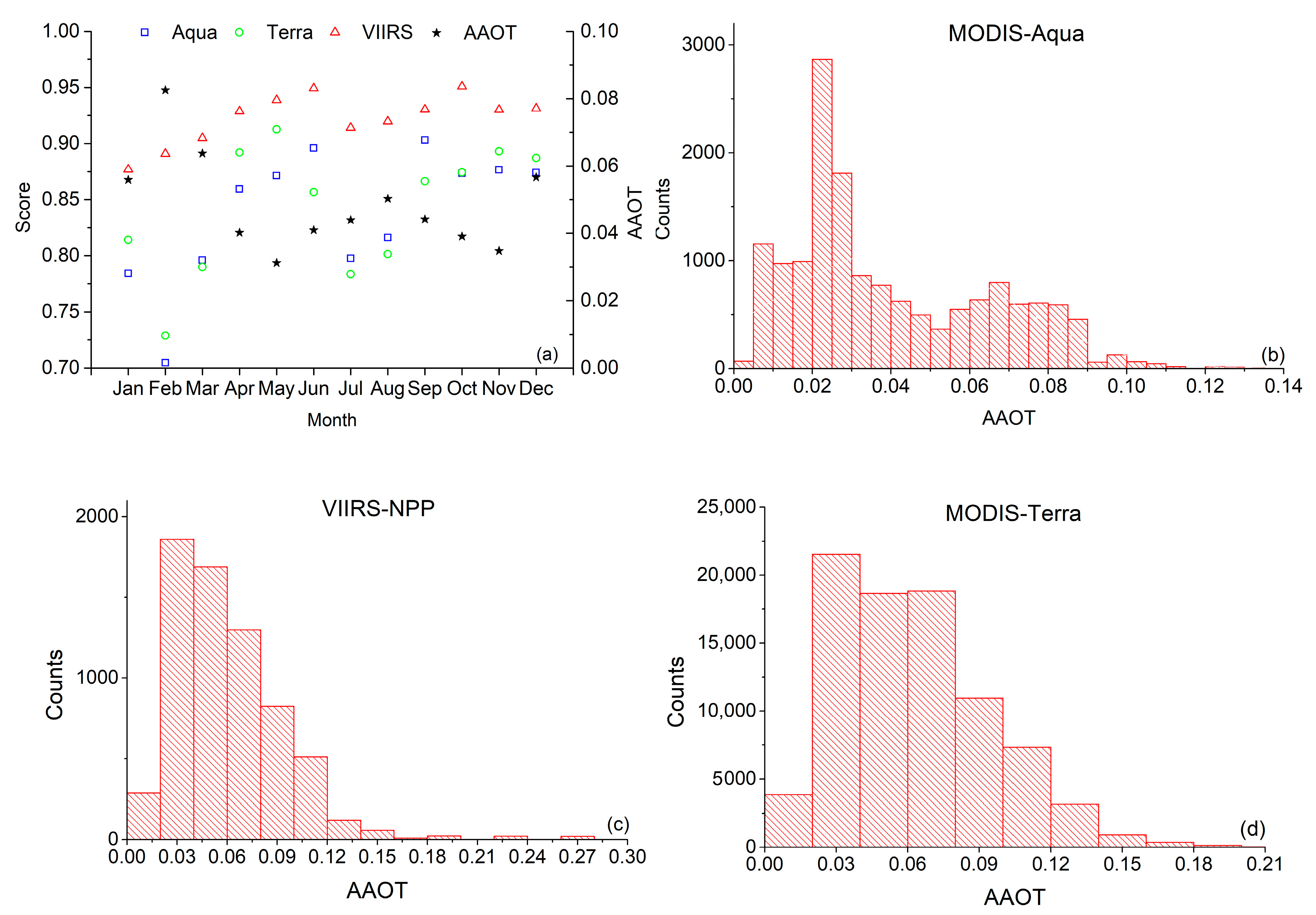
Remotesensing 13 00184 g010 550
Figure 10. Monthly absorption aerosol optical depth (AAOD) and QA score in the BB, which shows significant negative correlation between AAOD and score (a). Histogram of AAODs corresponding to the low quality (score < 0.5) pixels of MODIS–Aqua (b), VIIRS–NPP (c), and MODIS–Terra (d) daily Rrs(λ) products of BB in February.
Figure 10. Monthly absorption aerosol optical depth (AAOD) and QA score in the BB, which shows significant negative correlation between AAOD and score (a). Histogram of AAODs corresponding to the low quality (score < 0.5) pixels of MODIS–Aqua (b), VIIRS–NPP (c), and MODIS–Terra (d) daily Rrs(λ) products of BB in February.
Remotesensing 13 00184 g010
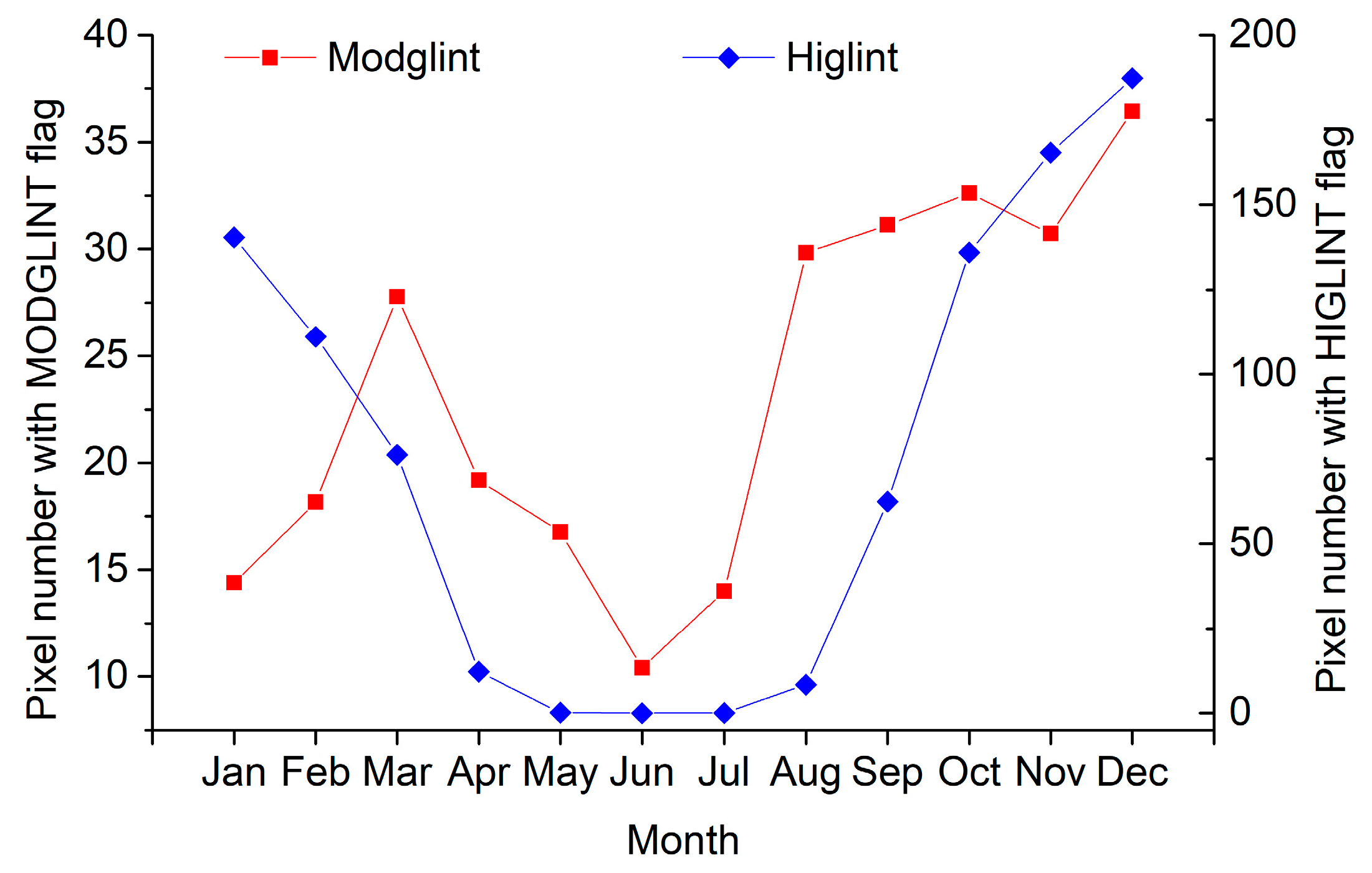
Remotesensing 13 00184 g011 550
Figure 11. Pixel numbers of level 2 Rrs(λ) with “MODGLINT” and “HIGLINT” flags corresponding to each level 3 pixel.
Figure 11. Pixel numbers of level 2 Rrs(λ) with “MODGLINT” and “HIGLINT” flags corresponding to each level 3 pixel.
Remotesensing 13 00184 g011
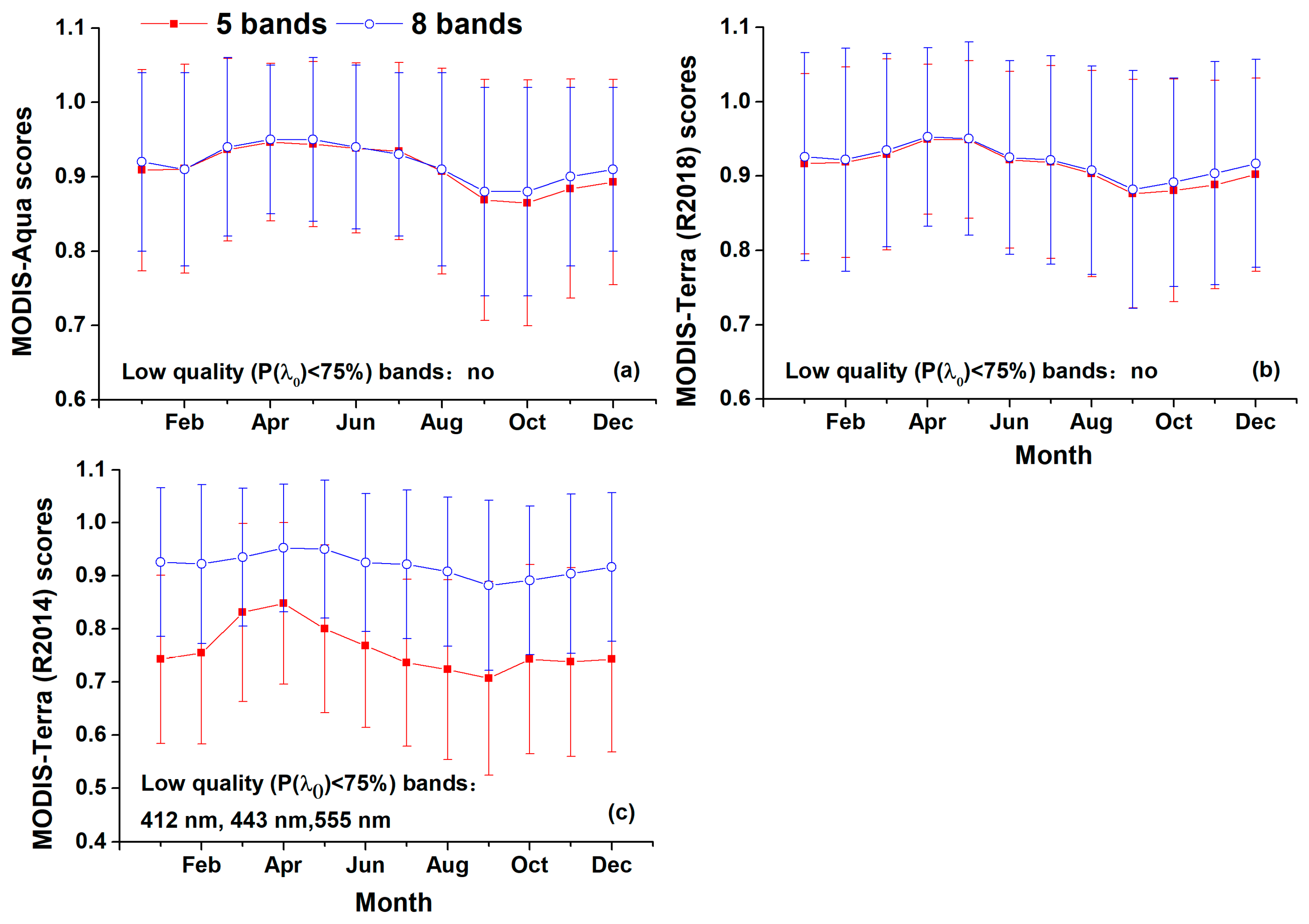
Remotesensing 13 00184 g012 550
Figure 12. Comparison between Rrs(λ) QA scores based on 5-band (red) and 8-band (purple) for MODIS-Aqua (a), MODIS-Terra (2018) (b), and MODIS-Terra (2014) (c).
Figure 12. Comparison between Rrs(λ) QA scores based on 5-band (red) and 8-band (purple) for MODIS-Aqua (a), MODIS-Terra (2018) (b), and MODIS-Terra (2014) (c).
Remotesensing 13 00184 g012
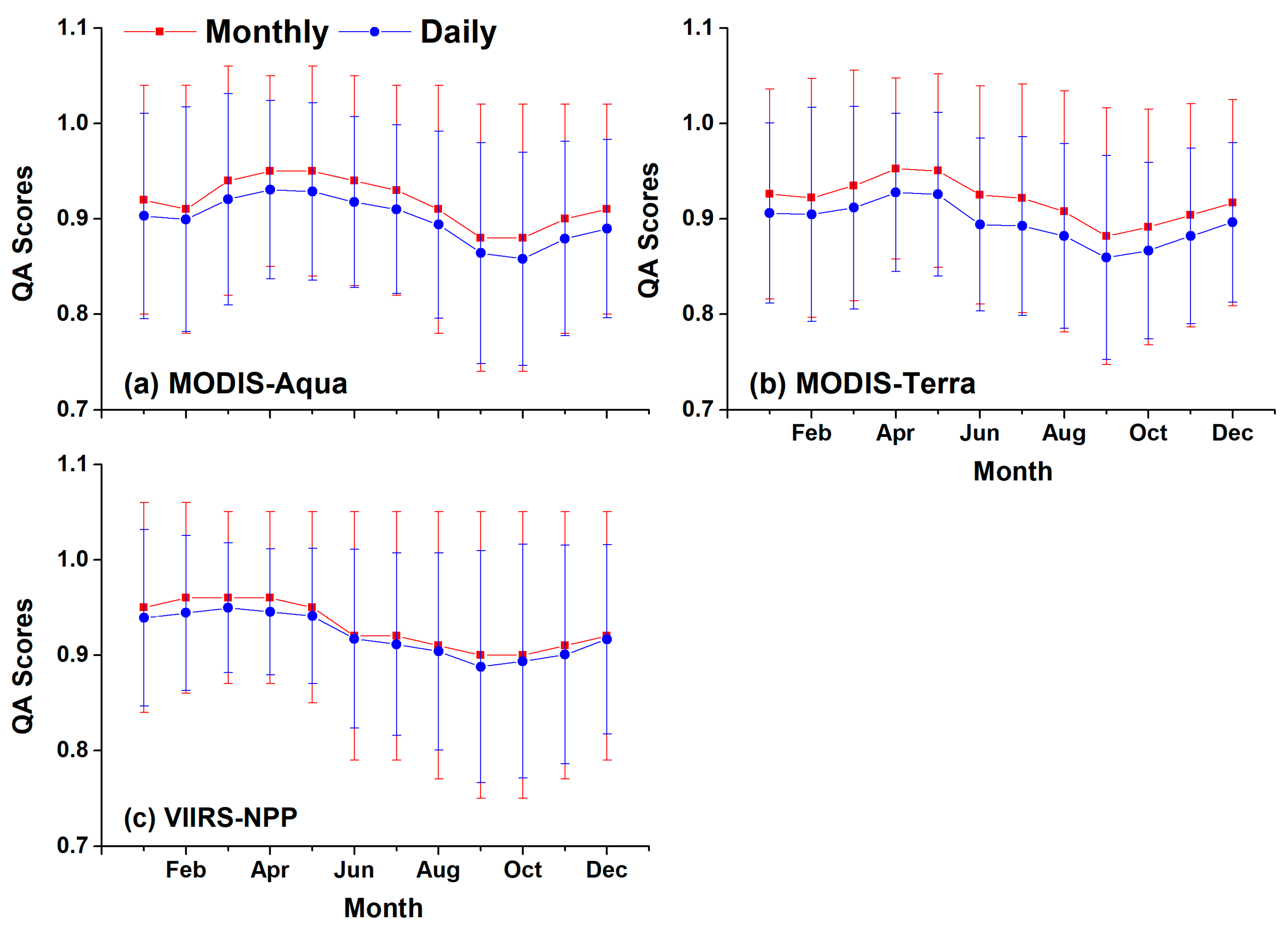
Remotesensing 13 00184 g013 550
Figure 13. Comparison between QA scores based on level 3 daily and monthly Rrs(λ) products from MODIS-Aqua (a), MODIS-Terra (b), and VIIRS-NPP (c).
Figure 13. Comparison between QA scores based on level 3 daily and monthly Rrs(λ) products from MODIS-Aqua (a), MODIS-Terra (b), and VIIRS-NPP (c).
Remotesensing 13 00184 g013
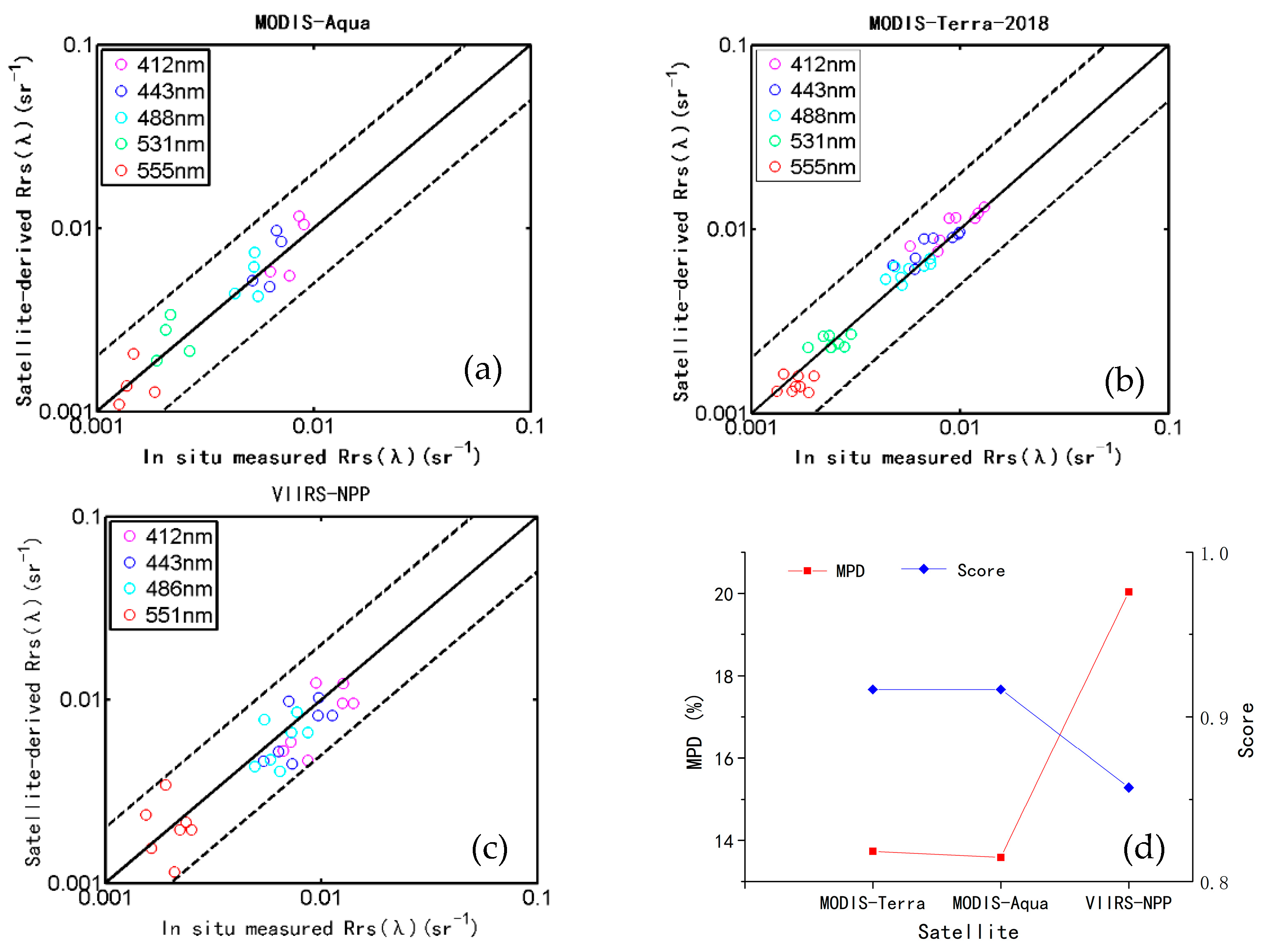
Remotesensing 13 00184 g014 550
Figure 14. Scatter plots of the satellite–derived Rrs(λ) versus in situ measurements (a–c). Solid line is 1:1 line. Dashed lines are 1:2 and 2:1 lines. The average scores and median absolute percent difference (MPD) of MODIS–Aqua, MODIS–Terra (R2018), and VIIRS–NPP level 2 Rrs(λ) products concurrent with in situ measurements (d).
Figure 14. Scatter plots of the satellite–derived Rrs(λ) versus in situ measurements (a–c). Solid line is 1:1 line. Dashed lines are 1:2 and 2:1 lines. The average scores and median absolute percent difference (MPD) of MODIS–Aqua, MODIS–Terra (R2018), and VIIRS–NPP level 2 Rrs(λ) products concurrent with in situ measurements (d).
Remotesensing 13 00184 g014
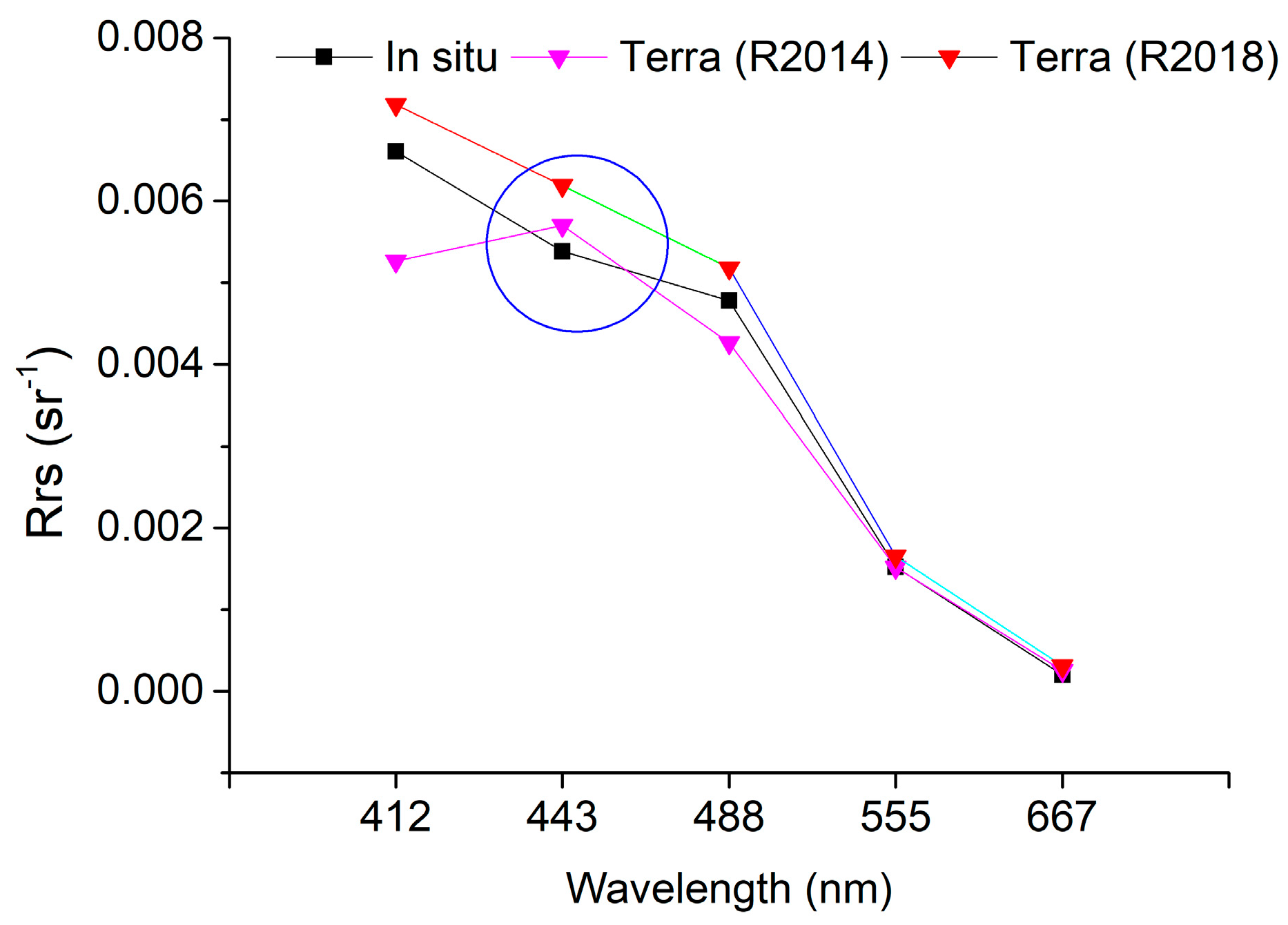
Remotesensing 13 00184 g015 550
Figure 15. Example of direct spectral comparison between in situ measurement and satellite retrievals at a match-up site. In this case, MODIS-Terra (R2014) fails to retrieve the actual spectral shape of Rrs(λ) and gets the lower QA score than MODIS-Terra (R2018), although its agreement with in situ data at all bands except for 412 nm band is good.
Figure 15. Example of direct spectral comparison between in situ measurement and satellite retrievals at a match-up site. In this case, MODIS-Terra (R2014) fails to retrieve the actual spectral shape of Rrs(λ) and gets the lower QA score than MODIS-Terra (R2018), although its agreement with in situ data at all bands except for 412 nm band is good.
Remotesensing 13 00184 g015
Table
Table 1. Scores and their standard deviations over the study area of MODIS-Aqua, MODIS-Terra (Versions R2018 and R2014) and VIIRS-NPP level 3 Rrs(λ) monthly products based on quality assurance (QA) method (Formula (1)), with 1 for a perfect spectrum and 0 for an unusable spectrum. Numbers in bold are the annual maximum and minimum of monthly scores. IO, BB, AS, and OZ represent the Indian Ocean, Bengal Bay, Arabian Sea and oligotrophic gyre zone in the southern Indian Ocean, respectively.
Table 1. Scores and their standard deviations over the study area of MODIS-Aqua, MODIS-Terra (Versions R2018 and R2014) and VIIRS-NPP level 3 Rrs(λ) monthly products based on quality assurance (QA) method (Formula (1)), with 1 for a perfect spectrum and 0 for an unusable spectrum. Numbers in bold are the annual maximum and minimum of monthly scores. IO, BB, AS, and OZ represent the Indian Ocean, Bengal Bay, Arabian Sea and oligotrophic gyre zone in the southern Indian Ocean, respectively.
AreaSensorJanuaryFebruaryMarchAprilMayJuneJulyAugustSeptemberOctoberNovemberDecemberAverage
IOMODIS-Aqua0.92 ± 0.120.91 ± 0.130.94 ± 0.120.95 ± 0.100.95 ± 0.110.94 ± 0.110.93 ± 0.110.91 ± 0.130.88 ± 0.140.88 ± 0.140.90 ± 0.120.91 ± 0.110.92 ± 0.12
MODIS-Terra R20140.80 ± 0.140.81 ± 0.150.86 ± 0.130.88 ± 0.120.84 ± 0.130.81 ± 0.130.78 ± 0.140.77 ± 0.140.75 ± 0.160.79 ± 0.140.80 ± 0.150.81 ± 0.140.81 ± 0.14
MODIS-Terra R20180.93 ± 0.110.92 ± 0.130.93 ± 0.120.95 ± 0.090.95 ± 0.10.92 ± 0.110.92 ± 0.120.91 ± 0.130.88 ± 0.130.89 ± 0.120.90 ± 0.120.92 ± 0.110.92 ± 0.12
VIIRS-NPP0.95 ± 0.110.96 ± 0.10.96 ± 0.090.96 ± 0.090.95 ± 0.10.92 ± 0.130.92 ± 0.130.91 ± 0.140.90 ± 0.150.90 ± 0.150.91 ± 0.140.92 ± 0.130.93 ± 0.12
BBMODIS-Aqua0.78 ± 0.190.70 ± 0.210.80 ± 0.20.86 ± 0.170.87 ± 0.160.90 ± 0.140. 80 ± 0.180.82 ± 0.170.90 ± 0.130.87 ± 0.150.88 ± 0.150.87 ± 0.150.83 ± 0.18
MODIS-Terra R20140.60 ± 0.160.55 ± 0.180.67 ± 0.160.76 ± 0.150.76 ± 0.150.74 ± 0.140.64 ± 0.170.65 ± 0.170.72 ± 0.140.70 ± 0.140.70 ± 0.150.69 ± 0.150.68 ± 0.16
MODIS-Terra R20180.81 ± 0.160.73 ± 0.190.79 ± 0.190.89 ± 0.150.91 ± 0.130.86 ± 0.150.78 ± 0.170.08 ± 0.170.87 ± 0.140.87 ± 0.130.89 ± 0.140.89 ± 0.130.84 ± 0.17
VIIRS-NPP0.88 ± 0.150.89 ± 0.130.9 ± 0.120.93 ± 0.120.94 ± 0.110.95 ± 0.10.91 ± 0.130.92 ± 0.110.93 ± 0.120.95 ± 0.10.93 ± 0.120.93 ± 0.110.92 ± 0.12
ASMODIS-Aqua0.93 ± 0.110.91 ± 0.130.86 ± 0.160.89 ± 0.140.87 ± 0.170.78 ± 0.190.83 ± 0.170.84 ± 0.180.83 ± 0.170.89 ± 0.140.87 ± 0.150.91 ± 0.130.88 ± 0.15
MODIS-Terra R20140.71 ± 0.120.72 ± 0.140.72 ± 0.140.77 ± 0.140.76 ± 0.180.68 ± 0.160.65 ± 0.160.67 ± 0.160.66 ± 0.160.75 ± 0.170.66 ± 0.170.70 ± 0.140.71 ± 0.15
MODIS-Terra R20180.92 ± 0.10.90 ± 0.130.85 ± 0.160.09 ± 0.120.88 ± 0.160.78 ± 0.160.79 ± 0.170.82 ± 0.160.83 ± 0.160.89 ± 0.120.88 ± 0.130.92 ± 0.120.88 ± 0.14
VIIRS-NPP0.96 ± 0.090.95 ± 0.10.94 ± 0.10.96 ± 0.080.96 ± 0.090.92 ± 0.130.94 ± 0.120.93 ± 0.120.93 ± 0.110.95 ± 0.10.93 ± 0.120.94 ± 0.110.95 ± 0.10
OZMODIS-Aqua0.95 ± 0.090.96 ± 0.070.99 ± 0.041.00 ± 0.030.99 ± 0.040.96 ± 0.080.94 ± 0.10.87 ± 0.130.79 ± 0.130.78 ± 0.110.88 ± 0.090.90 ± 0.080.92 ± 0.11
MODIS-Terra R20140.86 ± 0.090.88 ± 0.100.95 ± 0.070.95 ± 0.080.85 ± 0.110.76 ± 0.110.73 ± 0.110.75 ± 0.100.74 ± 0.110.77 ± 0.100.83 ± 0.100.85 ± 0.100.83 ± 0.10
MODIS-Terra R20180.96 ± 0.070.98 ± 0.070.99 ± 0.050.99 ± 0.040.99 ± 0.050.95 ± 0.090.92 ± 0.110.89 ± 0.130.83 ± 0.130.81 ± 0.110.88 ± 0.10.91 ± 0.080.92 ± 0.11
VIIRS-NPP0.95 ± 0.10.98 ± 0.060.99 ± 0.040.98 ± 0.070.95 ± 0.110.83 ± 0.160.83 ± 0.160.81 ± 0.170.78 ± 0.180.74 ± 0.170.81 ± 0.160.86 ± 0.130.88 ± 0.16
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Liu, R.; Zhang, J.; Cui, T.; Yu, H. Impact of Monsoon-Transported Anthropogenic Aerosols and Sun-Glint on the Satellite-Derived Spectral Remote Sensing Reflectance in the Indian Ocean. Remote Sens. 2021, 13, 184. https://doi.org/10.3390/rs13020184

AMA Style

Liu R, Zhang J, Cui T, Yu H. Impact of Monsoon-Transported Anthropogenic Aerosols and Sun-Glint on the Satellite-Derived Spectral Remote Sensing Reflectance in the Indian Ocean. Remote Sensing. 2021; 13(2):184. https://doi.org/10.3390/rs13020184

Chicago/Turabian Style

Liu, Rongjie, Jie Zhang, Tingwei Cui, and Haocheng Yu. 2021. "Impact of Monsoon-Transported Anthropogenic Aerosols and Sun-Glint on the Satellite-Derived Spectral Remote Sensing Reflectance in the Indian Ocean" Remote Sensing 13, no. 2: 184. https://doi.org/10.3390/rs13020184

APA Style

Liu, R., Zhang, J., Cui, T., & Yu, H. (2021). Impact of Monsoon-Transported Anthropogenic Aerosols and Sun-Glint on the Satellite-Derived Spectral Remote Sensing Reflectance in the Indian Ocean. Remote Sensing, 13(2), 184. https://doi.org/10.3390/rs13020184

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop