A Density-Based Algorithm for the Detection of Individual Trees from LiDAR Data
Abstract
:1. Introduction
2. Data and Method
2.1. Study Site and Available Data
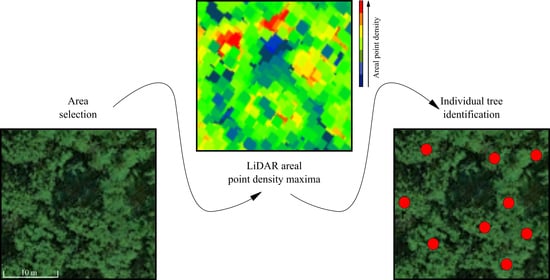
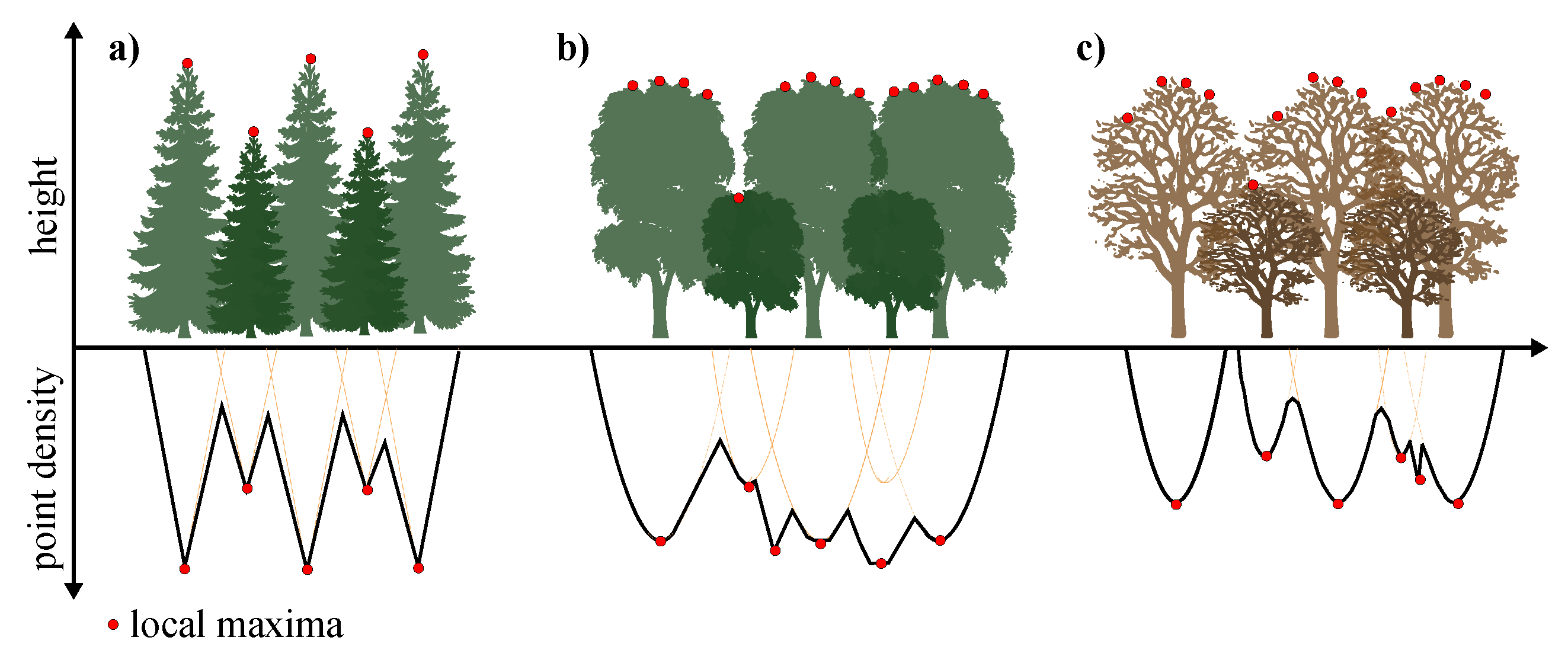
2.2. Presentation of the Algorithm
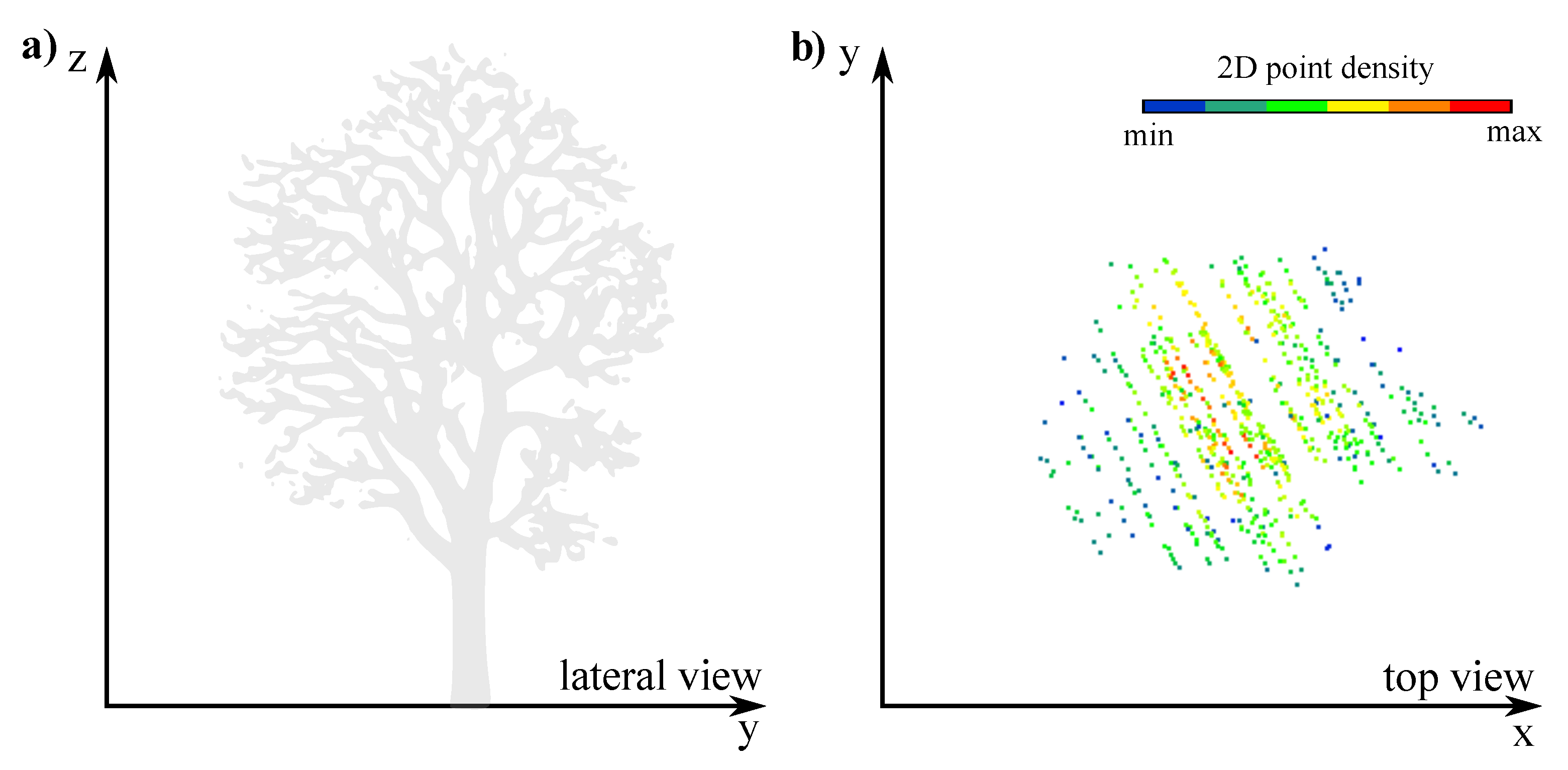
2.2.1. Pre-Processing
2.2.2. Workflow
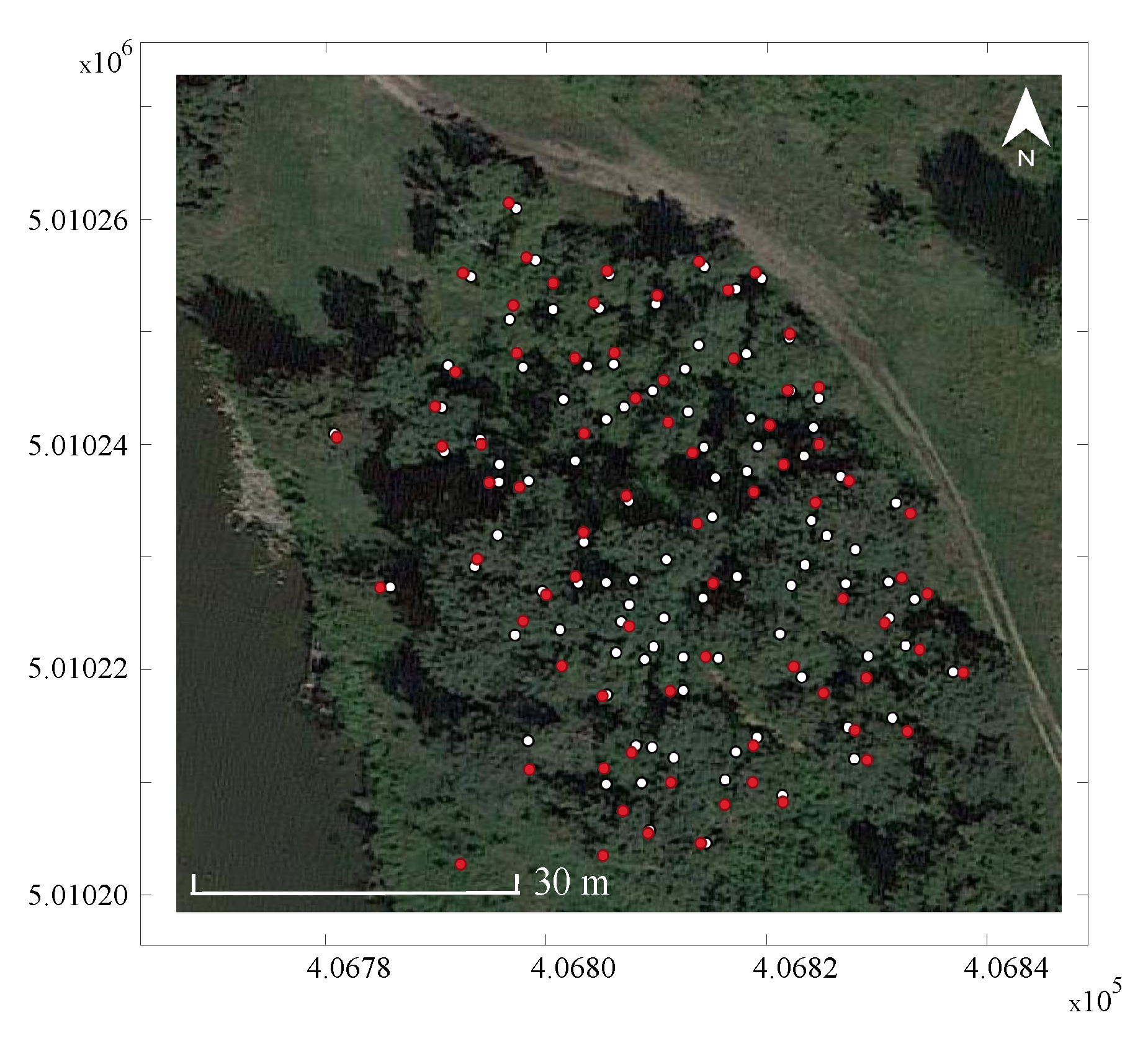
2.3. Accuracy Assessment
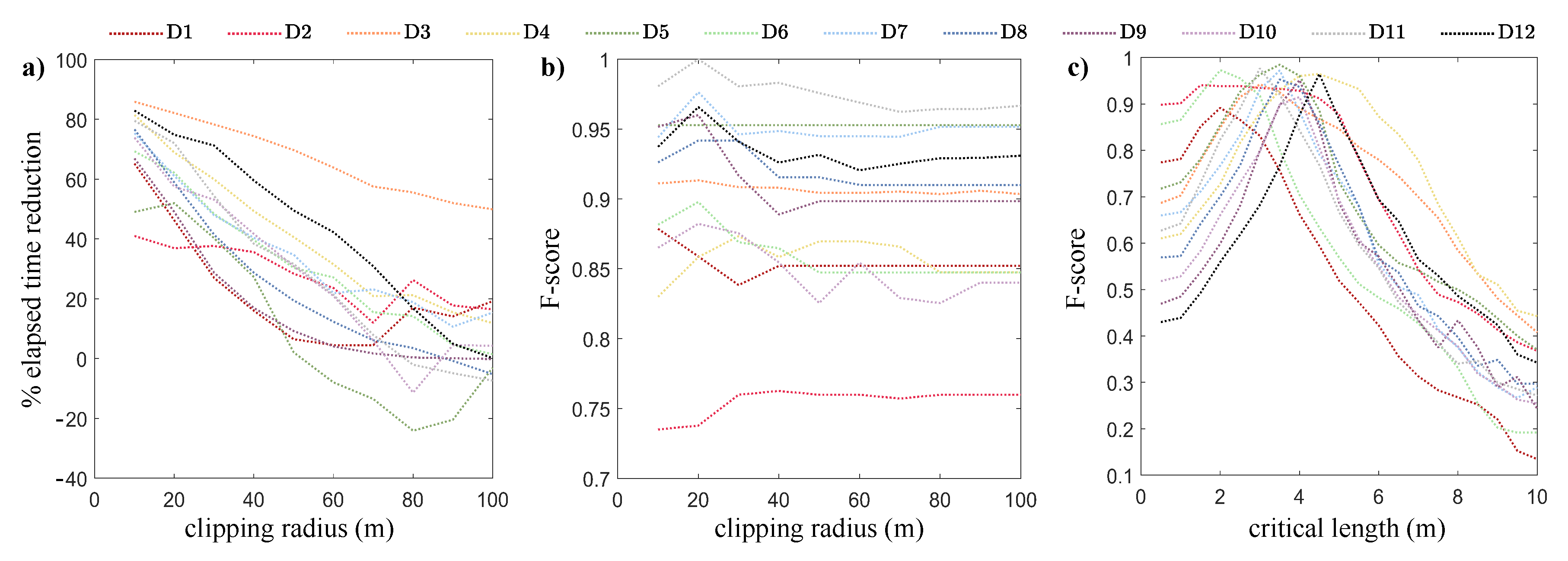
2.4. Sensitivity Analysis and the Parameter Setting
2.5. Application to Re-Sampled Point Clouds
3. Results
3.1. Algorithm Performance
3.2. Sensitivity Analysis Results
3.3. Re-Sampling Results
4. Discussion
4.1. Data for the Algorithm’s Application
4.2. Achieved Accuracy and the Influence of Data Quality
4.3. The Influence of the Parameter Setting
4.4. Cloud Re-Sampling and Low-Resolution Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Airborne Laser Scanning |
| CHM | Canopy Height Model |
| GIS | Geographic Information System |
| GPS | Global Positioning System |
| LiDAR | Light Detection And Ranging |
| RTK | Real Time Kinematic |
| TLS | Terrestrial Laser Scanning |
Appendix A. Algorithm Setup

References
- Flood, M. Laser altimetry: From science to commerical lidar mapping. Photogramm. Eng. Remote Sens. 2001, 67, 1209–1211, 1213–1217. [Google Scholar]
- Lindberg, E.; Holmgren, J. Individual tree crown methods for 3D data from remote sensing. Curr. For. Rep. 2017, 3, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Andújar, D.; Escolà, A.; Rosell-Polo, J.R.; Fernández-Quintanilla, C.; Dorado, J. Potential of a terrestrial LiDAR-based system to characterise weed vegetation in maize crops. Comput. Electron. Agric. 2013, 92, 11–15. [Google Scholar] [CrossRef] [Green Version]
- Eitel, J.U.; Magney, T.S.; Vierling, L.A.; Brown, T.T.; Huggins, D.R. LiDAR based biomass and crop nitrogen estimates for rapid, non-destructive assessment of wheat nitrogen status. Field Crops Res. 2014, 159, 21–32. [Google Scholar] [CrossRef]
- Reutebuch, S.E.; McGaughey, R.J.; Andersen, H.E.; Carson, W.W. Accuracy of a high-resolution lidar terrain model under a conifer forest canopy. Can. J. Remote Sens. 2003, 29, 527–535. [Google Scholar] [CrossRef]
- Klemas, V. Beach profiling and LIDAR bathymetry: An overview with case studies. J. Coast. Res. 2011, 27, 1019–1028. [Google Scholar] [CrossRef]
- Vastaranta, M.; Kantola, T.; Lyytikäinen-Saarenmaa, P.; Holopainen, M.; Kankare, V.; Wulder, M.A.; Hyyppä, J.; Hyyppä, H. Area-based mapping of defoliation of Scots pine stands using airborne scanning LiDAR. Remote Sens. 2013, 5, 1220–1234. [Google Scholar] [CrossRef] [Green Version]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sens. 2000, 66, 1367–1372. [Google Scholar]
- Li, Y.; Andersen, H.E.; McGaughey, R. A comparison of statistical methods for estimating forest biomass from light detection and ranging data. West. J. Appl. For. 2008, 23, 223–231. [Google Scholar] [CrossRef] [Green Version]
- Dalponte, M.; Reyes, F.; Kandare, K.; Gianelle, D. Delineation of individual tree crowns from ALS and hyperspectral data: A comparison among four methods. Eur. J. Remote Sens. 2015, 48, 365–382. [Google Scholar] [CrossRef] [Green Version]
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The utility of image-based point clouds for forest inventory: A comparison with airborne laser scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef] [Green Version]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q. Airborne lidar data processing and information extraction. Photogramm. Eng. Remote Sens. 2007, 73, 109. [Google Scholar]
- Andersen, H.E.; Reutebuch, S.E.; Schreuder, G.F. Automated individual tree measurement through morphological analysis of a LIDAR-based canopy surface model. In Proceedings of the 1st International Precision Forestry Symposium, Seattle, WA, USA, 17–20 June 2001; pp. 11–21. [Google Scholar]
- Lee, A.C.; Lucas, R.M. A LiDAR-derived canopy density model for tree stem and crown mapping in Australian forests. Remote Sens. Environ. 2007, 111, 493–518. [Google Scholar] [CrossRef]
- Coomes, D.A.; Dalponte, M.; Jucker, T.; Asner, G.P.; Banin, L.F.; Burslem, D.F.; Lewis, S.L.; Nilus, R.; Phillips, O.L.; Phua, M.H.; et al. Area-based vs tree-centric approaches to mapping forest carbon in Southeast Asian forests from airborne laser scanning data. Remote Sens. Environ. 2017, 194, 77–88. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-based and individual tree-based methods for predicting plot-level forest attributes. Remote Sens. 2010, 2, 1481–1495. [Google Scholar] [CrossRef] [Green Version]
- González-Ferreiro, E.; Diéguez-Aranda, U.; Barreiro-Fernández, L.; Buján, S.; Barbosa, M.; Suárez, J.C.; Bye, I.J.; Miranda, D. A mixed pixel-and region-based approach for using airborne laser scanning data for individual tree crown delineation in Pinus radiata D. Don plantations. Int. J. Remote Sens. 2013, 34, 7671–7690. [Google Scholar] [CrossRef]
- Corona, P.; Fattorini, L. Area-based lidar-assisted estimation of forest standing volume. Can. J. For. Res. 2008, 38, 2911–2916. [Google Scholar] [CrossRef] [Green Version]
- Magnussen, S.; Næsset, E.; Gobakken, T.; Frazer, G. A fine-scale model for area-based predictions of tree-size-related attributes derived from LiDAR canopy heights. Scand. J. For. Res. 2012, 27, 312–322. [Google Scholar] [CrossRef]
- Duncanson, L.; Dubayah, R. Monitoring individual tree-based change with airborne lidar. Ecol. Evol. 2018, 8, 5079–5089. [Google Scholar] [CrossRef]
- Rönnholm, P.; Hyyppä, J.; Hyyppä, H.; Haggrén, H.; Yu, X.; Kaartinen, H. Calibration of laser-derived tree height estimates by means of photogrammetric techniques. Scand. J. For. Res. 2004, 19, 524–528. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef] [Green Version]
- Kandare, K.; Ørka, H.O.; Chan, J.C.W.; Dalponte, M. Effects of forest structure and airborne laser scanning point cloud density on 3D delineation of individual tree crowns. Eur. J. Remote Sens. 2016, 49, 337–359. [Google Scholar] [CrossRef] [Green Version]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens. 2001, 39, 969–975. [Google Scholar] [CrossRef]
- Persson, A.; Holmgren, J.; Soderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sens. 2002, 68, 925–932. [Google Scholar]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ. 2003, 85, 290–303. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef] [Green Version]
- Heurich, M.; Weinacker, H. Automated tree detection and measurement in temperate forests of central Europe using laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 8. [Google Scholar]
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive methods for individual tree detection on airborne laser based canopy height model. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 187–191. [Google Scholar]
- Weinacker, H.; Koch, B.; Heyder, U.; Weinacker, R. Development of filtering, segmentation and modeling modules for lidar and multispectral data as a fundament of an automatic forest inventory system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef] [Green Version]
- Solberg, S.; Naesset, E.; Bollandsas, O.M. Single tree segmentation using airborne laser scanner data in a structurally heterogeneous spruce forest. Photogramm. Eng. Remote Sens. 2006, 72, 1369–1378. [Google Scholar] [CrossRef]
- Pang, Y.; Lefsky, M.; Andersen, H.E.; Miller, M.; Sherrill, K. Validation of the ICEsat vegetation product using crown-area-weighted mean height derived using crown delineation with discrete return lidar data. Can. J. Remote Sens. 2008, 34, S471–S484. [Google Scholar] [CrossRef]
- Maltamo, M.; Peuhkurinen, J.; Malinen, J.; Vauhkonen, J.; Packalén, P.; Tokola, T. Predicting tree attributes and quality characteristics of Scots pine using airborne laser scanning data. Silva Fenn. 2009, 43, 507–521. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Ene, L.; Næsset, E.; Gobakken, T. Single tree detection in heterogeneous boreal forests using airborne laser scanning and area-based stem number estimates. Int. J. Remote Sens. 2012, 33, 5171–5193. [Google Scholar] [CrossRef]
- Jing, L.; Hu, B.; Li, J.; Noland, T. Automated delineation of individual tree crowns from LiDAR data by multi-scale analysis and segmentation. Photogramm. Eng. Remote Sens. 2012, 78, 1275–1284. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.A.; Hudak, A.T.; Vierling, L.A.; Loudermilk, E.L.; O’Brien, J.J.; Hiers, J.K.; Jack, S.B.; Gonzalez-Benecke, C.; Lee, H.; Falkowski, M.J.; et al. Imputation of individual longleaf pine (Pinus palustris Mill.) tree attributes from field and LiDAR data. Can. J. Remote Sens. 2016, 42, 554–573. [Google Scholar] [CrossRef]
- Bian, Y.; Zou, P.; Shu, Y.; Yu, R. Individual tree delineation in deciduous forest areas with LiDAR point clouds. Can. J. Remote Sens. 2014, 40, 152–163. [Google Scholar] [CrossRef]
- Hirata, Y.; Furuya, N.; Suzuki, M.; Yamamoto, H. Airborne laser scanning in forest management: Individual tree identification and laser pulse penetration in a stand with different levels of thinning. For. Ecol. Manag. 2009, 258, 752–760. [Google Scholar] [CrossRef]
- Duncanson, L.; Cook, B.; Hurtt, G.; Dubayah, R. An efficient, multi-layered crown delineation algorithm for mapping individual tree structure across multiple ecosystems. Remote Sens. Environ. 2014, 154, 378–386. [Google Scholar] [CrossRef]
- Zhao, D.; Pang, Y.; Li, Z.; Liu, L. Isolating individual trees in a closed coniferous forest using small footprint lidar data. Int. J. Remote Sens. 2014, 35, 7199–7218. [Google Scholar] [CrossRef]
- Kwak, D.A.; Lee, W.K.; Lee, J.H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. For. Res. 2007, 12, 425–434. [Google Scholar] [CrossRef]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens. 2003, 29, 633–649. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Smith, A.M.; Hudak, A.T.; Gessler, P.E.; Vierling, L.A.; Crookston, N.L. Automated estimation of individual conifer tree height and crown diameter via two-dimensional spatial wavelet analysis of lidar data. Can. J. Remote Sens. 2006, 32, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Yu, B.; Wu, Q.; Huang, Y.; Chen, Z.; Wu, J. Individual tree crown delineation using localized contour tree method and airborne LiDAR data in coniferous forests. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 82–94. [Google Scholar] [CrossRef]
- Rahman, M.; Gorte, B. Tree crown delineation from high resolution airborne lidar based on densities of high points. In Proceedings of the ISPRS Workshop Laserscanning 2009, ISPRS XXXVIII (3/W8), Paris, France, 1–2 September 2009. [Google Scholar]
- Richardson, J.J.; Moskal, L.M. Strengths and limitations of assessing forest density and spatial configuration with aerial LiDAR. Remote Sens. Environ. 2011, 115, 2640–2651. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Li, J.; Jing, L.; Judah, A. Improving the efficiency and accuracy of individual tree crown delineation from high-density LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 145–155. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. An efficient approach to 3D single tree-crown delineation in LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 108, 219–233. [Google Scholar] [CrossRef]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
- Holmgren, J.; Lindberg, E. Tree crown segmentation based on a geometric tree crown model for prediction of forest variables. Can. J. Remote Sens. 2013, 39, S86–S98. [Google Scholar] [CrossRef]
- Holmgren, J.; Lindberg, E. Tree crown segmentation based on a tree crown density model derived from Airborne Laser Scanning. Remote Sens. Lett. 2019, 10, 1143–1152. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A bottom-up approach to segment individual deciduous trees using leaf-off lidar point cloud data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- Tiede, D.; Hochleitner, G.; Blaschke, T. A full GIS-based workflow for tree identification and tree crown delineation using laser scanning. In Proceedings of the ISPRS Workshop CMRT, Vienna, Austria, 29–30 August 2005; Volume 5. [Google Scholar]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W., Jr. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
- Véga, C.; Hamrouni, A.; El Mokhtari, S.; Morel, J.; Bock, J.; Renaud, J.P.; Bouvier, M.; Durrieu, S. PTrees: A point-based approach to forest tree extraction from lidar data. Int. J. Appl. Earth Obs. Geoinf. 2014, 33, 98–108. [Google Scholar] [CrossRef]
- Ayrey, E.; Fraver, S.; Kershaw, J.A., Jr.; Kenefic, L.S.; Hayes, D.; Weiskittel, A.R.; Roth, B.E. Layer stacking: A novel algorithm for individual forest tree segmentation from LiDAR point clouds. Can. J. Remote Sens. 2017, 43, 16–27. [Google Scholar] [CrossRef]
- Ma, Z.; Pang, Y.; Wang, D.; Liang, X.; Chen, B.; Lu, H.; Weinacker, H.; Koch, B. Individual Tree Crown Segmentation of a Larch Plantation Using Airborne Laser Scanning Data Based on Region Growing and Canopy Morphology Features. Remote Sens. 2020, 12, 1078. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.; Gorte, B. Individual tree detection based on densities of high points of high resolution airborne LiDAR. In Proceedings of the GEOBIA, 2008—Pixels, Objects, Intelligence: GEOgraphic Object Based Image Analysis for the 21st Century, Calgary, AB, Canada, 5–8 August 2008; University of Calgary: Calgary, AB, Canada, 2008; pp. 350–355. [Google Scholar]
- Rahman, M.; Gorte, B. Tree filtering for high density airborne LiDAR data. In Proceedings of the International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008. [Google Scholar]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-D mapping of a multi-layered Mediterranean forest using ALS data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Paris, C.; Valduga, D.; Bruzzone, L. A hierarchical approach to three-dimensional segmentation of LiDAR data at single-tree level in a multilayered forest. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4190–4203. [Google Scholar] [CrossRef]
- Zhen, Z.; Quackenbush, L.J.; Zhang, L. Trends in automatic individual tree crown detection and delineation—Evolution of LiDAR data. Remote Sens. 2016, 8, 333. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Yang, B.; Dong, Z.; Shaker, A. A new method for 3D individual tree extraction using multispectral airborne LiDAR point clouds. ISPRS J. Photogramm. Remote Sens. 2018, 144, 400–411. [Google Scholar] [CrossRef]
- Gupta, S.; Weinacker, H.; Koch, B. Comparative analysis of clustering-based approaches for 3-D single tree detection using airborne fullwave lidar data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef] [Green Version]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppä, J.; Kaartinen, H.; Kukko, A.; Holopainen, M. Automatic plot-wise tree location mapping using single-scan terrestrial laser scanning. Photogramm. J. Finl. 2011, 22, 37–48. [Google Scholar]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the RANSAC algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef] [Green Version]
- Trochta, J.; Krůček, M.; Vrška, T.; Král, K. 3D Forest: An application for descriptions of three-dimensional forest structures using terrestrial LiDAR. PLoS ONE 2017, 12, e0176871. [Google Scholar] [CrossRef] [Green Version]
- Kuželka, K.; Slavík, M.; Surovỳ, P. Very High Density Point Clouds from UAV Laser Scanning for Automatic Tree Stem Detection and Direct Diameter Measurement. Remote Sens. 2020, 12, 1236. [Google Scholar] [CrossRef] [Green Version]
- Roussel, J.R.; Caspersen, J.; Béland, M.; Thomas, S.; Achim, A. Removing bias from LiDAR-based estimates of canopy height: Accounting for the effects of pulse density and footprint size. Remote Sens. Environ. 2017, 198, 1–16. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A probabilistic interpretation of precision, recall and F-score, with implication for evaluation. In Proceedings of the European Conference on Information Retrieval, Santiago de Compostela, Spain, 21–23 March 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar]
- Bechtold, W.A. Crown-diameter prediction models for 87 species of stand-grown trees in the eastern United States. South. J. Appl. For. 2003, 27, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Pretzsch, H.; Biber, P.; Uhl, E.; Dahlhausen, J.; Rötzer, T.; Caldentey, J.; Koike, T.; Van Con, T.; Chavanne, A.; Seifert, T.; et al. Crown size and growing space requirement of common tree species in urban centers, parks, and forests. Urban For. Urban Green. 2015, 14, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Graham, A.N.; Coops, N.C.; Tompalski, P.; Plowright, A.; Wilcox, M. Effect of ground surface interpolation methods on the accuracy of forest attribute modeling using unmanned aerial systems-based digital aerial photogrammetry. Int. J. Remote Sens. 2020, 41, 3287–3306. [Google Scholar] [CrossRef]
- Habib, M.; Alzubi, Y.; Malkawi, A.; Awwad, M. Impact of interpolation techniques on the accuracy of large-scale digital elevation model. Open Geosci. 2020, 12, 190–202. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, L.; Chen, Q.; Wang, G.; Luo, P.; Sharma, R.P.; He, P.; Li, M.; Wang, M.; Duan, G. Analysis of the Spatial Differences in Canopy Height Models from UAV LiDAR and Photogrammetry. Remote Sens. 2020, 12, 2884. [Google Scholar] [CrossRef]
- Lovell, J.; Jupp, D.; Newnham, G.; Coops, N.; Culvenor, D. Simulation study for finding optimal lidar acquisition parameters for forest height retrieval. For. Ecol. Manag. 2005, 214, 398–412. [Google Scholar] [CrossRef]
- Holmgren, J.; Nilsson, M.; Olsson, H. Simulating the effects of lidar scanning angle for estimation of mean tree height and canopy closure. Can. J. Remote Sens. 2003, 29, 623–632. [Google Scholar] [CrossRef]
- Gaulton, R.; Malthus, T.J. LiDAR mapping of canopy gaps in continuous cover forests: A comparison of canopy height model and point cloud based techniques. Int. J. Remote Sens. 2010, 31, 1193–1211. [Google Scholar] [CrossRef]
- Disney, M.I.; Kalogirou, V.; Lewis, P.; Prieto-Blanco, A.; Hancock, S.; Pfeifer, M. Simulating the impact of discrete-return lidar system and survey characteristics over young conifer and broadleaf forests. Remote Sens. Environ. 2010, 114, 1546–1560. [Google Scholar] [CrossRef]
- Keränen, J.; Maltamo, M.; Packalen, P. Effect of flying altitude, scanning angle and scanning mode on the accuracy of ALS based forest inventory. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 349–360. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Jones, S.; Wang, T.; Heurich, M.; Zhu, X.; Shi, Y. Large off-nadir scan angle of airborne LiDAR can severely affect the estimates of forest structure metrics. ISPRS J. Photogramm. Remote Sens. 2018, 136, 13–25. [Google Scholar] [CrossRef]
- Mielcarek, M.; Stereńczak, K.; Khosravipour, A. Testing and evaluating different LiDAR-derived canopy height model generation methods for tree height estimation. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 132–143. [Google Scholar] [CrossRef]
- García, M.; Riaño, D.; Chuvieco, E.; Danson, F.M. Estimating biomass carbon stocks for a Mediterranean forest in central Spain using LiDAR height and intensity data. Remote Sens. Environ. 2010, 114, 816–830. [Google Scholar] [CrossRef]
- Mitchell, B.; Walterman, M.; Mellin, T.; Wilcox, C.; Lynch, A.M.; Anhold, J.; Falk, D.A.; Koprowski, J.; Laes, D.; Evans, D.; et al. Mapping vegetation structure in the Pinaleño Mountains using lidar-phase 3: Forest inventory modeling. In RSAC-100007-RPT1; US Department of Agriculture, Forest Service, Remote Sensing Applications Center: Salt Lake City, UT, USA, 2012; 17p. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. BioScience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Gaveau, D.L.; Hill, R.A. Quantifying canopy height underestimation by laser pulse penetration in small-footprint airborne laser scanning data. Can. J. Remote Sens. 2003, 29, 650–657. [Google Scholar] [CrossRef]
- Meng, X.; Currit, N.; Zhao, K. Ground filtering algorithms for airborne LiDAR data: A review of critical issues. Remote Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef] [Green Version]
- Parkan, M. Digital Forestry Toolbox for Matlab/Octave. Zenodo. 2018. Available online: https://zenodo.org/badge/latestdoi/58712667 (accessed on 27 August 2020).
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote sensing technologies for enhancing forest inventories: A review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef] [Green Version]
- Camporeale, C.; Ridolfi, L. Noise-induced phenomena in riparian vegetation dynamics. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Vesipa, R.; Camporeale, C.; Ridolfi, L. Noise-driven cooperative dynamics between vegetation and topography in riparian zones. Geophys. Res. Lett. 2015, 42, 8021–8030. [Google Scholar] [CrossRef] [Green Version]
- Latella, M.; Bertagni, M.B.; Vezza, P.; Camporeale, C. An integrated methodology to study riparian vegetation dynamics: From field data to impact modeling. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002094. [Google Scholar] [CrossRef] [PubMed]
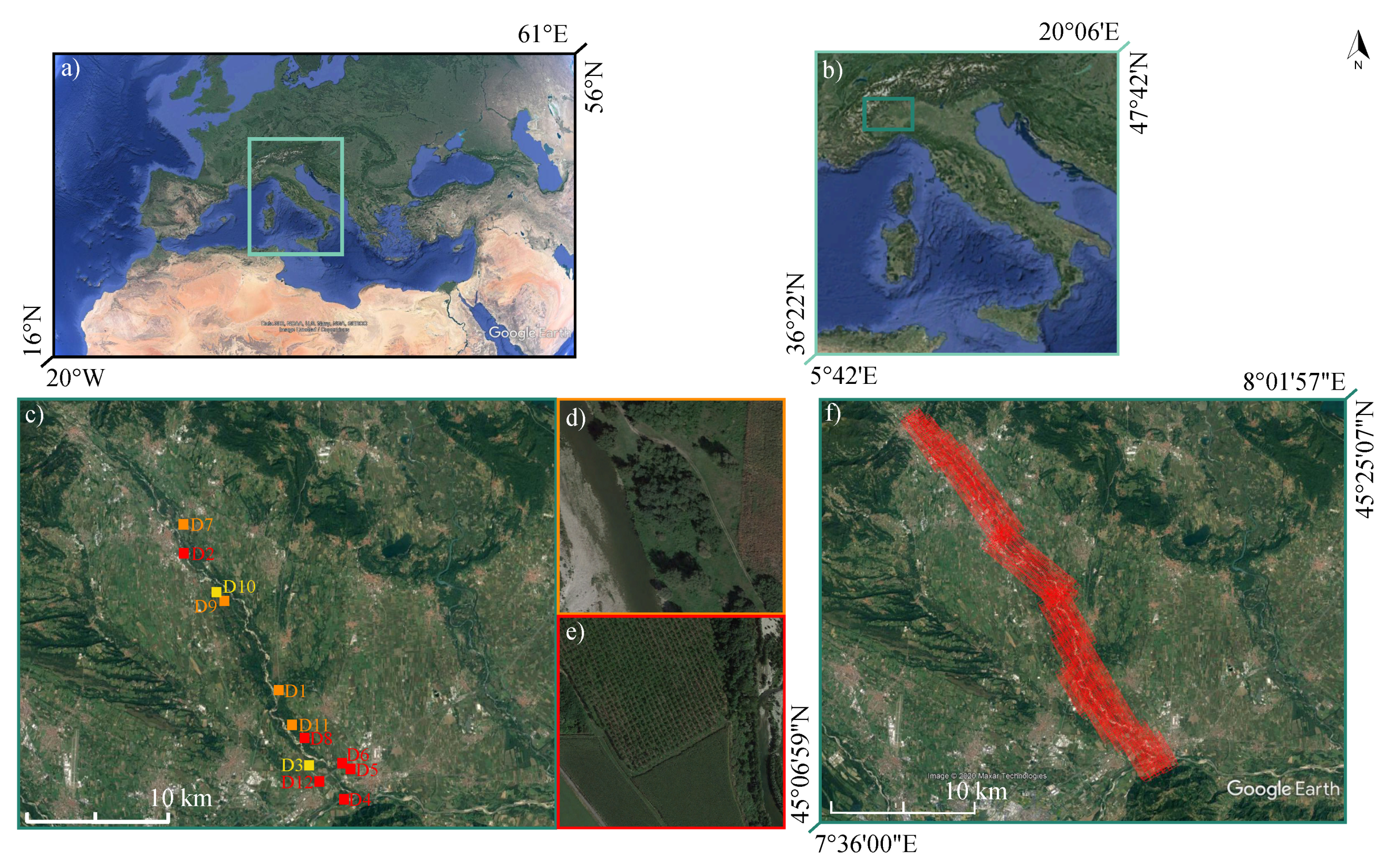




| Area ID | Coordinates | Tree | Tree | Tree | Perimeter | Area | Point | Notes |
|---|---|---|---|---|---|---|---|---|
| Pattern | Species | Age | (m) | (ha) | Density | |||
| D1 | 451422.27N; | random | Populus spp., | mature | 240 | 0.41 | 8.7 ± 4.4 | - |
| 074845.10E | Robinia Ps. | |||||||
| D2 | 451901.73N; | regular | Populus spp. | various | 620 | 2.40 | 7.5 ± 4.2 | - |
| 074416.98E | ||||||||
| D3 | 451206.02N; | mixed | Populus spp. | young | 834 | 4.39 | 8.7 ± 3.7 | - |
| 075026.61E | ||||||||
| D4 | 451058.61N; | regular | Populus spp. | various | 332 | 0.68 | 5.8 ± 2.1 | a warehouse |
| 075207.15E | 4 × 4 ×2 m | |||||||
| D5 | 451144.09N; | regular | Populus spp. | mature | 313 | 0.40 | 10.2 ± 3.4 | - |
| 075136.33E | ||||||||
| D6 | 451140.61N; | regular | Populus spp. | mature | 308 | 0.57 | 9.6 ± 3.6 | - |
| 075138.04E | ||||||||
| D7 | 452002.58N; | random | Populus spp. | various | 339 | 0.62 | 13.5 ± 7.5 | fence |
| 074401.05E | height: 2.5 m | |||||||
| D8 | 451225.45N; | regular | Populus spp., | mature | 316 | 0.41 | 17.8 ± 8.1 | - |
| 075032.02E | Quercus spp. | |||||||
| D9 | 451806.05N; | random | Robinia Ps. | mature | 250 | 0.27 | 10.1 ± 5.4 | power lines |
| 074603.51E | ||||||||
| D10 | 451808.24N; | mixed | Populus spp., | mature | 357 | 0.81 | 8.2 ± 4.6 | - |
| 074559.95E | Robinia Ps. | |||||||
| D11 | 451234.08N | random | Populus spp., | mature | 435 | 1.20 | 11.9 ± 7.2 | - |
| 075006.51E | Quercus spp. | |||||||
| D12 | 451206.08N; | regular | Populus spp. | mature | 572 | 1.93 | 8.7 ± 3.8 | - |
| 075026.58E |
| Area ID | # of Trees | # of Detected Trees | Recall | Precision | F-Score | Position Error (m) | Stem-to-Top Distance (m) | ||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | |||||||
| D1 | 98 | 76 | 0.78 | 0.96 | 0.86 | 1.25 | 0 | 2.12 | 0.79 |
| D2 | 284 | 166 | 0.58 | 1.00 | 0.74 | 0.80 | 0 | 2.08 | 0.63 |
| D3 | 543 | 620 | 1.00 | 0.84 | 0.92 | 0.81 | 0 | 2.06 | 0.62 |
| D4 | 102 | 133 | 1.00 | 0.75 | 0.86 | 0.86 | 0 | 1.67 | 0.65 |
| D5 | 132 | 144 | 1.00 | 0.91 | 0.95 | 0.82 | 0 | 1.79 | 0.53 |
| D6 | 151 | 123 | 0.81 | 1.00 | 0.90 | 0.74 | 0 | 1.35 | 0.54 |
| D7 | 130 | 125 | 0.96 | 0.99 | 0.98 | 0.78 | 0 | 1.70 | 0.66 |
| D8 | 109 | 97 | 0.89 | 1.00 | 0.94 | 1.00 | 0 | 1.31 | 0.60 |
| D9 | 65 | 60 | 0.92 | 1.00 | 0.96 | 0.91 | 0 | 1.19 | 0.56 |
| D10 | 185 | 147 | 0.79 | 0.99 | 0.78 | 0.91 | 0 | 1.91 | 0.55 |
| D11 | 210 | 210 | 1.00 | 1.00 | 1.00 | 0.73 | 0 | 1.50 | 0.63 |
| D12 | 305 | 317 | 1.00 | 0.93 | 0.97 | 0.86 | 0 | 1.83 | 0.70 |
| Area ID | Elapsed Time (s) | Number of Points |
|---|---|---|
| D1 | 41.87 | 19,510 |
| D2 | 4.28 | 4500 |
| D3 | 195.09 | 97,568 |
| D4 | 36.55 | 24,679 |
| D5 | 11.42 | 9995 |
| D6 | 17.43 | 13,391 |
| D7 | 142.93 | 45,617 |
| D8 | 59.91 | 29,935 |
| D9 | 34.75 | 15,860 |
| D10 | 55.00 | 31,865 |
| D11 | 123.91 | 58,808 |
| D12 | 413.62 | 127,192 |
| Area ID | Real Spacing (m) | Optimal Spacing (m) | Computed Spacing (m) |
|---|---|---|---|
| D1 | 2.5 | 2.0 | 2.8 |
| D2 | 6.0 | 1.5 | 5.8 |
| D3 | 3.0 | 3.0 | 2.5 |
| D4 | 8.0 | 4.0 | 2.8 |
| D5 | 5.0 | 3.5 | 2.8 |
| D6 | 2.5 | 2.0 | 3.1 |
| D7 | 3.5 | 3.5 | 3.3 |
| D8 | 3.5 | 3.5 | 3.8 |
| D9 | 4.0 | 4.0 | 4.1 |
| D10 | 4.0 | 4.0 | 4.2 |
| D11 | 3.0 | 3.0 | 3.1 |
| D12 | 5.0 | 4.5 | 4.4 |
| Advantages | Limitations | Notes |
|---|---|---|
| Low sensitivity to the tree spatial arrangement and the presence of understory vegetation. | Better performance in homogenous stands. | Splitting of datasets into homogenous areas before its application. |
| Working on the entire point clouds. | Long computation time for high number of input points. | In the case of large datasets, algorithm’s parallelization or dataset’s sub-sampling. |
| Requiring 2 points·m as minimum point density | Worse performance if dealing with local data inaccuracies | Data quality inspection before its application. |
| Good accuracy with the default parameter setting. | Necessity of field calibration for the derived treetops height. | Visual inspection of the study areas before its application. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Latella, M.; Sola, F.; Camporeale, C. A Density-Based Algorithm for the Detection of Individual Trees from LiDAR Data. Remote Sens. 2021, 13, 322. https://doi.org/10.3390/rs13020322
Latella M, Sola F, Camporeale C. A Density-Based Algorithm for the Detection of Individual Trees from LiDAR Data. Remote Sensing. 2021; 13(2):322. https://doi.org/10.3390/rs13020322
Chicago/Turabian StyleLatella, Melissa, Fabio Sola, and Carlo Camporeale. 2021. "A Density-Based Algorithm for the Detection of Individual Trees from LiDAR Data" Remote Sensing 13, no. 2: 322. https://doi.org/10.3390/rs13020322
APA StyleLatella, M., Sola, F., & Camporeale, C. (2021). A Density-Based Algorithm for the Detection of Individual Trees from LiDAR Data. Remote Sensing, 13(2), 322. https://doi.org/10.3390/rs13020322