Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China
Abstract
:1. Introduction
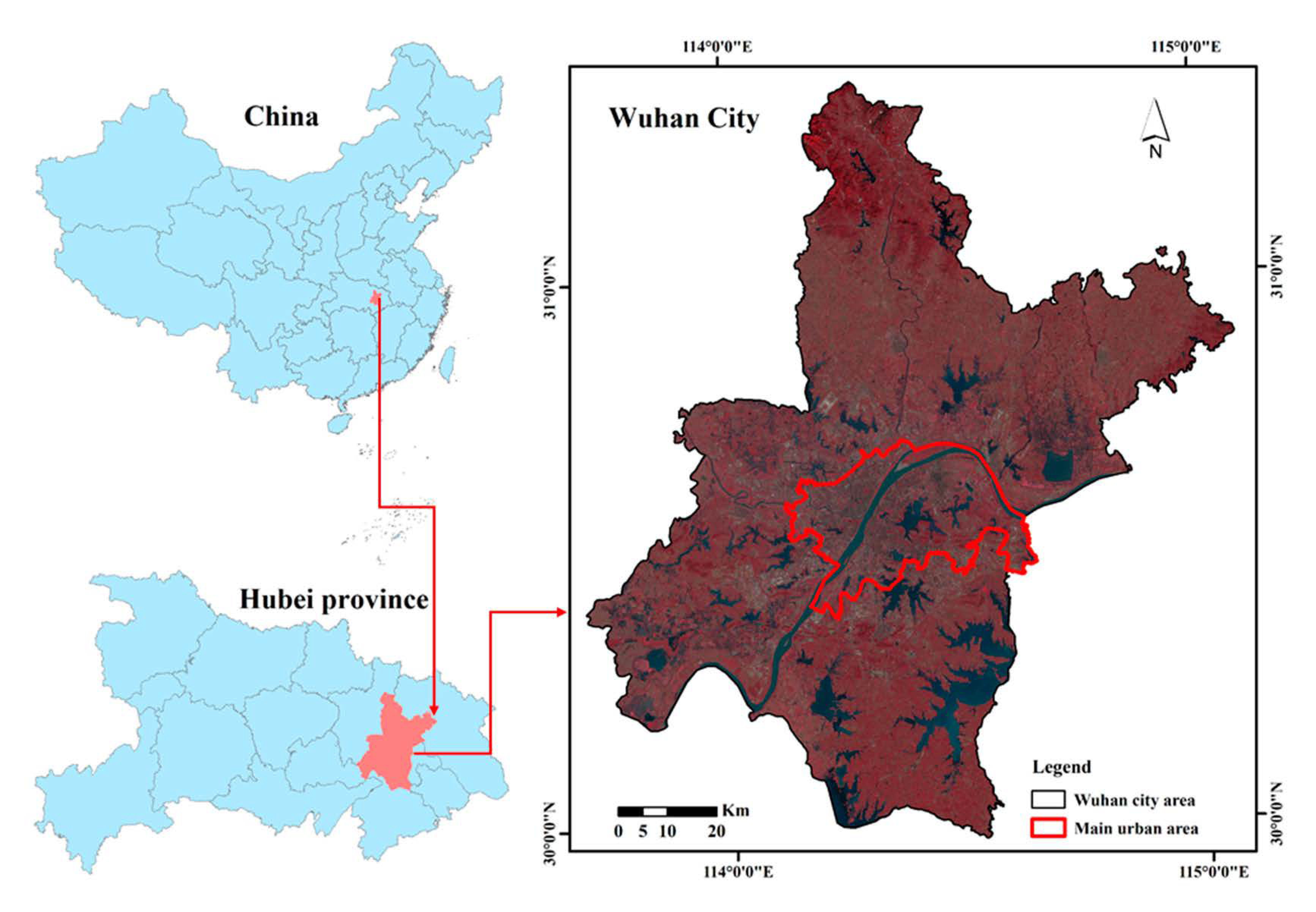
2. Study Area
3. Data and Methods
3.1. LST Retrieval from Landsat Images
3.2. Landsat Images
3.3. Spatial Analysis of LST
3.3.1. Spatial Pattern analysis
3.3.2. Geodetector Analysis
3.3.3. Land-Cover Data
4. Results
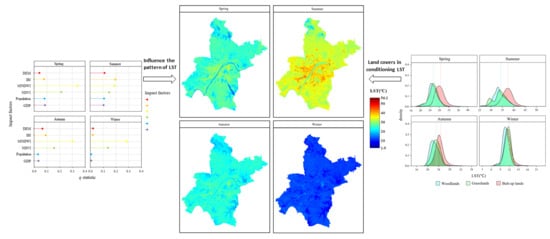
4.1. Spatial Distribution of LST
4.2. Spatial Patterns of LST
4.3. Quantifying the Contribution of Impact Factors to LST
4.4. Land Cover Analysis of LST
5. Discussion
5.1. Effects of Impact Factors on LST
5.2. The Role of Different Land Covers in Conditioning LST
6. Conclusions
- (1)
- LST in Wuhan shows spatial aggregations, with high temperature areas mainly distributed in the built-up areas and low temperature areas mainly distributed in water and woodland areas. In summer, during the study period, the average temperature difference among different land covers rose to 6.2 °C, while in winter, this average difference dropped to 1.9 °C.
- (2)
- Physical and socio-economic factors and their interactions were responsible for the patterns of LST differences in Wuhan. Among them, MNDWI, IBI, and NDVI, relating to the distribution of water areas, built-up, and green spaces and their interactions, were the main factors affecting temperature differences.
- (3)
- In spring and summer, the water area and urban green spaces (woodland and grassland) registered an LST of up to 5.4 °C and 2.6 °C lower than the built-up lands, respectively. From this perspective, water area and urban green spaces plays an extraordinary role in improving the thermal comfort of the city and preventing the occurrence of high temperature heat stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Sensor | Date | Remarks | |||
|---|---|---|---|---|---|
| 2013-04-26 | 2013-05-12 | 2015-03-31 | 2016-03-01 | Spring | |
| 2016-04-18 | 2018-04-08 | ||||
| 2013-06-13 | 2013-07-31 | 2015-08-22 | 2016-06-05 | Summer | |
| 2016-07-23 | 2017-07-26 | 2019-06-14 | 2019-08-01 | ||
| Landsat-8 | 2019-08-17 | ||||
| 2013-09-17 | 2013-11-04 | 2013-11-20 | 2014-10-06 | Autumn | |
| 2014-10-22 | 2015-10-25 | 2015-11-26 | 2017-10-30 | ||
| 2018-09-15 | 2018-11-02 | 2019-10-20 | 2019-11-05 | ||
| 2013-12-06 | 2014-01-23 | 2017-02-16 | 2017-12-17 | Winter | |
| 2019-12-07 |
References
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Ferguson, B.; Fisher, K.; Golden, J.; Hair, L.; Haselbach, L.; Hitchcock, D.; Kaloush, K.; Pomerantz, M.; Tran, N.; Waye, D. Reducing Urban Heat Islands: Compendium of Strategies; EPA: Washington, DC, USA, 2008. [Google Scholar]
- Grimmond, S. Urbanization and global environmental change: Local effects of urban warming. Geogr. J. 2007, 173, 83–88. [Google Scholar] [CrossRef]
- Plocoste, T.; Jacoby-Koaly, S.; Molinié, J.; Petit, R.H. Evidence of the effect of an urban heat island on air quality near a landfill. Urban Clim. 2014, 10, 745–757. [Google Scholar] [CrossRef]
- Steeneveld, G.J.; Klompmaker, J.O.; Groen, R.J.A.; Holtslag, A.A.M. An urban climate assessment and management tool for combined heat and air quality judgements at neighbourhood scales. Resour. Conserv. Recycl. 2018, 132, 204–217. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2016, 577, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite remote sensing of surface urban heat islands: Progress, challenges, and perspectives. Remote Sensing. 2019, 11, 48. [Google Scholar] [CrossRef] [Green Version]
- Nichol, J.E.; Fung, W.Y.; Lam, K.-S.; Wong, M.S. Urban heat island diagnosis using ASTER satellite images and ‘in situ’ air temperature. Atmos. Res. 2009, 94, 276–284. [Google Scholar] [CrossRef]
- Schwarz, N.; Schlink, U.; Franck, U.; Grossmann, K. Relationship of land surface and air temperatures and its implications for quantifying urban heat island indicators-an application for the city of Leipzig (Germany). Ecol. Indic. 2012, 18, 693–704. [Google Scholar] [CrossRef]
- Smoliak, B.V.; Snyder, P.K.; Twine, T.E.; Mykleby, P.M.; Hertel, W.F. Dense network observations of the twin cities canopy-layer urban heat island. J. Appl. Meteorol. Climatol. 2015, 54, 1899–1917. [Google Scholar] [CrossRef]
- Clay, R.; Guan, H.; Wild, N.; Bennett, J.; Ewenz, C. Urban heat island traverses in the city of Adelaide, South Australia. Urban Climate 2016, 17, 89–101. [Google Scholar] [CrossRef]
- Voogt, J. How Researchers Measure Urban Heat Islands; State and Local Climate and Energy Program, Heat Island Effect, Urban Heat Island Webcasts and Conference Calls; United States Environmental Protection Agency (EPA): Washington, DC, USA, 2007. [Google Scholar]
- Mirzaei, P.A.; Haghighat, F. Approaches to study urban heat island—Abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Anniballe, R.; Bonafoni, S.; Pichierri, M. Spatial and temporal trends of the surface and air heat island over Milan using MODIS data. Remote Sens. Environ. 2014, 150, 163–171. [Google Scholar] [CrossRef]
- Jin, M.L.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 044004. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Jiang, S.; Wang, J.; Zhou, C.; Wang, X.; Lee, X. Comparing the diurnal and seasonal variabilities of atmospheric and surface urban heat islands based on the Beijing urban meteorological network. J. Geophys. Res. Atmos. 2017, 122, 2131–2154. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Duan, S.-B.; Han, X.-J.; Huang, C.; Li, Z.-L.; Wu, H.; Qian, Y.; Gao, M.-F.; Leng, P. Land Surface Temperature Retrieval from Passive Microwave Satellite Observations: State-of-the-Art and Future Directions. Remote Sens. 2020, 12, 2573. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Voogt, J.A. Urban Heat Islands: Hotter Cities. 2004. Available online: www.actionbioscience.org/environment/voogt.html (accessed on 18 January 2021).
- Hu, L.; Brunsell, N.A. The impact of temporal aggregation of land surface temperature data for surface urban heat island (SUHI) monitoring. Remote Sens. Environ. 2013, 134, 162–174. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of local Moran’s I and GIS to identify pollution hotspots of Pb in urban soils of Galway, Ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Ding, H.; Shi, W. Land-use/land-cover change and its influence on surface temperature: A case study in Beijing City. Int. J. Remote. Sens. 2013, 34, 5503–5517. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Y.; Shi, W. Using Local Moran’s I Statistics to Estimate Spatial Autocorrelation of Urban Economic Growth in Shandong Province, China. In Proceedings of the 5th International Conference on Geo-Spatial Knowledge and Intelligence, Chiang Mai, Thailand, 8–10 December 2017; Yuan, H., Geng, J., Liu, C., Bian, F., Surapunt, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 848, pp. 32–39. [Google Scholar] [CrossRef]
- Yuan, Y.M.; Cave, M.; Zhang, C.S. Using Local Moran’s I to identify contamination hotspots of rare earth elements in urban soils of London. Appl. Geochem. 2018, 88, 167–178. [Google Scholar] [CrossRef]
- Ervin, E.D.; Flietstra, T.; Liu, Y.; Rollin, P.; Knust, B. Spatial Patterns of Hantavirus Pulmonary Syndrome in California and Nevada. In Proceedings of the 2014 Council of State and Territorial Epidemiologists Annual Conference, Nashville, TN, USA, 22–26 June 2014. [Google Scholar]
- Lemus-Canovas, M.; Martin-Vide, J.; Moreno-Garcia, C.M.; Lopez-Bustins, J.A. Estimating barcelona’s metropolitan daytime hot and cold poles using Landsat-8 land surface temperature. Sci. Total Environ. 2019, 699, 134307. [Google Scholar] [CrossRef]
- Rao, P.K. Remote sensing of urban “heat islands” from an environmental satellite. Bull. Am. Meteorol. Soc. 1972, 53, 647–648. [Google Scholar]
- Dousset, B.; Gourmelon, F. Satellite multi-sensor data analysis of urban surface temperatures and landcover. ISPRS J. Photogramm. Remote. Sens. 2003, 58, 43–54. [Google Scholar] [CrossRef]
- Streutker, D.R. Satellite-measured growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
- Morabito, M.; Crisci, A.; Guerri, G.; Messeri, A.; Congedo, L.; Munafò, M. Surface urban heat islands in Italian metropolitan cities: Tree cover and impervious surface influences. Sci. Total Environ. 2021, 751, 142334. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wang, G.; Yao, R.; Wang, L.; Yu, D.; Gui, X. Investigating surface urban heat islands in South America based on MODIS data from 2003–2016. Remote Sens. 2019, 11, 1212. [Google Scholar] [CrossRef] [Green Version]
- Guha, S.; Govil, H.; Dey, A.; Gill, N. Analytical study of land surface temperature with NDVI and NDBI using Landsat 8 OLI and TIRS data in Florence and Naples city, Italy. Eur. J. Remote Sens. 2018, 51, 667–678. [Google Scholar] [CrossRef]
- Nurwanda, A.; Honjo, T. The prediction of city expansion and land surface temperature in Bogor City, Indonesia. Sustain. Cities Soc. 2019, 52, 101772. [Google Scholar] [CrossRef]
- Algretawee, H.; Rayburg, S.; Neave, M. Estimating the effect of park proximity to the central of Melbourne city on Urban Heat Island (UHI) relative to Land Surface Temperature (LST). Ecol. Eng. 2019, 138, 374–390. [Google Scholar] [CrossRef]
- Masoudi, M.; Tan, P.Y.; Liew, S.C. Multi-city comparison of the relationships between spatial pattern and cooling effect of urban green spaces in four major Asian cities. Ecol. Indic. 2019, 98, 200–213. [Google Scholar] [CrossRef]
- Yao, L.; Li, T.; Xu, M.; Xu, Y. How the landscape features of urban green space impact seasonal land surface temperatures at a city-block-scale: An urban heat island study in Beijing, China. Urban For. Urban Green. 2020, 52, 126704. [Google Scholar] [CrossRef]
- Dissanayake, D.M.S.L.B. Land Use Change and Its Impacts on Land Surface Temperature in Galle City, Sri Lanka. Climate 2020, 8, 65. [Google Scholar] [CrossRef]
- Kotharkar, R.; Surawar, M. Land use, land cover, and population density impact on the formation of canopy urban heat islands through traverse survey in the Nagpur urban area, India. J. Urban Plan. Dev. 2016, 142. [Google Scholar] [CrossRef]
- Huang, G.L.; Cadenasso, M.L. People, landscape, and urban heat island: Dynamics among neighborhood social conditions, land cover and surface temperatures. Landsc. Ecol. 2016, 31, 2507–2515. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.L.; Liu, Y.X.; Li, H.L.; Wu, J.S. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Xie, Q.J.; Zhou, Z.X. Impact of urbanization on Urban Heat Island effect based on TM imagery in Wuhan, China. Environ. Eng. Manag. J. 2015, 14, 647–655. [Google Scholar] [CrossRef]
- Yang, J.; Gong, J.; Gao, J.; Ye, Q. Stationary and systematic characteristics of land use and land cover change in the national central cities of China using intensity analysis: A case study of Wuhan City. Resour. Sci. 2019, 41, 701–716. [Google Scholar] [CrossRef]
- Shen, H.F.; Huang, L.W.; Zhang, L.P.; Wu, P.H.; Zeng, C. Long-Term and Fine-Scale Satellite Monitoring of the Urban Heat Island Effect by the Fusion of Multitemporal and Multi-Sensor Remote Sensed Data: A 26-Year Case Study of the City of Wuhan in China. Remote Sens. Environ. 2016, 172, 109–125. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, J.; Yang, X.; Fang, C.; Liang, Y. Quantifying the seasonal contribution of coupling urban land use types on urban heat island using land contribution index: A case study in Wuhan, China. Sustain. Cities Soc. 2019, 44, 666–675. [Google Scholar] [CrossRef]
- Cao, L.; Li, P.; Zhang, L. Impact of Impervious Surface on Urban Heat Island in Wuhan, China. In Proceedings of the International Conference on Earth Observation Data Processing and Analysis (ICEODPA), Wuhan, China, 28–30 December 2008; International Society for Optics and Photonics: Bellingham, DC, USA, 2008; Volume 7285, p. 72855H. [Google Scholar]
- Gui, X.; Wang, L.; Yao, R.; Yu, D.; Li, C. Investigating the urbanization process and its impact on vegetation change and urban heat island in Wuhan, China. Environ. Sci. Pollut. Res. 2019, 26, 30808–30825. [Google Scholar] [CrossRef]
- Huang, L.; Shen, H.; Wu, P.; Zhang, L.; Zeng, C. Relationships Analysis of Land Surface Temperature with Vegetation Indicators and Impervious Surface Fraction by Fusing Multi-Temporal and Multi-Sensor Remotely Sensed Data. In Proceedings of the Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Li, L.; Tan, Y.; Ying, S.; Yu, Z.; Li, Z.; Lan, H. Impact of land cover and population density on land surface temperature: Case study in Wuhan, China. J. Appl. Remote Sens. 2014, 8, 084993. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, Q.; Ouyang, W. Impact of urban climate landscape patterns on land surface temperature in Wuhan, China. Sustainability 2017, 9, 1700. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Lu, D.; Xu, C.; Li, Y.; Chen, M. Spatial heterogeneity and its changes of population on the two sides of Hu Line. Acta Geogr. Sin. 2017, 72, 148–160. [Google Scholar] [CrossRef]
- Hu, M.; Lin, H.; Wang, J.; Xu, C.; Tatem, A.J.; Meng, B.; Zhang, X.; Liu, Y.; Wang, P.; Wu, G. The risk of COVID-19 transmission in train passengers: An epidemiological and modelling study. Clin. Infect. Dis. 2020. [Google Scholar] [CrossRef]
- Wang, H.; Liu, L.; Yin, L.; Shen, J.; Li, S. Exploring the complex relationships and drivers of ecosystem services across different geomorphological types in the Beijing-Tianjin-Hebei region, China (2000–2018). Ecol. Indic. 2020, 121, 107116. [Google Scholar] [CrossRef]
- Tao, H.; Liao, X.; Li, Y.; Xu, C.; Zhu, G.; Cassidy, D.P. Quantifying influences of interacting anthropogenic-natural factors on trace element accumulation and pollution risk in karst soil. Sci. Total Environ. 2020, 721, 137770. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.F.; Xu, C.D. Geodetector: Principle and prospective. Acta Geogr. Sinic. 2017, 72, 116–134. [Google Scholar]
- Wei, X.; Wang, J.; Wu, S.; Xin, X.; Liu, W. Comprehensive evaluation model for water environment carrying capacity based on vposrm framework: A case study in Wuhan, China. Sustain. Cities Soc. 2019, 50, 101640. [Google Scholar] [CrossRef]
- Wuhan Bureau of Statistics. Statistical Bulletin of Wuhan National Economic and Social Development in 2019. Available online: http://tjj.wuhan.gov.cn/tjfw/tjgb/202004/t20200429_1191417.shtml (accessed on 29 March 2020).
- Qian, Z.; He, Q.; Lin, H.M.; Kong, L.; Liao, D.; Dan, J.; Wang, B. Association of daily cause-specific mortality with ambient particle air pollution in Wuhan, China. Environ. Res. 2007, 105, 380–389. [Google Scholar] [CrossRef]
- Han, Y.; Li, S.; Zheng, Y. Predictors of nutritional status among community-dwelling older adults in Wuhan, China. Public Health Nutr. 2009, 12, 1189–1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Susskind, J.; Rosenfield, J.; Reuter, D.; Chahine, M.T. Remote sensing of weather and climate parameters from HIRS2/MSU on TIROS-N. J. Geophys. Res. Space Phys. 1984, 89, 4677. [Google Scholar] [CrossRef]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Mattar, C.; Cristobal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Chatterjee, R.S.; Singh, N.; Thapa, S.; Sharma, D.; Kumar, D. Retrieval of land surface temperature (LST) from Landsat TM 6 and TIRS data by single channel radiative transfer algorithm using satellite and ground-based inputs. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 264–277. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving landsurface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Murayama, Y. Geo-simulation of land use/cover scenarios and impacts on land surface temperature in Sapporo, Japan. Sustain. Cities Soc. 2020, 63, 102432. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Artis, D.A.; Carnahan, W.H. Survey of emissivity variability in thermography of urban areas. Remote Sens. Environ. 1982, 12, 313–329. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, Z.; Teng, M.; Wang, P. A multi-temporal Landsat TM data analysis of the impact of land use and land cover changes on the urban heat island effect. J. Food Agric. Environ. 2012, 10, 803–809. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Van de Griend, A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar] [CrossRef]
- Tapper, N.J. Urban influences on boundary layer temperature and humidity: Results from Christchurch, New Zealand. Atmospheric Environment. Part B. Urban Atmos. 1990, 24, 19–27. [Google Scholar] [CrossRef]
- Kuttler, W.; Weber, S.; Schonnefeld, J.; Hesselschwerdt, A. Urban/rural atmospheric water vapour pressure differences and urban moisture excess in Krefeld, Germany. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 2005–2015. [Google Scholar] [CrossRef]
- Isaya Ndossi, M.; Avdan, U. Application of Open Source Coding Technologies in the Production of Land Surface Temperature (LST) Maps from Landsat: A PyQGIS Plugin. Remote Sens. 2016, 8, 413. [Google Scholar] [CrossRef] [Green Version]
- Dhakar, R.; Sehgal, V.K.; Chakraborty, D.; Sahoo, R.N.; Mukherjee, J. Field scale wheat LAI retrieval from multispectral sentinel 2A-MSI and Landsat 8-OLI imagery: Effect of atmospheric correction, image resolutions and inversion techniques. Geocarto Int. 2019, 1–21. [Google Scholar] [CrossRef]
- Song, J.; Du, S.; Feng, X.; Guo, L. The relationships between landscape compositions and land surface temperature: Quantifying their resolution sensitivity with spatial regression models. Landsc. Urban Plan. 2014, 123, 145–157. [Google Scholar] [CrossRef]
- ArcGIS Version 10.0; Environmental Systems Research Institute: Redlands, CA, USA, 2010.
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Q.S.; Liu, J.; Zhang, Y.; Jiang, X.J.; Yang, Y.M. Study on the spatial differentiation of the populations on both sides of the “Qinling-Huaihe Line” in China. Sustainability 2020, 12, 4545. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, L.; Li, X.C.; Zhang, C.C.; Shi, T.Z.; Wu, X.Y.; Yang, C.; Gao, W.X.; Li, Q.Q.; Wu, G.F. Exploring annual urban expansions in the Guangdong-Hong Kong-Macau Greater Bay Area: Spatiotemporal features and driving factors in 1986–2017. Remote Sens. 2020, 12, 2615. [Google Scholar] [CrossRef]
- Wu, R.; Zhang, J.; Bao, Y.; Zhang, F. Geographical detector model for influencing factors of industrial sector carbon dioxide emissions in Inner Mongolia, China. Sustainability 2016, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Xia, J.; Zou, L.; Hong, S. Quantifying the influences of natural factors and human activities on NDVI changes in the Hanjiang river basin, China. Remote Sens. 2020, 12, 3780. [Google Scholar] [CrossRef]
- Xu, H.Q. A new index for delineating built-up land features in satellite imagery. Int. J. Remote Sens. 2008, 29, 4269–4276. [Google Scholar] [CrossRef]
- Xu, H.Q. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Brown, S. Measures of Shape: Skewness and Kurtosis. Available online: http://brownmath.com/stat/shape.htm (accessed on 18 January 2021).
- Wang, H.; Gao, J.; Hou, W. Quantitative attribution analysis of soil erosion in different geomorphological types in karst areas: Based on the geodetector method. J. Geogr. Sci. 2019, 29, 271–286. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Wu, Z.; Tan, J. The relationship between land surface temperature and land use/land cover in Guangzhou, China. Environ. Earth Sci. 2012, 65, 1687–1694. [Google Scholar] [CrossRef]
- Zhi, Y.; Shan, L.; Ke, L.; Yang, R. Analysis of Land Surface Temperature Driving Factors and Spatial Heterogeneity Research Based on Geographically Weighted Regression Model. Complexity 2020. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, S.; Chen, F.; Ye, H.; Wang, C.; Zhu, C. The impacts of rapid urbanization on the thermal environment: A remote sensing study of Guangzhou, South China. Remote Sens. 2012, 4, 2033–2056. [Google Scholar] [CrossRef] [Green Version]
- Peng, W.; Zhou, J.; Wen, L.; Xue, S.; Dong, L. Land surface temperature and its impact factors in Western Sichuan Plateau, China. Geocarto Int. 2017, 32, 919–934. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Li, W.; Ma, R. Examining urban thermal environment dynamics and relations to biophysical composition and configuration and socio-economic factors: A case study of the Shanghai metropolitan region. Sustain. Cities Soc. 2018, 40, 284–295. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Chen, L.; Li, M.; Huang, F.; Xu, S. Relationships of LST to NDBI and NDVI in Wuhan City Based on Landsat ETM+ Image. In Proceedings of the 6th International Congress on Image and Signal. Processing (CISP), Hangzhou, China, 16–18 December 2013; IEEE: Piscataway, NJ, USA, 2013; Volume 2, pp. 840–845. [Google Scholar]
- Zhang, Q.; Wu, Z.; Yu, H.; Zhu, X.; Shen, Z. Variable Urbanization Warming Effects across Metropolitans of China and Relevant Driving Factors. Remote Sens. 2020, 12, 1500. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.W.; Zhang, Z.; Tang, M.; Ji, X.Y.; Hou, M.F. Spatio-temporal scale effect and driving mechanism of thermal environment and land surface cover in Nanjing. Ecol. Environ. Sci. 2020, 29, 1403–1411. [Google Scholar] [CrossRef]
- Lu, D.D. Economic belt construction is the best choice of economic development layout: The enormous potential for the Changjiang River Economic Belt. Sci. Geogr. Sin. 2014, 34, 769–772. [Google Scholar] [CrossRef]
- Chen, Y.D. Setting up an enterprise with sincerity, making port thriving by creating. Building up Wuhan port as main hub of shipping in Changjiang River and main channel of logistics in middle China—An interview with Guqiangsheng—General manager of Wuhan Port Group Co., Ltd. Port. Sci. Technol. 2012, 7, 1–3. [Google Scholar] [CrossRef]
- Lee, S.H.; Song, C.K.; Baik, J.J.; Park, S.U. Estimation of anthropogenic heat emission in the Gyeong-In region of Korea. Theor. Appl. Climatol. 2009, 96, 291–303. [Google Scholar] [CrossRef]
- Walawender, J.P.; Szymanowski, M.; Monika, J.H. Land surface temperature patterns in the urban agglomeration of Krakow (Poland) derived from Landsat-7/ETM+ data. Pure Appl. Geophys. 2014, 171, 913–940. [Google Scholar] [CrossRef] [Green Version]
- Yin, C.; Yuan, M.; Lu, Y.; Huang, Y.; Liu, Y. Effects of urban form on the urban heat island effect based on spatial regression model. Sci. Total Environ. 2018, 634, 696–704. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; He, B.J.; Li, L.G.; Wang, H.B.; Darko, A. Profile and concentric zonal analysis of relationships between land use/land cover and land surface temperature: Case study of Shenyang, China. Energy Build. 2017, 155, 282–295. [Google Scholar] [CrossRef]
- Hua, A.K.; Ping, O.W. The influence of land-use/land-cover changes on land surface temperature: A case study of Kuala Lumpur metropolitan city. Eur. J. Remote Sens. 2018, 51, 1049–1069. [Google Scholar] [CrossRef] [Green Version]
- Le, K.J.; Fang, L.M.; He, X.B.; Zheng, X.Y. Relationship between forest city landscape pattern and thermal environment: A case study of Longquan City, China. Chin. J. Appl. Ecol. 2019, 30, 3066–3074. [Google Scholar] [CrossRef]
- Van Hove, L.W.A.; Jacobs, C.M.J.; Heusinkveld, B.G.; Elbers, J.A.; Van Driel, B.L.; Holtslag, A.A.M. Temporal and spatial variability of urban heat island and thermal comfort within the Rotterdam agglomeration. Build. Environ. 2015, 83, 91–103. [Google Scholar] [CrossRef] [Green Version]
- Lima Alves, E.; Lopes, A.; Lima Alves, E.D.; Lopes, A. The Urban Heat Island effect and the role of vegetation to address the negative impacts of local climate changes in a small Brazilian City. Atmosphere 2017, 8, 18. [Google Scholar] [CrossRef] [Green Version]
- Jalan, S.; Sharma, K. Spatio-temporal assessment of land use/ land cover dynamics and Urban Heat Island of Jaipur City using satellite data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-8, 767–772. [Google Scholar] [CrossRef] [Green Version]







| Minimum/Maximum (°C) | Mean/Standard Deviation (°C) | ||||||
|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter |
| 4.1/43.8 | 12.9/56.1 | 13.2/40.3 | 1.9/24.0 | 24.8/2.8 | 33.2/3.2 | 23.1/1.9 | 11.6/1.5 |
| Area (km2) | Area Proportion (%) | |||||||
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| Not Significant | 6265.1 | 6324.4 | 6913.9 | 7298.0 | 72.98 | 73.67 | 80.53 | 84.99 |
| High–High clusters | 721.2 | 1020.0 | 297.8 | 452.5 | 8.40 | 11.88 | 3.47 | 5.27 |
| High–Low outliers | 22.4 | 3.5 | 3.7 | 43.0 | 0.26 | 0.04 | 0.04 | 0.50 |
| Low–High outliers | 280.2 | 213.2 | 180.9 | 104.0 | 2.26 | 2.48 | 2.11 | 1.21 |
| Low–Low clusters | 1296.3 | 1024.2 | 1188.8 | 688.9 | 15.10 | 11.93 | 13.85 | 8.02 |
| Minimum/Maximum (°C) | Mean/Standard Deviation (°C) | |||||||
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| Not Significant | 11.6/43.5 | 24.6/53.5 | 15.3/38.6 | 4.7/22.5 | 25.2/2.0 | 33.1/2.0 | 23.4/1.5 | 11.7/1.2 |
| High–High clusters | 23.4/43.8 | 32.5/56.1 | 23.1/40.3 | 11.5/24.0 | 29.0/1.9 | 38.4/2.1 | 26.4/1.6 | 13.5/1.0 |
| High–Low outliers | 22.9/32.3 | 33.9/43.1 | 24.3/28.3 | 11.7/22.4 | 26.2/0.6 | 37.5/1.9 | 26.0/1.1 | 13.3/1.0 |
| Low–High outliers | 14.3/25.3 | 26.4/34.7 | 15.3/24.2 | 6.4/12.3 | 21.6/1.7 | 30.2/1.2 | 21.0/0.7 | 9.4/1.1 |
| Low–Low clusters | 4.1/25.9 | 12.9/35.5 | 13.2/23.9 | 1.9/12.2 | 20.1/2.0 | 29.0/3.0 | 20.4/1.3 | 9.1/1.1 |
| Spring | Summer | |||||||||||
| DEM | IBI | MNDWI | NDVI | Population | GDP | DEM | IBI | MNDWI | NDVI | Population | GDP | |
| DEM | 0.042 | 0.112 | ||||||||||
| IBI | 0.118 | 0.079 | 0.282 | 0.198 | ||||||||
| MNDWI | 0.388 | 0.455 | 0.342 | 0.306 | 0.439 | 0.190 | ||||||
| NDVI | 0.273 | 0.313 | 0.470 | 0.215 | 0.270 | 0.340 | 0.301 | 0.148 | ||||
| Population | 0.120 | 0.139 | 0.422 | 0.282 | 0.082 | 0.200 | 0.249 | 0.320 | 0.230 | 0.109 | ||
| GDP | 0.134 | 0.152 | 0.435 | 0.295 | 0.097 | 0.089 | 0.208 | 0.258 | 0.322 | 0.236 | 0.115 | 0.111 |
| Autumn | Winter | |||||||||||
| DEM | IBI | MNDWI | NDVI | Population | GDP | DEM | IBI | MNDWI | NDVI | Population | GDP | |
| DEM | 0.066 | 0.022 | ||||||||||
| IBI | 0.154 | 0.092 | 0.048 | 0.020 | ||||||||
| MNDWI | 0.371 | 0.411 | 0.301 | 0.306 | 0.308 | 0.284 | ||||||
| NDVI | 0.241 | 0.268 | 0.338 | 0.158 | 0.170 | 0.168 | 0.300 | 0.138 | ||||
| Population | 0.094 | 0.112 | 0.335 | 0.185 | 0.031 | 0.029 | 0.034 | 0.304 | 0.159 | 0.007 | ||
| GDP | 0.106 | 0.118 | 0.336 | 0.195 | 0.037 | 0.039 | 0.037 | 0.040 | 0.310 | 0.164 | 0.012 | 0.009 |
| Skewness | Kurtosis | |||||||
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| Croplands | 2.99 | 3.08 | 3.02 | 2.84 | 8.22 | 8.98 | 9.00 | 7.25 |
| Woodlands | 2.12 | 2.68 | 1.79 | 2.40 | 3.68 | 6.98 | 1.85 | 5.18 |
| Grasslands | 1.48 | 2.65 | 2.43 | 2.48 | 0.77 | 6.34 | 4.98 | 5.42 |
| Built-up lands | 2.19 | 1.75 | 2.57 | 2.67 | 3.66 | 1.68 | 5.97 | 6.44 |
| Water areas | 1.71 | 2.65 | 1.50 | 0.64 | 1.74 | 6.97 | 1.18 | −1.34 |
| Minimum/Maximum (°C) | Mean/Standard Deviation (°C) | |||||||
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| Croplands | 4.7/38.9 | 14.5/50.7 | 13.7/34.3 | 3.4/19.8 | 25.5/1.7 | 33.2/2.1 | 23.5/1.3 | 12.0/0.9 |
| Woodlands | 4.1/38.8 | 12.9/53.7 | 13.9/38.6 | 4.9/23.5 | 23.4/2.7 | 31.2/3.5 | 21.7/1.9 | 11.1/1.4 |
| Grasslands | 4.8/39.4 | 22.3/48.7 | 16.6/32.9 | 7.5/18.6 | 25.3/1.6 | 33.3/2.2 | 23.1/1.4 | 11.6/1.1 |
| Built-up lands | 5.2/43.8 | 20.6/56.1 | 13.2/40.3 | 1.9/24.0 | 27.5/2.5 | 36.9/3.0 | 24.7/1.6 | 12.1/1.2 |
| Water areas | 3.6/38.2 | 14.2/48.6 | 15.2/33.4 | 5.2/18.6 | 22.1/1.9 | 30.7/1.8 | 21.3/1.5 | 10.2/1.1 |
| Minimum/Maximum (°C) | Mean/Standard Deviation (°C) | |||||||
|---|---|---|---|---|---|---|---|---|
| Spring | Summer | Autumn | Winter | Spring | Summer | Autumn | Winter | |
| Woodlands | 18.1/37.5 | 25.8/44.9 | 16.8/31.2 | 7.5/17.1 | 25.7/2.1 | 34.3/2.7 | 23.0/1.6 | 11.3/1.1 |
| Grasslands | 18.1/39.4 | 25.9/48.2 | 16.9/33.0 | 7.6/18.7 | 26.0/2.2 | 34.4/3.0 | 23.6/1.5 | 11.9/1.2 |
| Built-up lands | 16.6/43.7 | 26.1/52.1 | 14.0/37.8 | 2.3/24.0 | 28.6/2.3 | 37.7/2.5 | 24.9/1.6 | 12.1/1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Wang, X.; Cai, X.; Yang, C.; Lu, X. Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sens. 2021, 13, 323. https://doi.org/10.3390/rs13020323
Chen L, Wang X, Cai X, Yang C, Lu X. Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sensing. 2021; 13(2):323. https://doi.org/10.3390/rs13020323
Chicago/Turabian StyleChen, Liang, Xuelei Wang, Xiaobin Cai, Chao Yang, and Xiaorong Lu. 2021. "Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China" Remote Sensing 13, no. 2: 323. https://doi.org/10.3390/rs13020323
APA StyleChen, L., Wang, X., Cai, X., Yang, C., & Lu, X. (2021). Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sensing, 13(2), 323. https://doi.org/10.3390/rs13020323