Analyzing the Spatiotemporal Uncertainty in Urbanization Predictions
Abstract
1. Introduction
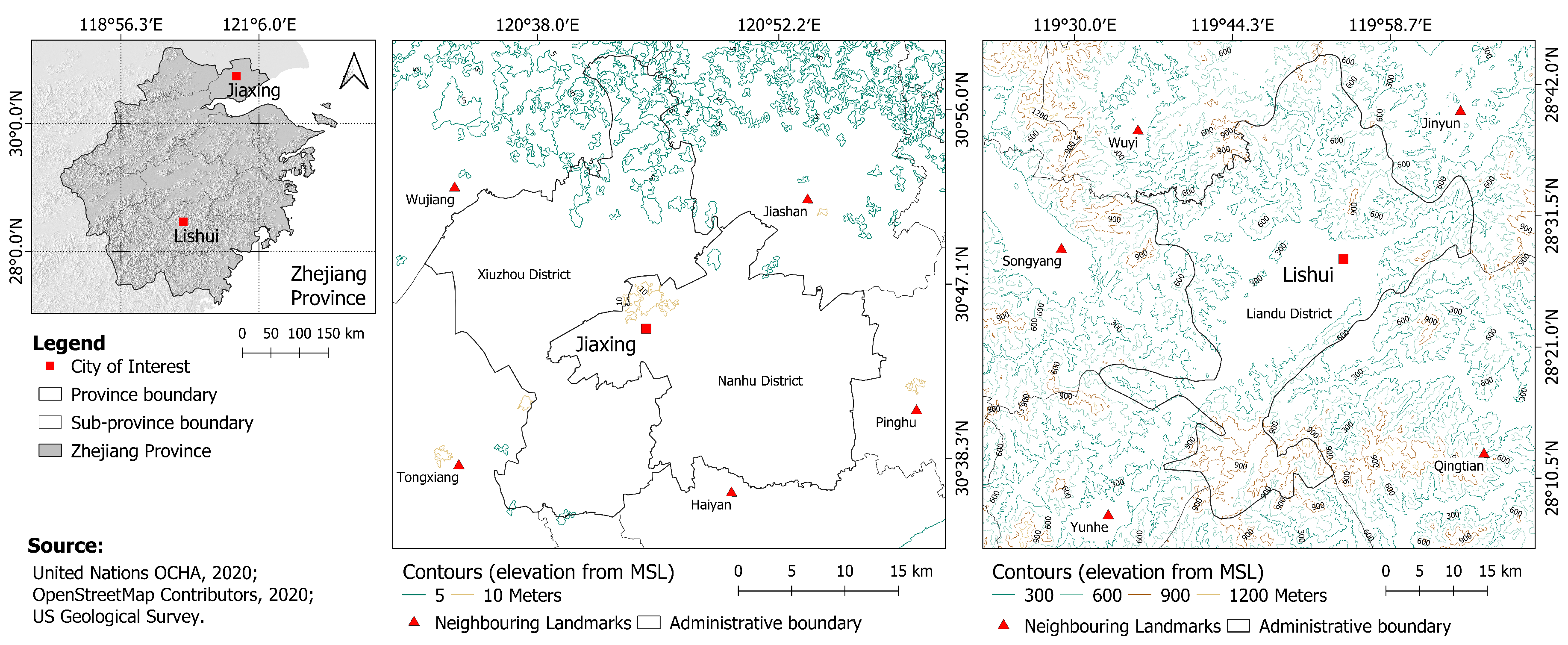
2. Materials and Methods
2.1. Input Data for Urban Growth Modeling
2.2. Sleuth CA Urban Growth Model
2.3. ML-Based Urban Growth Framework
2.4. Uncertainty Analysis of Urban Growth
- The yearly urbanization from 2015 to 2040, where 2015 is the last historical year, and the data from 2016 to 2040 corresponds to predictions.
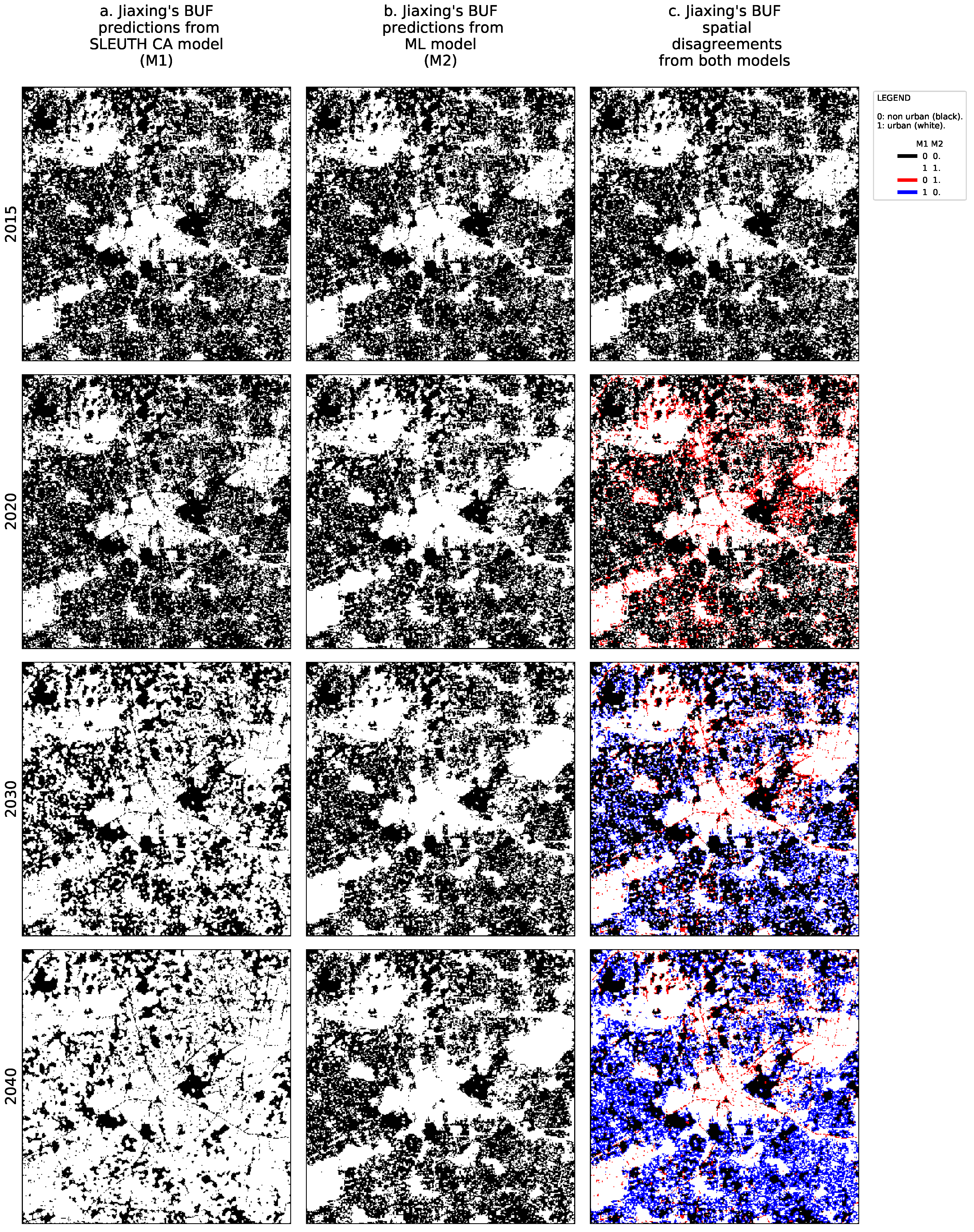
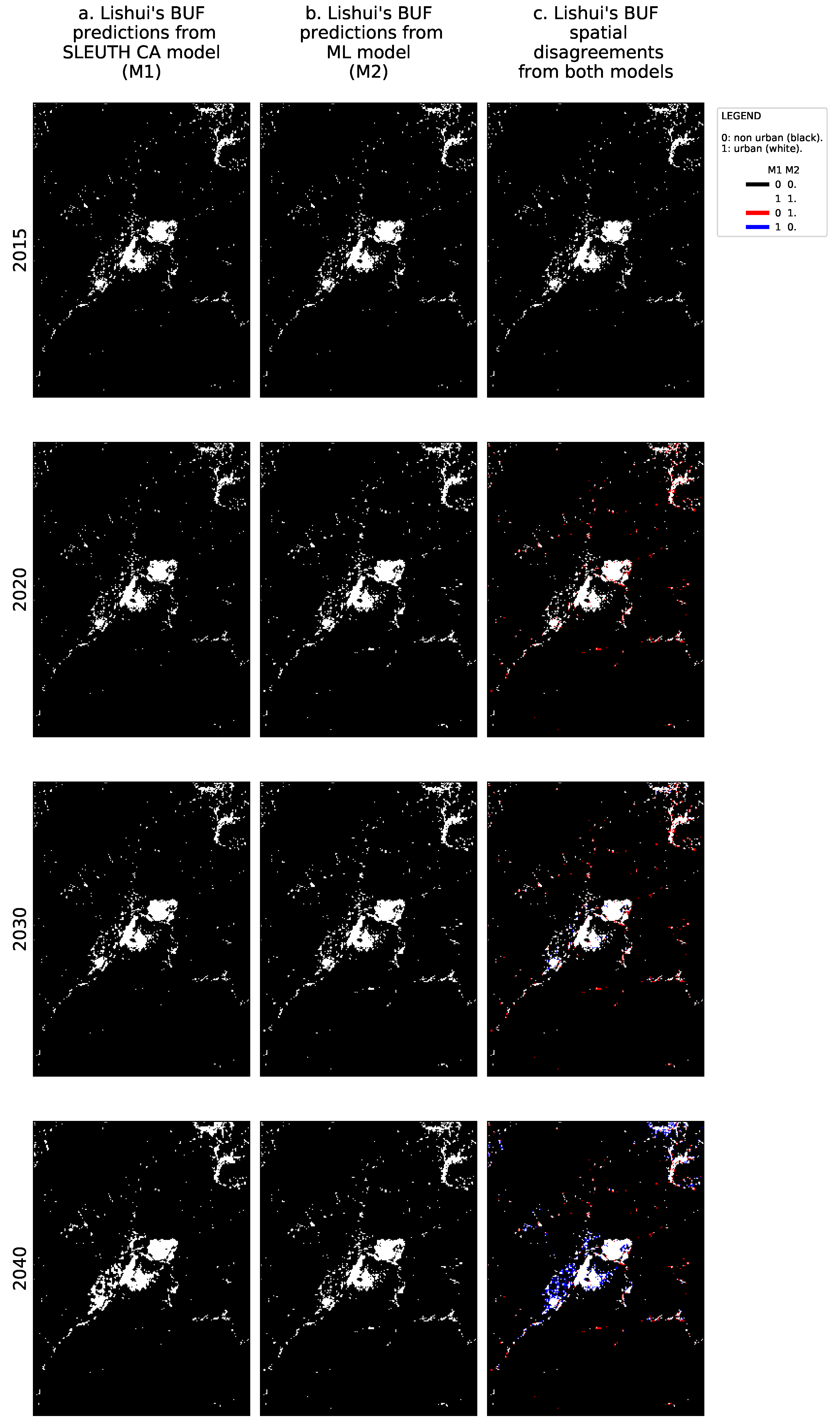
- An instantaneous spatial difference between the models for each decade, i.e.,: 2020, 2030, and 2040.
- The cumulative spatial agreement and disagreement of predicted urban areas from 2016 to 2040 removing the common urban areas that already existed in 2015 to ease the visual inspection.
- A histogram with the “signed” differences in predicted urbanization times between the models to reveal if one of the models tends to predict urbanization earlier than the other.
- A histogram with the “unsigned” differences in predicted urbanization times between the models to understand how long does it take them to reach an agreement within the simulation horizon.
- A time series showing the evolution of the spatial agreement of the urban predictions of both models over time excluding the existing urban areas of 2015. In this case, we propose an agreement index S through Equations (2) and (3), where the sum occurs over all pixels, is the reference year (which in our case is equal to 2015 because it is the last historical year), the sub-index refers to the predictions from the SLEUTH CA model, while corresponds to the predictions from the ML urban growth framework, and is an acronym for the binary urban footprint. In our convention, a value of one in BUF indicates an urban area, whereas a value of zero indicates a non-urban area. The proposed agreement index can be seen as a special variant of the intersection over union (IoU) that blocks de-urbanization effects and prevents over estimating the spatial agreement, as it is relative to the last known and common urbanization state for both models. Notice that when de-urbanization is prohibited from the forecasts of both models, Equation (3) reduces to Equation (4). Also notice that S varies from zero to one as the two predicted binary urban footprints move away from a total spatial disagreement to a perfect spatial agreement.
- A time series of two frequently used indices in the literature. The first index is known as the zero-mean normalized cross-correlation (ZNCC), see Equations (5) and (6), where is the expected-value operator computed as the arithmetic mean across all the spatial coordinates. The ZNCC can change from −1 to 1, and the closer it gets to 1, the better the spatial agreement.The second index is known as the sum of absolute differences (SAD), and we computed it using Equation (7). The SAD is greater than or equal to zero, and the closer to zero the better the spatial agreement.Notice that both indices assess the “instantaneous” level of spatial agreement between the urbanization predictions of both models over time, as they are computed directly over the yearly predictions, i.e.,: without discarding de-urbanization effects nor the urban areas that existed in 2015.
3. Results
3.1. Sleuth CA
3.2. ML-Based Urban Growth Framework
3.3. Uncertainty Analysis of Urban Growth
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GHSL | Global human settlement layer |
| BUF | Binary urban footprint |
| POP | Population distribution |
| LULCC | Land-uses and land-cover changes |
| DEM | Digital elevation map |
| SAD | Sum of absolute differences |
| SSD | Sum of square differences |
| MSE | Mean squared error |
| RMSE | Root mean square error |
| FP | False positive |
| ZNCC | Zero-mean normalized cross correlation |
| IoU | Intersection over union |
| KDE | Kernel density estimation |
| Probability density function | |
| CA | Cellular automaton |
| ML | Machine learning |
Appendix A. Auxiliary Tables for SLEUTH CA Model Calibration
| Stage | Monte Carlo Iteration | Diffusion | Breed | Spread | Slope | Road Gravity |
|---|---|---|---|---|---|---|
| Lishui: size of each image layer 704 rows × 518 columns | ||||||
| Coarse | 5 | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] |
| Fine | 8 | [25, 100, 15] | [1, 100, 10] | [13, 38, 5] | [75, 100, 5] | [50, 100, 10] |
| Final | 10 | [25, 100, 5] | [41, 61, 2] | [11, 15, 1] | [75, 100, 2] | [50, 100, 5] |
| Derive coeff | 150 | [25, 25, 1] | [53, 53, 1] | [13, 13, 1] | [77, 77, 1] | [95, 95, 1] |
| Predict | 200 | 32 | 67 | 17 | 68 | 96 |
| Jiaxing: size of each image layer 451 rows × 442 columns | ||||||
| Coarse | 5 | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] | [0, 100, 25] |
| Fine | 8 | [88, 100, 4] | [13, 38, 5] | [13, 38, 5] | [25, 100, 15] | [25, 100, 15] |
| Final | 10 | [92, 100, 1] | [13, 38, 2] | [18, 28, 2] | [85, 100, 3] | [25, 100, 5] |
| Derive coeff | 150 | [98, 98, 1] | [15, 15, 1] | [26, 26, 1] | [85, 85, 1] | [65, 65, 1] |
| Predict | 200 | 100 | 15 | 27 | 1 | 74 |
| Lishui | Jiaxing | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| OSM | Diff | Brd | Sprd | Slp | RG | OSM | Diff | Brd | Sprd | Slp | RG |
| Coarse calibration, runs: 3125, time: 1 h 18 m | Coarse calibration, runs: 3125, time: 1 h 31 m | ||||||||||
| 0.593 | 25 | 1 | 25 | 75 | 50 | 0.71 | 100 | 25 | 25 | 100 | 25 |
| 0.581 | 25 | 100 | 25 | 100 | 100 | 0.711 | 100 | 25 | 25 | 100 | 50 |
| 0.577 | 100 | 50 | 25 | 100 | 75 | 0.639 | 100 | 25 | 25 | 25 | 100 |
| Fine calibration, runs: 12,960, time: 7 h 37 m | Fine calibration, runs: 5184, time: 3 h 22 m | ||||||||||
| 0.751 | 25 | 41 | 13 | 75 | 100 | 0.844 | 100 | 13 | 28 | 85 | 25 |
| 0.748 | 25 | 61 | 13 | 80 | 90 | 0.829 | 100 | 13 | 28 | 100 | 70 |
| 0.741 | 100 | 51 | 13 | 100 | 50 | 0.824 | 92 | 38 | 18 | 85 | 100 |
| Final calibration, runs: 125,840, time: 4 d 11 m | Final calibration, runs: 67,392, time: 2 d 9 h 52 m | ||||||||||
| 0.764 | 25 | 53 | 13 | 77 | 95 | 0.841 | 98 | 15 | 26 | 85 | 65 |
| 0.760 | 40 | 51 | 13 | 85 | 60 | 0.838 | 100 | 13 | 28 | 85 | 25 |
| 0.755 | 25 | 55 | 14 | 79 | 70 | 0.834 | 100 | 13 | 28 | 88 | 35 |
Appendix B. Additional Figures for the Ml-Based Urban Growth Framework



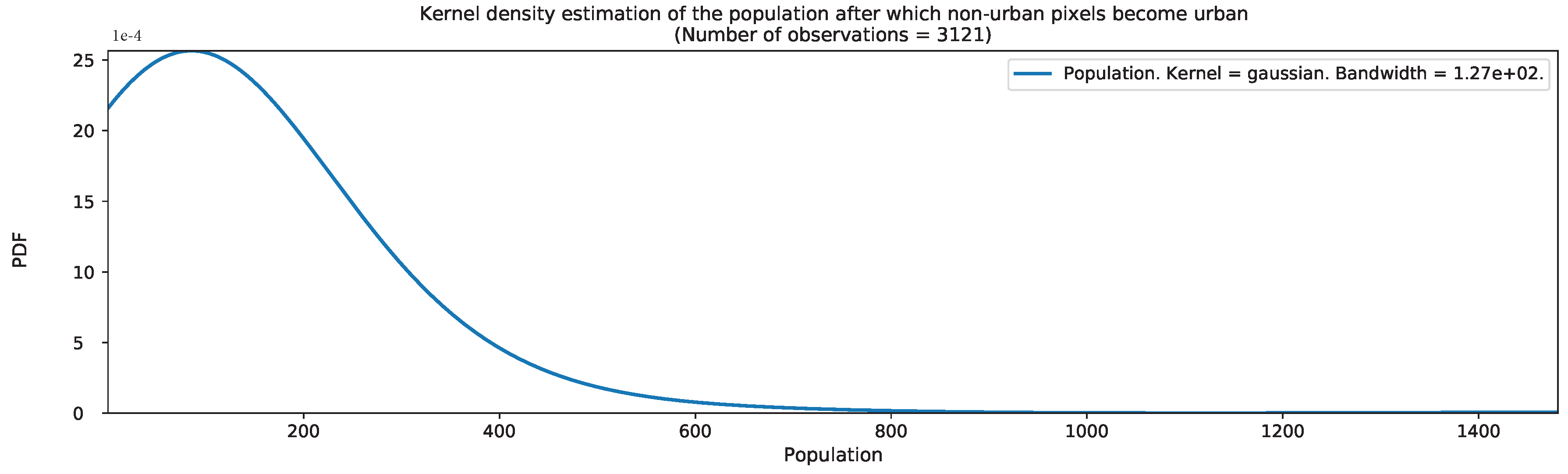




Appendix C. Land Use Recoding for Jiaxing and Lishui
- Urban.
- Agricultural.
- Rangeland.
- Forest Land.
- Water.
- Wetland.
- Barren Land.
- Tundra. This category was not available in Jiaxing nor Lishui.
- Perennial Snow or Ice. This category was not available in Jiaxing nor Lishui.
| Old Parent Class | Old Class | Pixel Value | New Class | Pixel Value |
|---|---|---|---|---|
| Grassland | Grass | 23 | Rangeland | 3 |
| Herbaceous green space | 24 | Rangeland | 3 | |
| Wetlands | Herbaceous wetlands | 33 | Wetland | 6 |
| Lake | 34 | Water | 5 | |
| Reservoir/pit | 35 | Water | 5 | |
| River | 36 | Water | 5 | |
| Canal | 37 | Water | 5 | |
| Arable land | Paddy field | 41 | Agriculture | 2 |
| Dry land | 42 | Barren land | 7 | |
| Artificial Surface | Residential | 51 | Urban | 1 |
| Industrial | 52 | Urban | 1 | |
| Transportation | 53 | Urban | 1 | |
| Mining farm | 54 | Urban | 1 | |
| Other | Bare rock | 65 | Barren land | 7 |
| Bare soil | 66 | Rangeland | 3 | |
| Woodland | Evergreen broad-leaved forest | 101 | Forest land | 4 |
| Deciduous broad-leaved forest | 102 | Forest land | 4 | |
| Evergreen coniferous forest | 103 | Forest land | 4 | |
| Deciduous coniferous forest | 104 | Forest land | 4 | |
| Coniferous and broad-leaved mixed forest | 105 | Forest land | 4 | |
| Evergreen broad-leaved shrub forest | 106 | Forest land | 4 | |
| Deciduous broad-leaved forest | 107 | Forest land | 4 | |
| Evergreen coniferous forest | 108 | Forest land | 4 | |
| Arbor | 109 | Rangeland | 3 | |
| Bush field | 110 | Rangeland | 3 | |
| Arbor green space | 111 | Rangeland | 3 | |
| Shrubland | 112 | Rangeland | 3 |
References
- United Nations. World Population Prospects 2019: Data Booket. ST/ESA/SER.A/424; Technical Report; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2019; Available online: https://population.un.org/wpp/Publications/Files/WPP2019_DataBooklet.pdf (accessed on 28 December 2020).
- United Nations. Population Facts; Technical Report 4, United Nations; Department of Economic and Social Affairs: New York, NY, USA, 2019; Available online: https://www.un.org/en/development/desa/population/migration/publications/populationfacts/docs/MigrationStock2019_PopFacts_2019-04.pdf (accessed on 28 December 2020).
- Kim, S.; Rowe, P.G. Does large-sized cities’ urbanisation predominantly degrade environmental resources in China? Relationships between urbanisation and resources in the Changjiang Delta Region. Int. J. Sustain. Dev. World Ecol. 2012, 19, 321–329. [Google Scholar] [CrossRef][Green Version]
- Guan, C.; Rowe, P.G. In pursuit of a well-balanced network of cities and towns: A case study of the Changjiang Delta Region in China. Environ. Plan. Urban Anal. City Sci. 2018, 45, 548–566. [Google Scholar] [CrossRef]
- Yang, J.; Shi, F.; Sun, Y.; Zhu, J. A Cellular Automata Model Constrained by Spatiotemporal Heterogeneity of the Urban Development Strategy for Simulating Land-use Change: A Case Study in Nanjing City, China. Sustainability 2019, 11, 4012. [Google Scholar] [CrossRef]
- Güneralp, B.; Seto, K. Futures of global urban expansion: Uncertainties and implications for biodiversity conservation. Environ. Res. Lett. 2013, 8, 1–10. [Google Scholar] [CrossRef]
- Cohen, B. Urban growth in developing countries: A review of current trends and a caution regarding existing forecasts. World Dev. 2004, 32, 23–51. [Google Scholar] [CrossRef]
- Seto, K.C.; Güneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Makse, H.A.; Havlin, S.; Stanley, H.E. Modelling urban growth patterns. Nature 1995, 377, 608. [Google Scholar] [CrossRef]
- Herold, M.; Goldstein, N.C.; Clarke, K.C. The spatiotemporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ. 2003, 86, 286–302. [Google Scholar] [CrossRef]
- Aghion, P.; Durlauf, S. Handbook of Economic Growth, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 2. [Google Scholar]
- Lung, T.; Lübker, T.; Ngochoch, J.K.; Schaab, G. Human population distribution modelling at regional level using very high resolution satellite imagery. Appl. Geogr. 2013, 41, 36–45. [Google Scholar] [CrossRef]
- Wu, J.; Li, R.; Ding, R.; Li, T.; Sun, H. City expansion model based on population diffusion and road growth. Appl. Math. Model. 2017, 43, 1–14. [Google Scholar] [CrossRef]
- Nduwayezu, G.; Sliuzas, R.; Kuffer, M. Modeling urban growth in Kigali city Rwanda. Rwanda J. 2017, 1. [Google Scholar] [CrossRef]
- Bhowmick, A.R.; Sardar, T.; Bhattacharya, S. Estimation of growth regulation in natural populations by extended family of growth curve models with fractional order derivative: Case studies from the global population dynamics database. Ecol. Informat. 2019, 53, 100980. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, X.; Wang, K.; Huang, L.; Shahtahmassebi, A.; Gan, M.; Weston, M. Delimiting Urban Growth Boundary through Combining Land Suitability Evaluation and Cellular Automata. Sustainability 2017, 9, 2213. [Google Scholar] [CrossRef]
- Santos, M.; Yang, J.; Liu, W.; Li, Y.; Li, X.; Ge, Q. Simulating Intraurban Land Use Dynamics under Multiple Scenarios Based on Fuzzy Cellular Automata: A Case Study of Jinzhou District, Dalian. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Batty, M. Classifying urban models. Environ. Plan. Plan. Des. 2016, 43, 251–256. [Google Scholar] [CrossRef]
- Clarke, K. A decade of cellular urban modeling with SLEUTH: Unresolved issues and problems. Plan. Support Syst. Cities Reg. 2008, 3, 47–60. [Google Scholar]
- Batty, M. Cellular Automata and Urban Form: A Primer. J. Am. Plan. Assoc. 1997, 63, 266–274. [Google Scholar] [CrossRef]
- Guzman, L.A.; Escobar, F.; Peña, J.; Cardona, R. A cellular automata-based land-use model as an integrated spatial decision support system for urban planning in developing cities: The case of the Bogotá region. Land Use Policy 2020, 92, 104445. [Google Scholar] [CrossRef]
- Gómez, J.A.; Patiño, J.E.; Duque, J.C.; Passos, S. Spatiotemporal Modeling of Urban Growth Using Machine Learning. Remote Sens. 2019, 12, 109. [Google Scholar] [CrossRef]
- Liu, D.; Clarke, K.C.; Chen, N. Integrating spatial nonstationarity into SLEUTH for urban growth modeling: A case study in the Wuhan metropolitan area. Comput. Environ. Urban Syst. 2020, 84, 101545. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 3:1–3:39. [Google Scholar] [CrossRef]
- Chen, M.; Liu, W.; Lu, D.; Chen, H.; Ye, C. Progress of China’s new-type urbanization construction since 2014: A preliminary assessment. Cities 2018, 78, 180–193. [Google Scholar] [CrossRef]
- Tan, Y. Exploration of the Development Path of Featured Small Towns with Zhejiang Characteristics; Zhejiang University Press: Hangzhou, China, 2013. [Google Scholar]
- China Statistical Yearbook; China Statistics Press: Beijing, China, 2018; Available online: https://www.chinayearbooks.com/china-statistical-yearbook-2018.html (accessed on 28 December 2020).
- Zhejiang Statistical Yearbook; China Statistics Press: Beijing, China, 2019; Available online: https://www.chinayearbooks.com/zhejiang-statistical-yearbook-2019.html (accessed on 28 December 2020).
- Liu, X.; Huang, Y.; Xu, X.; Li, X.; Li, X.; Ciais, P.; Lin, P.; Gong, K.; Ziegler, A.D.; Chen, A.; et al. High-spatiotemporal-resolution mapping of global urban change from 1985 to 2015. Nat. Sustain. 2020. [Google Scholar] [CrossRef]
- Chinese Academy of Sciences. Institute of Geographic Sciences and Natural Resources Research. Available online: http://english.igsnrr.cas.cn/ (accessed on 28 December 2020).
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4; Technical Report; International Centre for Tropical Agriculture (CIAT): Valle del Cauca, Colombia, 2008; Available online: http://srtm.csi.cgiar.org (accessed on 28 December 2020).
- OpenStreetMap Contributors. Planet OSM, 2017. Available online: https://planet.osm.org (accessed on 28 December 2020).
- Schiavina, M.; Freire, S.; MacManus, K. GHS-POP R2019A-GHS Population grid Multitemporal (1975–1990–2000–2015); European Commission, Joint Research Centre (JRC) [Dataset]: Brussels, Belgium, 2019. [Google Scholar] [CrossRef]
- Dietzel, C.; Clarke, K.C. Toward optimal calibration of the SLEUTH land use change model. Trans. GIS 2007, 11, 29–45. [Google Scholar] [CrossRef]
- Duque, J.C.; Ye, X.; Folch, D.C. spMorph: An exploratory space-time analysis tool for describing processes of spatial redistribution. Pap. Reg. Sci. 2015, 94, 629–651. [Google Scholar] [CrossRef]
- Taleb, N.N.; Bar-Yam, Y.; Cirillo, P. On single point forecasts for fat tailed variables. Int. J. Forecast. 2020. Available online: https://forecasters.org/wp-content/uploads/Talebetal_03082020.pdf (accessed on 28 December 2020). [CrossRef]




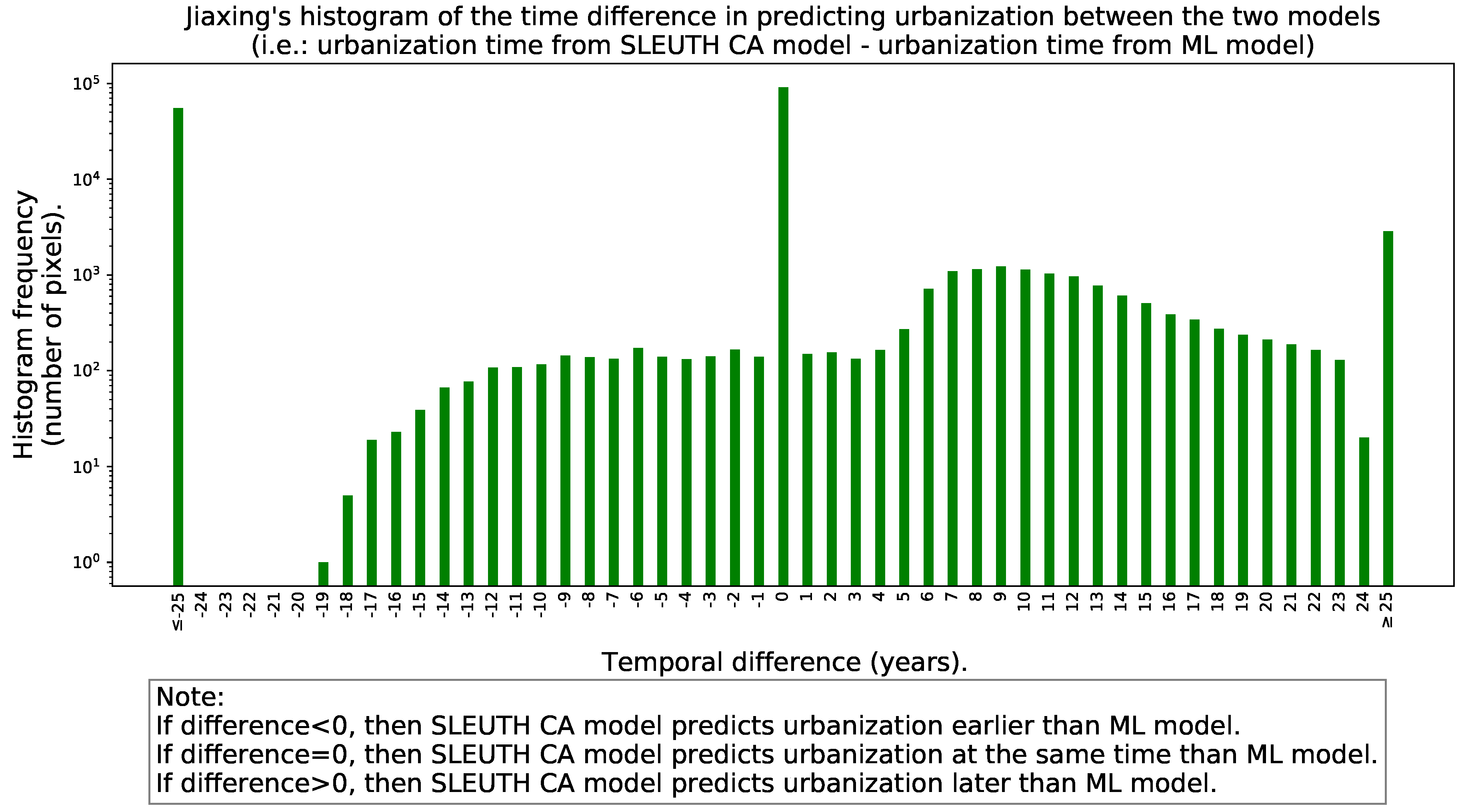
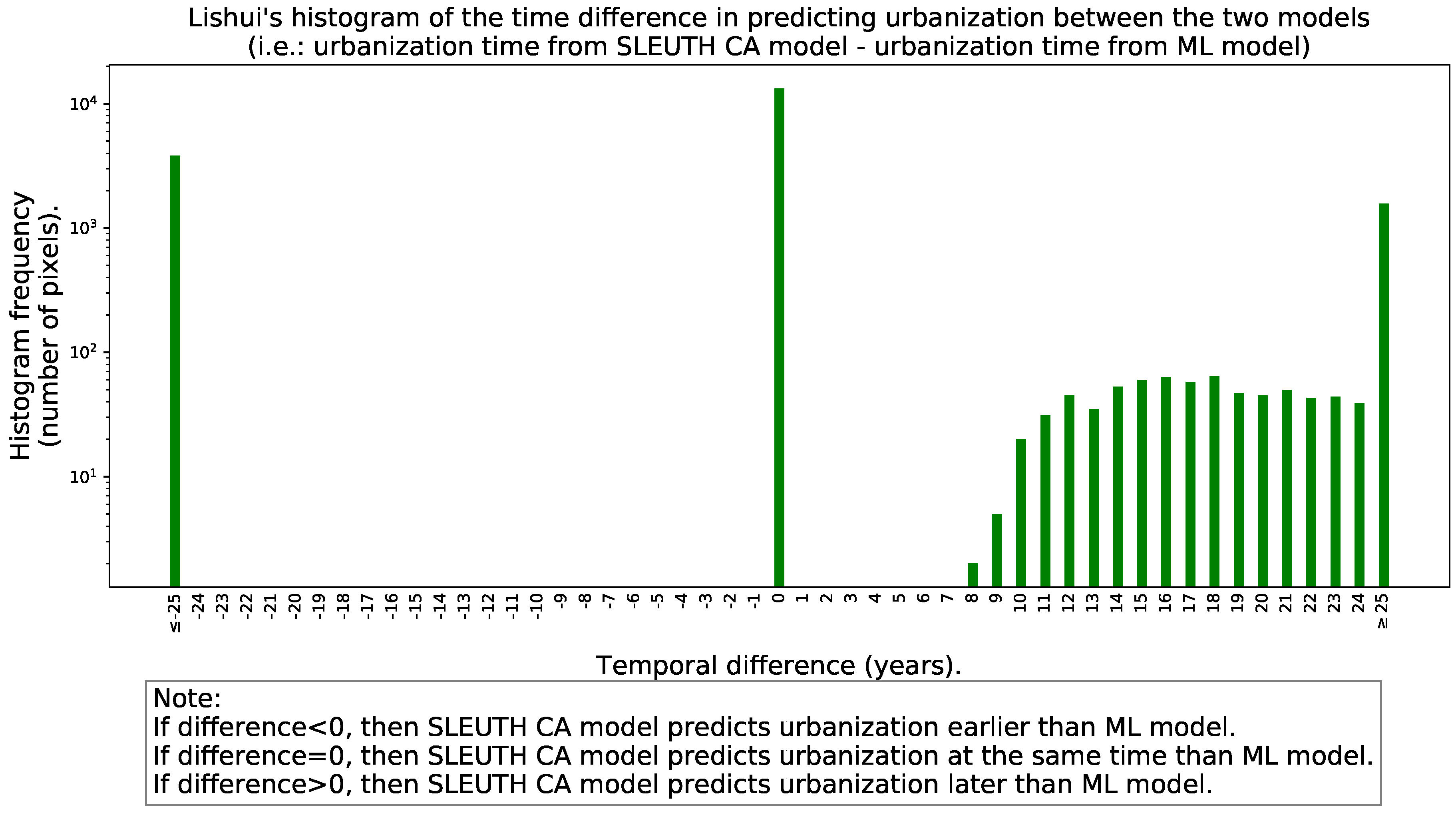






| Characteristics | SLEUTH CA | ML Framework |
|---|---|---|
| Does it expect the input variables in raster format? | Yes | Yes |
| Does it encode human intuition or human rules? | Yes | No |
| Does it require manual tuning or calibration? | Yes | No |
| Is it model driven or data driven? | Model (and data) driven | Data driven |
| Can it include additional independent variables with ease? | Yes with additional rules | Yes |
| What does the output depend on? | Output depends only on previous state(s) | Output depends on previous state(s) and inputs |
| Does it support future deterministic urban interventions? | Not in the standard implementation | Yes |
| Does it use population distribution as the main urban-growth driver? | No. Require manual input | Yes |
| Does the prediction change every time the model is run? | Yes | No |
| What is the key performance indicator of model fitness? | Shape index that measures the spatial fit between the model’s growth | For population distribution: SAD, SSD, RMSE, Pearson’s correlation coefficient. For binary urban footprint: FP rate, error rate, ZNCC, accuracy, F score, and the IoU, which is also known as the Jaccard index |
| Does it require expert knowledge to calibrate or train the model? | Yes | No |
| Does the model estimate get better with more training data? | Yes or no. Depending on the time and space dimension of data | Yes |
| Is it widely used in the literature? | Yes | Not yet, it is very recent |
| Variable Name | Data Source | Digital Format | Original Resolution | Temporal Availability | Used by SLEUTH CA | Used by ML Framework |
|---|---|---|---|---|---|---|
| Binary urban footprint | Obtained from [30] | Raster | 30 m × 30 m | 1990–2015 | Yes | Yes |
| Land use | Obtained from IGSNRR [31] through LULCC classifications | Raster | 100 m × 100 m | 1990, 2000, 2010 | Yes (Recoded using Anderson Level I classification—see Appendix B) | Yes (residential and industrial uses) |
| Terrain slope | Derived from DEM in SRTM [32] | Raster | 90 m × 90 m | 2015 | Yes | Yes |
| Hillshade | Derived from DEM in SRTM [32] | Raster | 90 m × 90 m | 2015 | Yes | No |
| Water bodies | Obtained from IGSNRR [31] through LULCC classifications | Raster | 100 m × 100 m | 1990, 2000, 2010 | Yes | Yes |
| Roads | OSM [33] | Vector | - | 2018–2019 | Yes | No |
| Potential of Roads | Derived from OSM [33] through Equation (1) | Raster | 100 m × 100 m | 2018–2019 | No | Yes |
| Population distribution | GHSL pop [34] | Raster | 250 m × 250 m | 1990, 2000, 2015 | No | Yes |
| Maximum population capacity | Derived from population distribution and binary urban footprint | Raster | 100 m × 100 m | 2015 | No | Yes |
| Official population projections | China Statistical Yearbooks [28,29] | Tabular | Administrative units | 1978–2018 for Jiaxing. 1991–2018 for Lishui | No | Yes |
| Prediction Coefficient | Value for Jiaxing | Value for Lishui |
|---|---|---|
| Diffusion | 100 | 32 |
| Breed | 15 | 67 |
| Spread | 27 | 17 |
| Slope | 1 | 68 |
| Road Gravity | 74 | 96 |
| Task | Time for Jiaxing | Time for Lishui |
|---|---|---|
| Pre-processing | 6.31 min | 11.74 min |
| Training | 98.29 min | 176.15 min |
| Model selection | 6.60 min | 7.20 min |
| Test | 4.77 min | 5.77 min |
| Simulation | 58.79 min | 62.46 min |
| Total | 174.76 min | 263.32 min |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, J.A.; Guan, C.; Tripathy, P.; Duque, J.C.; Passos, S.; Keith, M.; Liu, J. Analyzing the Spatiotemporal Uncertainty in Urbanization Predictions. Remote Sens. 2021, 13, 512. https://doi.org/10.3390/rs13030512
Gómez JA, Guan C, Tripathy P, Duque JC, Passos S, Keith M, Liu J. Analyzing the Spatiotemporal Uncertainty in Urbanization Predictions. Remote Sensing. 2021; 13(3):512. https://doi.org/10.3390/rs13030512
Chicago/Turabian StyleGómez, Jairo Alejandro, ChengHe Guan, Pratyush Tripathy, Juan Carlos Duque, Santiago Passos, Michael Keith, and Jialin Liu. 2021. "Analyzing the Spatiotemporal Uncertainty in Urbanization Predictions" Remote Sensing 13, no. 3: 512. https://doi.org/10.3390/rs13030512
APA StyleGómez, J. A., Guan, C., Tripathy, P., Duque, J. C., Passos, S., Keith, M., & Liu, J. (2021). Analyzing the Spatiotemporal Uncertainty in Urbanization Predictions. Remote Sensing, 13(3), 512. https://doi.org/10.3390/rs13030512









