Empirical Orthogonal Function Analysis and Modeling of Global Tropospheric Delay Spherical Harmonic Coefficients
Abstract
:1. Introduction
2. Data
2.1. ERA-5 Data
2.2. Global Tropospheric Delay SH Coefficients Set
3. Construction of the EOF-Based Model
3.1. Empirical Orthogonal Function and Analysis
3.1.1. EOF Method
3.1.2. Timing Characteristics of Ai(h)
3.2. EGtrop Model Construction
4. Results
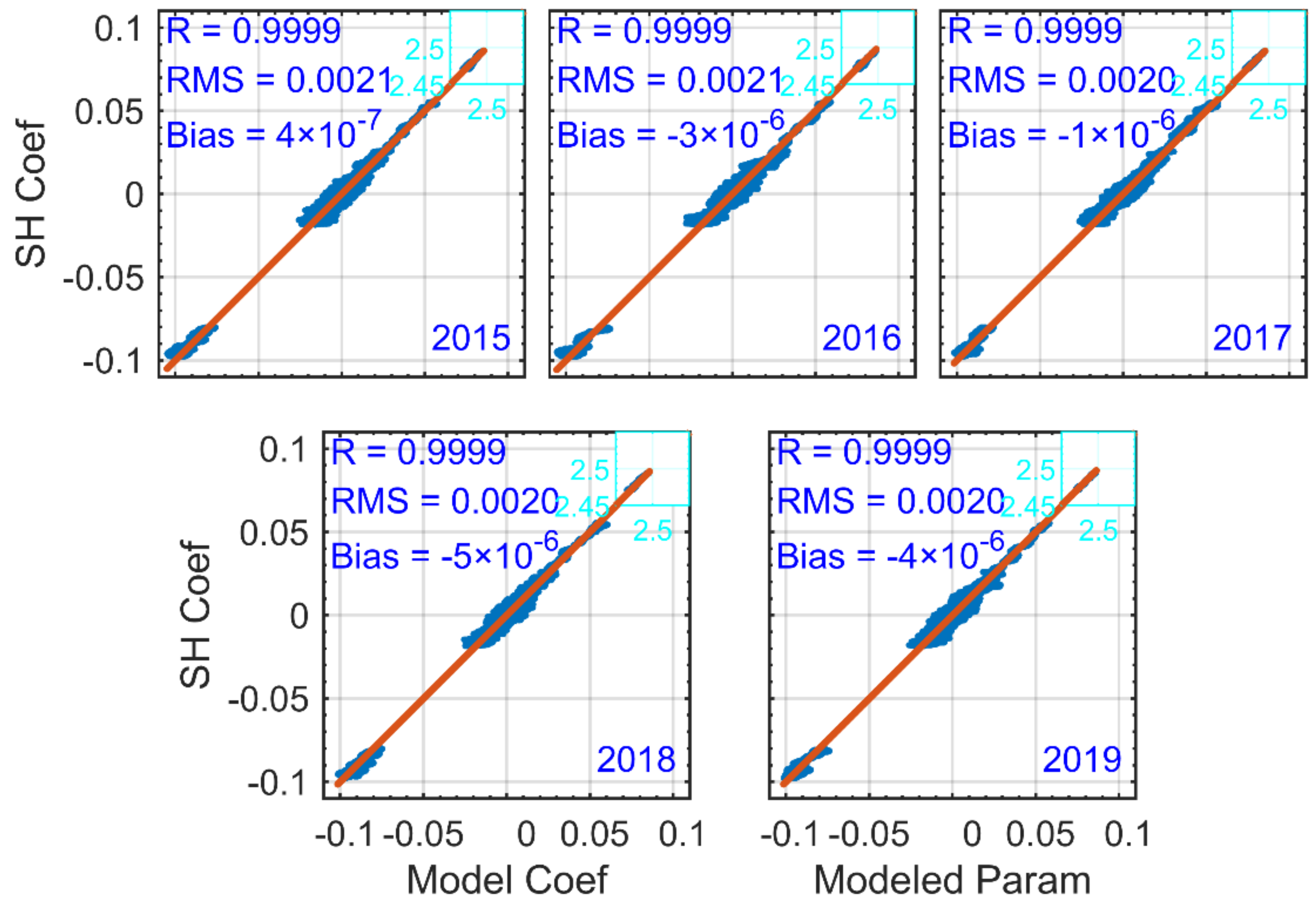
4.1. Global Tropospheric Delay SH Coefficients Set Validation
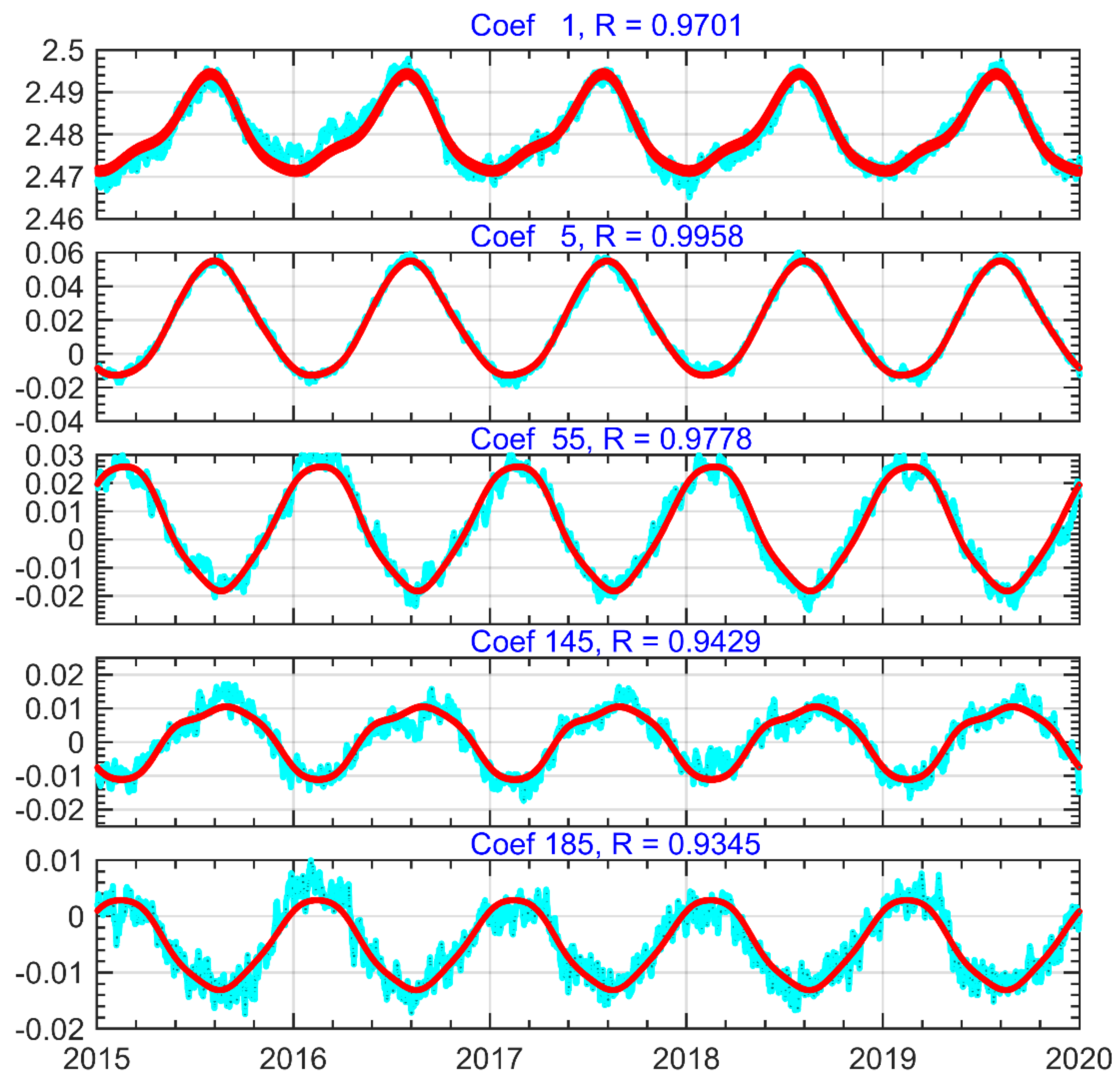
4.2. Verification of SH Coefficient for EGtrop Model
4.3. Verification of the Tropospheric Delay for EGtrop Model
5. Conclusions
- 1.
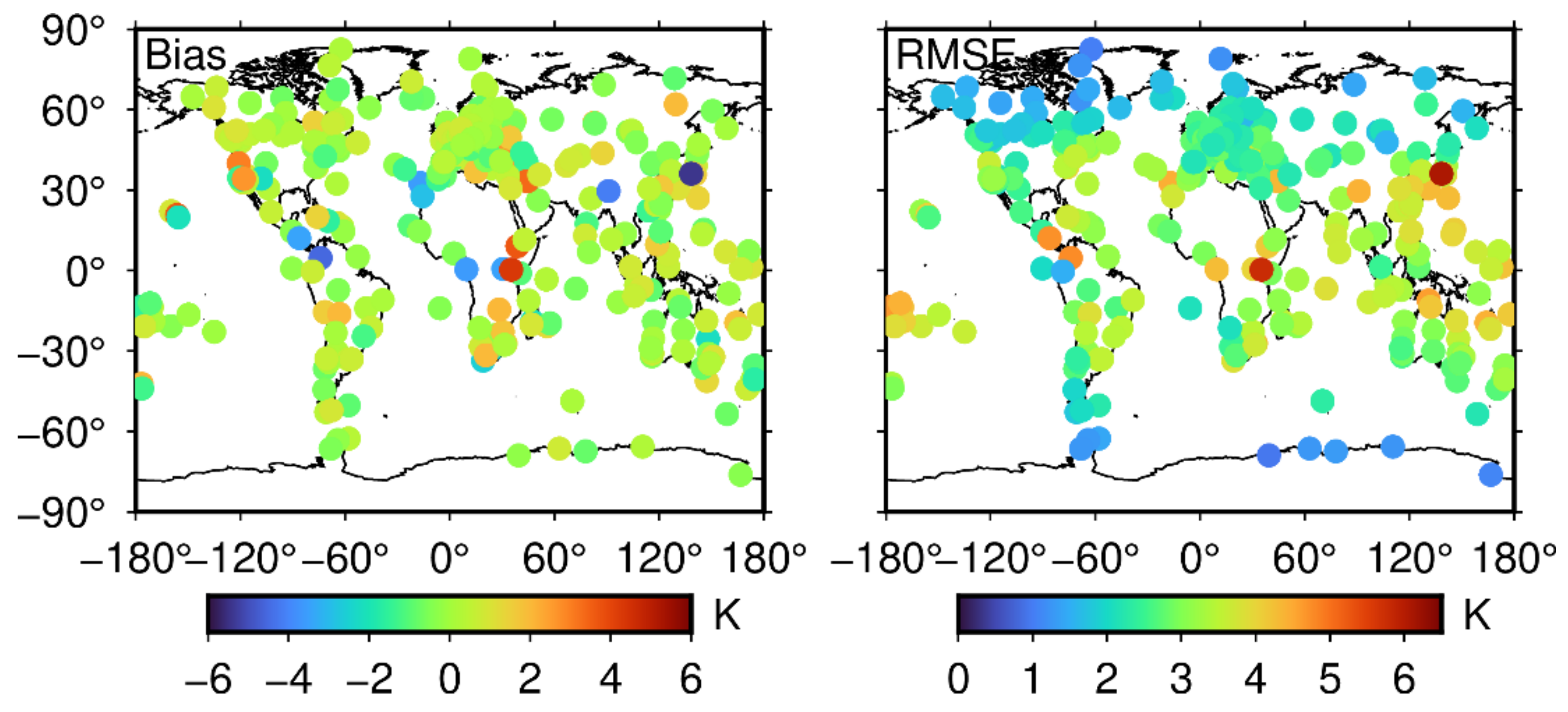
- This study adopts a spherical harmonic function to fit the tropospheric delay calculated with global ERA-5 meteorological data at each time, and an SH coefficients dataset is obtained in the calculation, which is convenient for EOF decomposition and formula fitting. It is verified that the SH_set yield a good accuracy (ERA-5 ZTD, Bias: −1.0 × 10−4 cm; RMSE: 1.97 cm; IGS ZTD, Bias: 0.08 cm; RMSE: 2.6 cm), indicating the feasibility and reliability of this strategy, which provides a reference for near-real-time model products.
- 2.
- Based on the analysis of the SH_set data from 2015 to 2019, it is found that the spherical harmonic coefficients exhibit a certain periodic variation. Based on this phenomenon, this study implements the EOF method and trigonometric functions to establish an SH coefficients model for the SH_set data called EGtrop and combines it with the spherical harmonic function to complete the establishment of the global tropospheric delay model. The results indicate that the accuracy of the new model is higher than that of GPT2w and UNB3m on the different reference data. In addition, through verification of the model accuracy, it is found that the EGtrop model is applicable not only at the global scale but also at the regional scale, and this model yields the advantage of local enhancement.
- 3.
- Compared to GGOS tropospheric delay grid data, the SH_set proposed in this study experiences a slight loss of accuracy, but it greatly reduces the number of parameters and is more convenient for users.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Ifadis, I.M. Space to earth techniques: Some considerations on the zenith wet path delay parameters. Survey Rev. 1993, 32, 130–144. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. 2006, 33, 160–176. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, H.S. Tropospheric Effect on Electromagnetically Measured Range: Prediction from Surface Weather Data. Radio Sci. 1971, 6, 357–367. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Ou, J.; Li, H.; Li, Z. A new global zenith tropospheric delay model IGGtrop for GNSS applications. Chin. Sci. Bull. 2012, 57, 2132–2139. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Contract report for Nav Canada by the Geodetic Research Laboratory, Department of Geodesy and Geomatics Engineering Technical Report No. 187; University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Collins, J.; Langley, R. The residual tropospheric propagation delay: How bad can it get? In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; The Institute of Navigation: Washington, DC, USA, 1998; pp. 729–738. [Google Scholar]
- Li, W.; Yuan, Y.; Ou, J.; He, Y. IGGtrop_SH and IGGtrop_rH: Two Improved Empirical Tropospheric Delay Models Based on Vertical Reduction Functions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5276–5288. [Google Scholar] [CrossRef]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS Tropospheric Correction Model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zhang, B.; Yao, Y. A Global Model for Estimating Tropospheric Delay and Weighted Mean Temperature Developed with Atmospheric Reanalysis Data from 1979 to 2017. Remote Sens. 2019, 11, 1893. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Yao, Y.; Shi, J.; Zhang, Q.; Peng, W. Development of Global Tropospheric Empirical Correction Model with High Temporal Resolution. Remote Sens. 2020, 12, 721. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zhang, B.; Yao, Y. An ERA5-Based Model for Estimating Tropospheric Delay and Weighted Mean Temperature Over China With Improved Spatiotemporal Resolutions. Earth Space Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, X.; Li, Z.; Qiu, C.; Zhang, J.; Li, H.; Li, L. A New Four-Layer Inverse Scale Height Grid Model of China for Zenith Tropospheric Delay Correction. IEEE Access 2020, 8, 210171–210182. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Dvinskikh, N.I. Expansion of ionospheric characteristics fields in empirical orthogonal functions. Adv. Space Res. 1988, 8, 179–187. [Google Scholar] [CrossRef]
- Mao, T.; Wan, W.; Yue, X.; Sun, L.; Zhao, B.; Guo, J. An empirical orthogonal function model of total electron content over China. Radio Sci. 2008, 43. [Google Scholar] [CrossRef]
- Zhang, M.L.; Liu, C.; Wan, W.; Liu, L.; Ning, B. A global model of the ionospheric F2 peak height based on EOF analysis. Ann. Geophys. 2009, 27, 3203–3212. [Google Scholar] [CrossRef] [Green Version]
- Ercha, A.; Zhang, D.H.; Xiao, Z.; Hao, Y.Q.; Ridley, A.J.; Moldwin, M. Modeling ionospheric foF2 by using empirical orthogonal function analysis. Ann. Geophys. 2011, 29, 1501–1515. [Google Scholar] [CrossRef] [Green Version]
- Ercha, A.; Zhang, D.; Ridley, A.J.; Xiao, Z.; Hao, Y. A global model: Empirical orthogonal function analysis of total electron content 1999–2009 data. J. Geophys. Res. Space Phys. 2012, 117, A03328. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zhang, S.-R.; Coster, A.J.; Fang, G. EOF analysis and modeling of GPS TEC climatology over North America. J. Geophys. Res. Space Phys. 2015, 120, 3118–3129. [Google Scholar] [CrossRef]
- Le, H.; Yang, N.; Liu, L.; Chen, Y.; Zhang, H. The latitudinal structure of nighttime ionospheric TEC and its empirical orthogonal functions model over North American sector. J. Geophys. Res. Space Phys. 2017, 122, 963–977. [Google Scholar] [CrossRef]
- Andima, G.; Amabayo, E.B.; Jurua, E.; Cilliers, P.J. Modeling of GPS total electron content over the African low-latitude region using empirical orthogonal functions. Ann. Geophys. 2019, 37, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newslett 2016, 147, 5–6. [Google Scholar]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Li, S.; Xu, T.; Jiang, N.; Yang, H.; Wang, S.; Zhang, Z. Regional Zenith Tropospheric Delay Modeling Based on Least Squares Support Vector Machine Using GNSS and ERA5 Data. Remote Sens. 2021, 13, 1004. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Uwamahoro, J.C.; Habarulema, J.B. Modelling total electron content during geomagnetic storm conditions using empirical orthogonal functions and neural networks. J. Geophys. Res. Space Phys. 2015, 120, 11000–11012. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Yao, Y.; Xu, X.; Hu, Y. Precision Analysis of GGOS Tropospheric Delay Product and Its Application in PPP. Acta Geod. Cartogr. Sin. 2017, 46, 278–287. [Google Scholar] [CrossRef]

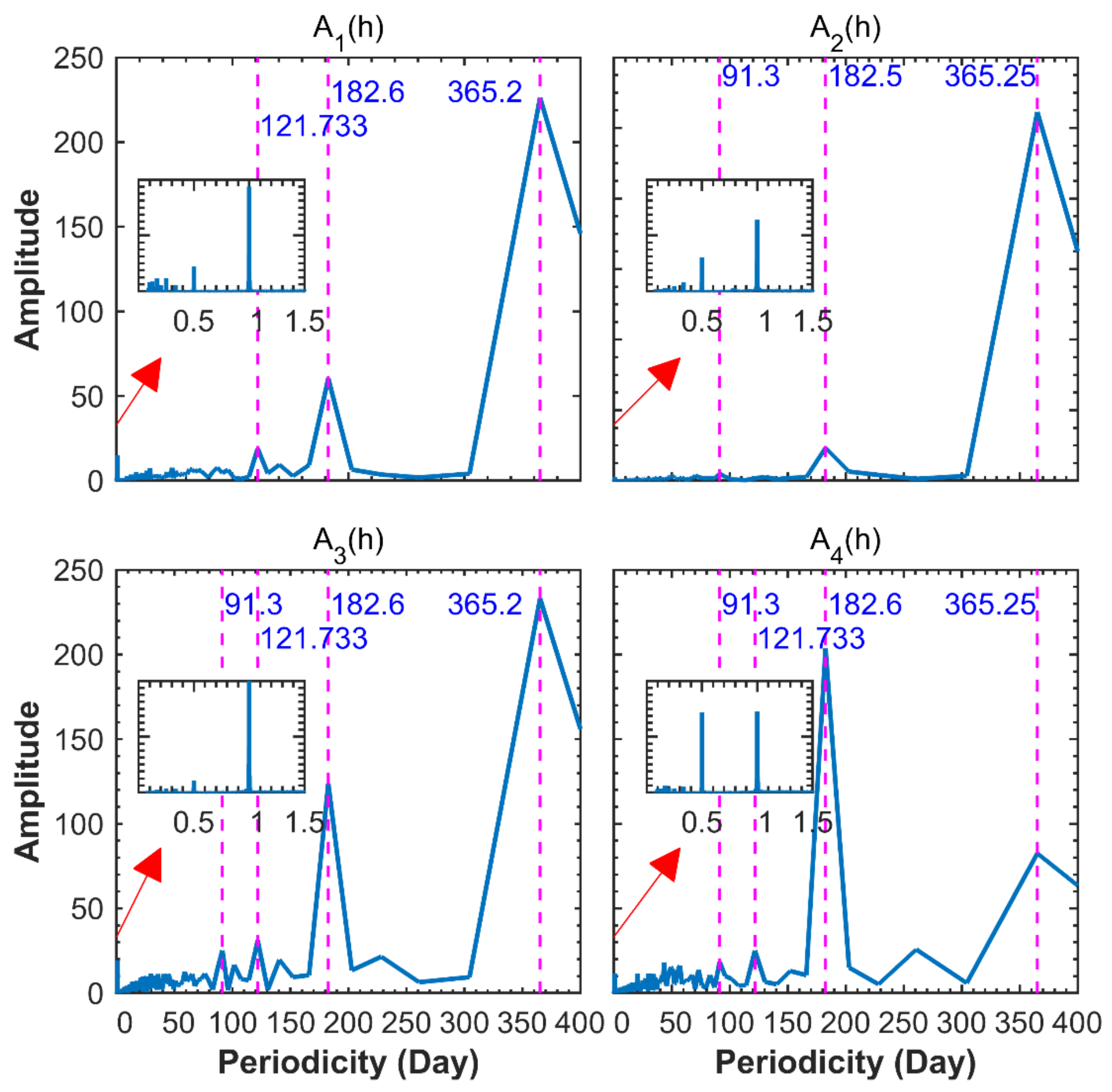

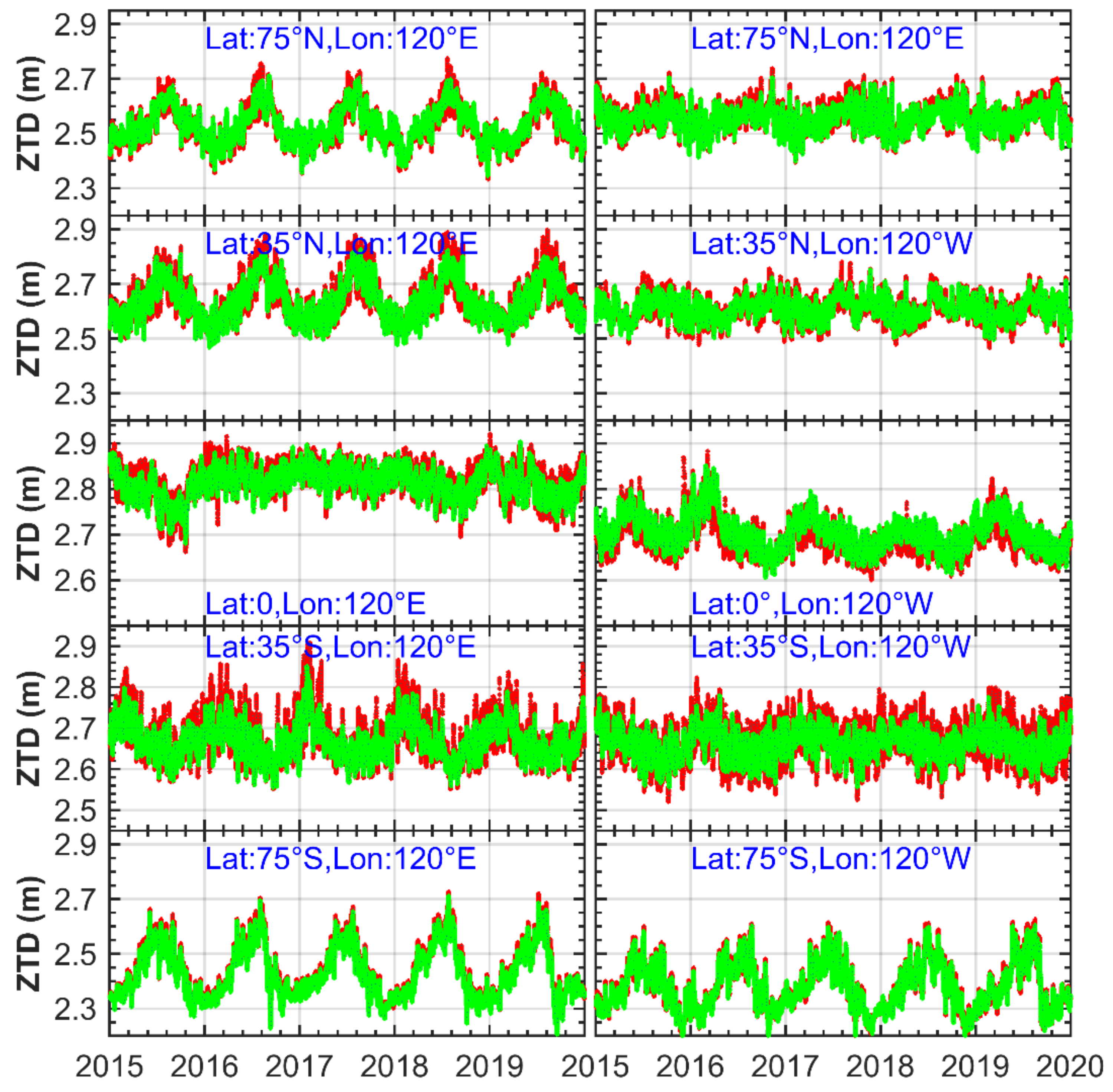

| EOF Mode | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Variances (%) | 99.9503 | 0.0184 | 0.0040 | 0.0031 | 0.0029 | 0.0014 |
| Cumulative var. (%) | 99.9503 | 99.9687 | 99.9727 | 99.9758 | 99.9787 | 99.9801 |
| Year | Bias [cm] | RMSE [cm] | ||||
|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | |
| 2015 | −5.78 | 4.03 | −1.1 × 10−4 | 0.38 | 6.64 | 1.98 |
| 2016 | −5.97 | 3.78 | −1.0 × 10−4 | 0.40 | 6.91 | 2.01 |
| 2017 | −5.99 | 3.79 | −1.1 × 10−4 | 0.39 | 6.79 | 1.93 |
| 2018 | −6.28 | 3.72 | −1.1 × 10−4 | 0.41 | 7.01 | 1.97 |
| 2019 | −6.00 | 3.73 | −1.1 × 10−4 | 0.42 | 6.74 | 1.96 |
| Mean | −1.0 × 10−4 | 1.97 | ||||
| Bias [cm] | RMSE [cm] | |||||
|---|---|---|---|---|---|---|
| Min | Max | Mean | Min | Max | Mean | |
| EGtrop | −10.84 | 6.04 | −0.25 | 1.06 | 11.69 | 3.79 |
| GPT2w | −9.20 | 16.11 | −1.02 | 1.19 | 15.79 | 4.32 |
| UNB3m | −13.28 | 17.32 | 3.11 | 1.06 | 17.72 | 6.60 |
| Data | Area | Error [cm] | Asia | Europe | Oceania | Africa | North America | South America | Antarctica | |
|---|---|---|---|---|---|---|---|---|---|---|
| Model | ||||||||||
| IGS ZTD | EGtrop | Bias | 1.73 | −0.27 | 2.93 | 0.36 | 1.33 | 0.90 | 1.05 | |
| RMSE | 4.97 | 3.14 | 3.66 | 3.09 | 3.98 | 4.09 | 3.36 | |||
| GPT2w | Bias | −0.11 | −0.33 | 0.17 | 0.41 | −0.30 | 1.01 | 0.02 | ||
| RMSE | 4.55 | 3.37 | 3.53 | 3.05 | 4.04 | 4.19 | 2.45 | |||
| UNB3m | Bias | −1.11 | −2.44 | 4.44 | 2.30 | 2.19 | 0.51 | 8.70 | ||
| RMSE | 6.29 | 4.32 | 6.27 | 4.82 | 5.28 | 5.44 | 9.48 | |||
| Radiosonde ZTD | EEtrop | Bias | 0.89 | 0.06 | 3.24 | −0.27 | 1.33 | −0.52 | 0.96 | |
| RMSE | 3.69 | 3.54 | 3.89 | 3.74 | 4.02 | 4.36 | 2.66 | |||
| GPT2w | Bias | −0.95 | 0.72 | 2.38 | −0.23 | −0.41 | −0.32 | −0.13 | ||
| RMSE | 3.49 | 3.52 | 3.20 | 3.59 | 3.88 | 4.43 | 2.64 | |||
| UNB3m | Bias | −0.10 | −0.42 | 8.70 | 5.22 | 0.63 | −0.60 | 9.00 | ||
| RMSE | 3.65 | 4.03 | 9.21 | 7.44 | 4.22 | 6.35 | 9.57 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Liu, H.; Xu, G.; Lu, Z. Empirical Orthogonal Function Analysis and Modeling of Global Tropospheric Delay Spherical Harmonic Coefficients. Remote Sens. 2021, 13, 4385. https://doi.org/10.3390/rs13214385
Ma Y, Liu H, Xu G, Lu Z. Empirical Orthogonal Function Analysis and Modeling of Global Tropospheric Delay Spherical Harmonic Coefficients. Remote Sensing. 2021; 13(21):4385. https://doi.org/10.3390/rs13214385
Chicago/Turabian StyleMa, Yongchao, Hang Liu, Guochang Xu, and Zhiping Lu. 2021. "Empirical Orthogonal Function Analysis and Modeling of Global Tropospheric Delay Spherical Harmonic Coefficients" Remote Sensing 13, no. 21: 4385. https://doi.org/10.3390/rs13214385
APA StyleMa, Y., Liu, H., Xu, G., & Lu, Z. (2021). Empirical Orthogonal Function Analysis and Modeling of Global Tropospheric Delay Spherical Harmonic Coefficients. Remote Sensing, 13(21), 4385. https://doi.org/10.3390/rs13214385






