Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Landslide Historical Inventory
2.3. Landslides Susceptibility Influencing Factors
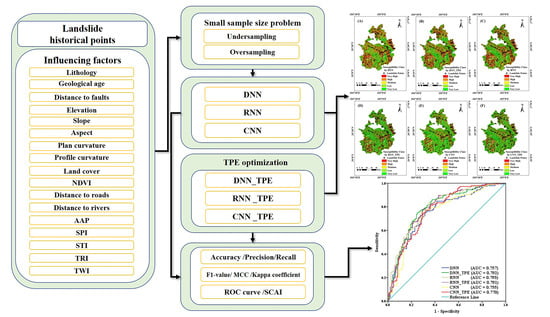
3. Methods
3.1. Data Pretreatment
3.1.1. Geodatabase Construction
3.1.2. Sample Selection
3.2. Multi-Collinearity Analysis
3.3. DNN Model
3.4. RNN Model
3.5. CNN Model
3.6. TPE Optimization
3.7. Model Validation Methods
4. Results
4.1. Factors Multi-Collinearity Analysis and Importance
4.2. The Optimization Process of TPE
4.3. Landslide Susceptibility Assessment and Mapping
4.4. Model Validation and Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Zhu, A.; Miao, Y.; Yang, L.; Bai, S.; Liu, J.; Hong, H. Comparison of the presence-only method and presence-absence method in landslide susceptibility mapping. Catena 2018, 171, 222–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. Study on Risk Assessment, Early Warning and Management of Geological Disasters Caused by Extreme Rainfall—A Case Study of Southeastern Mountains in Jilin Province, 1st ed.; Science Press: Beijing, China, 2017; p. 1. (In Chinese) [Google Scholar]
- Fan, X.; Scaringi, G.; Korup, O.; West, A.J.; Westen, C.J.; Tanyas, H.; Hovius, N.; Hales, T.C.; Jibson, R.W.; Allstadt, K.E.; et al. Earthquake-Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 2019, 57, 421–503. [Google Scholar] [CrossRef] [Green Version]
- Gao, Z.; Ding, M.; Huang, T.; Hu, X. Geohazard vulnerability assessment in Qiaojia seismic zones, SW China. Int. J. Disaster Risk Reduct. 2021, 52, 101928. [Google Scholar] [CrossRef]
- Zhang, F.; Peng, J.; Huang, X.; Lan, H. Hazard assessment and mitigation of non-seismically fatal landslides in China. Nat. Hazards 2021, 106, 785–804. [Google Scholar] [CrossRef]
- Lin, Q.; Lima, P.; Steger, S.; Glade, T.; Jiang, T.; Zhang, J.; Liu, T.; Wang, Y. National-scale data-driven rainfall induced landslide susceptibility mapping for China by accounting for incomplete landslide data. Geosci. Front. 2021, 12, 101248. [Google Scholar] [CrossRef]
- Pereira, S.; Santos, P.P.; Zêzere, J.L.; Tavares, A.O.; Garcia, R.A.C.; Oliveira, S.C. A landslide risk index for municipal land use planning in Portugal. Sci. Total Environ. 2020, 735, 139463. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Smith, H.G.; Spiekermann, R.; Betts, H.; Neverman, A.J. Comparing methods of landslide data acquisition and susceptibility modelling: Examples from New Zealand. Geomorphology 2021, 381, 107660. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly assessing earthquake-induced landslide susceptibility on a global scale using random forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Jia, G.; Alvioli, M.; Gariano, S.L.; Marchesini, I.; Guzzetti, F.; Tang, Q. A global landslide non-susceptibility map. Geomorphology 2021, 389, 107804. [Google Scholar] [CrossRef]
- Bălteanu, D.; Micu, M.; Jurchescu, M.; Malet, J.; Sima, M.; Kucsicsa, G.; Dumitrică, C.; Petrea, D.; Mărgărint, M.C.; Bilaşco, Ş.; et al. National-scale landslide susceptibility map of Romania in a European methodological framework. Geomorphology 2020, 371, 107432. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, S. GIS-based comparative study of Bayes network, Hoeffding tree and logistic model tree for landslide susceptibility modeling. Catena 2021, 203, 105344. [Google Scholar] [CrossRef]
- Chen, L.; Guo, H.; Gong, P.; Yang, Y.; Zuo, Z.; Gu, M. Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput. Geosci. 2021, 156, 104899. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, Y.; Huang, F.; Fan, X.; Huang, J. Landslide susceptibility zonation method based on C5.0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 2021, 12, 101249. [Google Scholar] [CrossRef]
- Stanley, T.A.; Kirschbaum, D.B.; Sobieszczyk, S.; Jasinski, M.F.; Borak, J.S.; Slaughter, S.L. Building a landslide hazard indicator with machine learning and land surface models. Environ. Model. Softw. 2020, 129, 104692. [Google Scholar] [CrossRef]
- Li, L.; Lan, H. Integration of Spatial Probability and Size in Slope-Unit-Based Landslide Susceptibility Assessment: A Case Study. Int. J. Environ. Res. Public Health 2020, 17, 8055. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, S.; Roy, A.K.; Martha, T.R. Landslide susceptibility assessment using Information Value Method in parts of the Darjeeling Himalayas. J. Geol. Soc. India 2013, 82, 351–362. [Google Scholar] [CrossRef]
- Shu, H.; Guo, Z.; Qi, S.; Song, D.; Pourghasemi, H.R.; Ma, J. Integrating Landslide Typology with Weighted Frequency Ratio Model for Landslide Susceptibility Mapping: A Case Study from Lanzhou City of Northwestern China. Remote Sens. 2021, 13, 3623. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, L.; Wang, S.; Lari, S. Regional landslide susceptibility zoning with considering the aggregation of landslide points and the weights of factors. Landslides 2014, 11, 399–409. [Google Scholar] [CrossRef]
- Tan, Q.; Bai, M.; Zhou, P.; Hu, J.; Qin, X. Geological hazard risk assessment of line landslide based on remotely sensed data and GIS. Measurement 2021, 169, 108370. [Google Scholar] [CrossRef]
- Saha, A.; Saha, S. Comparing the efficiency of weight of evidence, support vector machine and their ensemble approaches in landslide susceptibility modelling: A study on Kurseong region of Darjeeling Himalaya, India. Remote Sens. Appl. Soc. Environ. 2020, 19, 100323. [Google Scholar] [CrossRef]
- Tang, Y.; Feng, F.; Guo, Z.; Feng, W.; Li, Z.; Wang, J.; Sun, Q.; Ma, H.; Li, Y. Integrating principal component analysis with statistically-based models for analysis of causal factors and landslide susceptibility mapping: A comparative study from the loess plateau area in Shanxi (China). J. Clean. Prod. 2020, 277, 124159. [Google Scholar] [CrossRef]
- Yi, Y.N.; Zhang, Z.J.; Zhang, W.C.; Xu, Q.; Deng, C.; Li, Q.L. GIS-based earthquake-triggered-landslide susceptibility mapping with an integrated weighted index model in Jiuzhaigou region of Sichuan Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 1973–1988. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Zhang, J.; Zhang, Y.; Lang, Q. Applying a Series and Parallel Model and a Bayesian Networks Model to Produce Disaster Chain Susceptibility Maps in the Changbai Mountain area, China. Water 2019, 11, 2144. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.H.; Ge, T.T.; Tian, W.; Liou, Y.A. Debris Flow Susceptibility Mapping Using Machine-Learning Techniques in Shigatse Area, China. Remote Sens. 2019, 11, 2801. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Du, G.L.; Zhang, Y.S.; Iqbal, J.; Yang, Z.H.; Yao, X. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mt. Sci. 2017, 14, 249–268. [Google Scholar] [CrossRef]
- Long, N.; De Smedt, F. Analysis and Mapping of Rainfall-Induced Landslide Susceptibility in A Luoi District, Thua Thien Hue Province, Vietnam. Water 2019, 11, 51. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.T.; Song, C.; Yang, Y.; Xu, C.D.; Guo, F.; Xie, L. New method for landslide susceptibility mapping supported by spatial logistic regression and GeoDetector: A case study of Duwen Highway Basin, Sichuan Province, China. Geomorphology 2019, 324, 62–71. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.F.; Chen, C.W.; Khosravi, K.; Yang, Y.; Pham, B.T. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Shahri, A.A.; Spross, J.; Johansson, F.; Larsson, S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena 2019, 183, 104225. [Google Scholar] [CrossRef]
- Novellino, A.; Cesarano, M.; Cappelletti, P.; Di Martire, D.; Di Napoli, M.; Ramondini, M.; Sowter, A.; Calcaterra, D. Slow-moving landslide risk assessment combining Machine Learning and InSAR techniques. Catena 2021, 203, 105317. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pourghasemi, H.R.; Indra, P.; Dholakia, M.B. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naive bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Rong, G.; Alu, S.; Li, K.; Su, Y.; Zhang, J.; Zhang, Y.; Li, T. Rainfall Induced Landslide Susceptibility Mapping Based on Bayesian Optimized Random Forest and Gradient Boosting Decision Tree Models—A Case Study of Shuicheng County, China. Water 2020, 12, 3066. [Google Scholar] [CrossRef]
- Aktas, H.; San, B.T. Landslide susceptibility mapping using an automatic sampling algorithm based on two level random sampling. Comput. Geosci. 2019, 133, 104329. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Dou, J.; Chang, K.T.; Chen, S.S.; Yunus, A.P.; Liu, J.K.; Xia, H.; Zhu, Z.F. Automatic Case-Based Reasoning Approach for Landslide Detection: Integration of Object-Oriented Image Analysis and a Genetic Algorithm. Remote Sens. 2015, 7, 4318–4342. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.C.; Hong, H.Y. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef] [PubMed]
- Ali, S.A.; Parvin, F.; Vojteková, J.; Costache, R.; Linh, N.T.T.; Pham, Q.B.; Vojtek, M.; Gigović, L.; Ahmad, A.; Ghorbani, M.A. GIS-based landslide susceptibility modeling: A comparison between fuzzy multi-criteria and machine learning algorithms. Geosci. Front. 2021, 12, 857–876. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying deep learning and benchmark machine learning algorithms for landslide susceptibility modelling in Rorachu river basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Sun, D.L.; Wen, H.J.; Wang, D.Z.; Xu, J.H. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Rong, G.; Li, K.; Han, L.; Alu, S.; Zhang, J.; Zhang, Y. Hazard Mapping of the Rainfall–Landslides Disaster Chain Based on GeoDetector and Bayesian Network Models in Shuicheng County, China. Water 2020, 12, 2572. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, R.; Liu, X.; Ju, N.; Xie, M. Field survey of a catastrophic high-speed long-runout landslide in Jichang Town, Shuicheng County, Guizhou, China, on July 23, 2019. Landslides 2020, 17, 1415–1427. [Google Scholar] [CrossRef]
- China Geological Survey. Available online: http://www.cgs.gov.cn (accessed on 21 May 2021).
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef] [PubMed]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2019, 78, 4017–4034. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, W.; Hong, H. Application of frequency ratio, weights of evidence and evidential belief function models in landslide susceptibility mapping. Geocarto Int. 2017, 32, 619–639. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Fang, Z.; Peng, L.; Hong, H. Potential of Ensemble Learning to Improve Tree-Based Classifiers for Landslide Susceptibility Mapping. IEEE J.-STARS 2020, 13, 4642–4662. [Google Scholar] [CrossRef]
- Jebur, M.N.; Pradhan, B.; Tehrany, M.S. Optimization of landslide conditioning factors using very high-resolution airborne laser scanning (LiDAR) data at catchment scale. Remote Sens. Environ. 2014, 152, 150–165. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Verbiest, N.; Ramentol, E.; Cornelis, C.; Herrera, F. Preprocessing noisy imbalanced datasets using SMOTE enhanced with fuzzy rough prototype selection. Appl. Soft Comput. 2014, 22, 511–517. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.; Liem, N.V.; Trinh, P.T. Comparing the prediction performance of a Deep Learning Neural Network model with conventional machine learning models in landslide susceptibility assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Chen, H.; Zeng, Z.; Tang, H. Landslide Deformation Prediction Based on Recurrent Neural Network. Neural Process. Lett. 2015, 41, 169–178. [Google Scholar] [CrossRef]
- Xu, S.; Niu, R. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China. Comput. Geosci. 2018, 111, 87–96. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Cai, X.; Liu, Y.; Zhu, B. A Novel Gaussian–Bernoulli Based Convolutional Deep Belief Networks for Image Feature Extraction. Neural Process. Lett. 2019, 49, 305–319. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y. Artificial Intelligence Image Recognition Method Based on Convolutional Neural Network Algorithm. IEEE Access 2020, 8, 125731–125744. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Self-Learning Random Forests Model for Mapping Groundwater Yield in Data-Scarce Areas. Nat. Resour. Res. 2019, 28, 757–775. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the 24th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; pp. 2546–2554. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Shen, X.; Cao, L. Tree-Species Classification in Subtropical Forests Using Airborne Hyperspectral and LiDAR Data. Remote Sens. 2017, 9, 1180. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.H.; Xia, J.B.; Zhang, S.L.; Yan, J.K.; Ai, X.C.; Dai, K.B. An efficient intrusion detection system based on support vector machines and gradually feature removal method. Expert Syst. Appl. 2012, 39, 424–430. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Nhu, V.H.; Hoang, N.D.; Nguyen, H.; Ngo, P.; Bui, T.T.; Hoa, P.V.; Samui, P.; Bui, D.T. Effectiveness assessment of Keras based deep learning with different robust optimization algorithms for shallow landslide susceptibility mapping at tropical area. Catena 2020, 188, 104458. [Google Scholar] [CrossRef]
- Süzen, M.L.; Doyuran, V. A comparison of the GIS based landslide susceptibility assessment methods: Multivariate versus bivariate. Environ. Geol. 2004, 45, 665–679. [Google Scholar] [CrossRef]
- Alatorre, L.C.; Sanchez-Andres, R.; Cirujano, S.; Begueria, S.; Sanchez-Carrillo, S. Identification of Mangrove Areas by Remote Sensing: The ROC Curve Technique Applied to the Northwestern Mexico Coastal Zone Using Landsat Imagery. Remote Sens. 2011, 3, 1568–1583. [Google Scholar] [CrossRef] [Green Version]
- Tsangaratos, P.; Ilia, I.; Hong, H.Y.; Chen, W.; Xu, C. Applying Information Theory and GIS-based quantitative methods to produce landslide susceptibility maps in Nancheng County, China. Landslides 2017, 14, 1091–1111. [Google Scholar] [CrossRef]
- Keras Tuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 21 May 2021).
- Choi, J.; Oh, H.J.; Lee, H.J.; Lee, C.; Lee, S. Combining landslide susceptibility maps obtained from frequency ratio, logistic regression, and artificial neural network models using ASTER images and GIS. Eng. Geol. 2012, 124, 12–23. [Google Scholar] [CrossRef]
- Esper Angillieri, M.Y. Debris flow susceptibility mapping using frequency ratio and seed cells, in a portion of a mountain international route, Dry Central Andes of Argentina. Catena 2020, 189, 104504. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]



















| Influencing Factors | Variable Type | Resolution | Unit | Class | ||||
|---|---|---|---|---|---|---|---|---|
| 5 | 4 | 3 | 2 | 1 | ||||
| Lithology | Discrete | - | - | Claystone | Basalt | Sandstone | Dolomite | Limestone |
| Geological age | Discrete | - | - | Devonian | Carboniferous | Permian | Triassic | Jurassic |
| Distance to Faults | Continuous | - | m | <500 | 500~700 | 700~1000 | 1000~2000 | >2000 |
| Elevation | Continuous | 30 × 30 m | m | 2079~2863 | 1827~2079 | 1570~1827 | 1248~1570 | 633~1248 |
| Slope | Continuous | 30 × 30 m | ° | 40.05~74.74 | 28.58~40.05 | 19.70~28.58 | 11.56~19.70 | 0~11.56 |
| Aspect | Discrete | 30 × 30 m | - | Sunny slope | Semi-sunny slope | Flat | Semi-shady slope | Shady slope |
| Plan curvature | Discrete | 30 × 30 m | - | >0.33 | 0.10~0.33 | −0.10~0.10 | −0.33~−0.10 | <−0.33 |
| Profile curvature | Discrete | 30 × 30 m | - | >0.42 | 0.11~0.42 | −0.11~0.11 | −0.42~−0.11 | <−0.42 |
| Land cover | Discrete | 30 × 30 m | - | Impervious surface | Cropland, bare land | Shrubland | Forest, grassland | Wetland, water, snow/ice |
| NDVI | Continuous | 30 × 30 m | - | <0.111 | 0.111~0.162 | 0.162~0.201 | 0.201~0.247 | >0.247 |
| Distance to roads | Continuous | - | m | <500 | 500~700 | 700~1000 | 1000~2000 | >2000 |
| Distance to rivers | Continuous | - | m | <500 | 500~700 | 700~1000 | 1000~2000 | >2000 |
| AAP | Continuous | 30 × 30 m | mm | 1272~1353 | 1212~1272 | 1150~1212 | 1080~1150 | 981~1080 |
| SPI | Continuous | 30 × 30 m | - | >1000 | 500~1000 | 100~500 | 0~100 | 0 |
| STI | Continuous | 30 × 30 m | - | >20 | 10~20 | 1~10 | 0~1 | 0 |
| TRI | Continuous | 30 × 30 m | - | 91~342 | 58~91 | 38~58 | 22~38 | 0~22 |
| TWI | Continuous | 30 × 30 m | - | 11.87~23.50 | 8.73~11.87 | 6.61~8.73 | 5.00~6.61 | 1.85~5.00 |
| Model | Hyperparameter | Initial Value | Domain Space |
|---|---|---|---|
| DNN | Units | 35 | [10, 100] |
| Dropout rate | 0 | [0, 0.50] | |
| Batch size | 1 | [1, 100] | |
| Epoch | 50 | [10, 100] | |
| Optimizers | Adam | [Adam, Adamax, Sgd, Rmsprop, Adagrad, Adadelta, Nadam] | |
| RNN | Units | 50 | [10, 100] |
| Dropout rate | 0 | [0, 0.50] | |
| Batch size | 1 | [1, 100] | |
| Epoch | 50 | [10, 100] | |
| Optimizers | Adam | [Adam, Adamax, Sgd, Rmsprop, Adagrad, Adadelta, Nadam] | |
| CNN | Fitters | 20 | [10, 100] |
| Kernel size | 3 | [1, 10] | |
| Pooling size | 2 | [1, 10] | |
| Units | 50 | [10, 100] | |
| Dropout rate | 0 | [0, 0.50] | |
| Epoch | 100 | [10, 200] | |
| Optimizers | Adam | [Adam, Adamax, Sgd, Rmsprop, Adagrad, Adadelta, Nadam] |
| Explanatory Variable | Multi-Collinearity Statistics | |
|---|---|---|
| VIF | Tolerance | |
| Lithology | 1.533 | 0.652 |
| Geological age | 1.234 | 0.810 |
| Faults | 1.666 | 0.600 |
| Elevation | 1.775 | 0.563 |
| Slope | 2.911 | 0.343 |
| Aspect | 1.078 | 0.928 |
| Plan curvature | 1.502 | 0.666 |
| Profile curvature | 1.483 | 0.674 |
| Land cover | 1.249 | 0.801 |
| NDVI | 1.193 | 0.838 |
| Roads | 1.122 | 0.891 |
| Rivers | 1.150 | 0.869 |
| AAP | 1.864 | 0.537 |
| SPI | 6.085 | 0.164 |
| STI | 5.132 | 0.195 |
| TRI | 3.257 | 0.307 |
| TWI | 4.802 | 0.208 |
| Model | Hyperparameter | Initial Value | TPE Optimization Result |
|---|---|---|---|
| DNN | Units | 35 | 96 |
| Dropout rate | 0 | 0.395 | |
| Batch size | 1 | 38 | |
| Epoch | 50 | 42 | |
| Optimizers | Adam | Adam | |
| RNN | Units | 50 | 95 |
| Dropout rate | 0 | 0.357 | |
| Batch size | 1 | 42 | |
| Epoch | 50 | 69 | |
| Optimizers | Adam | Adam | |
| CNN | Fitters | 20 | 20 |
| Kernel size | 3 | 6 | |
| Pooling size | 2 | 2 | |
| Units | 50 | 69 | |
| Dropout rate | 0 | 0.177 | |
| Epoch | 100 | 177 | |
| Optimizers | Adam | RmsProp |
| DNN | DNN_TPE | RNN | RNN_TPE | CNN | CNN_TPE | |
|---|---|---|---|---|---|---|
| Accuracy | 0.715 | 0.743 | 0.719 | 0.712 | 0.722 | 0.733 |
| Precision | 0.701 | 0.733 | 0.676 | 0.697 | 0.735 | 0.745 |
| Recall | 0.750 | 0.764 | 0.840 | 0.750 | 0.694 | 0.708 |
| F1 | 0.725 | 0.748 | 0.749 | 0.722 | 0.714 | 0.726 |
| MCC | 0.432 | 0.487 | 0.451 | 0.425 | 0.445 | 0.466 |
| Kappa | 0.431 | 0.486 | 0.438 | 0.424 | 0.444 | 0.465 |
| Model | DNN | DNN_TPE | RNN | RNN_TPE | CNN | CNN_TPE | ||
|---|---|---|---|---|---|---|---|---|
| SCAI | ||||||||
| Class | ||||||||
| Very low | 3.3079 | 2.3431 | 2.7134 | 2.6216 | 1.9600 | 1.8397 | ||
| Low | 1.5043 | 1.6599 | 1.6960 | 0.9992 | 1.0252 | 1.0706 | ||
| Medium | 1.0784 | 1.2582 | 1.4446 | 0.5926 | 1.0597 | 0.8669 | ||
| High | 0.7650 | 0.9212 | 0.7055 | 0.6436 | 0.5241 | 0.5801 | ||
| Very high | 0.5022 | 0.4431 | 0.4636 | 0.4650 | 0.3882 | 0.4871 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rong, G.; Li, K.; Su, Y.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sens. 2021, 13, 4694. https://doi.org/10.3390/rs13224694
Rong G, Li K, Su Y, Tong Z, Liu X, Zhang J, Zhang Y, Li T. Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sensing. 2021; 13(22):4694. https://doi.org/10.3390/rs13224694
Chicago/Turabian StyleRong, Guangzhi, Kaiwei Li, Yulin Su, Zhijun Tong, Xingpeng Liu, Jiquan Zhang, Yichen Zhang, and Tiantao Li. 2021. "Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment" Remote Sensing 13, no. 22: 4694. https://doi.org/10.3390/rs13224694
APA StyleRong, G., Li, K., Su, Y., Tong, Z., Liu, X., Zhang, J., Zhang, Y., & Li, T. (2021). Comparison of Tree-Structured Parzen Estimator Optimization in Three Typical Neural Network Models for Landslide Susceptibility Assessment. Remote Sensing, 13(22), 4694. https://doi.org/10.3390/rs13224694