Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model
Abstract
:1. Introduction
2. Signal Processing and Height Inversion
2.1. Signal Processing
2.1.1. Data Fetch
2.1.2. Coherent Integration
2.1.3. Retracking and Incoherent Average
2.2. Height Inversion
2.2.1. Delay Estimation and Error Correction
2.2.2. Height Retrieval and Precision Calculation
3. Construction of Coherent Integration Time Optimization Model
3.1. The Reconstruction of Altimetric Precision Model
3.2. The Relationship between Model Parameters and Coherent Integration Time
3.2.1. Altimetric Sensitivity
3.2.2. Effective Incoherent Average Number
4. Results and Application
4.1. Validation of Coherent Integration Time Optimization Model
4.1.1. Altimetric Sensitivity
4.1.2. Effective Incoherent Average Number
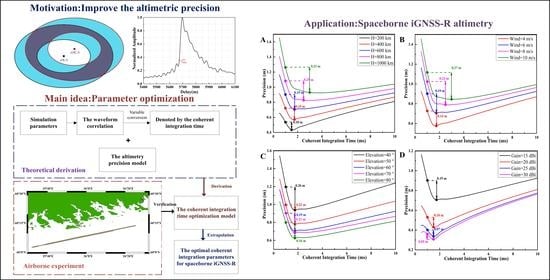
4.2. Application of Coherent Integration Time Optimization Model
4.2.1. Model Application: Airborne Experiment Scenario
4.2.2. Model Application: Extrapolation to Spaceborne Scenario
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Lowe, S.T.; Zuffada, C.; LaBrecque, J.L.; Lough, M.; Lerma, J.; Young, L.E. An ocean-altimetry measurement using reflected GPS signals observed from a low-altitude aircraft. IEEE Int. Geosci. Remote Sens. Symp. 2000, 5, 2185–2187. [Google Scholar] [CrossRef]
- Beyerle, G.; Hocke, K. Observation and simulation of direct and reflected GPS signals in radio occultation experiments. Geophys. Res. Lett. 2001, 28, 1895–1898. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–150. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Camps, A.; Ramos-Perez, I.; Rius, A. Experimental evaluation of GNSS reflectometry altimetric precision using the P(Y) and C/A signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1493–1500. [Google Scholar] [CrossRef]
- Li, W.; Yang, D.; D’Addio, S.; Martin-Neira, M. Partial interferometric processing of reflected GNSS signals for ocean altimetry. Geophys. Res. Lett. 2014, 11, 1509–1513. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martin-Neira, M.; Fabra, F.; Nogues-Correig, O.; Ribo, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Feng, W.; Yang, D.; Li, W.; Wei, Y. On-ground retracking to correct distorted waveform in spaceborne global navigation satellite system-reflectometry. Remote Sens. 2017, 9, 643. [Google Scholar] [CrossRef] [Green Version]
- Hajj, G.A. Theoretical description of a bistatic system for ocean altimetry using the GPS signa. Radio Sci. 2003, 38, 1001–1019. [Google Scholar] [CrossRef]
- Fernando Marchan-Hernandez, J.; Camps, A.; Rodriguez-Alvarez, N.; Valencia, E.; Bosch-Lluis, X.; Ramos-Perez, I. An efficient algorithm to the simulation of delay-Doppler maps of reflected global navigation satellite system signals. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2733–2740. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martin-Neira, M. Altimetric analysis of the sea-surface GPS-reflected signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Rodríguez, E. Altimetry for non-Gaussian oceans: Height biases and estimation of parameters. J. Geophys. Res. 1988, 93, 14107–14120. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. Global ocean altimetry with GNSS reflections from TechDemoSat-1. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4088–4097. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Assessment of spaceborne GNSS-R ocean altimetry performance using CYGNSS mission raw data. IEEE Trans. Geosci. Remote Sens. 2019, 58, 238–250. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wu, F.; Cui, Z.; Kang, G. A necessary model to quantify the scanning loss effect in spaceborne iGNSS-R ocean altimetry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1619–1627. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, W.; Wu, F.; Kang, G.; Li, Z.; Wang, Q.; Cui, Z. Increasing the number of sea surface reflected signals received by GNSS-Reflectometry altimetry satellite using the nadir antenna observation capability optimization method. Remote Sens. 2019, 11, 2473. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M.; D’Addio, S.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS ocean altimeter in-orbit demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- You, H.I.; Garrison, J.L.; Heckler, G.; Zavorotny, V.U. Stochastic voltage model and experimental measurement of ocean-scattered GPS signal statistics. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2160–2169. [Google Scholar] [CrossRef]
- Garrison, J.L. A statistical model and simulator for ocean-reflected GNSS signals. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6007–6019. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribo, S.; Martin-Neira, M. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea surface wind speed retrieval from the first Chinese GNSS-R mission: Technique and preliminary results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Fabra, F.; Cardellach, E.; Ribo, S.; Li, W.; Rius, A.; Carlos Arco-Fernandez, J.; Nogués-Correig, O.; Praks, J.; Rouhe, E.; Seppänen, J.; et al. Is accurate synoptic altimetry achievable by means of interferometric GNSS-R? Remote Sens. 2019, 11, 505. [Google Scholar] [CrossRef] [Green Version]
- Ribo, S.; Arco-Fernandez, J.C.; Cardellach, E.; Fabra, F.; Li, W.; Nogues-Correig, O.; Rius, A.; Martín-Neira, M. A software-defined GNSS reflectometry recording receiver with wide-bandwidth, multi-band capability and digital beam-forming. Remote Sens. 2017, 9, 450. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Camps, A.; Valencia, E.; Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Ramos-Perez, I.; Carreno-Luengo, H. Retracking considerations in spaceborne GNSS-R altimetry. GPS Solut. 2012, 16, 507–518. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Mashburn, J.; Axelrad, P.; Lowe, S.T.; Larson, K.M. An assessment of the precision and accuracy of altimetry retrievals for a monterey bay GNSS-R experiment. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4660–4668. [Google Scholar] [CrossRef]
- D’Addio, S.; Martin-Neira, M.; di Bisceglie, M.; Galdi, C.; Martin Alemany, F. GNSS-R altimeter based on Doppler multi-looking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1452–1460. [Google Scholar] [CrossRef]
- D’Addio, S.; Martin-Neira, M. Comparison of processing techniques for remote sensing of earth-exploiting reflected radio-navigation signals. Electron. Lett. 2013, 49, 292–293. [Google Scholar] [CrossRef]
- Fan, M.; Zhang, B.; Wang, F. Semi-codeless based P(Y) code autocorrelation GNSS-R sea surface altimetry method. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 398–404. [Google Scholar] [CrossRef]
- Martin, F.; Camps, A.; Park, H.; D’Addio, S.; Martin-Neira, M.; Pascual, D. Cross-correlation waveform analysis for conventional and interferometric GNSS-R approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1560–1572. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Domènech, E.V.; Pascual, D.; Martin, F.; Rius, A.; Ribo, S.; Benito, J.; Andrés-Beivide, A.; Saameno, P.; et al. Optimization and performance analysis of interferometric GNSS-R altimeters: Application to the Paris IoD mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1436–1451. [Google Scholar] [CrossRef]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the GNSS-R specular reflection point positioning accuracy using the gravity field normal projection reflection reference surface combination correction method. Remote Sens. 2018, 11, 33. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Zheng, W.; Li, Z.; Liu, Z. Improving the positioning accuracy of satellite-borne GNSS-R specular reflection point on sea surface based on the ocean tidal correction positioning method. Remote Sens. 2019, 11, 1626. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Park, H.; Camps, A.; Fabra, F.; Rius, A. GNSS-R Derived Centimetric Sea Topography: An Airborne Experiment Demonstration. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 1468–1478. [Google Scholar] [CrossRef]
- Goodman, J.W.; Narducci, L.M. Statistical Optics. Phys. Today 1986, 39, 126. [Google Scholar] [CrossRef]









| Design Parameter | Value |
|---|---|
| Receiver height | ~3000 m |
| Transmitter altitude | 20,200 km |
| Receiver velocity | 50 m/s |
| Antenna temperature | 200 K |
| Antenna gain | 15 dBi |
| Elevation angle | 70° |
| Processing interval | 39,102–40,721 |
| Power waveform processing time | 1 s |
| Wind speed | 7 m/s |
| Process method | iGNSS-R |
| Sampling frequency | 80 MHz |
| Carrier frequency | 1575.42 MHz (GPS L1) |
| Receiver bandwidth | 35 MHz |
| Waveform retracking method | DER |
| Filter bandwidth | 12 MHz |
| Design Parameter | Value |
|---|---|
| Receiver bandwidth | 35 MHz |
| Antenna temperature | 200 K |
| Transmitter altitude | 20,200 km |
| Process method | iGNSS-R |
| Sampling rate | 80 MHz |
| Carrier frequency | 1575.42 MHz (GPS L1) |
| Waveform retracking method | DER |
| Filter bandwidth | 12 MHz |
| Power waveform processing time | 1 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zheng, W.; Wu, F.; Liu, Z. Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model. Remote Sens. 2021, 13, 4715. https://doi.org/10.3390/rs13224715
Sun X, Zheng W, Wu F, Liu Z. Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model. Remote Sensing. 2021; 13(22):4715. https://doi.org/10.3390/rs13224715
Chicago/Turabian StyleSun, Xuezhi, Wei Zheng, Fan Wu, and Zongqiang Liu. 2021. "Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model" Remote Sensing 13, no. 22: 4715. https://doi.org/10.3390/rs13224715
APA StyleSun, X., Zheng, W., Wu, F., & Liu, Z. (2021). Improving the iGNSS-R Ocean Altimetric Precision Based on the Coherent Integration Time Optimization Model. Remote Sensing, 13(22), 4715. https://doi.org/10.3390/rs13224715