Evaluating the Correlation between Thermal Signatures of UAV Video Stream versus Photomosaic for Urban Rooftop Solar Panels
Abstract
:1. Introduction
2. Method
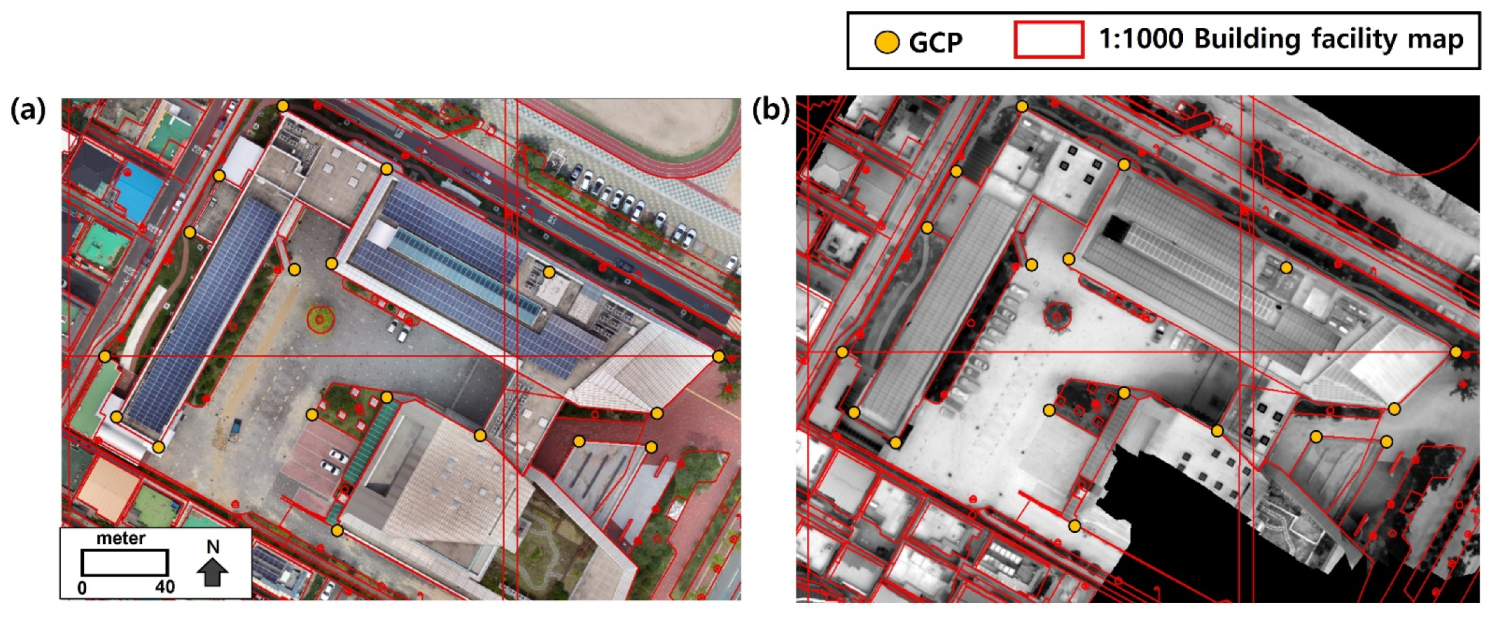
2.1. Experimental Target
2.2. Acquisition of UAV Thermal Imagery
2.3. Video-Based Thermal Frame Mosaic
2.4. Evaluating Performance of Video Mosaics in Thermal Deficiency Inspections
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wood Mackenzie. U.S. Solar Market Insight: Q2 2020. Available online: https://www.woodmac.com/industry/power-and-renewables/us-solar-market-insight (accessed on 7 May 2021).
- U.S. Census Bureau. 2020 Characteristics of New Housing. Available online: https://www.census.gov/construction/chars (accessed on 17 May 2021).
- United States Census Bureau. National and State Housing Unit Estimates: 2010 to 2019. Available online: https://www.census.gov/construction/chars/highlights.html (accessed on 15 October 2021).
- Um, J.-S. Drones as Cyber-Physical Systems; Springer: Singapore, 2019. [Google Scholar]
- Yao, Y.; Hu, Y. Recognition and location of solar panels based on machine vision. In Proceedings of the 2017 2nd Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Wuhan, China, 16–18 June 2017; pp. 7–12. [Google Scholar]
- Jurca, T.; Tulcan-Paulescu, E.; Dughir, C.; Lascu, M.; Gravila, P.; Sabata, A.D.; Luminosu, I.; Sabata, C.D.; Paulescu, M. Global Solar Irradiation Modeling and Measurements in Timisoara. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2011; Volume 1387, pp. 253–258. [Google Scholar]
- Um, J.-S.; Wright, R. ‘Video Strip Mapping (VSM)’ for Time-sequential Monitoring of Revegetation of a Pipeline Route. Geocarto Int. 1999, 14, 24–35. [Google Scholar] [CrossRef]
- Um, J.S.; Wright, R. A comparative evaluation of video remote sensing and field survey for revegetation monitoring of a pipeline route. Sci. Total. Environ. 1998, 215, 189–207. [Google Scholar] [CrossRef]
- Um, J.S.; Wright, R. Video strip mosaicking: A two-dimensional approach by convergent image bridging. Int. J. Remote Sens. 1999, 20, 2015–2032. [Google Scholar] [CrossRef]
- Lee, D.H.; Park, J.H. Developing Inspection Methodology of Solar Energy Plants by Thermal Infrared Sensor on Board Unmanned Aerial Vehicles. Energies 2019, 12, 2928. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Zhang, L.; Wu, T.; Zhang, H.; Sun, X. Detection and location of fouling on photovoltaic panels using a drone-mounted infrared thermography system. J. Appl. Remote Sens. 2017, 11, 016026. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Tran, L.H. Application of graph segmentation method in thermal camera object detection. In Proceedings of the 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 24–27 August 2015; pp. 829–833. [Google Scholar]
- Leira, F.S.; Johansen, T.A.; Fossen, T.I. Automatic detection, classification and tracking of objects in the ocean surface from UAVs using a thermal camera. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–10. [Google Scholar]
- Gómez-Candón, D.; Virlet, N.; Labbé, S.; Jolivot, A.; Regnard, J.-L. Field phenotyping of water stress at tree scale by UAV-sensed imagery: New insights for thermal acquisition and calibration. Precis. Agric. 2016, 17, 786–800. [Google Scholar] [CrossRef]
- Wu, J.; Dong, Z.; Zhou, G. Geo-registration and mosaic of UAV video for quick-response to forest fire disaster. In Proceedings of the MIPPR 2007: Pattern Recognition and Computer Vision, Wuhan, China, 15–17 November 2007; p. 678810. [Google Scholar]
- Kelly, J.; Kljun, N.; Olsson, P.-O.; Mihai, L.; Liljeblad, B.; Weslien, P.; Klemedtsson, L.; Eklundh, L. Challenges and Best Practices for Deriving Temperature Data from an Uncalibrated UAV Thermal Infrared Camera. Remote Sens. 2019, 11, 567. [Google Scholar] [CrossRef] [Green Version]
- Um, J.-S. Evaluating patent tendency for UAV related to spatial information in South Korea. Spat. Inf. Res. 2018, 26, 143–150. [Google Scholar] [CrossRef]
- Hwang, Y.-S.; Schlüter, S.; Park, S.-I.; Um, J.-S. Comparative Evaluation of Mapping Accuracy between UAV Video versus Photo Mosaic for the Scattered Urban Photovoltaic Panel. Remote Sens. 2021, 13, 2745. [Google Scholar] [CrossRef]
- Hwang, Y.-S.; Lee, J.-J.; Park, S.-I.; Um, J.-S. Exploring explainable range of in-situ portable CO 2 sensor signatures for carbon stock estimated in forestry carbon project. Sens. Mater. 2019, 31, 3773. [Google Scholar]
- Park, S.-I.; Ryu, T.-H.; Choi, I.-C.; Um, J.-S. Evaluating the Operational Potential of LRV Signatures Derived from UAV Imagery in Performance Evaluation of Cool Roofs. Energies 2019, 12, 2787. [Google Scholar] [CrossRef] [Green Version]
- Hwang, Y.; Um, J.-S. Exploring causal relationship between landforms and ground level CO2 in Dalseong forestry carbon project site of South Korea. Spat. Inf. Res. 2017, 25, 361–370. [Google Scholar] [CrossRef]
- Um, J.-S. Performance evaluation strategy for cool roof based on pixel dependent variable in multiple spatial regressions. Spat. Inf. Res. 2017, 25, 229–238. [Google Scholar] [CrossRef]
- Lee, J.-J.; Hwang, Y.-S.; Park, S.-I.; Um, J.-S. Comparative Evaluation of UAV NIR Imagery versus in-situ Point Photo in Surveying Urban Tributary Vegetation. J. Environ. Impact Assess. 2018, 27, 475–488. [Google Scholar] [CrossRef]
- Um, J.-S. Valuing current drone CPS in terms of bi-directional bridging intensity: Embracing the future of spatial information. Spat. Inf. Res. 2017, 25, 585–591. [Google Scholar] [CrossRef]
- Park, S.-I.; Hwang, Y.-S.; Lee, J.-J.; Um, J.-S. Evaluating Operational Potential of UAV Transect Mapping for Wetland Vegetation Survey. J. Coast. Res. 2021, 114, 474–478. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, X.; Ai, G.; Zhang, Y.; Zuo, Y. Generating a High-Precision True Digital Orthophoto Map Based on UAV Images. ISPRS Int. J. Geo-Inf. 2018, 7, 333. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-I.; Hwang, Y.-S.; Um, J.-S. Estimating blue carbon accumulated in a halophyte community using UAV imagery: A case study of the southern coastal wetlands in South Korea. J. Coast. Conserv. 2021, 25, 38. [Google Scholar] [CrossRef]
- Conte, P.; Girelli, V.A.; Mandanici, E. Structure from Motion for aerial thermal imagery at city scale: Pre-processing, camera calibration, accuracy assessment. ISPRS Int. J. Geo-Inf. 2018, 146, 320–333. [Google Scholar] [CrossRef]
- Hwang, Y.; Um, J.-S.; Hwang, J.; Schlüter, S. Evaluating the Causal Relations between the Kaya Identity Index and ODIAC-Based Fossil Fuel CO2 Flux. Energies 2020, 13, 6009. [Google Scholar] [CrossRef]
- Hwang, Y.; Um, J.-S. Performance evaluation of OCO-2 XCO2 signatures in exploring casual relationship between CO2 emission and land cover. Spat. Inf. Res. 2016, 24, 451–461. [Google Scholar] [CrossRef]
- Tian, M.; Zou, X.; Weng, F. Use of Allan Deviation for Characterizing Satellite Microwave Sounder Noise Equivalent Differential Temperature (NEDT). IEEE Geosci. Remote Sens. Lett. 2015, 12, 2477–2480. [Google Scholar] [CrossRef]
- Weng, F.; Zou, X.; Sun, N.; Yang, H.; Tian, M.; Blackwell, W.J.; Wang, X.; Lin, L.; Anderson, K. Calibration of Suomi national polar-orbiting partnership advanced technology microwave sounder. J. Geophys. Res. Atmos. 2013, 118, 11–187. [Google Scholar] [CrossRef]
- Hwang, Y.; Um, J.-S.; Schlüter, S. Evaluating the Mutual Relationship between IPAT/Kaya Identity Index and ODIAC-Based GOSAT Fossil-Fuel CO2 Flux: Potential and Constraints in Utilizing Decomposed Variables. Int. J. Environ. Res. Public Health 2020, 17, 5976. [Google Scholar] [CrossRef]
- Troy, A.; Morgan Grove, J.; O’Neil-Dunne, J. The relationship between tree canopy and crime rates across an urban–rural gradient in the greater Baltimore region. Landsc. Urban Plan. 2012, 106, 262–270. [Google Scholar] [CrossRef]
- Martins, J.P.A.; Trigo, I.F.; Ghilain, N.; Jimenez, C.; Göttsche, F.-M.; Ermida, S.L.; Olesen, F.-S.; Gellens-Meulenberghs, F.; Arboleda, A. An All-Weather Land Surface Temperature Product Based on MSG/SEVIRI Observations. Remote Sens. 2019, 11, 3044. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Li, J.; Zhao, D.; Zhu, J. A fieldwork study on the diurnal changes of urban microclimate in four types of ground cover and urban heat island of Nanjing, China. Build. Environ. 2008, 43, 7–17. [Google Scholar] [CrossRef]
- Kordecki, A.; Palus, H.; Bal, A. Practical vignetting correction method for digital camera with measurement of surface luminance distribution. Signal Image Video Process. 2016, 10, 1417–1424. [Google Scholar] [CrossRef] [Green Version]
- Pix4D SA. Pix4Dmapper 4.1 User Manual; Pix4D: Lusanne, Switzerland, 2017. [Google Scholar]
- Tu, Y.-H.; Phinn, S.; Johansen, K.; Robson, A. Assessing Radiometric Correction Approaches for Multi-Spectral UAS Imagery for Horticultural Applications. Remote Sens. 2018, 10, 1684. [Google Scholar] [CrossRef] [Green Version]
- Pinceti, P.; Profumo, P.; Travaini, E.; Vanti, M. Using drone-supported thermal imaging for calculating the efficiency of a PV plant. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Herraiz, Á.H.; Marugán, A.P.; Márquez, F.P.G. Optimal Productivity in Solar Power Plants Based on Machine Learning and Engineering Management. In International Conference on Management Science and Engineering Management; Springer: Cham, Switzerland, 2019; pp. 983–994. [Google Scholar]
- Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IPSJ Trans. Comput. Vis. Appl. 2017, 9, 16. [Google Scholar] [CrossRef]
- Jiang, J.; Niu, X.; Guo, R.; Liu, J. A Hybrid Sliding Window Optimizer for Tightly-Coupled Vision-Aided Inertial Navigation System. Sensors 2019, 19, 3418. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| UAV (DJI Matrice 200 V2) | Camera (DJI Zenmuse XT2) | |||
|---|---|---|---|---|
| Weight | 4.69 kg | Pixel numbers (width × height) | 640 × 512 | |
| Maximum flight altitude | 3000 m (flight altitude used in this experiment: 80 m) | Sensor size (width × height) | 10.88 × 8.7 mm | |
| Focal length * | 19 mm | |||
| Hovering accuracy | z (height) | Vertical, ±0.1 m Horizontal, ±0.3 m | Spectral band | 7.5–13.5 μm |
| x, y (location) | Horizontal, ±1.5 m or ±0.3 m (Downward Vision System) | Full frame rates | 30 Hz | |
| Maximum flight speed | 61.2 km/h (P-mode) | Sensitivity [NEDT]/Aperture | <0.05 °C, f/1.0 | |
| Category | Autopilot | 7.5 Frames/s | 1 Frame/s | 0.5 Frames/s | |
|---|---|---|---|---|---|
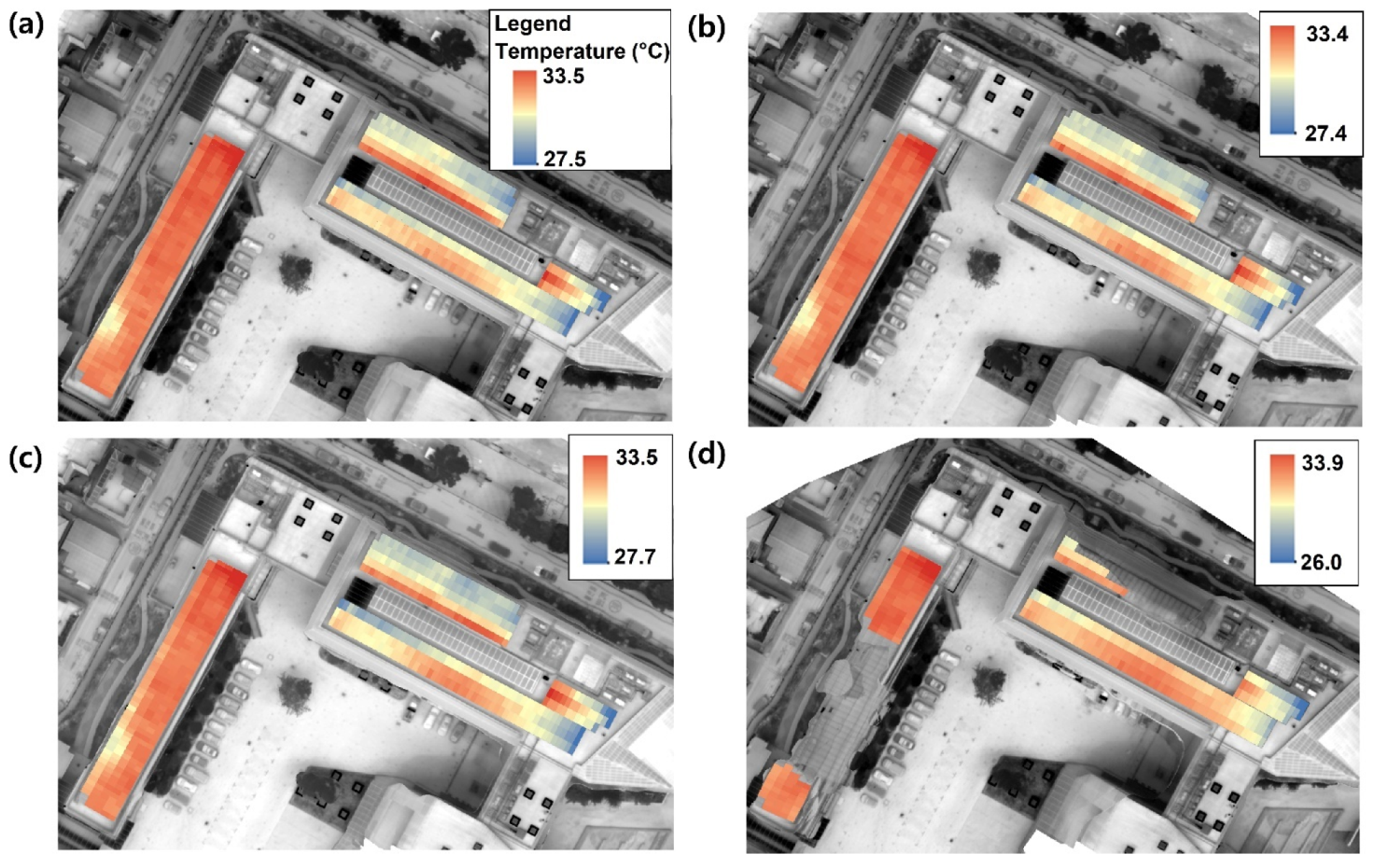
| SPSTs of solar cells detected in solar panels | Min | 26.03 | 26.02 | 25.38 | 24.63 |
| Max | 38.50 | 38.36 | 37.51 | 38.24 | |
| Mean | 31.50 | 31.47 | 31.47 | 31.60 | |
| Standard deviation | 0.57 | 0.58 | 0.60 | 0.59 | |
| Numbers of detected solar panels | 645 | 645 | 645 | 359 | |
| SPSTs of individual solar panels | Min | 27.46 | 27.44 | 27.74 | 26.02 |
| Max | 33.47 | 33.42 | 33.46 | 33.95 | |
| Mean | 31.52 | 31.52 | 31.53 | 31.64 | |
| Standard deviation | 0.98 | 0.97 | 0.98 | 1.15 | |
| Frame Intervals | |||
|---|---|---|---|
| Numbers of solar panels | 645 | 645 | 359 |
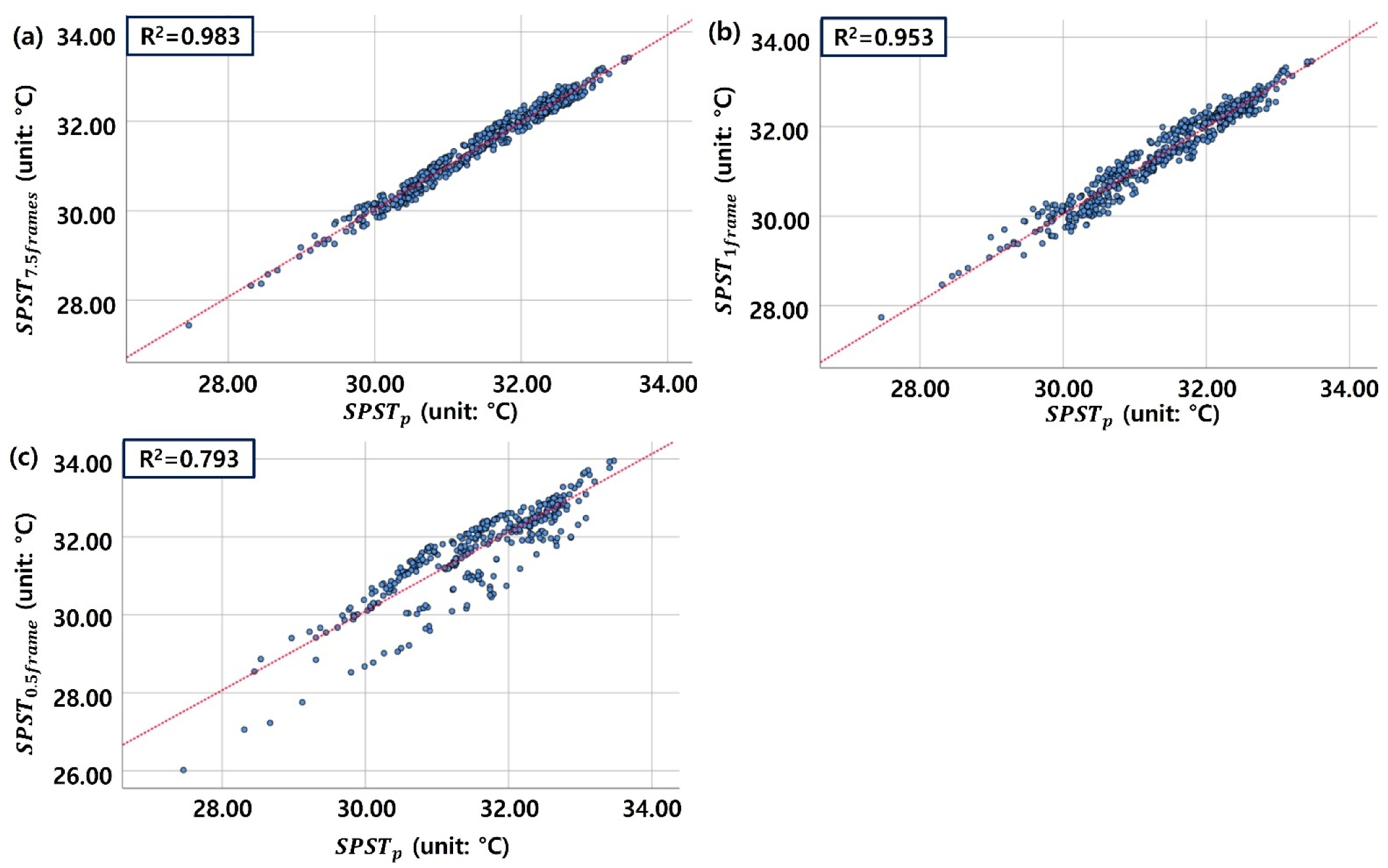
| Unstandardized coefficient (°C) | 1.001 * | 0.977 * | 0.785 * |
| t-statistic | 176.860 * | 114.540 * | 36.958 * |
| VIF | 1.00 | 1.00 | 1.00 |
| Pearson correlation | 0.991 * | 0.976* | 0.890 * |
| R2 | 0.983 | 0.953 | 0.793 |
| RMSE (°C) | 0.14 | 0.21 | 0.53 |
| Overlapping rate (%) | 99 | 97 | 88 |
| Frame Intervals | ||||
|---|---|---|---|---|
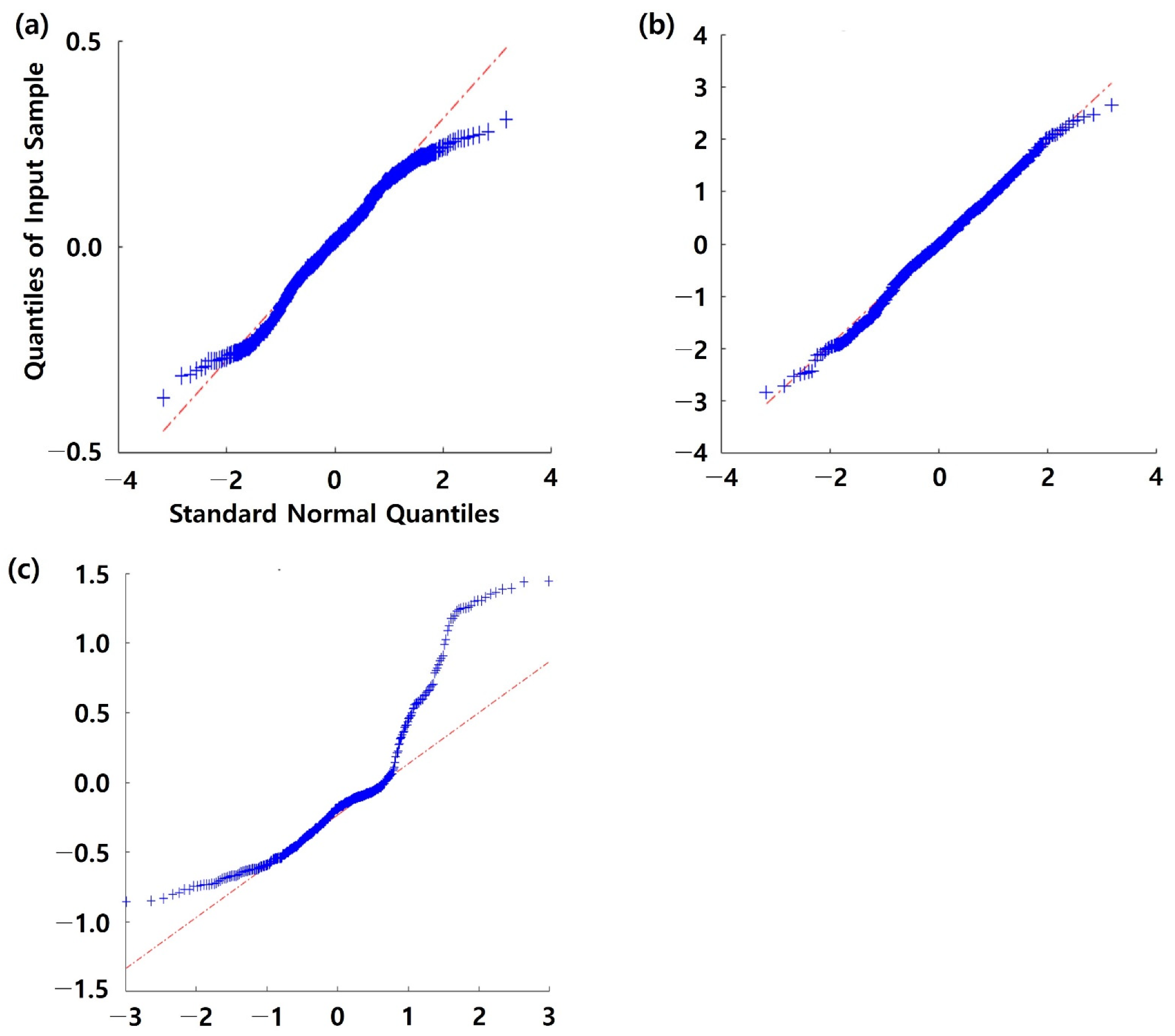
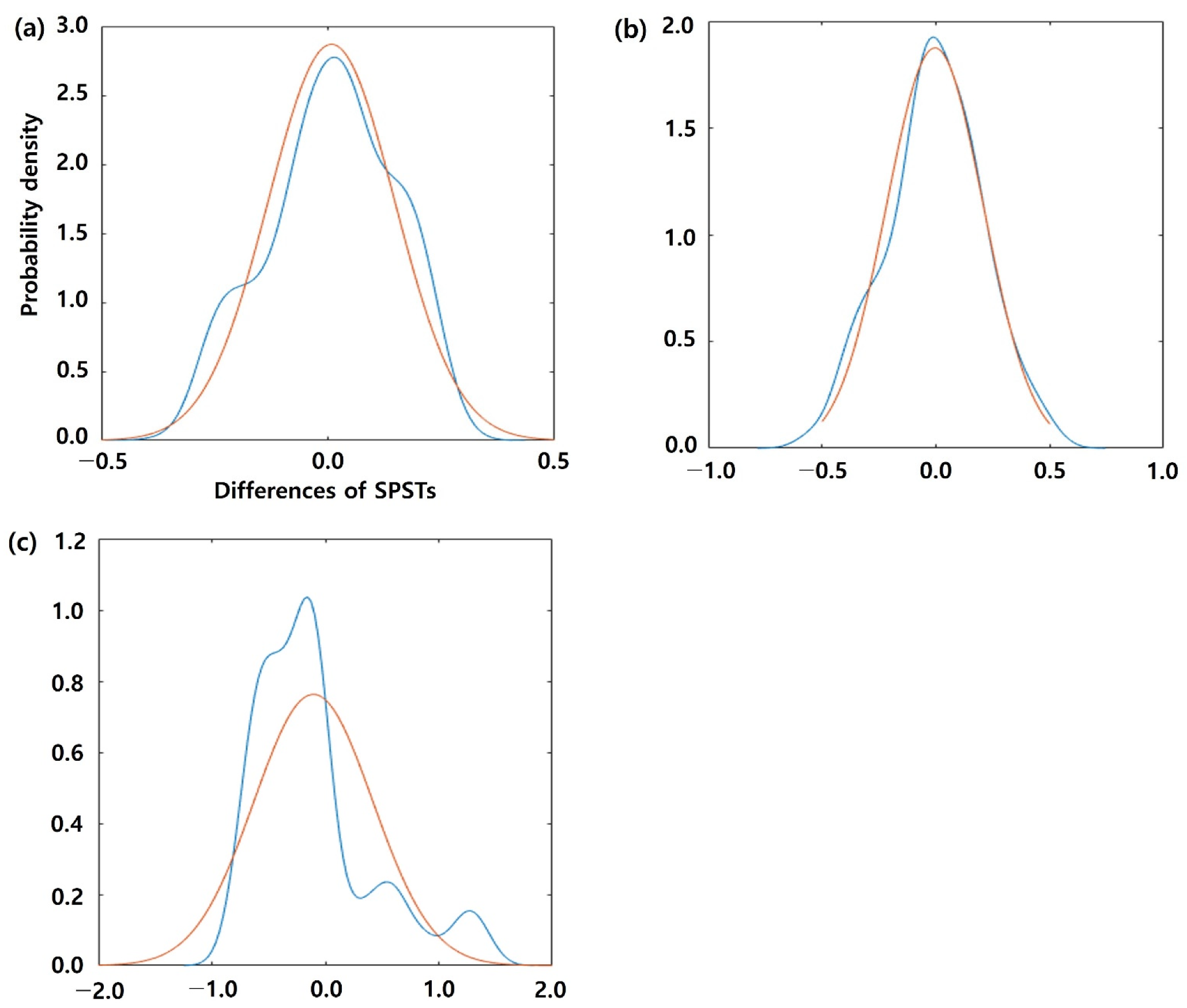
| Number of solar panels | Negative (−) difference with | 293 | 323 | 268 |
| Positive (+) difference with | 352 | 322 | 91 | |
| Temperature difference (°C) | Min | −0.366 | −0.604 | −0.855 |
| Max | 0.310 | 0.563 | 1.446 | |
| Mean | 0.007 | −0.005 | −0.106 | |
| Sum | 4.357 | −3.283 | −38.02 | |
| Standard deviation | 0.14 | 0.21 | 0.52 | |
| Frame Intervals | 2D Key Point Observations | Matched 2D Key Points Per Image (Mean) | Average Density * (/m3) | Area Covered (ha) | Flight Duration (m:s) |
|---|---|---|---|---|---|
| 1,038,092 | 2749 | 5.3 | 4.69 | 28:00 | |
| 932,947 | 3571 | 21.10 | 1.99 | 02:09 | |
| 571,406 | 3019 | 15.76 | 1.85 | 02:09 | |
| 161,712 | 1902 | 13.28 | 1.34 | 02:09 | |
| Longer frame intervals (15 frames/2 s → 1 frame/1 s → 1 frame/2 s) have lower overlapping rates (99 → 97 → 88%), fewer matched 2D key points per image (3571 → 3019 → 1902), and average density (21.10/m3 → 15.76/m3 → 13.28/m3). has lower overlapping rates (95%), the number of matched 2D key points (2749), and average density (5.3/m3) compared with and having smaller covered areas. | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, Y.-S.; Schlüter, S.; Lee, J.-J.; Um, J.-S. Evaluating the Correlation between Thermal Signatures of UAV Video Stream versus Photomosaic for Urban Rooftop Solar Panels. Remote Sens. 2021, 13, 4770. https://doi.org/10.3390/rs13234770
Hwang Y-S, Schlüter S, Lee J-J, Um J-S. Evaluating the Correlation between Thermal Signatures of UAV Video Stream versus Photomosaic for Urban Rooftop Solar Panels. Remote Sensing. 2021; 13(23):4770. https://doi.org/10.3390/rs13234770
Chicago/Turabian StyleHwang, Young-Seok, Stephan Schlüter, Jung-Joo Lee, and Jung-Sup Um. 2021. "Evaluating the Correlation between Thermal Signatures of UAV Video Stream versus Photomosaic for Urban Rooftop Solar Panels" Remote Sensing 13, no. 23: 4770. https://doi.org/10.3390/rs13234770
APA StyleHwang, Y.-S., Schlüter, S., Lee, J.-J., & Um, J.-S. (2021). Evaluating the Correlation between Thermal Signatures of UAV Video Stream versus Photomosaic for Urban Rooftop Solar Panels. Remote Sensing, 13(23), 4770. https://doi.org/10.3390/rs13234770








