Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R
Abstract
:1. Introduction
2. Materials and Methods
2.1. GNSS-R Geometry
2.2. Algorithm Principle
3. Results and Discussion
3.1. Experimental Data
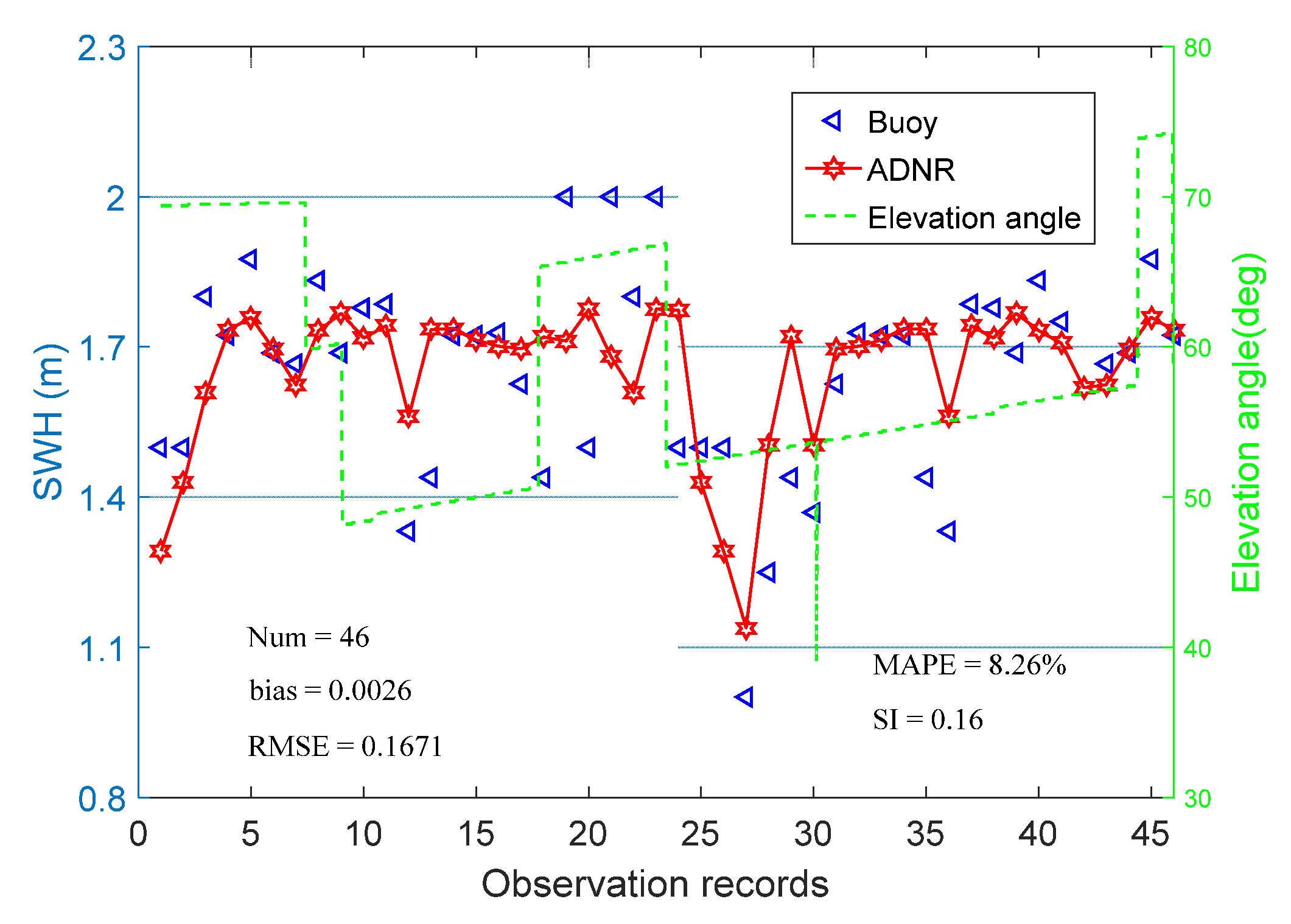
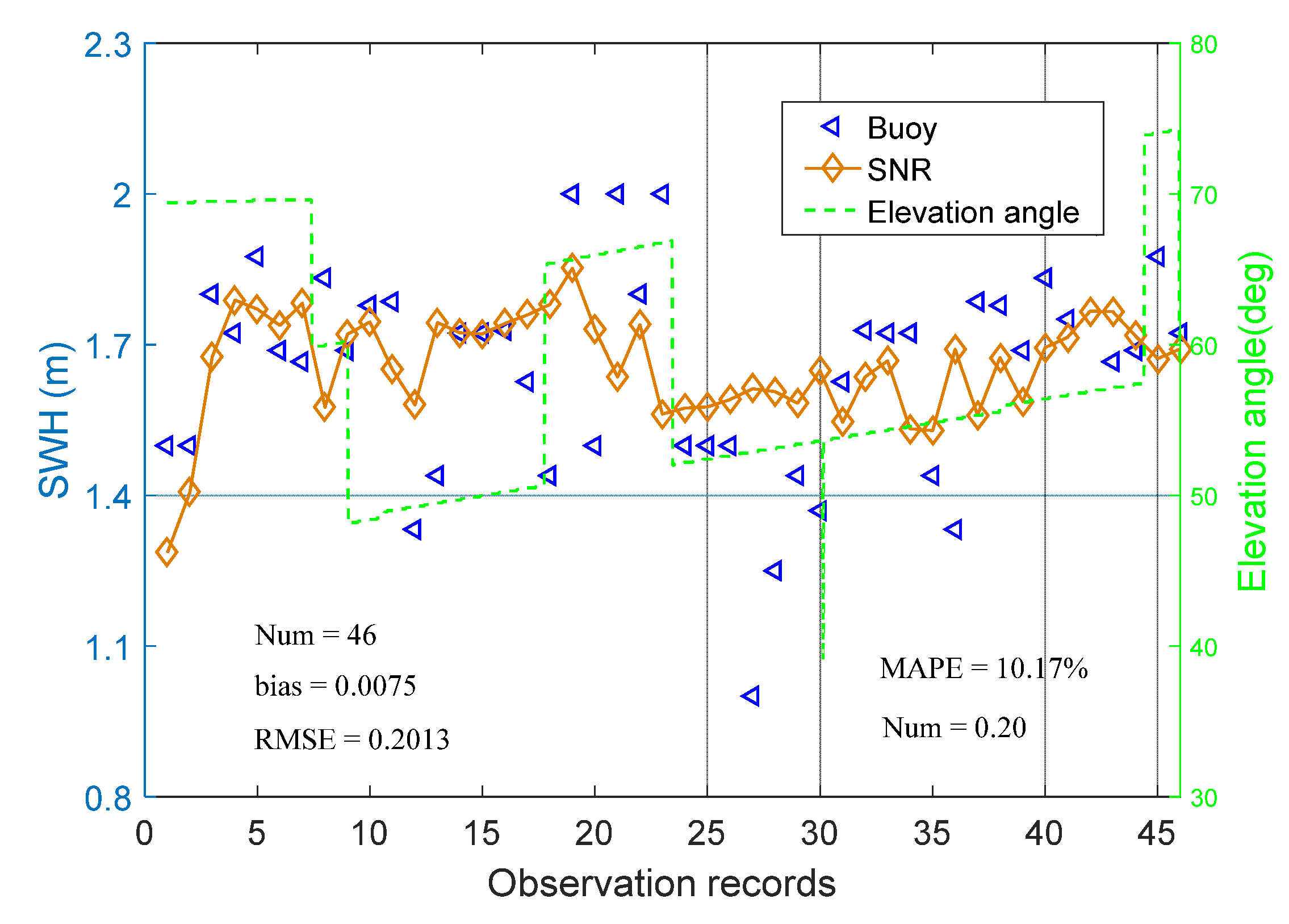
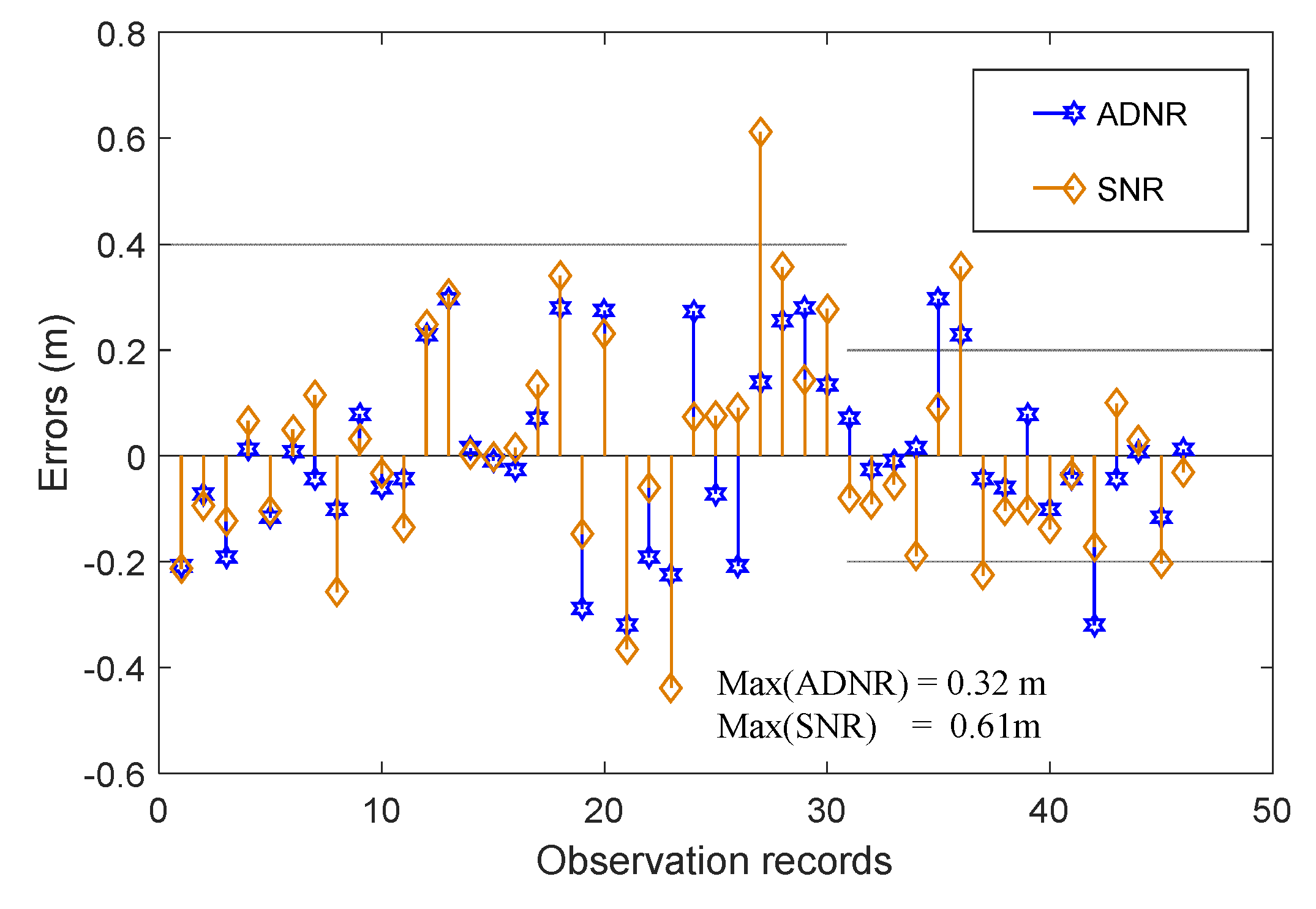
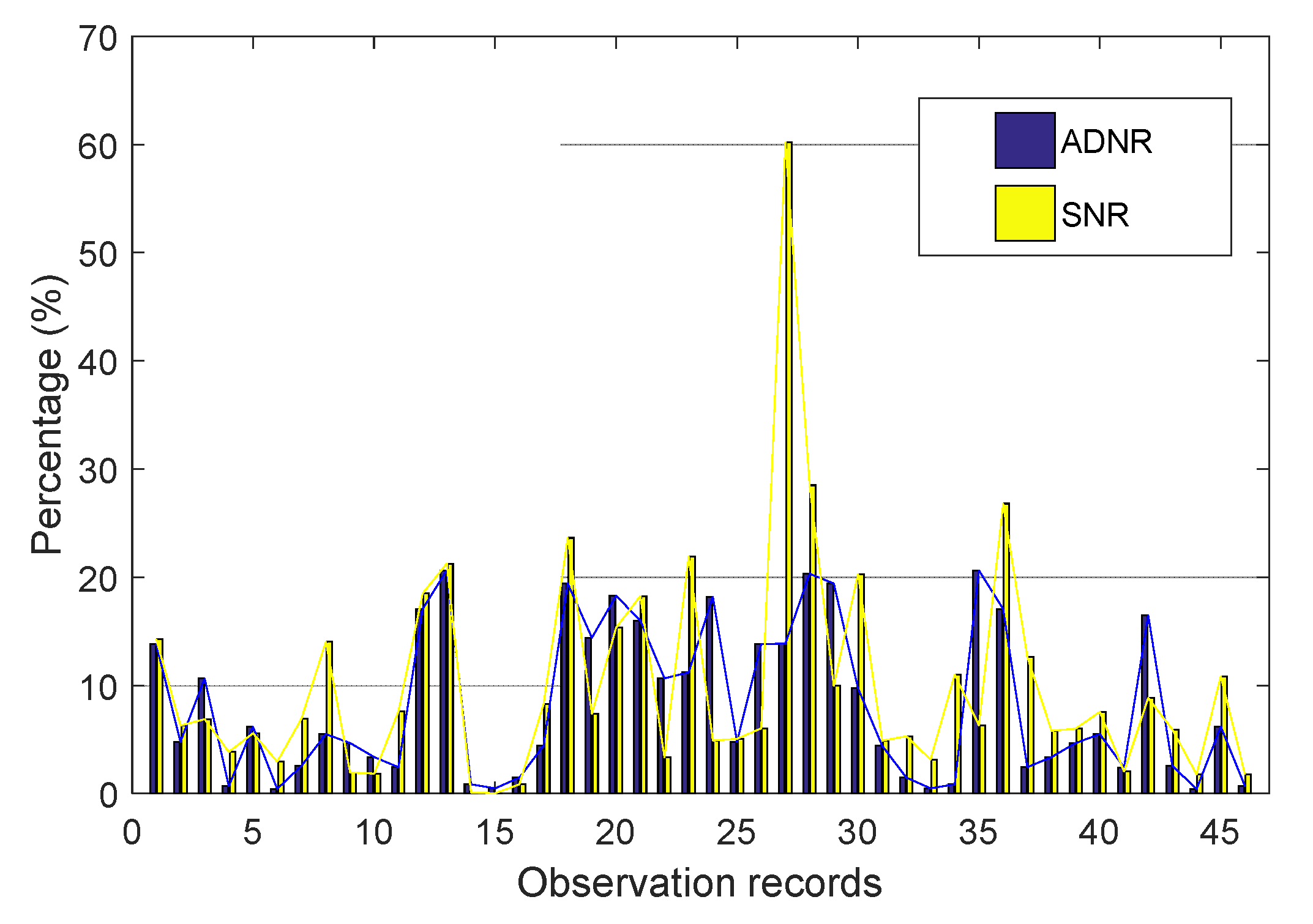
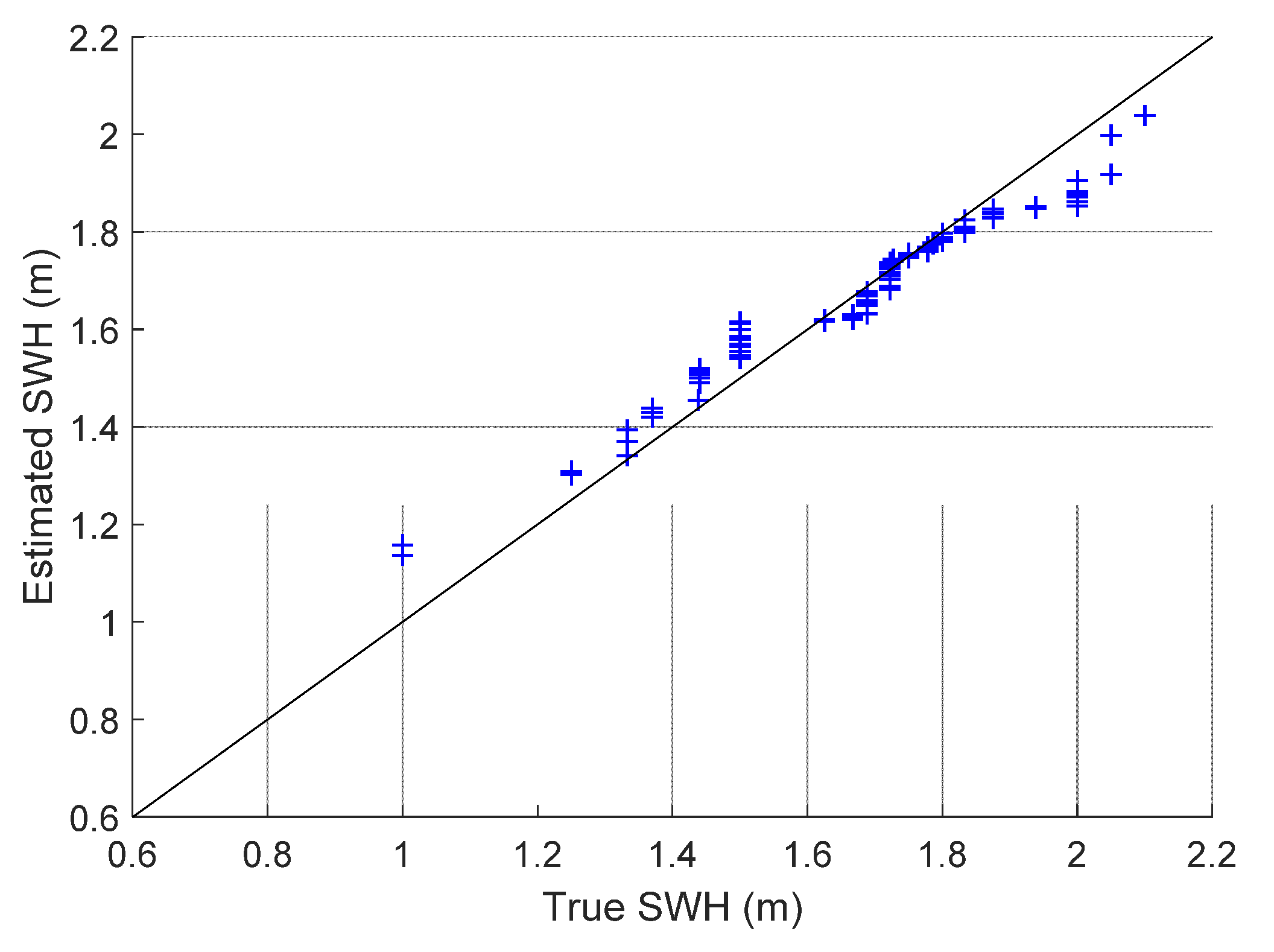
3.2. SWH Retrieval Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bao, Q.; Lin, M.; Zhang, Y.; Dong, X.; Lang, S.; Gong, P. Ocean Surface Current Inversion Method for a Doppler Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6505–6516. [Google Scholar] [CrossRef]
- Wan, J.; Guo, W.; Zhao, F.; Wang, C. HY-2A Altimeter Time Tag Bias Estimation Using Reconstructive Transponder. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1431–1435. [Google Scholar] [CrossRef]
- Pires, N.; Fernandes, M.J.; Gommenginger, C.; Scharroo, R. Improved Sea State Bias Estimation for Altimeter Reference Missions with Altimeter-Only Three-Parameter Models. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1448–1462. [Google Scholar] [CrossRef]
- Wu, K.; Li, X.-M.; Huang, B. Retrieval of Ocean Wave Heights from Spaceborne SAR in the Arctic Ocean with a Neural Network. J. Geophys. Res. Oceans 2021, 126, e2020JC016946. [Google Scholar] [CrossRef]
- Rodger, M.; Guida, R. Classification-Aided SAR and AIS Data Fusion for Space-Based Maritime Surveillance. Remote Sens. 2020, 13, 104. [Google Scholar] [CrossRef]
- Angnuureng, D.B.; Jayson-Quashigah, P.-N.; Almar, R.; Stieglitz, T.C.; Anthony, E.J.; Aheto, D.W.; Appeaning Addo, K. Application of Shore-Based Video and Unmanned Aerial Vehicles (Drones): Complementary Tools for Beach Studies. Remote Sens. 2020, 12, 394. [Google Scholar] [CrossRef] [Green Version]
- Lowe, M.K.; Adnan, F.A.F.; Hamylton, S.M.; Carvalho, R.C.; Woodroffe, C.D. Assessing Reef-Island Shoreline Change Using UAV-Derived Orthomosaics and Digital Surface Models. Drones 2019, 3, 44. [Google Scholar] [CrossRef] [Green Version]
- Specht, C.; Lewicka, O.; Specht, M.; Dąbrowski, P.; Burdziakowski, P. Methodology for Carrying out Measurements of the Tombolo Geomorphic Landform Using Unmanned Aerial and Surface Vehicles near Sopot Pier, Poland. J. Mar. Sci. Eng. 2020, 8, 384. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Voronovich, A.G. Recent Progress on Forward Scattering Modeling for GNSS Reflectometry. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3814–3817. [Google Scholar]
- Yan, Q.; Huang, W.; Foti, G. Quantification of the Relationship Between Sea Surface Roughness and the Size of the Glistening Zone for GNSS-R. IEEE Geosci. Remote Sens. Lett. 2017, 15, 237–241. [Google Scholar] [CrossRef]
- Slater, L.B. From Minitrack to NAVSTAR: The Early Development of the Global Positioning System, 1955–1975. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Baburov, V.I.; Ivantsevich, N.V.; Sauta, O.I. GLONASS Technologies for Controlling the Fields of Short-Range Navigation and Landing Systems. In Proceedings of the 24th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), St. Petersburg, Russia, 29–31 May 2017; pp. 1–4. [Google Scholar]
- Bedrich, S.; Bauch, A.; Laverty, J.; Moudrak, A.; Schafer, W. Design of the Galileo Precise Time Facility (PTF). In Proceedings of the 18th European Frequency and Time Forum, Guildford, UK, 5–7 April 2004; Volume 2004, pp. 476–483. [Google Scholar]
- Wang, F.; Zhang, B.; Yang, D.; Li, W.; Zhu, Y. Sea-State Observation Using Reflected BeiDou GEO Signals in Frequency Domain. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1656–1660. [Google Scholar] [CrossRef]
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to Ocean Altimetry. ESA J. 1993, 17, 331–335. [Google Scholar]
- Wang, F.; Yang, D.; Li, W.; Yang, W. On-Ground Retracking to Correct Distorted Waveform in Spaceborne Global Navigation Satellite System-Reflectometry. Remote Sens. 2017, 9, 643. [Google Scholar] [CrossRef] [Green Version]
- Park, H.; Camps, A.; Pascual, D.; Kang, Y.; Onrubia, R.; Querol, J.; Alonso-Arroyo, A. A Generic level 1 Simulator for Spaceborne GNSS-R Missions and Application to GEROS-ISS Ocean Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4645–4659. [Google Scholar] [CrossRef] [Green Version]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-Reflectometry on TechDemoSat-1: Early Mission Operations and Exploitation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Statistical Derivation of Wind Speeds from CYGNSS Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3955–3964. [Google Scholar] [CrossRef]
- Gleason, S.; Johnson, J.; Ruf, C.; Bussy-Virat, C. Characterizing Background Signals and Noise in Spaceborne GNSS Reflection Ocean Observations. IEEE Geosci. Remote Sens. Lett. 2020, 17, 587–591. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Effects of PRN-Dependent ACF Deviations on GNSS-R Wind Speed Retrieval. IEEE Geosci. Remote Sens. Lett. 2019, 16, 327–331. [Google Scholar] [CrossRef]
- Wang, F.; Yang, D.; Yang, L. Feasibility of Wind Direction Observation Using Low-Altitude Global Navigation Satellite System-Reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 5063–5075. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Camps, A.; Park, H.; Pascual, D.; Onrubia, R.; Martín, F. Retrieval of Significant Wave Height and Mean Sea Surface Level Using the GNSS-R Interference Pattern Technique: Results from a Three-Month Field Campaign. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3198–3209. [Google Scholar] [CrossRef] [Green Version]
- Peng, Q.; Jin, S. Significant Wave Height Estimation from Space-Borne Cyclone-GNSS Reflectometry. Remote Sens. 2019, 11, 584. [Google Scholar] [CrossRef] [Green Version]
- Yan, Q.; Huang, W. Sea Ice Sensing from GNSS-R Data Using Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1510–1514. [Google Scholar] [CrossRef]
- Gao, F.; Xu, T.; Meng, X.; Wang, N.; He, Y.; Ning, B. A Coastal Experiment for GNSS-R Code-Level Altimetry Using BDS-3 New Civil Signals. Remote Sens. 2021, 13, 1378. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 537–543. [Google Scholar] [CrossRef]
- Roggenbuck, O.; Reinking, J.; Lambertus, T. Determination of Significant Wave Heights Using Damping Coefficients of Attenuated GNSS SNR Data from Static and Kinematic Observations. Remote Sens. 2019, 11, 409. [Google Scholar] [CrossRef] [Green Version]
- Soulat, F.; Caparrini, M.; Germain, O.; Lopez-Dekker, P.; Taani, M.; Ruffini, G. Sea State Monitoring Using Coastal GNSS-R. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Caparrini, M.; Egido, A.; Soulat, F.; Germain, O.; Farres, E.; Dunne, S.; Ruffini, G. Oceanpal: Monitoring Sea State with a GNSS-R Coastal Instrument. In Proceedings of the International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 5080–5083. [Google Scholar]
- Shah, R.; Garrison, J.L. Application of the ICF Coherence Time Method for Ocean Remote Sensing Using Digital Communication Satellite Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1584–1591. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R Minimum Variance Wind Speed Estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J. Development and Application of Big Data in the Field of Satellite Navigation. Wirel. Commun. Mob. Comput. 2021, 2021, 8850350. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, L.; Li, Y. Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R. Remote Sens. 2021, 13, 4806. https://doi.org/10.3390/rs13234806
Qin L, Li Y. Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R. Remote Sensing. 2021; 13(23):4806. https://doi.org/10.3390/rs13234806
Chicago/Turabian StyleQin, Lingyu, and Ying Li. 2021. "Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R" Remote Sensing 13, no. 23: 4806. https://doi.org/10.3390/rs13234806
APA StyleQin, L., & Li, Y. (2021). Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R. Remote Sensing, 13(23), 4806. https://doi.org/10.3390/rs13234806




