A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner
Abstract
:1. Introduction
2. Materials and Methods
2.1. Used Instruments
2.1.1. Terrestrial Measurements
2.1.2. UAV DJI Matrice 300
2.1.3. Laser Scanner DJI Zenmuse L1
2.1.4. DJI Zenmuse P1
2.2. Testing Area
2.3. Terrestrial Measurements and Data Acquisition
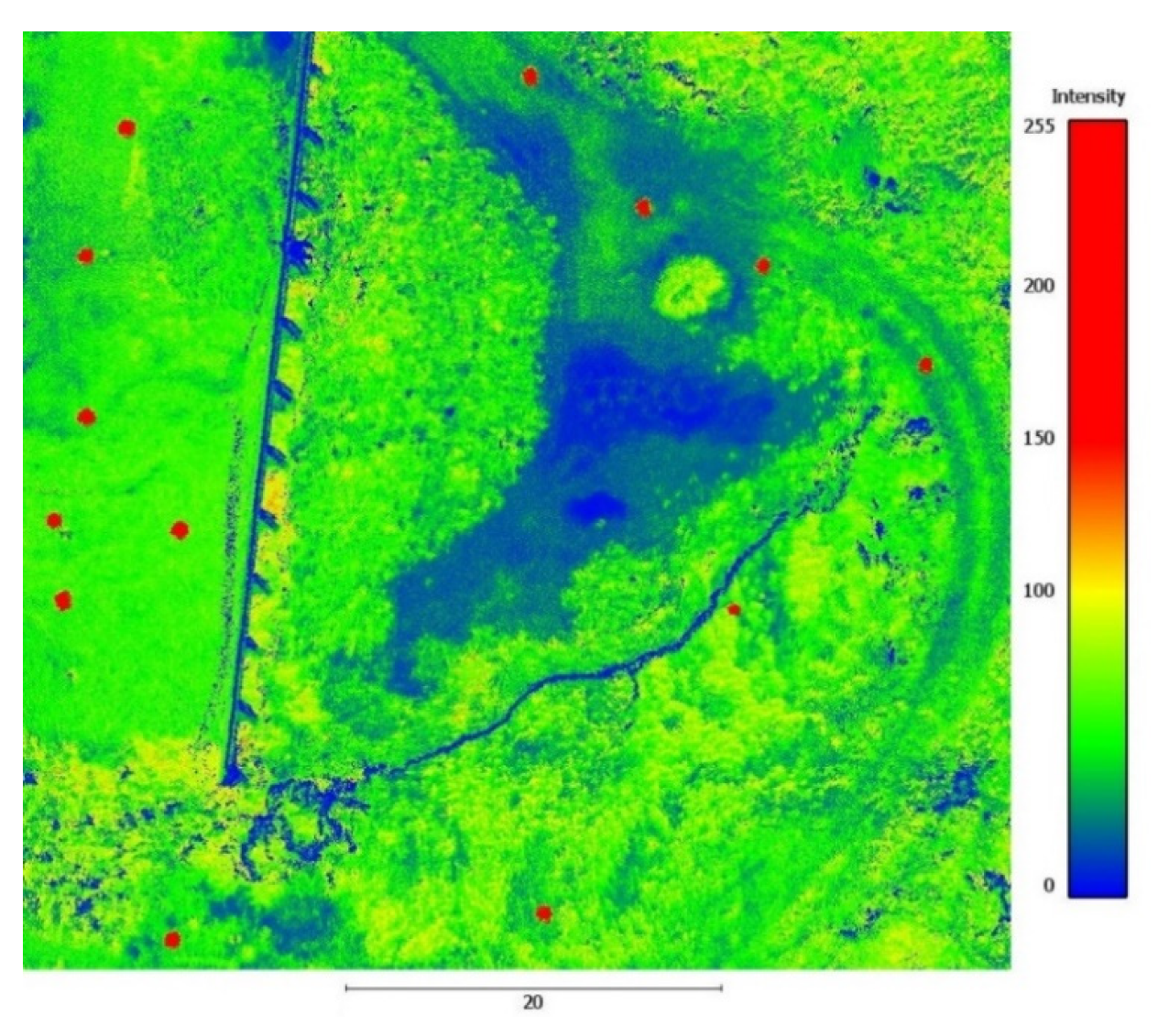
2.3.1. Stabilization of (Ground) Control Points
2.3.2. Terrestrial Measurements
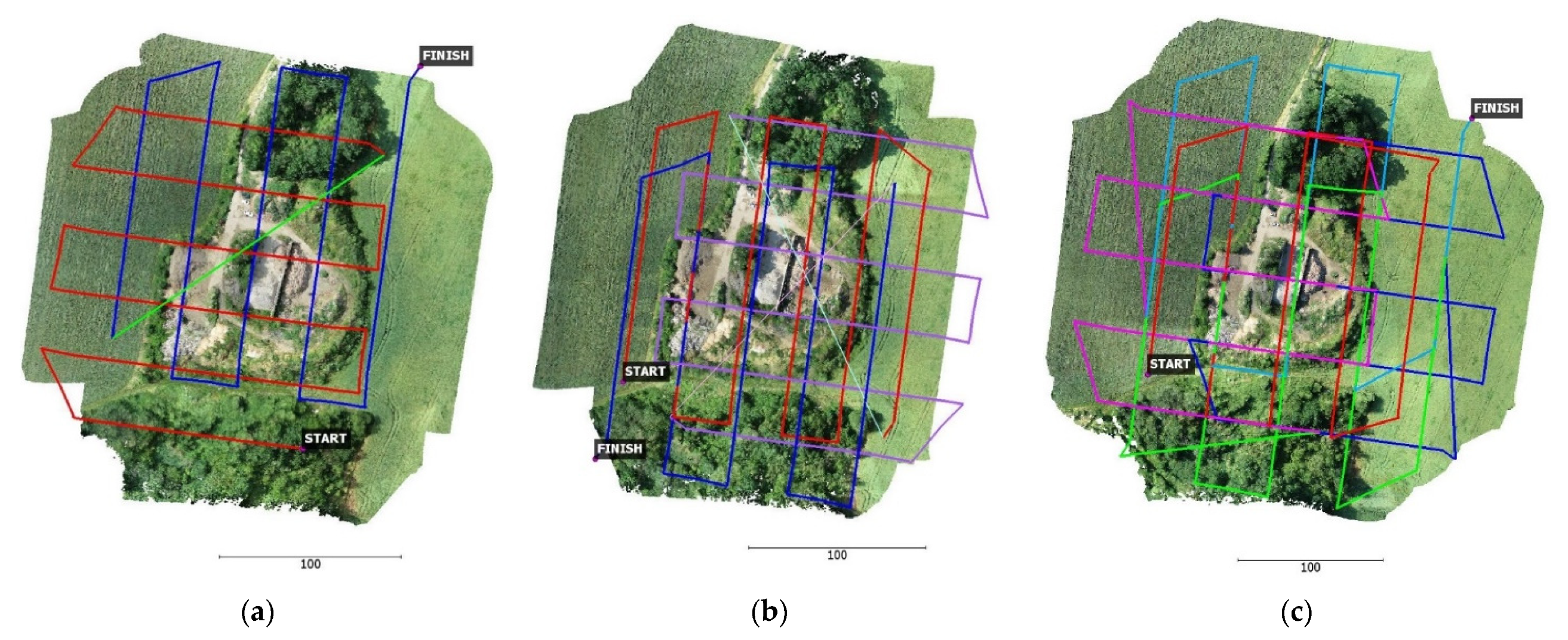
2.3.3. DJI Zenmuse L1 Data Acquisition (Lidar Data)
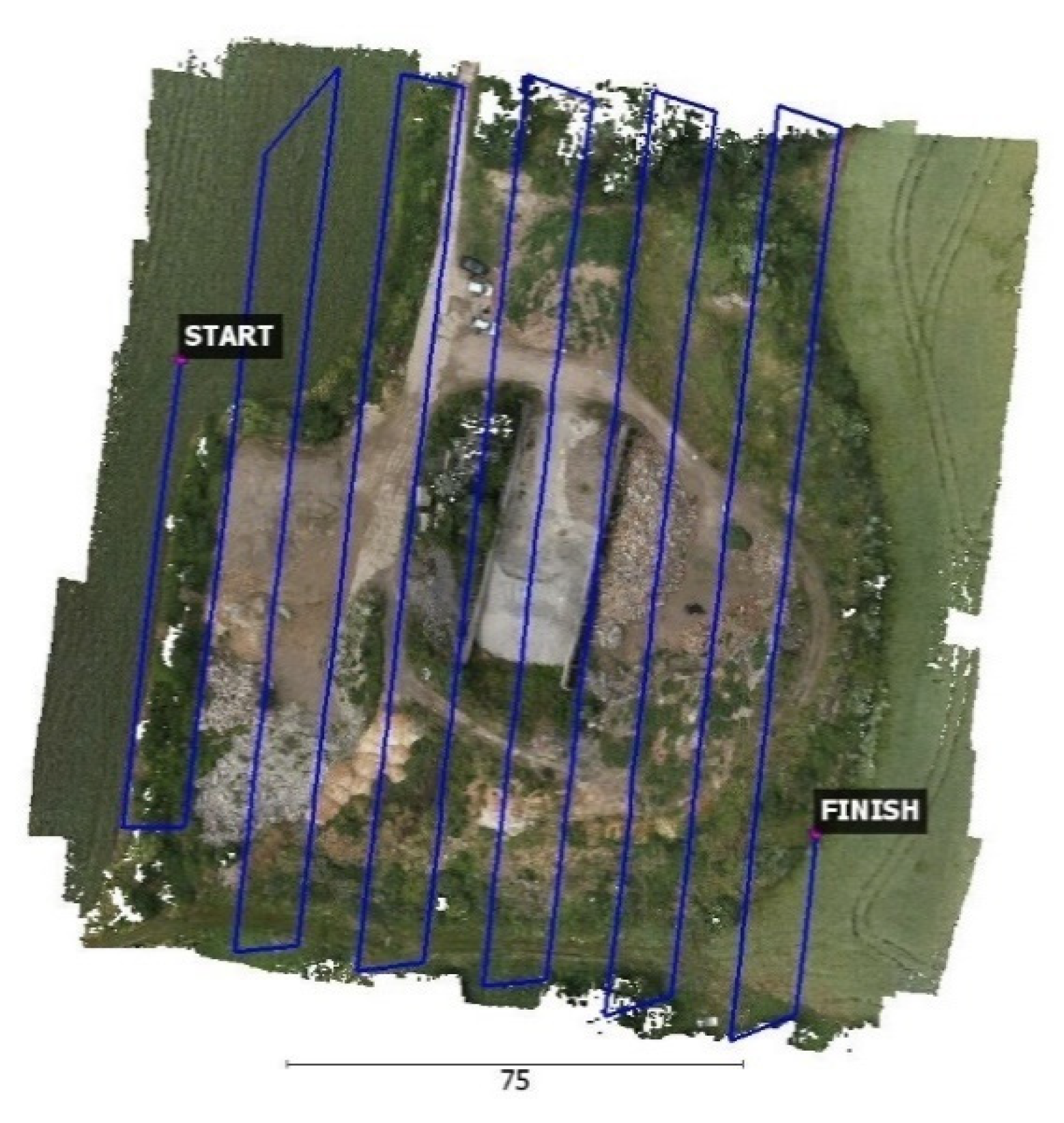
2.3.4. Reference Data Acquisition with DJI Zenmuse P1 (Photogrammetric Data)
2.4. Data Processing and Calculations
2.4.1. Processing of DJI Zenmuse P1 Data (Photogrammetric Data)
2.4.2. Processing of Zenmuse L1 Data (Lidar Data)
2.5. Algorithms of Accuracy Assessment
2.5.1. Global Accuracy of the Point Cloud
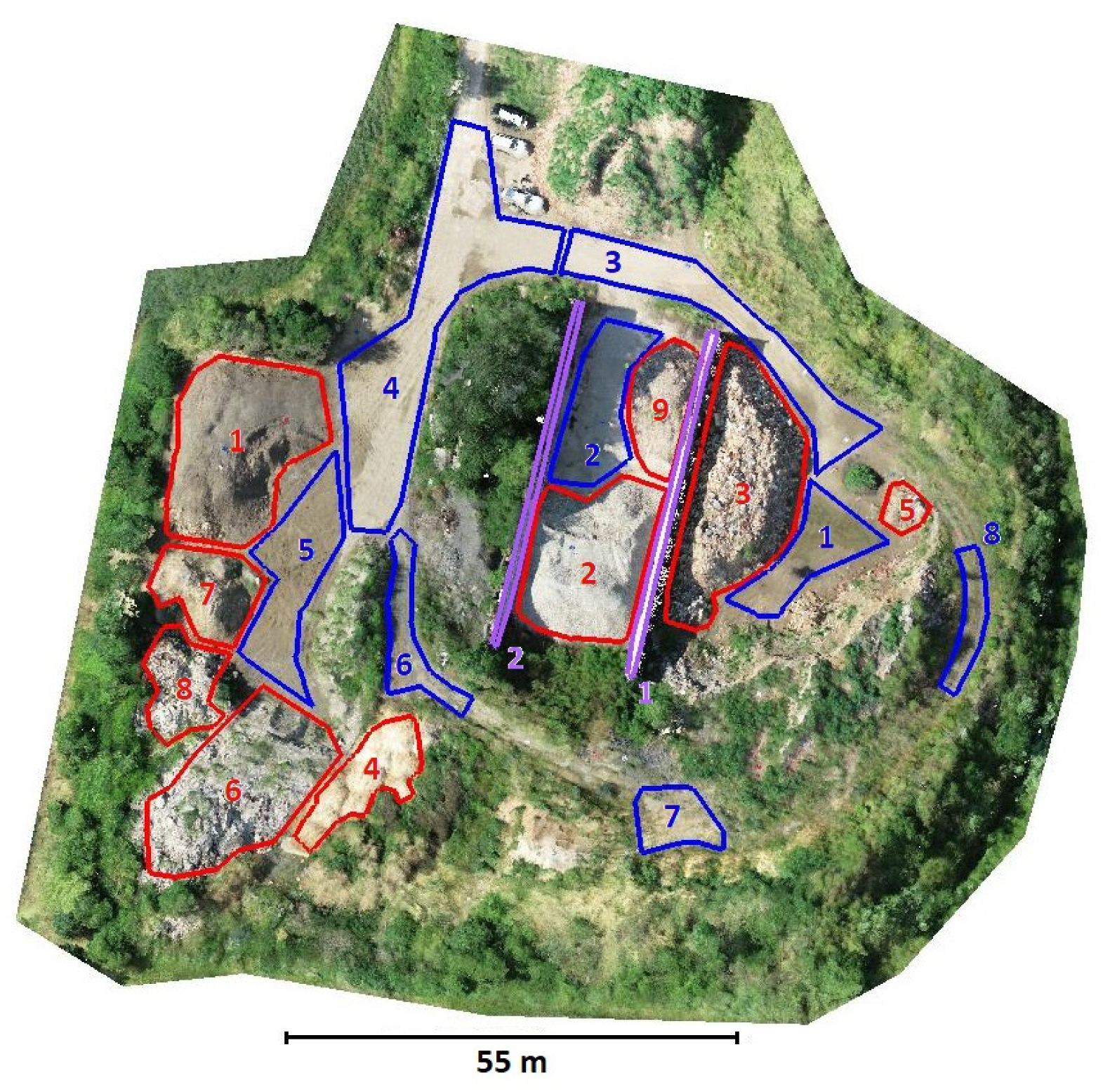
2.5.2. Evaluation of the Local Accuracy of the Point Cloud
2.5.3. Color Information Shift
3. Results
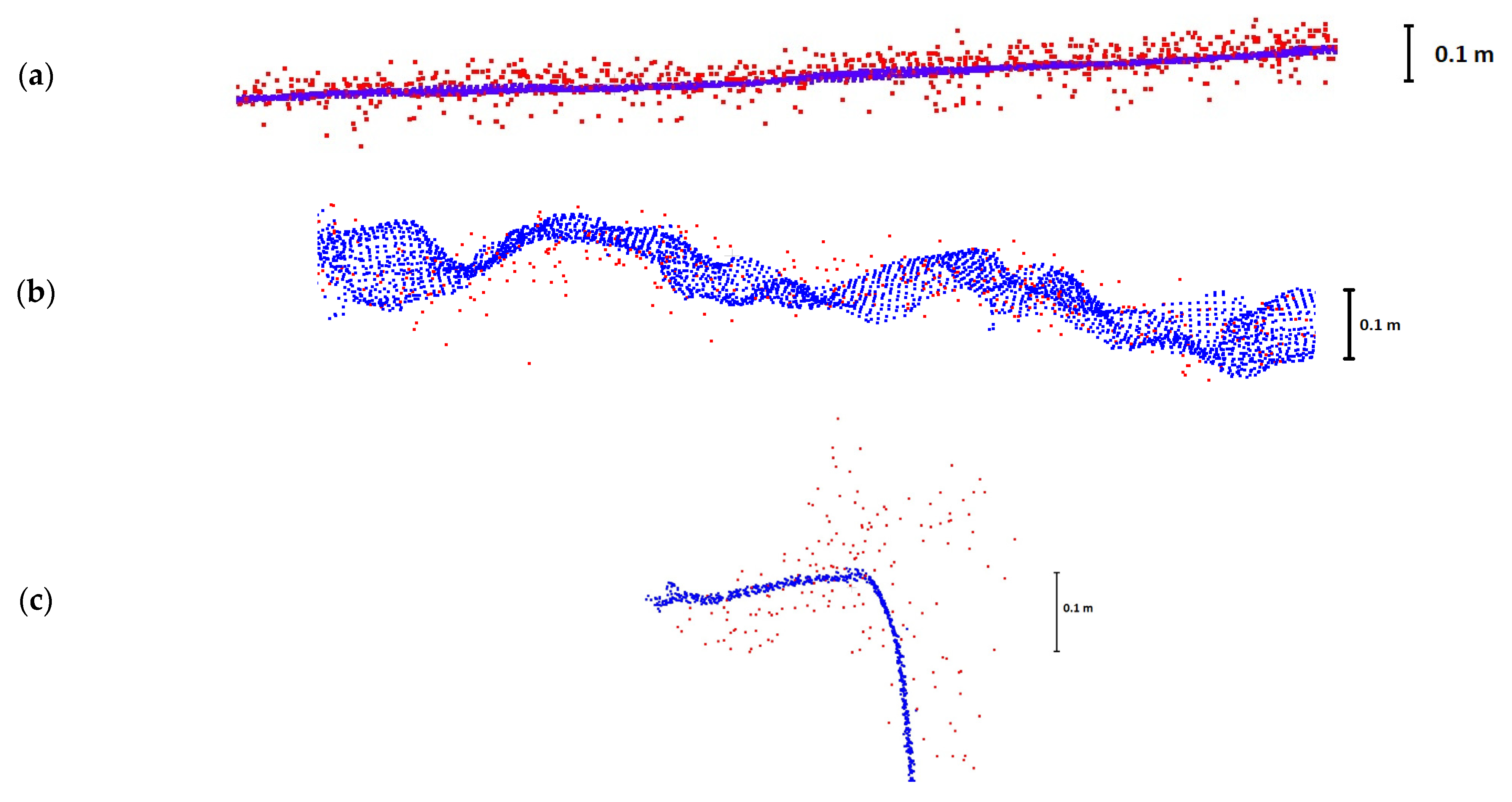
3.1. Visual Evaluation of the Point Clouds
3.2. Global Accuracy of the Point Cloud
3.3. Local Accuracy on the Vegetation-Free Areas
3.4. The Shift of the Color Information
4. Discussion
5. Conclusions
- Testing should be carried out in an area with surfaces that are approximately horizontal, vertical, and generally rugged, all without vegetation.
- Prior to data acquisition, targets covered with a reflective film should be placed in the area and their coordinates determined using a reference method with accuracy superior to the expected accuracy of the tested system.
- The UAV–lidar system point cloud should be supplemented with a reference point cloud (e.g., SfM as in our case) of the test area with significantly higher accuracy and detail.
- The coordinates of the centers of targets are determined in the cloud using reflection intensities. Using these data, the systematic georeferencing error is calculated and removed from the cloud by linear transformation.
- The resulting point cloud accuracy is determined as the RMSE of the distances between the reference (in our case, SfM) and tested (lidar) clouds for individual surfaces.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Detailed Results—RMSE of Lidar Point Clouds vs. SfM Point Cloud
| Flight L1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | All |
|---|---|---|---|---|---|---|---|---|---|
| 50 m_1 | 0.033 | 0.032 | 0.030 | 0.031 | 0.035 | 0.036 | 0.025 | 0.028 | 0.032 |
| 50 m_2 | 0.031 | 0.028 | 0.029 | 0.027 | 0.033 | 0.034 | 0.028 | 0.029 | 0.030 |
| 70 m | 0.052 | 0.037 | 0.039 | 0.044 | 0.048 | 0.045 | 0.041 | 0.045 | 0.044 |
| Flight L1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | All |
|---|---|---|---|---|---|---|---|---|---|---|
| 50 m_1 | 0.036 | 0.028 | 0.036 | 0.027 | 0.038 | 0.039 | 0.038 | 0.068 | 0.031 | 0.038 |
| 50 m_2 | 0.037 | 0.029 | 0.035 | 0.028 | 0.034 | 0.044 | 0.038 | 0.051 | 0.033 | 0.038 |
| 70 | 0.052 | 0.037 | 0.045 | 0.036 | 0.049 | 0.052 | 0.051 | 0.064 | 0.039 | 0.048 |
| Flight L1 | 1 | 2 | All |
|---|---|---|---|
| 50 m_1 | 0.025 | 0.052 | 0.038 |
| 50 m_2 | 0.029 | 0.027 | 0.027 |
| 70 | 0.045 | 0.053 | 0.049 |
References
- Urban, R.; Štroner, M.; Kuric, I. The use of onboard UAV GNSS navigation data for area and volume calculation. Acta Montan. Slovaca 2020, 25, 361–374. [Google Scholar] [CrossRef]
- Kovanič, Ľ.; Blistan, P.; Štroner, M.; Urban, R.; Blistanova, M. Suitability of Aerial Photogrammetry for Dump Documentation and Volume Determination in Large Areas. Appl. Sci. 2021, 11, 6564. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y. Applications of Unmanned Aerial Vehicles in Mining from Exploration to Reclamation: A Review. Minerals 2020, 10, 663. [Google Scholar] [CrossRef]
- Klouček, T.; Komárek, J.; Surový, P.; Hrach, K.; Janata, P.; Vašíček, B. The Use of UAV Mounted Sensors for Precise Detection of Bark Beetle Infestation. Remote Sens. 2019, 11, 1561. [Google Scholar] [CrossRef] [Green Version]
- Moudrý, V.; Beková, A.; Lagner, O. Evaluation of a high resolution UAV imagery model for rooftop solar irradiation estimates. Remote Sens. Lett. 2019, 10, 1077–1085. [Google Scholar] [CrossRef]
- Kovanič, Ľ.; Blistan, P.; Urban, R.; Štroner, M.; Blišťanová, M.; Bartoš, K.; Pukanská, K. Analysis of the Suitability of High-Resolution DEM Obtained Using ALS and UAS (SfM) for the Identification of Changes and Monitoring the Development of Selected Geohazards in the Alpine Environment—A Case Study in High Tatras, Slovakia. Remote Sens. 2020, 12, 3901. [Google Scholar] [CrossRef]
- Jaud, M.; Bertin, S.; Beauverger, M.; Augereau, E.; Delacourt, C. RTK GNSS-Assisted Terrestrial SfM Photogrammetry without GCP: Application to Coastal Morphodynamics Monitoring. Remote Sens. 2020, 12, 1889. [Google Scholar] [CrossRef]
- Žabota, B.; Kobal, M. Accuracy Assessment of UAV-Photogrammetric-Derived Products Using PPK and GCPs in Challenging Terrains: In Search of Optimized Rockfall Mapping. Remote Sens. 2021, 13, 3812. [Google Scholar] [CrossRef]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G.; Lingua, A. Uav Photogrammetry and Vhr Satellite Imagery for Emergency Mapping. The October 2020 Flood in Limone Piemonte (Italy). ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B3-2, 727–734. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry Using UAV-Mounted GNSS RTK: Georeferencing Strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Vacca, G.; Dessì, A.; Sacco, A. The Use of Nadir and Oblique UAV Images for Building Knowledge. ISPRS Int. J. Geo-Inf. 2017, 6, 393. [Google Scholar] [CrossRef] [Green Version]
- Losè, L.T.; Chiabrando, F.; Tonolo, F.G. Boosting the Timeliness of UAV Large Scale Mapping. Direct Georeferencing Approaches: Operational Strategies and Best Practices. ISPRS Int. J. Geo-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef] [Green Version]
- McMahon, C.; Mora, O.; Starek, M. Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping. Drones 2021, 5, 50. [Google Scholar] [CrossRef]
- Padró, J.-C.; Muñoz, F.-J.; Planas, J.; Pons, X. Comparison of four UAV georeferencing methods for environmental monitoring purposes focusing on the combined use with airborne and satellite remote sensing platforms. Int. J. Appl. Earth Obs. Geo-Inf. 2019, 75, 130–140. [Google Scholar] [CrossRef]
- Koska, B.; Křemen, T. The combination of laser scanning and structure from motion technology for creation of accurate exterior and interior orthophotos of St. Nicholas Baroque church. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 133–138. [Google Scholar] [CrossRef] [Green Version]
- Křemen, T. Advances and Trends in Geodesy, Cartography and Geoinformatics II. In Advances and Trends in Geodesy, Cartography and Geoinformatics II; CRC Press: London, UK, 2020; pp. 44–49. [Google Scholar]
- Blistan, P.; Jacko, S.; Kovanič, Ľ.; Kondela, J.; Pukanská, K.; Bartoš, K. TLS and SfM Approach for Bulk Density Determination of Excavated Heterogeneous Raw Materials. Minerals 2020, 10, 174. [Google Scholar] [CrossRef] [Green Version]
- Pukanská, K.; Bartoš, K.; Bella, P.; Gašinec, J.; Blistan, P.; Kovanič, Ľ. Surveying and High-Resolution Topography of the Ochtiná Aragonite Cave Based on TLS and Digital Photogrammetry. Appl. Sci. 2020, 10, 4633. [Google Scholar] [CrossRef]
- Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Flöry, S.; Nussbaumer, L. Concept and Performance Evaluation of a Novel UAV-Borne Topo-Bathymetric LiDAR Sensor. Remote Sens. 2020, 12, 986. [Google Scholar] [CrossRef] [Green Version]
- Jakovljevic, G.; Govedarica, M.; Alvarez-Taboada, F.; Pajic, V. Accuracy Assessment of Deep Learning Based Classification of LiDAR and UAV Points Clouds for DTM Creation and Flood Risk Mapping. Geosciences 2019, 9, 323. [Google Scholar] [CrossRef] [Green Version]
- Balsi, M.; Esposito, S.; Fallavollita, P.; Melis, M.G.; Milanese, M. Preliminary Archeological Site Survey by UAV-Borne Lidar: A Case Study. Remote Sens. 2021, 13, 332. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Cheng, Y.-T.; Zhou, T.; Ravi, R.; Hasheminasab, S.M.; Flatt, J.E.; Troy, C.; Habib, A. Evaluation of UAV LiDAR for Mapping Coastal Environments. Remote Sens. 2019, 11, 2893. [Google Scholar] [CrossRef] [Green Version]
- Shaw, L.; Helmholz, P.; Belton, D.; Addy, N. Comparison of UAV lidar and imagery for beach monitoring. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII-2/W13, 589–596. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, T.; Jansen, K.; Miller, J. Analysis of UAS Flight Altitude and Ground Control Point Parameters on DEM Accuracy along a Complex, Developed Coastline. Remote Sens. 2020, 12, 2305. [Google Scholar] [CrossRef]
- Feroz, S.; Abu Dabous, S. UAV-Based Remote Sensing Applications for Bridge Condition Assessment. Remote Sens. 2021, 13, 1809. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, Y.; Xiao, W.; Hu, Z. A review of UAV monitoring in mining areas: Current status and future perspectives. Int. J. Coal Sci. Technol. 2019, 6, 320–333. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Zhao, H.; Yang, R.; Liu, H.; Li, S.; Liu, J. An Entropy-Weighting Method for Efficient Power-Line Feature Evaluation and Extraction from LiDAR Point Clouds. Remote Sens. 2021, 13, 3446. [Google Scholar] [CrossRef]
- Dihkan, M.; Mus, E. Automatic detection of power transmission lines and risky object locations using UAV LiDAR data. Arab. J. Geosci. 2021, 14, 567. [Google Scholar] [CrossRef]
- Salach, A.; Bakuła, K.; Pilarska, M.; Ostrowski, W.; Górski, K.; Kurczyński, Z. Accuracy Assessment of Point Clouds from LiDAR and Dense Image Matching Acquired Using the UAV Platform for DTM Creation. ISPRS Int. J. Geo-Inf. 2018, 7, 342. [Google Scholar] [CrossRef] [Green Version]
- Gomes Pereira, L.; Fernandez, P.; Mourato, S.; Matos, J.; Mayer, C.; Marques, F. Quality Control of Outsourced LiDAR Data Acquired with a UAV: A Case Study. Remote Sens. 2021, 13, 419. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.; Zhang, K.; Wang, S.; Han, Y. UAV-Borne LiDAR Crop Point Cloud Enhancement Using Grasshopper Optimization and Point Cloud Up-Sampling Network. Remote Sens. 2020, 12, 3208. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Development and Performance Assessment of a Low-Cost UAV Laser Scanner System (LasUAV). Remote Sens. 2018, 10, 1094. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2020, 13, 77. [Google Scholar] [CrossRef]
- Jon, J.; Koska, B.; Pospíšil, J. Autonomous airship equipped by multi-sensor mapping platform. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-5/W1, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Fuad, N.A.; Ismail, Z.; Majid, Z.; Darwin, N.; Ariff, M.F.M.; Idris, K.M.; Yusoff, A.R. Accuracy evaluation of digital terrain model based on different flying altitudes and conditional of terrain using UAV LiDAR technology. IOP Conf. Series Earth Environ. Sci. 2018, 169, 012100. [Google Scholar] [CrossRef] [Green Version]
- Siwiec, J. Comparison of Airborne Laser Scanning of Low and High Above Ground Level for Selected Infrastructure Objects. J. Appl. Eng. Sci. 2018, 8, 89–96. [Google Scholar] [CrossRef] [Green Version]
- Pilarska, M.; Ostrowski, W.; Bakuła, K.; Górski, K.; Kurczyński, Z. The potential of light laser scanners developed for unmanned aerial vehicles—The review and accuracy. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLII-2/W2, 87–95. [Google Scholar] [CrossRef] [Green Version]





| Weight | Approx. 6.3 kg (With One Gimbal) |
|---|---|
| Max. transmitting distance (Europe) | 8 km |
| Max. flight time | 55 min |
| Dimensions | 810 × 670 × 430 mm |
| Max. payload | 2.7 kg |
| Max. speed | 82 km/h |
| Dimensions | 152 × 110 × 169 mm |
| Weight | 930 ± 10 g |
| Maximum Measurement Distance | 450 m at 80% reflectivity, 190 m at 10% reflectivity |
| Recording Speed | Single return: max. 240,000 points/s; Multiple return: max. 480,000 points/s |
| System Accuracy (1σ) | Horizontal: 10 cm per 50 m; Vertical: 5 cm per 50 m |
| Distance Measurement Accuracy (1σ) | 3 cm per 100 m |
| Beam Divergence | 0.28° (Vertical) × 0.03° (Horizontal) |
| Maximum Registered Reflections | 3 |
| RGB camera Sensor Size | 1 in |
| RGB Camera Effective Pixels | 20 Mpix (5472 × 3078) |
| Weight | 787 g |
| Dimensions | 198 × 166 × 129 mm |
| CMOS Sensor size | 35.9 × 24 mm |
| Number of Effective Pixels | 45 Mpix |
| Pixel Size | 4 µm |
| Resolution | 8192 × 5460 pix |
| X [m] | Y [m] | Z [m] | Total Error [m] | |
|---|---|---|---|---|
| Camera positions | 0.018 | 0.022 | 0.035 | 0.045 |
| GCPs | 0.003 | 0.002 | 0.006 | 0.007 |
| CPs | 0.002 | 0.002 | 0.011 | 0.011 |
| Flight | Number of Points (Total) | Number of Points (Cropped) | Average Point Density/m2 | Resolution [mm] |
|---|---|---|---|---|
| P1 | 274,363,655 | 77,849,698 | 6551 | 12 |
| L1_50 m_1 | 85,362,025 | 21,940,068 | 1846 | 23 |
| L1_50 m_2 | 129,145,833 | 34,263,928 | 2882 | 19 |
| L1_70 m | 214,350,916 | 40,576,864 | 3413 | 17 |
| Flight L1 | Type of Transformation | RMSE [m] | RMSEX [m] | RMSEY [m] | RMSEZ [m] |
|---|---|---|---|---|---|
| 50 m_1 | Original cloud | 0.036 | 0.054 | 0.019 | 0.022 |
| Translation | 0.013 | 0.016 | 0.013 | 0.007 | |
| 2.5D transformation | 0.013 | 0.016 | 0.013 | 0.007 | |
| 3D transformation | 0.012 | 0.016 | 0.013 | 0.005 | |
| 50 m_2 | Original cloud | 0.025 | 0.024 | 0.020 | 0.030 |
| Translation | 0.015 | 0.016 | 0.017 | 0.012 | |
| 2.5D transformation | 0.015 | 0.016 | 0.016 | 0.012 | |
| 3D transformation | 0.014 | 0.016 | 0.016 | 0.010 | |
| 70 m | Original cloud | 0.029 | 0.035 | 0.030 | 0.019 |
| Translation | 0.014 | 0.019 | 0.010 | 0.012 | |
| 2.5D transformation | 0.014 | 0.019 | 0.011 | 0.012 | |
| 3D transformation | 0.013 | 0.019 | 0.011 | 0.007 |
| Flight L1 | Type of Transformation | TX [m] | TY [m] | TZ [m] | Rz [°] | Rx [°] | Ry [°] |
|---|---|---|---|---|---|---|---|
| 50 m_1 | Original cloud | ||||||
| Translation | 0.052 | −0.014 | 0.021 | ||||
| 2.5D transformation | 0.052 | −0.014 | 0.021 | −0.0001 | |||
| 3D transformation | 0.052 | −0.014 | 0.021 | −0.0001 | −0.0084 | −0.0080 | |
| 50 m_2 | Original cloud | ||||||
| Translation | 0.018 | −0.011 | 0.027 | ||||
| 2.5D transformation | 0.018 | −0.011 | 0.027 | 0.0046 | |||
| 3D transformation | 0.018 | −0.011 | 0.027 | 0.0046 | −0.0135 | −0.0053 | |
| 70 m | Original cloud | ||||||
| Translation | 0.030 | −0.028 | 0.015 | ||||
| 2.5D transformation | 0.030 | −0.028 | 0.015 | −0.0050 | |||
| 3D transformation | 0.030 | −0.028 | 0.015 | −0.0050 | −0.0126 | −0.0212 |
| Flight L1 | Flat Surfaces | Rugged Surfaces | Vertical Surfaces |
|---|---|---|---|
| 50 m_1 | 0.032 | 0.038 | 0.038 |
| 50 m_2 | 0.030 | 0.038 | 0.027 |
| 70 m | 0.044 | 0.048 | 0.049 |
| Flight L1 | Shift | X (m) | Y (m) | Z (m) | Distance (m) |
|---|---|---|---|---|---|
| 50 m_1 | Mean | 0.076 | −0.196 | 0.000 | 0.210 |
| St. dev | 0.028 | 0.036 | 0.042 | ||
| 50 m_2 | Mean | −0.271 | −0.163 | −0.102 | 0.332 |
| St. dev | 0.069 | 0.051 | 0.027 | ||
| 70 m | Mean | −0.221 | 0.335 | −0.139 | 0.425 |
| St. dev | 0.054 | 0.071 | 0.043 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Štroner, M.; Urban, R.; Línková, L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sens. 2021, 13, 4811. https://doi.org/10.3390/rs13234811
Štroner M, Urban R, Línková L. A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sensing. 2021; 13(23):4811. https://doi.org/10.3390/rs13234811
Chicago/Turabian StyleŠtroner, Martin, Rudolf Urban, and Lenka Línková. 2021. "A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner" Remote Sensing 13, no. 23: 4811. https://doi.org/10.3390/rs13234811
APA StyleŠtroner, M., Urban, R., & Línková, L. (2021). A New Method for UAV Lidar Precision Testing Used for the Evaluation of an Affordable DJI ZENMUSE L1 Scanner. Remote Sensing, 13(23), 4811. https://doi.org/10.3390/rs13234811






