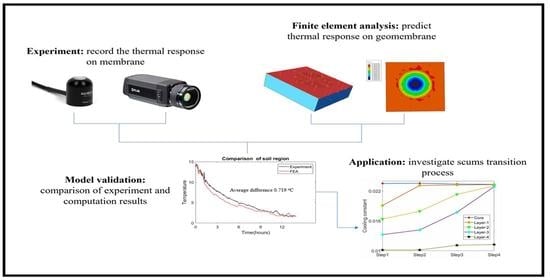
2.2. Finite Element Model
A finite element (FE) model of the experimental setup was constructed within the commercial package ABAQUS [
24], based on the geometry shown in
Figure 4 and the model details in
Table 4.
The relevant boundary conditions for the model are indicated in more detail in
Figure 5, in a cross-sectional view. The intensity of the incident solar radiation is denoted by
. Heat transfer from the top surface of the geomembrane occurs by convection and radiation [
25,
26]:
The convective heat flux
is characterised by Newton’s law
where
denote, respectively, the membrane temperature and ambient temperature at a time instant
t and
denotes the convective heat transfer coefficient. Radiative heat transfer for the HDPE membrane satisfied the Stefan–Boltzmann law, adapted for grey-body radiation [
25,
26]. Allowing for a radiative heat flux from the surroundings, the net radiative heat flux at the surface of a geomembrane can be written as follows:
where
must now be interpreted as absolute temperatures,
denotes the Stefan–Boltzmann constant and
the emissivity, which is equal to the absorptivity
according to Kirchoff’s law. For the range of temperatures encountered in this context, the difference
is relatively small compared with the absolute ambient temperature
, so Equation (3) can be rewritten in the form
Accordingly, Equation (1) can now be rewritten as
According to the experimental measurements of Pelte et al. [
27], a representative value for the combined heat transfer coefficient for a horizontal geomembrane is
, and this value was used in the FE model. The other relevant thermal properties for the model are summarised in
Table 5.
For simplicity, it is assumed that there is no heat flux across the external boundaries of the model on the underside of the membrane, i.e.,
as shown in
Figure 5. However, the membrane is assumed to be in perfect thermal contact with the soil substrate in the soil region, i.e., both temperature and heat flux are continuous across that interface.
The next step in characterising the cooling kinetics is to estimate the Biot number
where
k denotes the thermal conductivity and
denotes an appropriate characteristic length, which in this case can be assumed to be the membrane thickness. This leads to
. As this value is less than 0.1, the temperature gradient across the membrane thickness can be ignored [
25,
26]. Accordingly, the heat balance for a geomembrane on air (or biogas) can be written as follows:
where
denote, respectively, the membrane’s density, specific heat and thickness. Assuming for simplicity that the ambient temperature can be regarded as being constant, or only slowly time varying, Equation (7) can be integrated to obtain
where
denotes the initial temperature and
b the cooling constant. The exponential decay law in Equation (8) applies strictly only for the geomembrane in contact with air or biogas. However, as shown in our previous work [
9,
10,
11], it is also possible to allocate a value of the cooling constant for regions where the geomembrane is in contact with soil (simulating scum) by fitting the (measured or calculated) thermal transients to an exponential decay law.
The FE model was used to analyse the temperature change on the HDPE geomembrane, using the measured solar intensity and ambient temperature as inputs. The geometry of the FE model is shown in
Figure 4 with a mesh size of 1 mm.
The experiments described in
Section 2.1 used clayey soil since it is reported that clayey soil has similar density [
28,
29], thermal conductivity [
30,
31] and specific heat [
32,
33] as scumbergs. The thermal properties of each material are summarised in
Table 5. The emissivity of the HDPE geomembrane at the WTP is approximately 0.9 [
9,
10,
11]. The thermal expansion effect of the HDPE geomembrane was neglected in this study because it does not affect the thermal transient response. The time-dependent thermal FE analysis was conducted over a 24 h period with a time step of 100 s.
To simulate the effect of scum accumulation, the FE model of the soil substrate region in
Figure 4 was modified, as shown in
Figure 6. The substrate was partitioned into six regions, as indicated schematically in
Figure 6a, and in plan view and cross-sectional view in
Figure 6b,c, respectively. The thermal properties changed stepwise across those regions, from those appropriate for liquid sewage, which was simulated as water, to those of hard scum (cf.
Table 5), through 3 intermediate values obtained by linear interpolation, as indicated in
Figure 7. The extreme values are based on those reported in [
33,
34], and their applicability for the WTP will be further discussed below.
The progressive accumulation of scum was simulated through a stepwise change in properties over time. The model was subjected to 12 cycles of the same 24 h variation in solar intensity and ambient temperature described above. These 12 cycles were grouped into four sets lasting 3 days each. The thermal properties were varied stepwise over 4 time steps corresponding to these four sets, as summarised in
Table 6. During each step, the temperature profile on the membrane surface was monitored at five locations corresponding to the five regions identified in
Figure 6, viz. core, and layer 1 through layer 4. The geomembrane thickness and boundary conditions were the same as in
Section 2.