Orthorectification of Helicopter-Borne High Resolution Experimental Burn Observation from Infra Red Handheld Imagers
Abstract
:1. Introduction
2. Background
3. Objectives
4. Experimental Burn Data
5. Orthorectification Algorithms
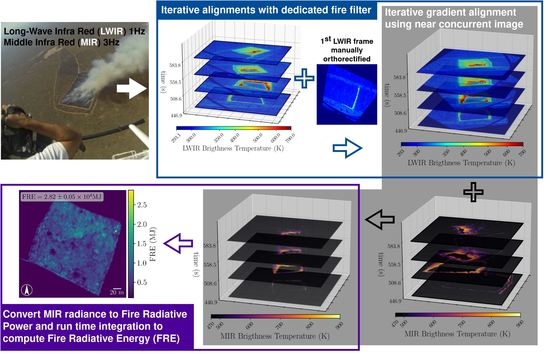
5.1. Algorithms for Long Wave Infra Red
5.1.1. Algorithm 1
| Algorithm 1 Iterative orthorectification using LWIR image background | |
| ▹ manual orthorectification | |
| for do | |
| and | ▹ reference image update |
| ▹ feature and area-based alignment, see step 5 in Figure S4 | |
| ▹ projection on Im | |
| ▹ algorithm stability | |
| ▹ orthorectification | |
| ▹ performance assessment | |
| if | ▹ quality flag |
5.1.2. Algorithm 2
| Algorithm 2 Recursive optimization of LWIR alignment | |
| for do | |
| ▹ reference image update, | |
| ▹ cooling area mask | |
| , ) | ▹ cooling area feature emphasis |
| ▹ alignment, see steps 4 and 5 in Figure S6 | |
| ▹ adjustment | |
| ▹ arrival time map update | |
5.2. Algorithms for Mid Infra Red Images
5.2.1. Algorithm 3
| Algorithm 3 Orthorectification of MIR image | |
| for in set of LWIR orthorectified images do | |
| ▹ select near-concurrent MIR images | |
| ▹ apply initial warp to perspective | |
| , ) | ▹ enhanced cooling area similarity |
| = | ▹ apply area-based alignment (see Figure S7) |
| ▹ compute orthorectification | |
5.2.2. Algorithm 4
| Algorithm 4 Iterative Optimization of MIR image Orthorectification | |
| ▹ input set of MIR orthorectified images | |
| ) | |
| run twice: | |
| for in do | |
| ▹ select reference neighbor image | |
| , ) | ▹ enhanced cooling area similarity |
| = | ▹ apply area-based alignment |
| ▹ compute orthorectification | |
6. Application to KNP14 Data Set
6.1. Application of Algorithms 1 and 2 to LWIR Images
6.1.1. Algorithm Parameter Calibration
6.1.2. Image Outlier Filtering
6.2. Application of Algorithms 3 and 4 to MIR Images
7. Discussion
7.1. Orthorectification Accuracy
7.2. Resulting KNP14 Data Set
7.3. Application to Fire Radiative Power Time Series Estimation
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| IR | Infra Red |
| BT | Brightness Temperature |
| LWIR | Long Wave Infra Red |
| MIR | Middle Infra Red |
| VIS | Visible |
| GCP | Ground Control Point |
| SSIM | Structural Similarity Index Metric |
| ROS | Rate Of Spread |
| FI | Fire Intensity |
| FRP | Fire Radiative Power |
| FRE | Fire Radiative Energy |
References
- Prichard, S.; Larkin, N.S.; Ottmar, R.; French, N.H.; Baker, K.; Brown, T.; Clements, C.; Dickinson, M.; Hudak, A.; Kochanski, A.; et al. The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns. Atmosphere 2019, 10, 66. [Google Scholar] [CrossRef] [Green Version]
- Andela, N.; Morton, D.C.; Giglio, L.; Chen, Y.; Van Der Werf, G.R.; Kasibhatla, P.S.; DeFries, R.S.; Collatz, G.J.; Hantson, S.; Kloster, S.; et al. A human-driven decline in global burned area. Science 2017, 356, 1356–1362. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, G.; Wooster, M.J. Global impact of landscape fire emissions on surface level PM2.5 concentrations, air quality exposure and population mortality. Atmos. Environ. 2021, 252, 118210. [Google Scholar] [CrossRef]
- Doerr, S.H.; Santín, C. Global trends in wildfire and its impacts: Perceptions versus realities in a changing world. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2016, 371. [Google Scholar] [CrossRef]
- Abram, N.J.; Henley, B.J.; Sen Gupta, A.; Lippmann, T.J.R.; Clarke, H.; Dowdy, A.J.; Sharples, J.J.; Nolan, R.H.; Zhang, T.; Wooster, M.J.; et al. Connections of climate change and variability to large and extreme forest fires in southeast Australia. Commun. Earth Environ. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Singleton, M.P.; Thode, A.E.; Sánchez Meador, A.J.; Iniguez, J.M. Increasing trends in high-severity fire in the southwestern USA from 1984 to 2015. For. Ecol. Manag. 2019, 433, 709–719. [Google Scholar] [CrossRef]
- Kochanski, A.K.; Jenkins, M.A.; Yedinak, K.; Mandel, J.; Beezley, J.; Lamb, B. Toward an integrated system for fire, smoke and air quality simulations. Int. J. Wildland Fire 2016, 25, 534. [Google Scholar] [CrossRef] [Green Version]
- Coen, J.L. Modeling Wildland Fires: Of the Coupled Atmosphere-Wildland Fire Environment Model (CAWFE); Technical Report, NCAR Technical Note NCAR/TN-500+STR; NCAR: Boulder, CO, USA, 2013. [Google Scholar] [CrossRef]
- Mandel, J.; Beezley, J.D.; Kochanski, A.K. Coupled atmosphere-wildland fire modeling with WRF 3.3 and SFIRE. Geosci. Model Dev. 2011, 4, 591–610. [Google Scholar] [CrossRef] [Green Version]
- Kochanski, A.K.; Jenkins, M.A.; Mandel, J.; Beezley, J.D.; Krueger, S.K. Real time simulation of 2007 Santa Ana fires. For. Ecol. Manag. J. 2013, 294, 136–149. [Google Scholar] [CrossRef] [Green Version]
- Filippi, J.B.; Bosseur, F.; Pialat, X.; Santoni, P.A.; Strada, S.; Mari, C. Simulation of Coupled Fire/Atmosphere Interaction with the MesoNH-ForeFire Models. J. Combust. 2011, 2011, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Filippi, J.B.; Bosseur, F.; Mari, C.; Lac, C. Simulation of a Large Wildfire in a Coupled Fire-Atmosphere Model. Atmosphere 2018, 9, 218. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Kochanski, A.; Baker, K.R.; Mell, W.; Linn, R.; Paugam, R.; Mandel, J.; Fournier, A.; Jenkins, M.A.; Goodrick, S.; et al. Fire behaviour and smoke modelling: Model improvement and measurement needs for next-generation smoke research and forecasting systems. Int. J. Wildland Fire 2019, 28, 570. [Google Scholar] [CrossRef] [Green Version]
- Ottmar, R.D.; Hiers, J.K.; Butler, B.W.; Clements, C.B.; Dickinson, M.B.; Hudak, A.T.; O’Brien, J.J.; Potter, B.E.; Rowell, E.M.; Strand, T.M.; et al. Measurements, datasets and preliminary results from the RxCADRE project—2008, 2011 and 2012. Int. J. Wildland Fire 2016, 25, 1. [Google Scholar] [CrossRef]
- Hudak, A.T.; Dickinson, M.B.; Bright, B.C.; Kremens, R.L.; Loudermilk, E.L.; O’Brien, J.J.; Hornsby, B.S.; Ottmar, R.D. Measurements relating fire radiative energy density and surface fuel consumption—RxCADRE 2011 and 2012. Int. J. Wildland Fire 2016, 25, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Butler, B.; Teske, C.; Jimenez, D.; O’Brien, J.; Sopko, P.; Wold, C.; Vosburgh, M.; Hornsby, B.; Loudermilk, E. Observations of energy transport and rate of spreads from low-intensity fires in longleaf pine habitat—RxCADRE 2012. Int. J. Wildland Fire 2016, 25, 76–89. [Google Scholar] [CrossRef] [Green Version]
- Mueller, E.V.; Skowronski, N.; Clark, K.; Gallagher, M.; Kremens, R.; Thomas, J.C.; El Houssami, M.; Filkov, A.; Hadden, R.M.; Mell, W.; et al. Utilization of remote sensing techniques for the quantification of fire behavior in two pine stands. Fire Saf. J. 2017, 91, 845–854. [Google Scholar] [CrossRef] [Green Version]
- Clements, C.B.; Kochanski, A.K.; Seto, D.; Davis, B.; Camacho, C.; Lareau, N.P.; Contezac, J.; Restaino, J.; Heilman, W.E.; Krueger, S.K.; et al. The FireFlux II experiment: A model-guided field experiment to improve understanding of fire–atmosphere interactions and fire spread. Int. J. Wildland Fire 2019, 28, 308. [Google Scholar] [CrossRef] [Green Version]
- McRae, D.J.; Jin, J.Z.; Conard, S.G.; Sukhinin, A.I.; Ivanova, G.A.; Blake, T.W. Infrared characterization of fine-scale variability in behavior of boreal forest fires. Can. J. For. Res. 2005, 35, 2194–2206. [Google Scholar] [CrossRef]
- Pastor, E.; Planas, E. Infrared imagery on wildfire research. Some examples of sound capabilities and applications. In Proceedings of the 2012 3rd International Conference on Image Processing Theory, Tools and Applications, IPTA 2012, Istanbul, Turkey, 15–18 October 2012; pp. 31–36. [Google Scholar] [CrossRef]
- Paugam, R.; Wooster, M.J.; Roberts, G. Use of handheld thermal imager data for airborne mapping of fire radiative power and energy and flame front rate of spread. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3385–3399. [Google Scholar] [CrossRef]
- Zajkowski, T.J.; Dickinson, M.B.; Hiers, J.K.; Holley, W.; Williams, B.W.; Paxton, A.; Martinez, O.; Walker, G.W. Evaluation and use of remotely piloted aircraft systems for operations and research—RxCADRE 2012. Int. J. Wildland Fire 2016, 25, 114. [Google Scholar] [CrossRef]
- Allison, R.; Johnston, J.; Craig, G.; Jennings, S.; Allison, R.S.; Johnston, J.M.; Craig, G.; Jennings, S. Airborne Optical and Thermal Remote Sensing for Wildfire Detection and Monitoring. Sensors 2016, 16, 1310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moran, C.J.; Seielstad, C.A.; Cunningham, M.R.; Hoff, V.; Parsons, R.A.; Queen, L.; Sauerbrey, K.; Wallace, T. Deriving Fire Behavior Metrics from UAS Imagery. Fire 2019, 2, 36. [Google Scholar] [CrossRef] [Green Version]
- Pérez, Y.; Pastor, E.; Planas, E.; Plucinski, M.; Gould, J. Computing forest fires aerial suppression effectiveness by IR monitoring. Fire Saf. J. 2011, 46, 2–8. [Google Scholar] [CrossRef]
- Rios, O.; Pastor, E.; Valero, M.M.; Planas, E. Short-term fire front spread prediction using inverse modelling and airborne infrared images. Int. J. Wildland Fire 2016, 25, 1033. [Google Scholar] [CrossRef] [Green Version]
- Pastor, E.; Àgueda, A.; Andrade-Cetto, J.; Muñoz, M.; Pérez, Y.; Planas, E. Computing the rate of spread of linear flame fronts by thermal image processing. Fire Saf. J. 2006, 41, 569–579. [Google Scholar] [CrossRef] [Green Version]
- Valero, M.M.; Verstockt, S.; Butler, B.; Jimenez, D.; Rios, O.; Mata, C.; Queen, L.; Pastor, E.; Planas, E. Thermal Infrared Video Stabilization for Aerial Monitoring of Active Wildfires. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2817–2832. [Google Scholar] [CrossRef]
- Biggs, R.; Biggs, H.C.; Dunne, T.T.; Govender, N.; Potgieter, A.L. Experimental burn plot trial in the Kruger National Park: History, experimental design and suggestions for data analysis. Koedoe 2003, 46, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Govender, N.; Trollope, W.S.W.; van Wilgen, B.W. The effect of fire season, fire frequency, rainfall and management on fire intensities in savanna vegetation in South Africa. J. Appl. Ecol. 2006, 43, 748–758. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; Gomez-Dans, J.; Roy, D.; Wooster, M.; Lajas, D. 3D radiative transfer modelling of fire impacts on a two-layer savanna system. Remote Sens. Environ. 2011, 115, 1866–1881. [Google Scholar] [CrossRef]
- Wooster, M.J.; Freeborn, P.H.; Archibald, S.; Oppenheimer, C.; Roberts, G.J.; Smith, T.E.; Govender, N.; Burton, M.; Palumbo, I. Field determination of biomass burning emission ratios and factors via open-path FTIR spectroscopy and fire radiative power assessment: Headfire, backfire and residual smouldering combustion in African savannahs. Atmos. Chem. Phys. 2011, 11, 11591–11615. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Oliva, P.; Giglio, L.; Csiszar, I.A. The New VIIRS 375m active fire detection data product: Algorithm description and initial assessment. Remote Sens. Environ. 2014, 143, 85–96. [Google Scholar] [CrossRef]
- Fischer, C.; Klein, D.; Kerr, G.; Stein, E.; Lorenz, E.; Frauenberger, O.; Borg, E. Data Validation and Case Studies using the TET-1 Thermal Infrared Satellite System. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 1177–1182. [Google Scholar] [CrossRef] [Green Version]
- Evangelidis, G.D.; Psarakis, E.Z. Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1858–1865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bovik, A.; Wang, Z.; Sheikh, H.; Bovik, A.; Sheikh, H. Structural Similarity Based Image Quality Assessment. In Signal Processing and Communications; CRC Press: Boca Raton, FL, USA, 2005; Chapter 7; pp. 225–241. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision; Springer: London, UK, 2011; pp. 43–1–43–23. [Google Scholar] [CrossRef]
- Evangelidis, G.D. IAT: A Matlab Toolbox for Image Alignment. 2013. Available online: https://sites.google.com/site/imagealignment/ (accessed on 24 November 2021).
- Bouguet, J.Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the Algorithm; Technical Report; Microprocessor Research Labs, Intel Corporation: Santa Clara, CA, USA, 2001. [Google Scholar] [CrossRef]
- Valero, M.M.; Verstockt, S.; Mata, C.; Jimenez, D.; Queen, L.; Rios, O.; Pastor, E.; Planas, E. Image Similarity Metrics Suitable for Infrared Video Stabilization during Active Wildfire Monitoring: A Comparative Analysis. Remote Sens. 2020, 12, 540. [Google Scholar] [CrossRef] [Green Version]
- Wooster, M.J.; Roberts, G.; Smith, A.M.S.; Johnston, J.; Freeborn, P.; Amici, S.; Hudak, A.T. Thermal Remote Sensing of Active Vegetation Fires and Biomass Burning Events. In Remote Sensing and Digital Image Processing; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 17, pp. 347–390. [Google Scholar] [CrossRef] [Green Version]
- Hampel, F.R. The influence curve and its role in robust estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Mell, W.E.; Linn, R.R. FIRETEC and WFDS Modeling of Fire Behavior and Smoke in Support of FASMEE—Final Report to the Joint Fire Science Program | FRAMES. 2017. Available online: https://www.fs.usda.gov/pnw/projects/firetec-and-wfds-modeling-fire-behavior-and-smoke-support-fasmee (accessed on 24 November 2021).
- Ciullo, V.; Rossi, L.; Pieri, A. Experimental Fire Measurement with UAV Multimodal Stereovision. Remote Sens. 2020, 12, 3546. [Google Scholar] [CrossRef]
- Valero, M.M.; Rios, O.; Planas, E.; Pastor, E. Automated location of active fire perimeters in aerial infrared imaging using unsupervised edge detectors. Int. J. Wildland Fire 2018, 27, 241–256. [Google Scholar] [CrossRef] [Green Version]
- Wooster, M.J.; Roberts, G.; Perry, G.L.W.; Kaufman, Y.J. Retrieval of biomass combustion rates and totals from fire radiative power observations: FRP derivation and calibration relationships between biomass consumption and fire radiative energy release. J. Geophys. Res 2005, 110, 24311. [Google Scholar] [CrossRef]
- Kremens, R.L.; Smith, A.M.; Dickinson, M.B. Fire Metrology: Current and Future Directions in Physics-Based Measurements. Fire Ecol. 2010, 6, 13–35. [Google Scholar] [CrossRef]
- Dickinson, M.B.; Hudak, A.T.; Zajkowski, T.; Loudermilk, E.L.; Schroeder, W.; Ellison, L.; Kremens, R.L.; Holley, W.; Martinez, O.; Paxton, A.; et al. Measuring radiant emissions from entire prescribed fires with ground, airborne and satellite sensors—RxCADRE 2012. Int. J. Wildland Fire 2016, 25, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.J.; Razinger, M.; Schultz, M.G.; Suttie, M.; et al. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef] [Green Version]
- Schroeder, W.; Ellicott, E.; Ichoku, C.; Ellison, L.; Dickinson, M.B.; Ottmar, R.D.; Clements, C.; Hall, D.; Ambrosia, V.; Kremens, R. Integrated active fire retrievals and biomass burning emissions using complementary near-coincident ground, airborne and spaceborne sensor data. Remote Sens. Environ. 2014, 140, 719–730. [Google Scholar] [CrossRef] [Green Version]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN5: 2006 update. Proc. SPIE 2006, 6233, 62331F. [Google Scholar] [CrossRef]
- Nolde, M.; Plank, S.; Richter, R.; Klein, D.; Riedlinger, T. The DLR FireBIRD Small Satellite Mission: Evaluation of Infrared Data for Wildfire Assessment. Remote Sens. 2021, 13, 1459. [Google Scholar] [CrossRef]
- Rochoux, M.C.; Ricci, S.; Lucor, D.; Cuenot, B.; Trouvé, A. Towards predictive data-driven simulations of wildfire spread—Part I: Reduced-cost ensemble Kalman filter based on a polynomial chaos surrogate model for parameter estimation. Nat. Hazards Earth Syst. Sci. 2014, 14, 2951–2973. [Google Scholar] [CrossRef] [Green Version]
- Rochoux, M.C.; Emery, C.; Ricci, S.; Cuenot, B.; Trouvé, A. Towards predictive data-driven simulations of wildfire spread—Part II: Ensemble Kalman Filter for the state estimation of a front-tracking simulator of wildfire spread. Nat. Hazards Earth Syst. Sci. 2015, 15, 1721–1739. [Google Scholar] [CrossRef] [Green Version]









| Burn Plot | Skukuza4 | Skukuza6 | Shabeni1 | Shabeni3 |
|---|---|---|---|---|
| First available visible image. White arrow shows the North. |  |  |  |  |
| Ignition day | 26 August 2014 | 26 August 2014 | 22 August 2014 | 22 August 2014 |
| Ignition time (LT) | 13:26 | 10:59 | 13:00 | 11:00 |
| Plot size (ha) | ||||
| terrain elevation (m) | ||||
| Fuel load (kg/ha) / moisture (%) | 4128/ | 2654/ | 4777/25 | 4678/ |
| Average T (C) | 33 | 30 | 32 | 28 |
| Average (%) | 48 | 60 | 23 | 42 |
| Mean wind speed (m s) | ||||
| Mean wind direction () | 140 | 160 | 320 | 320 |
| Fire duration (min) | ||||
| Corner fire | yes | yes | no | no |
| Number of images LWIR/MIR/VIS | 486/1437/396 | 980/1838/1065 | 527/1819/650 | 1650/1513/1620 |
| Matching satellite | VIIRS | TET | VIIRS | TET |
| Comments | Smoky plume and large front depth. | Multiple fronts. Weak fire on the eastern side. MIR camera set with a filter blocking 30% of the radiation. | Intense fire, with two spotting ignitions outside the plot. | Slow moving backfires followed by one intense front merging. LWIR images are slightly blurred. |
| Camera | Optris PI 400 LWIR | Agema 550 MIR | Gopro Hero 2 VIS |
|---|---|---|---|
| Wave length (m) | –14 | RGB | |
| Sensor size (pixels) | |||
| Field of view () | 53 | 40 | 58 |
| Nominal frame rate (Hz) | ∼1–2 | 3 | ∼1–2 |
| Temperature range (K) | 253 to 1173 | 473 to 1073 | - |
| Comment | IR filter removed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paugam, R.; Wooster, M.J.; Mell, W.E.; Rochoux, M.C.; Filippi, J.-B.; Rücker, G.; Frauenberger, O.; Lorenz, E.; Schroeder, W.; Main, B.; et al. Orthorectification of Helicopter-Borne High Resolution Experimental Burn Observation from Infra Red Handheld Imagers. Remote Sens. 2021, 13, 4913. https://doi.org/10.3390/rs13234913
Paugam R, Wooster MJ, Mell WE, Rochoux MC, Filippi J-B, Rücker G, Frauenberger O, Lorenz E, Schroeder W, Main B, et al. Orthorectification of Helicopter-Borne High Resolution Experimental Burn Observation from Infra Red Handheld Imagers. Remote Sensing. 2021; 13(23):4913. https://doi.org/10.3390/rs13234913
Chicago/Turabian StylePaugam, Ronan, Martin J. Wooster, William E. Mell, Mélanie C. Rochoux, Jean-Baptiste Filippi, Gernot Rücker, Olaf Frauenberger, Eckehard Lorenz, Wilfrid Schroeder, Bruce Main, and et al. 2021. "Orthorectification of Helicopter-Borne High Resolution Experimental Burn Observation from Infra Red Handheld Imagers" Remote Sensing 13, no. 23: 4913. https://doi.org/10.3390/rs13234913
APA StylePaugam, R., Wooster, M. J., Mell, W. E., Rochoux, M. C., Filippi, J.-B., Rücker, G., Frauenberger, O., Lorenz, E., Schroeder, W., Main, B., & Govender, N. (2021). Orthorectification of Helicopter-Borne High Resolution Experimental Burn Observation from Infra Red Handheld Imagers. Remote Sensing, 13(23), 4913. https://doi.org/10.3390/rs13234913