SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks
Abstract
:1. Introduction
2. Datasets and Observations
2.1. The Swarm Satellites
2.2. Earthquake Case Study
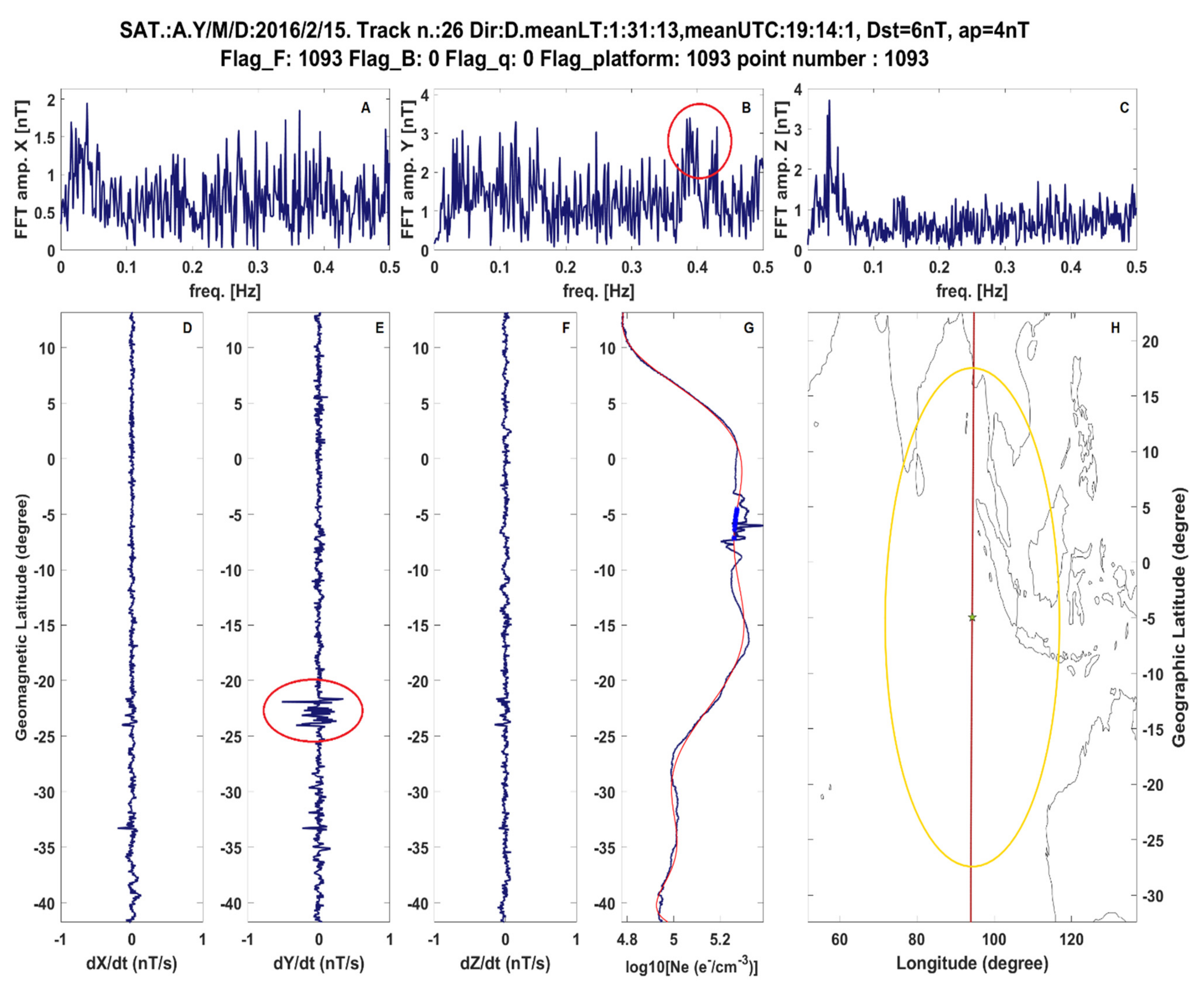
2.2.1. 2016 Sumatra Earthquake
2.2.2. The Ecuador Earthquake Occurred on 16 April 2016
2.3. Dataset and Preprocessing
3. Methodology
3.1. Data Preprocessing
3.2. Deep Learning Network Architecture
3.3. Performance Evaluation
4. Results
4.1. Considering Various Input Sequence Lengths
4.2. Data Comparing Nighttime Versus Daytime
4.3. Considering Various Spatial Windows
4.4. Considering the Magnitude of the Earthquake
4.5. Considering Unbalanced Datasets
4.6. Comparative Analysis of Other Classifiers
5. Discussions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moore, G.W. Magnetic Disturbances preceding the 1964 Alaska Earthquake. Nature 1964, 203, 508–509. [Google Scholar] [CrossRef]
- Davies, K.; Baker, D.M. Ionospheric effects observed around the time of the Alaskan earthquake of March 28, 1964. J. Geophys. Res. 1965, 70, 2251–2253. [Google Scholar] [CrossRef]
- Parrot, M.; Li, M. Demeter results related to seismic activity. URSI Radio Sci. Bull. 2015, 2015, 18–25. [Google Scholar]
- De Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential earthquake precursory pattern from space: The 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Piscini, A.; Campuzano, S.A.; De Carvalho, W.V.J.O. Pre-earthquake chain processes detected from ground to satellite altitude in preparation of the 2016–2017 seismic sequence in Central Italy. Remote Sens. Environ. 2019, 229, 93–99. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Soldani, M.; Piscini, A.; Sabbagh, D.; Cianchini, G.; Perrone, L.; Orlando, M. Swarm Satellite Magnetic Field Data Analysis Prior to 2019 Mw = 7.1 Ridgecrest (California, USA) Earthquake. Geosciences 2020, 10, 502. [Google Scholar] [CrossRef]
- Zhu, K.; Fan, M.; He, X.; Marchetti, D.; Li, K.; Yu, Z.; Chi, C.; Sun, H.; Cheng, Y. Analysis of Swarm Satellite Magnetic Field Data Before the 2016 Ecuador (Mw = 7.8) Earthquake Based on Non-negative Matrix Factorization. Front. Earth Sci. 2021, 9, 1976. [Google Scholar] [CrossRef]
- Christodoulou, V.; Bi, Y.; Wilkie, G. A tool for Swarm satellite data analysis and anomaly detection. PLoS ONE 2019, 14, e0212098. [Google Scholar] [CrossRef] [PubMed]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Jin, S. Anomalous seismo-LAI variations potentially associated with the 2017 Mw = 7.3 Sarpol-e Zahab (Iran) earthquake from Swarm satellites, GPS-TEC and climatological data. Adv. Space Res. 2019, 64, 143–158. [Google Scholar] [CrossRef]
- Marchetti, D.; Akhoondzadeh, M. Analysis of Swarm satellites data showing seismo-ionospheric anomalies around the time of the strong Mexico (Mw = 8.2) earthquake of 08 September 2017. Adv. Space Res. 2018, 62, 614–623. [Google Scholar] [CrossRef]
- Zhu, K.; Li, K.; Fan, M.; Chi, C.; Yu, Z. Precursor Analysis Associated With the Ecuador Earthquake Using Swarm A and C Satellite Magnetic Data Based on PCA. IEEE Access 2019, 7, 93927–93936. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Piscini, A.; Cianchini, G. Multi precursors analysis associated with the powerful Ecuador (MW = 7.8) earthquake of 16 April 2016 using Swarm satellites data in conjunction with other multi-platform satellite and ground data. Adv. Space Res. 2018, 61, 248–263. [Google Scholar] [CrossRef] [Green Version]
- Parrot, M. Statistical analysis of automatically detected ion density variations recorded by DEMETER and their relation to seismic activity. Ann. Geophys. 2012, 55. [Google Scholar] [CrossRef]
- Yan, R.; Parrot, M.; Pinçon, J.-L. Statistical Study on Variations of the Ionospheric Ion Density Observed by DEMETER and Related to Seismic Activities. J. Geophys. Res. Space Phys. 2017, 122, 12,421–12,429. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Shen, X.; Parrot, M.; Zhang, X.; Zhang, Y.; Yu, C.; Yan, R.; Liu, D.; Lu, H.; Guo, F.; et al. Primary Joint Statistical Seismic Influence on Ionospheric Parameters Recorded by the CSES and DEMETER Satellites. J. Geophys. Res. Space Phys. 2020, 125. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Pavon-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchetti, D.; De Santis, A.; Jin, S.; Campuzano, S.A.; Cianchini, G.; Piscini, A. Co-Seismic Magnetic Field Perturbations Detected by Swarm Three-Satellite Constellation. Remote Sens. 2020, 12, 1166. [Google Scholar] [CrossRef] [Green Version]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef] [PubMed]
- Rouet-Leduc, B.; Hulbert, C.; Johnson, P.A. Continuous chatter of the Cascadia subduction zone revealed by machine learning. Nat. Geosci. 2018, 12, 75–79. [Google Scholar] [CrossRef]
- Ross, Z.E.; Trugman, D.T.; Hauksson, E.; Shearer, P.M. Searching for hidden earthquakes in Southern California. Science 2019, 364, 767–771. [Google Scholar] [CrossRef] [Green Version]
- Xiong, P.; Long, C.; Zhou, H.; Battiston, R.; Zhang, X.; Shen, X. Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sens. 2020, 12, 3643. [Google Scholar] [CrossRef]
- Xiong, P.; Tong, L.; Zhang, K.; Shen, X.; Battiston, R.; Ouzounov, D.; Iuppa, R.; Crookes, D.; Long, C.; Zhou, H. Towards advancing the earthquake forecasting by machine learning of satellite data. Sci. Total Environ. 2021, 771, 145256. [Google Scholar] [CrossRef] [PubMed]
- Xiong, P.; Long, C.; Zhou, H.; Battiston, R.; De Santis, A.; Ouzounov, D.; Zhang, X.; Shen, X. Pre-Earthquake Ionospheric Perturbation Identification Using CSES Data via Transfer Learning. Front. Environ. Sci. 2021, 9, 9255. [Google Scholar] [CrossRef]
- Olsen, N.; Friis-Christensen, E.; Floberghagen, R.; Alken, P.; Beggan, C.D.; Chulliat, A.; Doornbos, E.; da Encarnação, J.T.; Hamilton, B.; Hulot, G.; et al. The Swarm Satellite Constellation Application and Research Facility (SCARF) and Swarm data products. Earth Planets Space 2013, 65, 1189–1200. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Pinheiro, K.J.; Jackson, A.; Finlay, C.C. Measurements and uncertainties of the occurrence time of the 1969, 1978, 1991, and 1999 geomagnetic jerks. Geochem. Geophys. Geosyst. 2011, 12. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An improved coupling model for the lithosphere-atmosphere-ionosphere system. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Spogli, L.; Cianchini, G.; Pavón-Carrasco, F.J.; Franceschi, G.D.; Di Giovambattista, R.; Perrone, L.; Qamili, E.; Cesaroni, C.; et al. Magnetic Field and Electron Density Data Analysis from Swarm Satellites Searching for Ionospheric Effects by Great Earthquakes: 12 Case Studies from 2014 to 2016. Atmosphere 2019, 10, 371. [Google Scholar] [CrossRef] [Green Version]
- Dobrovolsky, I.; Zubkov, S.; Miachkin, V. Estimation of the size of earthquake preparation zones. Pure Appl. Geophys. 1979, 117, 1025–1044. [Google Scholar] [CrossRef]
- Spogli, L.; Sabbagh, D.; Regi, M.; Cesaroni, C.; Perrone, L.; Alfonsi, L.; Di Mauro, D.; Lepidi, S.; Campuzano, S.A.; Marchetti, D.; et al. Ionospheric Response Over Brazil to the August 2018 Geomagnetic Storm as Probed by CSES-01 and Swarm Satellites and by Local Ground-Based Observations. J. Geophys. Res. Space Phys. 2021, 126. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX symposium on operating systems design and implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Oh, K.-S.; Jung, K. GPU implementation of neural networks. Pattern Recognit. 2004, 37, 1311–1314. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, CA, USA, 3–8 December 2012; pp. 2951–2959. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. I-115–I-123. [Google Scholar]
- Japkowicz, N.; Stephen, S. The class imbalance problem: A systematic study. Intell. Data Anal. 2002, 6, 429–449. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, CA, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Němec, F.; Santolík, O.; Parrot, M.; Berthelier, J.J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Němec, F.; Santolík, O.; Parrot, M. Decrease of intensity of ELF/VLF waves observed in the upper ionosphere close to earthquakes: A statistical study. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Píša, D.; Němec, F.; Parrot, M.; Santolík, O. Attenuation of electromagnetic waves at the frequency ~1.7 kHz in the upper ionosphere observed by the DEMETER satellite in the vicinity of earthquakes. Ann. Geophys. 2012, 55, 157–163. [Google Scholar] [CrossRef]
- Píša, D.; Němec, F.; Santolík, O.; Parrot, M.; Rycroft, M. Additional attenuation of natural VLF electromagnetic waves observed by the DEMETER spacecraft resulting from preseismic activity. J. Geophys. Res. Space Phys. 2013, 118, 5286–5295. [Google Scholar] [CrossRef] [Green Version]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Liu, J.-Y.; Hattori, K.; Han, P. Multiparameter Assessment of Pre-Earthquake Atmospheric Signals. Pre-Earthq. Process. 2018, 339–359. [Google Scholar] [CrossRef]
- Freund, F.T.; Heraud, J.A.; Centa, V.A.; Scoville, J. Mechanism of unipolar electromagnetic pulses emitted from the hypocenters of impending earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 47–65. [Google Scholar] [CrossRef]
- Wu, L.-X.; Qin, K.; Liu, S.-J. GEOSS-Based Thermal Parameters Analysis for Earthquake Anomaly Recognition. Proc. IEEE 2012, 100, 2891–2907. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.A.; Solovieva, M.; Molchanov, O.A. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Pulinets, S.A.; Ouzounov, D.P.; Karelin, A.V.; Davidenko, D.V. Physical bases of the generation of short-term earthquake precursors: A complex model of ionization-induced geophysical processes in the lithosphere-atmosphere-ionosphere-magnetosphere system. Geomagn. Aeron. 2015, 55, 521–538. [Google Scholar] [CrossRef]
- Freund, F.T. Pre-earthquake signals—Part I: Deviatoric stresses turn rocks into a source of electric currents. Nat. Hazards Earth Syst. Sci. 2007, 7, 535–541. [Google Scholar] [CrossRef] [Green Version]
- Soter, S. Macroscopic seismic anomalies and submarine pockmarks in the Corinth–Patras rift, Greece. Tectonophysics 1999, 308, 275–290. [Google Scholar] [CrossRef]
- Riggio, A.; Santulin, M. Earthquake forecasting: A review of radon as seismic precursor. Boll. Di Geofis. Teor. Ed Appl. 2015, 56. [Google Scholar]
- Gold, T.; Soter, S. Fluid ascent through the solid lithosphere and its relation to earthquakes. Pure Appl. Geophys. 1985, 122, 492–530. [Google Scholar] [CrossRef]
- Kumar, A.; Walia, V.; Singh, S.; Bajwa, B.S.; Dhar, S.; Yang, T.F. Earthquake precursory studies at Amritsar Punjab, India using radon measurement techniques. Int. J. Phys. Sci. 2013, 7, 5669–5677. [Google Scholar]
- Muto, J.; Yasuoka, Y.; Miura, N.; Iwata, D.; Nagahama, H.; Hirano, M.; Ohmomo, Y.; Mukai, T. Preseismic atmospheric radon anomaly associated with 2018 Northern Osaka earthquake. Sci. Rep. 2021, 11, 7451. [Google Scholar] [CrossRef] [PubMed]
- Omori, Y.; Nagahama, H.; Yasuoka, Y.; Muto, J. Radon degassing triggered by tidal loading before an earthquake. Sci. Rep. 2021, 11, 4092. [Google Scholar] [CrossRef]
- Fu, C.-C.; Lee, L.-C.; Yang, T.F.; Lin, C.-H.; Chen, C.-H.; Walia, V.; Liu, T.-K.; Ouzounov, D.; Giuliani, G.; Lai, T.-H.; et al. Gamma Ray and Radon Anomalies in Northern Taiwan as a Possible Preearthquake Indicator around the Plate Boundary. Geofluids 2019, 2019, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kuo, C.L.; Huba, J.D.; Joyce, G.; Lee, L.C. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Wan, W.; Zhou, C.; Zhang, X.; Liu, Y.; Shen, X. A study of the ionospheric disturbances associated with strong earthquakes using the empirical orthogonal function analysis. J. Asian. Earth Sci. 2019, 171, 225–232. [Google Scholar] [CrossRef]
- Yao, Y.B.; Chen, P.; Zhang, S.; Chen, J.J.; Yan, F.; Peng, W.F. Analysis of pre-earthquake ionospheric anomalies before the global M = 7.0+ earthquakes in 2010. Nat. Hazards Earth Syst. Sci. 2012, 12, 575–585. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Wang, M.; Yu, T.; Xu, G.; Wan, W.; Liu, L. Ionospheric total electron content variations prior to the 2008 Wenchuan Earthquake. Int. J. Remote Sens. 2010, 31, 3545–3557. [Google Scholar] [CrossRef]












| DataSet | Night/Daytime | Spatial Feature | Input Sequence Length | Earthquake Magnitude/No. of Real Earthquakes/Positive to Negative Ratio |
|---|---|---|---|---|
| DataSet 01 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 60 continuous points | above 4.8/9017/1:1 |
| DataSet 02 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 80 continuous points | above 4.8/9017/1:1 |
| DataSet 03 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 04 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 50 continuous points | above 4.8/9017/1:1 |
| DataSet 05 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 40 continuous points | above 4.8/9017/1:1 |
| DataSet 06 | Daytime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 07 | Nighttime | with its center at the epicenter and a deviation of 3° | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 08 | Nighttime | with its center at the epicenter and a deviation of 5° | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 09 | Nighttime | with its center at the epicenter and a deviation of 7° | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 10 | Nighttime | with its center at the epicenter and a deviation of 10° | 70 continuous points | above 4.8/9017/1:1 |
| DataSet 11 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | 4.8~5.2/5136/1:1 |
| DataSet 12 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | 5.2~5.8/2793/1:1 |
| DataSet 13 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | 5.8~7.5/853/1:1 |
| DataSet 14 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:2 |
| DataSet 15 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:3 |
| DataSet 16 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:4 |
| DataSet 17 | Nighttime | with its center at the epicenter and the Dobrovolsky radius | 70 continuous points | above 4.8/9017/1:5 |
| Method | DataSet | MCC | F1 | Accuracy | AUC of Class 0 | AUC of Class 1 | AUC of Class 2 |
|---|---|---|---|---|---|---|---|
| SafeNet | DataSet 01 | 0.684 | 0.830 | 0.830 | 0.910 | 0.929 | 0.500 |
| DataSet 02 | 0.654 | 0.825 | 0.825 | 0.894 | 0.927 | 0.539 | |
| DataSet 03 | 0.717 | 0.846 | 0.846 | 0.931 | 0.946 | 0.545 | |
| DataSet 04 | 0.690 | 0.829 | 0.829 | 0.899 | 0.907 | 0.500 | |
| DataSet 05 | 0.662 | 0.812 | 0.812 | 0.920 | 0.907 | 0.515 | |
| DataSet 06 | 0.653 | 0.805 | 0.805 | 0.881 | 0.871 | 0.534 | |
| DataSet 07 | 0.665 | 0.812 | 0.812 | 0.909 | 0.917 | 0.521 | |
| DataSet 08 | 0.659 | 0.809 | 0.809 | 0.912 | 0.919 | 0.500 | |
| DataSet 09 | 0.644 | 0.801 | 0.801 | 0.909 | 0.917 | 0.531 | |
| DataSet 10 | 0.657 | 0.809 | 0.809 | 0.913 | 0.921 | 0.505 | |
| DataSet 11 | 0.510 | 0.697 | 0.697 | 0.869 | 0.898 | 0.537 | |
| DataSet 12 | 0.517 | 0.706 | 0.706 | 0.860 | 0.883 | 0.518 | |
| DataSet 13 | 0.656 | 0.812 | 0.812 | 0.896 | 0.915 | 0.539 | |
| DataSet 14 | 0.661 | 0.835 | 0.835 | 0.875 | 0.916 | 0.522 | |
| DataSet 15 | 0.687 | 0.830 | 0.830 | 0.911 | 0.907 | 0.530 | |
| DataSet 16 | 0.665 | 0.819 | 0.819 | 0.911 | 0.925 | 0.523 | |
| DataSet 17 | 0.657 | 0.814 | 0.814 | 0.908 | 0.926 | 0.545 | |
| CNN | DataSet 03 | 0.635 | 0.825 | 0.825 | 0.859 | 0.908 | 0.520 |
| LSTM | DataSet 03 | 0.643 | 0.824 | 0.824 | 0.880 | 0.923 | 0.520 |
| DNN | DataSet 03 | 0.660 | 0.834 | 0.834 | 0.890 | 0.930 | 0.509 |
| GBM | DataSet 03 | 0.613 | 0.813 | 0.813 | 0.882 | 0.923 | 0.538 |
| RF | DataSet 03 | 0.450 | 0.742 | 0.742 | 0.836 | 0.876 | 0.519 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, P.; Marchetti, D.; De Santis, A.; Zhang, X.; Shen, X. SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks. Remote Sens. 2021, 13, 5033. https://doi.org/10.3390/rs13245033
Xiong P, Marchetti D, De Santis A, Zhang X, Shen X. SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks. Remote Sensing. 2021; 13(24):5033. https://doi.org/10.3390/rs13245033
Chicago/Turabian StyleXiong, Pan, Dedalo Marchetti, Angelo De Santis, Xuemin Zhang, and Xuhui Shen. 2021. "SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks" Remote Sensing 13, no. 24: 5033. https://doi.org/10.3390/rs13245033
APA StyleXiong, P., Marchetti, D., De Santis, A., Zhang, X., & Shen, X. (2021). SafeNet: SwArm for Earthquake Perturbations Identification Using Deep Learning Networks. Remote Sensing, 13(24), 5033. https://doi.org/10.3390/rs13245033









