Vegetation Drought Vulnerability Mapping Using a Copula Model of Vegetation Index and Meteorological Drought Index
Abstract
:1. Introduction
2. Data and Methods
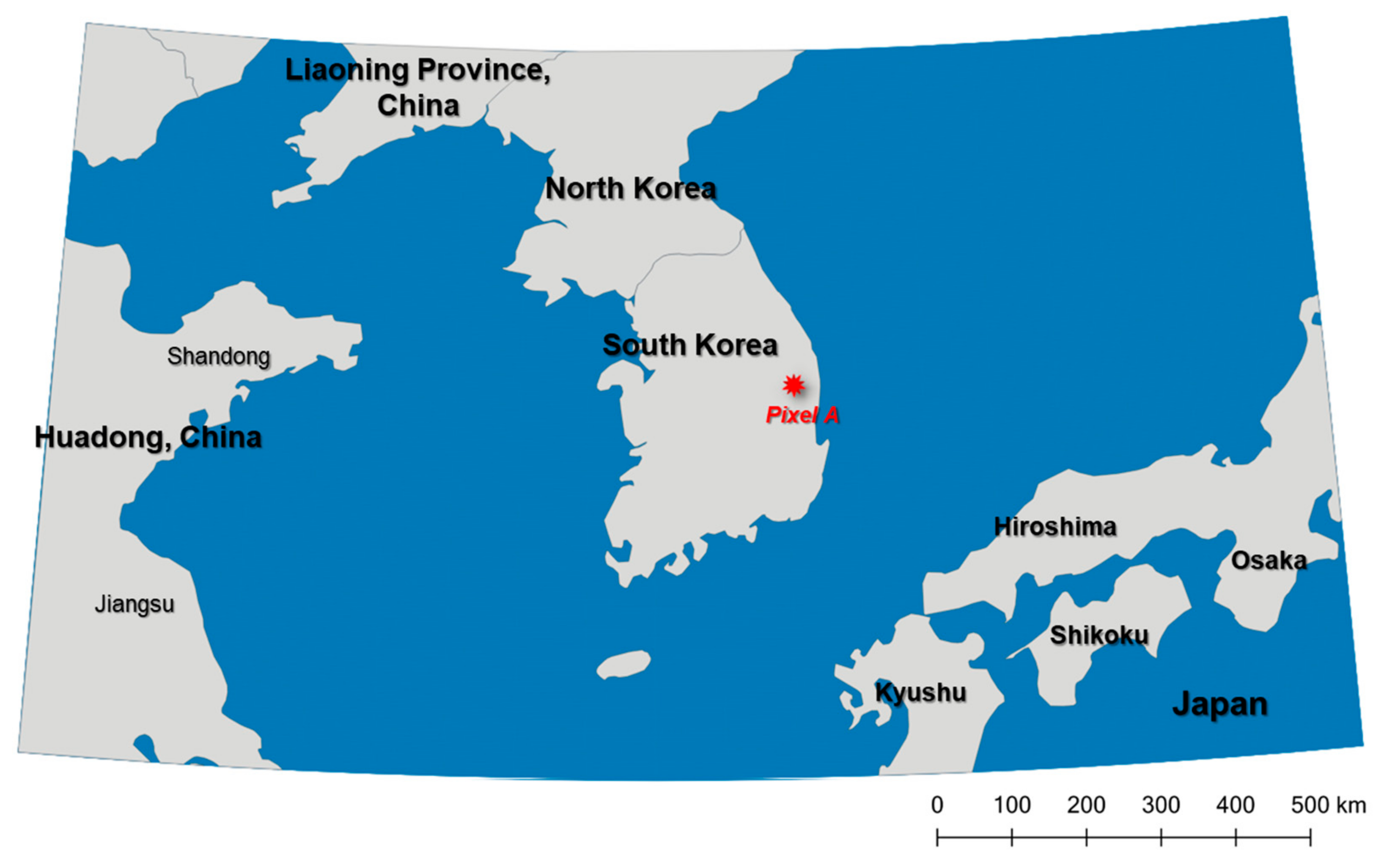
2.1. Data and Study Area
2.2. Drought Indices
2.3. Vegetation Health Index
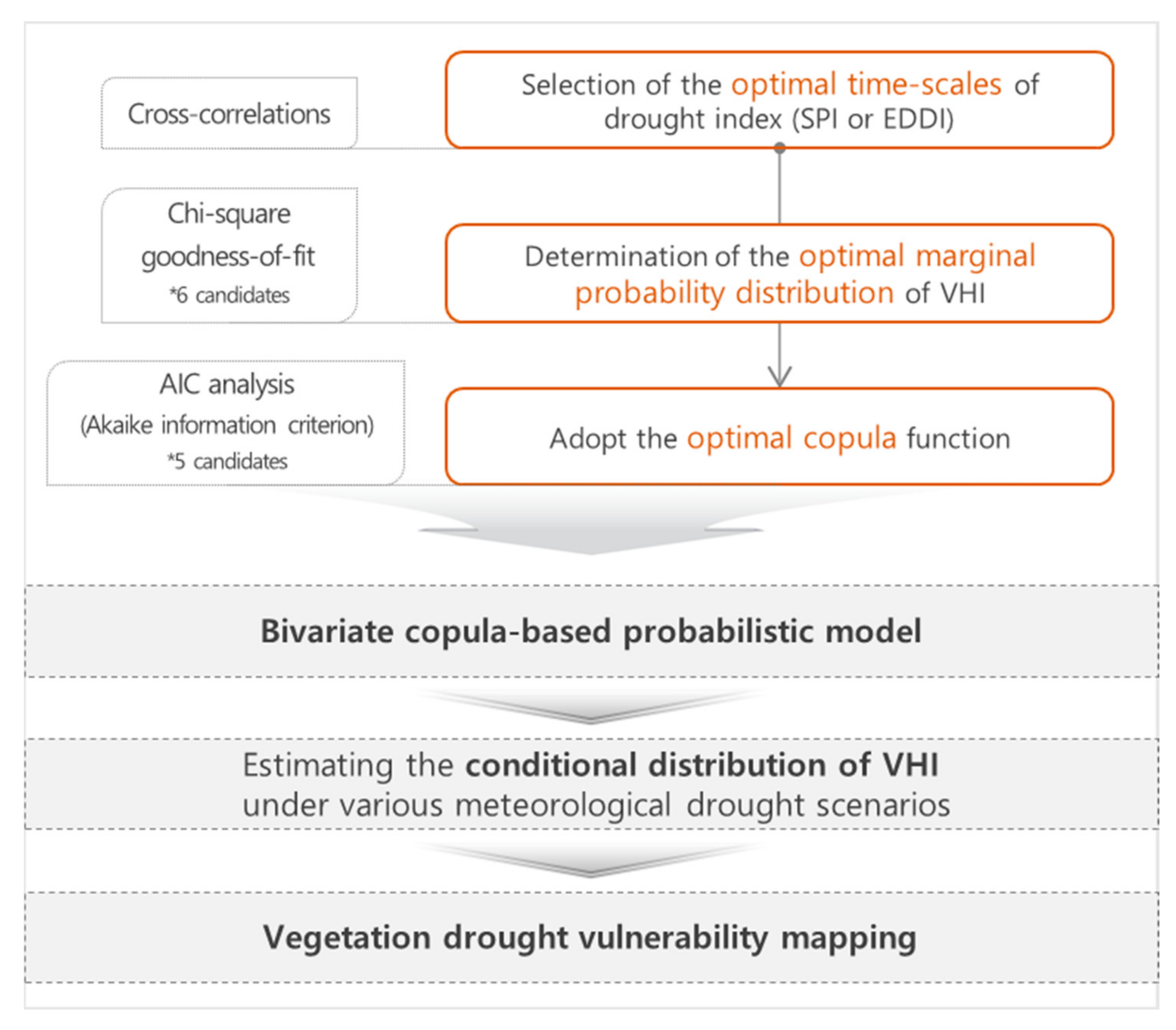
2.4. Bivariate Copula-Based Probabilistic Model
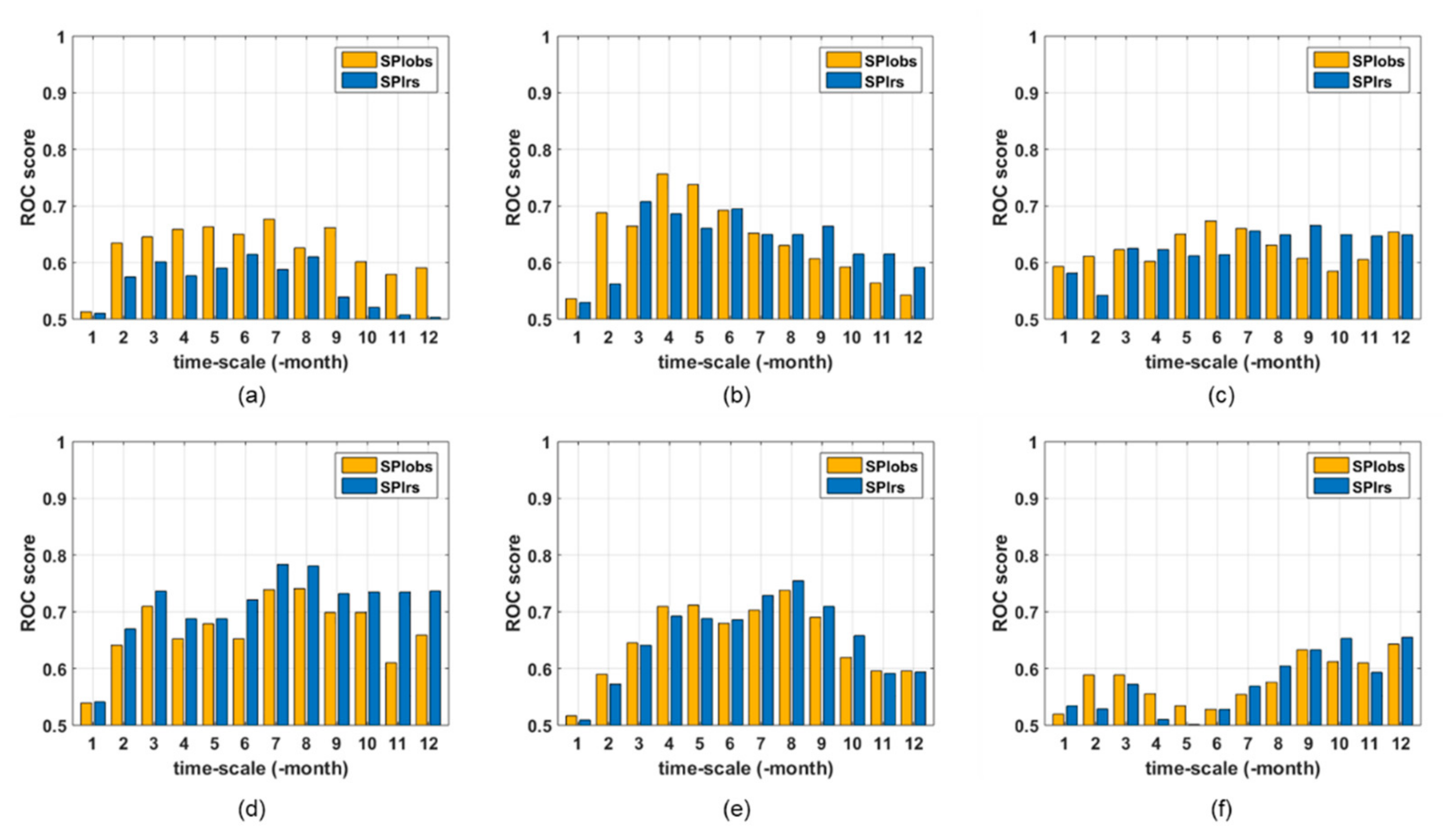
3. Applicability of Drought Indices Using Satellite Remote Sensing Data
4. Result and Discussion
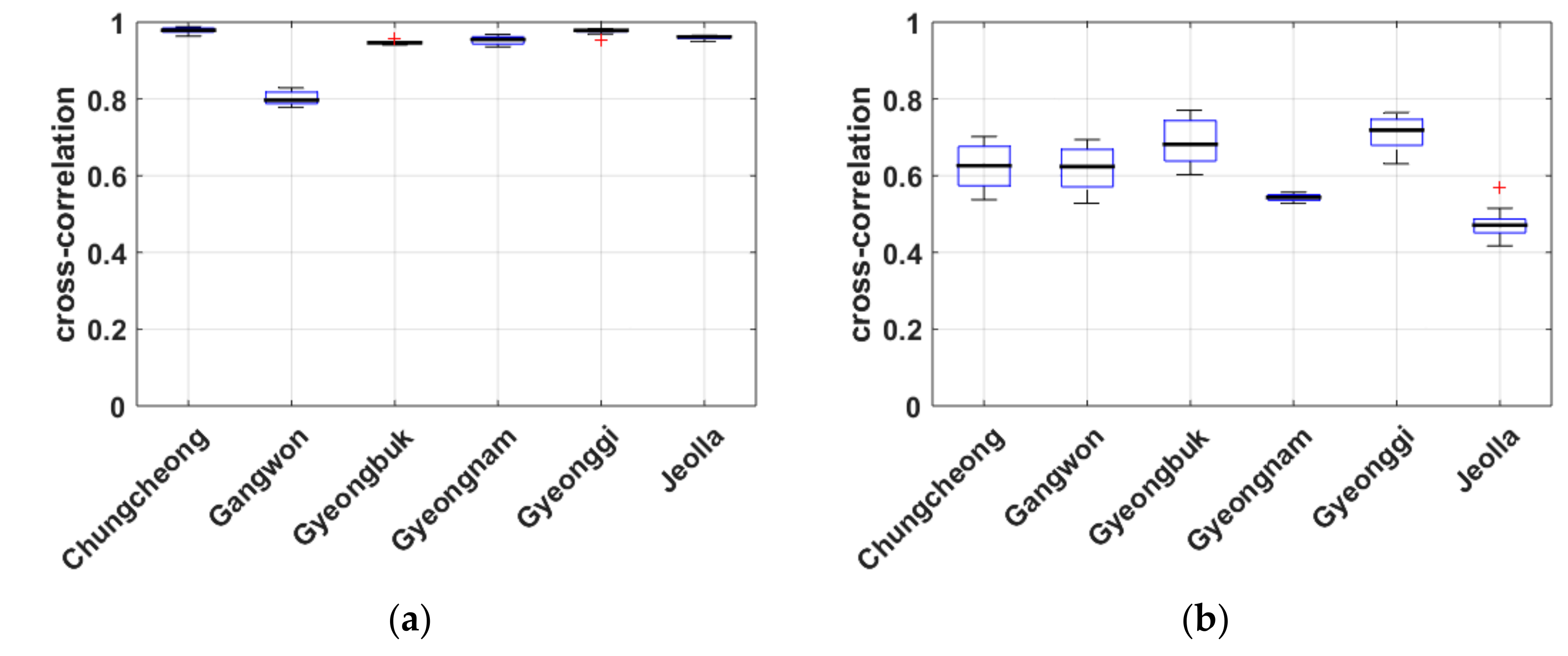
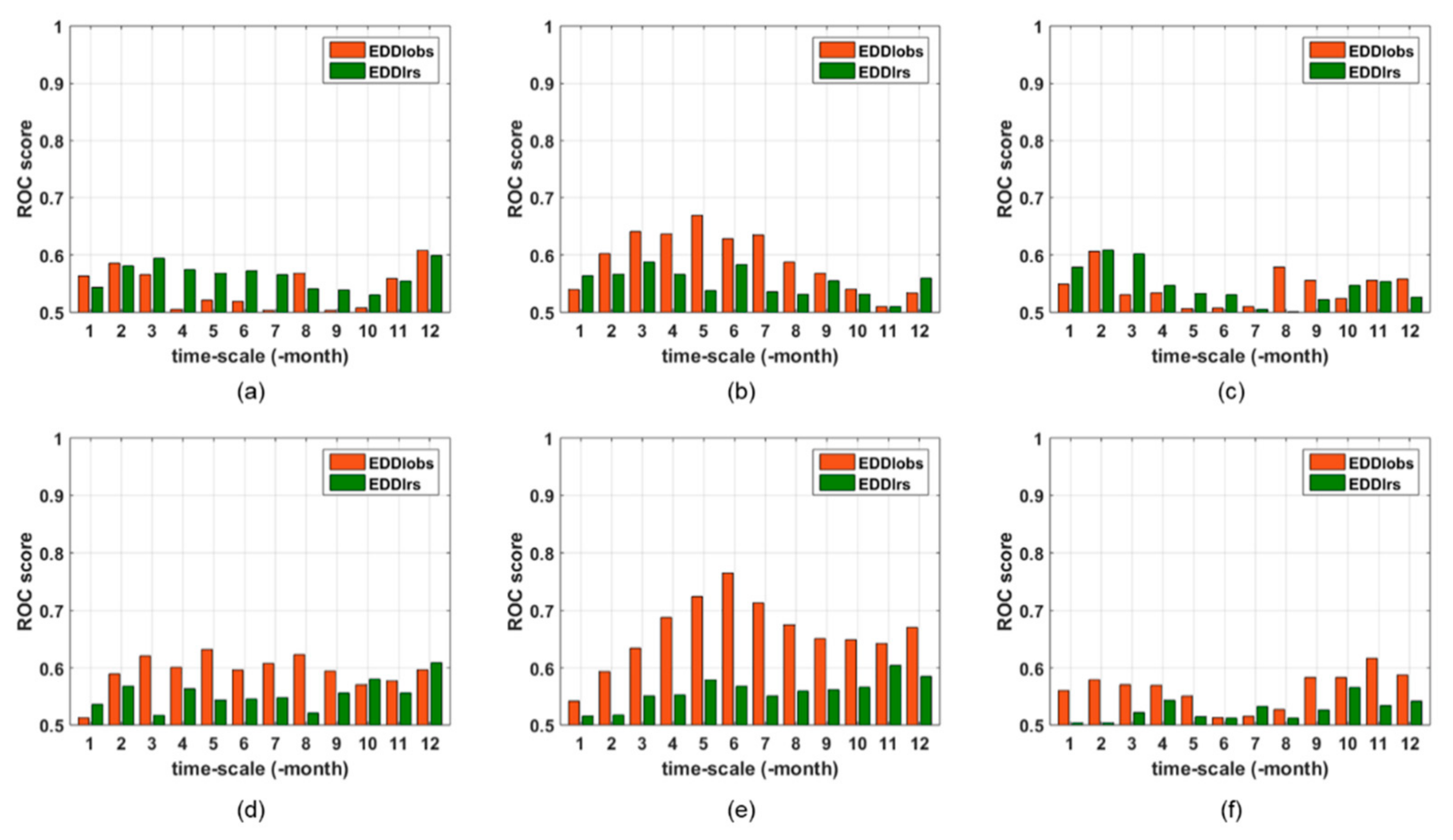
4.1. Time Scale for Drought Index
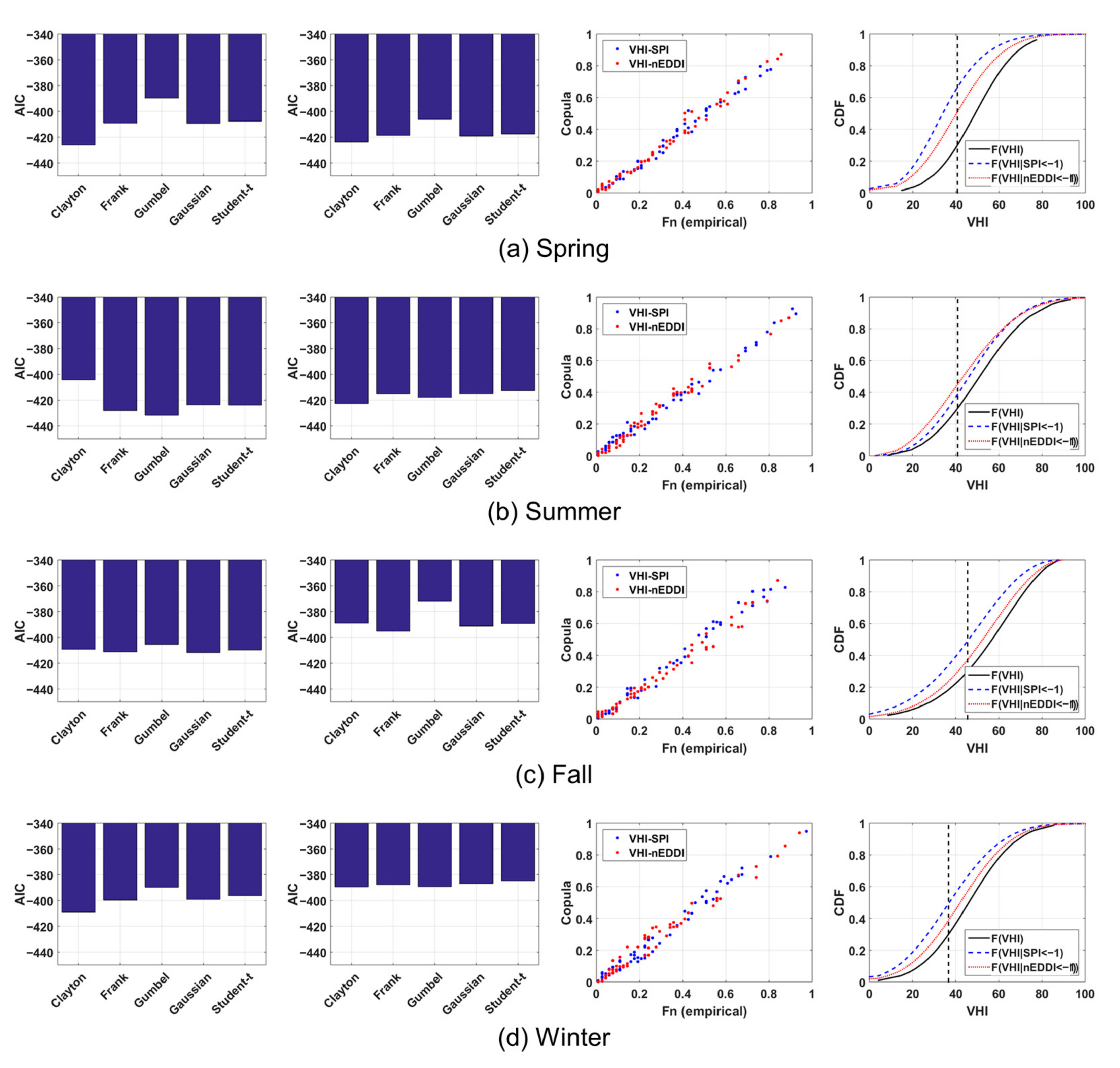
4.2. Bivariate Copula-Based Probabilistic Model
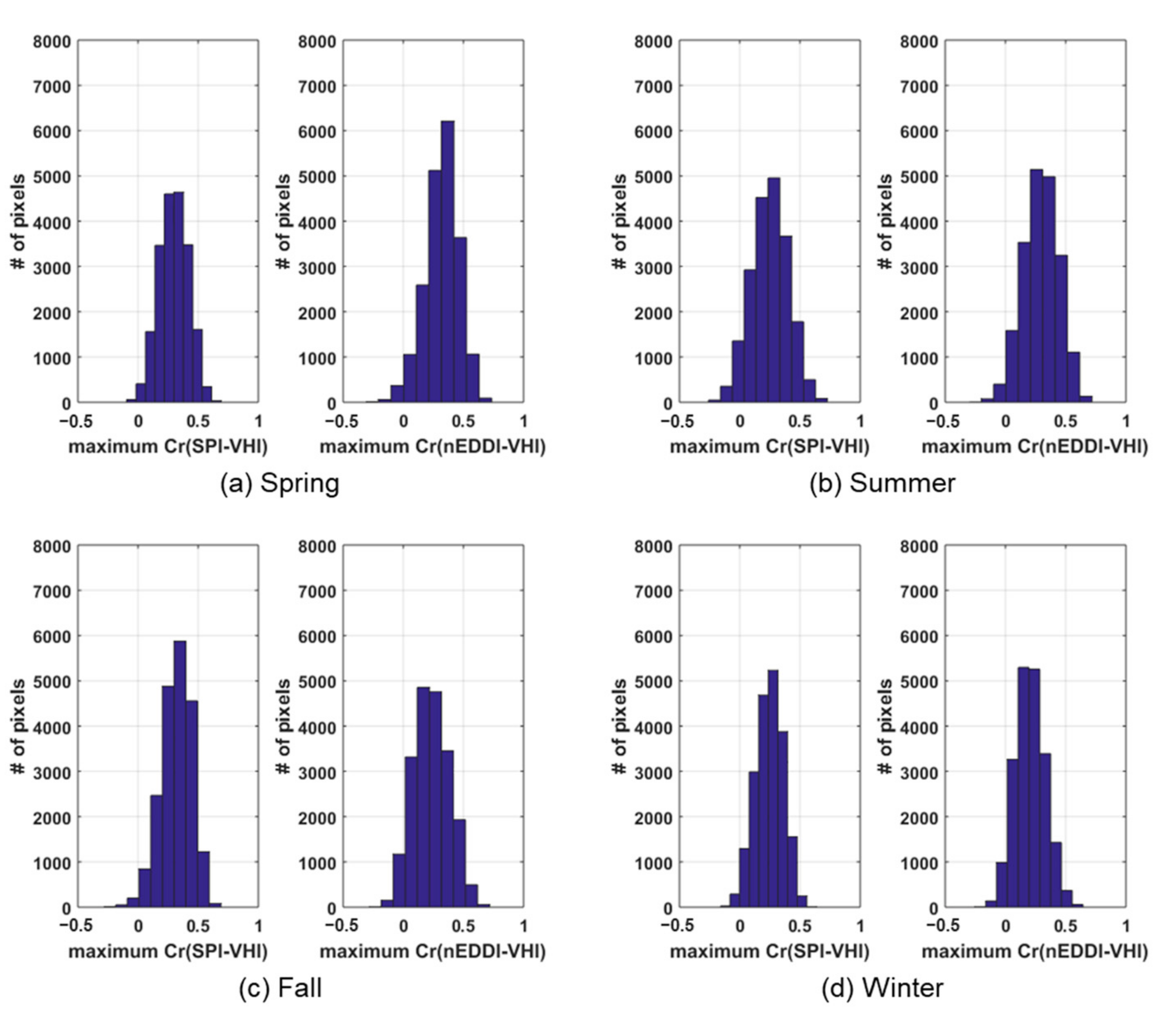
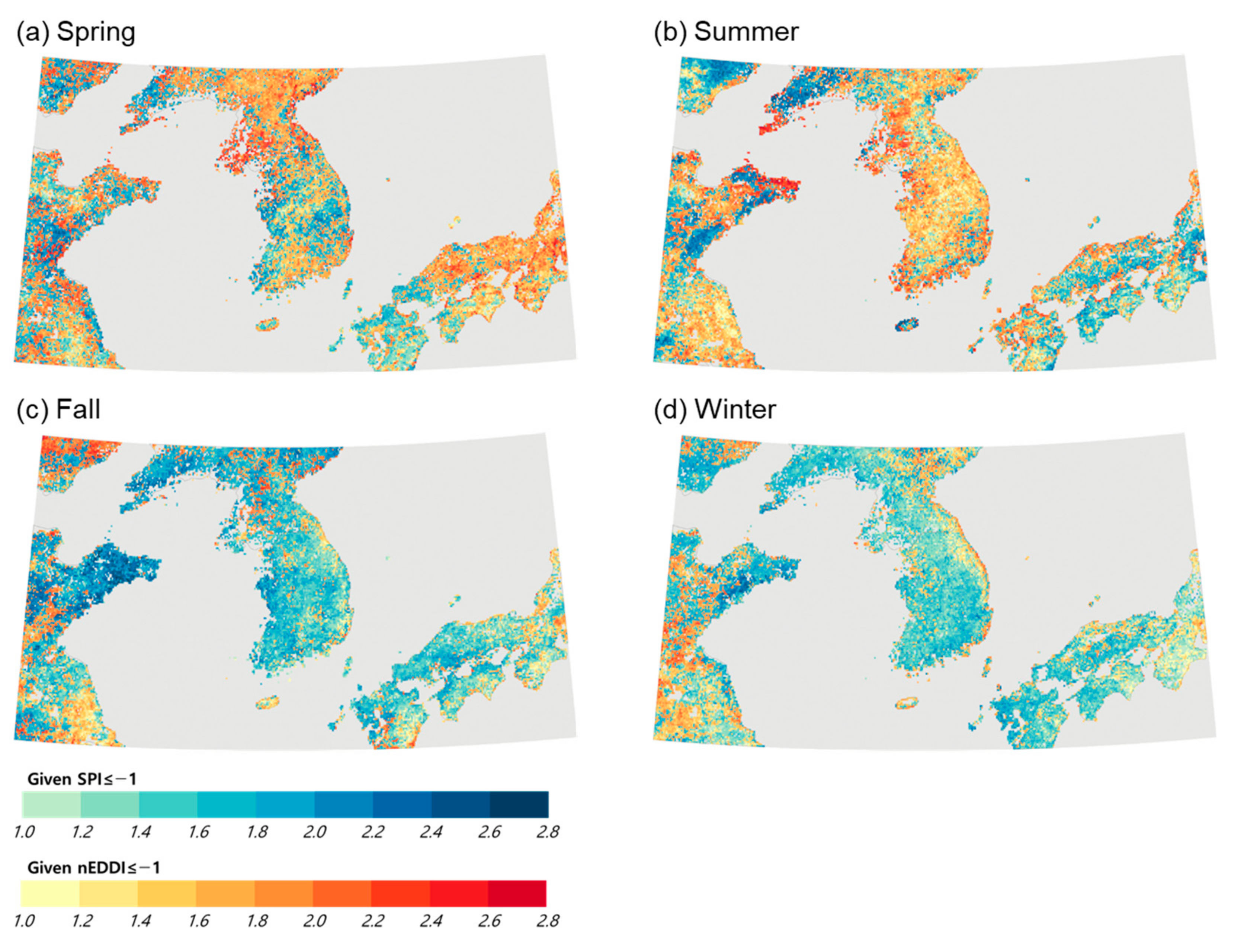
4.3. Vegetation Drought Vulnerability Mapping
4.4. Relative Importance on Vegetation Drought
4.5. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sönmez, F.K.; Kömüscü, A.Ü.; Erkan, A.; Turgu, E. An Analysis of Spatial and Temporal Dimension of Drought Vulnerability in Turkey Using the Standardized Precipitation Index. Nat. Hazards 2005, 35, 243–264. [Google Scholar] [CrossRef]
- Delbiso, T.D.; Altare, C.; Rodriguez-Llanes, J.M.; Doocy, S.; Guha-Sapir, D. Drought and Child Mortality: A Meta-Analysis of Small-Scale Surveys from Ethiopia. Sci. Rep. 2017, 7, 2212. [Google Scholar] [CrossRef] [Green Version]
- Fang, W.; Huang, Q.; Huang, S.; Yang, J.; Meng, E.; Li, Y. Optimal Sizing of Utility-Scale Photovoltaic Power Generation Complementarily Operating with Hydropower: A Case Study of the World’s Largest Hydro-Photovoltaic Plant. Energy Convers. Manag. 2017, 136, 161–172. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L.; Li, P.; Ma, L. Bivariate Probabilistic Quantification of Drought Impacts on Terrestrial Vegetation Dynamics in Mainland China. J. Hydrol. 2019, 577, 123980. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS Land Surface Temperature and Normalized Difference Vegetation Index products for Monitoring Drought in the Southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Hassan, M.M.; Smith, A.C.; Walker, K.; Rahman, M.; Southworth, J. Rohingya Refugee Crisis and Forest Cover Change in Teknaf, Bangladesh. Remote Sens. 2018, 10, 689. [Google Scholar] [CrossRef] [Green Version]
- Aadhar, S.; Mishra, V. High-Resolution near Real-Time Drought Monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef] [Green Version]
- Dutta, R. Drought Monitoring in the Dry Zone of Myanmar Using MODIS Derived NDVI and Satellite Derived CHIRPS Precipitation Data. Sustain. Agric. Res. 2018, 7, 46. [Google Scholar] [CrossRef] [Green Version]
- Al-Hedny, S.M.; Muhaimeed, A.S. Drought Monitoring for Northern Part of Iraq Using Temporal NDVI and Rainfall Indices. In Environmental Remote Sensing and Gis in Iraq; Springer: Cham, Switzerland, 2019; pp. 301–331. [Google Scholar] [CrossRef]
- Boyd, I.L.; Freer-Smith, P.H.; Gilligan, C.A.; Godfray, H.C.J. The Consequence of Tree Pests and Diseases for Ecosystem Services. Science 2013, 342, 1235773. [Google Scholar] [CrossRef]
- Gouveia, C.; Trigo, R.; Beguería, S.; Vicente-Serrano, S. Drought Impacts on Vegetation Activity in the Mediterranean Region: An Assessment Using Remote Sensing Data and Multi-Scale Drought Indicators. Glob. Planet. Chang. 2016, 151, 15–27. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Ren, H.; Tansey, K.; Zheng, Y.; Ghent, D.; Liu, X.; Yan, L. Agricultural Drought Monitoring Using European Space Agency Sentinel 3A Land Surface Temperature and Normalized Difference Vegetation Index Imageries. Agric. For. Meteorol. 2019, 279, 107707. [Google Scholar] [CrossRef]
- Kogan, F.N. Global Drought Watch from Space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar] [CrossRef]
- Wang, H.; Lin, H.; Liu, D. Remotely Sensed Drought Index and Its Responses to Meteorological Drought in Southwest China. Remote Sens. Lett. 2014, 5, 413–422. [Google Scholar] [CrossRef]
- Chen, C.; Son, N.; Chiang, S.; Chang, L.; Valdez, M. Drought Monitoring in Cultivated Areas of Central America Using Multi-temporal MODIS Data. Geomat. Nat. Hazards Risk 2016, 8, 402–417. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-Y.; Sur, C.; Kim, J.-S.; Lee, J.-H. Evaluation of Multi-Sensor Satellite Data for Monitoring Different Drought Impacts. Stoch. Environ. Res. Risk Assess. 2018, 32, 2551–2563. [Google Scholar] [CrossRef]
- Almamalachy, Y.S.; Al-Quraishi, A.M.F.; Moradkhani, H. Agricultural Drought Monitoring Over Iraq Utilizing MODIS Products. In Environmental Remote Sensing and GIS in Iraq; Springer: Cham, Switzerland, 2019; pp. 253–278. [Google Scholar] [CrossRef]
- Javed, T.; Li, Y.; Rashid, S.; Li, F.; Hu, Q.; Feng, H.; Chen, X.; Ahmad, S.; Liu, F.; Pulatov, B. Performance and Relationship of Four Different Agricultural Drought Indices for Drought Monitoring in China’s Mainland Using Remote Sensing Data. Sci. Total Environ. 2020, 759, 143530. [Google Scholar] [CrossRef]
- Li, B.; Tao, S.; Dawson, R.W. Relations between AVHRR NDVI and Ecoclimatic Parameters in China. Int. J. Remote Sens. 2002, 23, 989–999. [Google Scholar] [CrossRef]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The Impacts of Climate Change on Water Resources and Agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Salama, M.S.; Su, Z. Assessment of Vegetation Dynamics and Their Response to Variations in Precipitation and Temperature in the Tibetan Plateau. Clim. Chang. 2010, 103, 519–535. [Google Scholar] [CrossRef]
- Peng, S.; Chen, A.; Xu, L.; Cao, C.; Fang, J.; Myneni, R.; Pinzon, E.J.; Tucker, C.J.; Piao, S. Recent Change of Vegetation Growth Trend in China. Environ. Res. Lett. 2011, 6, 044027. [Google Scholar] [CrossRef]
- Cong, N.; Wang, T.; Nan, H.; Ma, Y.; Wang, X.; Myneni, R.B.; Piao, S. Changes in Satellite-Derived Spring Vegetation Green-up Date and Its Linkage to Climate in China from 1982 to 2010: A Multimethod Analysis. Glob. Chang. Biol. 2012, 19, 881–891. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, J.; Liu, L.; Wang, Z.; Ding, M.; Yang, X. NDVI-Based Vegetation Changes and Their Responses to Climate Change from 1982 to 2011: A Case Study in the Koshi River Basin in the Middle Himalayas. Glob. Planet. Chang. 2013, 108, 139–148. [Google Scholar] [CrossRef]
- Piao, S.; Nan, H.; Huntingford, C.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Peng, S.; Ahlström, A.; Canadell, J.G.; Cong, N.; et al. Evidence for a Weakening Relationship between Interannual Temperature Variability and Northern Vegetation Activity. Nat. Commun. 2014, 5, 5018. [Google Scholar] [CrossRef] [Green Version]
- Won, J.; Choi, J.; Lee, O.; Seo, J.; Kim, S. Weighting Coefficient Estimation of Vegetation Health Index for Ecological Drought Analysis. J. Wetl. Res. 2020, 22, 275–285. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, J.; Wang, X.; Peng, X.; Cai, H. Spatial and Temporal Effects of Drought on Chinese Vegetation under Different Coverage Levels. Sci. Total Environ. 2020, 716, 137166. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, L.; Feng, L.; Zhang, M.; Yao, R. Drought Characteristics and its Impact on Changes in Surface Vegetation from 1981 to 2015 in the Yangtze River Basin, China. Int. J. Clim. 2019, 40, 3380–3397. [Google Scholar] [CrossRef]
- Rousta, I.; Olafsson, H.; Moniruzzaman, M.; Zhang, H.; Liou, Y.-A.; Mushore, T.; Gupta, A. Impacts of Drought on Vegetation Assessed by Vegetation Indices and Meteorological Factors in Afghanistan. Remote Sens. 2020, 12, 2433. [Google Scholar] [CrossRef]
- Liu, Z.; Li, C.; Zhou, P.; Chen, X. A Probabilistic Assessment of the Likelihood of Vegetation Drought under Varying Climate Conditions across China. Sci. Rep. 2016, 6, 35105. [Google Scholar] [CrossRef] [Green Version]
- Poonia, V.; Jha, S.; Goyal, M.K. Copula Based Analysis of Meteorological, Hydrological and Agricultural Drought Characteristics across Indian River Basins. Int. J. Clim. 2021, 31, 4637–4652. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate Rainfall Frequency Distributions Using Archimedean Copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Goswami, U.P.; Hazra, B.; Goyal, M.K. Copula-Based Probabilistic Characterization of Precipitation Extremes over North Sikkim Himalaya. Atmos. Res. 2018, 212, 273–284. [Google Scholar] [CrossRef]
- Uttarwar, S.B.; Barma, S.D.; Mahesha, A. Bivariate Modeling of Hydroclimatic Variables in Humid Tropical Coastal Region Using Archimedean Copulas. J. Hydrol. Eng. 2020, 25, 05020026. [Google Scholar] [CrossRef]
- Jha, S.; Das, J.; Sharma, A.; Hazra, B.; Goyal, M.K. Probabilistic Evaluation of Vegetation Drought Likelihood and Its Implications to Resilience across India. Glob. Planet. Chang. 2019, 176, 23–35. [Google Scholar] [CrossRef]
- Wang, L.; Huang, S.; Huang, Q.; Leng, G.; Han, Z.; Zhao, J.; Guo, Y. Vegetation Vulnerability and Resistance to Hydrometeorological Stresses in Water- and Energy-Limited Watersheds Based on a Bayesian Framework. CATENA 2020, 196, 104879. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L.; Guo, Y. Probabilistic Assessment of Remote Sensing-Based Terrestrial Vegetation Vulnerability to Drought Stress of the Loess Plateau in China. Remote Sens. Environ. 2019, 232, 111290. [Google Scholar] [CrossRef]
- Oo, H.T.; Zin, W.W.; Kyi, C.C.T. Analysis of Streamflow Response to Changing Climate Conditions Using SWAT Model. Civ. Eng. J. 2020, 6, 194–209. [Google Scholar] [CrossRef]
- Ning, T.; Zhou, S.; Chang, F.; Shen, H.; Li, Z.; Liu, W. Interaction of Vegetation, Climate and Topography on Evapotranspiration Modelling at Different Time Scales within the Budyko Framework. Agric. For. Meteorol. 2019, 275, 59–68. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W.; Hong, Y.; Gourley, J.J.; Yu, Z. Vegetation Greening and Climate Change Promote Multidecadal Rises of Global Land Evapotranspiration. Sci. Rep. 2015, 5, 15956. [Google Scholar] [CrossRef]
- Nabaei, S.; Sharafati, A.; Yaseen, Z.M.; Shahid, S. Copula Based Assessment of Meteorological Drought Characteristics: Regional Investigation of Iran. Agric. For. Meteorol. 2019, 276–277, 107611. [Google Scholar] [CrossRef]
- Abeysingha, N.S.; Rajapaksha, U.R.L.N. SPI-Based Spatiotemporal Drought over Sri Lanka. Adv. Meteorol. 2020, 2020, 9753279. [Google Scholar] [CrossRef] [Green Version]
- Bhunia, P.; Das, P.; Maiti, R. Meteorological Drought Study Through SPI in Three Drought Prone Districts of West 1202 Bengal, India. Earth Syst. Environ. 2020, 4, 43–55. [Google Scholar] [CrossRef]
- Pham, Q.B.; Yang, T.-C.; Kuo, C.-M.; Tseng, H.-W.; Yu, P.-S. Coupling Singular Spectrum Analysis with Least Square Support Vector Machine to Improve Accuracy of SPI Drought Forecasting. Water Resour. Manag. 2021, 35, 847–868. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Hobbins, M.T.; Wood, A.; McEvoy, D.J.; Huntington, J.L.; Morton, C.; Anderson, M.; Hain, C. The Evaporative Demand Drought Index. Part I: Linking Drought Evolution to Variations in Evaporative Demand. J. Hydrometeorol. 2016, 17, 1745–1761. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, Y.; Cho, S.; Youn, Y.; Kim, N.; Lee, Y. A Comparison between the Reference Evapotranspiration Products for Croplands in Korea: Case Study of 2016–2019. Korean J. Remote Sens. 2020, 36, 1465–1483. [Google Scholar] [CrossRef]
- Yoon, D.H.; Nam, W.H.; Lee, H.J.; Hong, E.M.; Kim, T. Drought Hazard Assessment Using MODIS-Based Evaporative Stress Index (ESI) and ROC Analysis. J. Korean Soc. Agric. Eng. 2020, 62, 51–61. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, S.Y.; Kim, M.G.; Chung, I.M. Hydrological Drought Analysis and Monitoring Using Multiple Drought Indices: The Case of Mulrocheon Watershed. KSCE J. Civ. Environ. Eng. Res. 2021, 41, 477–484. [Google Scholar] [CrossRef]
- Peng, J.; Dadson, S.; Hirpa, F.; Dyer, E.; Lees, T.; Miralles, D.G.; Vicente-Serrano, S.M.; Funk, C. A pan-African High-Resolution Drought Index Dataset. Earth Syst. Sci. Data 2020, 12, 753–769. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Zhang, Y.; Ren, X.; Yao, Y.; Hao, Z.; Cai, W. Evaluation of CHIRPS and Its Application for Drought Monitoring over the Haihe River Basin, China. Nat. Hazards 2018, 92, 155–172. [Google Scholar] [CrossRef]
- Wu, W.; Li, Y.; Luo, X.; Zhang, Y.; Ji, X.; Li, X. Performance Evaluation of the CHIRPS Precipitation Dataset and Its Utility in Drought Monitoring over Yunnan Province, China. Geomat. Nat. Hazards Risk 2019, 10, 2145–2162. [Google Scholar] [CrossRef] [Green Version]
- Pandey, V.; Srivastava, P.; Singh, S.; Petropoulos, G.; Mall, R. Drought Identification and Trend Analysis Using Long-Term CHIRPS Satellite Precipitation Product in Bundelkhand, India. Sustainability 2021, 13, 1042. [Google Scholar] [CrossRef]
- Sandeep, P.; Reddy, G.O.; Jegankumar, R.; Kumar, K.A. Monitoring of Agricultural Drought in Semi-Arid Ecosystem of Peninsular India through Indices Derived from Time-Series CHIRPS and MODIS Datasets. Ecol. Indic. 2020, 121, 107033. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements—FAO IRRIGATION and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Tirivarombo, S.; Osupile, D.; Eliasson, P. Drought Monitoring and Analysis: Standardised Precipitation Evapotranspiration Index (SPEI) and Standardised Precipitation Index (SPI). Phys. Chem. Earth Parts A/B/C 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Al-Quraishi, A.M.F.; Qader, S.H.; Wu, W. Drought Monitoring Using Spectral and Meteorological Based Indices Combination: A Case Study in Sulaimaniyah, Kurdistan Region of Iraq. In Environmental Remote Sensing and GIS in Iraq; Springer: Cham, Switzerland, 2019; pp. 377–393. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, L.; Zhang, Y.; Guo, M.; Liu, X. Evaluation of Tropical Rainfall Measuring Mission (TRMM) Satellite Precipitation Products for Drought Monitoring over the Middle and Lower Reaches of the Yangtze River Basin, China. J. Geogr. Sci. 2020, 30, 53–67. [Google Scholar] [CrossRef] [Green Version]
- Harisuseno, D. Meteorological Drought and its Relationship with Southern Oscillation Index (SOI). Civ. Eng. J. 2020, 6, 1864–1875. [Google Scholar] [CrossRef]
- Salimi, H.; Asadi, E.; Darbandi, S. Meteorological and Hydrological Drought Monitoring Using Several Drought Indices. Appl. Water Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Won, J.; Kim, S. Future Drought Analysis Using SPI and EDDI to Consider Climate Change in South Korea. Water Supply 2020, 20, 3266–3280. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global Warming and 21st Century Drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef] [Green Version]
- Karnauskas, K.B.; Donnelly, J.P.; Anchukaitis, K.J. Future Freshwater Stress for Island Populations. Nat. Clim. Chang. 2016, 6, 720–725. [Google Scholar] [CrossRef]
- Won, J.; Jang, S.; Kim, K.; Kim, S. Applicability of the Evaporative Demand Drought Index. J. Korean Soc. Hazard Mitig. 2018, 18, 431–442. [Google Scholar] [CrossRef] [Green Version]
- Yao, N.; Li, Y.; Lei, T.; Peng, L. Drought Evolution, Severity and Trends in Mainland China over 1961–2013. Sci. Total Environ. 2018, 616–617, 73–89. [Google Scholar] [CrossRef]
- Noguera, I.; Domínguez-Castro, F.; Vicente-Serrano, S. Flash Drought Response to Precipitation and Atmospheric Evaporative Demand in Spain. Atmosphere 2021, 12, 165. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula Based Multisite Model for Daily Precipitation Simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.D.; Ryu, J.S.; Oh, K.R.; Jeong, S.M. An Application of Copulas-Based Joint Drought Index for Determining Comprehensive Drought Conditions. J. Korean Soc. Hazard Mitig. 2012, 12, 223–230. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Filho, W.L.; Yin, J.; Hu, R.; Wang, J.; Yang, C.; Yin, S.; Bao, Y.; Ayal, D.Y. Assessing Vegetation Response to Multi-Time-Scale Drought across Inner Mongolia Plateau. J. Clean. Prod. 2018, 179, 210–216. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation Thresholds of Meteorological Drought for Triggering Hydrological Drought at Various Levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef]
- Ryu, J.S.; Ahn, J.; Kim, S. An Application of Drought Severity-Area-Duration Curves Using Copulas-Based Joint Drought Index. J. Korea Water Resour. Assoc. 2012, 45, 1043–1050. [Google Scholar] [CrossRef]
- Dehghani, M.; Saghafian, B.; Zargar, M. Probabilistic Hydrological Drought Index Forecasting Based on Meteorological Drought Index Using Archimedean Copulas. Hydrol. Res. 2019, 50, 1230–1250. [Google Scholar] [CrossRef]
- Júnior, R.L.D.R.; Silva, F.D.D.S.; Costa, R.L.; Gomes, H.B.; Pinto, D.D.C.; Herdies, D.L. Bivariate Assessment of Drought Return Periods and Frequency in Brazilian Northeast Using Joint Distribution by Copula Method. Geosciences 2020, 10, 135. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Wang, Z.; Yang, H.; Di, D.; Zhao, Y.; Liang, Q. A New Copula-Based Standardized Precipitation Evapotranspiration Streamflow Index for Drought Monitoring. J. Hydrol. 2020, 585, 124793. [Google Scholar] [CrossRef]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-Based JOINT Drought INDEX Using SPI and EDDI and Its Application to Climate Change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar] [CrossRef]
- Sadegh, M.; Ragno, E.; AghaKouchak, A. Multivariate Copula Analysis Toolbox (MvCAT): Describing Dependence and Underlying Uncertainty Using a Bayesian Framework. Water Resour. Res. 2017, 53, 5166–5183. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency Analysis via Copulas: Theoretical Aspects and Applications to Hydrological Events. Water Resour. Res. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Ghaleb, F.; Mario, M.; Sandra, A.N. Regional Landsat-Based Drought Monitoring from 1982 to 2014. Climate 2015, 3, 563–577. [Google Scholar] [CrossRef] [Green Version]
- Orimoloye, I.; Ololade, O.; Mazinyo, S.; Kalumba, A.; Ekundayo, O.; Busayo, E.; Akinsanola, A.; Nel, W. Spatial Assessment of Drought Severity in Cape Town Area, South Africa. Heliyon 2019, 5, e02148. [Google Scholar] [CrossRef] [Green Version]
- Cornelissen, J.H.; van Bodegom, P.; Aerts, R.; Callaghan, T.V.; van Logtestijn, R.; Alatalo, J.; Chapin, F.S.; Gerdol, R.; Gudmundsson, J.; Gwynn-Jones, D.; et al. Global Negative Vegetation Feedback to Climate Warming Responses of Leaf Litter Decomposition Rates in Cold Biomes. Ecol. Lett. 2007, 10, 619–627. [Google Scholar] [CrossRef]
- Huang, S.; Zheng, X.; Ma, L.; Wang, H.; Huang, Q.; Leng, G.; Meng, E.; Guo, Y. Quantitative Contribution of Climate Change and Human Activities to Vegetation cover Variations Based on GA-SVM Model. J. Hydrol. 2020, 584, 124687. [Google Scholar] [CrossRef]
- Wang, S.; Mo, X.; Hu, S.; Liu, S.; Liu, Z. Assessment of Droughts and Wheat Yield Loss on the North China Plain with an Aggregate Drought Index (ADI) Approach. Ecol. Indic. 2018, 87, 107–116. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, X. Rapid Reduction in Ecosystem Productivity Caused by Flash Droughts Based on Decade-Long FLUXNET Observations. Hydrol. Earth Syst. Sci. 2020, 24, 5579–5593. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, X.; Otkin, J.A. Remote Sensing of the Impact of Flash Drought Events on Terrestrial Carbon Dynamics over China. Carbon Balance Manag. 2020, 15, 20. [Google Scholar] [CrossRef]
- Qu, S.; Wang, L.; Lin, A.; Zhu, H.; Yuan, M. What Drives the Vegetation Restoration in Yangtze River Basin, China: Climate Change or Anthropogenic Factors? Ecol. Indic. 2018, 90, 438–450. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X. Intercomparison and Evaluation of Three Global High-Resolution Evapotranspiration Products across China. J. Hydrol. 2018, 566, 743–755. [Google Scholar] [CrossRef]
- Moreira, A.A.; Ruhoff, A.L.; Roberti, D.R.; Souza, V.D.A.; da Rocha, H.R.; Paiva, R. Assessment of Terrestrial Water Balance Using Remote Sensing Data in South America. J. Hydrol. 2019, 575, 131–147. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of Twelve Evapotranspiration Products from Machine Learning, Remote Sensing and Land Surface Models over Conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Wang, H.; Lv, X.; Zhang, M. Sensitivity and Attribution Analysis of Vegetation Changes on Evapotranspiration with the Budyko Framework in the Baiyangdian Catchment, China. Ecol. Indic. 2020, 120, 106963. [Google Scholar] [CrossRef]
- Talsma, C.J.; Good, S.P.; Miralles, D.G.; Fisher, J.B.; Martens, B.; Jimenez, C.; Purdy, A.J. Sensitivity of Evapotranspiration Components in Remote Sensing-Based Models. Remote Sens. 2018, 10, 1601. [Google Scholar] [CrossRef] [Green Version]
- Ainsworth, E.A.; Rogers, A. The Response of Photosynthesis and Stomatal Conductance to Rising [CO2]: Mechanisms and Environmental Interactions. Plant Cell Environ. 2007, 30, 258–270. [Google Scholar] [CrossRef]
- Dijkstra, F.A.; Blumenthal, D.; Morgan, J.A.; LeCain, D.R.; Follett, R.F. Elevated CO2 Effects on Semi-Arid Grassland Plants in Relation to Water Availability and Competition. Funct. Ecol. 2010, 24, 1152–1161. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, P.C.D.M.K.A. Potential Evapotranspiration and Continental Drying. Nat. Clim. Chang. 2016, 6, 946–949. [Google Scholar] [CrossRef]
- Swann, A.L.S.; Hoffman, F.M.; Koven, C.D.; Randerson, J.T. Plant Responses to Increasing CO2 Reduce Estimates of Climate Impacts on Drought Severity. Proc. Natl. Acad. Sci. USA 2016, 113, 10019–10024. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Xiao, J.; Zhou, Y.; Zheng, Y.; Li, J.; Xiao, H. Drought Events and Their Effects on Vegetation Productivity in China. Ecosphere 2016, 7, e01591. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, Q.; Singh, V.P.; Shi, P. Seasonal Vegetation Response to Climate Change in the Northern Hemisphere (1982–2013). Glob. Planet. Chang. 2016, 148, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Schwinning, S.; Starr, B.; Ehleringer, J. Summer and Winter Drought in a Cold Desert Ecosystem (Colorado Plateau) Part I: Effects on Soil Water and Plant Water Uptake. J. Arid. Environ. 2005, 60, 547–566. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, J.; Li, J.; Wang, K.; Lei, L.; Guo, H. The 2010 Spring Drought Reduced Primary Productivity in Southwestern China. Environ. Res. Lett. 2012, 7, 045706. [Google Scholar] [CrossRef] [Green Version]

| Data | Product | Period | Spatial Resolution |
|---|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | MOD13C2 | 2001 to present | 0.05° |
| Land Surface Temperature (LST) | MOD11C3 | 0.05° | |
| Precipitation | CHIRPS | 0.05° | |
| Potential Evapotranspiration (PET) | MOD16A2 | 500 m |
| Past Drought Event Record | |||
|---|---|---|---|
| Drought | Non-Drought | ||
| Drought Index | Dry | Hit (H) | False (F) |
| Normal or Wey | Missing (M) | Negative hit (N) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Won, J.; Seo, J.; Lee, J.; Lee, O.; Kim, S. Vegetation Drought Vulnerability Mapping Using a Copula Model of Vegetation Index and Meteorological Drought Index. Remote Sens. 2021, 13, 5103. https://doi.org/10.3390/rs13245103
Won J, Seo J, Lee J, Lee O, Kim S. Vegetation Drought Vulnerability Mapping Using a Copula Model of Vegetation Index and Meteorological Drought Index. Remote Sensing. 2021; 13(24):5103. https://doi.org/10.3390/rs13245103
Chicago/Turabian StyleWon, Jeongeun, Jiyu Seo, Jeonghoon Lee, Okjeong Lee, and Sangdan Kim. 2021. "Vegetation Drought Vulnerability Mapping Using a Copula Model of Vegetation Index and Meteorological Drought Index" Remote Sensing 13, no. 24: 5103. https://doi.org/10.3390/rs13245103
APA StyleWon, J., Seo, J., Lee, J., Lee, O., & Kim, S. (2021). Vegetation Drought Vulnerability Mapping Using a Copula Model of Vegetation Index and Meteorological Drought Index. Remote Sensing, 13(24), 5103. https://doi.org/10.3390/rs13245103







