Corrections for radiometric calibration differences between AIRS and SNPP-CrIS, and between NOAA20 and SNPP-CrIS are determined after their respective radiances are converted to the CHIRP SRF. Two approaches are used for determination of inter-satellite biases. Most of this section concentrates on the bias differences between AIRS and SNPP-CrIS since (a) SNPP-CrIS is used as the CHIRP radiance standard, and (b) AIRS and CrIS are very different instruments with significant SRF differences. The NOAA20-CrIS bias differences with SNPP-CrIS are significantly smaller, which is unsurprising since the CrIS instruments aboard SNPP and NOAA20 are nearly identical, even though the NOAA20 CrIS blackbody design is thought to be an improvement over the SNPP version. SNPP-CrIS is presently used as the CHIRP radiance standard since it has overlapped with AIRS for a much longer time, allowing more extended inter-comparisons than AIRS with NOAA20 CrIs.
Two techniques are used to evaluate bias differences between satellites as summarized above, SNOs and large statistical inter-comparisons of radiances. The location of SNOs varies with the pair of satellites under consideration since the details of the orbit geometry determine the SNO locations and time differences.
Figure 6 summarizes the latitude sampling of the AIRS:SNPP-CrIS sets and the IASI:SNPP-CrIS SNOs. The AIRS:SNPP-CrIS SNOs use a maximum spatial offset of 13 km and temporal offset of 10 min. While these SNOs peak near ±78
there are a considerable number of SNOs occurring at all latitudes. The IASI:SNPP-CrIS SNOs, for maximum offsets of 13 km and 20 min, peak very sharply at ±73
and are therefore not particularly representative of the global mean. The IASI:NOAA20-CrIS SNO sampling is similar to that for SNPP-CrIS.
Note that there are no SNPP:NOAA20 SNOs [
21] since SNPP and NOAA20 are in essentially identical orbits except for a half-orbit along track separation. However, it is possible to use IASI as a SNO transfer standard by taking the double difference (NOAA20−IASI)
SNO− (SNPP − IASI)
SNO = (NOAA20 − SNPP)
SNO, which was also used in [
21], but for only a small number of SNOs (~1000) and only those in the north polar area. The double-difference approach using AIRS as the SNO transfer standard can also be used for the CHIRP channels that exist for AIRS derived CHIRP.
The latitude sampling for global equal-area sampling is also shown since that was used to build the statistical sampling data set. These statistical data sets are a 1% random, equal-area, sample for AIRS and the two CrIS instruments, taken over a 12 month period. We consider this statistical set of samplings more appropriate than SNO samplings for climate applications, since the statistical samplings are area-weighted and therefore represent accurate global samplings. The SNO samplings for AIRS and IASI are heavily weighted to very high latitudes and therefore they sample a highly aliased set of radiances that are far from globally representative. However, if the sensor calibration differences for any given spectral channel can indeed be mostly characterized by constant BT differences, then the SNO results will be very similar to the global statistical sampling results, and indeed they are very similar. Although we use the statistical intercomparisons to convert the AIRS and NOAA20-CrIS calibration to SNPP-CrIS, we use the calibration differences between the statistical samplings and SNO approach to estimate the uncertainties in the calibration conversions.
In order to minimize the effects of any drift in any of these instruments, a common time period of 1 March 2018 to 28 February 2019, was used for both the SNO and statistical data sets. This particular time period allowed a full year comparison between SNPP and NOAA20 CrIS, starting soon after NOAA20-CrIS began scientific operations, and before SNPP-CrIS suffered an outage of several months due to the failure of side-1 midwave electronics module. Only days when each instrument had a total number of observations within 2% of each other were used to minimize any aliasing. This ensures that all three sensors sampled the same underlying statistical set of data. For brevity, these data sets are referred to as the “2018” sets. Using a common 12-month time period for the radiometric correction of NOAA-20 CrIS and AIRS to the SNPP CrIS radiometric calibration provides the reference time (zero-offset) for application of any future improvements in stability in the three input sensor radiance records presently used for producing CHIRP.
The 1% statistical samplings used here contained approximately 3.7 million observations. The SNOs for AIRS:SNPP-CrIS had ~1.5 million paired samples, while the SNOs for IASI:SNPP-CrIS and IASI:NOAA20-CrIS sets each contain ~65 thousand observations. Note that for this work, all SNO and statistical samplings average over all 9 CrIS FOVs (focal plane detectors).
3.1. CHIRP:AQ and CHIRP:J1 Bias Offsets versus CHIRP:SN
AIRS is a grating spectrometer with 2378 spectral channels arranged over 17 different detector arrays. Each AIRS channel has a slightly different SRF with non-uniform center frequency spacings characteristic of grating instruments. A non-negligible number of channels either have very high noise or are inoperable. In addition, as discussed earlier, the AIRS L1c product contains a number of simulated channels that are located in-between detector modules. Conversion of AIRS L1c to the CHIRP SRF requires knowledge of a considerable number of AIRS channels, as illustrated in
Figure 2 to create a CHIRP channel radiance.
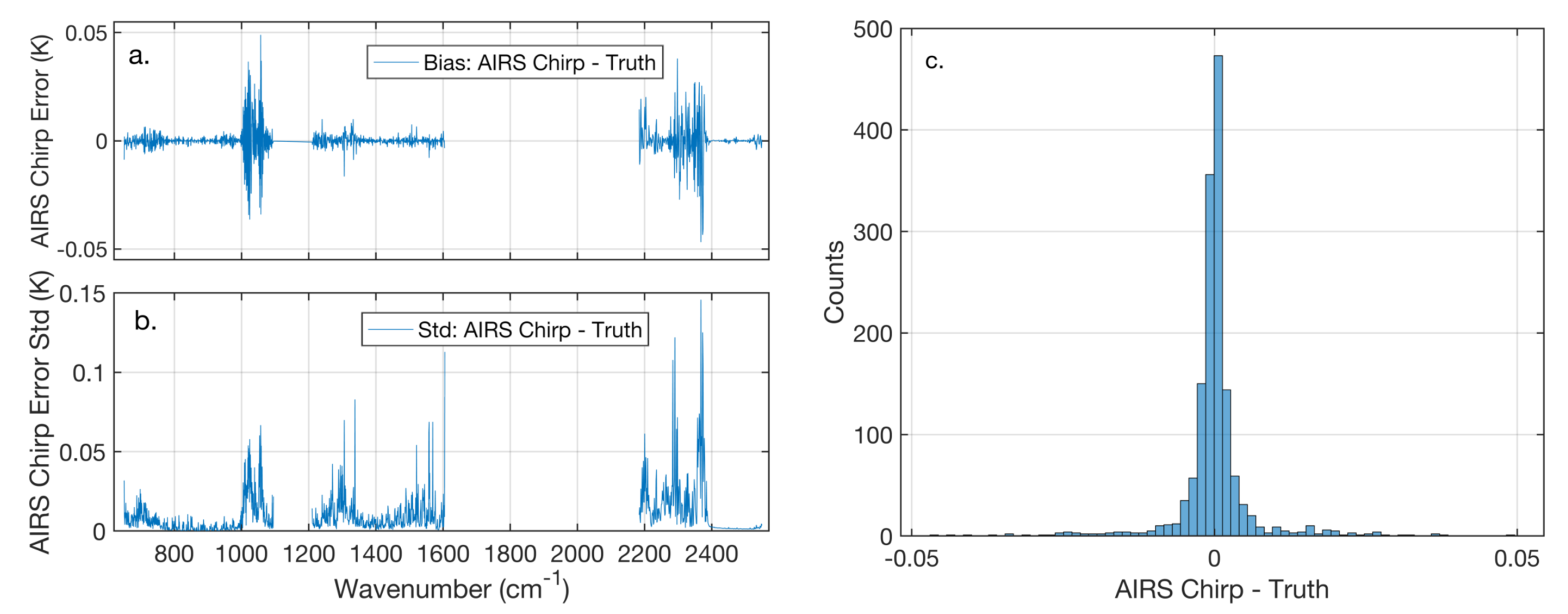
One primary diagnostic of the quality and heritage of a CHIRP channel created from AIRS is the fraction of AIRS synthetic radiances used to create a CHIRP channel radiance. The AIRS L1c product provides a per-granule summary of the number of times each channel has been synthesized, L1cNumSynth. We linearize the AIRS to CHIRP conversion and apply this to L1cNumSynth to get corresponding values for CHIRP. These are normalized as a fraction and becomes the CHIRP field “synth_frac”, indicating the level of simulated data used to create that channel. Users should avoid channels with high values of synth_frac, although these channel will likely introduce very little bias and have very representative standard deviations relative to RTA calculations. Probably the most dangerous use of these channels would be to sense minor constituents, which were not part of the statistical training used to create their radiances. Note that synth_frac will generally not change significantly over time, although it may increase for a short time when an AIRS channel has a short-term noise (POP) event. It will also change if an AIRS detector ceases operation, or vice-versa, but these are very infrequent events.
Fortunately, a very large percentage of the CHIRP channels have synth_frac values below 0.02, and these form a large enough ensemble of channels for existing retrieval or NWP applications.
Figure 7 is a sample CHIRP spectrum derived from AIRS for a randomly selected day, 18 August 2018. The red plus markers indicate CHIRP channels where synth_frac is less than 0.02. Qualitatively the channels with synth_frac less than 0.02 are distributed over a wide range of BT values including those sensing temperature, water vapor, ozone, methane, and other minor gases. Approximately 55% of the AIRS derived CHIRP channels have synth_frac below 0.02, and an additional 20% of channels have synth_frac between 0.02 and 0.25.
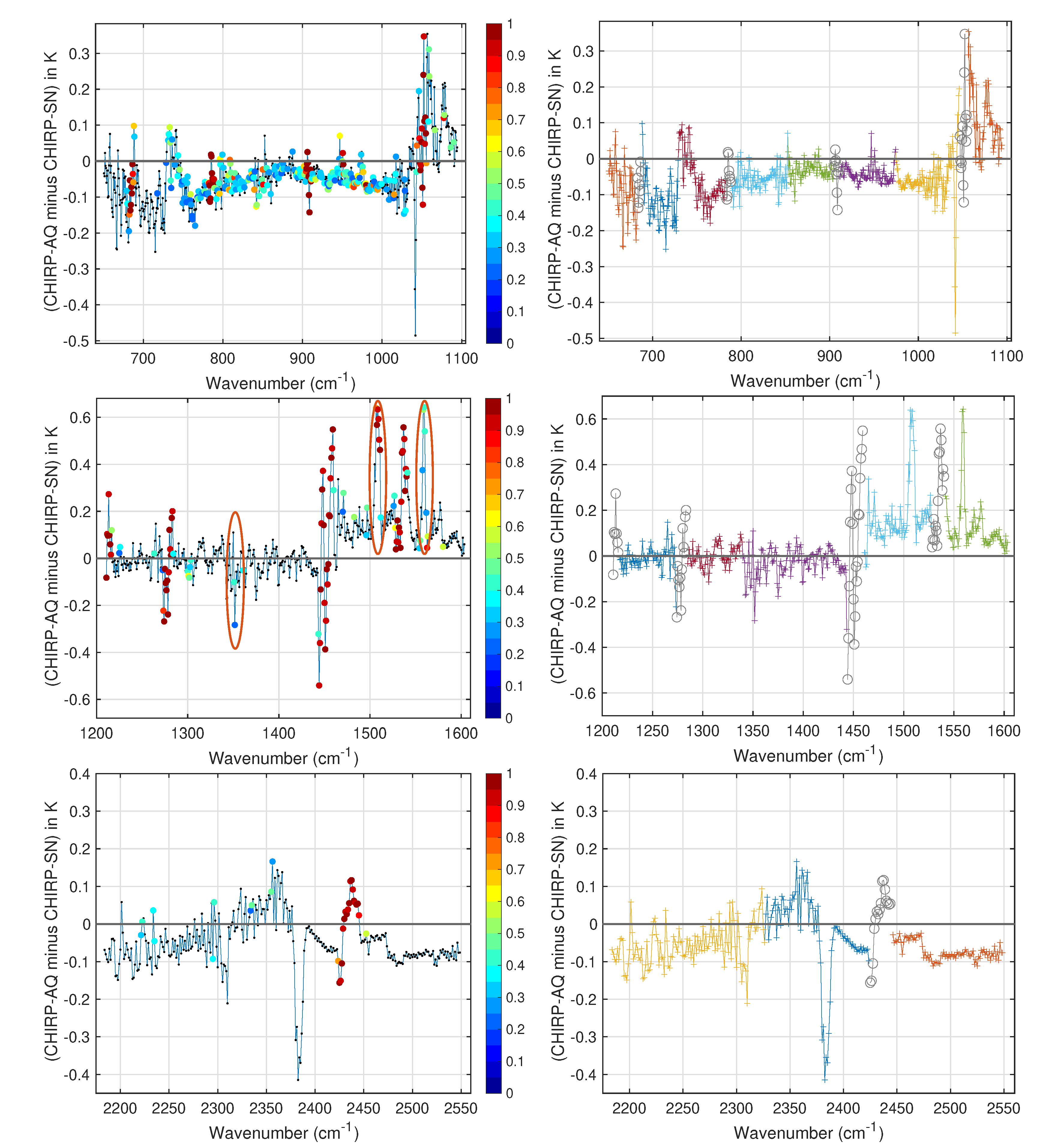
Figure 8 summarizes the (CHIRP-AQ minus CHIRP-SN) bias for all CHIRP-AQ channels. The colors denote the locations of different AIRS detector modules that contribute to CHIRP-AQ. These biases were derived from the 1 percent random subset of AIRS and SNPP-CrIS radiances for 2018. Small corrections are required to compare the means of the AIRS versus CrIS statistical samples in
Figure 8 since these two instruments have slightly different mean secant viewing angles which for AIRS is 1.2225, while the mean for CrIS (over all 9 FOVs) is 1.2433, or a difference of AIRS minus CrIS = −0.0208. The AIRS and CrIS BT means are corrected for this small secant offset by interpolating the BT means tabulated by secant angle, to the mean secant angle for all samples. This correction varies from ~−0.1 K to +0.05 K depending on the spectral region and is only required to inter-compare the statistical BT means in order to derive bias offsets.
CHIRP-AQ minus CHIRP-SN biases were also derived using SNOs. The difference between (CHIRP-AQ minus CHIRP-SN) using the statistical data set compared to the SNO data set are also shown in
Figure 8 (black dots). These two techniques give very similar bias differences, which suggests that any scene dependence of the inter-satellite biases are relatively small. The standard deviation over all CHIRP channels, between these two bias estimation, approaches 0.006 K ± 0.030 K (statistical minus SNO approach), suggesting that the accuracy of the statistically derived biases is on the order of 0.03 K.
Figure 9 repeats the (CHIRP-AQ minus CHIRP-SN) biases shown in
Figure 8 but with filled circles added to indicate the CHIRP channels with synth_frac greater than 0.02 (left column). The biases in the left column are repeated in the right column, but now with the locations of the AIRS L1c detector arrays shown in different colors (as in
Figure 8) and with the AIRS L1c filled gap channels denoted by gray lines and circles.
These curves clearly show that CHIRP channels located in the AIRS spectral gaps have very high synth_frac values and should be avoided in general. There are just a few regions, circled in red, where CHIRP synth_frac values are high that are not located in AIRS L1c filled-gaps in the midwave band. These AIRS channels have extremely high noise or are completely inoperable. The CHIRP channels with high synth_frac values generally also have higher biases relative to CHIRP:SN, which is expected since they are derived from AIRS L1c channels containing synthetic radiances. The synthetic CHIRP channels in the window region are quite accurate, while those in the midwave water band have bias errors of up to 0.6 K.
These synthetic biases are removed in CHIRP, but additional analysis is needed to determine their overall quality. However, as stated above, there is generally no need to use these channels for retrievals or assimilation. The wavelength dependence of the remaining good channels is, of course, some combination of bias errors due to AIRS and SNPP-CrIS.
It is possible to recognize spectral dependencies of the biases that correlate with locations of AIRS detector arrays. For example, there is a considerable shift between the high wavenumber end of the AIRS M11 array and the low wavenumber end of the M10 array, near 728 cm. The AIRS M-05 detector array covering the 1056–1136 cm range is known to have calibration issues so it is not surprising that the biases are larger in that region. The bias differences in the midwave region are very small for good channels, although the 1460–1605 cm region that covers the M-04a and M-04b detector arrays is offset by ~0.05 K from the biases of the other midwave modules.
The large negative bias feature in the shortwave band near 2382 cm
coincides with very low scene temperatures which can be difficult to calibrate accurately in the shortwave. In addition, the BT values increase very rapidly with wavenumber past 2382 cm
. This suggests that very small errors in either instrument’s SRF wing could contribute to larger than normal errors at the channel center. Similar behavior is seen in the NOAA20-CrIS minus SNPP-CrIS biases discussed in the
Section 3.2.
The long-term stability of CHIRP, as discussed in
Section 1, is determined by the combination of the parent instrument stability, and the accuracy of the inter-instrument calibration adjustments. It is far better to characterize individual instrument’s stability using their radiances in native format rather than in the context of CHIRP, since CHIRP consists of linear combinations of parent channels (except for the longwave band when CrIS is the parent instrument).
A partial examination of the relative stability of AIRS and SNPP-CrIS is shown in
Figure 10 that illustrates the variability in the relative calibration between these two sensors, at least over the nominal 2015–2020 time frame (actual times are 1 March 2015 through 28 February 2020). The standard deviation derived from the five yearly averages of the CHIRP-AQ minus CHIRP-SN calibration bias is seen to generally be below 0.005 K, except in the very cold shortwave channels, and in the AIRS M-05 array, which is well-known to have performance problems. Moreover, a linear fit of the five yearly biases over time has a trend (slope) of nearly zero, as shown in red. The observed trends are all at or below the 2-
uncertainty in the slope, shown in gray. This emphasizes the unimportance of the exact choice of year for computing the calibration bias offsets, since their relative calibration differences are quite constant in time.
3.2. CHIRP (NOAA20-CrIS-SNPP-CrIS) Bias Offsets
The CHIRP:J1 and CHIRP:SN bias offsets were also computed two different ways as outlined in the beginning of
Section 3. The SNO approach uses IASI (METOP-A) as a transfer standard since there are no SNOs between SNPP and NOAA20. This restricts inter-comparisons of SNPP to NOAA20 CrIS to narrow bands at high latitudes near ±73
, unlike the AIRS:SNPP-CrIS SNOs which include all latitudes, although they are also more numerous at high latitudes, as shown in
Figure 6. The latitude sampling of the AIRS:NOAA20:CrIS SNOs are similar to those for the AIRS:SNPP:CrIS SNOs, but since AIRS cannot provide the 1605 to 1750 cm
CHIRP channels, IASI SNOs were the better choice for SNO inter-comparisons. The conversion of of IASI radiances to CHIRP format follows the double-fourier transform approach described in [
21], except instead of converting to an interferometer with the CrIS OPDs, we convert to the CHIRP OPDs.
Figure 16 shows the mean biases for the NOAA20 and SNPP-CrIS radiances using (a) the 1% equal-area weighted 2018 statistical data set, (b) SNOs via a double-difference using IASI on METOP-A, and (c) SNOs between AIRS and NOAA20-CrIS, which are missing the high wavenumber end of the midwave band. Note that the BT difference range of this figure is almost 3.5× smaller than the corresponding figure for the AIRS and SNPP:CrIS biases (
Figure 8). This is not unexpected since the two CrIS instruments are essentially identical.
The agreement among these three estimates for the NOAA20-CrIS bias offset from SNPP-CrIS appear to vary with band, and vary within the band in the shortwave. As with the AIRS:SNPP-CrIS bias offsets, the statistically derived bias offset is used when creating the CHIRP data set, given its more uniform sampling. Following our discussion of the AIRS:SNPP-CrIS bias errors, a nominal estimate of the uncertainty in the AIRS:SNPP-CrIS bias is the difference between the statistically derived bias and IASI SNO double difference bias. The standard deviation, over all CHIRP channels, between these two bias estimation approaches is 0.008 K ± 0.035 K (statistical minus SNO approach), suggesting that the accuracy of the statistically derived biases is on the order of 0.035 K, very similar to the AIRS:SNPP-CrIS bias estimate uncertainty. These biases are quite similar to those derived by Wang and Chen [
21] using small samples of polar-only data, although our peak differences are generally somewhat smaller than their results.
Note that the use of IASI SNOs as a transfer standard to establish calibration offsets between SNPP- and NOAA20-CrIS also suggests that any future gaps that could occur in the overlap of two CrIS instruments in the JPSS series should still permit inter-satellite radiometric calibration corrections. If the “third party” or transfer standard satellite (e.g., IASI) is in operation for a long-enough time period, and this time period overlaps both version of CrIS, then the double-difference SNO approach used here allows for calibration offset corrections between two CrIS sensors that were not in orbit simultaneously. Therefore the CHIRP data product calibration traceability can potentially span CrIS satellite operation gaps if they do not last too long. Larger gaps that cannot use a third-party to inter-calibrate could possibly be corrected using the approaches applied in [
9] to estimate AIRS calibration stability, which included identifying offsets in the AIRS radiometry that took place due to instrument shutdowns of days to several weeks. The calibration standards in [
9] were the secular in-situ record of CO
, N
O, and ocean sea-surface temperatures, which are extremely well characterized and are stable enough to establish radiometric stability well below present climate trends.