On the Impact and Mitigation of Signal Crosstalk in Ground-Based and Low Altitude Airborne GNSS-R
Abstract
:1. Introduction
- From an estimation point of view, we assess the impact that a possible crosstalk may have on the reflected signal time-delay estimation performance, if not correctly accounted for. This is done by comparing the single source conditional maximum likelihood estimator (CMLE) performance in a dual source context with the corresponding single source CRB.
- By resorting to dual source estimators, we show the optimal time-delay estimation performance in a dual source crosstalk context, as a function of path separation and the reflected-to-direct signal amplitude ratio (RDR), compared to the corresponding dual source CRBs.
- As a complementary analysis of practical importance, we assess the robustness of such dual source estimators under a misspecified number of sources, i.e., when two sources are estimated, but crosstalk is not present in the signal.
- The performance of the VE, proposed in [40] for crosstalk mitigation, is compared to the CRB and non-coherent dual source estimators, which to the best of the authors’ knowledge is an important missing estimation performance analysis in the literature.
2. Theoretical Background
2.1. Preliminaries: A Geometrical Analysis
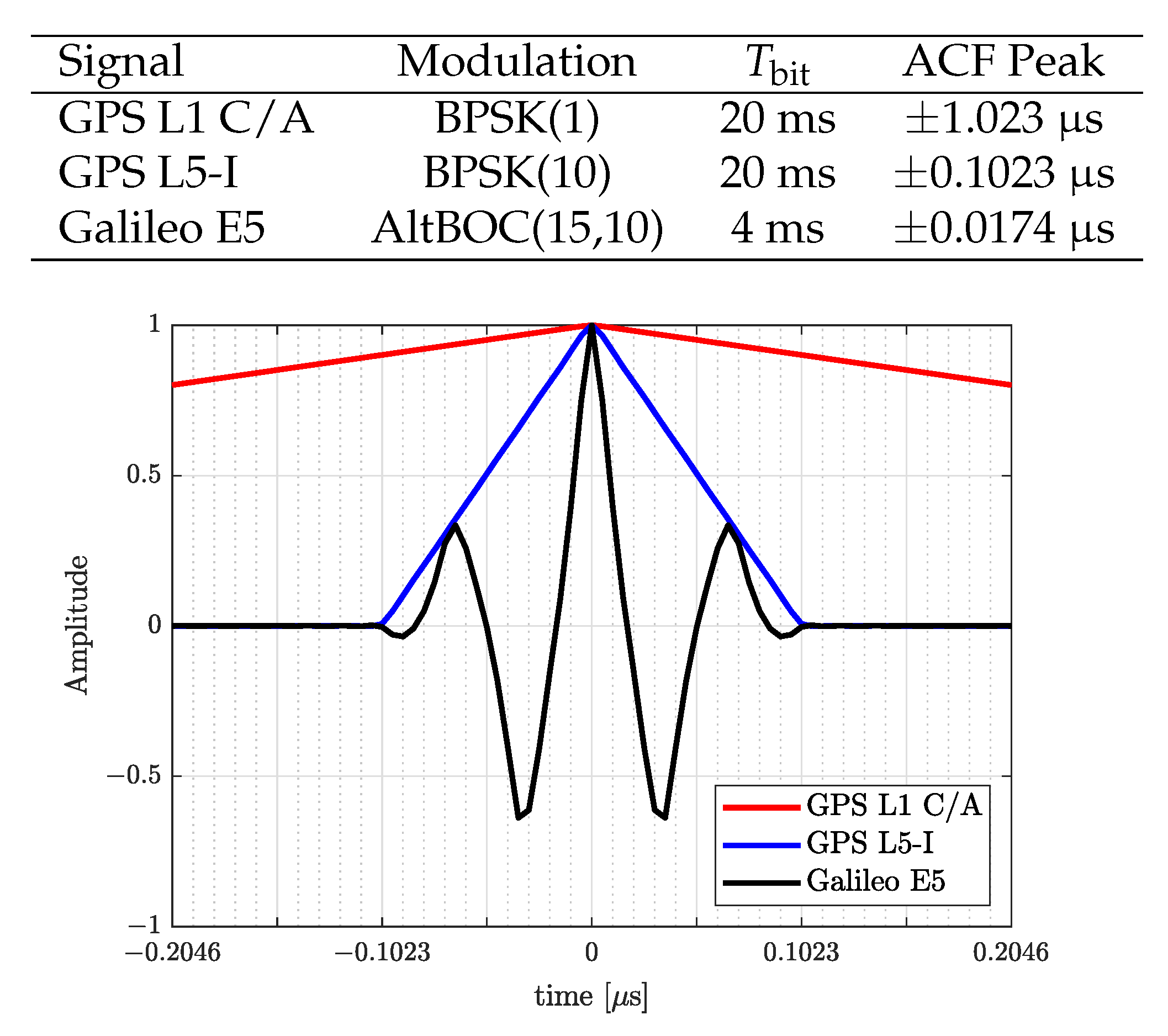
2.2. Single and Dual Source GNSS Signal Model
2.3. Single and Dual Source CRBs
3. Single/Dual Source Delay/Doppler/Phase Estimators
3.1. Single and Dual Source CMLEs
3.2. CLEAN-RELAX Estimator
3.3. Non-Coherent and Variance Estimators
4. Results and Discussions on Coherent Estimation
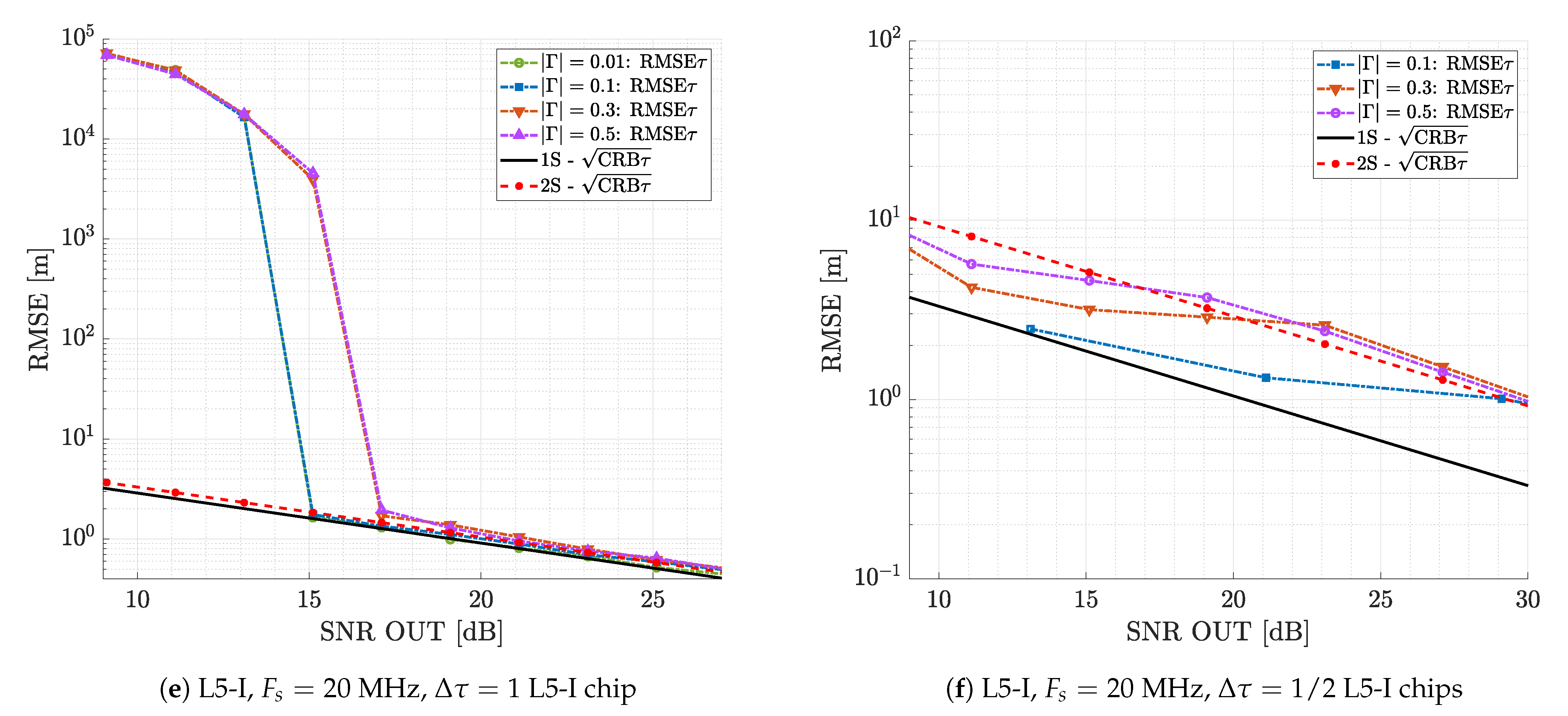
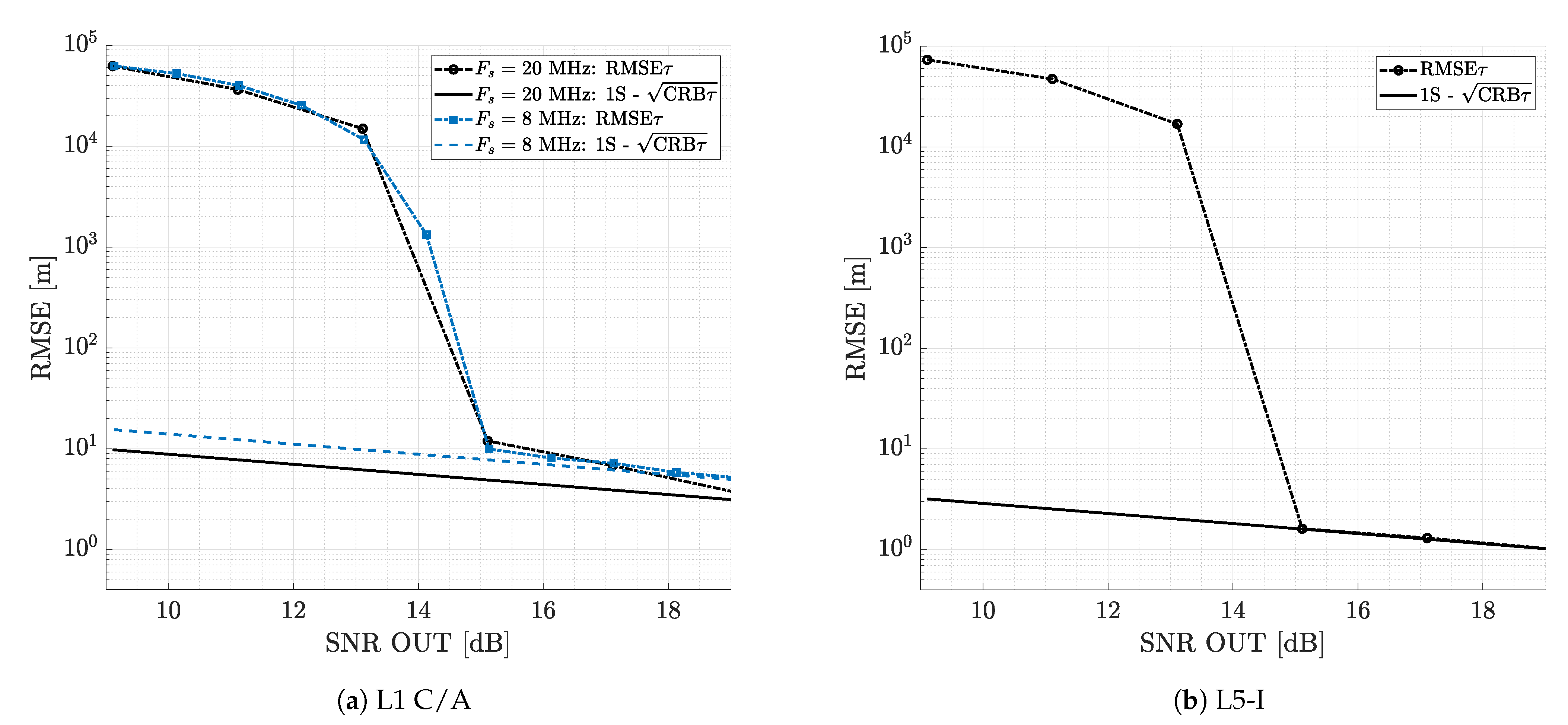
4.1. Crosstalk Impact on GNSS-R Time-Delay Estimation
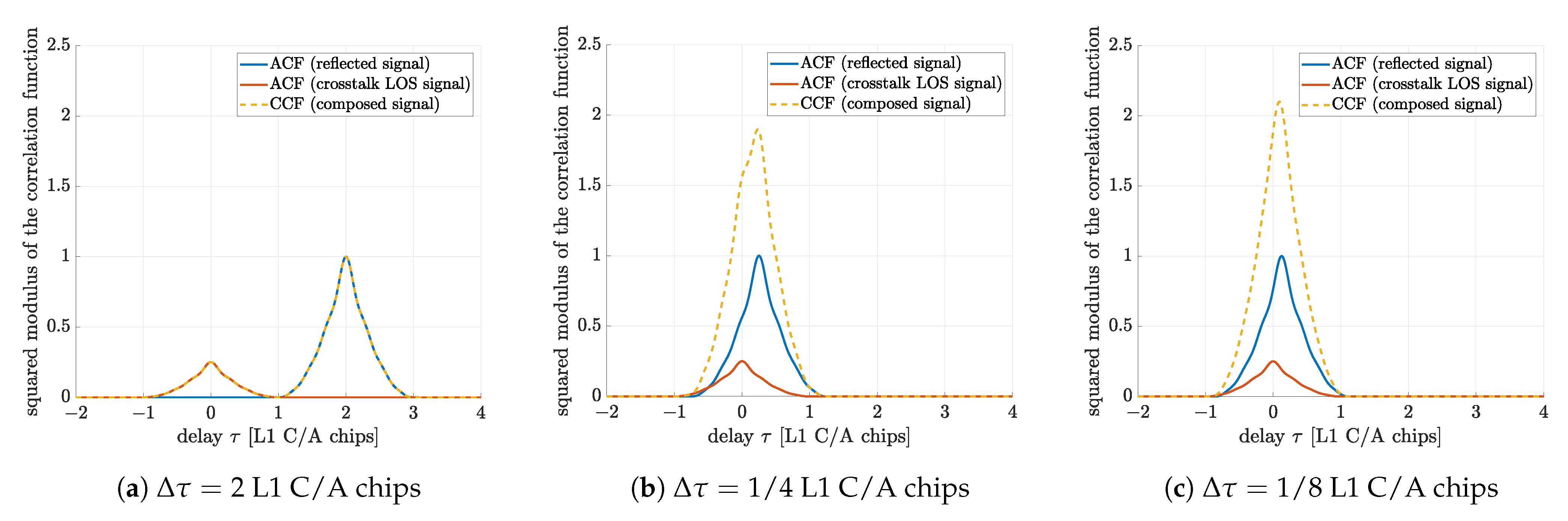
4.1.1. Analysis Setup
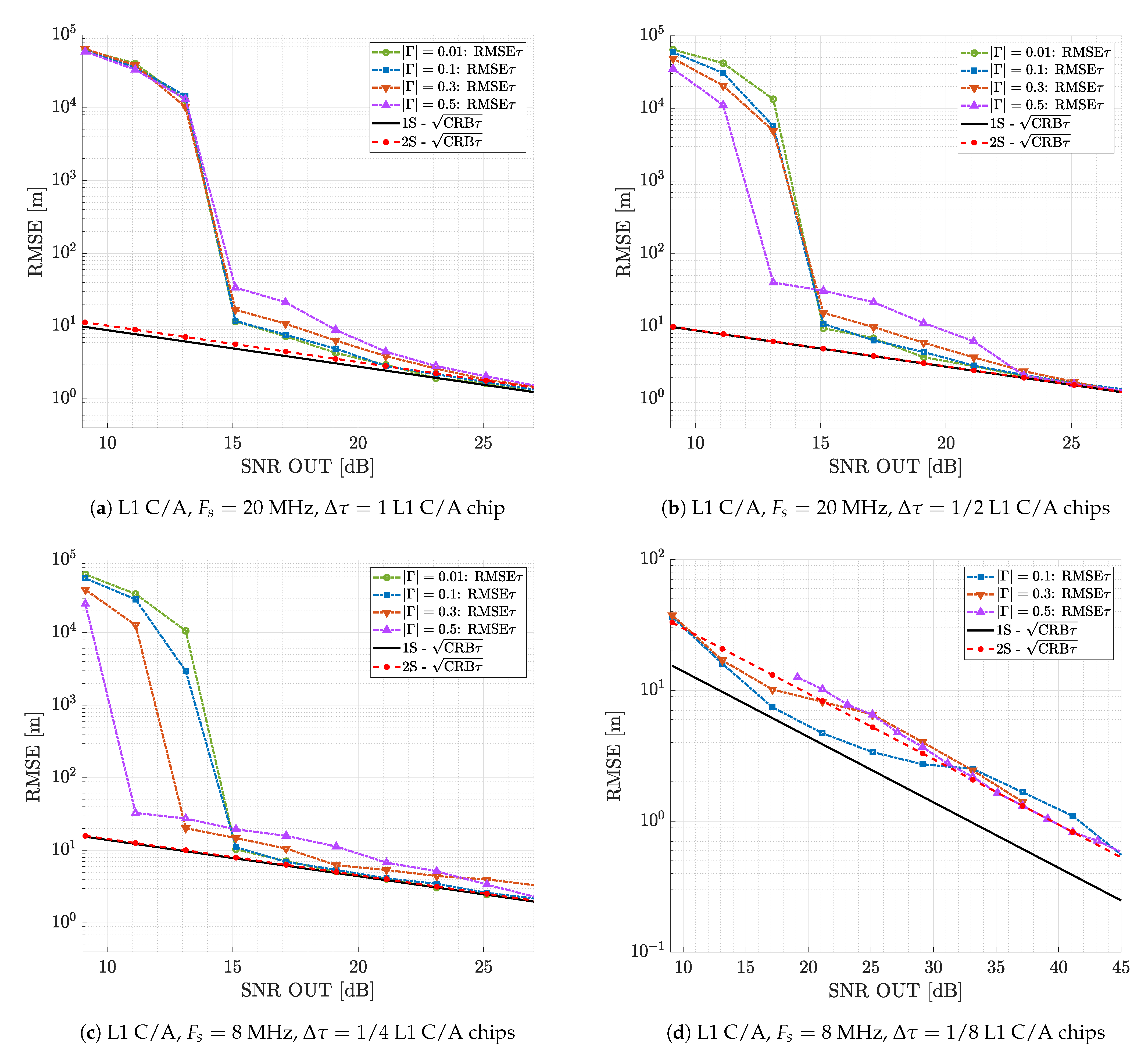
- Case (1): suboptimal single source estimation, that is two sources are present, but the corresponding estimator considers only one source.
- Case (2): optimal dual source estimation, that is it is known that two sources are present, and the corresponding estimator is matched to this.
4.1.2. Suboptimal Single Source Estimation
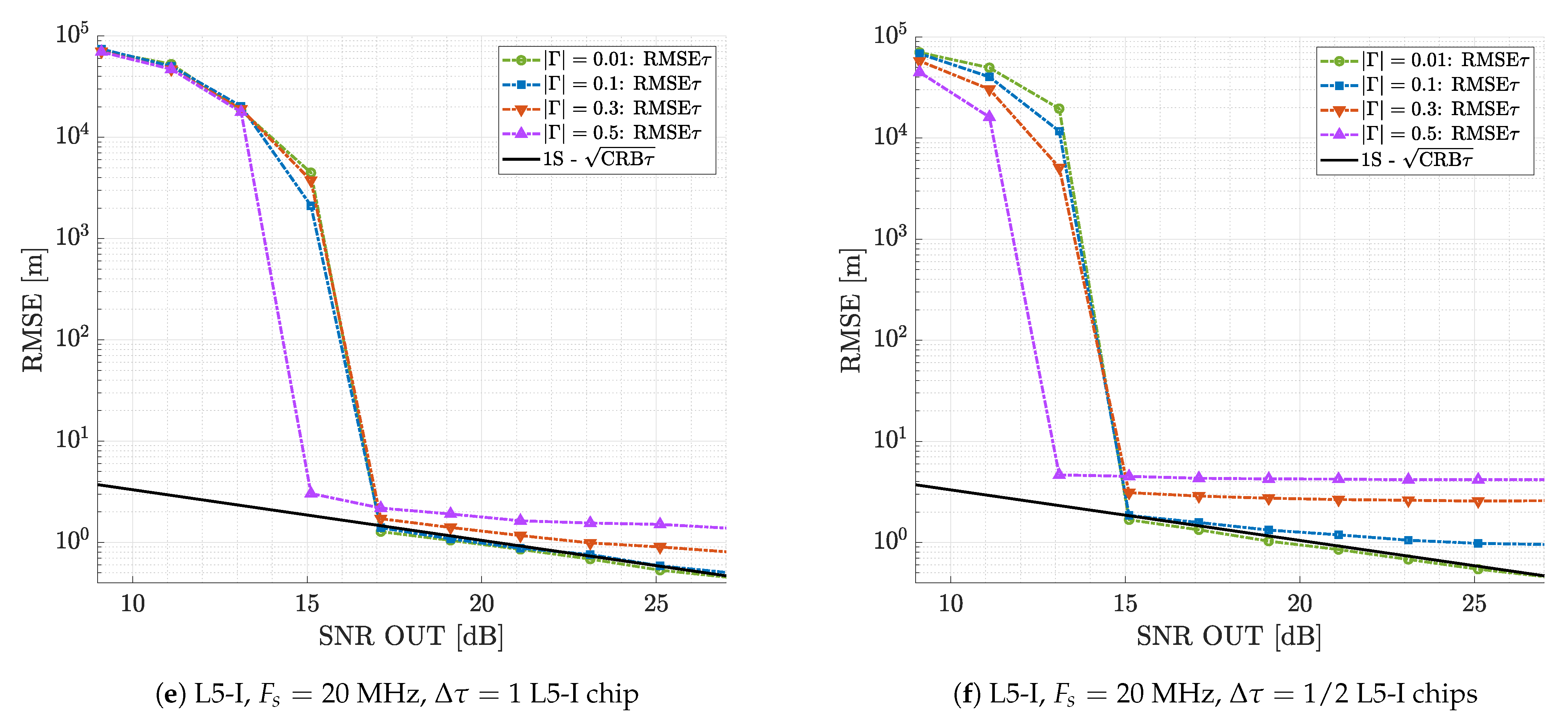
4.2. Optimal Dual Source Estimation
4.3. On the Dual Source Estimators’ Robustness: Misspecified Number of Sources
5. Results and Discussion on Non-Coherent Estimation
5.1. Analysis Setup
- Scenario #1: 20 PRNs, each one with a different random phase.
- Scenario #2: four blocks of five PRNs where (i) the first five PRNs have the same phase as the LOS signal and (ii) the other three blocks of five PRNs have three different random phases.
- Scenario #3: two blocks of 10 PRNs where (i) the first 10 PRNs have the same phase as the LOS signal and (ii) the other two blocks of five PRNs have two different random phases.
- Scenario #4: four blocks of five PRNs where (i) the first 15 PRNs have the same phase as the LOS signal and (ii) the remaining block of five PRNs has a random phase.
5.2. On the Estimation Performance of the Variance Estimator and Non-Coherent CRE
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Teunissen, P.J.G.; Montenbruck, O. (Eds.) Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on remote sensing using GNSS bistatic radar of opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.G.; Cardellach, E.; Xie, F. GNSS Remote Sensing: Theory, Methods and Applications; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Martín-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Application to Ocean Altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Katzberg, S.J.; Garrison, J.L. Utilizing GPS to Determine Ionospheric Delay over the Ocean; NASA Technical Memorandum 4750; 1996. Available online: https://ntrs.nasa.gov/citations/19970005019 (accessed on 11 February 2021).
- Anderson, K.D. Determination of Water Level and Tides Using Interferometric Observations of GPS Signals. J. Atmos. Ocean. Technol. 2000, 17, 1118–1127. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Perez, A.; Camps, A.; Ribó, S.; Cardellach, E.; Stroeve, J.; Nandan, V.; Itkin, P.; Tonboe, R.; Hendricks, S.; et al. Snow and Ice Thickness Retrievals Using GNSS-R: Preliminary Results of the MOSAiC Experiment. Remote Sens. 2020, 12, 4038. [Google Scholar] [CrossRef]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea Level Monitoring and Sea State Estimate Using a Single Geodetic Receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef] [Green Version]
- Treuhaft, R.N.; Lowe, S.T.; Zuffada, C.; Chao, Y. Two-cm GPS altimetry over Crater Lake. Geophys. Res. Lett. 2001, 28, 4343–4346. [Google Scholar] [CrossRef]
- Martín-Neira, M.; Caparrini, M.; Font-Rossello, J.; Lannelongue, S.; Vallmitjana, C.S. The PARIS concept: An experimental demonstration of sea surface altimetry using GPS reflected signals. IEEE Trans. Geosci. Remote Sens. 2001, 39, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Martín-Neira, M.; Colmenarejo, P.; Ruffini, G.; Serra, C. Altimetry precision of 1 cm over a pond using the wide-lane carrier phase of GPS reflected signals. Can. J. Remote Sens. 2002, 28, 394–403. [Google Scholar] [CrossRef]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.E.; LaBrecque, J.L. 5-cm precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29, 13-1–13-4. [Google Scholar] [CrossRef] [Green Version]
- Lowe, S.T.; Kroger, P.; Franklin, G.; LaBrecque, J.L.; Lerma, J.; Lough, M.; Marcin, M.R.; Muellerschoen, R.J.; Spitzmesser, D.; Young, L.E. A delay/Doppler-mapping receiver system for GPS-reflection remote sensing. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1150–1163. [Google Scholar] [CrossRef]
- Rius, A.; Aparicio, J.M.; Cardellach, E.; Martín-Neira, M.; Chapron, B. Sea surface state measured using GPS reflected signals. Geophys. Res. Lett. 2002, 29, 37-1–37-4. [Google Scholar] [CrossRef] [Green Version]
- Ruffini, G.; Soulat, F.; Caparrini, M.; Germain, O.; Martín-Neira, M. The eddy experiment: Accurate GNSS-R ocean altimetry from low altitude aircraft. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Marchan-Hernandez, J.F.; Camps, A.; Rodríguez-Álvarez, N.; Valencia, E.; Bosch-Lluis, X.; Ramos-Pérez, I. An efficient algorithm to the simulation of delay—Doppler maps of reflected Global Navigation Satellite System signals. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2733–2740. [Google Scholar] [CrossRef]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 38. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martín-Neira, M. Altimetric analysis of the sea-surface GPS-reflected signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribó, S.; Martín-Neira, M. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Park, H.; Pascual, D.; Camps, A.; Martin, F.; Alonso-Arroyo, A.; Carreno-Luengo, H. Analysis of Spaceborne GNSS-R Delay-Doppler Tracking. IEEE J. Sel. Topics Appl. Earth Observ. 2014, 7, 1481–1492. [Google Scholar] [CrossRef]
- Martín-Neira, M.; D’Addio, S.; Vitulli, R. Study of Delay Drift in GNSS-R Altimetry. IEEE J. Sel. Topics Appl. Earth Observ. 2014, 7, 1473–1480. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.R.; Rizos, C.; Qiao, L. Impact of Receiver Dynamics on Space-Based GNSS-R Altimetry. IEEE J. Sel. Topics Appl. Earth Observ. 2019, 12, 1974–1980. [Google Scholar] [CrossRef]
- Grieco, G.; Stoffelen, A.; Portabella, M. Rationale of GNSS Reflected Delay—Doppler Map (DDM) Distortions Induced by Specular Point Inaccuracies. IEEE J. Sel. Topics Appl. Earth Observ. 2020, 13, 3–13. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Rius, A.; Martín-Neira, M.; Fabra, F.; Nogues-Correig, O.; Ribό, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Martín, F.; Camps, A.; Park, H.; D’Addio, S.; Martín-Neira, M.; Pascual, D. Cross-Correlation Waveform Analysis for Conventional and Interferometric GNSS-R Approaches. IEEE J. Sel. Topics Appl. Earth Observ. 2014, 7, 1560–1572. [Google Scholar] [CrossRef]
- Pascual, D.; Camps, A.; Martin, F.; Park, H.; Arroyo, A.A.; Onrubia, R. Precision bounds in GNSS-R ocean altimetry. IEEE J. Select. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 1416–1423. [Google Scholar] [CrossRef]
- Martin, F.; D’Addio, S.; Camps, A.; Martín-Neira, M. Modeling and Analysis of GNSS-R Waveforms Sample-to-Sample Correlation. IEEE J. Sel. Topics Appl. Earth Observ. 2014, 7, 1545–1559. [Google Scholar] [CrossRef]
- Pascual, D.; Park, H.; Onrubia, R.; Arroyo, A.A.; Querol, J.; Camps, A. Crosstalk Statistics and Impact in Interferometric GNSS-R. IEEE J. Sel. Topics Appl. Earth Observ. 2016, 9, 4621–4630. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Park, H.; Camps, A.; Fabra, F.; Rius, A. GNSS-R derived centimetric sea topography: An airborne experiment demonstration. IEEE J. Sel. Topics Appl. Earth Observ. 2013, 6, 1468–1478. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Camps, A.; Ramos-Perez, I.; Rius, A. Experimental Evaluation of GNSS-Reflectometry Altimetric Precision Using the P(Y) and C/A Signals. IEEE J. Sel. Topics Appl. Earth Observ. 2014, 7, 1493–1500. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribó, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Cardellach, E.; Ao, C.O.; De la Torre, J.M.; Hajj, G.A. Carrier phase delay altimetry with GPS-reflection/occultation interferometry from low earth orbiters. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Ribó, S.; Martín-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Lake level and surface topography measured with spaceborne GNSS-reflectometry from CYGNSS Mission: Example for the lake Qinghai. Geophys. Res. Lett. 2018, 45, 13–332. [Google Scholar] [CrossRef]
- Lestarquit, L.; Peyrezabes, M.; Darrozes, J.; Motte, E.; Roussel, N.; Wautelet, G.; Frappart, F.; Ramillien, G.; Biancale, R.; Zribi, M. Reflectometry with an Open-Source Software GNSS Receiver: Use Case with Carrier Phase Altimetry. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2016, 9, 4843–4853. [Google Scholar] [CrossRef]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry with GNSS Reflected Signals. IEEE J. Select. Topics Appl. Earth Observ. Remote Sens. 2019, 13, 102–112. [Google Scholar] [CrossRef]
- Martin, F.; Camps, A.; Fabra, F.; Rius, A.; Martin-Neira, M.; D’Addio, S.; Alonso, A. Mitigation of Direct Signal Cross-Talk and Study of the Coherent Component in GNSS-R. IEEE Geosci. Remote Sens. Lett. 2015, 12, 279–283. [Google Scholar] [CrossRef]
- Das, P.; Ortega, L.; Vilà-Valls, J.; Vincent, F.; Chaumette, E.; Davain, L. Performance Limits of GNSS Code-Based Precise Positioning: GPS, Galileo & Meta-Signals. Sensors 2020, 20, 2196. [Google Scholar]
- Ortega, L.; Medina, D.; Vilà-Valls, J.; Vincent, F.; Chaumette, E. Positioning Performance Limits of GNSS Meta-Signals and HO-BOC Signals. Sensors 2020, 20, 3586. [Google Scholar] [CrossRef]
- Medina, D.; Ortega, L.; Vilà-Valls, J.; Closas, P.; Vincent, F.; Chaumette, E. Compact CRB for Delay, Doppler and Phase Estimation—Application to GNSS SPP & RTK Performance Characterization. IET Radar Sonar Navig. 2020, 14, 1537–1549. [Google Scholar]
- Das, P.; Vilà-Valls, J.; Vincent, F.; Davain, L.; Chaumette, E. A New Compact Delay, Doppler Stretch and Phase Estimation CRB with a Band-Limited Signal for Generic Remote Sensing Applications. Remote Sens. 2020, 12, 2913. [Google Scholar] [CrossRef]
- Lubeigt, C.; Ortega, L.; Vilà-Valls, J.; Lestarquit, L.; Chaumette, E. Joint Delay-Doppler Estimation Performance in a Dual Source Context. Remote Sens. 2020, 12, 3894. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing. In Radar Array Processing; Haykin, S., Litva, J., Shepherd, T.J., Eds.; Springer: Heidelberg, Germany, 1993; Chapter 4; pp. 99–151. [Google Scholar]
- Stoica, P.; Nehorai, A. Performances study of conditional and unconditional direction of arrival estimation. IEEE Trans. ASSP 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Renaux, A.; Forster, P.; Chaumette, E.; Larzabal, P. On the High-SNR Conditional Maximum-Likelihood Estimator Full Statistical Characterization. IEEE Trans. Signal Process. 2006, 54, 4840–4843. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Stoica, P. Efficient mixed-spectrum estimation with applications to target feature extraction. IEEE Trans. Signal Process. 1996, 44, 281–295. [Google Scholar]
- Townsend, B.R.; Fenton, P.C.; Van Dierendonck, K.J.; Richard Van Nee, D.J. Performance Evaluation of the Multipath Estimating Delay Lock Loop. Navigation 1995, 42, 502–514. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubeigt, C.; Ortega, L.; Vilà-Valls, J.; Lestarquit, L.; Chaumette, E. On the Impact and Mitigation of Signal Crosstalk in Ground-Based and Low Altitude Airborne GNSS-R. Remote Sens. 2021, 13, 1085. https://doi.org/10.3390/rs13061085
Lubeigt C, Ortega L, Vilà-Valls J, Lestarquit L, Chaumette E. On the Impact and Mitigation of Signal Crosstalk in Ground-Based and Low Altitude Airborne GNSS-R. Remote Sensing. 2021; 13(6):1085. https://doi.org/10.3390/rs13061085
Chicago/Turabian StyleLubeigt, Corentin, Lorenzo Ortega, Jordi Vilà-Valls, Laurent Lestarquit, and Eric Chaumette. 2021. "On the Impact and Mitigation of Signal Crosstalk in Ground-Based and Low Altitude Airborne GNSS-R" Remote Sensing 13, no. 6: 1085. https://doi.org/10.3390/rs13061085
APA StyleLubeigt, C., Ortega, L., Vilà-Valls, J., Lestarquit, L., & Chaumette, E. (2021). On the Impact and Mitigation of Signal Crosstalk in Ground-Based and Low Altitude Airborne GNSS-R. Remote Sensing, 13(6), 1085. https://doi.org/10.3390/rs13061085








