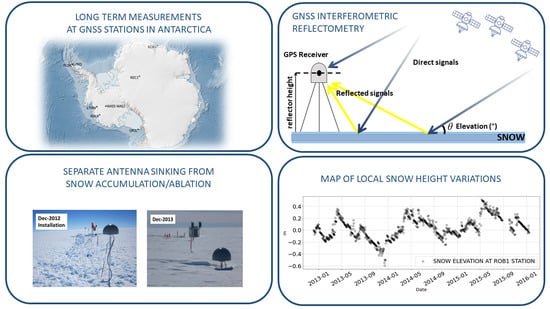
Long-Term Snow Height Variations in Antarctica from GNSS Interferometric Reflectometry
Abstract
:1. Introduction
2. Data and Methods
2.1. ROB1 and POLENET Antennas
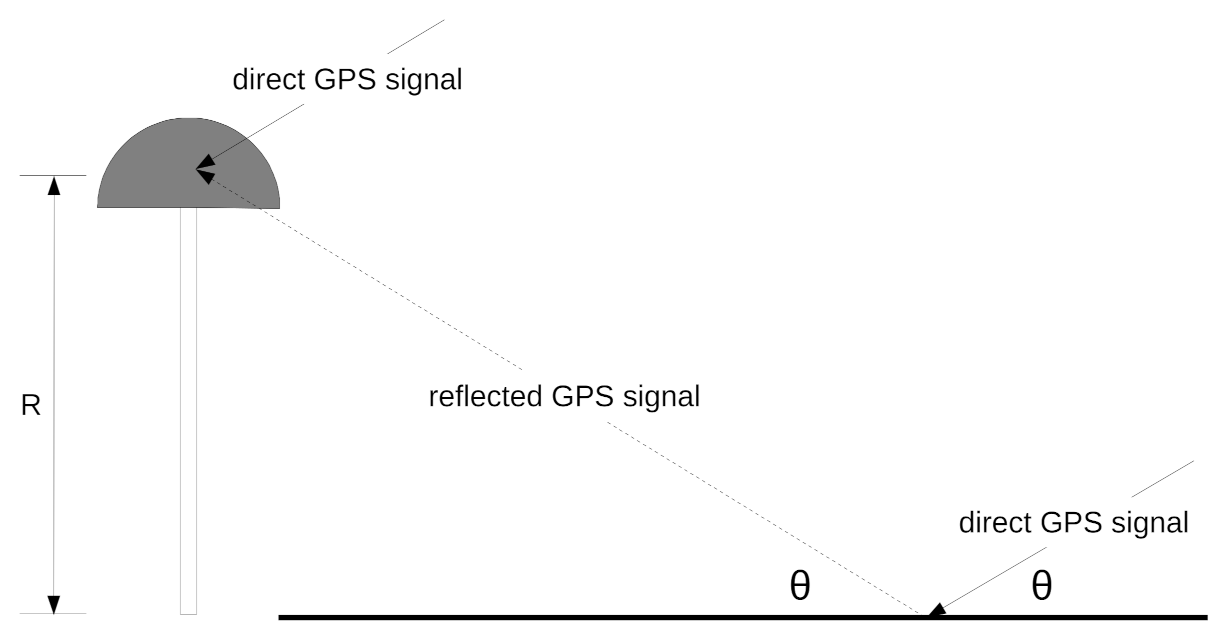
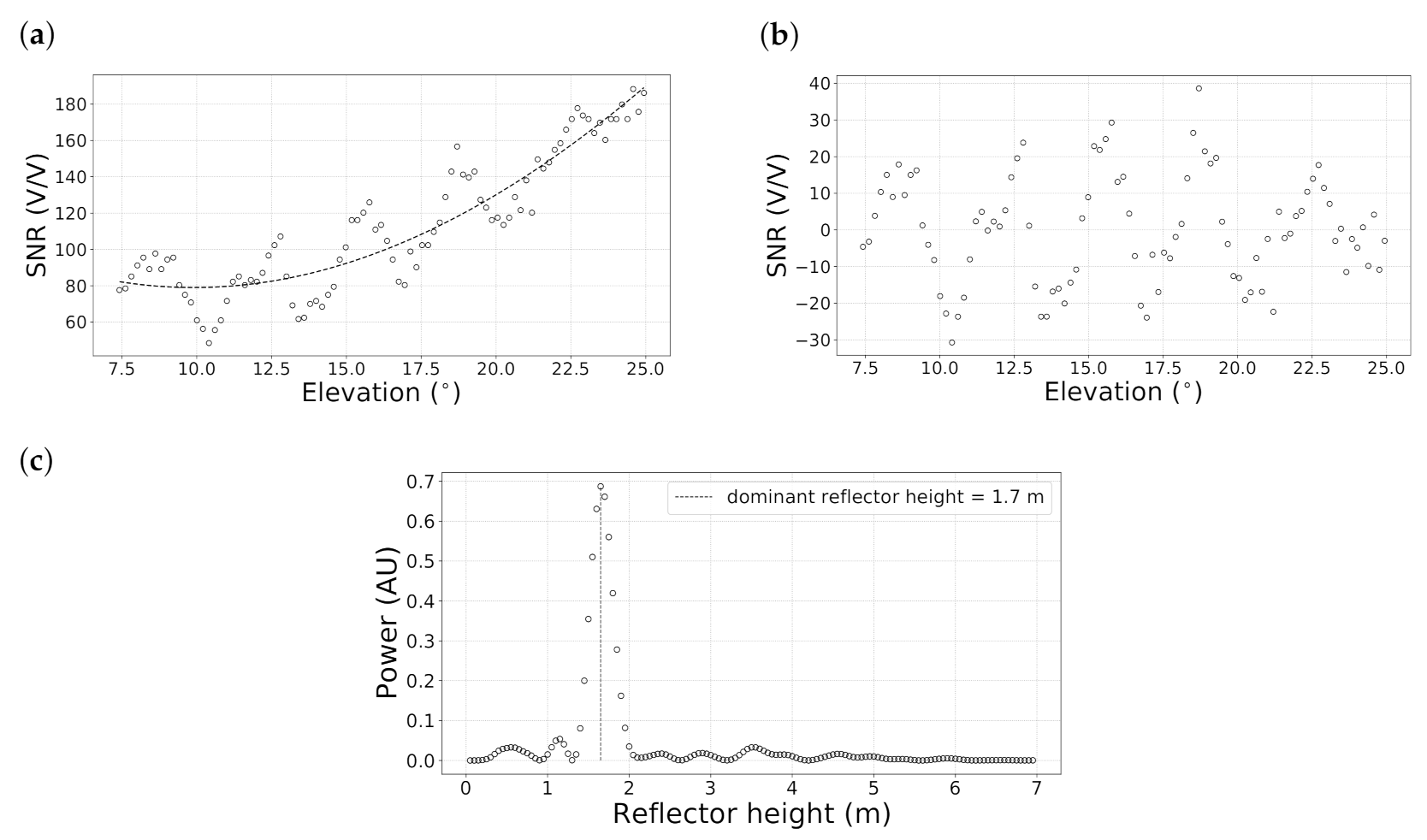
2.2. GNSS Interferometric Reflectometry
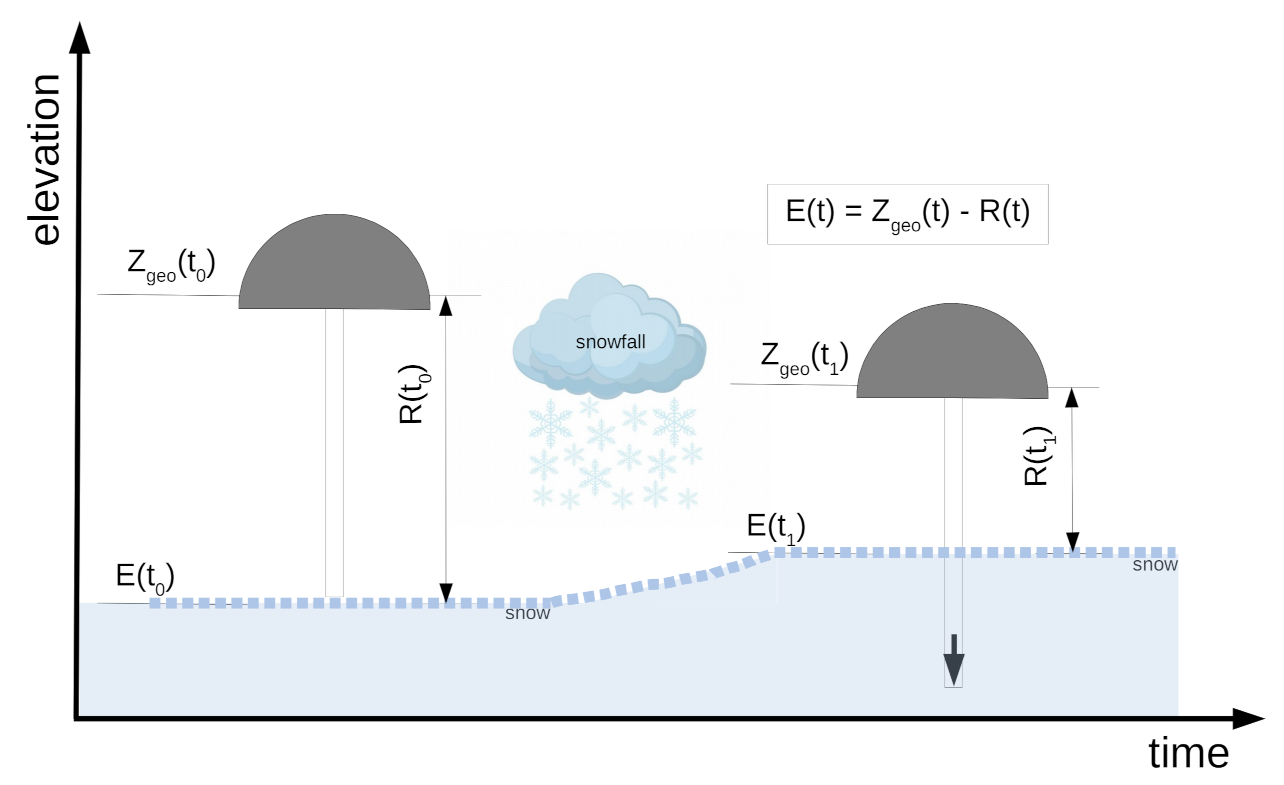
2.3. Measuring the Snow Surface Elevation
3. Results
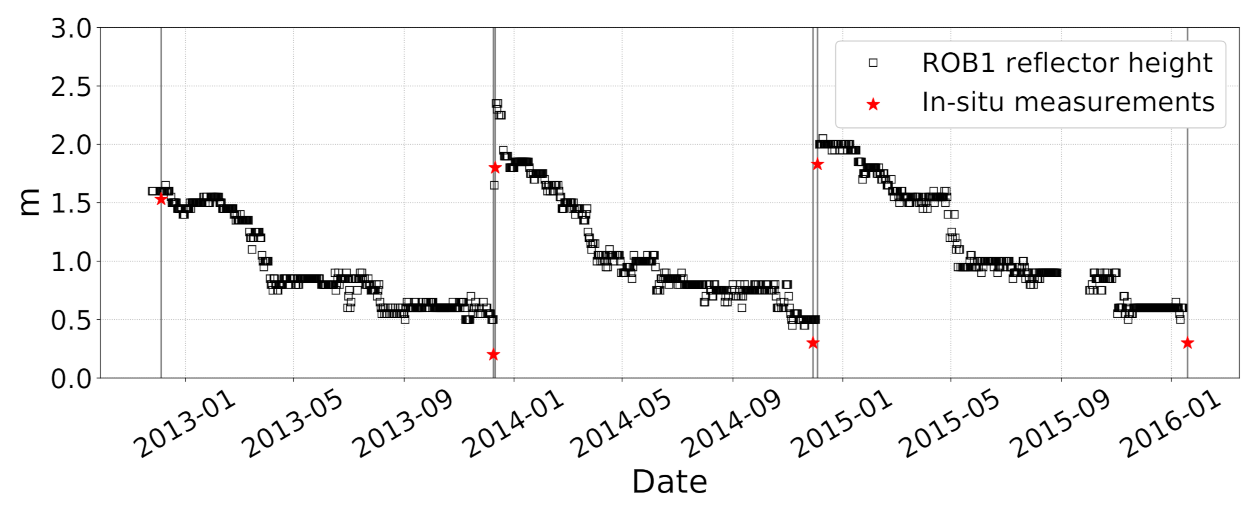
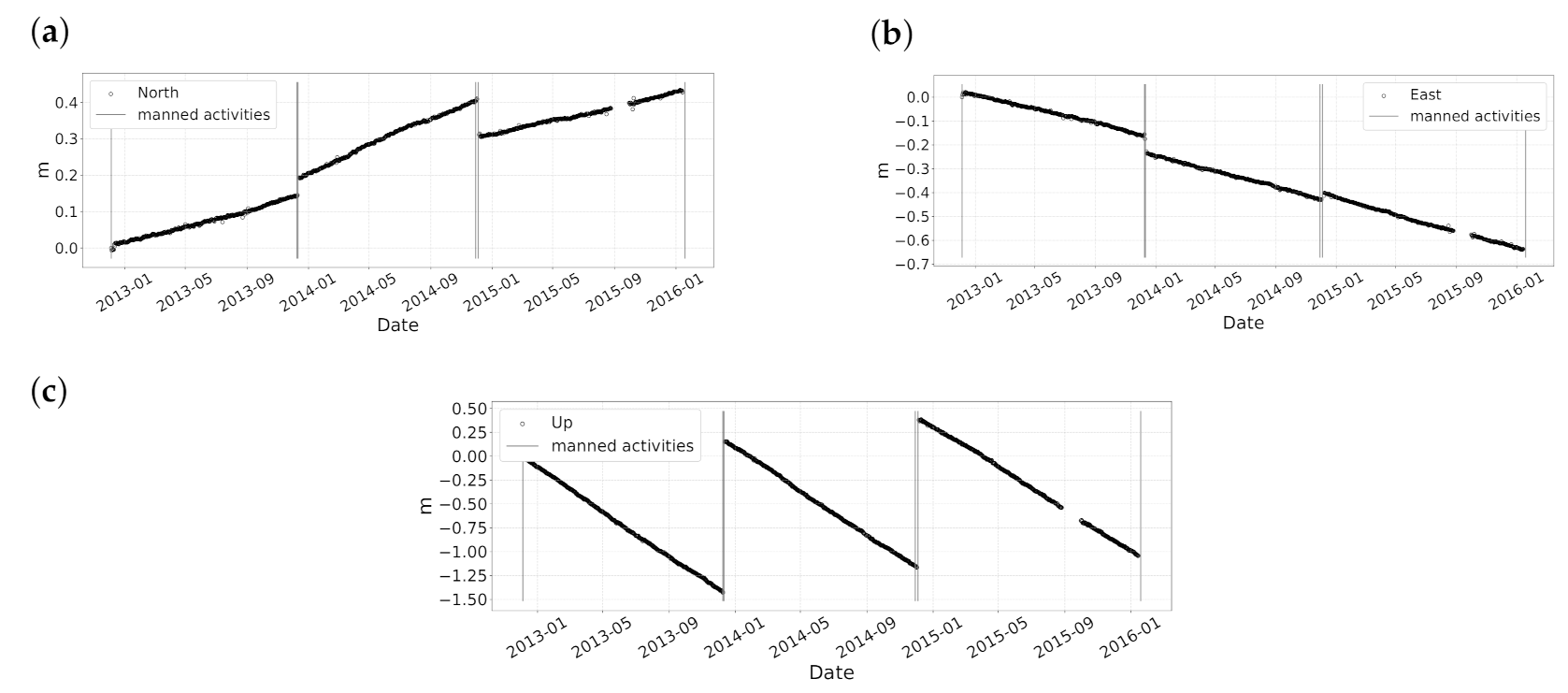
3.1. Antennas on an Ice Rise: ROB1
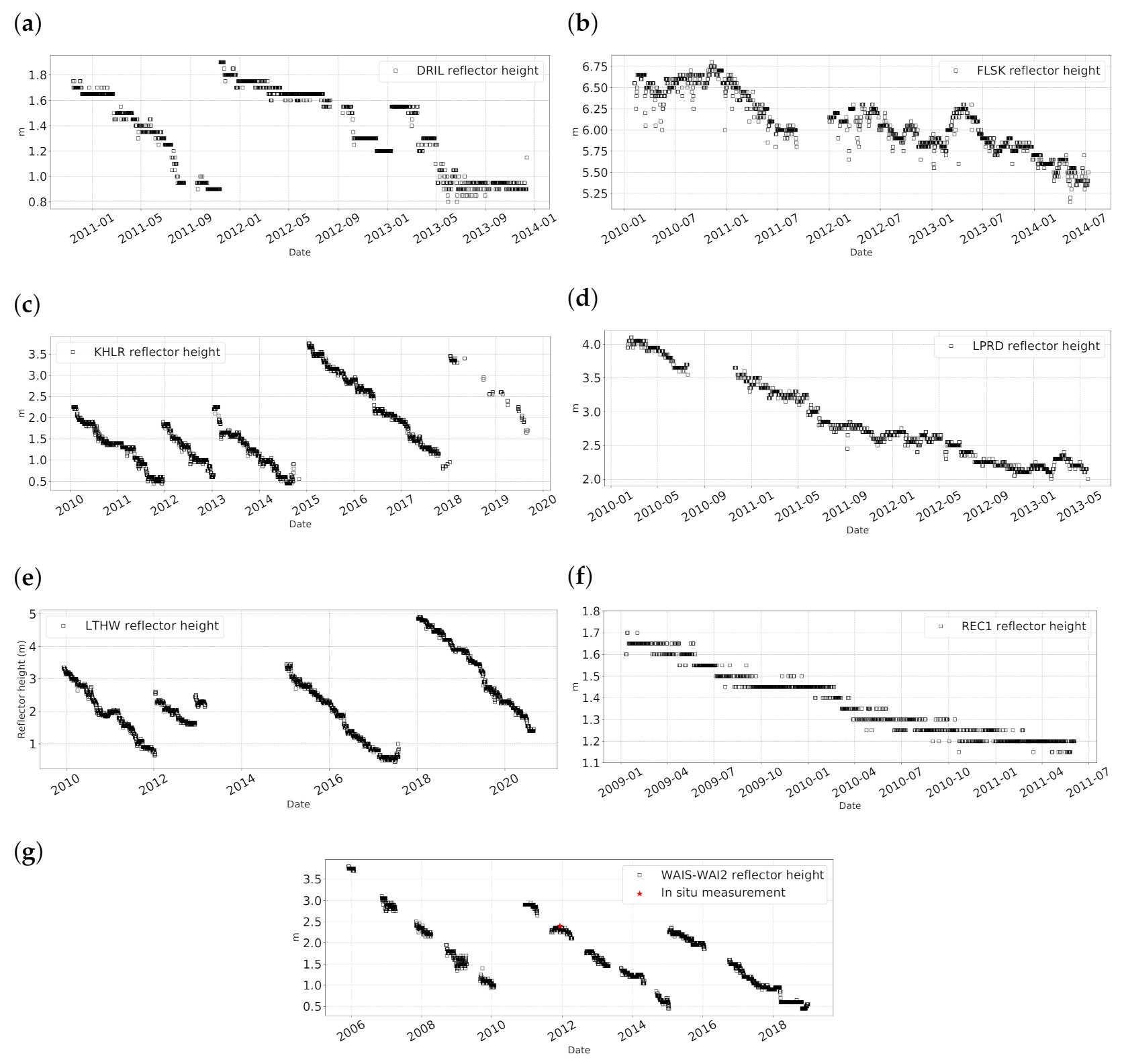
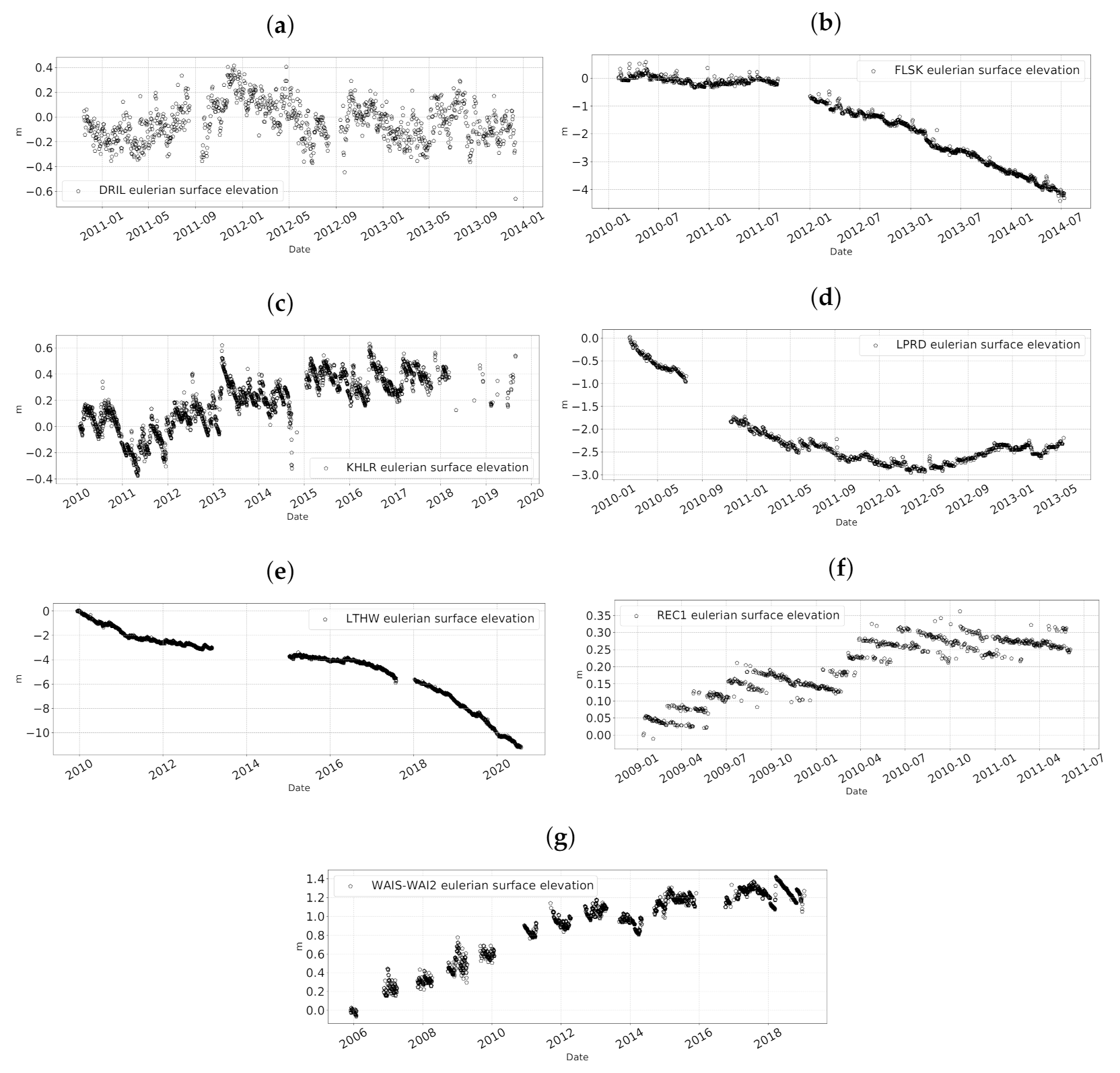
3.2. Antennas on a Moving Glacier: POLENET Antennas
4. Discussion
5. Conclusions
- For the LPRD station, located on the Leppard Glacier in the Antarctic Peninsula, we observe an overall decrease of the snow level of about three meters from 2010 to 2012, followed by a more stable period. However, the order of magnitude of the decrease is the same as the uncertainties of the REMA elevation model.
- For the FLSK antenna, located on the Flask Glacier in the Antarctic Peninsula, we observe a global decrease of more than four meters during the period 2010–2013, with an uncertainty of 2.5 m from the REMA elevation model.
- A prominent meltdown is observed for the LTHW antenna, located in the lower part of the Thwaites Glacier, with a global decrease between 2010 and 2020 of more than ten meters of the snow surface, a decrease one order of magnitude higher than the uncertainty obtained from the REMA elevation model.
- A positive trend in the snow surface elevation of 1.2 m from 2005 to 2019 (with an uncertainty of 0.4 m) was observed for station WAIS-WAI2, located on the West Antarctic Ice Sheet ice flow divide.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| GNSS-IR | GNSS Interferometric Reflectometry |
| GNSS PPP | GNSS Precise Point Positioning |
| REMA | Reference Elevation Model of Antarctica |
| SEC | Surface Elevation Changes |
| SMB | Surface Mass Balance |
| SNR | Signal-to-noise Ratio |
| WAIS | West Antarctic Ice Sheet |
References
- Fretwell, P.; Pritchard, H.D.; Vaughan, D.G.; Bamber, J.L.; Barrand, N.E.; Bell, R.; Bianchi, C.; Bingham, R.G.; Blankenship, D.D.; Casassa, G.; et al. Bedmap2: Improved ice bed, surface and thickness datasets for Antarctica. Cryosphere 2013, 7, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of GPS receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Nievinski, F.G. GPS snow sensing: Results from the EarthScope Plate Boundary Observatory. GPS Solut. 2013, 17, 41–52. [Google Scholar] [CrossRef]
- Shean, D.E.; Christianson, K.; Larson, K.M.; Ligtenberg, S.R.M.; Joughin, I.R.; Smith, B.E.; Stevens, C.M.; Bushuk, M.; Holland, D.M. GPS-derived estimates of surface mass balance and ocean-induced basal melt for Pine Island Glacier ice shelf, Antarctica. Cryosphere 2017, 11, 2655–2674. [Google Scholar] [CrossRef] [Green Version]
- Siegfried, M.R.; Medley, B.; Larson, K.M.; Fricker, H.A.; Tulaczyk, S. Snow accumulation variability on a West Antarctic ice stream observed with GPS reflectometry, 2007–2017. Geophys. Res. Lett. 2017, 44, 7808–7816. [Google Scholar] [CrossRef]
- Falconer, T.; Pyne, A.; Olney, M.; Curren, M. Operations overview for the ANDRILL McMurdo Ice Shelf Project, Antarctica. Terra Antart. 2007, 14, 131–140. [Google Scholar]
- Wiens, D.A.; Wilson, T.J.; Dietrich, R.O. POLENET: Polar Earth Observing Network for the International Polar Year. AGU Fall Meet. Abstr. 2007, U24D-03. [Google Scholar]
- Drews, R.; Matsuoka, K.; Martín, C.; Callens, D.; Bergeot, N.; Pattyn, F. Evolution of Derwael Ice Rise in Dronning Maud Land, Antarctica, over the last millennia. J. Geophys. Res. Earth Surf. 2015, 120, 564–579. [Google Scholar] [CrossRef] [Green Version]
- Scambos, T.; Truffer, M. Antarctica-PI Continuous-FLSK-Flask Glacier P.S. 2010. Available online: https://doi.org/10.7283/T5J964G3 (accessed on 6 February 2010).
- Antarctica-POLENET GPS Network-KHLR-Kohler Glacier P.S. 2010. Available online: https://doi.org/10.7283/T5XW4H37 (accessed on 24 January 2010).
- Scambos, T.; Truffer, M. Antarctica-PI Continuous-LPRD-Leppard Glacier P.S. 2010. Available online: https://doi.org/10.7283/T5DJ5CRC (accessed on 13 February 2010).
- Wilson, T. Antarctica-POLENET GPS Network-LTHW-Lower Thwaites Glacier P.S. 2009. Available online: https://doi.org/10.7283/T5NK3C7D (accessed on 12 December 2009).
- Scambos, T.; Bell, R. Antarctica-PI Continuous-REC1-Recovery Lakes 1 P.S. 2009. Available online: https://doi.org/10.7283/T5NZ85SS (accessed on 10 January 2009).
- Johns, B. Antarctica-Infrastructure GPS Network—WAIS-WAIS Divide Base Station P.S. 2006. Available online: https://doi.org/10.7283/T59K48F4 (accessed on 1 December 2005).
- Johns, B. Antarctica-Infrastructure GPS Network-WAI2-WAIS Divide P.S. 2011. Available online: https://doi.org/10.7283/T5ZC8133 (accessed on 8 December 2010).
- Larson, K.M.; Wahr, J.; Munneke, P.K. Constraints on snow accumulation and firn density in Greenland using GPS receivers. J. Glaciol. 2015, 61, 101–114. [Google Scholar] [CrossRef] [Green Version]
- Roesler, C.; Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2018, 22, 80. [Google Scholar] [CrossRef] [Green Version]
- Bergeot, N.; Chevalier, J.M.; Bruyninx, C.; Pottiaux, E.; Aerts, W.; Baire, Q.; Legrand, J.; Defraigne, P.; Huang, W. Near real-time ionospheric monitoring over Europe at the Royal Observatory of Belgium using GNSS data. J. Space Weather. Space Clim. 2014, 4, A31. [Google Scholar] [CrossRef] [Green Version]
- VanderPlas, J.T. Understanding the Lomb-Scargle Periodogram. Astrophys. J. Suppl. 2018, 236, 16. [Google Scholar] [CrossRef]
- Zimmermann, F.; Schmitz, B.; Klingbeil, L.; Kuhlmann, H. GPS Multipath Analysis Using Fresnel Zones. Sensors 2019, 19, 25. [Google Scholar] [CrossRef] [Green Version]
- Defraigne, P.; Guyennon, N.; Bruyninx, C. GPS Time and Frequency Transfer: PPP and Phase-Only Analysis. Int. J. Navig. Obs. 2008, 2008, 175468. [Google Scholar] [CrossRef] [Green Version]
- Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef] [Green Version]
- Nievinski, F.G.; Larson, K.M. Inverse Modeling of GPS Multipath for Snow Depth Estimation—Part I: Formulation and Simulations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6555–6563. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Sundal, A.; Briggs, K.; Muir, A.; Ridout, A.; Hogg, A.; Wingham, D. Increased ice losses from Antarctica detected by CryoSat-2. Geophys. Res. Lett. 2014, 41, 3899–3905. [Google Scholar] [CrossRef]
- Milillo, P.; Rignot, E.; Rizzoli, P.; Scheuchl, B.; Mouginot, J.; Bueso-Bello, J.; Prats-Iraola, P. Heterogeneous retreat and ice melt of Thwaites Glacier, West Antarctica. Sci. Adv. 2019, 5, eaau3433. [Google Scholar] [CrossRef] [Green Version]
- Scambos, T.; Bell, R.; Alley, R.; Anandakrishnan, S.; Bromwich, D.; Brunt, K.; Christianson, K.; Creyts, T.; Das, S.; DeConto, R.; et al. How much, how fast?: A science review and outlook for research on the instability of Antarctica’s Thwaites Glacier in the 21st century. Glob. Planet. Chang. 2017, 153, 16–34. [Google Scholar] [CrossRef]
- Shepherd, A.; Gilbert, L.; Muir, A.S.; Konrad, H.; McMillan, M.; Slater, T.; Briggs, K.H.; Sundal, A.V.; Hogg, A.E.; Engdahl, M.E. Trends in Antarctic Ice Sheet Elevation and Mass. Geophys. Res. Lett. 2019, 46, 8174–8183. [Google Scholar] [CrossRef] [Green Version]
- Behrangi, A.; Gardner, A.S.; Wiese, D.N. Comparative analysis of snowfall accumulation over Antarctica in light of Ice discharge and gravity observations from space. Environ. Res. Lett. 2020, 15, 104010. [Google Scholar] [CrossRef]
- Schröder, L.; Horwath, M.; Dietrich, R.; Helm, V.; van den Broeke, M.R.; Ligtenberg, S.R.M. Four decades of Antarctic surface elevation changes from multi-mission satellite altimetry. Cryosphere 2019, 13, 427–449. [Google Scholar] [CrossRef] [Green Version]




| Location | Start | Stop | Lon | Lat | |
|---|---|---|---|---|---|
| ROB1 | Derwael Ice Rise | 05 December 2012 | 14 January 2016 | 26.345 | −70.241 |
| DRIL | Ross Ice Shelf | 14 November 2010 | 12 December 2013 | 171.511 | −77.582 |
| FLSK | Flask Glacier | 06 February 2010 | 12 July 2014 | −62.897 | −65.752 |
| KHLR | Kohler Glacier | 24 January 2010 | 03 September 2019 | −120.729 | −76.155 |
| LPRD | Leppard Glacier | 13 February 2010 | 22 May 2013 | −62.903 | −65.953 |
| LTHW | Lower Thwaites Glacier | 12 December 2009 | 30 August 2020 | −107.782 | −76.458 |
| REC1 | Recovery Glacier | 10 January 2009 | 03 June 2011 | 18.905 | −82.812 |
| WAIS | West Antarctic | 01 December 2005 | 26 January 2010 | −112.054 | −79.467 |
| Ice Sheet Divide | |||||
| WAI2 | West Antarctic | 08 December 2010 | 19 January 2019 | −112.054 | −79.467 |
| Ice Sheet Divide |
| Ellipsoidal H | (ma) | (ma) | (ma) | REMA (m) | Annual Snow Variations | (ma) |
|---|---|---|---|---|---|---|
| 453.4 | 0.16 | −0.19 | −1.36 | - | ±30/50 cm | 0.08 ± 0.01 |
| Antenna | Dates | (m) | REMA (m) | (m) | (ma) | (ma) | |
|---|---|---|---|---|---|---|---|
| ROB1 | Start: 05 December 2012 Stop: 14 January 2016 | −0.6 | 0.4 | - | - | 0.08 ± 0.01 | 0.08 ± 0.01 |
| DRIL | Start: 14 November 2010 Stop: 12 December 2013 | 2359.3 | −243 | 0.6 ± 0.5 | - | 0.00 ± 0.16 | 0.00 ± 0.16 |
| FLSK | Start: 06 February 2010 Stop: 12 December 2013 | 194.4 | 1058.4 | 23.1 ± 2.5 | −4.5 | −0.16 ± 0.56 (2010) | −1.40 ± 0.56 (2012) |
| KHLR | Start: 24 January 2010 Stop: 26 August 2019 | 88.0 | 85.1 | 2.5 ± 0.6 | +0.4 | 0.06 ± 0.06 | 0.06 ± 0.06 |
| LPRD | Start: 13 February 2010 Stop: 22 May 2013 | 64.8 | 940.5 | 13.4 ± 2.6 | −2.5 | 0.48 ± 0.79 (2013) | −1.74 ± 0.79 (2010) |
| LTHW | Start: 12 December 2009 Stop: 31 July 2020 | 3596.4 | 666.4 | 14.4 ± 1.0 | −11.2 | −0.37 ± 0.09 (2012) | −2.48 ± 0.09 (2019) |
| REC1 | Start: 10 January 2009 Stop: 03 June 2011 | 4.4 | − 28.2 | 0.0 ± 0.4 | +0.3 | 0.11 ± 0.17 | 0.11 ± 0.17 |
| WAIS-WAI2 | Start: 01 December 2005 Stop: 19 January 2019 | −16.1 | −16.7 | 0.0 ± 0.4 | +1.2 | 0.15 ± 0.17 (2014) | 0.15 ± 0.17 (2010) |
| Basin | Period | (ma) | Antenna(s) | Period | (ma) |
|---|---|---|---|---|---|
| 6 | 2012–2016 | 0.032 | ROB1 | 01/2013–01/2016 | 0.076 |
| 26 | 2012–2016 | −0.181 | FLSK LPRD | 01/2012–07/2014 05/2012–05/2013 | −1.404 0.481 |
| 19 | 2012–2016 | −0.023 | WAIS-WAI2 | 2012–2016 | 0.066 |
| 21 | 2012–2016 | −0.415 | LTHW | 2012–2016 | −0.374 |
| 20 | 2012–2016 | −0.207 | KHLR | 2012–2016 | 0.064 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinat, E.; Defraigne, P.; Bergeot, N.; Chevalier, J.-M.; Bertrand, B. Long-Term Snow Height Variations in Antarctica from GNSS Interferometric Reflectometry. Remote Sens. 2021, 13, 1164. https://doi.org/10.3390/rs13061164
Pinat E, Defraigne P, Bergeot N, Chevalier J-M, Bertrand B. Long-Term Snow Height Variations in Antarctica from GNSS Interferometric Reflectometry. Remote Sensing. 2021; 13(6):1164. https://doi.org/10.3390/rs13061164
Chicago/Turabian StylePinat, Elisa, Pascale Defraigne, Nicolas Bergeot, Jean-Marie Chevalier, and Bruno Bertrand. 2021. "Long-Term Snow Height Variations in Antarctica from GNSS Interferometric Reflectometry" Remote Sensing 13, no. 6: 1164. https://doi.org/10.3390/rs13061164
APA StylePinat, E., Defraigne, P., Bergeot, N., Chevalier, J. -M., & Bertrand, B. (2021). Long-Term Snow Height Variations in Antarctica from GNSS Interferometric Reflectometry. Remote Sensing, 13(6), 1164. https://doi.org/10.3390/rs13061164