Quality of Orbit Predictions for Satellites Tracked by SLR Stations
Abstract
:1. Introduction
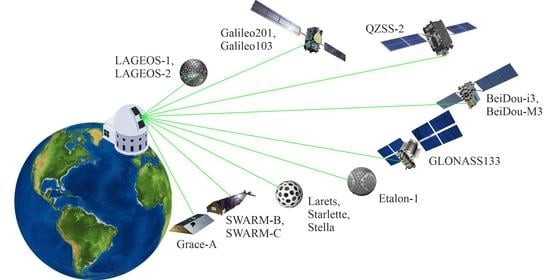
1.1. SLR
1.2. Orbit Predictions
1.3. The Goal of the Study
- How accurate predictions of satellite orbits are?
- Which prediction providers publish more accurate prediction files?
- What is the degradation of individual orbit components over time for different satellites?
1.4. Structure of the Paper
2. Methodology
2.1. Predicted Orbits
2.2. Precise Orbits
2.2.1. Precise Orbits of Geodetic Satellites
2.2.2. Precise Orbits of Navigation Satellites
2.2.3. Precise Orbits of Research LEO Satellites
2.3. Scheme of Multi-Source Data Processing
3. Results
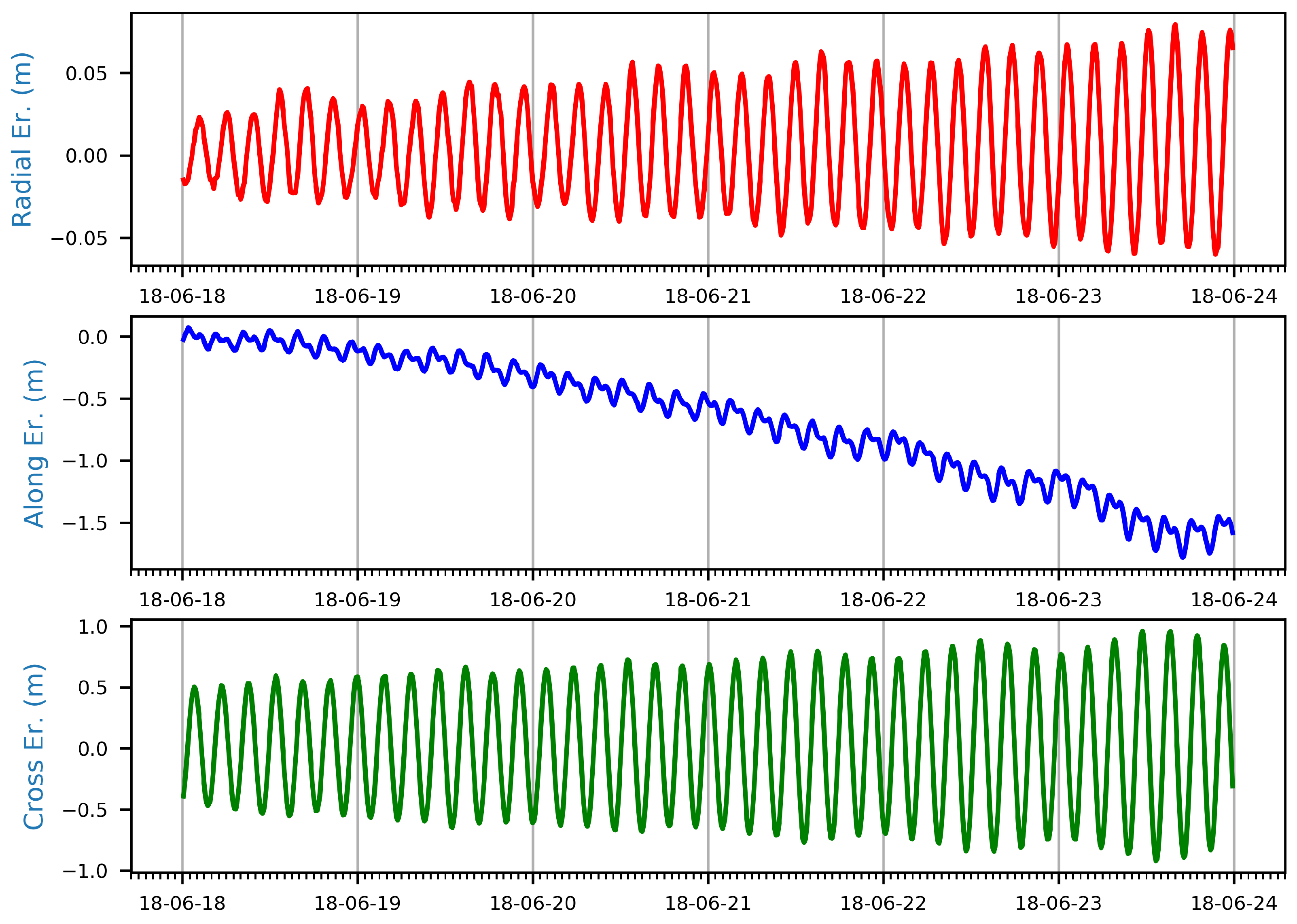
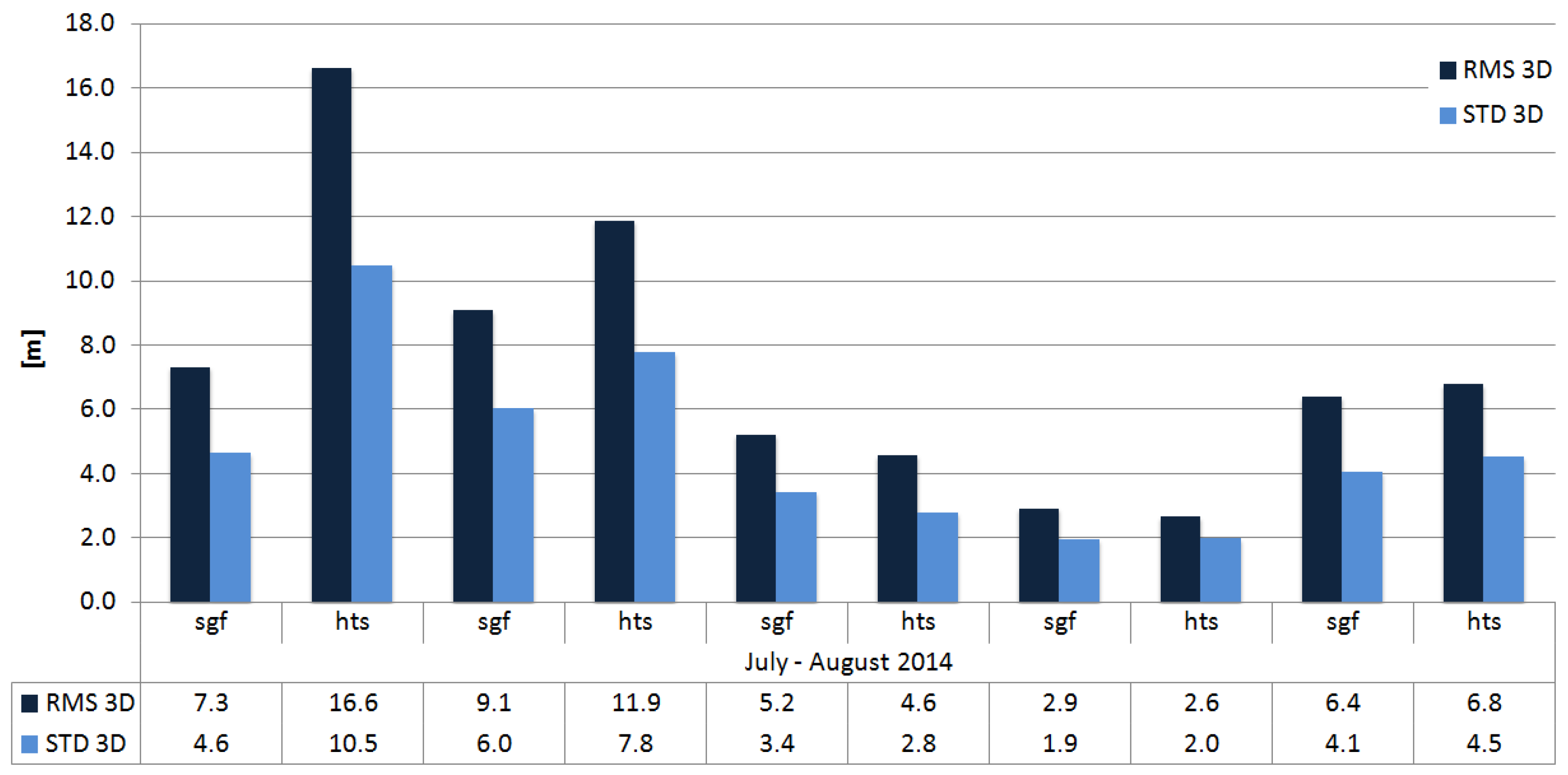
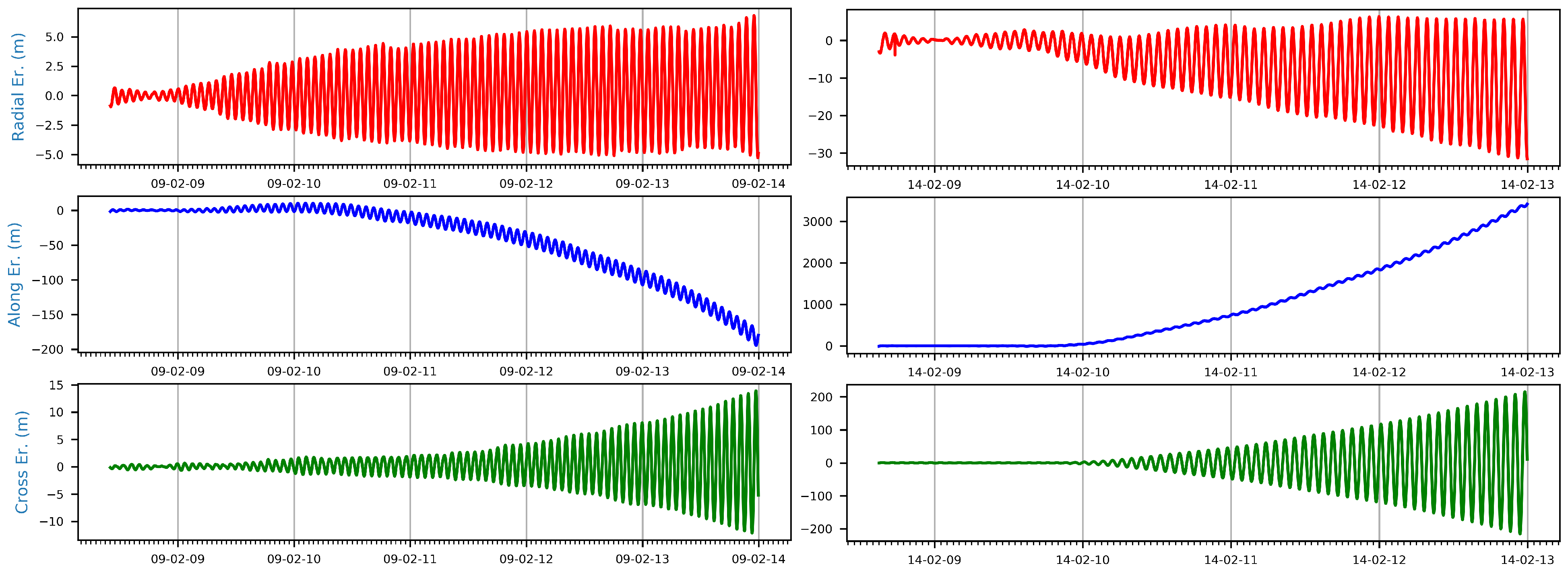
3.1. Quality of the Orbit Predictions—Geodetic Satellites
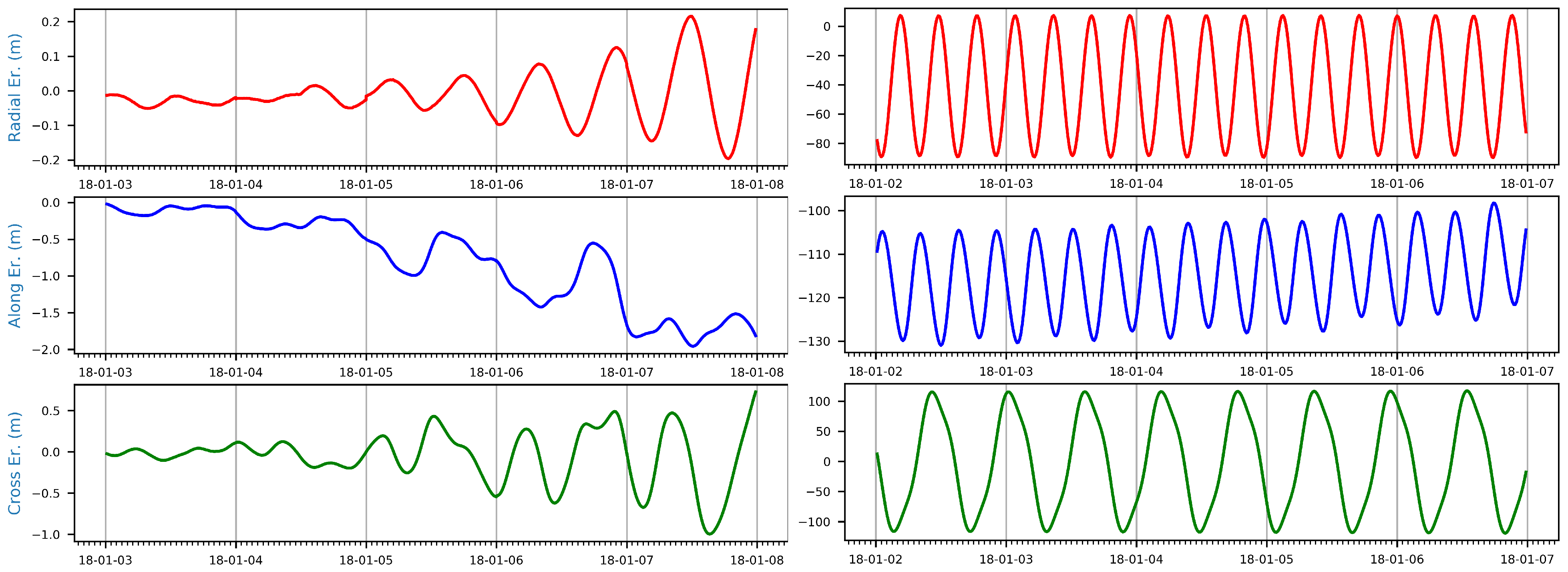
3.2. Quality of the Orbit Predictions—Navigation Satellites
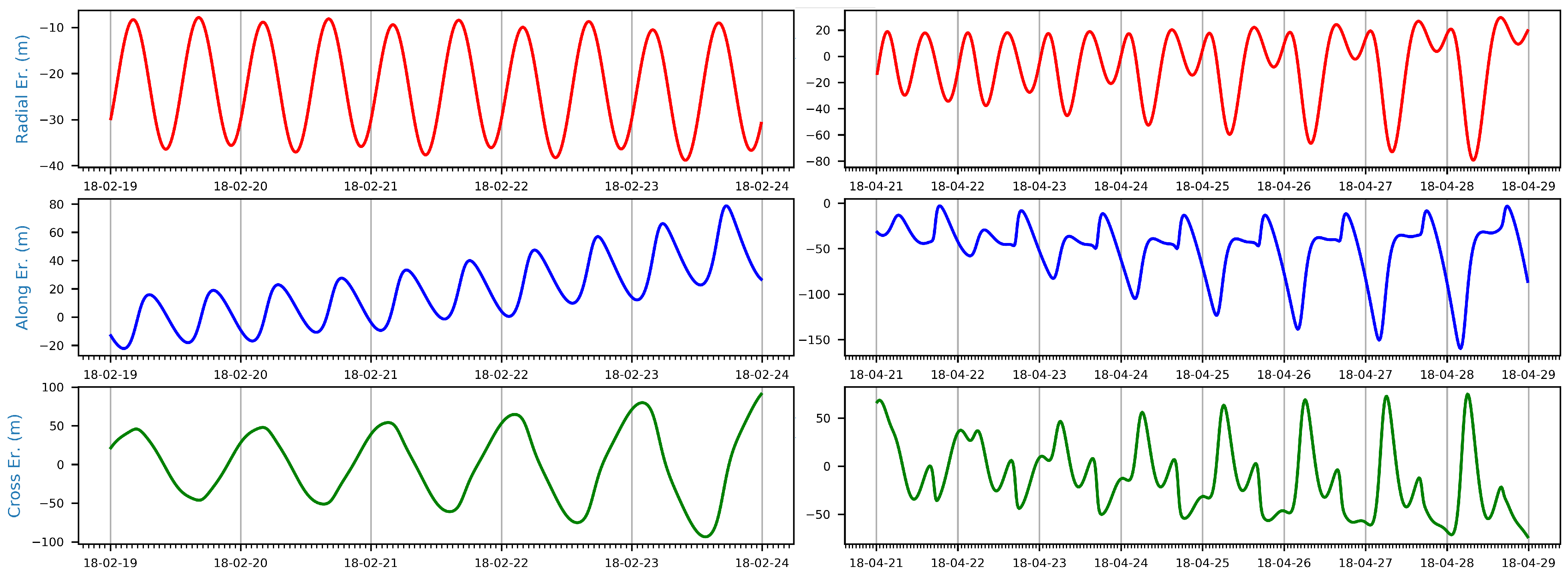
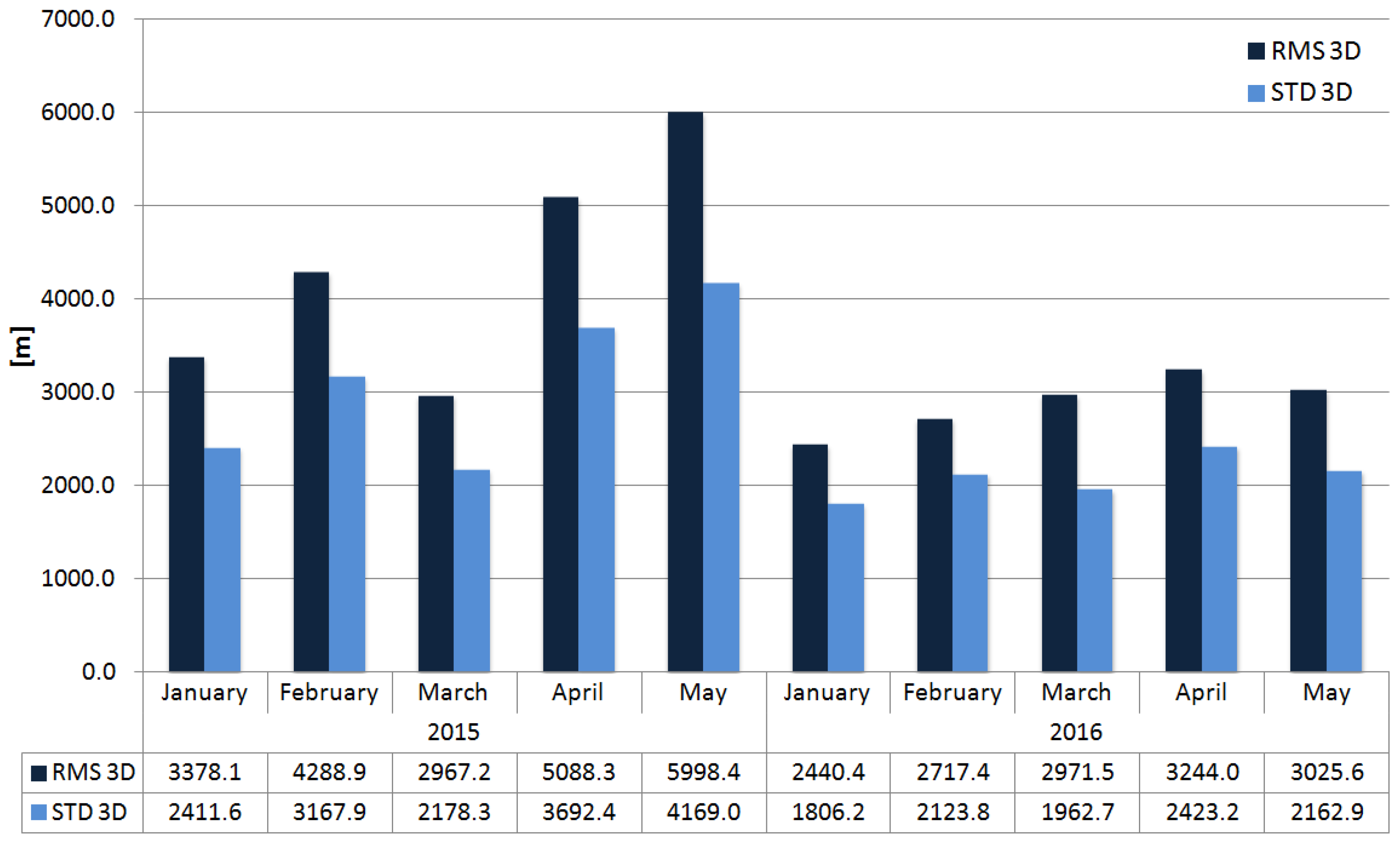
3.3. Quality of the Orbit Predictions—Research LEO Satellites
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GNSS | Global Navigation Satellite System |
| SLR | Satellite Laser Ranging |
| GPS | Global Positioning System |
| LEO | low-Earth orbit |
| ILRS | International Laser Ranging Service |
| LLR | Laser Retroreflector |
| CPF | Consolidated Prediction Format |
| CODE | Center for Orbit Determination in Europe |
| ECOM | empirical CODE orbit model |
| AIUB | Astronomical Institute University of Bern |
| ESOC | European Space Operations Centre |
| GAL | Galileo Control Centre |
| GFZ | German Research Centre for Geosciences |
| HTS | NASA GSFC SLR Mission Contractor, Greenbelt MD, USA |
| JAX | Japan Aerospace Exploration Agency |
| MCC | Mission Control Center, Russia |
| SGF | Space Geodesy Facility |
| QSS | Quazi-Zenith Satellite System Services |
| SSA | Space Situational Awareness |
| ESA | European Space Agency |
| MEO | Medium Earth orbit |
| GEO | Geostationary orbit |
| NOAA | National Oceanic and Atmospheric Administration |
| TIRV | Tuned Inter-Range Vector Range |
| MJD | modified Julian date |
| ITRF | International Terrestrial Reference Frame |
| SP3 | The Extended Standard Product 3 |
| ECEF | Earth-Centered Earth-Fixed |
| IERS | International Earth Rotation and Reference Systems Service |
| ASI | Italian Space Agency |
| UTC | Universal Time Coordinated |
| MGEX | Multi-GNSS-Experiment experiment |
| SRP | Solar radiation pressure |
| SRP Solar radiation pressure R | radial |
| S | along-track |
| W | cross-track |
| RMS | root mean square |
| STD | standard deviation |
| GLONASS | Globalnaja Nawigacionnaja Sputnikovaya Sistema |
| QZSS | Quasi–Zenith Satellite System |
References
- Zajdel, R.; Sośnica, K.; Bury, G. A new online service for the validation of multi-GNSS orbits using SLR. Remote Sens. 2017, 9, 1049. [Google Scholar] [CrossRef] [Green Version]
- Thaller, D.; Dach, R.; Seitz, M.; Beutler, G.; Mareyen, M.; Richter, B. Combination of GNSS and SLR observations using satellite co-locations. J. Geod. 2011, 85, 257–272. [Google Scholar] [CrossRef] [Green Version]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geod. 2018, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Bock, H.; Floberghagen, R. GOCE orbit predictions for SLR tracking. GPS Solut. 2011, 15, 129–137. [Google Scholar] [CrossRef]
- Urschl, C.; Beutler, G.; Gurtner, W.; Hugentobler, U.; Schaer, S. Contribution of SLR tracking data to GNSS orbit determination. Adv. Space Res. 2007, 39, 1515–1523. [Google Scholar] [CrossRef]
- Flohrer, C. Mutual validation of satellite-geodetic techniques and its impact on GNSS orbit modeling. In Geodätisch-Geophysikalische Arbeiten in der Schweiz; Schweizerische Geodätische Kommission: Zurich, Switzerland, 2008; Volume 75, ISBN 978-3-908440-19-2. [Google Scholar]
- Fritsche, M.; Sośnica, K.; Rodríguez-Solano, C.J.; Steigenberger, P.; Wang, K.; Dietrich, R.; Dach, R.; Hugentobler, U.; Rothacher, M. Homogeneous reprocessing of GPS, GLONASS and SLR observations. J. Geod. 2014, 88, 625–642. [Google Scholar] [CrossRef]
- Sośnica, K.; Thaller, D.; Dach, R.; Steigenberger, P.; Beutler, G.; Arnold, D.; Jäggi, A. Satellite laser ranging to GPS and GLONASS. J. Geod. 2015, 89, 725–743. [Google Scholar] [CrossRef] [Green Version]
- Sośnica, K.; Prange, L.; Kaźmierski, K.; Bury, G.; Drożdżewski, M.; Zajdel, R.; Hadaś, T. Validation of Galileo orbits using SLR with a focus on satellites launched into incorrect orbital planes. J. Geod. 2018, 92, 131–148. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Bauer, S.; Steinborn, J. Time bias service: Analysis and monitoring of satellite orbit prediction quality. J. Geod. 2019, 93, 2367–2377. [Google Scholar] [CrossRef]
- Wood, R. Improving orbit predictions. In Proceedings of the 11th International Laser Ranging Service Workshop, Deggendorf, Germany, 21–25 September 1998; Available online: https://cddis.nasa.gov/lw11/docs/imp_pred.pdf (accessed on 30 March 2021).
- Vetter, J.R. Fifty years of orbit determination. Johns Hopkins Apl Tech. Dig. 2007, 27, 239. [Google Scholar]
- Schutz, B.; Tapley, B.; Born, G.H. Statistical Orbit Determination; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Combrinck, L. Satellite Laser Ranging. In Sciences of Geodesy-I; Springer: Berlin/Heidelberg, Germany, 2010; pp. 301–338. [Google Scholar] [CrossRef]
- Seeber, G. Satellite Geodesy; (2nd Completely Rev. and Extended ed.); Walter de Gruyter: Berlin, Germany; New York, NY, USA, 2003. [Google Scholar]
- Gurtner, W. Near-real-time status exchange. In Proceedings of the 14th International Laser Ranging Service Workshop, San Fernando, Spain, 7–11 June 2004. [Google Scholar]
- Wood, R.; Gurtner, W. Herstmonceaux/Bern timebias service. In Proceedings of the 13th International Laser Ranging Service Workshop, Washington, DC, USA, 7–11 October 2002. [Google Scholar]
- Bobrinsky, N.; Del Monte, L. The space situational awareness program of the European Space Agency. Cosm. Res. 2010, 48, 392–398. [Google Scholar] [CrossRef]
- Peng, H.; Bai, X. Machine learning approach to improve satellite orbit prediction accuracy using publicly available data. J. Astronaut. Sci. 2020, 67, 762–793. [Google Scholar] [CrossRef]
- Lee, E.; Park, S.Y.; Hwang, H.; Choi, J.; Cho, S.; Jo, J.H. Initial orbit association and long-term orbit prediction for low earth space objects using optical tracking data. Acta Astronaut. 2020, 176, 247–261. [Google Scholar] [CrossRef]
- Ricklefs, R. Consolidated laser ranging prediction format: Field tests. In Proceedings of the 14th International Laser Ranging Service Workshop, San Fernando, Spain, 7–11 June 2004. [Google Scholar]
- Remondi, B.W. NGS Second Generation ASCII and Binary Orbit Formats and Associated Interpolation Studies. In Permanent Satellite Tracking Networks for Geodesy and Geodynamics, Proceedings of the International Association of Geodesy Symposia, Vienna, Austria, 11–24 August 1991; Mader, G.L., Ed.; Springer: Berlin/Heidelberg, Germany, 1993; Volume 109. [Google Scholar] [CrossRef]
- Hilla, S. The Extended Standard Product 3 Orbit Format. 2016. Available online: ftp://igs.org/pub/data/format/sp3d.pdf (accessed on 30 March 2021).
- Sośnica, K.; Jäggi, A.; Thaller, D.; Beutler, G.; Dach, R. Contribution of Starlette, Stella, and AJISAI to the SLR-derived global reference frame. J. Geod. 2014, 88, 789–804. [Google Scholar] [CrossRef] [Green Version]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical Note; Verlag des Bundesamts für Kar-tographie und Geodäsie: Frankfurt am Main, Germany, 2010; Volume 58.
- Dach, R.; Schaer, S.; Lutz, S.; Baumann, C.; Bock, H.; Orliac, E.; Prange, L.; Thaller, D.; Mervarta, L.; Jäggi, A.; et al. Center for Orbit Determination in Europe (CODE). In International GNSS Service: Technical Report 2013 (AIUB); Thaller, D., Mervarta, L., Jäggi, A., Eds.; IGS Central Bureau: Pasadena, CA, USA, 2013; pp. 21–34. [Google Scholar]
- Montenbruck, O.; Rizos, C.; Weber, R.; Weber, G.; Neilan, R.; Hugentobler, U. Getting a Grip on Mul-ti-GNSS—The International GNSS Service MGEX Campaign. GPS World 2013, 24, 44–49. [Google Scholar]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—The challenges of multi-GNSS data analysis. J. Geod. 2017, 91, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Bloßfeld, M.; Fritsche, M. Reducing the draconitic errors in GNSS geodetic products. J. Geod. 2014, 88, 559–574. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-stochastic orbit modeling techniques for low-Earth orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Bock, H.; Prange, L.; Meyer, U.; Beutler, G. GPS-only gravity field recovery with GOCE, CHAMP, and GRACE. Adv. Space Res. 2011, 47, 1020–1028. [Google Scholar] [CrossRef]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Brockmann, E.; Schaer, S.; Beutler, G.; Meindl, M.; Prange, L.; Bock, H.; Jäggi, A.; Ostini, L. GNSS processing at CODE: Status report. J. Geod. 2009, 83, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Dahle, C.; Arnold, D.; Bock, H.; Meyer, U.; Beutler, G.; van den Jssel, J. Swarm kine-matic orbits and gravity fields from 18 months of GPS data. Adv. Space Res. 2016, 57, 218–233. [Google Scholar] [CrossRef]
- Zhang, R.; Tu, R.; Zhang, P.; Liu, J.; Lu, X. Study of satellite shadow function model considering the overlapping parts of Earth shadow and Moon shadow and its application to GPS satellite orbit determination. Adv. Space Res. 2019, 63, 2912–2929. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Verdun, A. Ex-tended orbit modeling techniques at the CODE processing center of the International GPS Service for geodynamics (IGS): Theory and initial results. Manuscr. Geod. 1995, 19, 367–384. [Google Scholar]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef] [Green Version]
- Buchert, S.; Zangerl, F.; Sust, M.; André, M.; Eriksson, A.; Wahlund, J.E.; Opgenoorth, H. SWARM observations of equatorial electron densities and topside GPS track losses. Geophys. Res. Lett. 2015, 42, 2088–2092. [Google Scholar] [CrossRef]
- Sust, M.; Zangerl, F.; Montenbruck, O.; Buchert, S.; Garcia-Rodriguez, A. Spaceborne GNSS-receiving system performance prediction and validation. In Proceedings of the NAVITEC 2014, ESA Workshop on Satellite Navigation Technologies and GNSS Signals and Signal Processing 2014, Noordwijk, The Netherlands, 3 December 2014; pp. 3–5. Available online: http://www.cluster.irfu.se/scb/navitec_2014_sus_et_al_final_for_web.pdf (accessed on 30 March 2021).



| Agency | Abbreviations in CPF Files |
|---|---|
| Center for Orbit Determination in Europe (CODE), Astronomical Institute University of Bern (AIUB) | COD |
| European Space Operations Centre (ESOC) | ESA |
| Galileo Control Centre, DLR, Germany | GAL |
| GFZ German Research Centre for Geosciences | GFZ |
| NASA GSFC SLR Mission Contractor, Greenbelt MD, USA | HTS |
| Japan Aerospace Exploration Agency (JAXA), Japan | JAX |
| Mission Control Center, Russia | MCC |
| NERC Space Geodesy Facility (NSGF), formerly RGO, United Kingdom | NER/SGF |
| Quazi-Zenith Satellite System Services/NEC Corporation | QSS |
| Shanghai, China | SHA |
| Satellites | Total 1 | In Analysis | |||
|---|---|---|---|---|---|
| In Analysis | Equivalent | Analyzed | Equivalent | ||
| Geodesy | Etalon-1 | Etalon-2 | 10 | 6 | 7 |
| LEO | Grace A Swarm C | Grace B Swarm A | 28 | 3 | 5 |
| Navigation | Galileo101 Galileo201 | Galileo102, Galileo103, Galileo104, Galileo203-Galileo222 Galileo202 | 26 | 2 | 26 |
| Glonass133 | All other | 25 | 1 | 25 | |
| BeiDou-i3 BeiDou-M3 | I5, i6b, is1, is2 m1, m2, m9, m10, ms1,ms2 | 14 | 1 1 | 5 7 | |
| QZS1 | QZS2, QZS3, QZS4 | 4 | 1 | 4 | |
| GPS | - | 2 | 0 | 0 | |
| Lunar | - | - | 5 | 0 | - |
| Sum | 120 | 15 | 79 | ||
| Sum of all except the retroreflectors on the Moon and the GPS satellites | 113 | ||||
| LAGEOS-1 | LAGEOS-2 | Etalon-1 | Larets | Starlette | Stella | |
|---|---|---|---|---|---|---|
| Type of orbit | MEO | MEO | MEO | LEO | LEO | LEO |
| Inclination [deg] | 109.89 | 52.63 | 64.92 | 97.78 | 49.84 | 98.30 |
| Draconitic year [days] | 561 | 222 | 353.4 | 186.1 | 72.8 | 185.4 |
| Interval [days] | 56 | 22 | 35 | 19 | 7 | 18 |
| Number of years | 1(2018) | 1(2018) | 1(2018) | 1(2015) | 1(2014) | 1(2015) |
| LAGEOS-1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 | |||||||||||||||
| January | Februrary–March | April | June | August | |||||||||||
| hts | jax | sgf | hts | jax | sgf | hts | jax | sgf | hts | jax | sgf | hts | jax | sgf | |
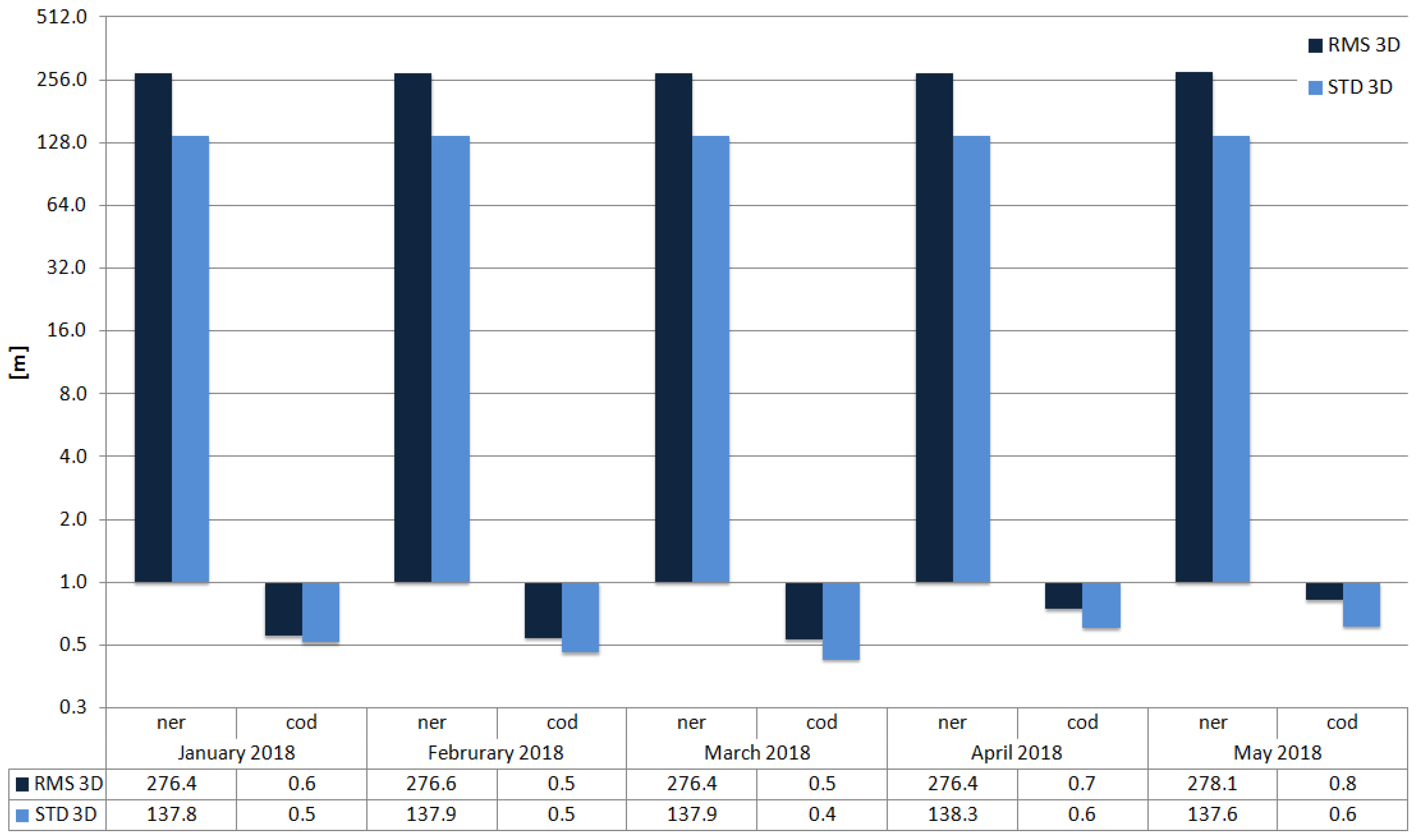
| RMS 3D | 17.6 | 1.8 | 0.3 | 10.7 | 1.4 | 0.4 | 88.2 | 1.2 | 0.4 | 24.4 | 0.8 | 0.4 | 20.4 | 2.4 | 0.3 |
| STD 3D | 12.4 | 0.9 | 0.3 | 8.0 | 0.7 | 0.3 | 56.5 | 0.6 | 0.3 | 17.2 | 0.4 | 0.3 | 16.0 | 1.2 | 0.2 |
| BeiDou-i3 | BeiDou-M3 | Galileo201 | Galileo101 | GLONASS133 | QZSS-1 | |
|---|---|---|---|---|---|---|
| Type of orbit | IGSO | MEO | MEO | MEO | MEO | GSO 1 |
| Inclination [deg] | 54.42 | 54.83 | 54.94 | 50.16 | 64.92 | 40.83 |
| Draconitic year [days] | 362.3 | 354.6 | 351.6 | 355.6 | 353.4 | 361.4 |
| Interval [days] | 36 | 35 | 36 | 36 | 36 | 36 |
| Number of years | 1(2018) | 1(2018) | 1(2018) | 1(2018) | 1(2018) | 1(2018) |
| GRACE-A | SWARM-B | SWARM-C | |
|---|---|---|---|
| Type of orbit | LEO | LEO | LEO |
| Inclination [deg] | 88.99 | 87.76 | 87.37 |
| Draconitic year [days] | 320.6 | 336 | 336 |
| Interval [days] | 32 | 34(32) | 34(32) |
| Number of years | 2(2009,2014) | 2(2015,2016) | 2(2015,2016) |
| Satellites | Prediction Centers | RMS 3D [m] | STD 3D [m] |
|---|---|---|---|
| Etalon1 | SGF (or JAX) | 1.1 | 0.8 |
| LAGEOS-1 | 0.4 | 0.3 | |
| LAGEOS-2 | 0.5 | 0.4 | |
| Larets | MCC (or SGF) | 95.3 | 60.4 |
| Starlette | SGF | 6.2 | 4.0 |
| Stella | 25.7 | 17.6 | |
| Galileo103 | ESA/COD | 2.0 | 0.9 |
| Galileo201 | 1.2 | 0.9 | |
| GLONASS133 | COD | 0.6 | 0.5 |
| BeiDou-i3 | SHA 1 | 64.6 | 53.3 |
| BeiDou-M3 | 71.3 | 48.0 | |
| QZS-1 | QSS 1 | 110.0 | 100.1 |
| GRACE-A | GFZ 1 | 832.8 2 | 229.8 2 |
| Swarm-B | ESA 1 | 1109.9 2 | 813.2 2 |
| Swarm-C | 2879.8 2 | 2095.7 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najder, J.; Sośnica, K. Quality of Orbit Predictions for Satellites Tracked by SLR Stations. Remote Sens. 2021, 13, 1377. https://doi.org/10.3390/rs13071377
Najder J, Sośnica K. Quality of Orbit Predictions for Satellites Tracked by SLR Stations. Remote Sensing. 2021; 13(7):1377. https://doi.org/10.3390/rs13071377
Chicago/Turabian StyleNajder, Joanna, and Krzysztof Sośnica. 2021. "Quality of Orbit Predictions for Satellites Tracked by SLR Stations" Remote Sensing 13, no. 7: 1377. https://doi.org/10.3390/rs13071377
APA StyleNajder, J., & Sośnica, K. (2021). Quality of Orbit Predictions for Satellites Tracked by SLR Stations. Remote Sensing, 13(7), 1377. https://doi.org/10.3390/rs13071377