A Novel Strategy to Reconstruct NDVI Time-Series with High Temporal Resolution from MODIS Multi-Temporal Composite Products
Abstract
:1. Introduction
2. Study Area and Data Requirement
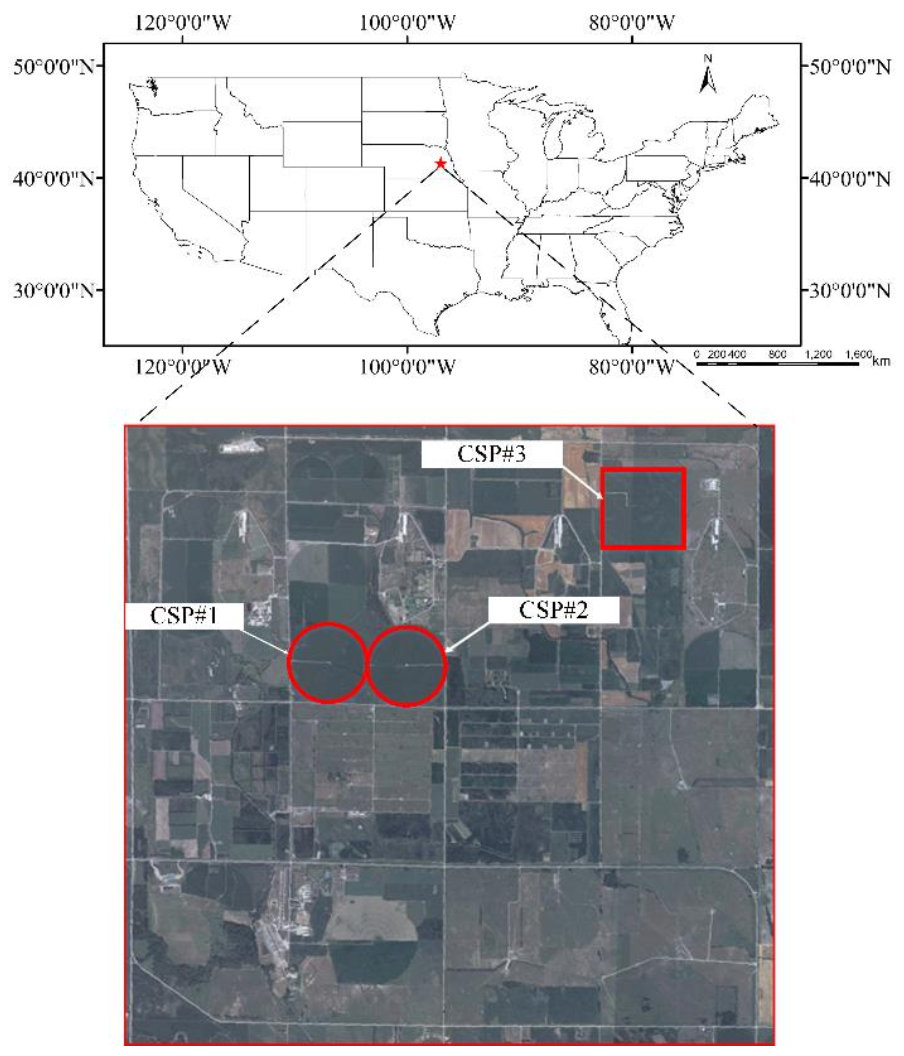
2.1. Study Area
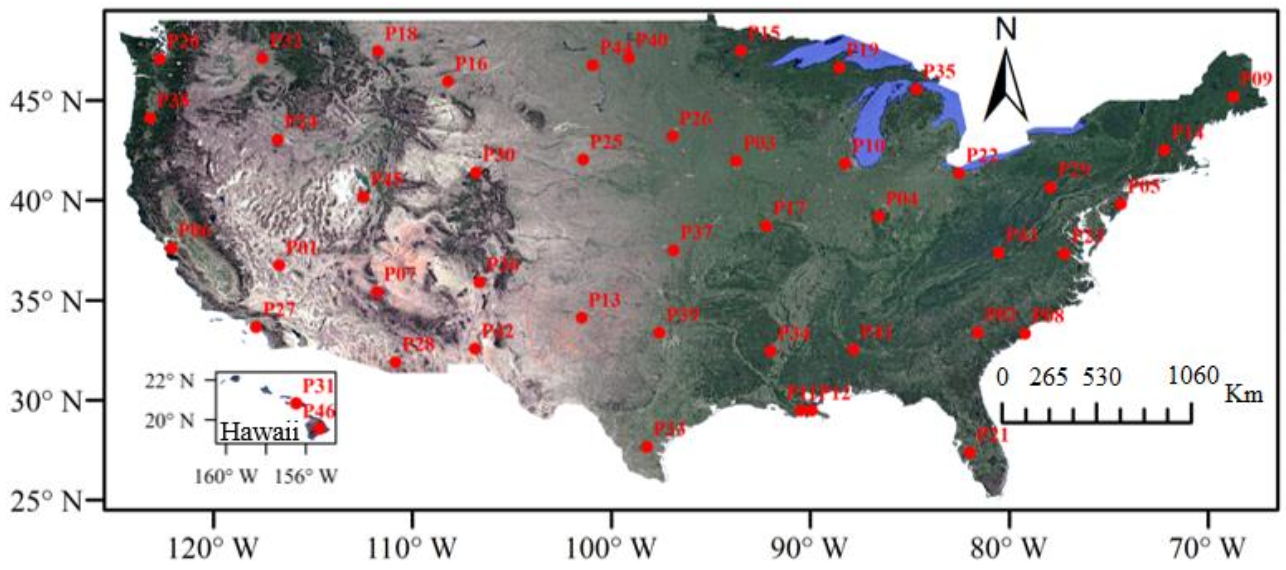
2.2. Data Requirement
2.2.1. Multi-Temporal NDVI Data
2.2.2. Cloud Mask Product
3. Methodology
3.1. HANTS
3.2. SG Filtering
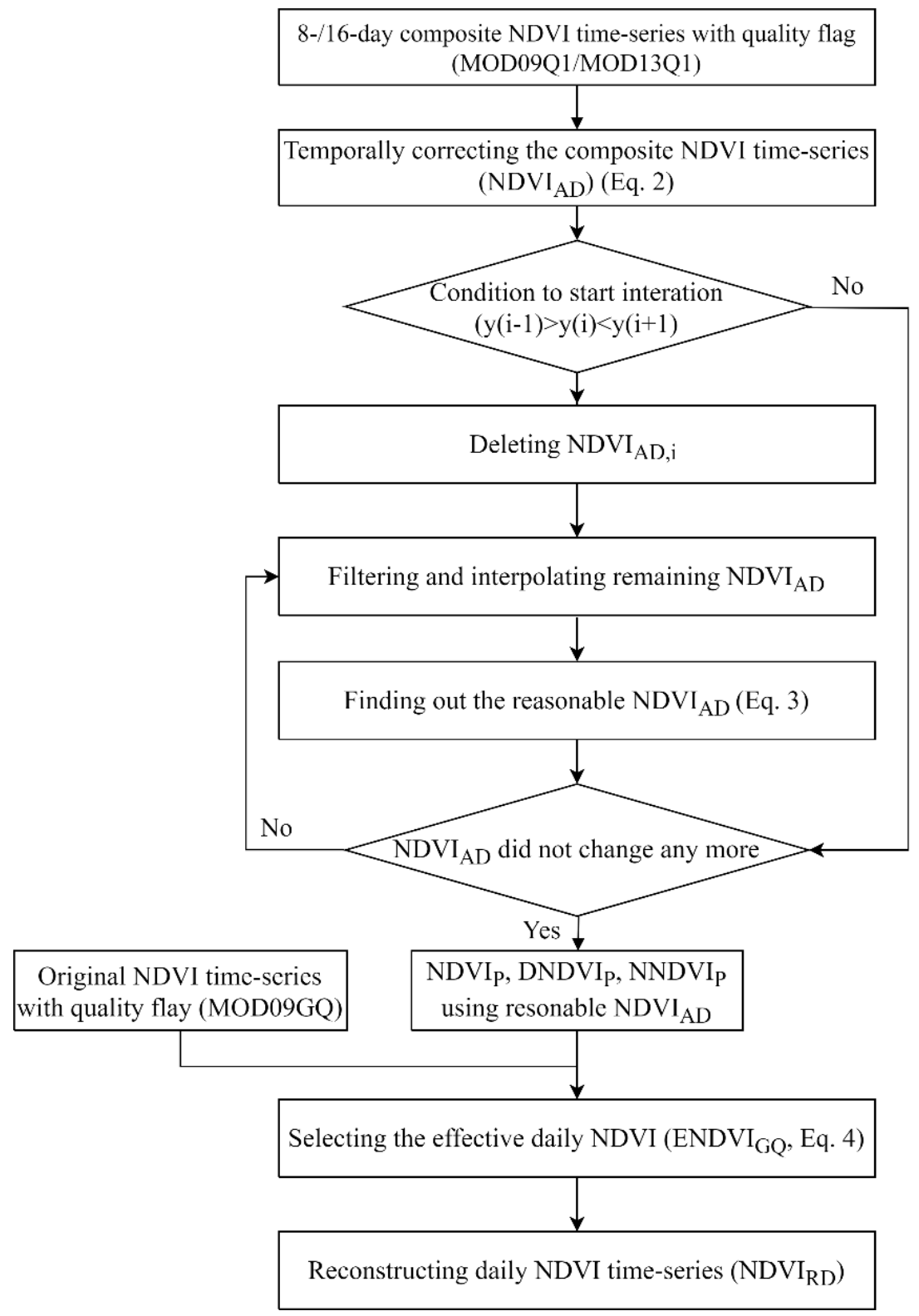
3.3. DAVIR-MUTCOP Method
3.4. Evaluation of the Method’s Performance
4. Results
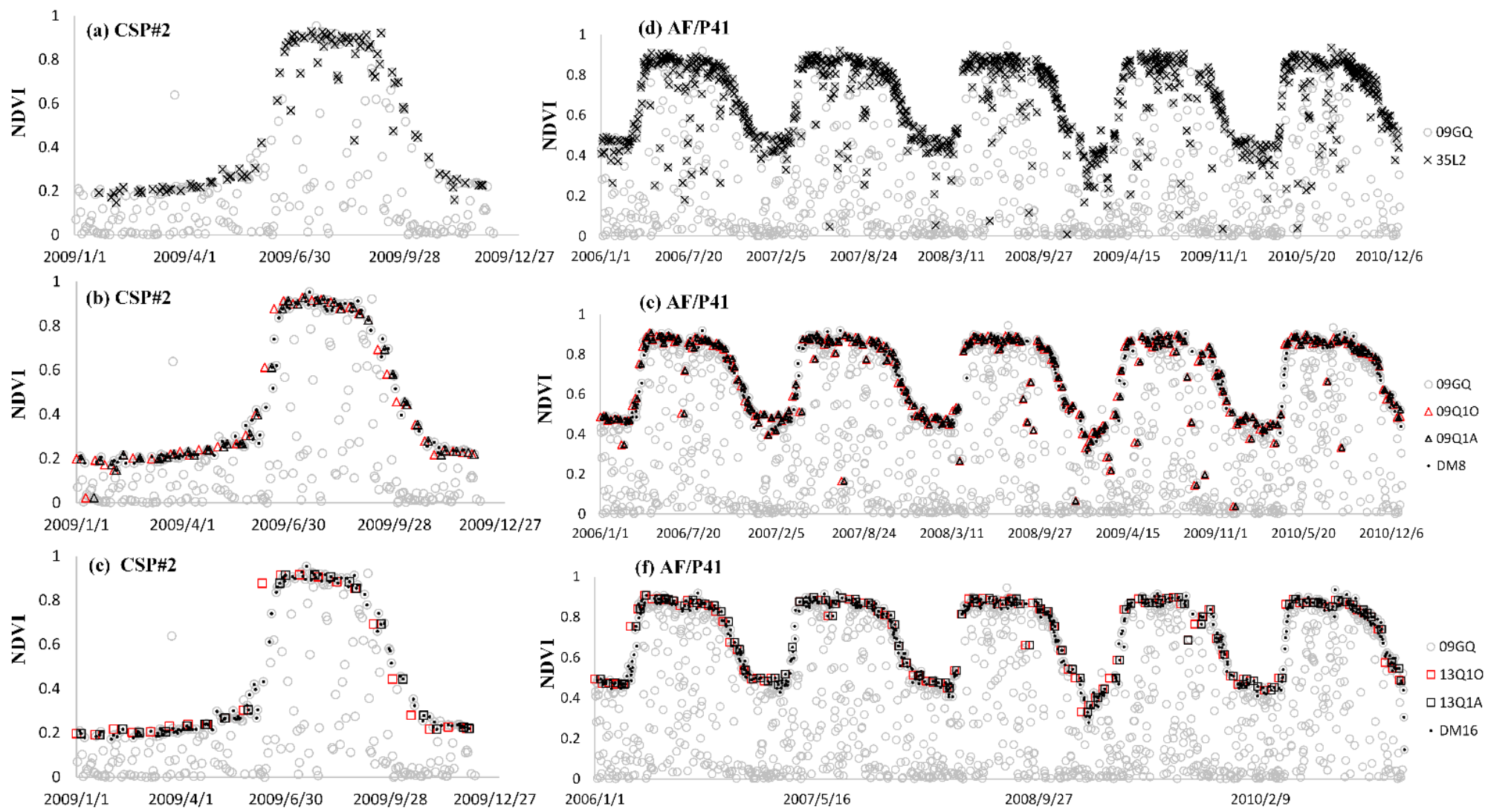
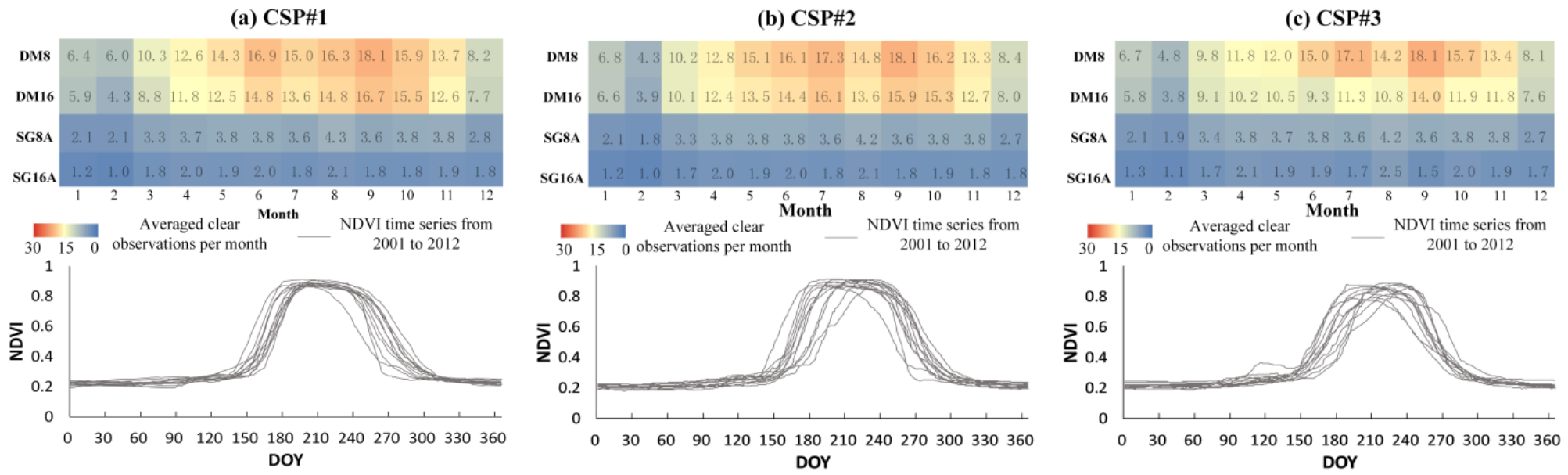
4.1. The MODIS Products
4.2. The Temporal Resolution of Different Reconstruction Stratiges
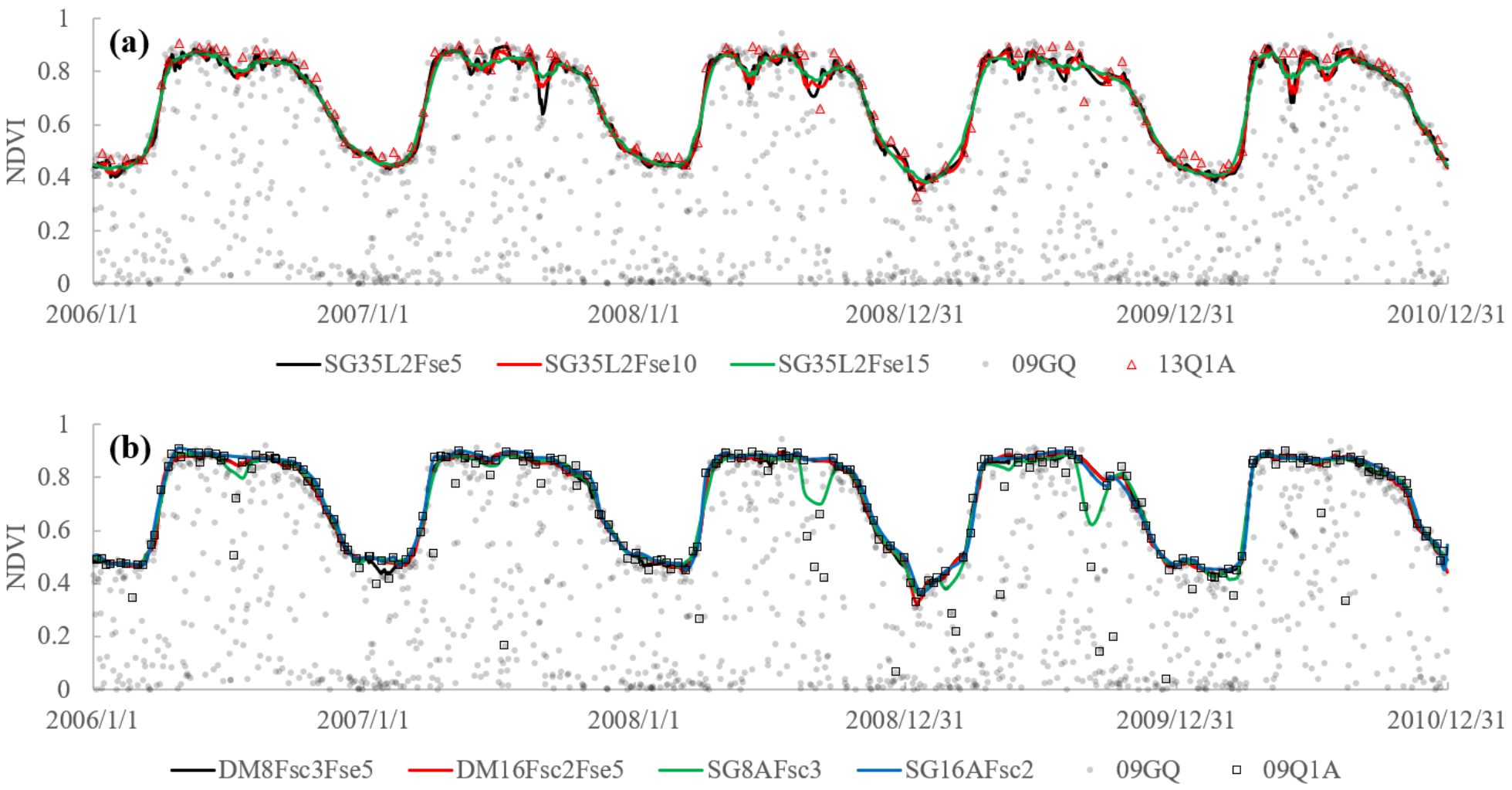
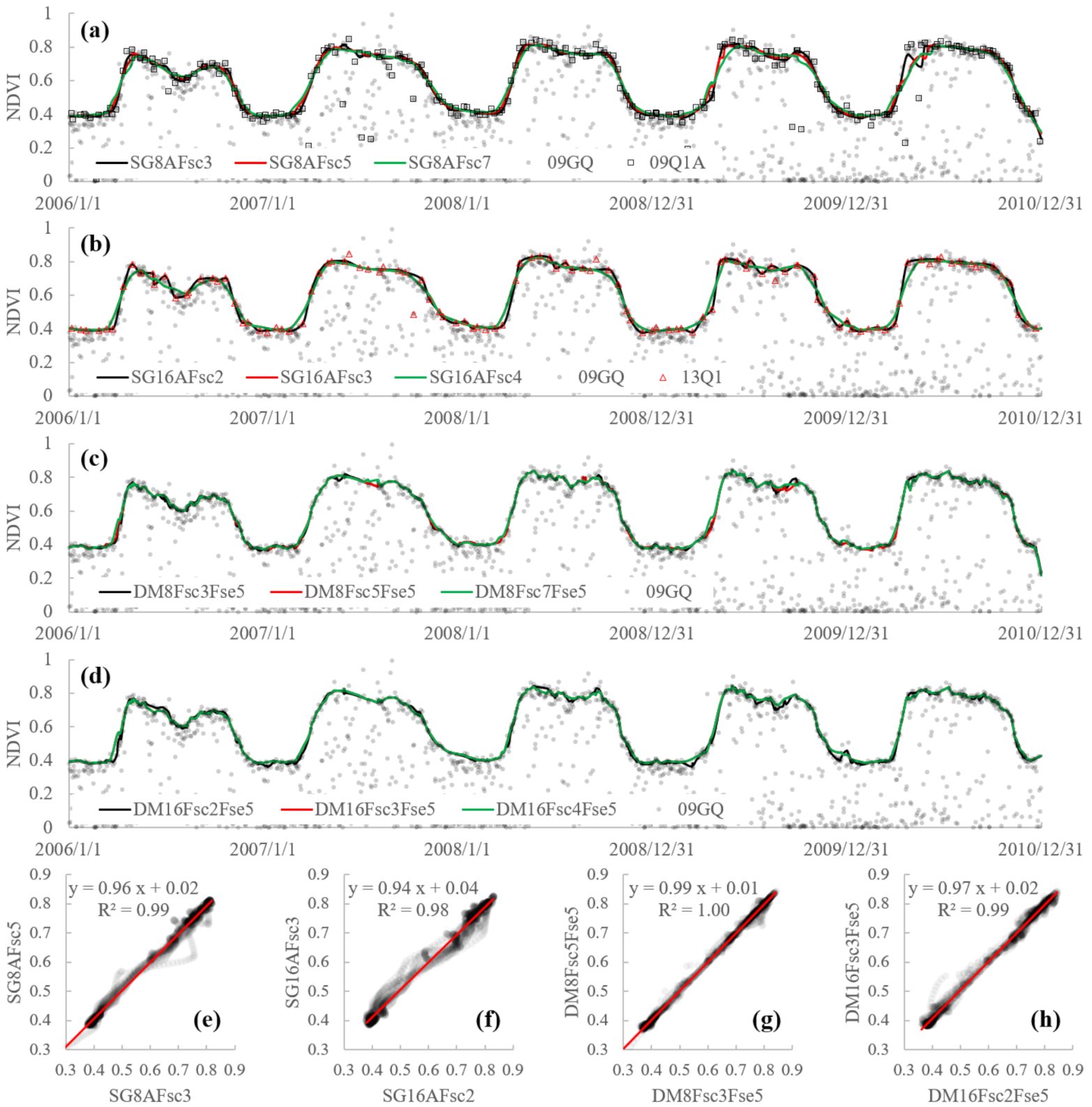
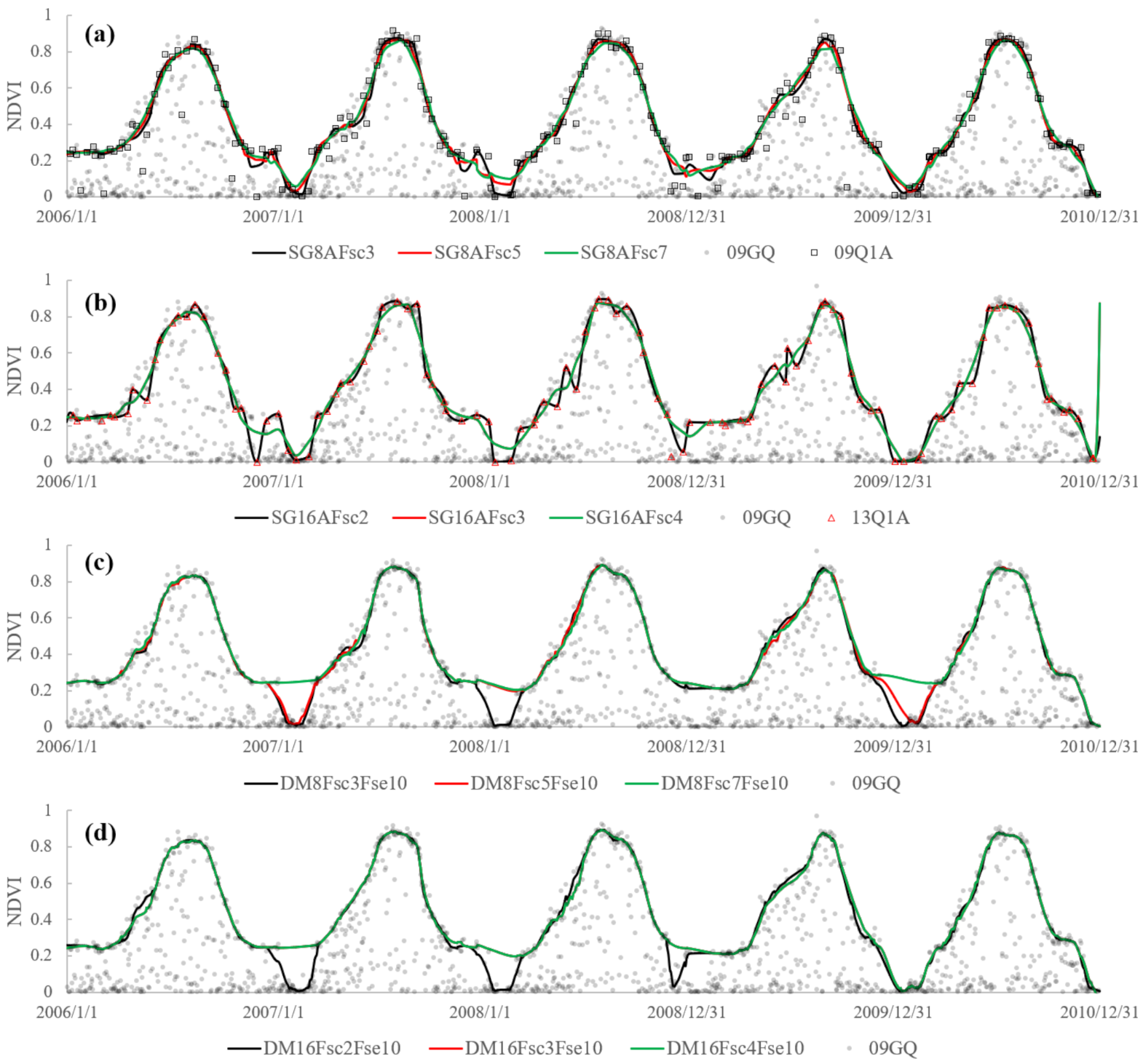
4.3. The Comparison of the NDVI Time-Series Curves Reconstructed by Different Stratiges
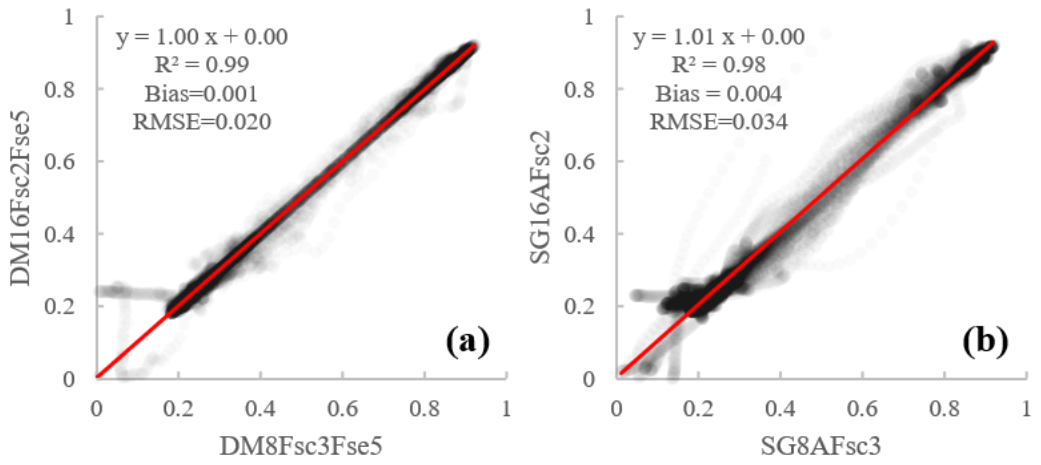
4.4. The Robustness of the Different Reconstruction Stratiges
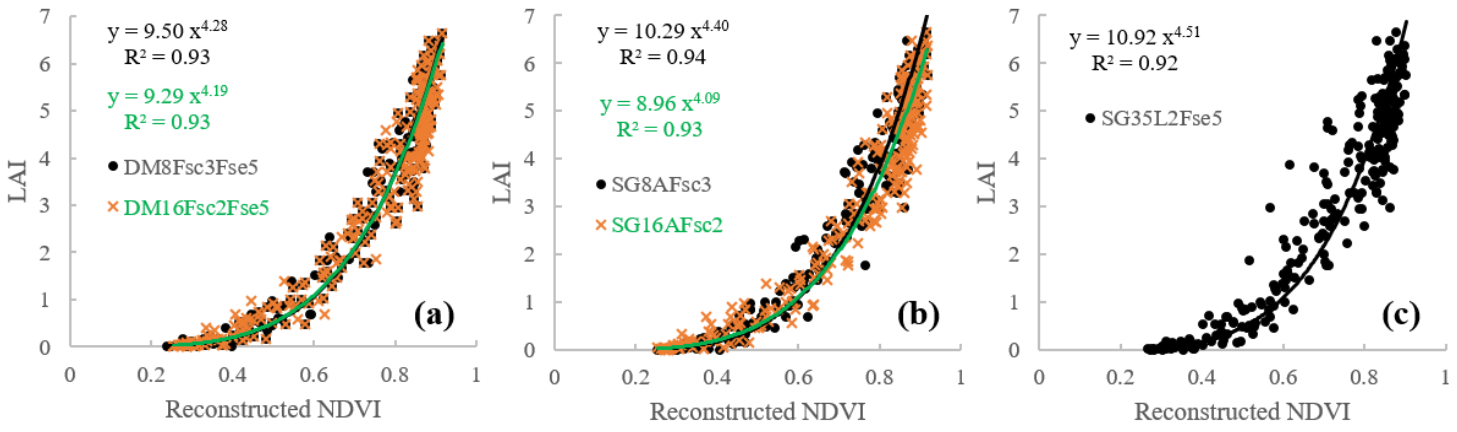
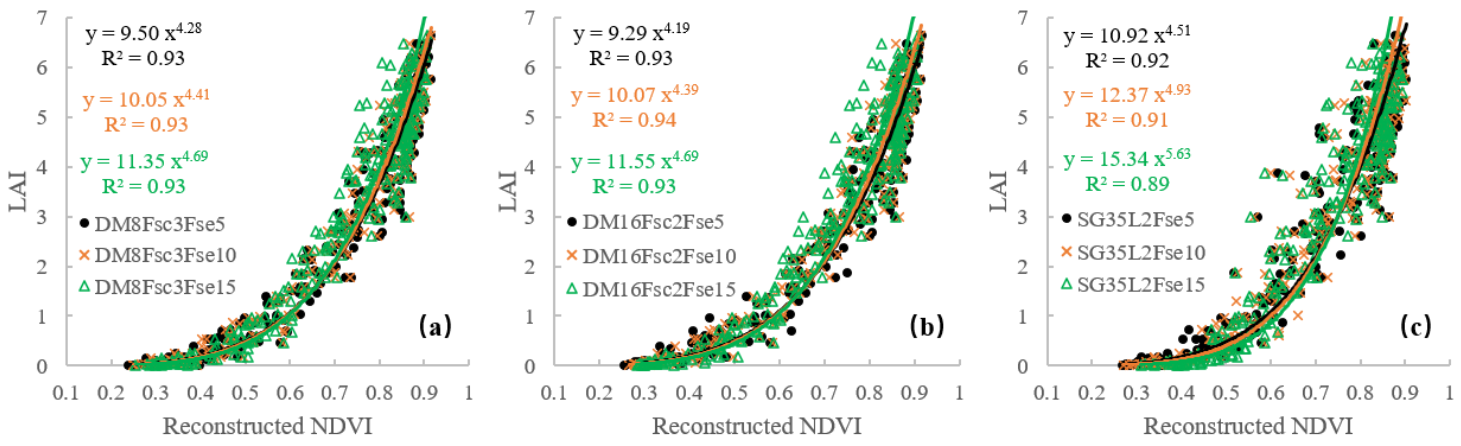
4.4.1. The Relationship between Ground-Observed LAI and Reconstructed NDVI
4.4.2. The Sensitiveness of the Reconstructed NDVI to Fsc
4.4.3. The Sensitiveness of the Reconstructed NDVI to Fse
5. Discussion
5.1. The Choice of Temporal Compositing Window
5.2. The Choice of the Filtering/Fitting Method and Parameters
5.3. The Potential Application of the DAVIR-MUTCOP Method in the Future
5.4. The Limitation of the DAVIR-MUTCOP Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Cai, Z.; Jönsson, P.; Jin, H.; Eklundh, L. Performance of Smoothing Methods for Reconstructing NDVI Time-Series and Estimating Vegetation Phenology from MODIS Data. Remote Sens. Basel 2017, 9, 1271. [Google Scholar] [CrossRef] [Green Version]
- Hird, J.N.; Mcdermid, G.J. Noise reduction of NDVI time series: An empirical comparison of selected techniques. Remote Sens. Environ. 2009, 113, 248–258. [Google Scholar] [CrossRef]
- De Beurs, K.M.; Townsend, P.A. Estimating the effect of gypsy moth defoliation using MODIS. Remote Sens. Environ. 2008, 112, 3983–3990. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. MODIS time-series imagery for forest disturbance detection and quantification of patch size effects. Remote Sens. Environ. 2005, 99, 462–470. [Google Scholar] [CrossRef]
- Nagai, S.; Saitoh, T.M.; Suzuki, R.; Nasahara, K.N.; Lee, W.; Son, Y.; Muraoka, H. The necessity and availability of noise-free daily satellite-observed NDVI during rapid phenological changes in terrestrial ecosystems in East Asia. For. Sci. Technol. 2011, 7, 174–183. [Google Scholar] [CrossRef]
- Narasimhan, R.; Stow, D. Daily MODIS products for analyzing early season vegetation dynamics across the North Slope of Alaska. Remote Sens. Environ. 2010, 114, 1251–1262. [Google Scholar] [CrossRef]
- Zeng, L.; Wardlow, B.D.; Wang, R.; Shan, J.; Tadesse, T.; Hayes, M.J.; Li, D. A hybrid approach for detecting corn and soybean phenology with time-series MODIS data. Remote Sens. Environ. 2016, 181, 237–250. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Tan, B.; Morisette, J.T.; Wolfe, R.E.; Gao, F.; Ederer, G.A.; Nightingale, J.; Pedelty, J.A. An Enhanced TIMESAT Algorithm for Estimating Vegetation Phenology Metrics from MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 361–371. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring Vegetation Phenology Using MODIS Time-Series Data. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Spruce, J.P.; Sader, S.; Ryan, R.E.; Smoot, J.; Kuper, P.; Ross, K.; Prados, D.; Russell, J.; Gasser, G.; McKellip, R.; et al. Assessment of MODIS NDVI time series data products for detecting forest defoliation by gypsy moth outbreaks. Remote Sens. Environ. 2011, 115, 427–437. [Google Scholar] [CrossRef]
- Hansen, M.C.; DeFries, R.S.; Townshend, J.R.G.; Sohlberg, R.; Dimiceli, C.; Carroll, M. Towards an operational MODIS continuous field of percent tree cover algorithm: Examples using AVHRR and MODIS data. Remote Sens. Environ. 2002, 83, 303–319. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Tian, F.; Fensholt, R.; Verbesselt, J.; Grogan, K.; Horion, S.; Wang, Y. Evaluating temporal consistency of long-term global NDVI datasets for trend analysis. Remote Sens. Environ. 2015, 163, 326–340. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Murakami, K.; Nagai, S. Evaluation of Sub-Pixel Cloud Noises on MODIS Daily Spectral Indices Based on in situ Measurements. Remote Sens. Basel 2011, 3, 1644–1662. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Jia, L.; Menenti, M.; Gorte, B. On the performance of remote sensing time series reconstruction methods—A spatial comparison. Remote Sens. Environ. 2016, 187, 367–384. [Google Scholar] [CrossRef]
- Nagai, S.; Saigusa, N.; Muraoka, H.; Nasahara, K.N. What makes the satellite-based EVI–GPP relationship unclear in a deciduous broad-leaved forest? Ecol. Res. 2010, 25, 359–365. [Google Scholar] [CrossRef]
- Sakamoto, T.; Yokozawa, M.; Toritani, H.; Shibayama, M.; Ishitsuka, N.; Ohno, H. A crop phenology detection method using time-series MODIS data. Remote Sens. Environ. 2005, 96, 366–374. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Sakamoto, T. Remote estimation of gross primary productivity in crops using MODIS 250m data. Remote Sens. Environ. 2013, 128, 186–196. [Google Scholar] [CrossRef]
- Housman, I.; Chastain, R.; Finco, M. An Evaluation of Forest Health Insect and Disease Survey Data and Satellite-Based Remote Sensing Forest Change Detection Methods: Case Studies in the United States. Remote Sens. Basel 2018, 10, 1184. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, W.J.; Huete, A.R.; Laing, T.W. MODIS vegetation index compositing approach: A prototype with AVHRR data. Remote Sens. Environ. 1999, 69, 264–280. [Google Scholar] [CrossRef]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance User’s Guide, Collection 6th ed. 2015. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD09_UserGuide_v1.4.pdf (accessed on 20 March 2021).
- Gao, X.; Huete, A.R.; Didan, K. Multisensor comparisons and validation of MODIS vegetation indices at the semiarid Jornada experimental range. IEEE Trans. Geosci. Remote. 2003, 41, 2368–2381. [Google Scholar]
- Miura, T.; Didan, K.; Huete, A.R.; Rodriguez, E.P. A performance evaluation of the MODIS vegetation index compositing algorithm. In Proceedings of the IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; pp. 1812–1814. [Google Scholar]
- Miura, T.; Huete, A.R.; Didan, K.; van Leeuwen, W.J.; Yoshioka, H. An assessment of the MODIS vegetation index compositing algorithm using quality assurance flags and sun/view angles. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 24–28 July 2000; pp. 545–547. [Google Scholar]
- Wessels, K.J.; Bachoo, A.; Archibald, S. Influence of composite period and date of observation on phenological metrics extracted from MODIS data. In Proceedings of the 33rd International Symposium on Remote Sensing of Environment: Sustaining the Millennium Development Goals, Stresa, Lago Magglore, Italy, 4–8 May 2009. [Google Scholar]
- McKellip, R.; Ryan, R.E.; Blonski, S.; Prados, D. Crop Surveillance Demonstration Using a Near-Daily MODIS Derived Vegetation Index Time Series. In Proceedings of the Third International Workshop on the Analysis of Multitemporal Remote Sensing Images, Biloxi, MS, USA, 16 May 2005; NASA Stennis Space Center: Biloxi, MS, USA. [Google Scholar]
- Guindin-Garcia, N.; Gitelson, A.A.; Arkebauer, T.J.; Shanahan, J.; Weiss, A. An evaluation of MODIS 8-and 16-day composite products for monitoring maize green leaf area index. Agric. For. Meteorol. 2012, 161, 15–25. [Google Scholar] [CrossRef] [Green Version]
- Colditz, R.R.; Ressl, R.A. The impact of the day of observation of image composites on adequate time series generation. In Proceedings of the SPIE Earth Resources and Environmental Remote Sensing/GIS Applications IV, Dresden, Germany, 24 October 2013. [Google Scholar]
- Testa, S.; Mondino EC, B.; Pedroli, C. Correcting MODIS 16-day composite NDVI time-series with actual acquisition dates. Eur. J. Remote Sens. 2014, 47, 285–305. [Google Scholar] [CrossRef]
- Thayn, J.B.; Price, K.P. Julian dates and introduced temporal error in remote sensing vegetation phenology studies. Int. J. Remote Sens. 2008, 29, 6045–6049. [Google Scholar] [CrossRef]
- Gatis, N.; Anderson, K.; Clement, E.G.; Luscombe, D.J.; Hartley, I.P.; Smith, D.; Brazier, R.E. Evaluating MODIS vegetation products using digital images for quantifying local peatland CO2 gas fluxes. Remote Sens. Ecol. Conserv. 2017, 3, 217–231. [Google Scholar] [CrossRef]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green leaf phenology at Landsat resolution: Scaling from the field to the satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, K. Misestimation of Growing Season Length Due to Inaccurate Construction of Satellite Vegetation Index Time Series. IEEE Geosci. Remote. Sens. Lett. 2019, 16, 1185–1189. [Google Scholar] [CrossRef]
- Ahl, D.E.; Gower, S.T.; Burrows, S.N.; Shabanov, N.V.; Myneni, R.B.; Knyazikhin, Y. Monitoring spring canopy phenology of a deciduous broadleaf forest using MODIS. Remote Sens. Environ. 2006, 104, 88–95. [Google Scholar] [CrossRef] [Green Version]
- Testa, S.; Soudani, K.; Boschetti, L.; Borgogno Mondino, E. MODIS-derived EVI, NDVI and WDRVI time series to estimate phenological metrics in French deciduous forests. Int. J. Appl. Earth Obs. 2018, 64, 132–144. [Google Scholar] [CrossRef]
- Xu, X.; Conrad, C.; Doktor, D. Optimising Phenological Metrics Extraction for Different Crop Types in Germany Using the Moderate Resolution Imaging Spectrometer (MODIS). Remote Sens. Basel 2017, 9, 254. [Google Scholar] [CrossRef] [Green Version]
- Qiu, B.; Feng, M.; Tang, Z. A simple smoother based on continuous wavelet transform: Comparative evaluation based on the fidelity, smoothness and efficiency in phenological estimation. Int. J. Appl. Earth Obs. 2016, 47, 91–101. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Pan, Z.; Hu, Y.; Cao, B. Construction of smooth daily remote sensing time series data: A higher spatiotemporal resolution perspective. Open Geospat. Data Softw. Stand. 2017, 2, 25. [Google Scholar] [CrossRef] [Green Version]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef] [Green Version]
- Van Leeuwen, W.J.; Huete, A.R.; Laing, T.W.; Didan, K. Vegetation change monitoring with spectral indices: The importance of view and sun angle standardized data. In Proceedings of the SPIE The International Society for Optical Engineering, Florence, Italy, 17 December 1999. [Google Scholar]
- Bhandari, S.; Phinn, S.; Gill, T. Assessing viewing and illumination geometry effects on the MODIS vegetation index (MOD13Q1) time series: Implications for monitoring phenology and disturbances in forest communities in Queensland, Australia. Int. J. Remote Sens. 2011, 32, 7513–7538. [Google Scholar] [CrossRef]
- Tittebrand, A.; Spank, U.; Bernhofer, C.H. Comparison of satellite-and ground-based NDVI above different land-use types. Theor. Appl. Climatol. 2009, 98, 171–186. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; Thackrah, G.; Quaife, T.; Barnsley, M. Comparison of MODIS broadband albedo over an agricultural site with ground measurements and values derived from Earth observation data at a range of spatial scales. Int. J. Remote Sens. 2004, 25, 5297–5317. [Google Scholar] [CrossRef]
- Gu, J.; Li, X.; Huang, C.; Okin, G.S. A simplified data assimilation method for reconstructing time-series MODIS NDVI data. Adv. Space Res. 2009, 44, 501–509. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, H.; Lu, N.; Yao, T.; Liang, T. Toward advanced daily cloud-free snow cover and snow water equivalent products from Terra–Aqua MODIS and Aqua AMSR-E measurements. J. Hydrol. 2010, 385, 23–35. [Google Scholar] [CrossRef]
- Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
- Luo, Y.; Trishchenko, A.P.; Khlopenkov, K.V. Developing clear-sky, cloud and cloud shadow mask for producing clear-sky composites at 250-m spatial resolution for the seven MODIS land bands over Canada and North America. Remote Sens. Environ. 2008, 112, 4167–4185. [Google Scholar] [CrossRef]
- Wilson, A.M.; Parmentier, B.; Jetz, W. Systematic land cover bias in Collection 5 MODIS cloud mask and derived products—A global overview. Remote Sens. Environ. 2014, 141, 149–154. [Google Scholar] [CrossRef]
- Wang, T.; Fetzer, E.J.; Wong, S.; Kahn, B.H.; Yue, Q. Validation of MODIS cloud mask and multilayer flag using CloudSat-CALIPSO cloud profiles and a cross-reference of their cloud classifications. J. Geophys. Res. Atmos. 2016, 121, 611–620. [Google Scholar] [CrossRef]
- Sun, L.; Gao, F.; Anderson, M.C.; Kustas, W.P.; Thenkabail, P.S. Remote Sensing Daily Mapping of 30 m LAI and NDVI for Grape Yield Prediction in California Vineyards. Remote Sens. Basel 2017, 9, 317. [Google Scholar] [CrossRef] [Green Version]
- Rumney, G.R. North America, climate of. In Climatology. Encyclopedia of Earth Science; Springer: Boston, MA, USA, 1987; pp. 612–624. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Xin, Q.; Li, J.; Li, Z.; Li, Y.; Zhou, X. Evaluations and comparisons of rule-based and machine-learning-based methods to retrieve satellite-based vegetation phenology using MODIS and USA National Phenology Network data. Int. J. Appl. Earth Obs. 2020, 93, 102189. [Google Scholar] [CrossRef]
- Eklundh, L.; Jönsson, P. TIMESAT 3.3 with seasonal trend decomposition and parallel processing Software Manual. 2017. Available online: http://web.nateko.lu.se/timesat/docs/TIMESAT33_SoftwareManual.pdf (accessed on 20 March 2021).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Wardlow, B.D.; Hu, S.; Zhang, X.; Zhou, G.; Peng, G.; Xiang, D.; Wang, R.; Meng, R.; Wu, W. A Novel Strategy to Reconstruct NDVI Time-Series with High Temporal Resolution from MODIS Multi-Temporal Composite Products. Remote Sens. 2021, 13, 1397. https://doi.org/10.3390/rs13071397
Zeng L, Wardlow BD, Hu S, Zhang X, Zhou G, Peng G, Xiang D, Wang R, Meng R, Wu W. A Novel Strategy to Reconstruct NDVI Time-Series with High Temporal Resolution from MODIS Multi-Temporal Composite Products. Remote Sensing. 2021; 13(7):1397. https://doi.org/10.3390/rs13071397
Chicago/Turabian StyleZeng, Linglin, Brian D. Wardlow, Shun Hu, Xiang Zhang, Guoqing Zhou, Guozhang Peng, Daxiang Xiang, Rui Wang, Ran Meng, and Weixiong Wu. 2021. "A Novel Strategy to Reconstruct NDVI Time-Series with High Temporal Resolution from MODIS Multi-Temporal Composite Products" Remote Sensing 13, no. 7: 1397. https://doi.org/10.3390/rs13071397
APA StyleZeng, L., Wardlow, B. D., Hu, S., Zhang, X., Zhou, G., Peng, G., Xiang, D., Wang, R., Meng, R., & Wu, W. (2021). A Novel Strategy to Reconstruct NDVI Time-Series with High Temporal Resolution from MODIS Multi-Temporal Composite Products. Remote Sensing, 13(7), 1397. https://doi.org/10.3390/rs13071397









