Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source and Pre-Processing
2.3. Overall Workflow
2.4. LST Retrieval
2.5. Land Cover Classification
2.6. Landscape Metrics-Based Analysis
2.7. Statistical Analysis
3. Results
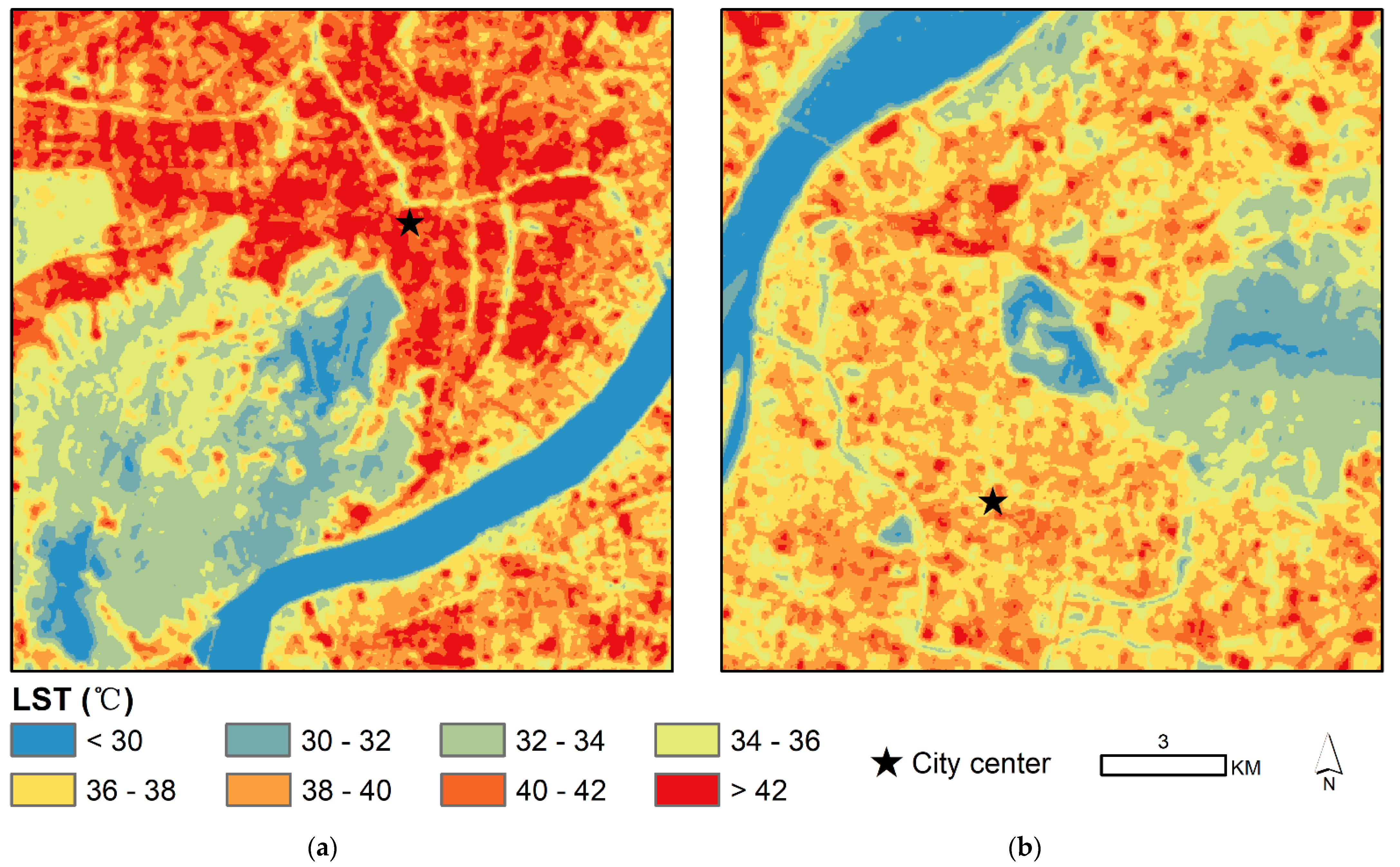
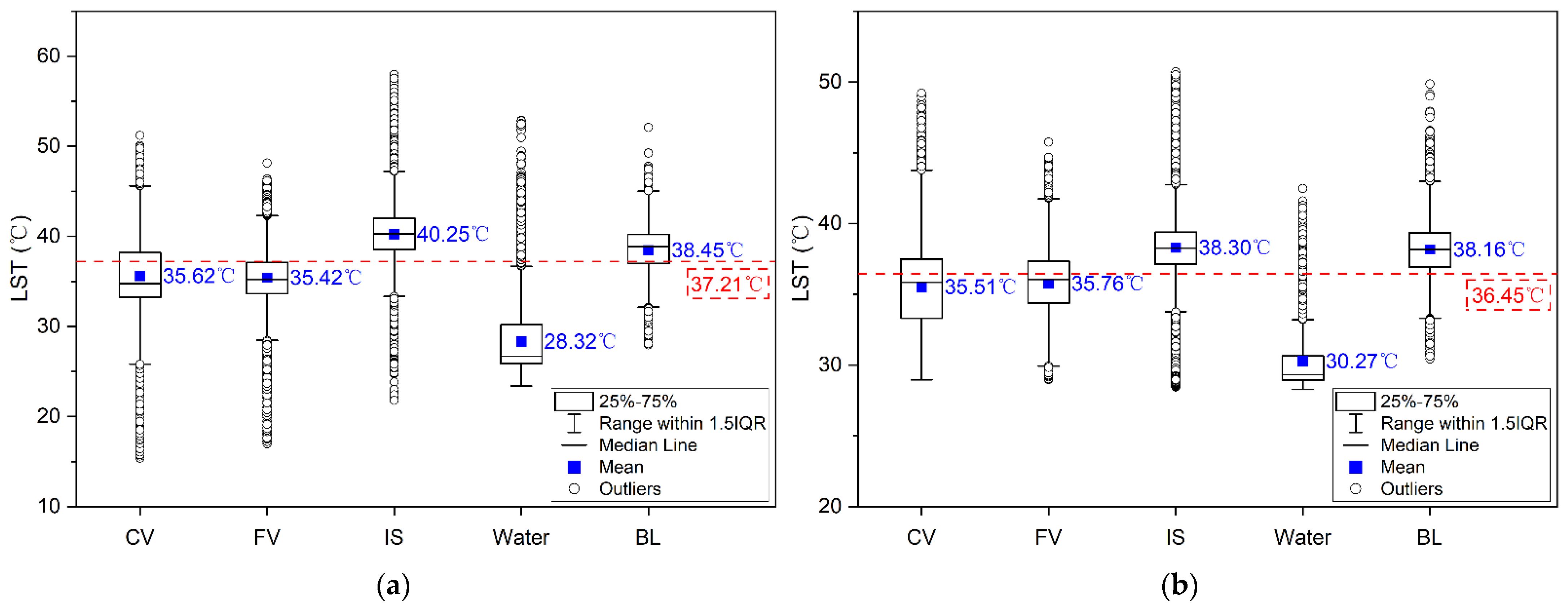
3.1. Spatial Distributions of Land Cover and LST
3.2. Drivers of LST Variations in the Lakes and Their Surrounding Areas
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pascual, J.I.; Lorente, N.; Song, Z.; Conrad, H.; Rust, H.P. Selectivity in vibrationally mediated single-molecule chemistry. Nature 2003, 423, 525–528. [Google Scholar] [CrossRef]
- Howard, L. The Climate of London; London Harvey and Dorton: London, UK, 1833; Volume 2, pp. 1818–1820. [Google Scholar]
- Hou, H.; Estoque, R.C. Detecting Cooling Effect of Landscape from Composition and Configuration: An Urban Heat Island Study on Hangzhou. Urban For. Urban Green. 2020, 53, 126719. [Google Scholar] [CrossRef]
- Ganeshan, M.; Murtugudde, R.; Imhoff, M.L. A multi-city analysis of the UHI-influence on warm season rainfall. Urban Clim. 2013, 6, 1–23. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Santamouris, M.; Cartalis, C.; Synnefa, A.; Kolokotsa, D. On the impact of urban heat island and global warming on the power demand and electricity consumption of buildings—A review. Energy Build. 2015, 98, 119–124. [Google Scholar] [CrossRef]
- Rocklöv, J.; Forsberg, B.; Ebi, K.; Bellander, T. Susceptibility to mortality related to temperature and heat and cold wave duration in the population of Stockholm County, Sweden. Glob. Health Action 2014, 7, 22737. [Google Scholar] [CrossRef] [Green Version]
- Wong, L.P.; Alias, H.; Aghamohammadi, N.; Aghazadeh, S.; Sulaiman, N.M.N. Urban heat island experience, control measures and health impact: A survey among working community in the city of Kuala Lumpur. Sustain. Cities Soc. 2017, 35, 660–668. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, M.; Hong, L.; Xian, X.; Yang, K. Temporal and Spatial Variation of Urban Heat Island Effect in Plateau Lake Region Based on RS—A 30-Year Case Study in Dianchi Basin. In Proceedings of the 2018 26th International Conference on Geoinformatics, Kunming, China, 28–30 June 2018; pp. 1–6. [Google Scholar]
- Hathway, E.A.; Sharples, S. The interaction of rivers and urban form in mitigating the Urban Heat Island effect: A UK case study. Build. Environ. 2012, 58, 14–22. [Google Scholar] [CrossRef] [Green Version]
- Moyer, A.N.; Hawkins, T.W. River effects on the heat island of a small urban area. Urban Clim. 2017, 21, 262–277. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Hu, L.; Sun, Y.; Collins, G.; Fu, P. Improved estimates of monthly land surface temperature from MODIS using a diurnal temperature cycle (DTC) model. ISPRS J. Photogramm. Remote Sens. 2020, 168, 131–140. [Google Scholar] [CrossRef]
- Chen, L.; Wang, X.; Cai, X.; Yang, C.; Lu, X. Seasonal Variations of Daytime Land Surface Temperature and Their Underlying Drivers over Wuhan, China. Remote Sens. 2021, 13, 323. [Google Scholar] [CrossRef]
- Cao, H.; Gao, B.; Gong, T.; Wang, B. Analyzing Changes in Frozen Soil in the Source Region of the Yellow River Using the MODIS Land Surface Temperature Products. Remote Sens. 2021, 13, 180. [Google Scholar] [CrossRef]
- Ngie, A.; Abutaleb, K.; Ahmed, F.; Darwish, A.; Ahmed, M. Assessment of urban heat island using satellite remotely sensed imagery: A review. S. Afr. Geogr. J. 2014, 96, 198–214. [Google Scholar] [CrossRef]
- Zhou, D.; Zhao, S.; Liu, S.; Zhang, L.; Zhu, C. Surface urban heat island in China’s 32 major cities: Spatial patterns and drivers. Remote Sens. Environ. 2014, 152, 51–61. [Google Scholar] [CrossRef]
- Clinton, N.; Gong, P. MODIS detected surface urban heat islands and sinks: Global locations and controls. Remote Sens. Environ. 2013, 134, 294–304. [Google Scholar] [CrossRef]
- Khorchani, M.; Vicente-Serrano, S.M.; Azorin-Molina, C.; Garcia, M.; Martin-Hernandez, N.; Peña-Gallardo, M.; Kenawy, A.E.; Domínguez-Castro, F. Trends in LST over the peninsular Spain as derived from the AVHRR imagery data. Global Planet. Chang. 2018, 166, 75–93. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, H.; Li, P.; Yin, Z. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Streutker, D.R. Satellite-measured growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
- Wu, C.; Li, J.; Wang, C.; Song, C.; Chen, Y.; Finka, M.; Rosa, D.L. Understanding the relationship between urban blue infrastructure and land surface temperature. Sci. Total. Environ. 2019, 694, 133742. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y. Water Bodies’ Cooling Effects on Urban Land Daytime Surface Temperature: Ecosystem Service Reducing Heat Island Effect. Sustainability 2019, 11, 787. [Google Scholar] [CrossRef] [Green Version]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban heat island effect: A systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Schwarz, N.; Manceur, A.M. Analyzing the Influence of Urban Forms on Surface Urban Heat Islands in Europe. J. Urban Plan. Dev. 2015, 141, A4014003. [Google Scholar] [CrossRef]
- Theeuwes, N.E.; Solcerová, A.; Steeneveld, G.J. Modeling the influence of open water surfaces on the summertime temperature and thermal comfort in the city. J. Geophys. Res.: Atmos. 2013, 118, 8881–8896. [Google Scholar] [CrossRef] [Green Version]
- Spronken-Smith, R.A.; Oke, T.R.; Lowry, W.P. Advection and the surface energy balance across an irrigated urban park. Int. J. Climatol. 2000, 20, 1033–1047. [Google Scholar] [CrossRef]
- Gunawardena, K.R.; Wells, M.J.; Kershaw, T. Utilising green and bluespace to mitigate urban heat island intensity. Sci. Total Environ. 2017, 584–585, 1040–1055. [Google Scholar] [CrossRef]
- Song, W.; Xu, Q.; Fu, X.; Zhang, P.; Pang, Y.; Song, D. Research on the Relationship between Water Diversion and Water Quality of Xuanwu Lake, China. Int. J. Environ. Res. Public Health 2018, 15, 1262. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Han, G.; Chen, M. Do water bodies play an important role in the relationship between urban form and land surface temperature? Sustain. Cities Soc. 2018, 39, 487–498. [Google Scholar] [CrossRef]
- Xu, S.; Liu, Y.; Qian, Y.; Wang, Q. The significance of the West Lake pattern and its heuristic implications for creating China’s heritage tourism economics. Tour. Manag. 2017, 58, 286–292. [Google Scholar] [CrossRef]
- Hangzhou Municipal Bureau of Statistics. An Overview of Hangzhou. Available online: http://tjj.hangzhou.gov.cn/ (accessed on 26 January 2021).
- Nanjing Municipal Bureau of Statistics. Nanjing Statistical Yearbook 2020. Available online: http://tjj.nanjing.gov.cn/material/njnj_2020/ (accessed on 26 January 2021).
- Wang, L.; Hou, H.; Weng, J. Ordinary least squares modelling of urban heat island intensity based on landscape composition and configuration: A comparative study among three megacities along the Yangtze River. Sustain. Cities Soc. 2020, 62, 102381. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Liu, T. Deep learning-based fusion of Landsat-8 and Sentinel-2 images for a harmonized surface reflectance product. Remote Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
- Fernandez-Beltran, R.; Baidar, T.; Kang, J.; Pla, F. Rice-Yield Prediction with Multi-Temporal Sentinel-2 Data and 3D CNN: A Case Study in Nepal. Remote Sens. 2021, 13, 1391. [Google Scholar] [CrossRef]
- Persson, H.J.; Jonzén, J.; Nilsson, M. Combining TanDEM-X and Sentinel-2 for large-area species-wise prediction of forest biomass and volume. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102275. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Windahl, E.; Beurs, K.d. An intercomparison of Landsat land surface temperature retrieval methods under variable atmospheric conditions using in situ skin temperature. Int. J. Appl. Earth Obs. Geoinf. 2016, 51, 11–27. [Google Scholar] [CrossRef] [Green Version]
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar] [CrossRef]
- Qin, Z.; Li, W.; Xu, B.; Chen, Z.; Liu, J. The estimation of land surface emissivity for Landsat TM6. Remote Sens. Land Resour. 2004, 16, 28–32,36,41. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Becker, F.; Choudhury, B.J. Relative sensitivity of normalized difference vegetation Index (NDVI) and microwave polarization difference Index (MPDI) for vegetation and desertification monitoring. Remote Sens. Environ. 1988, 24, 297–311. [Google Scholar] [CrossRef]
- Cadenasso, M.L.; Pickett, S.T.A.; Schwarz, K. Spatial heterogeneity in urban ecosystems: Reconceptualizing land cover and a framework for classification. Front. Ecol. Environ. 2007, 5, 80–88. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- O’Neill, R.V.; Krummel, J.R.; Gardner, R.H.; Sugihara, G.; Jackson, B.; Deangelis, D.L.; Milne, B.T.; Turner, M.G.; Zygmunt, B.; Christensen, S.W.; et al. Indices of landscape pattern. Landsc. Ecol. 1988, 1, 153–162. [Google Scholar] [CrossRef]
- Chen, A.; Yao, L.; Sun, R.; Chen, L. How many metrics are required to identify the effects of the landscape pattern on land surface temperature? Ecol. Indic. 2014, 45, 424–433. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y.; Myint, S.W. Effects of landscape composition and pattern on land surface temperature: An urban heat island study in the megacities of Southeast Asia. Sci. Total Environ. 2017, 577, 349–359. [Google Scholar] [CrossRef]
- Yao, L.; Li, T.; Xu, M.; Xu, Y. How the landscape features of urban green space impact seasonal land surface temperatures at a city-block-scale: An urban heat island study in Beijing, China. Urban For. Urban Green. 2020, 52, 126704. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, F. Effects of changing spatial extent on the relationship between urban forest patterns and land surface temperature. Ecol. Indic. 2020, 109, 105778. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, Ü.; Sawut, M.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Bartesaghi-Koc, C.; Osmond, P.; Peters, A. Spatio-temporal patterns in green infrastructure as driver of land surface temperature variability: The case of Sydney. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101903. [Google Scholar] [CrossRef]
- Masoudi, M.; Tan, P.Y.; Fadaei, M. The effects of land use on spatial pattern of urban green spaces and their cooling ability. Urban Clim. 2021, 35, 100743. [Google Scholar] [CrossRef]
- Masoudi, M.; Tan, P.Y. Multi-year comparison of the effects of spatial pattern of urban green spaces on urban land surface temperature. Landsc. Urban Plan. 2019, 184, 44–58. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 26 January 2021).
- Gupta, N.; Mathew, A.; Khandelwal, S. Analysis of cooling effect of water bodies on land surface temperature in nearby region: A case study of Ahmedabad and Chandigarh cities in India. Egypt. J. Remote Sens. Space Sci. 2019, 22, 81–93. [Google Scholar] [CrossRef]
- Pardoe, I. Multiple Linear Regression. In Applied Regression Modeling, 3rd ed.; Pardoe, I., Ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2020; Volume 3, pp. 96–100. [Google Scholar]
- Franklin, J.B.; Sathish, T.; Vinithkumar, N.V.; Kirubagaran, R. A novel approach to predict chlorophyll-a in coastal-marine ecosystems using multiple linear regression and principal component scores. Mar. Pollut. Bull. 2020, 152, 110902. [Google Scholar] [CrossRef]
- Yuan, D.; Elvidge, C.D. Comparison of relative radiometric normalization techniques. ISPRS J. Photogramm. Remote Sens. 1996, 51, 117–126. [Google Scholar] [CrossRef]
- Sun, R.; Chen, L. How can urban water bodies be designed for climate adaptation? Lands. Urban Plan. 2012, 105, 27–33. [Google Scholar] [CrossRef]
- Cheval, S.; Popa, A.-M.; Șandric, I.; Iojă, I.-C. Exploratory analysis of cooling effect of urban lakes on land surface temperature in Bucharest (Romania) using Landsat imagery. Urban. Clim. 2020, 34, 100696. [Google Scholar] [CrossRef]
- Zhang, Q.; Wen, Y.; Wu, Z.; Chen, Y. Seasonal Variations of the Cooling Effect of Water Landscape in High-density Urban Built-up Area: A Case Study of the Center Urban District of Guangzhou. Ecol. Environ. Sci. 2018, 27, 1323–1334. [Google Scholar] [CrossRef]
- Athukorala, D.; Murayama, Y. Spatial Variation of Land Use/Cover Composition and Impact on Surface Urban Heat Island in a Tropical Sub-Saharan City of Accra, Ghana. Sustainability 2020, 12, 7953. [Google Scholar] [CrossRef]
- Liu, F.; Hou, H.; Murayama, Y. Spatial Interconnections of Land Surface Temperatures with Land Cover/Use: A Case Study of Tokyo. Remote Sens. 2021, 13, 610. [Google Scholar] [CrossRef]
- Yu, B.; He, X.; Wei, L.; Chen, L.; Zhou, W. Primary exploration for construction of urban multilevel ventilation corridors system in Hangzhou. J. Meteorol. Sci. 2018, 38, 625–636. [Google Scholar] [CrossRef]
- Zhang, Y.; Rui, D.; Zhou, L. Nanjing Zhongshan Mountain Scenic’s Influence on the Air Quality in Main Urban Area. Environ. Monit. Forewarning 2010, 2, 47–50. [Google Scholar] [CrossRef]
- Fei, J.; Chen, W.; Bao, Q.; Zhang, W. Evolution Characteristics and Multi-Value of Scenic Byway of the West Lake Mountain Forest in Hangzhou. J. Chin. Urban For. 2020, 18, 98–102. [Google Scholar] [CrossRef]
- Jenerette, G.D.; Harlan, S.L.; Brazel, A.; Jones, N.; Larsen, L.; Stefanov, W.L. Regional relationships between surface temperature, vegetation, and human settlement in a rapidly urbanizing ecosystem. Lands. Ecol. 2007, 22, 353–365. [Google Scholar] [CrossRef]
- Soydan, O. Effects of landscape composition and patterns on land surface temperature: Urban heat island case study for Nigde, Turkey. Urban. Clim. 2020, 34, 100688. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, X.; Yang, Q.; Cao, Y. The turning point between urban vegetation and artificial surfaces for their competitive effect on land surface temperature. J.Clean. Prod. 2021, 292, 126034. [Google Scholar] [CrossRef]
- Kong, F.; Yin, H.; James, P.; Hutyra, L.R.; He, H.S. Effects of spatial pattern of greenspace on urban cooling in a large metropolitan area of eastern China. Lands. Urban Plan. 2014, 128, 35–47. [Google Scholar] [CrossRef]
- Fan, H.; Yu, Z.; Yang, G.; Liu, T.Y.; Liu, T.Y.; Hung, C.H.; Vejre, H. How to cool hot-humid (Asian) cities with urban trees? An optimal landscape size perspective. Agric. For. Meteorol. 2019, 265, 338–348. [Google Scholar] [CrossRef]
- Wang, R.; Hou, H.; Murayama, Y.; Derdouri, A. Spatiotemporal Analysis of Land Use/Cover Patterns and Their Relationship with Land Surface Temperature in Nanjing, China. Remote Sens. 2020, 12, 440. [Google Scholar] [CrossRef] [Green Version]
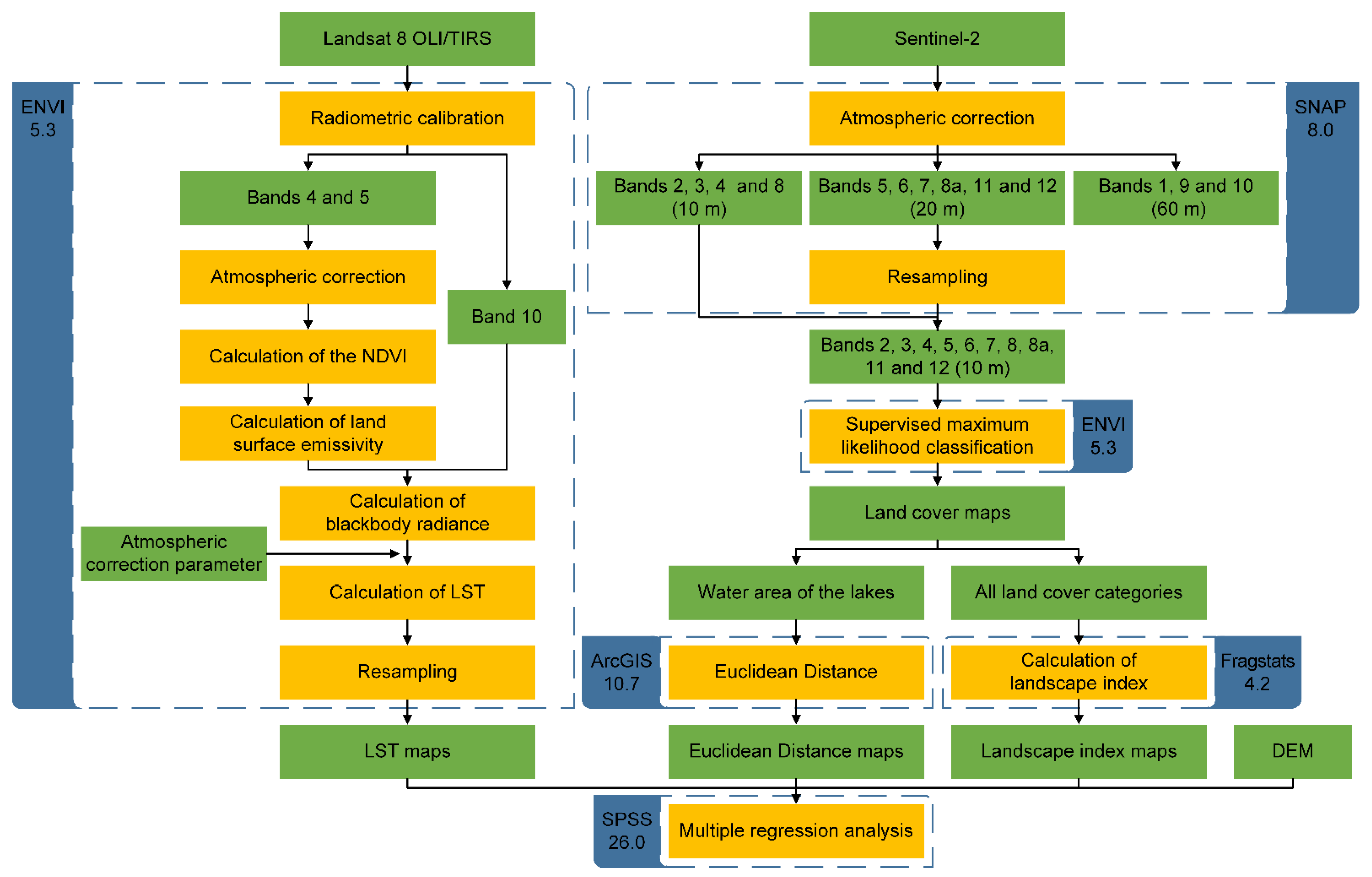


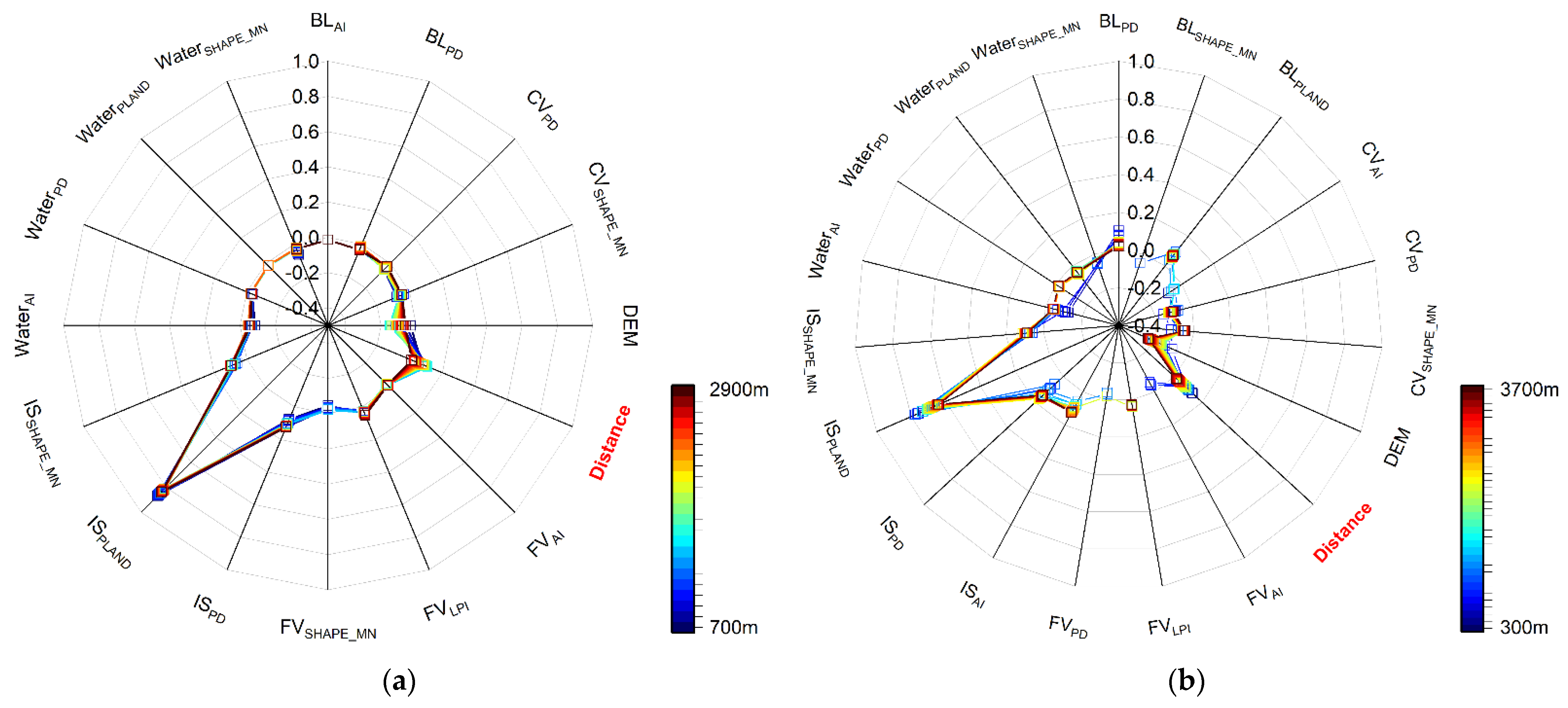
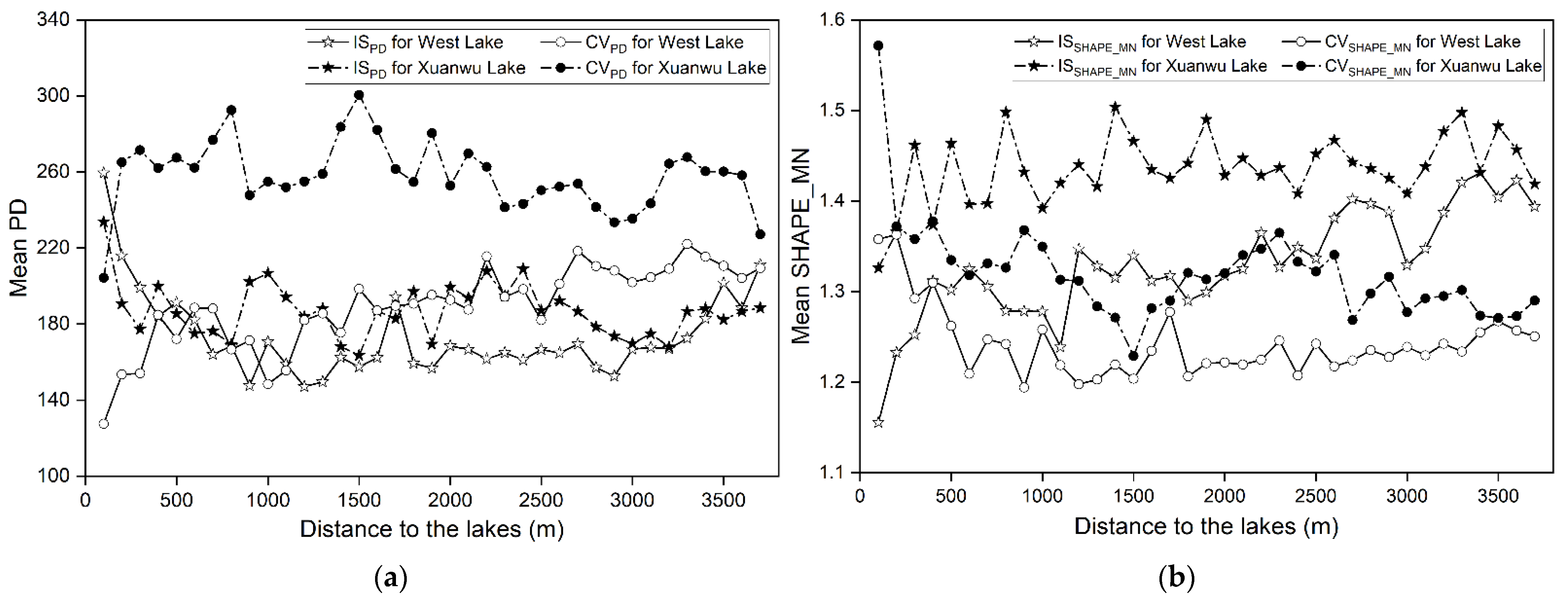
| Study Area | Platform | Resolution | Acquisition Data | Local Time |
|---|---|---|---|---|
| West Lake | Landsat 8 | 30 m | 22 July 2020 | 10:31:30 |
| Sentinel-2 | 10 m | 22 July 2020 | 10:35:51 | |
| Xuanwu Lake | Landsat 8 | 30 m | 13 September 2019 | 10:37:38 |
| Sentinel-2 | 10 m | 19 September 2019 | 10:45:51 |
| Category | Description |
|---|---|
| CV | Coarse-textured vegetation which includes forest, woodland and shrub land |
| FV | Fine-textured vegetation which includes cropland and grassland |
| IS | Impervious surface which includes buildings and pavements |
| BL | Bare lands which include bare soil and bare rock |
| Water | Water bodies which include natural-flowing river and lake as well as artificial pond and reservoir |
| Metrics (Abbreviation) | Equation (Unit) | Description |
|---|---|---|
| Percentage of landscape (PLAND) | The percentage of the landscape consisting of the corresponding patches. | |
| Largest patch index (LPI) | The percentage of the landscape comprised by the largest patch. | |
| Mean shape index (SHAPE_MN) | Mean shape index of the corresponding patches within an analysis unit. | |
| Aggregation index (AI) | The degree of the corresponding patches’ aggregation within an analysis unit. | |
| Patch density (PD) | The ratio of the corresponding patches’ number to the total landscape area within an analysis unit. |
| Model | R2 | ΔR2 | AIC | F | Model | R2 | ΔR2 | AIC | F |
|---|---|---|---|---|---|---|---|---|---|
| 700 m | 0.817 | 0.815 | −3642.549 | 475.977 *** | 1900 m | 0.854 | 0.853 | −12,057.291 | 1468.306 *** |
| 800 m | 0.820 | 0.819 | −4197.190 | 425.007 *** | 2000 m | 0.850 | 0.849 | −12,793.736 | 1519.813 *** |
| 900 m | 0.828 | 0.826 | −4821.972 | 561.296 *** | 2100 m | 0.843 | 0.843 | −13,502.545 | 1546.701 *** |
| 1000 m | 0.835 | 0.834 | −5454.464 | 670.202 *** | 2200 m | 0.840 | 0.839 | −14,323.481 | 1607.948 *** |
| 1100 m | 0.844 | 0.842 | −6161.756 | 677.878 *** | 2300 m | 0.833 | 0.833 | −15,061.922 | 1510.684 *** |
| 1200 m | 0.848 | 0.847 | −6838.319 | 780.868 *** | 2400 m | 0.829 | 0.828 | −15,915.979 | 1555.192 *** |
| 1300 m | 0.851 | 0.850 | −7501.743 | 816.920 *** | 2500 m | 0.825 | 0.825 | −16,762.030 | 1728.390 *** |
| 1400 m | 0.856 | 0.855 | −8228.796 | 933.408 *** | 2600 m | 0.823 | 0.822 | −17,648.922 | 1792.588 *** |
| 1500 m | 0.858 | 0.857 | −8975.791 | 1318.902 *** | 2700 m | 0.820 | 0.820 | −18,556.259 | 1858.858 *** |
| 1600 m | 0.858 | 0.857 | −9772.715 | 1128.923 *** | 2800 m | 0.815 | 0.815 | −19,416.599 | 1894.329 *** |
| 1700 m | 0.857 | 0.856 | −10,546.830 | 1301.174 *** | 2900 m | 0.807 | 0.806 | −20,228.078 | 1751.485 *** |
| 1800 m | 0.856 | 0.855 | −11,318.390 | 1393.030 *** |
| Model | R2 | ΔR2 | AIC | F | Model | R2 | ΔR2 | AIC | F |
|---|---|---|---|---|---|---|---|---|---|
| 300 m | 0.664 | 0.661 | −864.991 | 182.782 *** | 2100 m | 0.714 | 0.713 | −9074.115 | 568.348 *** |
| 400 m | 0.662 | 0.658 | −1203.617 | 151.728 *** | 2200 m | 0.718 | 0.717 | −9736.086 | 620.828 *** |
| 500 m | 0.654 | 0.651 | −1586.683 | 191.253 *** | 2300 m | 0.722 | 0.721 | −10,431.697 | 629.963 *** |
| 600 m | 0.658 | 0.655 | −1985.280 | 241.875 *** | 2400 m | 0.724 | 0.723 | −11,123.377 | 725.120 *** |
| 700 m | 0.681 | 0.676 | −2398.239 | 159.392 *** | 2500 m | 0.726 | 0.725 | −11,801.854 | 778.349 *** |
| 800 m | 0.678 | 0.675 | −2793.519 | 233.355 *** | 2600 m | 0.727 | 0.726 | −12,514.335 | 829.313 *** |
| 900 m | 0.690 | 0.687 | −3208.182 | 207.705 *** | 2700 m | 0.729 | 0.728 | −13,217.408 | 884.023 *** |
| 1000 m | 0.700 | 0.697 | −3624.970 | 248.397 *** | 2800 m | 0.732 | 0.731 | −13,957.272 | 949.271 *** |
| 1100 m | 0.708 | 0.706 | −4062.281 | 321.778 *** | 2900 m | 0.737 | 0.737 | −14,753.843 | 1030.338 *** |
| 1200 m | 0.718 | 0.715 | −4504.243 | 269.532 *** | 3000 m | 0.744 | 0.743 | −15,557.309 | 1120.447 *** |
| 1300 m | 0.721 | 0.719 | −4969.837 | 354.215 *** | 3100 m | 0.748 | 0.747 | −16,436.357 | 1206.056 *** |
| 1400 m | 0.726 | 0.724 | −5491.625 | 369.638 *** | 3200 m | 0.750 | 0.750 | −17,272.656 | 1281.379 *** |
| 1500 m | 0.723 | 0.721 | −5968.423 | 399.837 *** | 3300 m | 0.752 | 0.752 | −18,154.546 | 1358.456 *** |
| 1600 m | 0.717 | 0.715 | −6443.835 | 424.270 *** | 3400 m | 0.754 | 0.754 | −19,048.449 | 1438.198 *** |
| 1700 m | 0.710 | 0.708 | −6883.467 | 482.297 *** | 3500 m | 0.757 | 0.757 | −19,956.757 | 1526.397 *** |
| 1800 m | 0.704 | 0.703 | −7324.604 | 468.843 *** | 3600 m | 0.763 | 0.762 | −20,979.320 | 1646.591 *** |
| 1900 m | 0.699 | 0.698 | −7808.448 | 495.792 *** | 3700 m | 0.766 | 0.766 | −21,943.199 | 1749.128 *** |
| 2000 m | 0.707 | 0.706 | −8408.943 | 551.379 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Li, Y.; Hou, H.; Murayama, Y.; Wang, R.; Hu, T. Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing. Remote Sens. 2021, 13, 1526. https://doi.org/10.3390/rs13081526
Zheng Y, Li Y, Hou H, Murayama Y, Wang R, Hu T. Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing. Remote Sensing. 2021; 13(8):1526. https://doi.org/10.3390/rs13081526
Chicago/Turabian StyleZheng, Yaoyao, Yao Li, Hao Hou, Yuji Murayama, Ruci Wang, and Tangao Hu. 2021. "Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing" Remote Sensing 13, no. 8: 1526. https://doi.org/10.3390/rs13081526
APA StyleZheng, Y., Li, Y., Hou, H., Murayama, Y., Wang, R., & Hu, T. (2021). Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing. Remote Sensing, 13(8), 1526. https://doi.org/10.3390/rs13081526










