It can be seen that the center frequency of the B1C and B2a signals of BDS-3 are the same as the center frequency of the Galileo E1 and E5a signals. Therefore, some combinations with the same wavelength can be formed from the two systems.
2.1. Double-Differenced BDS-3 and Galileo Mathematical Model
The basic DD observation equations of pseudo-range and carrier phase measurements for a system ‘
’ (denotes BDS-3 and Galileo) and frequency band
can be expressed as follows:
where the symbol ‘
’ represents the DD operator;
and
represent the pseudo-range and carrier phase observation values of the corresponding system, respectively;
is the geometric distance between a satellite and a receiver;
is the first-order ionospheric delay at the first frequency;
is the first-order ionospheric scalar factor of the corresponding system;
is the tropospheric delay;
and
are the measurement noise of the pseudo-range and carrier phase, respectively; and
is the DD ambiguity of the corresponding system.
The corresponding linearized DD pseudo-range and carrier phase measurement equations can be expressed as follows:
where
is the linear coefficient matrix and
denotes the baseline parameters and atmospheric parameters.
Omitting the system superscript, the combined DD observation equations of quad-frequency signals can be written as follows [
16]:
where
where the coefficients
,
,
,
of the combinations are represented by
and
in BDS-3 and Galileo, respectively;
is a DD carrier phase observation of the combined signal; the expression of
is similar to
;
is the ionospheric scalar factor of the combined signal;
is the wavelength of the combined signal; and
is the velocity of light.
2.2. Determination of the EWL Ambiguity
Taking BDS-3 as an example, the EWL carrier phase measurements and the pseudo-range code measurements on B1C, B1I, B3I, and B2a can be used to form a set of observation equations, expressed as follows:
where the symbols
represent the DD pseudo-range observation residual vectors on B1C, B1I, B3I, and B2a, respectively;
represents the residual vector of DD carrier phase observations of an EWL signal;
is the design matrix of the baseline parameter
;
is the ionospheric scalar factor of an EWL signal;
represents the number of DD satellite pairs tracked in a current epoch;
is an identity matrix with dimension
;
and
represent an unknown DD ionospheric bias matrix and a DD EWL ambiguities matrix with dimension
, respectively; and the last terms
,
,
,
, and
are observed minus the computed (OMC) vectors from their corresponding observations.
Suppose that the combination coefficients of EWL are
, the covariance matrix of (9) can then be written as follows [
21]:
where
and
are the basic variances between undifferenced pseudo-range and carrier phase observations in the zenith direction, respectively;
denotes the Kronecker product;
is the DD weight matrix;
is the cofactor matrix that depends on the elevation of observations [
22];
is a linear transformation matrix used to transform the original observation matrix into a combined observation matrix; and
is a combination coefficient matrix of EWL. It is worth noting that, when calculating the long-baseline, Equation (8) needs to calculate the inter-satellite difference of the two stations separately and to then add them to obtain
.
2.4. Theoretical Precision of Triple- and Quad-Frequency EWL/WL Signals of BDS-3 and Galileo
Then, we analyzed the theoretical precision of the instantaneous ambiguity and range parameters at each step in the DD case.
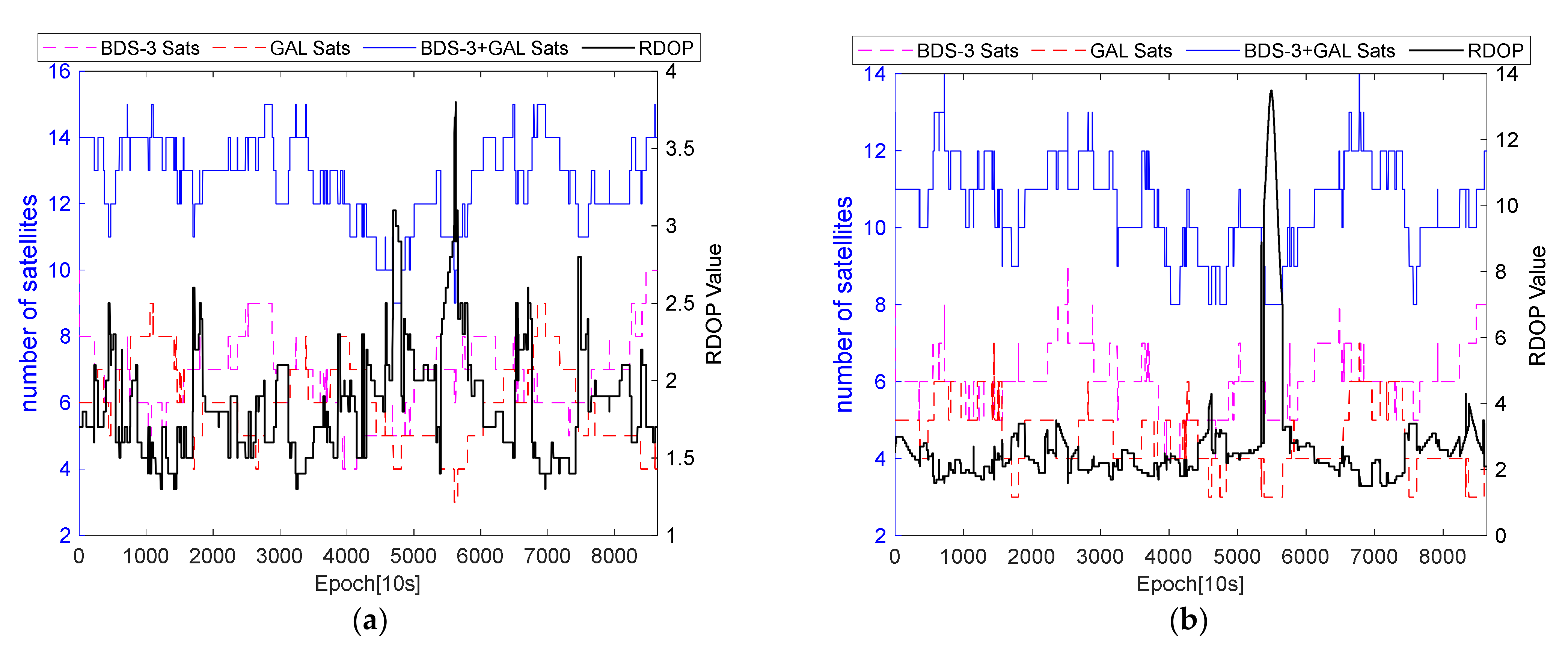
The precision of the GNSS positioning performance depends on the measurement noise of the observations and the strength of the geometric figures between the receivers and the GNSS satellites. The dilution of precision (DOP) factor is often used in positioning to quantitatively reflect the strength of the geometric figures [
25]. The calculation of the DOP value and the theoretical precision of the baseline can be expressed as follows [
26,
27]:
where
is the design matrix of the entire equations;
is the three-dimensional (3D) theoretical precision of the baseline parameters (DD range); and
is the normalized baseline noise variance, which is related to the noise of EWL/WL combinations. When the DOP (PDOP for absolute positioning and RDOP for relative positioning) for all satellites in view is equal to 1, the theoretical precision of station–satellite distance or baseline can be obtained [
28]. Therefore, assuming that RDOP is equal to 1, the theoretical baseline precision can be calculated using Equation (11).
Empirically, the DD pseudo-range and carrier phase precision are set as 50 cm and 5 mm, respectively. Various combinations can be formed based on the original observations. When the number of frequency increases, the number of optional combined signals also greatly increases, but most of them are unsuitable signals.
Assuming that the coefficient value
ranges from −10 to 10, some linearly independent EWL, second EWL, and WL combinations with a small noise amplitude factor and a small ionospheric scalar factor can be obtained in the two systems, respectively. Within this range, we first chose the combination with minimal theoretical DD ambiguity standard deviation (STD) as the first EWL, corresponding to the combination of BDS-3 (1,−1,0,0) and Galileo (0,−1,1,0), and the corresponding EWL ambiguity precisions were 0.041 cycles and 0.043 cycles (shown in
Table 2 and
Table 3), respectively. The first choice of second EWL combination was
m, and then, the combination with the minimum DD ambiguity STD within this wavelength range was selected. Ignoring the troposphere residuals and the orbital residuals,
Table 2 and
Table 3 show the theoretical parameter precisions of BDS-3 and Galileo when the RDOP value is 1, respectively. When no ambiguities were fixed, the precision of the baseline parameter was decided by the DD pseudo-range noise.
For the function model shown in Equations (7) and (10), when only observation noise is considered, the float ambiguities rounding success rates can be computed as follows [
29]:
where
is the random bias caused by observation noises.
It can be seen that the theoretical precisions of BDS-3 and Galileo are 1.012 m and 1.249 m, respectively. When only pseudo-range is used, DD range is more than 1.0 m and decimeter-level instantaneous positioning cannot be obtained. Additionally, after fixing the EWL, the DD range theoretical precisions of BDS-3 and Galileo are 0.949 m and 1.173 m, respectively, which have slight improvement. Similarly, if the second EWL is directly constrained by pseudo-ranges, the ambiguity STDs of BDS-3 and Galileo are 0.110 cycles and 0.070 cycles, respectively, and the a priori success rates are both greater than 99.9%, so they can be fixed reliably by rounding. In addition, it can be seen that using the fixed EWL observations as accurate pseudo-range observations to constrain second EWL ambiguities cannot greatly improve the precision of second EWL ambiguities. Moreover, the DD range is not improved by much after fixing the second EWL ambiguities compared with EWL, especially for Galileo. However, no matter for BDS-3 or Galileo, the precision of WL ambiguities has the same characteristics: the fixed EWL observations have little restriction on WL ambiguities, and the WL ambiguity STDs of BDS-3 and Galileo are 0.314 cycles and 0.358 cycles, respectively. Compared to without EWL constraints, the a priori success rate only increased by 2.3 and 2.5 percentage points. Nevertheless, the fixed second EWL can significantly improve the precision of WL ambiguities.
After using the fixed second EWL constraints, the WL ambiguity STDs of BDS-3 and Galileo are 0.209 cycles and 0.298 cycles, respectively, and the a priori success rates are 98.3% and 90.7%, respectively. Compared with the fixed EWL, it has been increased by 9.5 and 6.9 percentage points, respectively. Correspondingly, the quad-frequency WL AR of BDS-3 and Galileo in
Section 2.3 can be expressed as follows:
where
;
;
and
have the same expression; the superscript capitals ‘C’ and ‘E’ indicate BDS-3 and Galileo, respectively;
is a column matrix vector with n rows of elements, all being 1; and the subscripts ‘
c’ and ‘
e’ of the identity matrix are the dimensions of matrix, corresponding to the number of satellite pairs of BDS-3 and Galileo, respectively. It should be noted that the first two steps of the EWL and second EWL AR processes cannot be ignored.
In the above process, some suboptimal second EWL combinations have been eliminated, for example, the Galileo signal with a wavelength of 2.91 m. However, no suboptimal second EWL signal is eliminated in BDS-3. Therefore, in
Table 4, optimal EWL/WL combinations in different triple-frequency configurations are selected in BDS-3 and Galileo, respectively. The corresponding ambiguity precisions of EWL/WL and the theoretical DD ranges are given. As a comparison, the optimal triple-frequency configuration of GPS is added.
It can be seen that the DD ranges of two configurations of triple-frequency signals (B1C,B3I,B2a) and (B1I,B3I,B2a) in BDS-3 are 0.335 m and 0.349 m, respectively, of which the values are close to the quad-frequency case; therefore, these two configurations of triple-frequency signals can be selected as the optimal triple-frequency signals of BDS-3. As the long baseline is additionally affected by unmodeled errors, when the DD ranges of the two triple-frequency configurations are similar, the configuration with a smaller ambiguity STD is selected. It is easy to determine that the best configuration for Galileo is (E1,E5a,E6) because the ambiguity STD of this configuration is the same as that of quad-frequency, of which the value is 0.316 m. Following Equation (13), the corresponding EWL/WL equation is expressed as follows:
The quad-frequency combination scheme and the optimal triple-frequency combination scheme were selected, corresponding to the No. 1 and No. 3 combination schemes in
Table 5. In addition, in
Table 4, BDS-3 and Galileo have configurations of triple-frequency signals (B1C,B1I,B2a) and (E1,E5a,E5b) with the worst precision, respectively. It should be noted that ’worst’ here refers to the worst of all the combination schemes that have been selected in this experiment, but it is the best in the corresponding triple-frequency combined signals. Coincidentally, they correspond to the quad-frequency combination scheme without the constraints of the fixed second EWL in the second step and directly use fixed EWL to constrain WL ambiguities. Therefore, we added this combination scheme to the comparison as No. 2. Finally, the DD range a priori precisions of the combination of BDS-3 (B1C,B1I,B3I) and the combination of Galileo (E1,E5b,E6) are medium, and they also form a combination scheme for comparison, as No. 4. The corresponding coefficients of proposed combination schemes are shown in
Table 5.
According to
Table 5, there are two EWL combinations in BDS-3; the corresponding wavelengths are, respectively, 20.93 m and 3.26 m, which are quite different. There are three EWL combinations in Galileo, corresponding to wavelengths of 9.77 m, 4.19 m, and 2.93 m. All coefficients are plus or minus 1 or 0.