Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud
Abstract
:1. Introduction
- (1)
- The amount of point cloud is huge, making the point-by-point calculation of the distance between millions of power line points and the surrounding ground points prohibitive. Moreover, for the 3D spatial catenary curve of the conductor, it is complicated to calculate the point-to-curve distance directly in the 3D space.
- (2)
- The geographical environment within the power line corridor is complex, which brings difficulty to the accurate extraction of power lines. It spans over mountains, lakes, and terrains with great elevation fluctuation. Moreover, the tall trees could also occlude the collection of power line points, resulting in the sparsity or missing points along the power lines.
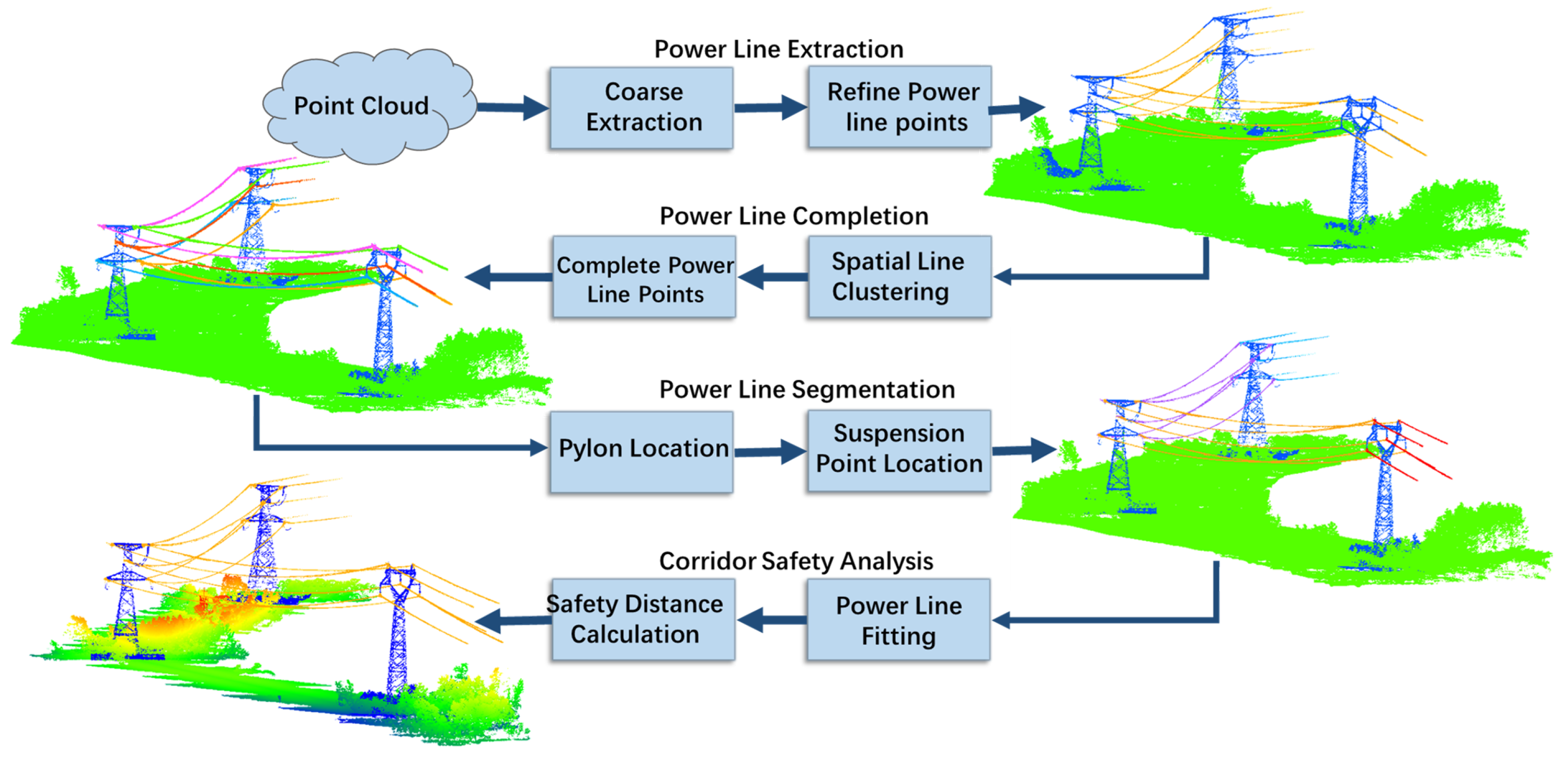
2. Methods
- (1)
- Power line extraction: Due to the different height distribution of LiDAR points of power lines, pylons and ground objects, the height histogram was adopted to extract power line points based on gridding. With the help of region growing, the extraction result was further refined by eliminating the false positives.
- (2)
- Power line completion: To complete the missing power line points, spatial line clustering was proposed to accurately classify the power lines from the perspective of projection. For each cluster of the power line, a local linear model was fitted for completing the false negatives.
- (3)
- Power line segmentation: The direction of the power lines varied with the terrains between consecutive pylons, so we needed to treat each span separately. Therefore, the pylon was located by the contextual relationship between power lines and pylon first. The suspension point of conductor on the pylon was then located by progressively searching the nearest intersection of power lines. As a result, the power line points were ready to be segmented span-by-span.
- (4)
- Corridor safety analysis: In order to calculate the distance between ground objects and the power lines, checking the 3D distance between ground points and the power line points in the 3D space was necessary. The points of the power line were distributed as a catenary curve in a vertical plane where the power line points could be fitted first. Then the distance could be simplified using the distance between a 3D spatial point and the catenary plane and the distance between a planar point and a 2D catenary curve.
- (1)
- The spatial line clustering is proposed to accurately classify and complete the power line points locally, which can greatly overcome the sparsity and missing of LiDAR points within the complex power line corridor.
- (2)
- The contextual relationship of the power line and pylon is well investigated by the grid-based analysis, so that pylon and the suspension point of power lines on the pylon are well extracted.
- (3)
- The catenary plane-based simplification of 3D spatial distance calculation between power lines and ground objects facilitates the survey of the power line corridor.
2.1. Extraction of Power Line Points
2.1.1. Coarse Extraction of Power Line Points
2.1.2. Refinement of Candidate Power Line Points
2.2. Completion of Power Line Points Using Spatial Line Clustering
2.2.1. Cases of Missing Power Line Points
- (1)
- Confusion with the pylon. After the region growing, part of the correctly extracted power line points were lost. As shown in Figure 6a, the power line points near the pylon were extracted as the pylon after the region growing, because they were reachable from the neighboring pylon.
- (2)
- (3)
- Underlying water. Due to the mirror reflection, there were no laser points from the water surface, which led to another false negative of power line points when power lines passed across the water surface. As shown in Figure 6c, for the cell located at the water, there was no point in the water surface. Since the empty layer between the ground and power line could not be found, the extraction of the power line could not be achieved.
2.2.2. Power Line Classification Using Spatial Line Clustering
2.2.3. Completion of Power Line Points
2.3. Power Line Segmentation Using the Suspension Points
2.3.1. Pylon Location Guided by Power Line
2.3.2. Suspension Point Location and Power Line Segmentation
- The horizontal center coordinate of pylon was calculated first. The vertical plane that passed through the center of the pylon and perpendicular to the direction of the power lines was used to segment the power line. As shown in Figure 12, the yellow plane in the first row is a vertical plane passing through the center of the pylon, which acts as the initial interface. It divided the power line points into red and blue parts.
- After fitting the red and the blue points respectively to get and , the intersection of and was calculated. Since the two lines in the 3D space might have been skew lines which did not intersect, we took the mid-point of the closest point pair of the skew lines as the intersection. As shown in the first row of Figure 12, and were the closest point pair of the skew lines, and the suspension points were the mid-point of . The blue plane was the ideal interface to divide the power lines. It can be seen that the were closer to the ideal plane than the original yellow plane.
- If the number of power line points on one side was too small, the intersection of the fitted line on the other side with the plane was directly regarded as the suspension point with no iteration. It often happened when the point cloud was sparse and the power line points were missing on one side.
- If the distance between suspension point and the plane was less than a threshold, the calculation stopped. Otherwise, as shown in the second row of Figure 12, it took a new vertical plane passed through the to re-divide the power line points, re-fitted the left and right straight lines, and calculated the intersections . The was regarded as the new suspension point. It can be seen that the new suspension point approached the ideal plane gradually.
- The above process was repeated until the distance of successive intersection and was less than a threshold.
2.4. Power Line Fitting and Corridor Safety Distance Calculation
2.4.1. Regularizing the Point Cloud
2.4.2. Fitting the Catenary Plane and Catenary Curve of Power Line
2.4.3. Calculate the Safety Distance
- For most cells that neither contained any power line points nor any power line points in the neighboring cells, they were safe with no report of safety distance.
- If the cell had power line points or had a power line in its neighborhood, we needed to calculate the safety distance of every object point in the cell.
3. Results
3.1. Experimental Data
3.2. Evaluation Methods
3.2.1. Evaluation of the Extraction Effect of Power Line Points
3.2.2. Spatial Positioning Accuracy of the Suspension Points
3.2.3. The Accuracy of the Safety Distance Calculation
3.3. Experimental Results
3.3.1. Results of Typical Corridors
3.3.2. The Extraction Accuracy of Power Line Points
3.3.3. The Positioning Accuracy of the Suspension Point
3.3.4. The Accuracy and Speed of the Distance Calculation
3.3.5. The Influence of Point Density
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lou, W.J.; Wu, D.G.; Su, J.; Gu, S.Q.; Jiang, W.D. Discussion on Wind-induced Swing Flashover and Conductor Wind Load of EHV Transmission Lines. High Volt. Eng. 2019, 045, 1249–1255. [Google Scholar]
- Chen, C.; Yang, B.; Song, S.; Peng, X.; Huang, R. Automatic Clearance Anomaly Detection for Transmission Line Corridors Utilizing UAV-Borne LIDAR Data. Remote Sens. 2018, 10, 613. [Google Scholar]
- Jardini, M.G.M.; Jacobsen, R.M.; Jardini, J.A.; Magrini, L.C.; Beltrame, A.M.K. Information System for the Vegetation Control of Transmission Lines Right-of-way. In Proceedings of the 2007 IEEE Power Tech, Lausanne, Switzerland, 1–5 July 2007. [Google Scholar]
- Ahmad, J.; Malik, A.S.; Xia, L.; Ashikin, N. Vegetation encroachment monitoring for transmission lines right-of-ways: A survey. Electr. Power Syst. Res. 2013, 95, 339–352. [Google Scholar] [CrossRef]
- Mills, S.; Gerardo Castro, M.P.; Li, Z.; Cai, J.; Hayward, R.; Mejias, L.; Walker, R.A. Evaluation of Aerial Remote Sensing Techniques for Vegetation Management in Power-Line Corridors. IEEE Trans. Geoence Remote Sens. 2010, 48, 3379–3390. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, B.; Xiao, W.; Liang, F.; Wang, Z. Automatic Extraction of High-Voltage Power Transmission Objects from UAV Lidar Point Clouds. Remote Sens. 2019, 11, 2600. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.; Wu, G.; Ye, X.; Huang, L.; Lei, J. A Novel Method to Reconstruct Overhead High-Voltage Power Lines Using Cable Inspection Robot LiDAR Data. Remote Sens. 2017, 9, 753. [Google Scholar]
- Yan, L.; Wu, W.; Li, T. Power transmission tower monitoring technology based on TerraSAR-X products. Proc. SPIE Int. Soc. Opt. Eng. 2011, 10, 82861E. [Google Scholar]
- Deng, S.; Zhang, J.; Li, P.; Yang, J. Power line detection from synthetic aperture radar imagery using coherence of co-polarisation and cross-polarisation estimated in the Hough domain. IET Radar Sonar Navig. 2012, 6, 873–880. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, X.; Chen, Z.; Wu, W.; Li, T. Risk assessment for wildfire occurrence in high-voltage power line corridors by using remote-sensing techniques: A case study in Hubei Province, China. Int. J. Remote Sens. 2016, 37, 4818–4837. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, Y.; Karady, G.G.; Heydt, G.T.; Olsen, R.G. The Utilization of Satellite Images to Identify Trees Endangering Transmission Lines. IEEE Trans. Power Deliv. 2009, 24, 1703–1709. [Google Scholar] [CrossRef]
- Jóźków, G.; Vander Jagt, B.; Toth, C. Experiments with UAS Imagery for Automatic Modeling of Power Line 3D Geometry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 403. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.C.; Lei, J.F.; Wang, X.P.; Zhao, L.; Tian, M.; Cao, W.B.; Yao, H.T.; Cai, B.B. Power line identification algorithm for aerial image in complex background. Bull. Surv. Mapp. 2019, 28–32. [Google Scholar] [CrossRef]
- Jadin, M.S.; Ghazali, K.H.; Taib, S. Thermal condition monitoring of electrical installations based on infrared image analysis. In Proceedings of the Electronics, Communications & Photonics Conference, Riyadh, Saudi Arabia, 27–30 April 2013. [Google Scholar]
- Zhang, W.F.; Peng, X.; Chen, R.; Chen, C.; Deng, Y.; Qian, J.; Xu, W. Intelligent Diagnostic Techniques of Abnormal Heat Defect in Transmission Lines Based on Unmanned Helicopter Infrared Video. Power Syst. Technol. 2014, 38, 1334–1338. [Google Scholar]
- Nardinocchi, C.; Balsi, M.; Esposito, S. Fully Automatic Point Cloud Analysis for Powerline Corridor Mapping. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8637–8648. [Google Scholar] [CrossRef]
- Chen, C.; Mai, X.M.; Song, S.; Peng, X.Y.; Xu, W.X.; Wang, K. Automatic power line extraction method for airborne laser point cloud data. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1600–1605. [Google Scholar]
- Jung, J.; Che, E.; Olsen, M.J.; Shafer, K.C. Automated and efficient powerline extraction from laser scanning data using a voxel-based subsampling with hierarchical approach. ISPRS J. Photogramm. Remote Sens. 2020, 163, 343–361. [Google Scholar] [CrossRef]
- Husain, A.; Vaishya, R.C. An automated method for power line points detection from terrestrial LiDAR data. In Emerging Technologies in Data Mining and Information Security; Springer: Berlin, Germany, 2019; pp. 459–472. [Google Scholar]
- Nasseri, M.H.; Moradi, H.; Nasiri, S.M.; Hosseini, R. Power Line Detection and Tracking Using Hough Transform and Particle Filter. In Proceedings of the 2018 6th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 23–25 October 2018. [Google Scholar]
- Zheng, L.; Yi, R. Fault diagnosis system for the inspection robot in power transmission lines maintenance. In Proceedings of the 2009 International Conference on Optical Instruments and Technology: Optoelectronic Imaging and Process Technology, Shanghai, China, 19–22 October 2009. [Google Scholar]
- Guan, H.; Yu, Y.; Li, J.; Ji, Z.; Zhang, Q. Extraction of power-transmission lines from vehicle-borne lidar data. Int. J. Remote Sens. 2016, 37, 229–247. [Google Scholar] [CrossRef]
- Xiaowei, Y.; Juha, H.; Mika, K.; Kimmo, N.; Kirsi, K.; Mikko, V.; Ville, K.; Harri, K.; Markus, H.; Eija, H. Comparison of Laser and Stereo Optical, SAR and InSAR Point Clouds from Air- and Space-Borne Sources in the Retrieval of Forest Inventory Attributes. Remote Sens. 2015, 7, 15933–15954. [Google Scholar]
- Blistan, P.; Kovanič, L.; Zelizňaková, V.; Palková, J. Using UAV photogrammetry to document rock outcrops. Acta Mont. Slovaca 2016, 21, 154–161. [Google Scholar]
- Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Zeybek, M.; İsmail, Ş. Point cloud filtering on UAV based point cloud. Measurement 2019, 133, 99–111. [Google Scholar] [CrossRef]
- Huang, H.; Brenner, C.; Sester, M. A generative statistical approach to automatic 3D building roof reconstruction from laser scanning data. ISPRS J. Photogramm. Remote Sens. 2013, 79, 29–43. [Google Scholar] [CrossRef]
- Aicardi, I.; Dabove, P.; Lingua, A.M.; Piras, M. Integration between TLS and UAV photogrammetry techniques for forestry applications. IForest Biogeosci. For. 2016, 10, e1–e7. [Google Scholar] [CrossRef] [Green Version]
- Garrido, M.; Paraforos, D.; Reiser, D.; Vázquez Arellano, M.; Griepentrog, H.; Valero, C. 3D Maize Plant Reconstruction Based on Georeferenced Overlapping LiDAR Point Clouds. Remote Sens. 2015, 7, 17077–17096. [Google Scholar] [CrossRef] [Green Version]
- Ituen, I.; Sohn, G. The Way Forward: Advances in Maintaining Right-of-Way of Transmission Lines. Geomatica 2010, 64, 451–462. [Google Scholar]
- Wang, Y.; Chen, Q.; Liu, L.; Zheng, D.; Li, C.; Li, K. Supervised Classification of Power Lines from Airborne LiDAR Data in Urban Areas. Remote Sens. 2017, 9, 771. [Google Scholar]
- Pu, S.; Xie, L.; Ji, M.; Zhao, Y.; Liu, W.; Wang, L.; Zhao, Y.; Yang, F.; Qiu, D. Real-time powerline corridor inspection by edge computing of UAV Lidar data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4213, 547–551. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, Z.; Hayward, R.; Walker, R.A.; Jin, H. Classification of Airborne LIDAR Intensity Data Using Statistical Analysis and Hough Transform with Application to Power Line Corridors. In Proceedings of the 2009 Digital Image Computing: Techniques and Applications, Melbourne, VIC, Australia, 1–3 December 2009; pp. 462–467. [Google Scholar]
- Melzer, T.B.C. Extraction and Modeling of Power Lines from ALS Point Clouds. In Proceedings of the Workshop, 28th Workshop of the Austrian Association for Pattern Recognition (OAGM), Salzburg, Austria, 22–23 May 2004; pp. 47–54. [Google Scholar]
- Yu, J.; Mu, C.; Feng, Y.M.; Dou, Y.J. Study on power line extraction from airborne LiDAR point cloud data. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1275–1279. [Google Scholar]
- Wang, P.H.; Xi, X.H.; Wang, C.; Xia, S.B. Study on power line fast extraction based airborne LiDAR data. Sci. Surv. Mapp. 2017, 42, 154–158. [Google Scholar]
- Awrangjeb, M. Extraction of Power Line Pylons and Wires Using Airborne LiDAR Data at Different Height Levels. Remote Sens. 2019, 11, 1798. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.F.; Wang, C.; Wang, J.; Zhou, J.; Ma, Y. Extraction of power lines from laser point cloud based on residual clustering method. Acta Geod. Et Cartogr. Sin. 2020, 49, 883. [Google Scholar]
- Jwa, Y.; Sohn, G.; Kim, H.B. Automatic 3D powerline reconstruction using airborne lidar data. Int. Arch. Photogramm. Remote Sens. 2009, 38, W8. [Google Scholar]
- Chen, C.; Peng, X.Y.; Song, S.; Wang, K.; Qian, J.J.; Yang, B.S. Safety Distance Diagnosis of Large Scale Transmission Line Corridor Inspection Based on LiDAR Point Cloud Collected With UAV. Power Syst. Technol. 2017, 041, 2723–2730. [Google Scholar]
- Blomley, R.; Jutzi, B.; Weinmann, M. Classification of Airborne Laser Scanning Data Using Geometric Multi-Scale Features and Different Neighbourhood Types. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. 2016, III-3, 169–176. [Google Scholar] [CrossRef] [Green Version]
- Liang, C.; Tong, L.; Wang, Y.; Li, M. Extraction of Urban Power Lines from Vehicle-Borne LiDAR Data. Remote Sens. 2014, 6, 3302–3320. [Google Scholar]
- Bo, G.; Huang, X.; Fan, Z.; Sohn, G. Classification of airborne laser scanning data using JointBoost. ISPRS J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar]
- Zhou, R.Q.; Xu, Z.H.; Peng, C.G.; Zhang, F.; Jiang, W.S. A JointBoost-based classification method of high voltage transmission corridor from airborne LiDAR point cloud. Sci. Surv. Mapp. 2019, 44, 21–27. [Google Scholar]
- Kim, H.B.; Sohn, G. Point-based Classification of Power Line Corridor Scene Using Random Forests. Photogramm. Eng. Remote Sens. 2013, 79, 821–833. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Z.; Hu, Q. A Model-Driven Approach for 3D Modeling of Pylon from Airborne LiDAR Data. Remote Sens. 2015, 7, 11501–11524. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.Y.; Song, S.; Qian, J.J.; Chen, C.; Wang, K.; Yang, Y.Q.; Zheng, X.G. Research on Automatic Positioning Algorithm of Power Transmission Towers Based on UAV LiDAR. Power Syst. Technol. 2017, 41, 3670–3677. [Google Scholar]
- Liu, Y.; Yang, B.S.; Liang, F.X. An automatically recognizing method for transmission towers from ALS point cloud. Bull. Surv. Mapp. 2019, 01, 34–38. [Google Scholar]
- Hongyun, S.; Tao, G.; Di, W.; Shichun, W.; Jian, Z.; Xin, L.; Xin, L. Power line suspension point location method based on laser point cloud. Laser Technol. 2020, 44, 364–370. [Google Scholar]
- Toschi, I.; Morabito, D.; Grilli, E.; Remondino, F.; Carlevaro, C.; Cappellotto, A.; Tamagni, G.; Maffeis, M. Cloud-Based Solution for Nationwide Power Line Mapping. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 119–126. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Liu, Z.J.; Wang, J. Extraction and Security Detection of Power Line Based on Laser Point Cloud Data. Laser J. 2017, 38, 48–51. [Google Scholar]
- Jwa, Y.; Sohn, G. A multi-level span analysis for improving 3D power-line reconstruction performance using airborne laser scanning data. In Proceedings of the ISPRS Technical Commission III Symposium PCV 2010—Photogrammetric Computer Vision and Image Analysis, Saint-Mandé, France, 1–3 September 2010. [Google Scholar]
- Redding, N.J. Implicit polynomials, orthogonal distance regression, and the closest point on a curve. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 191–199. [Google Scholar] [CrossRef]
- Silver, E.A.; Bischak, D.P.; Silveira, G.J.C.D. An efficient method for calculating the minimum distance from an operating point to a specific (hyperbolic) efficient frontier. IMA J. Manag. Math. 2009, 20, 251–261. [Google Scholar] [CrossRef]
- William, H. Numerical recipes in FORTRAN. The art of scientific computing. IEEE Concurr. 1997, 6, 79. [Google Scholar]
- Ostu, N. A threshold selection method from gray-histogram. IEEE Trans. Syst. Man Cybern. 1975, 11, 285–296. [Google Scholar]
- Foley, J.D.; Dam, A.V.; Feiner, S.; Hughes, J.F. Computer Graphics: Principles and Practice, 2nd ed.; Addison-Wesley Professional: Boston, MA, USA, 1996. [Google Scholar]
- Wu, L.F.; Chen, Y.P.; Chen, Y.H. Algorithms on calculating minimum distance between point and spatial parametric curves. Mach. Des. Manuf. 2011, 15–17. [Google Scholar]
- Jwa, Y.; Sohn, G. A Piecewise Catenary Curve Model Growing for 3D Power Line Reconstruction. Photogramm. Eng. Remote Sens. 2012, 78, 1227–1240. [Google Scholar] [CrossRef]




















| 220 kV | 500 kV | 750 kV | |
|---|---|---|---|
| Length (km) | 5.1 | 21.2 | 14.2 |
| Number of points (Million) | 36.93 | 170.92 | 64.13 |
| Density (points/m) | 63.0 | 89.3 | 49 |
| Number of pylons | 16 | 69 | 33 |
| 220 kV | 500 kV | 750 kV | |
|---|---|---|---|
| TP | 373,152 | 1,443,240 | 1,210,830 |
| FN | 987 | 2395 | 22,354 |
| FP | 1382 | 7315 | 26,565 |
| Precision | 0.9963 | 0.995 | 0.9785 |
| Recall | 0.9974 | 0.9983 | 0.9818 |
| F-score | 0.9969 | 0.9969 | 0.9802 |
| Voltage Level | Number of Points | Point-Lines Time/s | Point-Points Time/s | MAE/m | Time Ratio |
|---|---|---|---|---|---|
| 220 kV | 54,492 | 0.334 | 1256.285 | 0.03 | 3760 |
| 500 kV | 31,729 | 0.226 | 948.723 | 0.05 | 4198 |
| 750 kV | 29,977 | 0.287 | 962.924 | 0.02 | 3355 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Du, Y.; Shi, W. Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud. Remote Sens. 2021, 13, 1571. https://doi.org/10.3390/rs13081571
Huang Y, Du Y, Shi W. Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud. Remote Sensing. 2021; 13(8):1571. https://doi.org/10.3390/rs13081571
Chicago/Turabian StyleHuang, Yuchun, Yingli Du, and Wenxuan Shi. 2021. "Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud" Remote Sensing 13, no. 8: 1571. https://doi.org/10.3390/rs13081571
APA StyleHuang, Y., Du, Y., & Shi, W. (2021). Fast and Accurate Power Line Corridor Survey Using Spatial Line Clustering of Point Cloud. Remote Sensing, 13(8), 1571. https://doi.org/10.3390/rs13081571






